Learning from electronic health records across multiple sites: A communication-efficient and privacy-preserving distributed algorithm

Abstract

Objectives

We propose a one-shot, privacy-preserving distributed algorithm to perform logistic regression (ODAL) across multiple clinical sites.

Materials and Methods

ODAL effectively utilizes the information from the local site (where the patient-level data are accessible) and incorporates the first-order (ODAL1) and second-order (ODAL2) gradients of the likelihood function from other sites to construct an estimator without requiring iterative communication across sites or transferring patient-level data. We evaluated ODAL via extensive simulation studies and an application to a dataset from the University of Pennsylvania Health System. The estimation accuracy was evaluated by comparing it with the estimator based on the combined individual participant data or pooled data (ie, gold standard).

Results

Our simulation studies revealed that the relative estimation bias of ODAL1 compared with the pooled estimates was <3%, and the ratio of standard errors was <1.25 for all scenarios. ODAL2 achieved higher accuracy (with relative bias <0.1% and ratio of standard errors <1.05). In real data analysis, we investigated the associations of 100 medications with fetal loss during pregnancy. We found that ODAL1 provided estimates with relative bias <10% for 85% of medications, and ODAL2 has relative bias <10% for 99% of medications. For communication cost, ODAL1 requires transferring $p$ numbers from each site to the local site and ODAL2 requires transferring $(p\times p+p)$ numbers from each site to the local site, where $p$ is the number of parameters in the regression model.

Conclusions

This study demonstrates that ODAL is privacy-preserving and communication-efficient with small bias and high statistical efficiency.

INTRODUCTION

Electronic health records (EHRs) contain patient health information recorded during routine clinical care by various types of clinicians, including physicians, nurses, and other ancillary medical personnel. The last few decades have seen large-scale adoption of EHRs throughout the United States, including providers in rural communities,¹ although adoption in these settings was slower than that among larger, urban medical centers.² This availability of clinical data from EHRs throughout the United States, from small-scale clinics (eg, 1 or 2 providers) all the way to large academic medical centers, has led to new challenges and opportunities within the informatics community.

Data integration across different institutions and clinical sites can potentially accelerate knowledge discovery and enhance the generalizability of findings, and is consistent with the vision of a national-scale learning health system.^3–5 The growth of structured, analysis-ready clinical data has also resulted in formation of several collaborative groups and consortiums that were designed to specifically handle data integration challenges from across diverse institutions.^6,7 One organization is called the Observational Health Data Sciences and Informatics (OHDSI) consortium (https://ohdsi.org/). OHDSI has developed a Common Data Model that all community members conform with by transforming their local EHR data to the Common Data Model’s standards. This allows researchers to develop methods that can be simultaneously applied to many institutions. In addition, tools are made available in an open source framework to enable further advancement of analytic methods.^3,8,9

In many situations, it is not feasible to share patient-level data across sites or provide data to a central site, especially if sites exist in different countries. Distributed algorithms have been developed that decompose computational tasks into pieces within each site without sharing individual-level information.^10–14 Among them, Chen et al¹² proposed a distributed algorithm for linear regression. Owing to the existence of the close-form estimator for linear regression, the algorithm directly decomposes the estimator into parts that can be calculated separately in each site and then combined together without loss of information. The combined estimator is lossless, which means it is identical to the result where the model is fitted on the combined individual participant data (pooled data). Moreover, the algorithm is one-shot, which means transferring information across sites is required only once.

However, for other commonly used statistical models without close-form solutions, such as logistic regression or the Cox proportional hazards model, the analogy of Chen et al¹² is not available. The parameters of these models are often estimated by optimizing a likelihood function using the Newton method, which iteratively updates the parameter value until a convergence is reached. As a consequence, iterative distributed algorithms are developed to decompose each step of the Newton method and calculate them distributively. For example, Wu et al¹⁰ proposed an iterative algorithm for distributed logistic regression named GLORE (Grid binary LOgistic Regression) and successfully deployed it to the multi-institutional pSCANNER (patient-centered Scalable National Network for Effectiveness Research) network. Another iterative algorithm called WebDISCO (a web service for distributed Cox model learning) was developed for Cox proportional hazards model by the same research team.¹¹ These algorithms are lossless, yet the communication cost, which is characterized by the total number of bytes transferred per iteration and number of iterations needed, is often high, and therefore could lead to operational difficulty.

To avoid the iterative communication across sites, Duan et al¹⁵ proposed a one-shot distributed algorithm for logistic regression (ODAL), which requires transferring data from each site only once and does not require sharing patient-level data from participating institutional data contributors. Following this work, we incorporate a new one-shot algorithm (ODAL2) into the ODAL framework. With the help of transferring more digits, ODAL2 can reach higher estimation accuracy compared with the algorithm proposed in Duan et al refer to as ODAL1 hereafter and provide estimates nearly the same as the analysis based on the pooled data. In addition, our article provides the variance estimators for both ODAL1 and ODAL2, which allow quantification of the uncertainty, and enable the statistical inference procedures.

MATERIALS AND METHODS

In this section, we briefly introduce the ODAL1 algorithm proposed in Duan et al,¹⁵ and then propose the new algorithm ODAL2, in the context of distributed research networks. We begin with a brief introduction of the logistic regression model, which is arguably the most commonly used model to study impacts of risk factors on a binary outcome in biomedical sciences.

Logistic regression model

Consider a setting where we have $p-1$ risk factors, detonated by $x_1, x_2, \dots , x_{p-1}$. Let $x={\left(1, x_1, x_2, \dots , x_{p-1}\right)}^T$. The outcome Y is binary and the logistic regression model assumes

$$\mathit{logit}\left(\mathit{Pr}\left(Y=1\right)|x\right)=x^T\beta ,$$

where$\mathrm{ }\mathit{logit}\left(t\right)=\mathit{log}\{t/(1-t\left)\right\}$ and $\beta$ is the vector of intercept and regression coefficients.

Algorithms

Suppose that we have $N={\sum }_{j=1}^K{n}_j$ identically and independently distributed observations from K different sites. Let $(x_{\mathit{ij}}, Y_{\mathit{ij}})$ denote the i-th observation in the j-th clinical site. The global log-likelihood function combining data from all sites can be written as

$$L\left(\beta \right)=\frac{1}{N}\sum _{j=1}^K\sum _{i=1}^{n_j}[Y_{\mathit{ij}}{x}_{\mathit{ij}}^T\beta -\mathit{log}\{(1+\hspace{0.17em}\text{exp}\hspace{0.17em}{(x}_{\mathit{ij}}^T\beta \left)\right\}],$$

and the pooled estimator is obtained through maximum the previous function, that is,

$$\widehat{\beta }=\arg \underset{\mathrm{\beta }}{\max }L(\beta ).$$ (1)

This pooled estimator achieves the best possible estimation accuracy through directly combining the patient-level data from different sites, and therefore can be treated as the gold standard estimator. To avoid transferring patient-level data, we extend the distributed computing method proposed by Jordan et al¹³ and Wang et al¹⁴ and develop the following algorithms to estimate the coefficient $\beta$.

1. The first-order algorithm- -ODAL1

With the assumption that the patient-level data from one of the sites (termed as the local site) are accessible, Duan et al¹⁵ adopted the surrogate likelihood approach in Jordan et al¹³ and constructed the following first-order surrogate likelihood function as an approximation of the global likelihood function:

$${\stackrel{\sim }{L}}^1\left(\beta \right)=\mathrm{ }{L}_1\left(\beta \right)+\left\{\nabla L\left(\stackrel{-}{\beta }\right)-\nabla L_1\left(\stackrel{-}{\beta }\right)\right\}\beta ,$$ (2)

where $\stackrel{-}{\beta }$ is an initial value. The term $L_j\left(\beta \right)$ is the log-likelihood function of the $j$-th site defined as

$$L_j\left(\beta \right)=\frac{1}{n_j}\sum _{i=1}^{n_j}[Y_{\mathit{ij}}{x}_{\mathit{ij}}^T\beta -\mathit{log}\{(1+\hspace{0.17em}\text{exp}\hspace{0.17em}{(x}_{\mathit{ij}}^T\beta \left)\right\}],$$ (3)

and $j=1$ is assumed to be the local site where patient-level data are accessible. The term $\nabla L\left(\stackrel{-}{\beta }\right)$ is the first gradient of the likelihood function $L\left(\beta \right)$ evaluated at $\stackrel{-}{\beta }$, where

$$\nabla L\left(\stackrel{-}{\beta }\right)={\sum }_{j=1}^K{n_j\nabla L}_j\left(\stackrel{-}{\beta }\right)/N.$$ (4)

The gradient of the log-likelihood function of the $j$-th site is calculated as

$${\nabla L}_j\left(\stackrel{-}{\beta }\right)=\frac{1}{n_j}\sum _{i=1}^{n_j}\{Y_{\mathit{ij}}-p_{\mathit{ij}}(\stackrel{-}{\beta }) {\}x}_{\mathit{ij}}$$ (5)

where $p_{\mathit{ij}}\left(\stackrel{-}{\beta }\right)=\{1+\exp \left(-x_{\mathit{ij}}^T\stackrel{-}{\beta }\right){\}}^{-1}$. The quantity ${\nabla L}_j\left(\stackrel{-}{\beta }\right)$ is a p-dimensional vector. When ${\nabla L}_j\left(\stackrel{-}{\beta }\right)$ is transferred to the local site, $\nabla L\left(\stackrel{-}{\beta }\right)$ can be calculated by$\left(4\right)$. The terms $L_1\left(\beta \right)$ and $\nabla L_1\left(\stackrel{-}{\beta }\right)$in the surrogate likelihood function are obtained locally using the patient-level data from the local site. The ODAL1 estimator is then defined as

$$\stackrel{\sim }{{\beta }^1}=\arg \underset{\mathrm{\beta }}{\max }{\stackrel{\sim }{L}}^1\left(\beta \right).$$

Intuitively, a more accurate initial value $\stackrel{-}{\beta }$ increases the accuracy of $\stackrel{\sim }{{\beta }^1}$. A reasonable choice of $\stackrel{-}{\beta }$ suggested by Duan et al¹⁵ is the maximum likelihood estimator of the local likelihood, which does not require extra communication to obtain, that is,

$$\stackrel{-}{\beta }=\arg \underset{\mathrm{\beta }}{\max }{L}_1(\beta ).$$

We derived the variance estimator of $\stackrel{\sim }{{\beta }^1}$, which can be estimated within the local site by Supplementary equation S1.

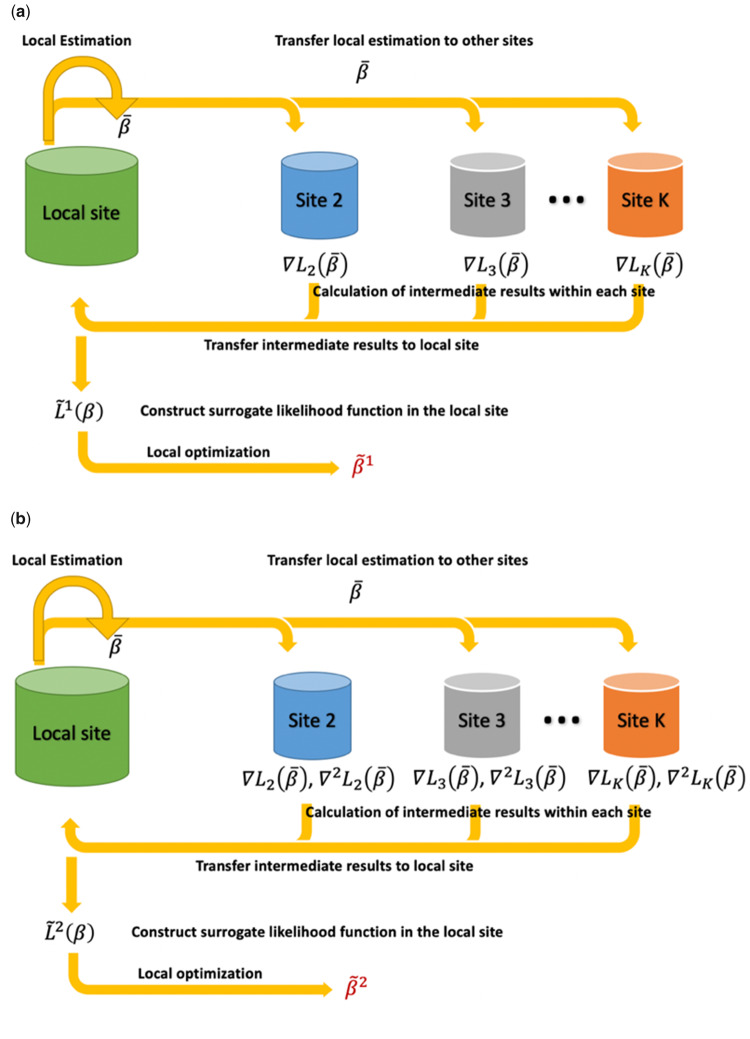
We summarize the ODAL1 in the following algorithm and also in Figure 1.

Figure 1.

Schematic illustration of the proposed one-shot, privacy-preserving distributed algorithm to perform logistic regression (ODAL) methods. (a) ODAL1: The initial value $\stackrel{-}{\beta }$ is obtained by fitting logistic model at the local site and is transfer to the other sites. Then the intermediate term $\nabla L_j\left(\stackrel{-}{\beta }\right)$ is evaluated at each site j (j = 2, …, K) and transferred back to the local site. Combined with $\nabla L_1\left(\stackrel{-}{\beta }\right)$ and $L_1(\beta )$, we obtain the first-order surrogate likelihood function ${\stackrel{\sim }{L}}^1(\beta )$ and the ODAL1 estimator is obtained by maximizing ${\stackrel{\sim }{L}}^1\left(\beta \right).$ (b) ODAL2: The initialization is the same as ODAL1, and the intermediate terms $\nabla L_j\left(\stackrel{-}{\beta }\right)$ and ${\nabla }^2{L}_j\left(\stackrel{-}{\beta }\right)$ are evaluated at each site and transferred back to the local site. Combined with $\nabla L_1\left(\stackrel{-}{\beta }\right)$, ${\nabla }^2{L}_1\left(\stackrel{-}{\beta }\right)$, and $L_1(\beta )$, we obtain the second-order surrogate function ${\stackrel{\sim }{L}}^2(\beta )$ and the ODAL2 estimator is obtained by maximizing ${\stackrel{\sim }{L}}^2\left(\beta \right).$

Algorithm 1.

ODAL1

1. Initial value: obtain $\stackrel{-}{\beta }=\arg \underset{\mathrm{\beta }}{\max }{L}_1(\beta )$ using data in the local site 1.

2. Initial communication: transfer $\stackrel{-}{\beta }$ to the other sites.

3. For site j = 2 to K,

4. do compute $\nabla L_j\left(\stackrel{-}{\beta }\right)$ using equation 5

5. transfer $\nabla L_j\left(\stackrel{-}{\beta }\right)$ to site 1

6. end

7. Compute the surrogate likelihood $\stackrel{\sim }{L^1}\left(\beta \right)$ using equation 2

8. Obtain $\stackrel{\sim }{{\beta }^1}=\arg \underset{\mathrm{\beta }}{\max }\stackrel{\sim }{L^1}\left(\beta \right)$

9. Obtain $V(\stackrel{\sim }{{\beta }^1)}$ using Supplementary Material equation S1

10. return $\stackrel{\sim }{{\beta }^1}$ and $V(\stackrel{\sim }{{\beta }^1)}$.

2. The second-order algorithm- -ODAL2

To achieve higher estimation accuracy, we propose the ODAL2 algorithm, which requires transferring small amount of extra aggregated information than ODAL1. More specifically, ODAL2 is based on the following second-order surrogate likelihood, which calculates the second-order gradient ${\nabla }^{2}L\left(\stackrel{-}{\beta }\right)$ in a distributed manner to further improve the approximation accuracy.

$${\stackrel{\sim }{L}}^2\left(\beta \right)=L_1\left(\beta \right)+{\left\{\nabla L\left(\stackrel{-}{\beta }\right)-\nabla L_1\left(\stackrel{-}{\beta }\right)\right\}}^T\beta +\frac{1}{2}{\left(\beta -\stackrel{-}{\beta }\right)}^T\left\{{\nabla }^{2}L\left(\stackrel{-}{\beta }\right)-{ \nabla }^2{L}_1\left(\stackrel{-}{\beta }\right)\right\}(\beta -\stackrel{-}{\beta }).$$ (6)

In the previous function, $L_1\left(\beta \right)$, $\nabla L_1\left(\stackrel{-}{\beta }\right)$ and ${\nabla }^2{L}_1\left(\stackrel{-}{\beta }\right)$ can be calculated from the local site. The term$\nabla L\left(\stackrel{-}{\beta }\right)$ is calculated the same way in equations 4 and 5, and ${\nabla }^{2}L\left(\stackrel{-}{\beta }\right)$ is calculated in a distributed way by ${\nabla }^{2}L\left(\stackrel{-}{\beta }\right)={\sum }_{j=1}^K{n_j{\nabla }^{2}L}_j\left(\stackrel{-}{\beta }\right)/N$, where ${{\nabla }^{2}L}_j\left(\beta \right)$ is defined as

$${{\nabla }^{2}L}_j\left(\beta \right)=\frac{1}{n_j}\sum _{i=1}^{n_j}{p}_{\mathit{ij}}\left(\stackrel{-}{\beta }\right)\{1-p_{\mathit{ij}}(\stackrel{-}{\beta }){\}x}_{\mathit{ij}}{x}_{\mathit{ij}}^T.$$

We note that the second-order gradient ${{\nabla }^{2}L}_j\left(\beta \right)$ is a $p\times p$matrix and contains only aggregated information. Similarly, the ODAL2 estimator is obtained by

$$\stackrel{\sim }{{\beta }^2}=\arg \underset{\mathrm{\beta }}{\max }{\stackrel{\sim }{L}}^2\left(\beta \right).$$

The algorithm is summarized below and in Figure 1.

Algorithm 2.

ODAL2

1. Initial value: obtain $\stackrel{-}{\beta }=\arg \underset{\mathrm{\beta }}{\max }{L}_1(\beta )$ using data in the local site 1.

2. Initial communication: transfer $\stackrel{-}{\beta }$ to the other sites.

3. For site j = 2 to K,

4. do compute $\nabla L_j\left(\stackrel{-}{\beta }\right),{\nabla }^2{L}_j\left(\stackrel{-}{\beta }\right)$

5. transfer $\nabla L_j\left(\stackrel{-}{\beta }\right),{\nabla }^2{L}_j\left(\stackrel{-}{\beta }\right)$ to site 1

6. end

7. Compute the surrogate likelihood $\stackrel{\sim }{L^2}\left(\beta \right)$ using equation (6)

8. Obtain $\stackrel{\sim }{{\beta }^2}=\arg \underset{\mathrm{\beta }}{\max }\stackrel{\sim }{L^2}\left(\beta \right)$

9. Obtain$V\left(\stackrel{\sim }{{\beta }^2}\right)$using Supplementary Material equation S2

10. return $\stackrel{\sim }{{\beta }^2}$ and $V\left(\stackrel{\sim }{{\beta }^2}\right)$

Simulation study

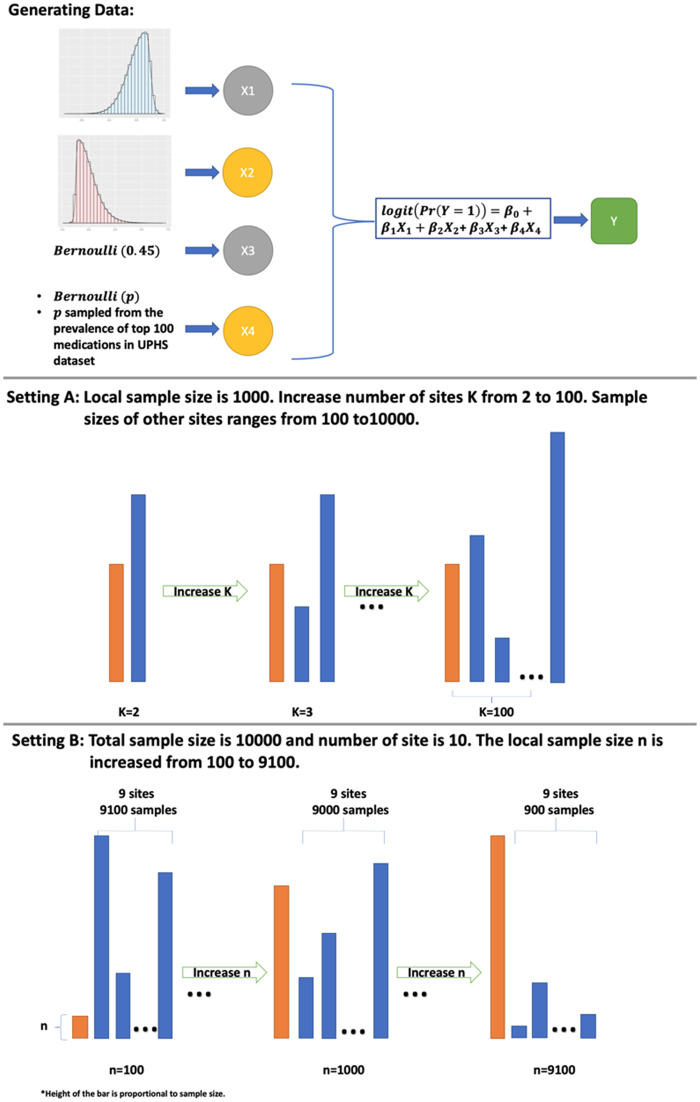
In our simulation study, we consider 4 risk factors: $x_1, x_2,x_3$, and $x_4$. The variables $x_1$ and $x_2$are continuous variables mimicking the standardized weight and age in the University of Pennsylvania Health System (UPHS) dataset, respectively. The variable $x_3$ is a binary variable generated from a Bernoulli distribution with probability 0.45, which matches the proportion of white patients in the UPHS dataset (see Table 1). The variable $x_4$ is a binary variable mimicking the medication status, which is also generated from a Bernoulli distribution, in which the probability of the Bernoulli distribution is sampled from the empirical distribution of the prevalence of the top 100 medications in the UPHS dataset. The histograms of the distributions used for $x_1$, $x_2$, and $x_4$ can be found in Supplementary Figure S1.

Table 1.

Demographics of Pregnancies Treated at the University of Pennsylvania Health System

Demographics	Normal Pregnancy (n = 30 810)	Fetal Loss (n = 4763)	P Value
Race/ethnicity
Whitea	13 911 (45.2)	2291 (48.1)
African American	12 918 (41.9)	1871 (39.3)
Other	1916 (6.2)	274 (5.8)
Asian	2065 (6.7)	327 (6.9)
Age, y	29.40	32.15	<.001
Weight, lb	123.45	115.43	<.001
Body mass index, kg/m2	16.95	16.61	.043

Values are n (%) or mean.

^aFor race, we only used a binary variable (for white vs other races/ethnicities including African American, Asian, Hispanic, etc.) in our regression model.

To account for a wide range of the possible association parameters, we randomly choose each of the regression parameters $\left({\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\right)$from a uniform distribution between (–1, 1). The intercept ${\beta }_0$is then chosen to maintain the prevalence of the outcome to be around 14%, which is close to the prevalence of fetal loss in the UPHS dataset (see Table 1). To evaluate the performance of the proposed algorithms, we design the following 2 simulation settings.

• A.We randomly generate data from K sites. The local site has 1000 samples and each of the other K-1 sites has ${10}^r*1000$ samples, where $r$is randomly chosen from –1 to 1. We perform separate simulations for different values of K ranging from 2 to 100.
• B.We randomly generate data for 10 000 patients, and divide the data in to 10 subsets where we assign n samples to the local site, and the other $9$sites randomly split the $(1000-n)$ samples. We perform separate simulations for different values of n ranging from 100 to 9100. This setting investigates the performance of ODAL when the relative size of the local site, compared with the total number of patients, increases from a small percentage to a large proportion.

A graphical illustration of the design of the simulation study can be found in Figure 2.

Figure 2.

Design of the simulation study. 1) Data are generated from a logistic regression with covariates X1, X2, X3, and X4; 2) Setting A considers the case in which the local sample size is fixed at 1000. The number of sites K is growing from 2 to 100; and 3) Setting B considers the case where total sample size is fixed at 10 000 and there are 10 sites in the network. The sample size in the local site grows from 100 to 9100.

We compare the estimates from the proposed ODAL1 and ODAL2 with the local estimate from equation 3 with $j=1$and the estimate from the GLORE algorithm in terms of the estimation accuracy of ${\beta }_4$. Relative bias and ratio of standard errors to the pooled estimate (gold standard) are used as metrics. We also record the number of iterations required by GLORE, and compare the amount of numbers transferred in each methods. The simulation study is conducted in R version 3.4.3 (R Foundation for Statistical Computing, Vienna, Austria) and the R code is provided in the Supplementary Material.¹⁶

Application of ODAL algorithms to study the association between medication and fetal loss

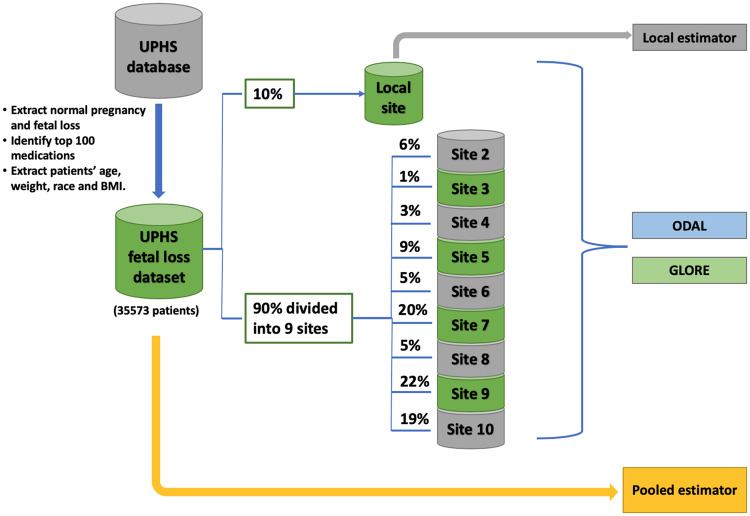
We evaluate our algorithms using data from UPHS, which covers a population that spans the entire Philadelphia Metropolitan area, including Southeastern Pennsylvania, Delaware, and Southern New Jersey. We extract data from UPHS for female patients whose pregnancy diagnosis was labeled as normal (ie, defined as those who are coded with any of the Z34 International Classification of Diseases–Tenth Revision codes or a V22 International Classification of Diseases–Ninth Revision code) and those patients with a fetal loss (ie, who are coded with any International Classification of Diseases–Ninth Revision code 630-639 or International Classification of Diseases–Tenth Revision code O00-O08). We select the 100 most common medications prescribed within 1 year before the first diagnosis of either the fetal loss or a normal pregnancy. For legal concern, we are not able to release the specific drug names in this article. Instead, we label them from 1 to 100. We exclude patients for whom no medication information is available. Demographic variables including age, race, body mass index (BMI), and weight are also extracted within 1 year before outcome (ie, normal pregnancy or fetal loss). Age, weight, and BMI are averaged across the 1-year period before the outcome. We fit logistic regression models to evaluate the risks of fetal loss associated with various medication exposures. Medications included in our analysis were prescribed at any time point from 1 year before first diagnosis of outcome until the diagnosis date of outcome. We include one medication at a time adjusting for maternal age, race, weight, and BMI.

To mimic a distributed network, we randomly extract 10% of the samples to construct the local site, and for the remaining data, we randomly split them into 9 subsets, in which each subset serves as a site in the network. We apply the ODAL algorithms and the GLORE algorithm using the 10 datasets. The pooled estimates are obtained by fitting regression models on the whole dataset, and the local estimates are obtained using patients in the local site only. See Figure 3 for a graphical illustration of the study design. This study was reviewed and approved by the University of Pennsylvania Institutional Review Board.

Figure 3.

Design of the real data evaluation. Patients with normal pregnancy and fetal loss are identified from the University of Pennsylvania Health System(UPHS) database and randomly divided into 10 sites. The local site has 10% of the data and the other 9 sites randomly split the rest of the data. Local estimator is conducted using data from the local site. The first-order one-shot, privacy-preserving distributed algorithm to perform logistic regression (ODAL1), ODAL2, and GLORE (Grid binary LOgistic Regression) are performed using the distributed data. The pooled analysis is performed using the whole fetal loss dataset.

RESULTS

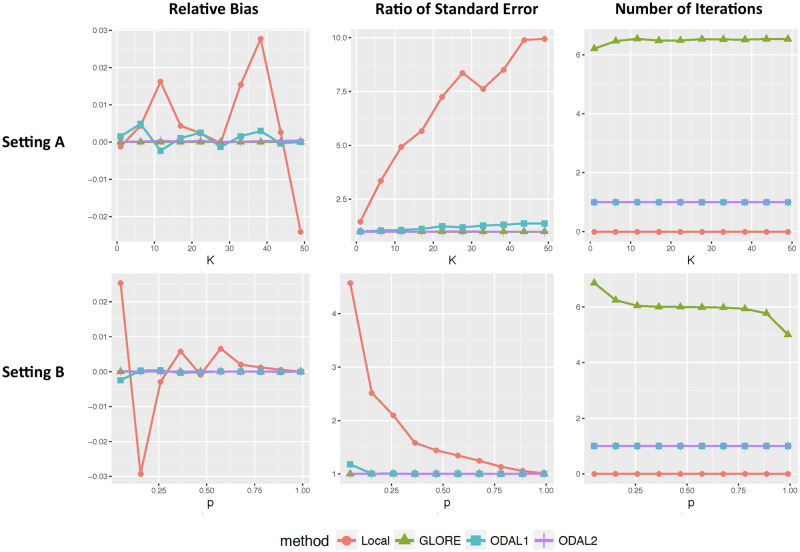
Evaluation of bias reduction through simulation studies

We presented the averaged relative bias, ratio of standard errors, and the number of iterations of each compared method across 500 replications in Figure 4. We verified that GLORE is lossless, in which bias is zero and the relative standard errors are equal to 1 for all scenarios. In setting A, when $K$ increases, the total sample size increases while the local sample size remains unchanged. Therefore, the relative bias and standard error of the local estimator increase due to increasing total sample size across sites. Compared with the pooled estimator, ODAL1 is observed to have small relative bias (<0.5%) and relative standard errors between 1.02 to 1.25. ODAL2 is more accurate, with a relative bias <0.1% and ratio of standard error <1.05. In setting B, when the total sample size is fixed, the performance of the local estimator improves as the local sample size increases. On the other hand, ODAL1 and ODAL2 have relative biases <0.3% for all local sample size settings.

Figure 4.

Relative biases and ratio of standard errors of the local estimator, first-order one-shot, privacy-preserving distributed algorithm to perform logistic regression (ODAL1), ODAL2, and GLORE (Grid binary LOgistic Regression) compared with the POOLED estimator under settings A and B.

For communication cost, GLORE requires between 5 and 7 rounds of communications until the algorithm converges, and for each iteration, it requires transferring $p\times p+p$ numbers from each site to a center. ODAL1 an ODAL2 require only 1 round of communication, where ODAL1 requires transferring $p$ numbers from each site to the local site, and ODAL2 requires transferring $p\times p+p\mathrm{ }$numbers from each site to the local site.

In summary, both ODAL1 and ODAL2 can achieve comparable estimation accuracy as the pooled estimator, while ODAL2 has a more robust accuracy performance than ODAL1. The communication costs of ODAL1 and ODAL2 are less than GLORE.

Validation using the UPHS fetal loss dataset

Table 1 shows the summary statistics of the demographic features of the UPHS dataset.

There were in total 30 810 normal pregnancies and 4763 fetal loss cases (prevalence of fetal loss is 13.43%) included in the dataset. The distributions of the age, weight, and BMI variables were significantly different in the groups of patients. For simplicity, we restricted our adjustment of race to a binary indicator variable of white vs other races/ethnicities including African American, Asian, Hispanic, etc.

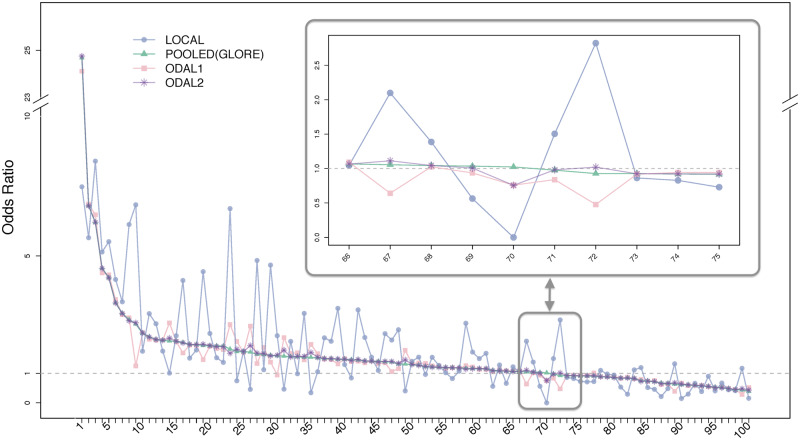
Figure 5 shows the estimated odds ratio for each medication using the 5 methods. As GLORE yields the same estimation results as the pooled estimator, we plot them using the same line and symbol. The drugs from the left to the right were sorted by the estimated odds ratio from the pooled dataset and labeled from 1 to 100. The estimated odds ratios and 95% confidence intervals from all 4 methods can be found in Supplementary Table S1. We found that for 99% of medications, ODAL2 has estimates with <10% of relative bias compared with the pooled estimator. ODAL1 has slightly larger bias compared with ODAL2, and ODAL1 provides estimates with relative bias <10% for 85% of the medications. For a clearer presentation, we zoomed in the region of 10 medications with odds ratio close to 1. The local estimates were observed to be highly inconsistent with the pooled estimates. For example, the odds ratio for the 72th drug was estimated to be 0.93 by the pooled estimator and 2.82 by the local estimator, while was estimated as 0.49 and 1.02 by ODAL1 and ODAL2, respectively. Regarding the communication cost, for the 100 medications, GLORE required 6-9 (with a mean value of 6.7) times of iteration to reach convergence.

Figure 5.

Odds ratio estimates from the first-order one-shot, privacy-preserving distributed algorithm to perform logistic regression (ODAL1), ODAL2, POOLED (identical to the estimates from GLORE [Grid binary LOgistic Regression]), and the local estimators for 100 medications and their associations with fetal loss. The 100 medications from left to right are sorted in descending order by their odds ratio, which was estimated from the pooled estimator. The list of drug name and estimations can be found in Supplementary Table S1. We zoom in on 10 drugs with odds ratios near 1 in the highlighted box.

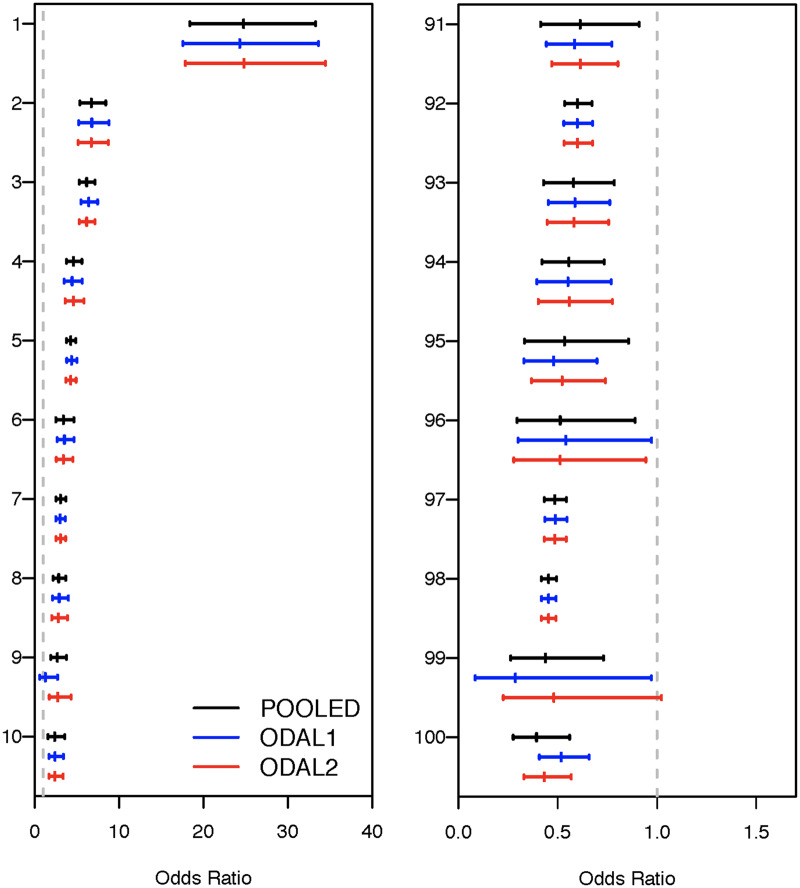
For further validation, we computed the odds ratios and the 95% confidence intervals of the top 10 drugs that are positively associated with fetal loss (harmful), and also of the top 10 drugs with negative association (protective), as shown in Figure 6, and compared our results with the information from Food and Drug Administration’s A-X category system, which is a pregnancy safety evaluation system for drugs. In the A-X system, category A drugs are drugs in which no fetal risk has been observed in controlled human studies, category B drugs are drugs with no evidence of fetal risk in animal models but for which well-controlled human studies are lacking, category C drugs are drugs in which fetal risk has been shown in animal models but the effects are unknown in humans, and categories D and X are drugs with known evidence of some fetal risk in humans and animals. Among the 10 “harmful” (which does not imply causation) drugs we identified, 6 were category D or X, each having known evidence of increase fetal loss risk in the literature, with 4 being known contraceptives. Three drugs were category C pain relievers.

Figure 6.

(Left panel) Point estimates and confidence intervals of odds ratios estimated from the first-order one-shot, privacy-preserving distributed algorithm to perform logistic regression (ODAL1), ODAL2, POOLED, and local estimators for top 10 medications positively associated with fetal loss. (Right panel) Point estimates and confidence intervals of odds ratios estimated from ODAL1, ODAL2, POOLED, and local estimators for top 10 medications negatively associated with fetal loss. The dashed gray line indicates an odds ratio of 1, indicating no difference in risk from that expected by chance.

In the 10 medications that are negatively associated with fetal loss (ie, “protective”), we found 8 types of prenatal vitamins, as well as folic acid, that are commonly considered beneficial for pregnancy. These findings are consistent with the literature on the importance of prenatal vitamins to prevent early term miscarriages and fetal loss.

In summary, the ODAL algorithms provide estimates that are highly consistent with the pooled estimates, and the identified associations are consistent with current understanding of these medications.

DISCUSSION

In this study, we proposed distributed algorithms, ODAL, for logistic regression through the construction of surrogate likelihood functions that act as good proxies of the global likelihood function without the need for sharing individual patient-level data across sites. The proposed algorithms are communication-efficient compared with the existing iterative algorithms. Although the estimates from ODAL is not completely identical to the pooled estimate, the consistency between ODAL with the pooled estimate is found to be extremely high over a wide spectrum of scenarios considered in simulation studies and real data analyses. In practice, when the total sample size or the local sample size becomes larger, the deviation between ODAL and the pooled estimator could be even lower.

In almost all cases, the accuracy of ODAL2 is higher than that of ODAL1 and is almost the same as the gold standard estimator. Although both ODAL algorithms are one-shot, ODAL1 requires transferring fewer digits than ODAL2 does. The data transferred from each site to the local site are $p$ numbers for ODAL1 and $p\times p+p$ numbers for ODAL2, where $p$ is the number of parameters in the logistic regression model. The iterative algorithm GLORE, on the other hand, requires transferring $\left(p\times p+p\right)*M$ numbers from each site to the central machine, where M is the number of iterations for the algorithm to reach a convergence. In practice, when fitting a relatively low-dimensional model, the extra communication cost of transferring $p\times p$ numbers is negligible. In this scenario, ODAL2 would be preferred as it can guarantee a better performance. However, in some applications, the number of predictors included in the model can be large, for example, when studying association between a certain disease and a large number of genetic variants jointly. In such cases, transferring$p\times p$ numbers is more challenging, and ODAL1 might be favored because it has less communication cost and can still provide reasonable estimation accuracy. On the other hand, if iterative communication is not a concern within the network, lossless methods such as GLORE are preferred.

Implementing ODAL is relatively easy in distributive networks such as ODHSI, as it does not require iterative communication. Iterative communication is a lengthy process whereby each individual site has to provide estimates and then the calculations are recomputed and improved. We found that other methods (such as GLORE) typically required 6 communication events. In practice, this would involve 6 different requests made by researchers to each individual site participating in a study. In many cases this is an untenable situation. However, using our methods and other data harmonization methods, such as those from the OHDSI collaboration, the number of iterative communications is greatly reduced (only 1 communication event is required). With the help of the Common Data Model, researchers at different clinical sites can initiate a common research question and transfer their data into the same format. For ODAL, one site serves as the local site and provides an initial estimation of the exposure-outcome relationship. This initial estimation is then provided to other sites, who calculate site-specific estimates. These calculations can be performed using prewritten code or software packages (see https://github.com/Penncil/OHDSI-PDA).

Limitations

Our data application is not based on a real distributed research network, but rather is done by splitting one dataset into different subsets. This ignores the potential heterogeneity of data across sites. It would be more meaningful to evaluate the performance of the ODAL algorithms in a real distributed network. Our study using EHR clinical data on medication exposure and risk of fetal loss shows that 13.43% of pregnancies in our cohort ended in fetal loss. Our cohort contained 30 810 normal pregnancies and 4763 fetal loss cases. This is about half of the expected rate between 25% and 50% of all pregnancies that end in fetal loss (or miscarriage).¹⁷ Therefore, our clinical data are underreporting the true effect of fetal loss; therefore, there may be additional pregnancies that were not captured. Based on our results, fetal loss is also likely underreported in clinical records. Therefore, our results on medication exposure and fetal outcome are limited to those reported in EHRs and may not apply to other pregnancies not captured in the clinical system. Moreover, the regression model in this study controlled only basic demographic variables such as age, sex, and race. There might be uncontrolled confounders that we would like to explore in the following work.

Future work

While our methods are motivated by the analysis of EHR data, ODAL can be applied in numerous other settings in which distributed analysis is needed. For example, for population and global health studies that utilize administrative data such as birth and death records, there is increasing concern with releasing data out of the local or national departments of health^18,19 Also, data from prospective cohorts, especially for environmental health studies, often cannot be shared outside of the parent study due to the collection of participants’ residential locations, timings of exposure and outcome, and other identifiers.^20–22

In the future, we plan to extend our method to other types of outcomes, such as categorical and time-to-event data. In addition, we are extending to high-dimensional setting in which the number of covariates is considered to be large compared with the total sample size. We are developing open-source software packages for directly implementing ODAL in distributed networks. We believe that our algorithms can be a useful complement to the existing distributed algorithms.

CONCLUSION

Here, we presented algorithms (ODAL) that allow for distributive analysis across multiple clinical datasets. The algorithms are privacy-preserving in the sense that patient-level data are not required to be transferred across sites. We studied both the first-order algorithm ODAL1 and is the second-order algorithm ODAL2 using simulated data and a real clinical EHR dataset from UPHS. Our simulation studies revealed that the relative estimation bias compared with the pooled estimator was <3% for all scenarios. ODAL2 achieved higher accuracy but required extra information transferred across sites. When evaluated against real clinical EHR data, we found that ODAL1 provided odds ratio estimates with relative bias <10% for 85% of medications and that ODAL2 has relative bias <10% for 99% of medications. In summary, we conclude that ODAL is a privacy-preserving and communication-efficient algorithm that provides accurate estimation and efficient statistical inference.

FUNDING

This work is supported in part by National Institutes of Health grants 1R01LM012607 (RD and YC), 1R01AI130460 (RD and YC), P50MH113840 (YC), 1R01AI116794 (JHM and YC) and R01LM009012 (JHM and YC).

AUTHOR CONTRIBUTIONS

RD and YC designed methods and experiments; MRB provided the dataset from the University of Pennsylvania Health System; RD designed the dataset generation and conducted simulation experiments; RD and MRB conducted data analysis; all authors interpreted the results and provided instructive comments; and RD, MRB, and YC drafted the main manuscript. All authors have approved the manuscript.

CONFLICT OF INTEREST STATEMENT

None declared.