Phenotypic memory drives population growth and extinction risk in a noisy environment

Abstract

Random environmental fluctuations pose major threats to wild populations. As patterns of environmental noise are themselves altered by global change, there is growing need to identify general mechanisms underlying their effects on population dynamics. This notably requires understanding and predicting population responses to the color of environmental noise, i.e. its temporal autocorrelation pattern. Here, we show experimentally that environmental autocorrelation has a large influence on population dynamics and extinction rates, which can be predicted accurately provided that a memory of past environment is accounted for. We exposed near to 1000 lines of the microalgae Dunaliella salina to randomly fluctuating salinity, with autocorrelation ranging from negative to highly positive. We found lower population growth, and twice as many extinctions, under lower autocorrelation. These responses closely matched predictions based on a tolerance curve with environmental memory, showing that non-genetic inheritance can be a major driver of population dynamics in randomly fluctuating environments.

The demography and extinction risk of wild populations is largely determined by responses to random fluctuations in their environment^1–7, the magnitude and predictability of which are currently altered by anthropogenic activities^8,9. In addition to their amplitude, stochastic (i.e., random) fluctuations are characterized by their temporal autocorrelation, which determines the extent to which one time step is a good predictor for the next. Temporal autocorrelation, sometimes described as the color of noise in reference to the spectral decomposition of random fluctuations, is a ubiquitous feature of natural systems^10,11. Because environmental autocorrelation characterizes the pattern and ordering of environmental noise rather than its magnitude, it was originally thought to be irrelevant to expected population dynamics in a stochastic environment, which instead were predicted to only depend on the mean and variance of environmental fluctuations in population growth³. However, more recent theory has shown that environmental autocorrelation may have a dramatic impact on population growth and extinction risk in a stochastic environment^12–16. The reason is that positive temporal autocorrelation facilitates phenotypic tracking of environmental fluctuations by phenotypic plasticity^17,18, evolutionary responses to natural selection¹⁹, or both, thereby modifying the mean and variance of population growth rates. However theoretical predictions are scarcer for negatively autocorrelated fluctuations, where high and low conditions alternate rapidly but predictably. More importantly, we lack empirical validation of this theory in a form that combines the realism of a continuously varying environment (such as temperature, humidity, salinity) with the high replication required to properly investigate responses to stochasticity. High replication is all the more important as environmental autocorrelation is expected to influence the variance of population size among independent realizations of stochastic population dynamics, therefore increasing extinction risk¹².

An increasing number of studies have inferred the level of environmental stochasticity in population growth in the wild^20,21 and the demographic consequences of environmental autocorrelation^22,23. However, attributing population size fluctuations to measured environmental factors is extremely challenging in the wild, where such factors may largely covary among each other, and the origin of their variation is unknown. Furthermore, observations from natural population generally consist of a single realization of a process with a limited number of time points (usually below 50), whereas assessing the range of likely outcomes for any stochastic process in the future requires many replicates, and/or long time spans. Experimental studies in the laboratory with short-lived organisms appears as a necessary bridge between theory and nature, because they allow testing theoretical predictions with ample replication and precision, potentially yielding general insights about population responses to environmental stochasticity. However, the few experimental studies about demographic consequences of environmental autocorrelation have had contrasting findings^24–27. To achieve significant progress on this question, we need to overcome the specificities of each individual system by establishing robust and general mechanistic links between environments and population demographic processes.

Such a link can be provided by environmental tolerance curves, which measure how fitness or its life history components (survival and fecundity) respond to abiotic environmental variables such as temperature or salinity. Tolerance curves are increasingly popular tools connecting physiology and ecology in response to climate change^28–30, notably because they share many commonalities across taxa and environmental factors, thus allowing for generalization. They are typically hump-shaped, with an optimum at some intermediate environmental value that coincides to some extent with the historical environment of the species^31,32. This non-linear relationship between the environment and absolute fitness is predicted to strongly drive effects of environmental stochasticity on population dynamics and extinction risk¹², but these predictions still largely lack empirical validation. Furthermore, environmental tolerance curves can potentially be influenced by the history of environments experienced by an individual^30,33–35 (phenotypic plasticity) or its ancestors³⁶ (trans-generational plasticity), but it is unclear to what extent population dynamics will be affected by such environmental memory effects. To answer these questions, we carried out a highly replicated experiment with a eukaryotic microorganism, in order to investigate how environmental autocorrelation influences population dynamics and extinction risk in a stochastic environment.

Results

We exposed six ancestral lineages (hereafter genotypes) of the facultative sexual microalgae Dunaliella salina to randomly varying salinities during 37 transfers (~100 generations). Using a liquid handling robot, we transferred each line twice a week (every 3 or 4 days), diluting 15% of the population of origin into fresh medium with controlled salinity, which differed across lines. More precisely, our treatments consisted of 164 time series with the same mean (µ = 2.4M NaCl) and variance (standard deviation σ = 1M NaCl), but 4 autocorrelation levels, from negative (ρ = -0.5) to highly positive (ρ = 0.9). In doing so, we modulated the pattern of salinity change between two successive transfers, without modifying the overall magnitude of fluctuations (Figure 1 a. and b., upper panel). Importantly, 39 (out of 41) time series within each treatment were different, independent realizations of the same stochastic process, allowing investigation of the variance introduced by environmental stochasticity, which is known to be an important driver of extinction risk^2,12. We tracked population densities and the proportion of extinct populations at each of 37 transfers (~100 generations, over 4 months) using optical density, fluorescence and flow cytometry. We then estimated the intrinsic rate of increase between each successive transfers, assuming continuous logistic growth following the 15% dilution (Figure 1c).

Figure 1. Salinity, growth rates and population dynamics for two time series with different environmental autocorrelations.

a. Times series number 19 for ancestral genotype AC and autocorrelation 0. b. Times series number 22 for ancestral genotype AC and autocorrelation 0.9. For the population growth rate, colors indicate whether growth rate compensates (blue, r > 0.542) or not (red) the bi-weekly dilution. Population size estimates and standard errors from the reverse gamma fit (solid line and ribbon) are represented together with the three raw measurements at each transfer (dots): cytometer counts (black), fluorescence (dark gray) and optical density (light gray). c. Estimated logistic population dynamics during transfers 14 to 19 (days 49 to 76), accounting for the biweekly dilution (arrows down). Red points and error bars correspond to the estimates and standard error for population size fitted in the model. Note that even when the population reaches high densities (here > 2.10⁵, while carrying capacity is estimated around 10⁶), the biweekly 15% dilution leads to nearly exponential growth after each transfer. The colored straight lines materialize the exponential phase, over which the population grows at rate r, the intrinsic rate of increase, colored in the same way as in the times series of r above.

In addition to three single strains (genotypes A: CCAP 19/18, B: CCAP 19/18 and C: CCAP 19/15), we used the three possible mixes of two of these strains (genotype AB, AC and BC), to test for potential advantages of genetic diversity on population dynamics. One of the single genotypes (B) grew too slowly to compensate for dilution at each transfer and got extinct rapidly (Extended Data 1) even in constant treatments, so it was discarded from further analysis.

Environmental autocorrelation strongly affects population size

Environmental stochasticity initially caused a rapid increase of variation in population size among our different lines of a same stochasticity treatment (as materialized by the dashed confidence interval in Figure 2.a.), as expected because population growth accumulates linearly on the log scale during a phase of exponential growth^2,12. The stochastic variation among lines then settled to an approximately constant value, characteristic of the stationary phase (days > 45, Figure 2a), where fluctuating population sizes spanned several orders of magnitude, in contrast with the small variance among replicates in constant environments (Extended Data 2). This is consistent with theory showing that stochastic environments can cause large fluctuations in population sizes around their expected carrying capacity^2,12,37.

Figure 2. Population dynamics in a stochastic environment.

Colors correspond to the temporal autocorrelation of salinity time series: -0.5: blue, 0: green, 0.5: orange, 0.9: red. a. Time series of population sizes under the 156 stochastic salinity series are plotted for genotype A (shaded lines), together with the exponential of the mean log population size (solid line) ± standard deviation (dashed lines). Population densities larger than 1000 cells.mL^-1 are plotted on the log scale, on which mean and standard deviation were also estimated, excluding extinct lines. Population sizes under 1000 are plotted on the linear scale, thus allowing tracking extinctions. b. Histograms of log-population size during the stationary phase for genotype A (day > 40). Panels c-f: Moments of the distribution of log population size during the stationary phase (computed on 22497 points). Different symbols represent different genotypes: A (■), C (+), AB (▲), AC (×) and BC (●), and bootstrapped 95% confidence interval are represented. The solid line represents the generalized linear regression on environmental autocorrelation.

The distribution of log-population size was asymmetric for all treatments and genotypes, with a negative skew causing an excess of very small populations undergoing high extinction risk (Figure 2.b. and e). Remarkably, this skewness is consistent with models of a moving optimum phenotype in a stochastic environment¹² - equivalent to models of tolerance curves with an optimum environment^12,35,38 -, but not necessarily with classic phenomenological models where noise is added to the population growth rate without an explicit tolerance curve^2,3,39. This suggests that fluctuations in our experimental populations are driven to some extent by the interplay of a stochastic environment with a hump-shaped tolerance curve with an optimum. However, density dependence in population growth also impacts the distribution of population size, modifying the influence of the stochastic environment^2,40. To control for this influence of density dependence, we analyzed the distribution of the intrinsic growth rate r, i.e. the rate of exponential growth at low population density, extracted from a model of continuous logistic growth (Figure 1.c). We found strong support for an asymmetrical distribution of r (ΔAIC = -3713 between a normal and a reverse gamma distribution), with an estimated skewness between -1.7 and -0.4 (Figure 3.d).

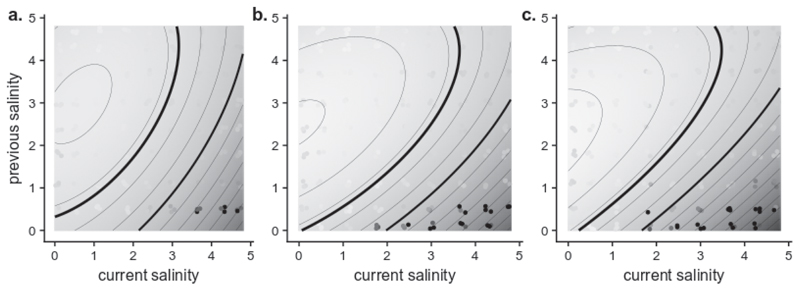
Figure 3. Population growth rate in response to environmental autocorrelation.

a. Tolerance curve with environmental memory relating growth rate r (intrinsic rate of increase) to the current (S_T) and previous salinities (S_{T - 1}), for genotype C (gray surface, black to light gray: r = -2 to r = 1), compared with the 3119 growth rates fitted under the reverse gamma model, under each autocorrelation treatment (points – same colors as Figure 2). The thick black line corresponds to the growth rate that allows overcoming the biweekly dilution (r = 0.542) and the thin black line shows r = 0. Ellipsoids at the bottom materialize the joint distributions of pre- and post-transfer salinities, under our four autocorrelation treatments. Panels b-e: Moments of the intrinsic rate of increase of lines A (■), C (+), AB (▲), AC (×) and BC (●) in the four autocorrelation treatments. Mean (b.), variance (c.), skewness (d.) and autocorrelation (e.) of r are plotted against environmental autocorrelation for all genotypes, with their standard errors. Predictions from the tolerance curve with (solid line) or without (dotted line) environmental memory are also plotted for genotype C.

Using the population sizes estimations obtained from the reverse gamma model, we found important differences between the dynamics of populations exposed to different autocorrelation treatments. For each of the genotype x autocorrelation treatment (from 438 to 833 data points), we computed the distributions of the population size during the stationary phase, and analyzed the influence of environmental autocorrelation on moments of these distributions. As environmental autocorrelation increased, populations underwent fewer episodes of negative growth, and smaller fluctuations in size (Figure 1). As a consequence, the mean (log) population size was larger under larger environmental autocorrelation (Figure 2c, slope = 0.71±0.11, p = 4.0.10^-5), contrary to classical population dynamics predictions where the expected intrinsic growth rate only depends on the mean and variance of the environment^3,4,6. The variance in log population size among replicate lines decreased with increasing autocorrelation (Figure 2d, slope = -3.0±0.71, p = 1.3.10^-3). This contrasts with the common theoretical prediction that higher autocorrelation generates long batches of good/bad environments in different lines, thereby increasing population size variance among lines^12–15, but is consistent with a contribution of environmental autocorrelation to phenotypic tracking of the environment (via phenotypic plasticity or genetic evolution), reducing the magnitude of population fluctuations¹⁹. We found a general trend for lower asymmetry (negative skewness closer to 0) with increasing temporal autocorrelation, but this effect highly depended on the strain (or mix) used and was not significant (Figure 3.d, slope = 0.19±0.25). Temporal autocorrelation of the stationary population size was highly variable within genotype x autocorrelation treatment (Figure 3.e). In particular, it was never found significantly different from 0, even in the highly autocorrelated treatment (ρ = 0.9), highlighting that temporal autocorrelation of the environmental factors translates only very weakly into autocorrelation of population sizes^25,41–43.

Environmental memory governs population dynamics

To reach more mechanistic insights into drivers of stochastic population dynamics in our experiment, we used the known salinity and population measurements to estimate a hump-shaped tolerance curve relating the intrinsic rate of increase r(T) following transfer T to the current salinity S_T,

$$r(T)=a_{univ}+b_{univ}\times S_T+c_{univ}\times S_T^2,$$ 1

where the subscript ‘univ’ is for univariate. This was compared to a bivariate tolerance curve that also includes an effect of memory of the previous environment (prior to the last transfer), via the salinity S_{T - 1},

$$r(T)=a+b\times S_{T-1}+c\times S_T+d\times S_{T-1}^2+e\times S_T^2+f\times S_{T-1}\times S_T$$ 2

where e determines the tolerance breadth with respect to the current environment, d the breadth of the environmental memory effect, and f the interaction between past and current salinity.

We fitted parameters of the tolerance curve with (equation 2) or without memory (equation 1), under the same model of logistic growth as in the first section, assuming a Gaussian distribution of the population size around its expected value (given the value at the previous time step). We found strong support for the generalized bivariate tolerance curve (ΔAIC < -10^-3 and p-values from likelihood ratio test < 10^-9 for all genotypes, see Supplementary Table 1), revealing an important impact of environmental memory on population growth. Growth rates were highest for populations transferred from high to low salinity, while populations transferred from low to high salinities declined (Figure 3.a), notably because of high mortality that could be detected by flow cytometry (Extended Data 3a, b, c).

To quantify the extent to which tolerance curves and memory effects explain the variation in growth within and across autocorrelation treatments, we derived the moments of population growth rates predicted by combining these tolerance curves with the realized salinity time series, and compared them to their estimated counterparts that do not use information about salinity (Supplementary Table 1). The tolerance curve with memory correctly predicted increases in the mean (slope = 0.069±0.009, p = 1.5.10^-5) and skewness (slope = 0.58±0.09, p = 2.9.10^-5) of population growth rates with increasing environmental autocorrelation, and a decrease in their variance (slope = -0.12±0.01, p = 2.18.10^-8), while all these effects were entirely missed by a memoryless tolerance curve (continuous vs dashed lines in Figure 3b, c, d). The predicted and observed responses to environmental autocorrelation were in very good quantitative agreement for the mean and variance of population growth rate (Figure 3b, c), and were qualitatively consistent for the skewness of population growth rate (Figure 3.d). Temporal autocorrelation of the growth rate displayed discrepancy between the fit from the data and prediction from the tolerance curves (Figure 3e). Nevertheless, the tolerance curve with memory allowed for negative autocorrelation of population growth rates despite positive environmental autocorrelation, as observed in the data but not possible with a memoryless tolerance curve.

A candidate mechanism: plasticity of glycerol content

Although a range of physiological mechanisms are probably involved in these population responses to salinity fluctuations, glycerol content is a key candidate phenotypic trait. Glycerol acts as an osmoregulator, with intracellular concentration responding nearly linearly to the environmental salinity⁴⁴. It is the major mechanism that makes Dunaliella a model species for salinity tolerance⁴⁴. To investigate the possible role of this metabolite in our population responses to salinity, we tracked the dynamics of intracellular glycerol following a change in salinity. When going from high (3.5M NaCl) to low salinity, intracellular glycerol concentration first changed almost immediately, with significant differences in glycerol contents as soon as 16 minutes after transfer in 0.5, 2 or 3.5M NaCl (Supplementary Table 1), probably through excretion⁴⁵, followed by a slower adjustment of glycerol level (Figure 4). In contrast, the reciprocal transfer from low (0.5M NaCl) to high salinity, which requires de novo production of glycerol⁴⁴, triggered slower change in glycerol content, with significant differences between transfer in 0.5 and in 2M NaCl found only after 135 minutes (Figure 4 and Supplementary Table 1). Most cells even died before their glycerol content could be measured in the transfer to the highest salinity (Figure 4). This is consistent with our observation that transitions from low to high salinity are more detrimental to the population dynamics than the reverse (Figure 3a).

Figure 4. Intracellular glycerol concentration in genotype C after transfer to a new salinity.

The transfers were at time = 0, from 0.5M (dashed lines) or 3.5M (solid lines), to 0.5M (blue), 2M (purple) and 3.5M (red) NaCl. Transfer from 0.5 to 3.5M caused high mortality, and thus could not be analyzed. Each measurement was replicated twice, and first-order standard errors (bars) were computed using the delta method, accounting for the independent errors of the extra-cellular, total glycerol and population size (cytometer) estimations. The first time point corresponds to 16 min post-transfer.

Extinction rates increase with decreasing autocorrelation

Nearly half the lines went extinct by the end of the experiment (Figure 5a). Environmental autocorrelation had a strong impact on extinction risk. Populations from low autocorrelation treatments (ρ = -0.5 and ρ = 0) went more extinct (72 and 61% extinct by the end of the experiment, median survival time: 77 days and 83 days, respectively) than populations from positive autocorrelation treatments (33 and 34% extinct by the end of the experiment for ρ = 0.5 and ρ = 0.9, respectively; p < 1.10^-4, log ranked test performed independently for all genotypes, see Supplementary Table 1 for details). We found no evidence for an effect of genetic variation on extinction risk in our experiment, as single-strain lines did not differ significantly from mixed-strain lines, and there was no indication that recombination contributed to population persistence in mixed-strain lines (Supplementary Information). Simulations using the tolerance curve with environmental memory combined with the actual times series of environments gave results qualitatively similar to our data (Figure 5b). By contrast, a memoryless tolerance curve reversed the predictions, with the lowest extinction risk predicted under negative or null autocorrelation. The reason for this reversal is that, without environmental memory (and neglecting rapid evolution), environmental autocorrelation does not help phenotypic tracking of the environmental optimum, and therefore has no direct effect on the distribution of population growth rates (dashed lines in Figure 3b-d), but only influences how growth rates are integrated into the population dynamics. Because all things being equal, more autocorrelated growth rates cause larger variance in population size (as confirmed in simulations without memory, p < 10^-3), they are expected to increase extinction risk in the absence of environmental memory^12,15. This effect is totally buffered by environmental memory: with higher mean and lower variance in growth rates, populations experiencing positively autocorrelated environments are less likely to fall below a critical threshold for extinction.

Figure 5. Population extinctions across environmental autocorrelations.

a. Survival curves (Kaplan-Meier) for the pooled genotypes A, AB, AC, BC and C, under the four autocorrelation treatments (same colors as in Figure 2). For each autocorrelation treatment, the solid lines show the estimated proportion of non-extinct populations, among the initial 195 populations (39 independent time series x 5 genotypes), and the dashed lines indicate 95% confidence bands. Stars and numbers indicate median survival times (times at which 50% of the populations has gone extinct) in the corresponding survival curve. b-c: Survival curves estimated from simulations parametrized with (b) or without (c) environmental memory, using the same salinity time series as in the experiment.

Discussion

Random environmental fluctuations largely contribute to natural baseline rates of extinction^1–6, which are currently aggravated by trends such as global climate change. Furthermore anthropogenic activities, beyond their effects on mean environments, are altering the patterns of these random fluctuations, including their temporal autocorrelation^8,9. There is thus is a pressing need to empirically characterize and quantify drivers of extinction risk in an autocorrelated stochastic environment. Using a highly replicated experiment with many independent environmental time series, we found that environmental autocorrelation can have a strong impact on population dynamics and extinction risk. In other words, extinction risk depends not only on the mean and variance of environmental fluctuations, but also on the order in which environments are encountered, within and across generations. This implies that the color of environmental noise, as increasingly documented in the ecological literature^{10,13,15,16,24–26}, is likely to be an important driver of population dynamics. Importantly, the impacts of environmental autocorrelation on population dynamics could be predicted accurately in our experiment using the simple and general concept of the environmental tolerance curve, which summarizes all influences of the environment with a few parameters. This validates the utility of this tool as a way to predict population dynamics in a changing environment, by connecting physiology to ecology²⁸. However, we only reached accurate predictions when an influence of past environment was accounted for in these tolerance curves.

The large influence of environmental memory on population dynamics in our experiment implies that the phenotype of an individual cell is partly affected by the environment experienced by its recent ancestor(s), which can be described as trans-generational phenotypic plasticity, or environment-dependent parental effect, a form on non-genetic inheritance³⁰. There is abundant evidence in microbes that prior exposure to stress can affect later stress responses⁴⁶, and such acclimation experiments generally span over several cellular generations. In our experiment, genetic evolution could in principle also contribute, because some lines are highly polymorphic, but the time scale of ~3 generations between transfers is not consistent with large evolutionary change between transfers. In addition, clones isolated from mixed BC populations displayed similar tolerance curves as the whole population (Extended Data 5), confirming that (trans-generational) phenotypic plasticity is the major mechanism responsible for this short-term environmental memory.

Our experiment included elements of realism that are uncommon in the laboratory, such as continuously distributed fluctuations of an environmental variable, and a large number of independent realization of the same stochastic process. This represents a large step towards bridging the gap between theory and natural populations on quantitative rather than qualitative grounds, an important goal for population ecology. Note that in our batch culture setting, the environment changed every 3 or 4 days, i.e. every 2 to 5 generations (depending on salinity) for our model species D. salina, while salinity remained constant during the interval between transfers. This means that the autocorrelation we report is not a value per generation or per unit time as in theoretical models, but across transfers. This limitation is common to any experiment that uses organisms with continuous overlapping generations in batch culture, since changing the environment continuously over time in a stochastic way is essentially impossible. Such discretization does not hamper our conclusions about the influence of environmental correlation on population growth and extinction risk in our experiment, but it should be kept in mind when comparing quantitatively the effect of environmental autocorrelation in our experiment versus in wild populations of higher organisms, where censuses and environmental measurements are made at regular intervals (typically a year²).

Microbes are inherently prone to transgenerational effects because they lack soma-germline differentiation, and therefore transmit their cytoplasm content and regulation factors to daughter cells upon reproduction. However, trans-generational effects mediated by non-genetic inheritance are increasingly documented in multicellular eukaryotes⁴⁷, and have been shown recently to affect demographic parameters in a fluctuating environment in an animal³⁶. This suggests that our results are also relevant to natural populations of larger organisms with conservation concerns, and that plasticity and non-genetic inheritance should generally be considered when investigating extinction risk in a randomly changing environment.

Methods

Dunaliella strains

We used two closely related strains of the facultative sexual microalgae Dunaliella salina, CCAP 19/12 (A) and CCAP 19/15 (C), and one more distant strain CCAP 19/18 (B). The lines were not axenic nor clonal when received from Culture Collection of Algae and Protozoan (Glasgow).We exposed them to increasing salinities (up to 4.8M) during several weeks to eliminate putative non-Dunaliella species of eukaryotes and finally isolated them by cell sorting (BD FACS Aria IIu, up to 10⁵ cells). We then initiated 1074 lines from six ancestral backgrounds, with either low or high genetic diversity. Single strain lines (A, B and C) were used for the low genetic diversity treatment, and high genetic diversity lines were initiated by a 50% mix of two strains (AB, BC and AC).

Experimental design

Each ancestral genetic background was exposed to three constant salinities (with 5 replicate lines per salinity), and 156 fluctuating salinity times series. The latter consisted of 39 independent time series (with the first one replicated 3 times) for each of four autocorrelation treatments: ρ = -0.5 (blue noise), ρ = 0 (white noise), ρ = 0.5 and ρ = 0.9 (red noise).

At each transfer, a 15% aliquot of each population was replicated in fresh medium with controlled salinity. The same dilution rate (d = 15%) was used in all treatments, and set so as to compensate for the intrinsic growth rate across variable environments for the slowest growing strain (strain B). However, growth rates were overestimated in our preliminary measurements, so that the dilution rate that we used caused the loss of most B lines before the end of the experiment.

Constant treatments were low ([NaCl] = 0.8M), medium (2.4M), and high (3.2M) salinities. The stochastic treatments involved continuously ranging, (near) normally distributed salinities, with same mean 2.4M and variance 1 among treatments, but temporal autocorrelation set by the treatment. We generated fluctuating salinity time series as follows:

• -Generate a first-order autoregressive (AR1) process of length 1000000, mean 2.4, variance 1 and autocorrelation set by the treatment. An AR1 process is a stationary Gaussian process, in which the value at a given time step is a linear combination of the value at the previous time step plus an independent normally distributed noise.
• -Truncate this theoretical process so as to keep only reachable salinity values. This involved removing salinities below 0 and above [NaCl]_max = 4.8M, as well as salinities that made the transition from the previous time point impossible because of the constraints imposed by the 15% dilution upon transfer.
• -Estimate the (reduced) variance of this truncated process
• -Increase input variance (step += 0.05) and repeat all previous steps, until the reduced variance V = 1 ± 0.01
• -Generate 39 times series of length 37 time steps for each autocorrelation treatment, using as input variance the value from the iterative search described above. The mean, variance, and temporal autocorrelation of these times series were checked to conform to their setpoint values. The distribution of salinities in all time series for the different autocorrelation treatments did not deviate from the expected Gaussian (Extended Data 4).

Transfers and growth

Experimental lines were cultured in 96 deep-well plates with artificial saline water + 2% Guillard’s F/2 marine water enrichment solution (Sigma; G0154-500ml). Lines were distributed in 18 plates, such that each combination of ancestral genotype x environmental treatment was equally represented in all plates. Population positions in each plate were then randomized across the 60 central wells (external wells were not used because they experience larger evaporation). A liquid handling robot (Biomek NX from Beckman) was used to serially transfer these lines twice per week (alternating three-day and four-day cycles) into fresh medium. The salinity in this new medium was set independently in each well by adjusting the volumes of a hyposaline ([NaCl]_min = 0M) and a hypersaline ([NaCl]_max = 4.8M) solution, following

$$\begin{array}{l}{V}_{\rho ,i,T}^{Hyper}=V_{tot}\frac{{\left[NaCl\right]}_{\rho ,i,T}-d{\left[NaCl\right]}_{\rho ,i,T-1,}}{{\left[NaCl\right]}_{max}}\\ V_{\rho ,i,T}^{Hypo}=V_{tot}-V_{\rho ,i,T}^{Hyper}\end{array}$$ 3

where [NaCl]_ρ,i,T and [NaCl]_{ρ,i,T - 1} are the setpoint salinities at transfers T and T - 1 (respectively) for time series i of autocorrelation treatment ρ, V_tot = 800 µL is the total volume of culture, and d = 15% is the dilution rate as defined above.

Plates were covered with plastic lids, sealed with Parafilm and placed at a fixed position in a growth chamber, with temperature set at 24°C, and light at 200 μmol.m^-2.s^-1 for 12:12h LD cycles.

Population density measures

After each transfer, cell density before dilution was measured using 3 complementary methods. We measured optical density (absorbance at 680nm) and fluorescence (excitation at 390-80nm, emission at 685-40 nm) in a 200 µL sample of the each population using a BMG ClarioStar spectrophotometer. Cells from the same sample were then counted by flow cytometry (Guava EasyCyte HT). Dunaliella cells were isolated from debris using forward scatter (FSC), side scatter (SSC), red (695/50 nm) and yellow (583/26 nm) fluorescence emissions (excitation 488 nm, See Extended Data 3a., b. and c. for details). Cytometer performance was checked using a standardized fluorescent bead reagent (EasyCheck Kit, Merck Millipore) before each measure. Because of time limitation, only half of the plates went into the flow cytometer after each transfer, while the remaining plates were read in the next transfer, such that each plate was passed through the flow cytometer once per week.

To calibrate among our different measures of population density, we first regressed the fluorescence and OD over the population density as estimated from cytometer counts (see Extended Data 3 d. and e.), excluding the data points where spectrometer measures were too low and exhibited high uncertainty (fluorescence < 400 and absorbance < 0.01). We obtained:

$$\begin{array}{l}{\left[Duna\right]}_{OD}=5273448(OD-O{D}_{blank})\\ {\left[Duna\right]}_{OD}=11.543428(Fluo-Flu{o}_{blank})\end{array}$$ 4

where OD_blank and Fluo_blank are the fluorescence and absorbance in wells known to be empty (control wells or extinct populations) within each given plate.

Statistical analysis

We analyzed population dynamics using an ad hoc state-space model. As typical in state-space models⁴⁸, our model comprised two main components: (i) an underlying, unobserved process describing the true stochastic dynamics of the populations size; (ii) and an observation model, which describes how this process translates into measurements, with errors that are independent after conditioning by the underlying process. We wrote an explicit likelihood function in C++ and optimized it in R (version 3.5.2), using the TMB package⁴⁹. R and C++ codes are available from the Dryad digital repository⁵⁵.

Observation model

In a preliminary experiment, we determined the error distributions of cytometer counts, absorbance and fluorescence error. We made replicated (x3) measured of population sizes in serial dilutions of a Dunaliella culture, with concentration ranging from 30 to 10⁶ cells.mL^-1, and fitted generalized linear regression between measurements and the known relative population sizes, expressed as a ratio of the maximal population size. We compared AIC from normal, lognormal, poisson and negative binomial models. Absorbance and fluorescence error were respectively normally and log-normally distributed, while cytometer measures followed a negative binomial distribution, with mean the actual population size. We thus used as the observation model for cytometer counts C, fluorescence F and absorbance OD,

$$\begin{array}{c}C\sim 𝒩ℬ(N,{\theta }_c)\\ log(F)\sim 𝒩(log(N),{\theta }_F)\\ OD\sim 𝒩(N,{\theta }_{OD})\end{array}$$ 5

where 𝒩ℬ denotes a negative binomial, N is the true population density (governed by the unobserved process), and the θ are parameters that control the error variances (or overdispersion for cytometer counts) of these measurements.

Process model

We assumed that population density followed continuous logistic growth:

$$\frac{\text{d}N{\left(t\right)}_{g,\rho ,i}}{\text{d}t}=r{\left(t\right)}_{g,\rho ,i}\left(1-\frac{N{\left(t\right)}_{g,\rho ,i}}{K_g}\right)$$ 6

where N(t)_g,ρ,i is the population density for the population from strain g, environmental treatment ρ, and time serie i at time t, K_g the carrying capacity of genotype g and r(t)_g,i,ρ its intrinsic growth rate in the environment experienced at time t. In the constant treatment analysis, K_g was also allowed to vary between salinity treatments (K_g,S).

Given that r(t)_g,ρ,i is constant over the time interval between two successive transfer, population size at transfer T + 1 can be implemented from population size at transfer T by integrating equation 6 (Δt_T,T+1 = 3 or 4 days), following a 15% dilution rate (d):

$$N{\left(T+1\right)}_{g,\rho ,i}=\frac{dN{\left(T\right)}_{g,\rho ,i}{e}^{\Delta t_{T,T+1}r{\left(T\right)}_{g,\rho ,i}}\times K_g}{K_g-dN{\left(T\right)}_{g,\rho ,i}\left(e^{\Delta t_{T,T+1}r{\left(T\right)}_{g,\rho ,i}}-1\right)}$$ 7

A convenient property of state-space models is that observation errors are independent conditional on the process⁵⁰ (and independent of the process). Therefore, the overall log-likelihood in our model was simply the sum of the log likelihood of the process (equation 7, 8, 9, 10) and that of all observations (equation 5), producing an explicit formula amenable to numerical optimization.

Density dependence analysis using constant treatments

As our model was unable to estimate density dependence directly from the time series of fluctuating salinities, we first analyzed the population dynamics from constant time series in an independent model for this purpose. We considered that both the intrinsic growth rate r_g,S and the carrying capacity K_g,S were constant across replicates and transfers for one strain g in one salinity S. The probability distribution of population size at transfer T + 1, for strain g and salinity treatment S is then

$$N{\left(T+1\right)}_{g,S,i}\sim logNormal\left(LogisticGrowth\left(N{\left(T\right)}_{g,S,i}\right),\beta \right)$$ 8

where LogisticGrowth(d N_g,S,i,T) is the continuous logistic function given by equation 8 and β is the process error. For each genotype, likelihood ratio test between a model where K_g,S was constant across salinity and a model where K_g,S varies with salinity was performed. We found that K_g,S differed significantly but slightly between salinity treatments (Extended Data 2 d), so we used a constant K_g for each genotype in further analysis.

Fluctuating growth analysis

Environmental fluctuations caused variation in the intrinsic rate of increase r in all our stochastic lines. The distribution of r results from the interaction between moments of the stochastic environment (mean, variance and autocorrelation) and the growth response of each genotype to the environment. The distribution of r may be characterized by its mean, variance, but also skewness¹² and potentially by the autocorrelation of r across transfers. We estimated the parameters of this distribution for each autocorrelation treatment x genotype, within the state space model described by equations 5 and 8. We fitted either an autocorrelated normal (equation 9) or a reverse gamma distribution (equation 10) for r(T)_g,ρ,i,

$$r{\left(T\right)}_{g,\rho ,i}\sim 𝒩\left(\left(1-{\rho }_r\right){\overline{r}}_{g,\rho }+{\rho }_{r_{g,\rho }}r{\left(T-1\right)}_{g,\rho ,i},\left(1-{\rho }_{r_{g,\rho }}^2\right){\sigma }_{r_{g,\rho }}^2\right)$$ 9

or

$$r_{{max}_{g,\rho }}-r{\left(T\right)}_{g,\rho ,i}\sim \Gamma \left({\alpha }_{g,\rho },{\beta }_{g,\rho }\right)$$ 10

where r_max, α_g,ρ and β_g,ρ are the maximal growth rate, the shape and the scale parameter for the gamma distribution for strain g in the ρ environment. Mean ${\overline{r}}_{g,\rho },$ standard deviation σ_g,ρ and skewness skew (r_g,ρ) were simultaneously estimated (estimation and standard error) from r_maxg,ρ, α_g,ρ and β_g,ρ using the ADREPORT procedure of the TMB package.

Population densities were estimated as random variables with a residual component of variation, and were hence only very weakly affected by the assumed shape of the growth rate distribution (r² > 0.99 between the normal and the reverse gamma estimates, see Extended Data 6). This allowed us to visualize the goodness of fit for the reverse gamma and the autocorrelated normal. Using the population size estimates, we computed the realized intrinsic growth rate, corrected for density dependence:

$${\widehat{r(T)}}_{g,\rho ,i}=\frac{Ln\left[\frac{K_g/d{\widehat{N(T)}}_{g,\rho ,i}+1}{K_g/N{\widehat{(T+1)}}_{g,\rho ,i}+1}\right]}{\Delta t_{T,T+1}}$$ 11

and plotted them against the predicted distribution fitted by the normal and reverse gamma model (Extended Data 1).

To assess the extent to which population fluctuations were driven by responses to fluctuating salinity, we then used salinity as an environmental covariate. We explicitly expressed the growth rate r(T)_g,ρ,i as a function of both the current (S_g,ρ,i,T) and the previous salinity S_g,ρ,i,T−1. We modeled a bivariate tolerance curve using a 2^nd order polynomial, with parameters depending on the strain g,

$$r{\left(T\right)}_{g,\rho ,i}^S=a_g+b_g\times S_{\rho ,i,T-1}+c_g\times S_{\rho ,i,T}+d_g\times S_{\rho ,i,T-1}^2+e_g\times S_{\rho ,i,T}^2+f_g\times S_{\rho ,i,T-1}\times S_{\rho ,i,T}$$ 12

leading to equation 2 in the main text.

Population size at T + 1 then followed a logistic growth (equation 7) with growth rate determined by current and previous salinity following equation 10, and we assumed a constant Gaussian distribution of the residuals generated by the process error, with standard deviation β:

$$\mathit{\text{log}}\left(N{\left(T+1\right)}_{g,S,i}\right)\sim 𝒩\left(\mathit{\text{log}}\left(LogisticGrowth(N{\left(T\right)}_{g,S,i,T},r{\left(T\right)}_{g,\rho ,i}^S)\right),\beta \right)$$ 13

Similar analysis was performed using only the salinity of growth (S_g,ρ,i,T) in order to fit a tolerance curve without environmental memory (equation 1 in the main text):

$$r{\left(T\right)}_{g,\rho ,i}^S=a_{univ,g}+b_{univ,g}\times S_{\rho ,i,T}+c_{univ,g}\times S_{\rho ,i,T}^2$$ 14

Moments of population density and intrinsic growth rates

We used the population density outputs of the gamma model (equation 10) to estimate the mean, variance, skewness and autocorrelation of log population density of non-extinct lines during the stationary phase (day > 40), for each autocorrelation treatment × genotype combination (39 independent lines over up to 26 transfers – replicates 2 and 3 of series 1 were excluded from this analysis). Confidence intervals for these estimates were obtained by bootstrap (1000 simulations), where population densities were sampled for each simulation from a normal distribution with mean and standard deviation given by their corresponding estimate and standard error. We then performed mixed linear regression between these computed moments and the environmental autocorrelation, with ancestral genotype as a random factor, using the R package lme4⁵¹. To include the uncertainty in the estimation of population size moments, we performed 1000 generalized linear regression with population moment sampled from a normal distribution with parameters their estimate and error, and corrected for multiple imputation using the R package MICE⁵².

Similar regressions were performed on 1000 simulations of the growth rate moments, sampled from a normal distribution with parameters the estimate and standard error obtained from the gamma model. Mean, variance, skewness estimates, and their associated errors, were directly fitted in the gamma model. Autocorrelation of the intrinsic rate of increase was computed using the realized population sizes estimated in the gamma model, with similar bootstrap and sampling as used for the population log density analysis.

Fitted moments of the intrinsic rate of increase were compared to analytical predictions based on the tolerance curves, with or without memory. Subsequent salinities in our time series closely follow a binormal distribution (except for a weak truncation caused by our experimental design, see Extended Data 4), with mean µ = 2.4M and variance σ² = 1 at both steps, and correlation given by the environmental autocorrelation ρ. Combining this with the tolerance curve with memory leads to explicit formulas in the Mathematica 11 notebook available from the Dryad repository⁵⁵. In particular, we found that the mean growth rate $\overline{r}$ increases linearly with the environmental autocorrelation ρ(E), while the variance Var(r) is a quadratic function of ρ(E). Analytic formula for the skewness and the variance are more complex, but show notably that environmental memory allows for negative autocorrelation of the growth rate ρ(r), even when the environment is positively autocorrelated, a pattern that we found in our data but that could not be achieved without a memory effect.

Without memory (equation 14), the moments of the distribution of growth rates take a simpler form, summarized in Supplementary Table 2 (details in Mathematica 11 notebook in Dryad digital repository⁵⁵). In the absence of environmental memory, the mean, variance and skewness of the intrinsic rate of increase do not change with environmental autocorrelation ρ. Skewness is always negative for humped-shaped tolerance curves (c_univ < 0). The effect of the environmental autocorrelation ρ(E) on the autocorrelation of the intrinsic rate of increase ρ(r) depends on the distance between the salinity optimum and the mean environment. When the phenotypic optimum corresponds to the mean environment, ρ(r) = ρ²(E), while ρ(r) tends rapidly towards ρ(E) as the mismatch between environmental mean and salinity optimum increases.

Survival analysis

We determined the extinction time for each population in the stochastic environment. Because OD, fluorescence and cytometry measures were not precise enough to discriminate between population sizes below 1000 cells.mL^-1, we considered that a population was extinct from the time it fell below an estimated 1000 cells.mL^-1 (corresponding to a small number of cytometer counts, and a negligible density compared with the carrying capacity close to 10⁶) and remained under this threshold for at least 5 transfers. After this delay, observed growth events that occurred only in 8 populations were due to contamination.

The survival responses in each treatment were then assessed by plotting the Kaplan-Meier survival curves (non-parametric model for the ratio of non-extinct populations through time), and analyzing differences in survival by log rank tests (ggsurvplot R package ⁵³). Independent analyses were performed for each genotype, and average extinction rates and autocorrelation effects were found similar in all genotypes except B. To illustrate these effects, we plotted the Kaplan-Meier survival curves and median survival time (time by which 50% of the population were extinct) for the joined genotypes in each autocorrelation treatment (Figure 5).

Simulations

Tolerance curves fitted with (equation 12) and without (equation 14) memory were used to simulate population dynamics under our fluctuating salinity treatments. Process noise and observation errors were not simulated. Population size variance was analyzed using the same bootstrap method as used for the real dynamics, except that here the true simulated population sizes were known and not sampled from their estimation distribution. Simulations did not include demographic stochasticity, so simulated lines were considered extinct after population densities were found below 1000 cells.mL^-1.

Intracellular glycerol dosage

A background culture of genotype C was used to measure variation in intracellular glycerol concentration in response to salinity changes. The ancestral population was cultivated in 2.4M for 10 days until it reached the late exponential phase. It was then split and acclimated for 7 days in 50mL flasks at low (0.5M) and high (3.5M NaCl) salinities. Each of these flasks was then split again and transferred to 0.5M, 2M and 3.5M NaCl in 50mL flasks, and sampled after 16, 45, 72 minutes, 2h15, 4h15 and 1 day for glycerol dosage.

Intracellular glycerol concentration was estimated from the difference between total and extra-cellular (after cell filtration) glycerol concentrations. 800µL Free Glycerol Reagent (Sigma Aldrich) was mixed to 200µL culture (with or without cells), and we measured optical density at 540nm after 5 minutes incubation at 37°C. Glycerol concentration was then interpolated from a (linear) standard curve. Dunaliella densities were also estimated by flow cytometry, and we made two independent replicates of all measures. Intracellular glycerol concentration per cell was computed as

$${\left[\text{glycerol}\right]}_{\text{intra}}=\frac{{\left[\text{glycerol}\right]}_{\text{total}}-{\left[\text{glycerol}\right]}_{\text{extra}}}{\left[Dunaliella\right]},$$

where [] denotes a density/concentration. We computed the first-order standard errors of the intra-cellular glycerol concentration using the delta method, accounting for the (independent) error of the cytometer, the total and the extracellular glycerol measures (Figure 4). We then performed Wald test to assess whether different glycerol levels were found under different treatments (Supplementary Table 1).

Extended Data

Extended Data Fig. 1. Population dynamics summary for each of the six ancestral genotypes.

(same color as Figure 2). a. Distribution of r: lines represent the estimated distribution fitted in the gamma model (solid lines) and histograms are based on the 3119 realized growth rates estimated from the population dynamics of each line, including residual deviation from the underlying model (gamma). b. Tolerance curves: lighter grey indicate higher growth rate, the thick bold line corresponds to the growth rate that allows overcoming the biweekly dilution (r = 0.542), and the thin bold line to r = 0.c. Estimated survival curves.

Extended Data Fig. 2. Population dynamics in constant salinities.

a. Time series of population sizes for all lines of ancestral genotype A in the 3 constant salinities (light blue: 0.8M, blue: 2.4M, dark blue: 3.2M – 5 replicates each) are plotted (shaded lines), together with the mean population size (solid line) ± standard deviation (dashed lines). Population sizes> 1000 are plotted on the log scale and mean and standard deviation were estimated on the log scale, excluding extinct lines. Note that at 3.2M, the population size slowly decreases over time because its exponential growth slightly undercompensates the biweekly dilution. b. Distribution of population size in genotype A during the stationary phase (except at 3.2M where no stationary phase is reached), for all constant environmental treatments. Note the reduced variances and skewnesses as compared with the stochastic environments (Figure 2). c. and d.: Growth rate (r) and carrying capacity (K) of all ancestral genetic backgrounds, estimated in the 3 constant salinities, with their standard errors. Salinity has a significant effect on K (p = 5.2.10^-15, likelihood ratio test), but this was neglected in the population dynamic analysis in fluctuating environment because the biweekly 15% dilution implied that exponential growth was prevalent in our experiment (Extended Data 1).

Extended Data Fig. 3. Raw measurements.

a, b and c. Cytometer (Guava® EasyCyte) plots. Dunaliella shape and size do not allow distinction from debris, but a gate can designed based on chlorophyll (red and yellow) autofluorescence. Dead cells were detectable after transfers from low to high salinity. They show an immediate decrease in red fluorescence, and are not taken into account when measuring population size. d and e. Regression between spectrometer measures (685nm fluorescence – 10722 points and 680nm optical density – 7332 points, see Supplementary Table 1 for details). Fluorescent values below 400 and optical density values below 0.01 (vertical lines) were discarded from the analysis and colors represent the day of each measure (from 0 (black) to 133 (light blue).

Extended Data Fig. 4. Salinity distribution in the stochastic treatments.

a. Salinity time series of 10 of the 39 independent lines for each of the four autocorrelation treatments (same colors as Figure 2). b. Distribution of salinities in the 39 independent salinity series experienced by the six ancestral genetic background in the four autocorrelation treatments. Note that truncation of salinities that could not be reached with our dilution level did not much affect the final distribution of salinities in our treatments, which was similar to the Gaussian expectation in the absence of truncation (line).

Extended Data Fig. 5. Tolerances curves of 3 clones from BC genotype under autocorrelation 0.

We measured exponential growth (starting 3 independent replicates from 5000 cells and measuring population size after 3 days) in 75 previous x current cross salinities ranging from 0.1 to 4.7M. Raw growth rate ranging from -1.5 (black) to 1 (light grey) were measured (dots) and bivariate tolerance curves (color and curves) were fitted using equation 12 (see Method section). Clones displayed similar plasticity as found in the total population (Extended Data 1, genotype BC).

Extended Data Fig. 6. Comparison between population sizes fitted in the state-space model including an autocorrelated normal (x) or a gamma (y) distribution of the intrinsic growth rate r.

The same colors and symbols as Figure 2 were used to represent autocorrelation and genotypes of the 22497 data points.