A methodology for evaluating tooth wear monitoring using timed automata modelling

Abstract

Objectives

Tooth wear is a multifactorial condition leading to the loss of dental hard tissues. A counselling/monitoring protocol is of importance in order to keep that loss as limited as possible. Since many factors are involved and a time span of decades is included, research to disentangle all these processes in patients is difficult. Instead, a modelling technique was used that is able to deal with time, costs and probabilistic and stochastic information. The aim was to shed light on the question: does a yearly or a once‐in‐five‐years counselling/monitoring protocol yield better outcome measures?

Methods

A so‐called timed automata model was adopted, analysed with the tool UPPAAL. To our knowledge, this is the first time that formal modelling is applied in dentistry. In this article, a UPPAAL model for the evaluation of tooth wear is described.

Results

Using the UPPAAL model, it was calculated that with a yearly counselling/monitoring protocol the severity of tooth wear at age 74, the total costs per person and the number of restorative treatments were less, and the number of so‐called “good years” was higher.

Conclusions

With the use of the UPPAAL model, it may be concluded that a yearly counselling/monitoring protocol can yield better outcome measures.

Clinical Significance

Regarding dentistry in general and tooth wear in particular, with the use of a timed automata model in UPPAAL, actual research questions can be answered, factors of influence in a multifactorial condition like tooth wear can be clarified, and future research topics can be determined.

1. INTRODUCTION

Tooth wear is a multifactorial condition leading to the loss of the dental hard tissues (enamel, dentin and cementum). Tooth wear is a common condition amongst adults and since it is an irreversible process, it increases with age. Since people will become older and keep their own dentition for a greater part of their lives (due to better care of caries and periodontitis), tooth wear will become a bigger problem.1

Studies amongst adults are rare, but those that are performed show this increase with age. The existing literature revealed that severe tooth wear increases from 2%‐3% at age 20 towards 12%‐17% at age 70.2, 3 When tooth wear progresses, it can cause problems for (a) the individuals, namely deterioration of aesthetic appearance, sensitivity, pain, discomfort and functional problems4 and hence an impaired oral health‐related quality of life5, 6; (b) the oral caregivers, namely having to perform restorative treatments of increasing complexity3, 7; for the community, meaning increasing costs because of dental and medical treatments or absenteeism.8 The latter issues are in the domain of “health economics”, a branch of economics concerned with issues related to efficiency, effectiveness, and value and behaviour in the production and consumption of health and health care. Because of the increasing costs for health care and dental health care, these issues are of importance.

Tooth wear can be divided in subgroups, namely mechanical wear and chemical wear. In addition, both subgroups can be divided in intrinsic and extrinsic.4 Intrinsic mechanical tooth wear (IMTW, attrition, tooth to tooth contact) is a physiological phenomenon that no one can escape, because it is a result of normal function (chewing). IMTW may accelerate due to sleep bruxism (grinding).9 The other three subgroups, namely extrinsic mechanical tooth wear (EMTW, abrasion, due to other factors), intrinsic chemical tooth wear (ICTW, erosion, due to stomach acid) and extrinsic chemical tooth wear (ECTW, erosion, due to an erosive diet) are considered as non‐physiological. The non‐physiological tooth wear processes may accelerate the amount of tissue loss and influence each other, thereby possibly leading to pathological tooth wear. As mentioned in the European Consensus Statement,7 not only the amount of tooth wear determines if tooth wear is pathological, but also the additional complaints of the patient.

Tooth wear can occur on all surfaces of the teeth.1 The loss of hard dental tissues on the surfaces that are involved in the occlusion and articulation (occlusal, incisal and palatal surfaces of the second sextant) is of more importance for the dentition than the other surfaces (non‐occlusal and non‐incisal surfaces).4 The loss on the occlusal and incisal surfaces will result in the loss of clinical crown height, resulting in disturbance of the maxillo‐mandibular relation. Consequently, when time progresses, these surfaces become more difficult to restore. This is the reason why the Tooth Wear Evaluation System (TWES) contains several grading systems with a focus on the surfaces involved in occlusion and articulation.4, 10

The dental team has two treatment options available, namely counselling/monitoring and a restorative treatment.7 Counselling means educating the patient about the possible causes of the existing tooth wear and, by considering the possible aetiological factors, take the appropriate preventive measures if possible. Monitoring can be done by quantifying the amount of tooth wear with an evaluation system, intra‐orally, on casts and/or on intra‐oral photographs.11 In the future, intra‐oral scans can be used to measure objectively the amount of loss of the dental hard tissues. The main goal of counselling and monitoring is to avoid further loss of hard dental tissues as much as possible, as well as measure and determine tooth material loss over time. By doing this, the start of a restorative treatment can be postponed or even avoided. Advantages of a restorative treatment can be the reduction of sensitivity and/or pain, the improvement of function and mastication, the improvement of oro‐facial aesthetics and the prevention of further loss of hard dental tissues and/or restorations. Disadvantages of restorative procedures are often overlooked and include the failure and/or fracture of the restorations and/or of the teeth. As soon as the restorative cycle is started, it is always necessary to re‐restore the dentition after some time, since restorations will not last for decades.12 Therefore, it is important to postpone the start to an older age of the patient as much as possible. Regarding the important question when to continue counselling/monitoring and when to start a restorative treatment, proposals for decision‐making have been formulated.4, 7

An important question is not only how to perform counselling and monitoring, but also which protocol should be used: at what time intervals and in which order do monitoring and counselling take place? Since so many factors are involved in the multifactorial tooth wear process and a long time span is involved (decades), research to disentangle all these processes on patients is extremely difficult. Therefore, instead of performing time‐consuming and expensive empirical research, it is an attractive alternative approach to construct a mathematical model of both tooth wear and the tooth wear monitoring, and then to analyse this model. This asks for a modelling technique that is able to deal with time, costs, and probabilistic and stochastic information. An example of such a modelling technique is the enhanced timed automata paradigm as implemented in the UPPAAL tool, developed by computer scientists in Uppsala, Sweden and Aalborg, Denmark.13, 14 This tool has not only been used widely in various computer science applications, but also in the medical field.15, 16 Many other modelling formalisms exist. In health care, the so‐called discrete‐event model (DEM) has been widely used; for a comparison between UPPAAL and DEM, we refer to.16 For our aim, we have chosen UPPAAL because of its compositionality (allowing to build a system out of smaller components) and its graphical user interface (which makes it easier to explain and discuss models with non‐experts in formal modelling).

To our knowledge, the present study is the first time that formal modelling is applied in dentistry. In this article, a UPPAAL model for tooth wear is developed based on evidence, while additionally, educated assumptions are made. The model exists of two parts, namely a “tooth wear evaluation part” and a “patient part”. The model, together with a detailed explanation, can be found at.17

So far, to our knowledge, no recommendations are proposed at what time interval counselling/monitoring is needed. Arbitrarily, we choose a short and a long interval, namely 1 year and 5 years, respectively, resulting in the question to be answered: does yearly counselling/monitoring or once‐in‐five‐years results in better outcome measures? Using the UPPAAL model, several outcome measures are calculated, amongst which the average TWES grade over a whole life, the total costs per person for a whole life, the average number of restorative treatments per person and the so‐called “good years”, that is, the years a person has a tooth wear score of grade 0, 1 or 2 (no, mild or moderate tooth wear).

2. METHODS

Firstly, the assumptions and evidence for several parameters that play an important role in tooth wear, as well as in monitoring and treating tooth wear, will be discussed. Secondly, how these aspects are dealt with in a UPPAAL model will be analysed in the next section. Finally, six outcome measures will be calculated, namely:

1. What are the average costs per patient?

2. What is the average number of restorative treatments per patient?

3. What is the expected average TWES score during the lifetime of a patient?

4. What is the average number of good years (ie the years with TWES score <3) per patient?

5. What is the chance that a patient underwent at least three restorative treatments?

6. What is the chance that a patient reaches TWES score 4?

2.1. Distribution of crown height and enamel thickness

Regarding the permanent dentition, two development eruption states are known, viz., the first eruption around 6 years of age (the four first molars and the eight incisors) and the second eruption around 12 years of age (the 4 second molars, the four canines and the eight premolars). In theory, there are two options for modelling, namely the permanent molars and the permanent incisors, since these teeth have erupted first. Therefore, these teeth, being longer at risk in the oral cavity than all the other permanent teeth, have a longer period of being at risk for tooth wear. It was therefore chosen to select the data of the first molars for the UPPAAL model. In future research, data of one of the other types of teeth can be used in this model, or even all types of teeth can be clustered.

It is important to model the variation of parameters like thickness of enamel and clinical crown height of the first molars. We model these parameters as a stochastic variable with a normal distribution. According to the existing evidence,18 the average enamel thickness is 1426 mu, ranging between 280 and 2010 mu. Note that the average is not in the centre of the interval; since a normal distribution is symmetric around the average, we approximate this interval by taking the average of the left (1426‐280) and right (2010‐1426) part of the interval. Hence, we use as interval [1426‐944,1426+944], so the approximated interval has length 1888 mu. Statistics show us that for a normal distribution, 99.7% of the values lie in an interval of length 6×sigma (where sigma is the standard deviation), so we take the standard deviation of the enamel thickness to be sigma=315 mu.

Based on,19 we assume that the clinical crown height of the first molars lies in the interval 5700 mu ± 750 mu. Here, we also assume a normal distribution, so the standard deviation of this distribution is sigma = 1500/6 = 250 mu.

2.2. Tooth wear parameters

Data of physiological tooth wear are scarce; we used the data of a group of Belgian researchers regarding the first molars, namely 29 mu/year.20 The non‐physiological tooth wear is determined by the existing prevalence data of non‐physiological tooth wear and the resulting aggravation of the total tooth wear (calculated based on the physiological tooth wear of 29 mu/year). The bruxism prevalence in adults is 10% 21 and the aggravation was considered to be 1/3 of the physiological wear, so an additional IMTW of 9 mu/year. The extrinsic mechanical tooth wear (EMTW) is not included, since this does not contribute to loss of clinical crown height in modern human beings. Intrinsic chemical tooth wear (ICTW) is caused by the stomach acid. The main reason for bringing the stomach content into the oral cavity is gastroesophageal reflux disease (GERD). The prevalence is modestly considered as 10% in adults, since the existing evidence has a broad range between 2.5% and 50% worldwide 22 and between 10% and 20% in the Western world.23 The aggravation was considered as an increase of four times the physiological wear (assumption). Finally, the fourth subgroup of tooth wear, namely extrinsic chemical tooth wear (ECTW), is caused by an acidic diet. Precise prevalence data are not available, but in modern society a dramatic lifestyle change has occurred, with an estimated increase of frequency and consumption of acidic foods and drinks of around 300% in the last two decades (01), nevertheless a modest percentage was considered, namely 20% in adults. The aggravation was considered as an increase of three times the physiological wear (assumption). It must be emphasised that the above and below chosen percentages were estimated deliberately on the low side of the spectrum, in order to produce outcomes as realistic as possible.

2.3. Cost and effects of counselling and measures

In this part of the methods, we have used the costs as they are currently prevailing in the Netherlands, since we also have used the prevalence data of tooth wear in the Dutch adult population.3 Of course, in other countries other prices will prevail; such prices and prevalence data could in principle be incorporated in the model. Regarding the Dutch prevalence data, it can be stated that they are equal to the prevalence data that were revealed in a review that used and composed data from different countries.2 If sleep bruxism is present, splint therapy will be started, which costs € 210.00, according to the dental fees in the Netherlands set by the Dutch Healthcare Authority.24 Reduction of the wear process is set at 50% (assumption). This is based on the fact that wearing an occlusal splint will reduce the tooth wear process to zero, but the success of a treatment depends, amongst others, on the patient compliance. The compliance of a patient will not be 100%. Regarding compliance of medication, percentages between 40% and 70% are reported 25; a search about the compliance of removable orthodontic appliance yielded percentages between 40% and 90%.26 Therefore, a modest calculation of the compliance of an occlusal splint is set at the mentioned 50%.

When reflux is presumed, a patient should be sent to his/her home physician. The home physician will start the regular treatment by prescribing the medication belonging to the disease, namely proton pump inhibitors (PPI).27, 28 The costs for the consultation and the medication is set at € 50.00, according to the fees in the Netherlands, set by the Dutch Healthcare Authority.29 There is evidence that a remission of the existing complaints can be achieved in 85%‐95% of the patients in the first 8 weeks, with one daily doses of a PPI, but a relapse can occur over time.28 Therefore, an expected reduction of the wear process is set at 50% (assumption), again a modest calculation, based on the above‐mentioned knowledge of the expected remission, possible relapse and a modest compliance.

When an acidic diet is discovered by the use of proper questionnaires and a tailored oral history taking, the calculation of the reduction of the tooth wear process is set at 10% (assumption). This is a conservative estimate, because changing the lifestyle of a patient is difficult. This counselling does not yield extra costs, so it is set at € 0.00.

Regarding the restorative treatments: if the tooth wear is grade 3 and age is over 50, or the tooth wear is grade 4, a restorative treatment is started. Here, we assume that during someone's lifespan, the maximum number of treatments is four. The restorative treatments 1 and 2 are set as non‐invasive treatments, following the described recommendations in the earlier mentioned consensus report.7 The assumption was made that if there is generalised tooth wear, meaning all teeth need to be restored, the first choice of treatment was, again following the consensus report,7 with the non‐invasive direct resin composite technique (estimation of the costs in the Netherlands € 4000.00).24 The restorative treatments 3 and 4 are set as partly invasive, partly non‐invasive, and the assumption was made that after two restorative non‐invasive cycles, a more invasive treatment is necessary. The assumption was made that all teeth need re‐restoration again, partly non‐invasive, but partly invasive with indirect techniques (estimation of the costs in the Netherlands € 12 000.00).24

2.4. The UPPAAL model

Many phenomena in science and technology can be modelled by so‐called automata, consisting of states (also called locations) and transitions between locations. Timed automata (TA)30 are finite‐state automata enriched with real‐valued clocks and synchronisation channels. All clocks in a TA model advance with the same rate, and transitions between the locations of an automaton depend on conditions on clocks. In particular, a guard defines when a transition may be taken, while an invariant is the condition for permanence in a location. A model may consist of several automata; automata may synchronise their transitions, with each participant performing one of two complementary actions (input and output) on a synchronisation channel associated with a transition. A set of clocks may also be reset by a transition, causing them to restart from 0. The models we will present here were implemented using the software tool UPPAAL,13 which adds a number of features to the basic definition of TA. Some of the extensions used in this paper are the use of clock derivatives, cost variables, stochastic variables and probabilistic transitions. We make use of the statistical model checking features of UPPAAL.14

2.5. Patient initialisation

The age of a patient is recorded by clock age (Figure 1). The patient starts in location Start, is allowed to remain there as long as age ≤10 and is allowed to take the outgoing transition when guard age ≥6 is satisfied (so the transition is taken on average when age = 8). In this transition, we stochastically determine the enamel thickness e, and 1/3rd of the clinical crown length d1, and d2 = 2 × d1.

Figure 1.

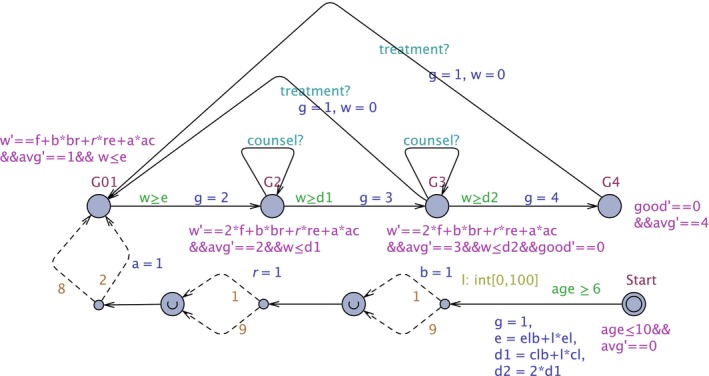
The Patient Model. This UPPAAL automaton models a patient: initialisation of variables, and the locations G01, G2, G3, and G4, corresponding to the tooth wear scores. Detailed explanation can be found in Ref.17 [Colour figure can be viewed at https://www.wileyonlinelibrary.com]

We want to turn the normal distribution for enamel thickness into a uniform distribution with the same mean and variation, since uniform distributions are directly supported in UPPAAL. If mean and variance of the distribution are preserved in the approximations, then according to a key theorem in statistics (the central limit theorem) the distribution function of the average of large numbers (larger than 30) of samples of a variable will not be affected; since in the model analysis hundreds of thousands of simulations will be used, the approximations are well justified.

Standard statistical theory tells us that the length of the uniformly distributed interval is given by sqrt 12  × sigma = 3464 × sigma. We saw above that sigma = 315 and the mean is 1426, so the length is 3.464 × 315 = 1091, and hence, the lower bound of uniform interval elb = 1426−545 = 881. We approximate the length of interval by el × 100 = 11 × 100; this means we can draw a random number between 1 and 100 and establish the enamel thickness e as e = elb+l × el. For 1/3rd of clinical crown height, similar calculations lead to a uniformly distributed interval with lower bound clb = 1750 and length cl×100 = 3×100, so d1 = clb+l × cl.

In our abstract model, we assume that the presence of bruxism, reflux and acid diet is being probabilistically decided right after a patient has left the start state. The parameters b (for bruxism), r (for reflux) and a (for acid diet) are set to 1 by probabilistic choices, with probabilities 0.1, 0.1 and 0.2, respectively.

2.6. Patient behaviour

The patient starts in location G01, where grading scores 0 and 1, so no wear or wear limited to the enamel; note that variable g has been set to the maximum score 1 in the transition from location Start (Figure 1). The total amount of tooth wear is recorded in variable w. A patient can remain in location G01 until w = e (so all enamel is gone), in location G2 until w = d1 (so 1/3rd of clinical crown length is gone), in location G3 until w = d2 (so loss of 2/3rd of clinical crown length) and indefinitely in the location G4.

The speed of the tooth wear is given by the derivative w' of the total amount of tooth wear w. It is composed of the physiological tooth wear f = 29 mu/year, the wear to bruxism b×br where br = 9 mu/year, the wear due to reflux r×re where re = 4 × f mu/year and the wear due to acid diet a×ac where ac = 3×f mu/year. We assume that if the enamel is gone, the physiological wear of the exposed dentine is twice as fast, so in locations G2 and G3 the physiological wear is 2 × f mu/year. Note that in location G4 we do not record tooth wear anymore (as it cannot get a worse grade score from there). Variable avg is used in the calculation of the average grade score during the lifetime of a patient: in each location, the derivative of avg is set to the grade score. The final average grade score of a patient of age 74 is avg/74.

If a treatment takes place (in G3 or G4), a transition is taken to location G01, the grade score g is set to 1, and the amount of tooth wear w is reset to 0.

2.7. Tooth wear evaluation: initialisation

We assume that monitoring, using the Tooth Wear Evaluation System (TWES) starts between age 11 and 15 (again an interval, to avoid that all patients have synchronised monitoring) (Figure 2). Clock p records the time since the last TWES monitoring.

Figure 2.

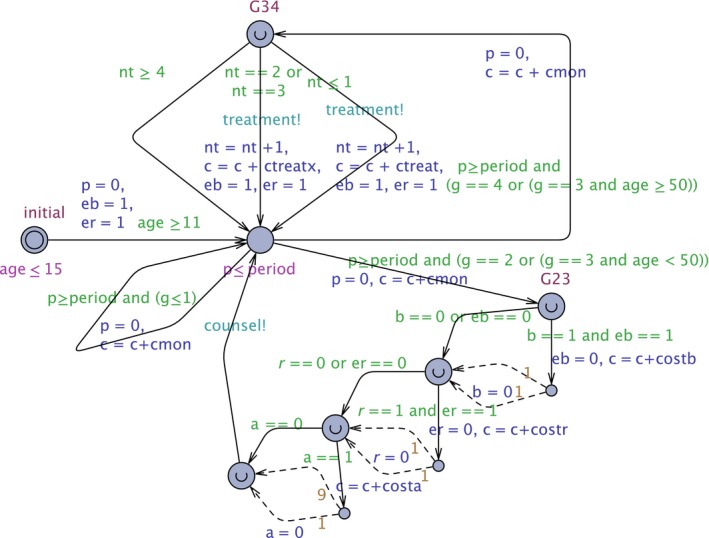
The TWES Model. This UPPAAL automaton models the periodic monitoring, counseling (starting from location G23), and treatment (starting from location G34). Detailed explanation can be found in Ref.17 [Colour figure can be viewed at https://www.wileyonlinelibrary.com]

Variables eb and er record whether bruxism and reflux are still treatable (in that case the value is 1, otherwise 0). If p = period and g = 1 or g = 0, a transition to the same location is taken and the cost c is updated with the cost of monitoring cmon (which we have here assumed to be 0). Clock p is reset to 0.

2.8. Tooth wear evaluation: counselling/monitoring

If g = 2 or g = 3 and age <50, location G23 is entered. From this location, a cascade of counselling transitions is taken (Figure 2):

• Bruxism: if it has not happened yet (eb = 1) with cost costb =€ 210.00, the variable b is reset to 0 with success probability 50%;

• Reflux: costr =€ 50.00, variable r is reset with success probability 50%;

• Acidic diet: costa =0, variable a is rest with success probability 10%.

Note that since bruxism and reflux are treated only once, variables eb respectively er are set to 0 when the treatment transitions are taken.

2.9. Tooth wear evaluation: restorative treatment

If g = 3 and age ≥50, or g = 4: a transition is taken to location G34. From that location, there are three possible transitions (Figure 2):

• If the number of treatments nt satisfies nt ≤1, we increment nt, add ctreat (4000, the cost of the first two treatments) to the cost c, and synchronise with the patient via channel treatment.

• If nt satisfies nt = 2 or nt = 3, we increment nt, add ctreatx (12 000, the cost of the third and fourth treatment) to cost c, and synchronise with the patient via channel treatment.

• If nt satisfies nt ≥4, we do nothing.

In case of a treatment we again enable the treatment of bruxism and reflux so we set eb and er to 1.

3. RESULTS

With the created UPPAAL model, random simulations can be performed. An example of such a random simulation is given in Figure 3, where the total amount of tooth wear w, the costs c and the TWES score g (multiplied by 1000 so it fits in the same scale as costs and tooth wear) have been plotted. A certain TWES score means that the patient has at least one tooth with such a score. This is in line with the way the prevalence data were obtained in the Netherlands3 and also in other prevalence studies.2 We see that for this particular random patient at age 15 a successful reflux treatment was performed, which augmented the costs by € 50.00 and decreased the speed of tooth wear. Around age 25 the patient reached TWES score 3, for which a treatment took place at age 50; note that the costs then increased by € 4000.00 and the tooth wear was reset to 0. Checking several such random simulations is important for gaining confidence in the validity of the model.

Figure 3.

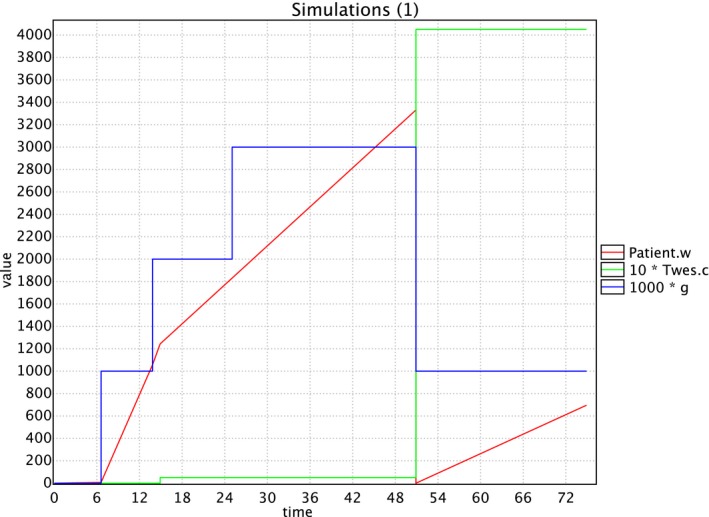
A random simulation. This figure combines the output of a random simulation of a patient between the age of 0 and 74 in one graph: the red line represents the tooth wear in micron, the green line represents the costs in euro, and the blue line represents the tooth wear score (multiplied by 1000 to be representable in the same graph) [Colour figure can be viewed at https://www.wileyonlinelibrary.com]

The model was analysed for performance properties by asking queries in a format required by UPAAL. For each property, the analysis was performed for a monitoring period of 1 year and for one of 5 years, where a population of 100.000 simulated patients was checked who all live 74 years. The “end‐year” of 74 was used, because in the prevalence study of tooth wear in the Dutch adult population, the oldest age group was 65‐74 years old, so these prevalent figures were available.3 We checked the difference between these periods for the following properties, specifying the UPPAAL query and the outcome for the two periods:

1. What are the average costs per patient? UPPAAL query: E[≤74; 100000](max: 10*Twes.c). Outcome period 1: € 4495.00 euro and period 5: € 5155.00.

2. What is the average number of restorative treatments per patients? UPPAAL query E[≤74; 100000](max:Twes.nt). Outcome period 1:1.03 and period 5:1.12.

3. What is the expected average TWES score during the lifetime of a patient? UPPAAL query: E[≤74; 100000](max:Patient.avg/74). Outcome period 1:1.17 and period 5:1.21.

4. What is the average number of good years (ie the years with TWES score ≤3) per patient? UPPAAL query: E[≤74; 100000](max: good). Outcome period 1:67.6 and period 5:66.2.

5. What is the chance that a patient has at least 3 restorative treatments? UPPAAL query Pr[≤74](<>Twes.nt==3). Outcome period 1:4% and period 5:7%.

6. What is the chance that a patient reaches TWES score 4? UPPAAL query: Pr[≤74](<>G4). Outcome period 1:14% and period 5:23%.

4. DISCUSSION

A modelling technique was used that is able to deal with time, with costs and with probabilistic and stochastic information. The aim was to shed light on the question: does a yearly or a once‐in‐five‐years counselling/monitoring protocol yield better outcome measures? Using the UPPAAL model, it was calculated that with a yearly counselling/monitoring protocol the average costs per person were less, the average number of restorative treatments needed were less, the expected average TWES score was less, the number of so‐called “good years” was higher, the chance that a patient has at least three restorative treatments was less, and the chance that a patient reaches TWES score 4 was less. Hence, we see that period 1 performs better than period 5 on all performance criteria. Of course, this outcome is valid under the modelling assumptions that have been made in creating the model. We like to stress that the fact that these modelling assumptions can be explicitly pointed out in the model enables a rational discussion about these assumptions. For instance, the prevalence of bruxism, reflux and acid diet is established in an abstract way when the patient is on average 8 years old; the model can be adapted in such a way that this prevalence is established at a more realistic age. To mention just another assumption, the costs for TWES counselling has been set at € 0.00 in this model. It is easy to adapt such an assumption: what if we set this cost at € 20.00? A simple adaptation in the model now shows that the average costs per patient for period 1 is now € 5605.00 and for period 5 it is € 5208.00; so now the costs for period 1 are higher while it continues to perform better on all other criteria. This might open a debate on whether the higher performance of 1‐year‐period TWES monitoring justifies the increased cost. Having a model where alternative and what‐if scenarios can easily be analysed is an important asset in such a debate.

Regarding the presented UPPAAL tooth wear model, one may conclude that a yearly counselling/monitoring interval can be better than an interval of once‐in‐five‐years on all aspects: average grade, average costs, average number of treatments, average number of “good years”, possibility of arriving in a situation of severe tooth wear and possibility of having three treatments. The outcomes belong to the field of “health economics”, in other words, the examined questions and results are issues related to the costs, efficiency and effectiveness of dental health and dental healthcare.

The model has been produced as a cooperation between dental researchers and computer science UPPAAL experts where the graphical user interface of the UPPAAL tool proved to be very beneficial to the mutual understanding of experts from different disciplines; tool and model could be used by a non‐expert in the modelling language to autonomously analyse variants of the model.31 The model incorporates evidence from dental research regarding some general dental aspects (eg enamel thickness, crown and lengths) and evidence regarding tooth wear (eg prevalence and physiological wear). Additionally, several assumptions were made, again when possible based on existing evidence. The results were better for the yearly counselling protocol (as opposed to a once‐in‐five‐years protocol) for all studied performance criteria. We will discuss the used evidence and assumptions one by one.

Regarding the prevalence data of tooth wear, the results of the Dutch survey3 are in line with a review regarding the prevalence data in adults.2 The decade distribution is used in other studies as well, and made the choice of 74 years as end point explainable.3 Of course there are many evaluation systems available which can hamper the comparison of several studies.2 Nevertheless, the evaluation system that was used has proven to be reliable.10 Regarding the used data for the enamel thickness,18 crown length19 and physiological wear,20 evidence is scarce but exists. Regarding the data used for setting the prevalence for bruxism,21 GERD 22, 23 and an acidic diet,1 there was a broad spectrum of evidence, in which case the lower values were chosen. The same was the case regarding the effect of several monitoring/treatment options on the compliance25, 26 and the costs.24, 29 The moment of eruption of the first permanent molars and the moment a virtual patient “enters the model” are both educated assumptions.

An important question is how our model relates to empirical evidence. Since the existing evidence has not been obtained for patients undergoing a TWES monitoring protocol, this is a highly non‐trivial question. Currently, we are working to relate variants of our model to the data reported in.3

It is important to obtain more confidence in the model by assessing the quality and robustness of the model. A first step has been taken in31 where both the realism of some assumptions and the sensitivity of the results with regard to several variables have been investigated. The main conclusion of31 is that the results are especially sensitive to the prevalence of reflux and acidic diet, and to the values of both physiological and chemical tooth wear. More empirical research is needed on these parameters to obtain more reliable outcomes. In addition, we are refining the model towards less abstract ways of dealing with the prevalence of pathological tooth wear. Our ultimate goal was to produce optimal monitoring and treatment protocols for personalised medicine, so by considering the specific conditions of a patient. It is our conviction that this will contribute to better dental care for the large amount of the adult population suffering from tooth wear.

Regarding dentistry in general and tooth wear in particular, with the use of a timed automata model in UPPAAL, actual research questions can be answered. With this method, factors of influence in a multifactorial condition like tooth wear can be clarified, and so future research topics can be determined.

Wetselaar P, Lobbezoo F, de Jong P, Choudry U, van Rooijen J, Langerak R. A methodology for evaluating tooth wear monitoring using timed automata modelling. J Oral Rehabil. 2020;47:353–360. 10.1111/joor.12908