Abstract
DNA confinement in a nanochannel typically is understood via mapping to the confinement of an equivalent neutral polymer by hard walls. This model has proven to be effective for confinement in relatively large channels where hairpin formation is frequent. An analysis of existing experimental data for Escherichia coli DNA extension in channels smaller than the persistence length, combined with an additional dataset for λ-DNA confined in a 34 nm wide channel, reveals a breakdown in this approach as the channel size approaches the Odijk regime of strong confinement. In particular, the predicted extension distribution obtained from the asymptotic solution to the weakly correlated telegraph model for a confined wormlike chain deviates significantly from the experimental distribution obtained for DNA confinement in the 34 nm channel, and the discrepancy cannot be resolved by treating the alignment fluctuations or the effective channel size as fitting parameters. We posit that the DNA-wall electrostatic interactions, which are sensible throughout a significant fraction of the channel cross section in the Odijk regime, are the source of the disagreement between theory and experiment. Dimensional analysis of the wormlike chain propagator in channel confinement reveals the importance of a dimensionless parameter, reflecting the magnitude of the DNA-wall electrostatic interactions relative to thermal energy, which has not been considered explicitly in the prevailing theories for DNA confinement in a nanochannel.
I. INTRODUCTION
When a DNA molecule is confined in a channel or pore the, excluded volume1 and the stiffness of the polymer chain2 cause the molecule to extend along the channel axis. It is particularly challenging to describe the thermodynamics of this process when the channel size, D, is commensurate with the persistence length, lp, of the polymer. For D ≪ lp, known as the Odijk regime,2 the chain is extended close to its contour length, L, with small fluctuations in alignment with respect to the channel axis.3–5 Conversely, for D ≫ lp, the polymer can easily form hairpin bends; the chain statistics here follow blob theory, described first by the marginal solution behavior embodied in the extended de Gennes regime6–9 and eventually cross over to the de Gennes regime for .1 While Odijk4 proposed an additional scaling regime between the classic Odijk behavior2 and the blob regimes,1 observing the scaling behavior in this so-called backfolded Odijk regime requires that the polymer exhibits a very large monomer anisotropy,10 the latter measured by the ratio of the persistence length to the effective width, , of the polymer. For DNA, the monomer anisotropy lp/ saturates at lp/ ≈ 10 at high ionic strength and decreases with decreasing ionic strength.11 As a result, DNA will not exhibit a backfolded Odijk regime.10 Rather, the extension of DNA confined in the channels near the persistence length typically appears as a smooth transition from the de Gennes scaling to the Odijk scaling, with an apparent extension scaling that is inverse in the channel size.7,12–16
Recently, two complementary theories have emerged that subsume the physics of the extended de Gennes regime and the backfolded Odijk regime into a single regime characterized by weak excluded volume interactions.17,18 The key result of both theories17,18 is the existence of a new scaling parameter, α, that represents the typical number of overlaps per hairpin bend in the chain, with the fractional extension of the chain scaling like α1/3. Importantly, the existence of the latter scaling law is not predicated on a large value of the monomer anisotropy. As a result, these theories17,18 should permit a description of DNA extension when D ≈ lp, a technologically important case19 for which the inequalities required in previous scaling theories4 cannot be satisfied.
DNA is a polyelectrolyte, and nanochannel confinement of DNA takes place in a system with charged walls. The varied electrostatic interactions in the physical system are captured within the prevailing neutral wormlike chain model by computing an effective width ,20 which accounts for the electrostatic contribution to the segmental excluded volume, a persistence length lp that includes contributions from both the intrinsic stiffness and the electrostatic repulsion along the DNA backbone,21 and an effective channel size Deff, which accounts for the region of the channel that is inaccessible to the DNA due to DNA-wall electrostatic interactions.7,22,23 Once this mapping is complete, the DNA extension within the nanochannel can be described using one of the myriad theories1,2,4,17,18 developed for the confinement of a neutral polymer between hard walls.
The present contribution addresses the applicability of this neutral wormlike chain model to describe the distribution of DNA extensions for channel sizes somewhat smaller than the persistence length and thus being proximate to the Odijk regime but not yet satisfying the strong inequality D ≪ lp. We take advantage of one of the new theories, the weakly correlated telegraph model,17 to facilitate this analysis. Recently, Ödman et al. have derived an asymptotic solution to the telegraph model for such small channels and proposed a method to augment that result to account for the effect of alignment fluctuations.24 This theory is reviewed in detail in Sec. II. The resulting probability distributions for the extension X of the chain are in remarkably good agreement with direct simulations of a confined, neutral wormlike chain25 when the variance due to alignment fluctuations corresponds to that in the Odijk regime.5 The agreement between simulation and theory persists down to values of α ≈ 0.3, well below the asymptotic requirement α ≫ 1 in the theory.25 The predictions of the telegraph model24 have also been compared to four of the experimental data points from Reinhart et al.,26 the latter obtained by stretching nick-labeled DNA for genome mapping in nanochannels at values of α ranging from 0.81 to 8.40.19 The results of this analysis are reproduced in Fig. 1. The qualitative agreement between theory and these particular experiments is satisfying, in particular, the presence of similar fat tails in both theoretical and experimental distributions. However, the agreement between theory and experiment becomes worse as the channel size decreases.24 This result is counterintuitive; decreasing the channel sizes better satisfies the asymptotic condition α ≫ 1, which suggests that the agreement between theory and experiment should improve with decreasing channel size. The published analysis24 only compared theory and experiment26 for two distances between nick labels and two channel sizes. We expand this comparison to the entire dataset26 in Sec. III; the discrepancy is prevalent throughout all of the data.
FIG. 1.
Comparison between the predictions of the telegraph model and experimental data in Ref. 26 for the difference between the chain extension, X, relative to the average chain extension, ⟨X⟩ for L = 28 125 bp and two channel sizes: (a) D = 40 nm and (b) D = 51 nm. Reproduced with permission from A. B. Bhandari and K. D. Dorfman, Biomicrofluidics 13, 044110 (2019). Copyright 2019 AIP Publishing LLC.
One possible source of the discrepancy between theory and experiment is a systematic bias in the experimental data engendered by the genome mapping method used to acquire the data. Explicitly, the DNA in the experimental dataset26 were obtained from Escherichia coli cells, labeled in a sequence-specific manner using a nicking enzyme, and then injected into the nanochannel device.19 In order to identify the genomic distance (in kilobase pairs, kbp) between two labels on a given DNA molecule, the label pattern of that molecule needs to be mapped to the reference genome for E. coli to identify the underlying sequence and, thus, the molecular distance.26 In our previous experiments, around 25%–35% of the molecules in a dataset that passed the thresholds of length ≥50 kbp and number of labels ≥5 did not align to the reference.26 DNA molecules that did not map to the reference were not included in the probability distribution. While many of the unmapped molecules arise from the high variability of the E. coli genome, molecules with the correct sequence that cannot be mapped may be due to hairpin folds, which would introduce a systematic bias that cannot be easily resolved using a genome mapping approach. In addition, the spectrum of GC content in the DNA sample may have also confounded the analysis,27 although this is not expected to be a significant factor for reasonably large separations between nick labels.23
To address these potential concerns about systematic errors in prior experimental work,26 we have undertaken a new experiment described in Sec. IV to attenuate all of these experimental artifacts. Explicitly, we repeated the experiments of Reinhart et al.26 using a single DNA sample, λ-phage DNA, without mapping to any reference so as to include all the data points for intact, non-overlapping DNA. Our experiments also probed the extension of DNA at a ratio D/lp = 0.62 and a concomitant value of α = 88.3. This ratio of D/lp is even closer to the Odijk regime than previous experiments,26 which only achieved a ratio down to D/lp = 0.70. Comparing the experimental data to the asymptotic solution of the telegraph model24 reveals that the discrepancy between theory and experiment continues to increase as D/lp decreases, underscoring the conclusions of the previous analysis24 and ruling out the systematic errors arising in the genome mapping approach26 on the qualitative conclusions of that analysis. We posit in Sec. V that the long-range effects of DNA-wall electrostatic interactions, which are not included in any of the theories for channel-confined polymers, are the source of the disagreement between the theory and experiment.
II. THEORY
The one-dimensional telegraph process describes a persistent random walk, where a particle moves with a fixed velocity on a line for some time T, randomly changing directions with a rate r. The weakly correlated telegraph process adds a small penalty ε for revisiting the same position along the walk, thereby penalizing frequent changes in direction. Werner et al.17 showed how the problem of a channel confined DNA molecule can be mapped onto the weakly correlated telegraph model in the limit of weak excluded volume interactions, i.e., for . The correspondence between the decay in velocity autocorrelation for the telegraph process and the decay in orientational correlations for an confined ideal wormlike chain provides the first step in the mapping, wherein is replaced by the average orientation a between the ideal polymer backbone and the channel axis and (2r)−1 is replaced by the global persistence length g, the latter describing the typical distance between hairpin turns in the absence of excluded volume interactions.28 Excluded volume appears in the penalty ε for overlapping segments of the confined polymer at a given position within the channel.17 Importantly, the trio of parameters (a, g, ε) describing the confined polymer problem can all be obtained from simulations of ideal, confined wormlike chains.17 The total time of the walk, T, corresponds to the contour length of the polymer, L.
Dimensional analysis of the telegraph model reveals that its parameters can only be combined into a single dimensionless number17
| (1) |
representing the typical number of overlaps per hairpin turn. The same scaling parameter was obtained by Chen18 via analysis of the self-consistent field equation description for a confined wormlike chain. The parameters appearing in Eq. (1) have been computed by Werner et al.17 over the range of channel sizes relevant to DNA confinement; one can readily map the primitive variables (lp, , D) describing the confined polymer problem to the telegraph model parameters via interpolation of the data in Ref. 17.
The region of the phase space immediately proximate to the Odijk regime corresponds to small channels, α ≫ 1, but long chains, L ≫ g; the crossover into the Odijk regime takes place when L ≪ g and α ≫ 1 such that there are no hairpin turns in the small channel. In the dual asymptotic limit α ≫ 1 and L ≫ g, the telegraph model can be solved.24 The leading order probability distribution for the chain extension is24
| (2) |
where is the normalization factor, X′ = X/(aL), and the action is
| (3) |
The predictions of Eq. (2) are in excellent agreement with numerical simulations of the weakly correlated telegraph process,24 verifying the asymptotic solution of the model.
The telegraph model treats the alignment of the polymer with the channel axis in a mean-field manner through the average alignment a between the polymer backbone and the channel axis and thus does not include the alignment fluctuations that are present in the Odijk regime.3,5 As the channel size decreases, the Odijk fluctuations become increasingly significant and eventually overwhelm the rapidly decreasing magnitude of the extension fluctuations due to hairpin formation at large values of α.17 To account for the Odijk fluctuations, Ödman et al.24 proposed augmenting the telegraph model with the Odijk regime fluctuations via the probability distribution
| (4) |
where
| (5) |
is a Gaussian with variance σ0.
In their comparison with experimental data,26 Ödman et al.24 treated σ0 as an adjustable parameter. In principle, we would anticipate that σ0 would be the variance in extension in the Odijk regime
| (6) |
obtained by Burkhardt et al. for a wormlike chain confined to a square channel.5 We have recently demonstrated25 that Eqs. (4)–(6) provide excellent agreement with pruned-enriched Rosenbluth (PERM) method simulations of confined wormlike chains. Indeed, we found that Eq. (4) captures simulation data down to α ≈ 0.3, well below the asymptotic limit α ≫ 1.
III. COMPARISON TO EXPERIMENTAL DATA FOR E. COLI
We begin our analysis of the telegraph model by comparing its predictions to a set of extension measurement distributions produced by Reinhart et al.26 for the MG1655 E. coli strain in five channel sizes, ranging from 40 nm to 51 nm, in a research-grade version of the Bionano Genomics Irys genome mapping system.19 The image data acquired in this system are similar to that in Fig. 2, which provides a representative image obtained using the approach described in Sec. IV A. The channel sizes used by Reinhart et al.26 were close to the DNA persistence length of 52 nm expected for the 0.5× TBE buffer used in those experiments, which has an ionic strength of 103 mM due to residual chemicals used for the nick-labeling reaction that remained in the running buffer.29 For each molecule, they extracted each section that contained at least 5 contiguous labels that were perfect matches to the reference genome; this region could include the entire molecule. The images provided measurements of the extension X (in nanometers), while the maps to the reference genome provided the corresponding contour lengths L (in base pairs, bp). A given molecule can contribute many measurements to the total data set, since they contain multiple labels.26,27 For comparison to the theory, we assume a conversion of 0.34 nm per base pair due to the low YOYO dye loading (1 dye molecule per 37 bp) used in the experiments. The probability distribution histograms for the experimental extension data used bin sizes of L = 250 bp for the separation between nick labels on the DNA to minimize the impact of errors in fluorophore localization on the measured the distance X between the labels. The minimum distance between labels was set to 2500 bp, to remove effects of the diffraction-limited optics on label resolution.30 Depending on the channel size, these experiments involved between 1839 and 9598 molecules, producing between 8.7 × 104 and 8.0 × 105 measurements of the extension X between label pairs. This data density is sufficient to produce histograms of X − ⟨X⟩ for a particular bin in L, where ⟨X⟩ is the average extension for label pairs within that bin.
FIG. 2.
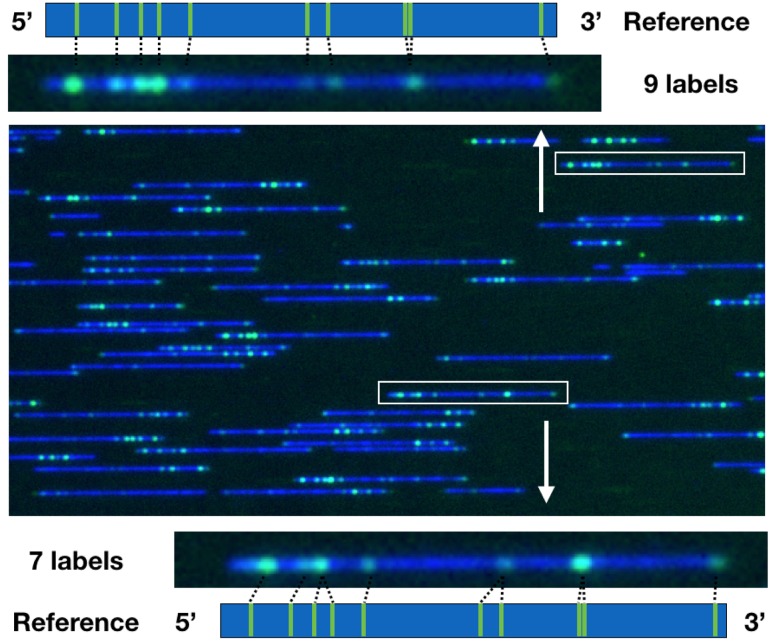
Composite, false-color image of λ-DNA molecules with backbone (blue) and the Nt.BspQI nick sites (green) obtained in 34 nm nanochannels. The representative λ-DNA molecules (in the white rectangular boxes) have 9 (upper panel) and 7 (bottom panel) resolvable labels, respectively. The distances between the nearest pairs of labels are measured and compared to the reference. A detailed discussion on filtering data for contour length and the correlation coefficient between the image and the reference is provided in Sec. IV A.
In their comparison of the telegraph model to experimental data, Ödman et al.24 selected two representative values of the contour length between separations, L = 28 125 bp and 53 125 bp, for both the smallest (40 nm) and largest (51 nm) channel sizes. The variance σ0 appearing in Eq. (5) was treated as an adjustable parameter to fit the right tail of the distribution, with the fitted value of σ0 being approximately twice that given by Eq. (6).24 For the effective channel size, Ödman et al. considered first the typical approximation7
| (7) |
where D is the physical channel size and is the Stigter effective width,20 which is 5.6 nm for the experimental conditions.29 For the experimental data in the 51 nm channel,26 the fitted value of σ0 led to excellent qualitative agreement between the theory and experiment. However, there was a significant discrepancy in the left tail for the 40 nm channel,24 which is evident in Fig. 1. Ödman et al. noted that this discrepancy is attenuated (but not eliminated) by assuming an effective channel size that is 2 nm larger than that computed by Eq. (7), and attributed the discrepancy to uncertainties in the actual channel size available to the channel. We will return to this issue in Sec. V.
The analysis by Ödman et al.24 suggests there may be a negative correlation for the agreement between theory and channel size, but this tentative conclusion rests on the analysis of only four data points and a qualitative analysis of the data. To provide a firm foundation for their conclusion, we have reanalyzed the entire dataset from Reinhart et al.,26 and a trio of statistical tests25 were applied to quantify the extent of the discrepancies between theory and experiment for each channel size.
Our analysis follows the approach of Ödman et al.,24 using Eqs. (4) and (5) to model the extension distribution and treating σ0 in Eq. (5) as an adjustable parameter. Table I provides the relevant experimental parameters and the corresponding telegraph parameter values needed to evaluate Eqs. (2) and (3). The fitted value of σ0, required for Eq. (4), was determined by fitting the right tail of distribution to the experimental data. These fitting parameters were obtained separately for each channel size D and each bin in L and appear in Fig. S4 of the supplementary material. The three smallest channels are fit by σ0 ≈ 1.5σOdijk, while the fitting to the two largest channels uses σ0 ≈ 2.5σOdijk. Inspired by the prior analysis, we used a 2 nm augmentation to the effective channel size in Eq. (7), allowing us to compare the full distributions to the best case scenario in Ref. 24.
TABLE I.
Telegraph model parameters for the channel sizes appearing in the experimental data from Reinhart et al.26 The DNA persistence length is lp = 52 nm and the effective width is = 5.6 nm. The effective channel size is 2 nm greater than that computed from Eq. (7) to mimic the best-case scenario of Ödman et al.24 The alignment of the DNA backbone with the channel axis, a, the global persistence length, g, and the scaling parameter, α, were obtained by interpolation to the simulation data of Werner et al.17
| D (nm) | Deff (nm) | a | g (nm) | α |
|---|---|---|---|---|
| 40 | 36.4 | 0.84 | 884 | 8.40 |
| 42 | 38.4 | 0.84 | 700 | 6.15 |
| 43 | 39.7 | 0.84 | 656 | 5.32 |
| 49 | 45.4 | 0.82 | 385 | 2.53 |
| 51 | 47.4 | 0.81 | 363 | 0.81 |
Figure 3 provides the comparison between theory and experiment26 over a wide range of contour lengths for the 40 nm channel and 51 nm channel considered previously by Ödman et al.24 The data obtained in the 42 nm, 43 nm, and 49 nm channels appear in Figs. S1–S3 of the supplementary material. Figure 3 confirms that the qualitative conclusions obtained by Ödman et al.24 for two values of L persist for the entire dataset. For the 51 nm channel [Figs. 3(c) and 3(d)], the experimental data and theoretical predictions are in excellent agreement, with the main difference being the smoothness of the theoretical result, which is obtained from numerical quadrature, when compared to the experimental data, which have significant pixelation due to the limited sampling in the tails of the distribution. In contrast, the 40 nm channel data [Figs. 3(a) and 3(b)] exhibit the significant discrepancy in the tails identified previously,24 which we now see for all values of L.
FIG. 3.
Comparison between the predictions of the telegraph model in Eq. (4) and the experimental data of Reinhart et al.26 for (a) D = 40 nm, experiment; (b) D = 40 nm, theory; (c) D = 51 nm, experiment; and (d) D = 51 nm, theory. Panels (a) and (c) reproduced with permission from Reinhart et al., J. Chem. Phys. 142, 064902 (2015). Copyright 2015 AIP Publishing LLC.
To quantify the degree of agreement between the theoretical and experimental distributions, we used three statistical tests in accordance with our previous work comparing simulations of confined, wormlike chains to the telegraph model.25 These tests require first converting the probability density functions for each horizontal slice in Fig. 3, which corresponds to the bin size at a fixed value of L, into cumulative density functions (CDFs), which are bounded on the interval [0, 1]. The first test computes the root-mean-square (rms) error between the experimental CDF and the theoretical CDF. The other two tests use an empirical distribution goodness of fit:31 (i) the Cramér-von Mises criterion, which provides uniform weighting to the data, and (ii) the Anderson-Darling criterion, which gives more weight in the test to the tails of the distribution. This procedure was repeated for the additional heat maps provided in Figs. S1–S3 of the supplementary material.
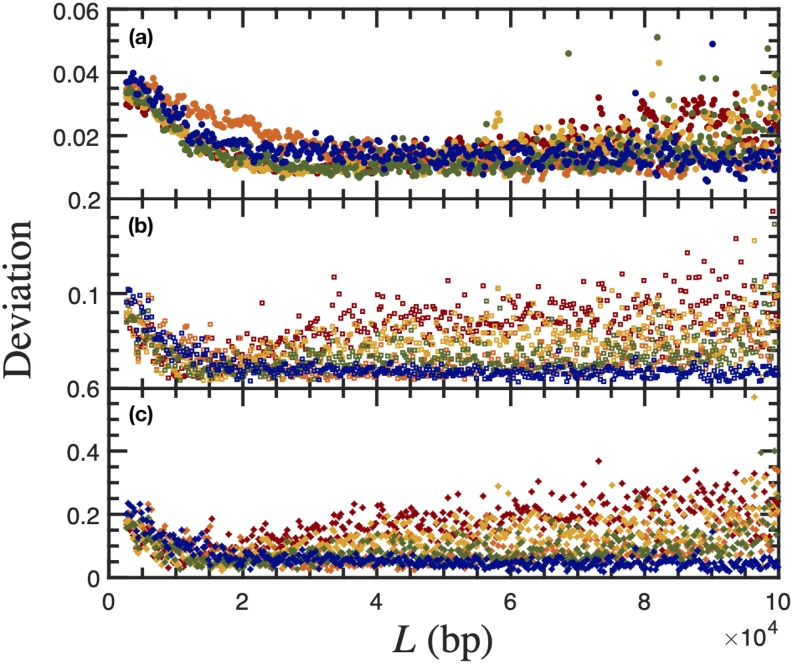
Figure 4 provides the results of the statistical tests as a function of contour length. The absolute values of the deviations measured by these statistical tests increase with the emphasis that the test puts on the tails of the distribution; the rms error in Fig. 4(a) is dominated by the central portion of the data, the Cramér-von Mises criterion in Fig. 4(b) incorporates information throughout the distribution with a uniform weight, and the Anderson-Darling criterion in Fig. 4(c) puts particular emphasis on the tails of the distribution. The overall trends revealed by these statistics are consistent, with the exception of the anomalously low values in the 42 nm channel. Figure S1 of the supplementary material shows that the extension distribution for the 42 nm channels is narrower than anticipated, consistent with previous observations about that particular dataset.26
FIG. 4.
The result of statistical tests for quantifying the degree of agreement between theory and experiments: (a) the rms error, (b) the Cramér-von Mises criterion, and (c) the Anderson-Darling criterion. Statistical data were obtained for 40 nm (red), 42 nm (orange), 43 nm (yellow), 49 nm (green), and 51 nm (blue) nanochannels using the probability distributions in Fig. 3 and Figs. S1–S3 of the supplementary material.
All of the data exhibit an initial decrease in the deviation with increasing contour length. We attribute this trend to the asymptotic nature of the solution to the telegraph model; the chain needs to be sufficiently long to form hairpin bends (L ≫ g), which is not satisfied for the shortest contour lengths. In general, this initial transient in the deviation as a function of the contour length decays at a label separation of approximately 20 kbp, supporting the smaller value of the contour length selected by Ödman et al.24
The main goal of our reanalysis of the experimental data26 with the telegraph model24 is to determine how the deviation between the theory and experiment depends on the channel size. Figure 5 provides the results obtained using each metric (rms error, Cramér-von Mises, and Anderson-Darling) as a function of channel size, where we have averaged the results in Fig. 4 from L = 20 kbp to L = 80 kbp to remove the aforementioned artifacts that arise at small and large molecular weights. The trends in Fig. 5 are consistent with the conclusions drawn by Ödman et al.24 from their analysis of a limited dataset: the deviation between experiment and theory increases with decreasing channel size, with the exception of the 42 nm channels. As noted in the context of Fig. 4, the magnitude of the deviations for the different statistical tests reflects their emphasis on the tails of the distribution, which is strongest for the Anderson-Darling test and weakest for the rms error.
FIG. 5.
The result of statistical tests as a function of channel size by averaging the results in Fig. 4 from L = 20 kbp to L = 80 kbp for quantifying the degree of agreement between theory and experiments: the rms error (red), the Cramér-von Mises criterion (yellow), and the Anderson-Darling criterion (blue). The boxes span from 25% to 75% of the data, with the lines indicating the median value. For the comparison between theory and simulation, the dashed line alternating between red and yellow indicates the value of 0.02 which was obtained by the rms error and Cramér-von Mises criterion; the blue dashed line is at the value of 0.07 obtained by the Anderson-Darling criterion.25
It can be challenging to readily interpret the magnitude of the deviations in Fig. 5 without a familiarity with these types of measurements. By way of comparison, we recall that the plots of the CDFs obtained from our recent simulations of confined wormlike chains25 were almost indistinguishable from the telegraph model CDFs for large values of α. The corresponding values of the statistical criteria for α > 1 were approximately 0.07 for the Anderson-Darling criterion (blue dashed line in Fig. 5) and 0.02 for both the rms error and the Cramér-von Mises criterion (dashed line alternating between red and yellow in Fig. 5). Figure 5 indicates that the deviations for the wider channels (49 nm and 51 nm) are similar to those obtained for comparisons between theory and simulation,25 but the deviations from the Cramér-von Mises criterion and the Anderson-Darling criterion are substantially higher for experiments than simulation as the channel size decreases. The rms error deviation remains roughly constant with the channel size, indicating that the theory does an adequate job in capturing the central portion of the probability distribution, which dominates the rms error.
It is important to note that the comparison between experiment and the telegraph theory leading to Fig. 5 allows σ0 to be a fitting parameter. Had we required the theoretical calculations to use the Odijk theory result in Eq. (6), which was the case in the comparison between simulation and theory,25 the deviations between experiment and theory would increase further.
IV. COMPARISON TO EXPERIMENTAL DATA FOR -DNA
Our reanalysis of the experimental data from Reinhart et al.,26 most notably the statistical tests in Fig. 5, suggest an increasing discrepancy between theory and experiment as the channel size decreases. However, one concern about the genome mapping approach used previously26 is that it requires mapping the labeled DNA back to the reference genome to obtain their contour length. Some molecules do not align to the reference genome, around 25%–35% of the molecules in a dataset. In cases where the lack of alignment is due to incomplete nick labeling or changes in the host genome, excluding these molecules does not impact our physical measurements. However, molecules that do not align for physical reasons, in particular, significant backfolding, are excluded from the final dataset. This is unlikely to be the source of the discrepancy, since we would expect the exclusion of such molecules to lead to the theory overestimating the left tail of the extension distribution; this is opposite to the behavior shown by Ödman et al.24 and the results in Figs. 3(a) and 3(b).
To rule out the confounding effects due to mapping to the reference genome to obtain the value of L, this section describes a new experiment using λ-DNA (48.5 kbp) as the model polymer. These experiments also took advantage of (i) an experimental protocol that removes the labeling chemicals prior to injection into the nanochannel,32,33 allowing us to lower the ionic strength to 48 mM and a corresponding persistence length21 of lp = 54.9 nm, and (ii) the Bionano Genomics Saphyr chip, which lowered the channel size to D = 34 nm while retaining the high-throughput required to obtain the tails of the extension probability densities.26 The latter channel size is similar to the 30 nm × 40 nm lower bound in the classic experiment by Reisner et al.,12 thereby probing a very low value D/lp = 0.62. If we adopt Eq. (7) as the approximation for the effective channel size and use the DNA effective width = 7.6 nm predicted by Stigter’s theory,20 the effective channel size is Deff = 26.4 nm and the ratio Deff/lp = 0.48 is considerably smaller than unity. We will examine the validity of this effective channel size in Sec. V.
A. Experimental method
λ-DNA (48.5 kbp, New England Biolabs) was labeled at the 5′-GCTCTTC-3 site using the nicking, labeling, repairing, and staining (NLRS) protocol.32,33 Briefly, the λ-DNA were nicked with the nicking enzyme Nt.BspQI, labeled by inserting a cy3-like fluorophore during the labeling step, repaired using Taq ligase, and stained by YOYO-1 at a dye to base pair ratio of 1:37. Drop dialysis with Tris-EDTA (TE) buffer was applied to remove the extra reagents in the previous steps and the DNA was suspended in the Bionano Genomics running buffer, which has an ionic strength of 48 mM. The experiment was conducted with a Bionano Genomics Saphyr chip, which contains an array of 34 nm wide nanochannels. The error in the nanochannel width is estimated as ±2.5 nm.23 The labeled molecules were driven into nanochannels by an electrokinetic system and then sequentially excited by a sapphire green laser (532 nm, 300 mW, Coherent) and an OBIS blue laser (488 nm, 300 mW, Coherent) to image the DNA backbone and nick labels, respectively, on a research-grade version of the Bionano Genomics Saphyr system. Figure 2 shows a typical false-color image from the experiment, with blue and green channels combined.
The acquired image stack includes a total of 1 241 907 molecules. The images were analyzed by Bionano Genomics’s image processing algorithm (available from Bionano Genomics) to identify the DNA molecules, measure the extension of their backbone (blue laser) along the channel axis, and measure the distance between nick sites (green laser). Owing to its use for genome mapping, the image processing algorithm reports its output in units of base pairs. The program output was converted to physical distances using the conversions 366 bp = 1 pixel for the algorithm, which is a built-in conversion factor in the code, and 1 pixel = 0.1083 µm for the microscope optics.
There exist a number of experimental challenges when using the high-throughput data obtained by this method for physical measurements, such as incomplete dye labeling, shear fragmentation and photocleavage of the DNA, and overlapping molecules, since the images are acquired without the typical low-throughput approach of screening the field of view to confirm that the molecules appear to be intact and labeled. These are not significant issues for the practice of genome mapping,19 since producing a consensus genome map essentially averages over the data. Since we are interested in analyzing the tails of the extension distribution, which involve the rare events, we need to ensure that we only analyzed intact, isolated λ-DNA molecules. To this end, we adopted the conservative approach of analyzing the extension distribution between the most distant pair of nick sites of λ-DNA, rather than the extension of the entire molecule, to ensure that the region between these nick sites (45 315 bp far apart) was intact. We also adopted a set of three filters that attenuate the effects of systematic errors in the dataset.
In the first filtering step, we confirmed that the molecule has the correct number of labels. The λ-DNA genome has ten 5′-GCTCTTC-3′ nick sites, illustrated in Fig. 6. However, proximate nick sites can merge into a single, diffraction-limited label if the distance between pairs of nick sites is less than 1500–2500 base pairs. This is always the case for the 8th and 9th nick sites, which are only separated by 473 bp. It is also possible that small hairpins can lead to a collapse of the other label pairs indicated in Fig. 6. As a consequence, an image of a completely labeled molecules will have between 7 and 9 resolvable labels. Figure 2 shows two representative molecules with 9 (upper panel) and 7 (bottom panel) resolvable labels, respectively. Requiring that all molecules meet this condition reduced the dataset to 612 121 molecules.
FIG. 6.
Scheme of λ-DNA reference with (a) the locations of all the nick sites counted from the 5′ end and the distance between every nearest pairs of nick sites and (b) a schematic molecule that illustrates the diffraction-limited spots. Due to the diffraction-limited optics, proximate nick sites can merge into a single label if the distance between pairs of nick sites is less than 1500–2500 bp. The pair of nick sites that always appear as a single label are labeled in red (the case of 8th and 9th nick sites); the nick sites that may be a single label due to fluctuations are labeled in yellow; all other resolvable nick sites are labeled in green.
In the second filtering step, we required that molecules have a backbone extension L between 14.0 µm and 16.5 µm. The latter value corresponds to fully extended λ-DNA. The former value corresponds to the distance between the first and last nick points if the molecule were stretched to the 91.2% extent predicted by Odijk’s theory,2,5 which is a robust lower bound since there is additional DNA on both sides of those nick sites. To ensure that our key conclusions are not affected by the choices for these upper and lower bounds, the supplementary material provides a sensitivity analysis to the parameter selection. This additional length filter reduced the total size of the dataset to 509 070 molecules.
Additional experimental artifacts can arise from small DNA fragments that become adsorbed to the walls and are imaged along with the free molecules, proximate DNA fragments within the channel that are erroneously identified as a single molecule,34 and free dye molecules.35 To attenuate these effects, the third filtering step checked that the labeling pattern on the DNA was consistent with the expected pattern for λ-DNA. While the scoring methods used in genome mapping could be used here, analogous to previous work,27,34 we chose to adopt a different approach that was tailored to the particular details of the reference λ-DNA pattern in Fig. 6 that can accommodate readily the diffraction-limited spots. For molecules with 9 labels, we computed the correlation coefficient between the measured distance between labels and the reference. For molecules with 8 labels, the same calculation was performed for all possible 8-label combinations of Fig. 6; the calculation for molecules with 7 labels used all possible 7-label combinations. In all cases, we considered both the patterns produced by Fig. 6 and their inverse, since the 5′-3′ orientation of the DNA within the nanochannel is not known. For completeness, all of these possible patterns are included in Fig. S5 of the supplementary material. We then selected the highest correlation obtained from all of the calculations for that molecule. Only those molecules whose largest correlation coefficient exceeded a cutoff of 0.98 were included for further analysis. This value was selected by first simulating 104 patterns by randomly selecting locations within the simulated molecule to insert a hairpin using the frequency and hairpin size predicted by Ödman et al. using the telegraph model.24 Simulated label locations below 1500 bp were assumed to merge into a single label, and simulated label locations between 1500 and 2500 bp were merged into single labels by selecting a uniformly distributed random variable between those two limits for each molecule and merging labels that were separated less than that value. The correlation coefficients for these simulated data with the reference produced the lowest value of 0.98. This final filter reduced the dataset to 166 340 molecules for analysis. Compared to the molecules left from the previous filtering step, around 67% molecules were removed in the last correlation coefficient filter. More data points could be included by lowering the cutoff of correlation coefficient, and the corresponding sensitivity analysis to the choice of the cutoff value is provided in the supplementary material. Inasmuch as the result from the sensitivity analysis in the supplementary material shows that the adjustment would only broaden the extension distribution and make our conclusion more significant, here we used the final dataset, 166 340 molecules, with the strictest cutoff setting for further discussion.
B. Results
The comparison of the experimental data with the telegraph model requires selecting an appropriate channel size Deff. We have considered the three possible cases listed in Table II. The typical approximation7 given by Eq. (7) furnishes Deff = 26.4 nm for a physical channel size D = 34 nm and the effective width = 7.6 nm at this ionic strength. We also considered the case where we neglect the long-ranged DNA-wall excluded volume interactions using the most likely channel size, corresponding to Deff = 34 nm, and the same assumption using the upper bound in the estimate for the channel size,23 Deff = 36.5 nm. We chose to examine the latter value to provide the most favorable possible comparison between the theory and experiment, as we know from prior work24 that the theory comes closer to the experimental data26 by increasing Deff. Nevertheless, if the overall modeling approach is applicable, we would expect the channel size Deff = 26.4 nm to be the best estimate based on the success of this approach in modeling DNA confinement in larger channels.7,36–38
TABLE II.
Telegraph model parameters for the channel sizes appearing in the experimental data obtained from λ-DNA in a D = 34 nm channel. The DNA persistence length is lp = 54.9 nm and the effective width is = 7.6 nm. The effective channel sizes considered are the estimated physical channel size (34 nm), the upper bound in the physical channel size (36.5 nm), and the approximation in Eq. (7). The alignment of the DNA backbone with the channel axis, a, the global persistence length, g, and the scaling parameter, α, were obtained by interpolation to the data of Werner et al.17 The values of σOdijk are calculated using Eq. (6). The value σ0 = 199 nm is the best-fit parameter to capture the right tail of the distribution and independent of the choice of Deff.
| Deff (nm) | a | g (nm) | α | σOdijk (nm) |
|---|---|---|---|---|
| 26.4 | 0.88 | 4436 | 88.3 | 43.2 |
| 34.0 | 0.85 | 1289 | 16.3 | 55.7 |
| 36.5 | 0.85 | 973 | 10.6 | 59.8 |
Figure 7 compares the predictions of the telegraph model to the experimental data for each of the values of Deff in Table II, using the telegraph model parameters in Table II. The dotted lines treat the alignment fluctuations using the Odijk variance σOdijk in Eq. (6), while the solid lines use the best-fit value σ0 = 199 following the approach used by Ödman et al.24 and our own analysis in Sec. III. We also provide a comparison between experiment and theory using the correction σ0 = 2σOdijk proposed by Ödman et al.24 in Fig. S8 of the supplementary material. Table III provides the statistical tests for comparison to the λ-DNA experiments.
FIG. 7.
Comparison between the predictions of telegraph model with σ0 = σOdijk (dotted lines) and the best fit for σ (solid lines) and the experimental data of λ-DNA (blue circles). The theoretical distributions were modeled at Deff = 36.5 nm (red), Deff = 34 nm (yellow), and Deff = 26.4 nm (green) nanochannels using the parameter values in Table II.
TABLE III.
Results of the statistical tests for the data in Fig. 7 and Fig. S8 of the supplementary material.
| σ0 = σOdijk | σ0 = 2σOdijk | Best fit σ0 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Deff (nm) | 26.4 | 34.0 | 36.5 | 26.4 | 34.0 | 36.5 | 26.4 | 34.0 | 36.5 |
| rms error | 0.10 | 0.093 | 0.090 | 0.083 | 0.069 | 0.065 | 0.040 | 0.040 | 0.040 |
| Cramér-von Mises | 0.22 | 0.19 | 0.198 | 0.16 | 0.12 | 0.11 | 0.039 | 0.037 | 0.036 |
| Anderson-Darling | 1.33 | 1.00 | 0.90 | 0.72 | 0.48 | 0.41 | 0.12 | 0.12 | 0.11 |
The disagreement between theory and experiment in the λ-DNA experiments is even more prominent for this small channel than we observed for the E. coli sample in the larger channels. These results indicate that the trend of increasing deviation with decreasing channel size is robust to the methodology, not an artifact of the genome mapping approach used previously.26 The shortcomings in the model are especially apparent when the Odijk variance is used to model the alignment fluctuations; the theory describes neither the right nor left tails.
Allowing the variance σ0 to be an adjustable parameter alleviates the problem somewhat by broadening the predicted distribution to better reflect the experimental results. However, there are two notable issues with this semiempirical approach. First, treating σ0 as a fitting parameter becomes less effective as the channel size decreases. We have already noted this effect in the context of Fig. 5, with the statistical measures of the deviation increasing with decreasing channel size. Comparing those results for E. coli DNA to Table III reveals a continued increase in the deviation between experiments and theory for the 34 nm channel, even when we make the questionable approximation of allowing the DNA to occupy the entire channel cross section. Second, the deviation between the best-fit value of σ0 and that predicted for the Odijk regime5 is increasing with decreasing channel size. The best-fit values of σ0 used by Ödman et al.24 were typically a factor of two larger than the Odijk theory for their limited analysis, and our analysis of the entire dataset (see Fig. S4 of the supplementary material) suggests this is a reasonable approximation. In contrast, Table III indicates that capturing qualitatively the experimental distribution for D = 34 nm required using a five-fold increase in the variance with respect to the Odijk theory. While combining the telegraph model with a fitted variance due to alignment fluctuations may provide a functional description of the experimental data, the inability to predict the required value of σ0—and the significant and growing deviations between the best-fit value and the Odijk theory with decreasing channel sizes—limits the predictive value of the model.
A possible source of the discrepancy between the theory and experiment lies in the parameters used to filter the outliers (incomplete labeling, fragmented molecules) in the dataset. We have taken a rather conservative approach to the filtering, as indicated by the attrition between the original dataset and those molecules that were deemed to be intact, λ-DNA. The supplementary material provides a sensitivity analysis to the parameter selection of the cutoff values for the length filter and the correlation coefficient filter. This additional analysis indicates that the disagreement between the theory and the experiment was unaffected by having a stricter restriction on the length filter. The disagreement becomes more prominent when lowering the cutoff values of correlation coefficient, which broadened the experimental distribution by including molecules that were previously excluded due to poor alignment. We thus conclude that our analysis is robust to the particular parameters choices used to filter the data.
V. DISCUSSION
It is clear from the analysis of our experimental data for E. coli DNA26 and λ-DNA that the agreement between the predictions of the telegraph model and the data becomes worse as the channel size decreases. The salient question is then whether the problem lies in the telegraph model itself or the applicability of this particular model to the experimental data. Since we have shown elsewhere25 that the predictions of Eq. (4) are in very close agreement with simulation data for a discrete wormlike chain model, it appears that the problem lies in the applicability of the this physical model to describe the experimental scenario.
The most likely shortcoming in the models used to describe DNA in nanochannel confinement is that these models1,4,17,18 are derived for a neutral polymer confined between hard walls. Using such models to interpret experimental data for DNA is predicated on the assumption that the confined polyelectrolyte physics can be mapped to an equivalent neutral polymer. The persistence length lp21,39,40 and DNA effective width 20 are mapped using polyelectrolyte theory for unconfined polymers. The challenge lies in the DNA-wall interactions, which are conventionally handled by defining an effective channel size Deff < D that accounts for the repulsion of the DNA from the walls.7,22
Let us consider, in the context of a relatively simple model, the extent to which DNA-wall electrostatic interactions are expected to affect the extension of DNA in a nanochannel. In this context, it is convenient to consider what happens in the Odijk regime, where the excluded volume effects are negligible. Following the notation of Chen,41 the Hamiltonian for a wormlike chain in an external potential is
| (8) |
where r is the spatial position within the channel, u is the (dimensionless) tangent vector to the backbone chain, t ∈ [0, 1] is the fractional distance along the polymer backbone, and kBT is the Boltzmann factor. The potential U[r(t), u(t)] is defined per unit length such that integration over t provides the total external energy for the chain. The propagator q(r, u; t) corresponding to Eq. (8) satisfies the modified diffusion equation41
| (9) |
The Odijk theory can be derived3 from the case of a neutral polymer interacting with hard walls, where the propagator satisfies
| (10) |
subject to appropriate boundary conditions on the hard walls.41 At the scaling level,3,42 using r ∼ D and balancing the two terms in the operator of Eq. (10) reveals that . The time in the propagator is then t ∼ λ/L, where
| (11) |
is the Odijk deflection length.2 Determining the extension of the chain requires computing the thermal fluctuations for an almost completely stretched chain2,5
| (12) |
The scaling leads to the well-known result2
| (13) |
The prefactor A can be obtained by solving Eq. (10) using ground-state dominance and appropriate boundary conditions for a hard wall.41,42 Alternatively, one can convert the problem into an accelerated particle model3,5 or simulate an ideal wormlike chain using a particle-based model.43 These different approaches all yield very similar results;41 we have typically invoked the result A = 0.182 74 obtained by Burkhardt et al.5 for square channels.
Now let us consider the case where there is a potential that governs the polymer-wall interactions, in excess of the infinite energy penalty associated with penetrating a hard wall. It proves convenient here to recast Eq. (9) into a dimensionless form. Following the preceding analysis, we define a dimensionless position , scaled tangent vector , and dimensionless time . Let us further write the dimensionless interaction potential ϕ(r, u) = U(r, u)/U0, where U0 is the maximum value of U. The dimensionless form of Eq. (9) is
| (14) |
where
| (15) |
is the polymer-wall interaction energy per deflection segment.
We would expect to recover the Odijk statistics from Eq. (14) in the limit β ≪ 1, independent of the particular form of ϕ(r, u). In this case, the polymer-wall interactions would represent a small correction, on par with other approximations in the Odijk theory.2 We would also expect to recover Eq. (13) for cases where the function ϕ(r, u) attenuates sufficiently fast such that βϕ(r, u) is sensible only in a thin boundary layer near the wall. In this case, it is convenient to define an effective channel size similar to Eq. (7) that approximates the exclusion of the DNA from the region immediately proximate to the wall, which is the standard approach for accounting for DNA-wall interactions when analyzing experimental data.7,22,23
For our purposes, we need to determine whether βϕ(r, u) is sufficiently attenuated at the experimental conditions used here (D = 34 nm, I = 48 mM). From Dobrynin’s theory,21 the persistence length is lp = 55 nm and the corresponding deflection segment length from Eq. (11) is λ = 40 nm. For the DNA-wall interaction energy, we adopt the simple model of a DNA segment of effective charge density νeff moving in an electrostatic potential ψ(z) = Ψwalle−κz created by the channel walls22
| (16) |
where z is the distance measured perpendicular to the surface of the wall. In the latter, the Debye length is
| (17) |
with ϵ0 being the permittivity of free space, ϵb = 80 is the dielectric constant of the buffer, NA is Avogadro’s number, and I is the ionic strength of the buffer. For our conditions, the Debye length is κ−1 = 1.4 nm. This model assumes, inter alia, that the electrostatic problem is one-dimensional. If the Odijk theory can be applied, this assumption will be reasonable since the DNA-wall interactions will be sensible only within a thin layer near the wall, which can be approximated as a flat interface without a significant contribution from the corners.
Both the effective charge of the DNA and the surface potential are affected by the ionic strength of the buffer. For νeff, we use the approach Stigter20 developed in the context of computing the effective width of DNA,
| (18) |
For a given ionic strength, νeff is computed numerically by matching the far-field solution of the Guoy-Chapman model for a charged cylinder of charge density ν to the far-field solution of the Debye-Hückel model for a charged cylinder of charge density νeff.44 Numerical data are available11 for as a function of ionic strength, which can be readily inverted into data for νeff via Eq. (18). For our experimental conditions, νeff = 4.2 e/nm.
For Ψwall, we need to compute the ζ potential of the surface,22
| (19) |
The ζ potential for fused silica can be obtained from the model of Behrens and Grier,45 which involves the simultaneous solution for the ζ potential,
| (20) |
and the surface charge density,
| (21) |
where pH = 8.6 is the typical buffer condition,23 and, for silica and glass, pK = 7.5 is the dissociation constant,46 C = 2.9 F/m2 is the Stern layer capacitance,46 and Γ = 8 nm−2 is the surface density of ionizable groups.47 The resulting wall potential is −77 mV.
Combining the estimates for λ and U0/L = νeffΨwall leads to β = 500. Clearly, one cannot completely ignore the wall-interaction term in Eq. (9). This conclusion agrees with intuition. DNA is a highly charged object and, in these buffer conditions, silica is also highly charged and repulsive for the DNA; any attempt to bring the DNA into contact with the wall is going to be strongly repelled.
The more relevant question is the length scale for the DNA-wall interactions. If the DNA-wall effect is short-ranged, then one still might expect to observe Odijk statistics for DNA in a nanochannel, albeit with an effective channel size that is somewhat smaller than the actual channel due to the local repulsion. Unfortunately, we find that the magnitude of the wall interaction term, βϕ, only decays to the relatively small value βϕ ≈ 0.1 after 8.5 Debye lengths. For our experiments, this decay length corresponds to z* = 12 nm away from the wall, a substantial fraction of the 17 nm half-width of the channel. It seems implausible that such a long-ranged interaction can be accurately captured by defining an effective channel size Deff = 10 nm.
It is worthwhile to consider whether the conclusions drawn for our particular experimental system (D = 34 nm, I = 48 nm) hold for other experimental systems that are proximate to the Odijk regime. Figure 8 provides data for the dimensionless wall interaction parameter β and the position z* where the wall interaction energy βϕ(z) decays to 0.1 kBT. The solid black curve extends the results for our particular channel size to a wide range of ionic strengths. Even at the relatively high ionic strength of 100 mM, the wall interaction remains sensible out to a considerable distance z*/D = 0.25. As the system probes deeper into the Odijk regime (D/lp = 0.1), the effect of wall interactions only becomes more important. We have also considered the marginal case of D = lp, where our analysis becomes suspect due to the emergence of excluded volume interactions. Neglecting that complication, we again see that DNA-wall electrostatic interactions remain very prominent at lower ionic strengths. Even at an ionic strength of 100 mM, the effect of a single wall continues to persist to almost 20% of the channel cross section. We thus conclude that the DNA-wall electrostatic interactions play an important role for all experimentally relevant scenarios for confinement in channels near the persistence length.
FIG. 8.
Plot of (a) the dimensionless wall interaction parameter β given by Eq. (15) and (b) the position z* at which the wall interaction potential βϕ(z) decays to 0.1kBT as a function of buffer ionic strength for channel sizes that are proximate to the Odijk regime. The dashed blue curve corresponds to D = lp, the solid black line corresponds to the ratio D = 0.62lp for a 34 nm channel and a 48 mM ionic strength, and the dashed-dotted gold line corresponds to D = 0.1lp. The black circles are the results of the analysis for the experiments of Sec. IV. Note that the ratio z*/D is the DNA-wall electrostatic interaction length due to a single wall relative to the entire channel size.
Clearly, the theoretical analysis pursued here is a simplified description of the experimental scenario, neglecting the effects of segmental excluded volume in the polymer model and treating the electrostatic problem without any ion correlation effects. It nevertheless illuminates two challenging directions for improving our understanding of DNA confinement in such small channels. At a fundamental level, it is worthwhile to examine how the Odijk theory is affected by polymer-wall interactions that are long-ranged. There is already evidence48 that the mapping to an effective channel size fails for sufficiently strong wall interactions. A more detailed analysis is possible by solving Eq. (10) for a model potential, following previous work on confinement of ideal chains,42 or by simulating the discrete wormlike chain model for small channel sizes.48 Such an analysis would also benefit by considering in detail the channel shape, rather than the simplified one-dimensional model used here. Moving past this relatively straightforward question poses significant challenges for theory and simulation, such as providing a more realistic electrostatic model that includes electrostatic correlations that would affect the DNA configuration49 and capturing the physical chemistry of the interactions between different ions and DNA.50,51
VI. CONCLUSIONS
While the confined neutral wormlike chain model has proven to be a robust model for describing DNA confinement in relatively wide nanochannels,36–38 where the electrostatic interactions are localized to a small region near the channel walls, the results presented here suggest that these interactions play an important role in governing the extension of DNA for channels close to the persistence length. This conclusion confers both challenges and opportunities. Developing a detailed model for the various electrostatic interactions taking place between a highly charged polyelectrolyte confined in close proximity to charged walls is not trivial, especially if ion correlation effects and the physicochemical details of the DNA and the particular ions play an important role. However, if such a polyelectrolyte model were available, it could be used to great benefit to understand the strong extension of DNA in nanochannels smaller than its persistence length, which underlies the genome mapping technology19 and, as our analysis suggests, remains an unsolved problem. We are optimistic that such a model could also be merged with the basic principles underlying the telegraph model since the idea of projecting the three-dimensional walk of the DNA onto an effective one-dimensional walk of the telegraph particle should be robust to the details of the walk that is being projected. In particular, analysis of the parameters in the telegraph model reveals that the scaling parameter α is most sensitive to the global persistence length,17 which itself is a very sensitive function of the channel size (for hard walls).10,28 Understanding how the global persistence length is affected by DNA-wall electrostatic interactions is the most promising route toward improving the agreement between theory and experiment for channel-confined DNA. Importantly, the global persistence length is a property of ideal wormlike chains,28 and there exists a powerful propagator approach52 for computing it. Modifying that approach52 to account for electrostatic interactions, even within the simple models used here, provides an enticing opportunity.
Our analysis of DNA-wall interactions also provides an interesting perspective on different methods for equilibrium stretching of DNA by channel confinement. Two general approaches have been proposed, the relatively high ionic strength, small channel approach used here19 and a low ionic strength, large channel approach.53,54 To date, the metric used to compare methods is the ratio of the channel size to persistence length, D/lp, since it is the relevant parameter for the Odijk theory in Eq. (13). Our analysis suggests that the DNA extension should be a function of both D/lp and the wall interaction parameter β in Eq. (15). A particularly strong test of our conclusions would be to examine these two approaches at the same values of D/lp < 1. The electrostatic interactions embodied in β, as well as the length scale describing their decay, will be different for the two systems due to the nonlinearity of the electrostatics models. If these experiments furnished different DNA extensions at the same value of the Odijk parameter D/lp, this would be a strong indication that DNA-wall electrostatic effects indeed play a prominent role.
SUPPLEMENTARY MATERIAL
See supplementary material for (i) additional figures equivalent to Fig. 2 for the other channel sizes, (ii) a figure of comparison between the best fit adjustable parameters, σ, and the corresponding σOdijk using Eq. (6) for each channel size D and each bin in L, (iii) all of the possible labeling patterns of λ-DNA, (iv) a sensitivity analysis to the parameter selection of the cutoff values for the length and the correlation coefficient filters, and (v) an additional figure equivalent to Fig. 6 using the correction σ0 = 2σOdijk.
ACKNOWLEDGMENTS
This work was supported by the National Institutes of Health (Grant No. R01-HG006851). J.G.R. is an employee of Bionano Genomics, Inc., which is commercializing nanochannel genome mapping.
REFERENCES
- 1.Daoud M. and de Gennes P. G., J. Phys. 38, 85 (1977). 10.1051/jphys:0197700380108500 [DOI] [Google Scholar]
- 2.Odijk T., Macromolecules 16, 1340 (1983). 10.1021/ma00242a015 [DOI] [Google Scholar]
- 3.Yang Y., Burkhardt T. W., and Gompper G., Phys. Rev. E 76, 011804 (2007). 10.1103/physreve.76.011804 [DOI] [PubMed] [Google Scholar]
- 4.Odijk T., Phys. Rev. E 77, 060901(R) (2008). 10.1103/physreve.77.060901 [DOI] [PubMed] [Google Scholar]
- 5.Burkhardt T. W., Yang Y., and Gompper G., Phys. Rev. E 82, 041801 (2010). 10.1103/physreve.82.041801 [DOI] [PubMed] [Google Scholar]
- 6.Brochard-Wyart F., Tanaka T., Borghi N., and De Gennes P. G., Langmuir 21, 4144 (2005). 10.1021/la0474114 [DOI] [PubMed] [Google Scholar]
- 7.Wang Y., Tree D. R., and Dorfman K. D., Macromolecules 44, 6594 (2011). 10.1021/ma201277e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dai L., Van Der Maarel J., and Doyle P. S., Macromolecules 47, 2445 (2014). 10.1021/ma500326w [DOI] [Google Scholar]
- 9.Werner E. and Mehlig B., Phys. Rev. E 90, 062602 (2014). 10.1103/physreve.90.062602 [DOI] [PubMed] [Google Scholar]
- 10.Muralidhar A., Tree D. R., and Dorfman K. D., Macromolecules 47, 8446 (2014). 10.1021/ma501687k [DOI] [Google Scholar]
- 11.Tree D. R., Muralidhar A., Doyle P. S., and Dorfman K. D., Macromolecules 46, 8369 (2013). 10.1021/ma401507f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Reisner W., Morton K. J., Riehn R., Wang Y. M., Yu Z., Rosen M., Sturm J. C., Chou S. Y., Frey E., and Austin R. H., Phys. Rev. Lett. 94, 196101 (2005). 10.1103/physrevlett.94.196101 [DOI] [PubMed] [Google Scholar]
- 13.Zhang C., Zhang F., van Kan J. A., and van der Maarel J. R. C., J. Chem. Phys. 128, 225109 (2008). 10.1063/1.2937441 [DOI] [PubMed] [Google Scholar]
- 14.Persson F., Utko P., Reisner W., Larsen N. B., and Kristensen A., Nano Lett. 9, 1382 (2009). 10.1021/nl803030e [DOI] [PubMed] [Google Scholar]
- 15.Cifra P., J. Chem. Phys. 131, 224903 (2009). 10.1063/1.3271830 [DOI] [PubMed] [Google Scholar]
- 16.Tree D. R., Wang Y., and Dorfman K. D., Phys. Rev. Lett. 110, 208103 (2013). 10.1103/physrevlett.110.208103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Werner E., Cheong G. K., Gupta D., Dorfman K. D., and Mehlig B., Phys. Rev. Lett. 119, 268102 (2017). 10.1103/physrevlett.119.268102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen J. Z., Phys. Rev. Lett. 121, 037801 (2018). 10.1103/physrevlett.121.043401 [DOI] [PubMed] [Google Scholar]
- 19.Lam E. T., Hastie A., Lin C., Ehrlich D., Das S. K., Austin M. D., Deshpande P., Cao H., Nagarajan N., Xiao M., and Kwok P. Y., Nat. Biotechnol. 30, 771 (2012). 10.1038/nbt.2303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Stigter D., Biopolymers 16, 1435 (1977). 10.1002/bip.1977.360160705 [DOI] [PubMed] [Google Scholar]
- 21.Dobrynin A. V., Macromolecules 38, 9304 (2005). 10.1021/ma051353r [DOI] [Google Scholar]
- 22.Reisner W., Pedersen J. N., and Austin R. H., Rep. Prog. Phys. 75, 106601 (2012). 10.1088/0034-4885/75/10/106601 [DOI] [PubMed] [Google Scholar]
- 23.Bhandari A. B., Reifenberger J. G., Chuang H.-M., Cao H., and Dorfman K. D., J. Chem. Phys. 149, 104901 (2018). 10.1063/1.5040458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ödman D., Werner E., Dorfman K. D., Doering C. R., and Mehlig B., Biomicrofluidics 12, 034115 (2018). 10.1063/1.5038417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bhandari A. B. and Dorfman K. D., “Simulations corroborate telegraph model predictions for the extension distributions of nanochannel confined DNA,” Biomicrofluidics 13, 044110 (2019). 10.1063/1.5109566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Reinhart W. F., Reifenberger J. G., Gupta D., Muralidhar A., Sheats J., Cao H., and Dorfman K. D., “Distribution of distances between DNA barcode labels in nanochannels close to the persistence length,” J. Chem. Phys. 142, 064902 (2015). 10.1063/1.4907552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chuang H.-M., Reifenberger J. G., Cao H., and Dorfman K. D., Phys. Rev. Lett. 119, 227802 (2017). 10.1103/physrevlett.119.227802 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Odijk T., J. Chem. Phys. 125, 204904 (2006). 10.1063/1.2400227 [DOI] [PubMed] [Google Scholar]
- 29.Reinhart W. F., Reifenberger J. G., Gupta D., Muralidhar A., Sheats J., Cao H., and Dorfman K. D., J. Chem. Phys. 147, 029901 (2017). 10.1063/1.4993458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang Y., Reinhart W. F., Tree D. R., and Dorfman K. D., Biomicrofluidics 6, 014101 (2012). 10.1063/1.3672691 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Stephens M. A., J. Am. Stat. Assoc. 69, 730 (1974). 10.1080/01621459.1974.10480196 [DOI] [Google Scholar]
- 32.Mak A. C. Y., Lai Y. Y. Y., Lam E. T., Kwok T. P., Leung A. K. Y., Poon A., Mostovoy Y., Hastie A. R., Stedman W., Anantharaman T., Andrews W., Zhou X., Pang A. W. C., Dai H., Chu C., Lin C., Wu J. J. K., Li C. M. L., Li J. W., Yim A. K. Y., Chan S., Sibert J., Dzakula Z., Cao H., Yiu S. M., Chan T. F., Yip K. Y., Xiao M., and Kwok P. Y., Genetics 202, 351 (2016). 10.1534/genetics.115.183483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zook J. M., Catoe D., McDaniel J., Vang L., Spies N., Sidow A., Weng Z., Liu Y., Mason C. E., Alexander N., Henaff E., McIntyre A. B., Chandramohan D., Chen F., Jaeger E., Moshrefi A., Pham K., Stedman W., Liang T., Saghbini M., Dzakula Z., Hastie A., Cao H., Deikus G., Schadt E., Sebra R., Bashir A., Truty R. M., Chang C. C., Gulbahce N., Zhao K., Ghosh S., Hyland F., Fu Y., Chaisson M., Xiao C., Trow J., Sherry S. T., Zaranek A. W., Ball M., Bobe J., Estep P., Church G. M., Marks P., Kyriazopoulou-Panagiotopoulou S., Zheng G. X., Schnall-Levin M., Ordonez H. S., Mudivarti P. A., Giorda K., Sheng Y., Rypdal K. B., and Salit M., Sci. Data 3, 160025 (2016). 10.1038/sdata.2016.25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Reifenberger J. G., Dorfman K. D., and Cao H., Analyst 140, 4887 (2015). 10.1039/c5an00343a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sheats J., Reifenberger J. G., Cao H., and Dorfman K. D., Biomicrofluidics 9, 064119 (2015). 10.1063/1.4938732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gupta D., Sheats J., Muralidhar A., Miller J. J., Huang D. E., Mahshid S., Dorfman K. D., and Reisner W., J. Chem. Phys. 140, 214901 (2014). 10.1063/1.4879515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gupta D., Miller J. J., Muralidhar A., Mahshid S., Reisner W., and Dorfman K. D., ACS Macro Lett. 4, 759 (2015). 10.1021/acsmacrolett.5b00340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Iarko V., Werner E., Nyberg L. K., Müller V., Fritzsche J., Ambjörnsson T., Beech J. P., Tegenfeldt J. O., Mehlig K., Westerlund F., and Mehlig B., Phys. Rev. E 92, 062701 (2015). 10.1103/physreve.92.062701 [DOI] [PubMed] [Google Scholar]
- 39.Skolnick J. and Fixman M., Macromolecules 10, 944 (1977). 10.1021/ma60059a011 [DOI] [Google Scholar]
- 40.Odijk T., J. Polym. Sci.: Polym. Phys. Ed. 15, 477 (1977). 10.1002/pol.1977.180150307 [DOI] [Google Scholar]
- 41.Chen J. Z. Y., Prog. Polym. Sci. 54-55, 3 (2016). 10.1016/j.progpolymsci.2015.09.002 [DOI] [Google Scholar]
- 42.Chen J. Z. Y., Macromolecules 46, 9837 (2013). 10.1021/ma4020824 [DOI] [Google Scholar]
- 43.Muralidhar A., Tree D. R., Wang Y., and Dorfman K. D., J. Chem. Phys. 140, 084905 (2014). 10.1063/1.4865965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stigter D., J. Colloid Interface Sci. 53, 296 (1975). 10.1016/0021-9797(75)90016-8 [DOI] [Google Scholar]
- 45.Behrens S. H. and Grier D. G., J. Chem. Phys. 115, 6716 (2001). 10.1063/1.1404988 [DOI] [Google Scholar]
- 46.Hiemstra T., de Witt J. C. M., and van Riemsdijk W. H., J. Colloid Interface Sci. 133, 105 (1989). 10.1016/0021-9797(89)90285-3 [DOI] [Google Scholar]
- 47.The Chemistry of Silica, edited by Iler R. K. (John Wiley & Sons, New York, 1979). [Google Scholar]
- 48.Cheong G. K., Li X., and Dorfman K. D., Phys. Rev. E 95, 022501 (2017). 10.1103/physreve.95.022501 [DOI] [PubMed] [Google Scholar]
- 49.Muthukumar M., Macromolecules 50, 9528 (2017). 10.1021/acs.macromol.7b01929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McFail-Isom L., Sines C. C., and Williams L. D., Curr. Opin. Struct. Biol. 9, 298 (1999). 10.1016/s0959-440x(99)80040-2 [DOI] [PubMed] [Google Scholar]
- 51.Jayaram B., Sharp K. A., and Honig B., Biopolymers 28, 975 (1989). 10.1002/bip.360280506 [DOI] [PubMed] [Google Scholar]
- 52.Chen J. Z. Y., Phys. Rev. Lett. 118, 247802 (2017). 10.1103/PhysRevLett.118.247802 [DOI] [PubMed] [Google Scholar]
- 53.Jo K., Dhingra D. M., Odijk T., de Pablo J. J., Graham M. D., Runnheim R., Forrest D., and Schwartz D. C., Proc. Natl. Acad. Sci. U. S. A. 104, 2673 (2007). 10.1073/pnas.0611151104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kim Y., Kim K. S., Kounovsky K. L., Chang R., Jung G. Y., de Pablo J. J., Jo K., and Schwartz D. C., Lab Chip 11, 1721 (2011). 10.1039/c0lc00680g [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for (i) additional figures equivalent to Fig. 2 for the other channel sizes, (ii) a figure of comparison between the best fit adjustable parameters, σ, and the corresponding σOdijk using Eq. (6) for each channel size D and each bin in L, (iii) all of the possible labeling patterns of λ-DNA, (iv) a sensitivity analysis to the parameter selection of the cutoff values for the length and the correlation coefficient filters, and (v) an additional figure equivalent to Fig. 6 using the correction σ0 = 2σOdijk.