Developing algorithms to predict adult onset internalizing disorders: An ensemble learning approach

Abstract

A growing literature is utilizing machine learning methods to develop psychopathology risk algorithms that can be used to inform preventive intervention. However, efforts to develop algorithms for internalizing disorder onset have been limited. The goal of this study was to utilize prospective survey data and ensemble machine learning to develop algorithms predicting adult onset internalizing disorders. The data were from Waves 1–2 of the National Epidemiological Survey on Alcohol and Related Conditions (n = 34,653). Outcomes were incident occurrence of DSM-IV generalized anxiety, panic, social phobia, depression, and mania between Waves 1–2. In total, 213 risk factors (features) were operationalized based on their presence/occurrence at the time of or before Wave 1. For each of the five internalizing disorder outcomes, super learning was used to generate a composite algorithm from several linear and non-linear classifiers (e.g., random forests, k-nearest neighbors). AUCs achieved by the cross-validated super learner ensembles were in the range of 0.76 (depression) to 0.83 (mania), and were higher than AUCs achieved by the individual algorithms. Individuals in the top 10% of super learner predicted risk accounted for 37.97% (depression) to 53.39% (social anxiety) of all incident cases. Thus, the algorithms achieved acceptable-to-excellent prediction accuracy with a high concentration of incident cases observed among individuals predicted to be highest risk. In parallel with the development of effective preventive interventions, further validation, expansion, and dissemination of algorithms predicting internalizing disorder onset/trajectory could be of great value.

Internalizing disorders (IDs) are the most common form of psychopathology; roughly one-third of the US population experiences an anxiety or mood disorder over their lifetime (Kessler et al., 2005). IDs also are highly chronic (Andrade et al., 2003; Yonkers et al., 2013) and thus consistently identified as a top cause of disease burden (James, 2018). Although IDs frequently onset in childhood and early adolescence, a large proportion of individuals experience first onset after the age of 18 (e.g., >50% of lifetime cases of panic disorder, agoraphobia, generalized anxiety disorder; roughly 75% of all lifetime mood disorder cases; Kessler et al., 2005).

Given their high prevalence and burden, significant efforts have been devoted to identifying ID risk factors. Literature has amassed on the importance of a wide range of factors, many of which can be assessed using self-report (e.g., socio-demographics; pre-existing symptoms of physical and mental disorders, stress/adversity; Grant et al., 2009; Kim-Cohen et al., 2003; McLaughlin et al., 2010; Scott et al., 2007). Although it is common for etiological studies to collect data on numerous ID risk factors, there have been limited efforts to determine how to use/combine all available risk factor data to generate composite algorithms (risk scores) that predict ID onset. The development of algorithms to predict ID onset could be used to inform preventive intervention; that is, to determine who is at highest-risk and possibly in need of (targeted) assessment or preventive intervention.

A recent review identified only four studies that have attempted to develop algorithms predicting the onset of generalized anxiety disorder, panic disorder, or bipolar disorders/mania (Bernardini et al., 2017). More work has been done to develop algorithms predicting the onset of depression (Bellón et al., 2011; King et al., 2013; King et al., 2008). For example, Wang and colleagues (2014) used data from the National Epidemiological Survey on Alcohol and Related Conditions (NESARC) and stepwise regression methods to develop a population-level algorithm for adult onset major depression (Wang et al., 2014). However, a limitation across most ID algorithm development studies (including Wang et al., 2014) has been the reliance on conventional regression methods that (a) are prone to model overfit (i.e., poor performance in hold-out data or an independent sample), particularly in the presence of highly correlated features, and (b) cannot flexibly capture nonlinear associations or interactions among predictors.

An alternative approach for developing algorithms for ID onset is to use (supervised) machine learning methods designed to optimize prediction. A growing literature is utilizing machine learning to develop algorithms for posttraumatic stress disorder/symptoms (e.g., in emergency settings; Galatzer-Levy et al., 2014), but there has been virtually no effort to use machine learning to develop algorithms that predict the onset of other IDs. In particular, ensemble methods have been used to develop optimized composite algorithms from several different approaches to prediction and which outperform individual (i.e., non-ensemble) algorithms (Kessler et al., 2014). The goal of the present study was to utilize prospective data from the NESARC and ensemble machine learning methods to develop algorithms predicting adult onset generalized anxiety disorder, panic disorder, social phobia, depression, and mania.

Method

Sample

Algorithms were developed using data from Waves 1–2 of the NESARC, a longitudinal representative household survey of US adults (Hasin and Grant, 2015). Although the NESARC focused extensively on substance use, the surveys assessed a wide range of DSM-IV mental disorders (including IDs) and associated risk factors. NESARC data previously has been used to develop algorithms for major depression onset (Wang et al., 2014) and is well-suited for supervised machine learning because of its prospective design, large sample, and rich assessment of ID risk factors. The Wave 1 NESARC interview was conducted in 2001–2002 (n=43,093). Wave 2 re-interviewed 34,653 of the Wave 1 respondents in 2004–2005. Details of the NESARC design and field procedures are available elsewhere (Grant et al., 2003).

Outcomes

Our goal was to develop algorithms predicting incident onset IDs in adulthood. Mental disorders were diagnosed using the Alcohol Use Disorder and Associated Disability Interview Schedule, DSM-IV Version (AUDADIS-IV). The AUDADIS-IV is a reliable fully structured diagnostic interview of DSM-IV substance use disorders, IDs, personality disorders, and associated risk factors (e.g., family history of psychopathology) that can be administered by trained lay diagnosticians (Grant et al., 2003). Whereas 12-month and lifetime disorders were assessed at Wave 1, a goal of Wave 2 was to assess disorders first occurring since Wave 1 (i.e., disorder incidence). Our outcomes were defined based on Wave 2 variables indicating incident occurrence (since Wave 1) of five DSM-IV disorder outcomes: generalized anxiety disorder (GAD), panic disorder (with or without agoraphobia; PDA), social phobia (SOC), depression (major depressive episode/disorder or dysthymia, DEP), and mania (manic or hypomanic episode). Models were developed for each outcome in a distinct subsample that excluded individuals with disorder incidence prior to Wave 1 (based on Wave 1 lifetime diagnoses): GAD (outcome n = 1,123; GAD sample n = 33,018), PDA (647; 32,714), SOC (560; 32,902), DEP (1,707; 27,769), mania (970; 32,496).

Features

The NESARC assessed the wide range of established ID risk factors including sociodemographics (Grant et al., 2009), physical health problems (Scott et al., 2007), other (pre-existing) mental disorders/symptoms (Kim-Cohen et al., 2003; Merikangas et al., 2003), personality traits (Krueger, 1999), stressful life events (Hammen, 2005; McLaughlin et al., 2010; Miloyan et al., 2018), childhood adversity/trauma exposure (Lindert et al., 2014; McLaughlin et al., 2010), and a family history of psychopathology (Beardselee et al., 1998). The Wave 1–2 surveys and codebooks were reviewed to identify all plausible risk factors (“features”) within these domains and with minimal missing data (i.e., we did not attempt to operationalize predictors based on questions that were “skipped” for >80% of respondents). Features were operationalized to reflect the presence/severity of the risk factor at the time of or prior to the Wave 1 assessment (prior to incident disorder onset). Features assessed at Wave 2 were determined to be present prior to Wave 1 (a) if they explicitly assessed experiences occurring prior to the age of 18 (Wave 1 respondents were ≥18), or (b) based on self-reported age of occurrence (e.g., reported ages of traumatic event occurring prior to age at Wave 1). This approach was used to capture directional associations between features and outcomes (i.e., risk factors preceding outcomes), and is more conservative than the approach used by Wang and colleagues (e.g., Wang et al. defined a predictor for discrimination experiences, which was assessed in Wave 2 and without questions to assess discrimination prior to Wave 1). The 213 features are summarized in Supplemental Tables 1–2.

Analysis method

All analyses were conducted in R (Team, 2013). Super learning (Polley et al., 2018; Van der Laan and Rose, 2011) was used to generate a prediction function for each of the five outcomes. The (a) identifying a user-specified “library” of classifiers (i.e., different approaches to prediction, described below), (b) implementing each classifier in the library using k-fold cross-validation (CV) to generate predicted values (10-fold CV described below), (c) regressing the outcome onto the CV predicted values from each classifier in the library (to determine the best weighted combination of the individual algorithms), and (d) fitting each classifier in the library on the full sample, and combining these fits with the weights generated in the prior step to estimate the super learner predicted values. Super learner analyses were not weighted because the majority of the classifiers included in the super learner library (see below) were not designed for complex survey design.

Classifiers.

Several different classifiers were included in the super learner library, both based on recent recommendations (LeDell et al., 2016) and because it was unknown what type of classifier(s) would result in optimized prediction. Nine classifiers were selected: logistic regression, least absolute shrinkage and selection operator (LASSO) penalized (logistic) regression, random forests, Bayesian main-terms logistic regression, generalized additive modeling, adaptive splines, k-nearest neighbors, linear support vector machines, and linear discriminant analysis. Classifier descriptions are provided in Supplemental Table 3.

In developing the super learner ensemble for each outcome, each classifier was implemented using five different feature subsets that were identified using super learning feature selection methods. Feature selection is a common data processing step in the machine learning literature (Galatzer-Levy et al., 2018). Although reducing the number of features may increase bias (reducing model accuracy), feature selection also mitigates risk of model overfit (reducing variance). Five feature sets were operationalized for each outcome. Four sets of non-collinear features were defined (for each outcome) based on features that had non-zero coefficients in LASSO models tuned to select a maximum of 5, 10, or 20 features, and when permitted to use as many features as possible (four LASSO feature sets were defined for each outcome). The fifth, in comparison, included all features with significant bivariate associations with the outcome (Wald χ² p < .05).

The classifiers were implemented on each of these feature sets rather than all 213 features because (a) some classifiers could perform better using a smaller number of features (e.g., collinearity could negatively impact performance), (b) we wanted to evaluate the extent to which utilizing a smaller number of features would affect model performance, (c) prior efforts to develop ID algorithms in the NESARC have used similar feature selection methods (e.g., identifying significant bivariate associations, selecting 10–20 with largest odds ratios among collinear sets; Wang et al., 2014), and (d) to mitigate computational intensity (by eliminating irrelevant features). To develop the super learner for each outcome, all nine classifiers were implemented using each of the five feature sets (44 individual algorithms were estimated to create the super learner for one outcome¹).

Cross-validation.

Super learning (and thus all classifier-predictor set combinations) was implemented using 10-fold CV. The 10-fold CV approach involved: (a) dividing all observations into 10 mutually exclusive subgroups of roughly equal size in terms of total number and number of outcome cases (for each outcome/sample), (b) fitting the model (i.e., classifier/predictor set combination) in 9 of the 10 blocks within each fold (i.e., the training set), and using the resulting fit to estimate predicted probabilities for observations in the one left-out block (i.e., the validation/test set), and (c) repeating this process until cross-validated (CV) predicted probabilities are estimated for all observations (for any given classifier-predictor set combination) and all classifier-predictor set combinations (including the consolidated super learner ensembles). In other words, predicted values were estimated for all observations based on a model developed in a mutually exclusive subsample. In comparison, Wang et al. (2014) split the NESARC into training and validation/test samples based on US consensus region (training: Northeast/Midwest/South regions, test: West region). Ten-fold CV has advantages over split-sample validation including increased sample size (all observations are utilized as both training and test cases) and reduced likelihood of model overfit (because not relying on a single/arbitrary sample split; see James et al., 2013)

Model Performance.

To evaluate and compare the performance of the super learner to the individual classifiers, area under the receiver operating characteristic (ROC) curves (AUC) and their 95% confidence intervals (CI) were calculated using the CV predicted probabilities (expressed to four decimals for increased precision). In addition, two approaches were used to operationalize high risk cut-points. First, cut-point were operationalized for all algorithms based on the threshold at which Youden’s Index was maximized (the point on the ROC curve where sensitivity + specificity was highest). Second, super learner risk tiers were created by rank ordering predicted values and dividing respondents into 20 equal groups (ventiles of risk). Operating characteristics were calculated based on Youden’s Index and the ventiles of risk. Sensitivity and positive predictive value were prioritized over specificity and negative predictive value given the primary goal of identifying true-positive cases.

Results

Feature selection

Details of which variables were selected in each feature set for each outcome are presented in Supplemental Tables 4–6 (including bivariate odds ratios). The Figure 1 Word Cloud summarizes those selected most frequently across feature sets and outcomes. Five features were selected for all outcomes and in >20 of the 25 total feature sets (in the largest font in the Word Cloud): having a lifetime PTSD diagnosis prior to Wave 1 (for interpretative purposes, odds ratios [ORs] = 4.9–5.7, χ²₁ = 340.8–588.9), number of attention deficit-hyperactivity disorder symptoms in childhood (ORs = 1.1–1.2, χ²₁ = 223.8–967.7), SF-12v2 Mental Disability summary score at Wave 1 (higher score indicates better health, ORs = 0.9, χ²₁ = 188.2–544.9), number of childhood adversities (ORs = 1.3, χ²₁ = 230.0–478.6), and being the victim of sexual assault prior to Wave 1 (ORs = 3.1–4.3, χ²₁ = 222.3–297.3). Several other features also were selected for more than one (but not all five) outcomes across the restrictive (5, 10, or 20) LASSO feature sets (see Supplemental Table 6). A limited number of features were selected for a single ID (e.g., subclinical social anxiety fears and SOC; self-perceived health and PDA; unemployment in the past 12-months and DEP; subclinical elevated mood and number of illicit drugs used in past 12-months and mania).

Figure 1.

Word cloud of the features selected most frequently across predictor sets and outcomes (larger font indicates higher frequency of selection).

Best performing algorithms

A summary of the best performing individual classifiers using each feature set, and performance of the five super learner ensembles, are presented in Table 1 (see Supplemental Tables 7–11 for super learner weights, AUCs, and operating characteristics for all algorithms based on Youden’s Index). Based on AUC, linear discriminant analysis (LDA), generalized additive modeling (GAM), and LASSO were consistently the best performing classifiers. The best performing CV individual algorithm for each outcome was: (a) GAD - LDA (max 20 features, AUC = 0.7988 [0.7863–0.8113]), (b) PDA - LASSO (all bivariate features, AUC = 0.7796 [0.7620–0.7972]), (c) SOC - GAM (max 20 features, AUC = 0.7942 [0.7756–0.8129]), (d) DEP - LASSO (all bivariate features, AUC = 0.7552 [0.7435–0.7668]), and (e) Mania – LASSO (all bivariate features, AUC = 0.8249 [0.8119–0.8379]). AUCs of the best performing algorithms using a maximum of five features was lower and ranged between 0.7281 (0.7155–0.7407; DEP) and 0.7862 (0.7711–0.8013; mania). Several other classifier-feature set combinations resulted in similar but lower AUCs than the best classifier-feature sets combinations (Supplemental Tables 7–11), including the logistic regression models. At least seven (of the nine) total classifiers and 16 (of the 44) total classifier-feature set combinations were represented with non-zero weights in the super learner ensemble for each outcome. The CV super learner ensembles achieved slightly higher AUCs than the individual algorithms, with AUCs ranging between 0.7572 (95% CI = 0.7455–0.7688; DEP) and 0.8261 (0.8131–0.8392; mania). When the super learner coefficients were applied to the full sample (i.e., non-CV), AUCs increased but were not indicative of model overfit (i.e., AUC approaching 1)². Calibration slopes and Brier scores indicated acceptable calibration of the ensembles (slopes = 1.09–1.16, Brier scores = 0.016–0.053; slope near 1.0 and Brier score near 0 indicate better calibration, Van Calster et al. 2016).

Table 1.

Best performing 10-fold cross-validated models across feature sets and outcomes

	Outcome
	Generalized anxiety disorder	Panic disorder	Social phobia	Depression	Mania
Base Rate/Incidence, %	3.40	1.98	1.70	6.15	2.99
Best Individual Algorithm/Performance
Max 5 Features1	LDA	LDA	GAM	GAM	LDA
AUC (95% CI)	0.7669 (0.7529–0.7810)	0.7752 (0.7572–0.7933)	0.7350 (0.7118–0.7581)	0.7281 (0.7155–0.7407)	0.7862 (0.7711–0.8013)
SL Weight	n/a	n/a	n/a	n/a	n/a
Max 10 Features1	LDA	LASSO	GAM	GAM	GAM
AUC (95% CI)	0.7821 (0.7687–0.7956)	0.7634 (0.7447–0.7822)	0.7739 (0.7536–0.7942)	0.7498 (0.7380–0.7616)	0.8169 (0.8036–0.8302)
SL Weight	n/a	0.0214	<.001	0.0400	<.001
Max 20 Features1	LDA	LDA	GAM	GAM	GAM
AUC (95% CI)	0.7988 (0.7863–0.8113)	0.7752 (0.7572–0.7933)	0.7942 (0.7756–0.8129)	0.7504 (0.7387–0.7620)	0.8231 (0.8103–0.8360)
SL Weight	0.1283	n/a	0.1604	0.0428	0.0548
All LASSO Features (n=101–104)1	LDA	LASSO	LASSO	Splines	LDA
AUC (95% CI)	0.7869 (0.7734–0.8004)	0.7678 (0.7492–0.7865)	0.7867 (0.7670–0.8063)	0.7472 (0.7354–0.7590)	0.8128 (0.7988–0.8269)
SL Weight	0.1022	0.0361	0.1039	0.0673	0.1119
All Significant Features (n=151–180)1	LASSO	LASSO	LASSO	LASSO	LASSO
AUC (95% CI)	0.7975 (0.7849–0.8101)	0.7796 (0.7620–0.7972)	0.7751 (0.7548–0.7954)	0.7552 (0.7435–0.7668)	0.8249 (0.8119–0.8379)
SL Weight	0.0586	0.1142	n/a	0.0829	0.1142
Ensemble Performance
Number of classifiers used in the ensemble (max 9)	9	9	7	9	9
Number of algorithms used in the ensemble (max 44)	25	27	16	26	28
Superlearner CV AUC
AUC (95% CI)	0.7991 (0.7865–0.8117)	0.7813 (0.7638–0.7988)	0.7990 (0.7803–0.8177)	0.7572 (0.7455–0.7688)	0.8261 (0.8131–0.8392)
Superlearner Full Sample AUC
AUC (95% CI)	0.8174 (0.8057–0.8292)	0.8163 (0.8008–0.8319)	0.8369 (0.8206–0.8531)	0.7779 (0.7668–0.7890)	0.8553 (0.8444–0.8662)

Abbreviations. AUC, area under the receiver operating characteristic curve; 95% CI, 95% confidence interval; SL weight, super learner weight (n/a indicates weight of 0); LDA, linear discriminant analysis; GAM, generalized additive modeling; LASSO, least absolute shrinkage and selection operator; Splines, multivariate adaptive polynomial splines.

¹See Supplemental Tables 4–6 for the variables selected for each feature set and outcome

Super learner operating characteristics

Between 21.09% and 35.57% of each outcome-specific sample had a predicted value above the optimized Youden’s Index risk threshold (Table 2). Individuals with predicted values above the optimized risk thresholds accounted for 69.01% (DEP) to 81.75% (GAD) of all incidence cases of the outcomes (sensitivity). The rate of the outcomes among individuals above the risk threshold (PPV) ranged from 5.16% (PDA) to 14.19% (DEP). Sensitivity and PPV were 2.30 (GAD) to 3.41 (SOC) times greater than their expected values. In comparison, specificity (range = 66.05% [GAD] to 79.79% [SOC]) and NPV (range = 97.28% [DEP] to 99.40% [SOC] were 1.01 (PDA; SOC) to 1.04 (DEP) times greater than their expected values.

Table 2.

Super learner performance based on optimized risk cut-point (Youden’s Index)

	Optimal risk threshold1	% sample above threshold	Sensitivity	PPV	(O/E)2	Specificity	NPV	(O/E)3
Generalized Anxiety Disorder	.021	35.57	81.75	7.82	2.30	66.05	99.04	1.03
Panic Disorder	.015	29.18	76.20	5.16	2.61	71.77	99.34	1.01
Social Phobia	.018	21.09	71.96	5.81	3.41	79.79	99.40	1.01
Depression	.052	29.89	69.01	14.19	2.31	72.68	97.28	1.04
Mania	.021	26.79	79.69	8.88	2.97	74.84	99.17	1.02

Abbreviations. PPV, positive predictive value; NPV, negative predictive value.

¹Optimal risk threshold is the optimal predicted value (0–1 range) multiplied by 100 for increased precision (0–100 range)

²Observed (O) / Expected (E) sensitivity is calculated by dividing the observed sensitivity (above the optimized threshold) by the expected sensitivity (i.e., the % of the sample above the optimized risk threshold). O/E PPV is calculated by dividing the observed PPV (above the optimized risk threshold) by the overall rate/incidence (true positive rate) of the outcome and is equivalent to O/E sensitivity.

³O/E specificity is calculated by dividing the observed specificity (below the optimized threshold) by the expected sensitivity (i.e., % of sample below the optimized risk threshold). O/E NPV is calculated by dividing the observed NPV (above the optimized risk threshold) by the overall true negative rate of the outcome and is equivalent to O/E specificity.

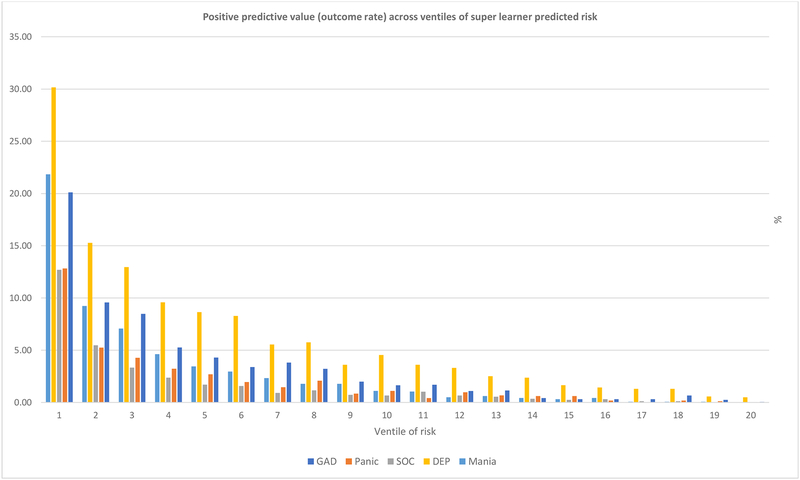
Individuals in the top 5% of predicted risk accounted for 24.55% (DEP) to 37.52% (SOC) of all incidence cases of the outcomes (Figure 2), whereas those in the top 10% of predicted risk accounted for 36.97% (DEP) to 53.39% (SOC) of all incident cases (sensitivity). The outcome rates (PPV) in the top 5% of risk ranged from 12.70% (SOC) to 30.17% (DEP) (Figure 3) and in the top 10% of risk from 9.05% (PDA) to 22.72% (DEP). Sensitivity/PPV was 4.91–7.50 times the expected value (5%) among individuals in the top 5% of predicted risk, 3.70–5.34 times the expected value (10%) among those in the top 10% (the “top decile”), and remained above the expected value across the top five ventiles for all five IDs.

Figure 2.

Sensitivity (proportion of outcome cases) across ventiles of super learner predicted risk.

Figure 3.

Positive predictive value (outcome rate) across ventiles of super learner predicted risk.

Discussion

This is the first study to use ensemble machine learning to develop algorithms predicting the first onset of several IDs. The CV and full-sample super learner ensembles achieved AUCs indicating acceptable (AUC ≥0.70) to excellent (AUC ≥0.80) prediction (Hosmer et al., 2013). As expected, the CV super learners achieved higher AUCs than the best performing CV individual algorithms. However, the magnitude of these differences were relatively small for several classifier-feature set combinations (e.g., ΔAUC <.01), including when the classifiers were restricted to a maximum of five features. Along these lines, the comparable but slightly lower AUCs of the logistic regression models based on non-collinear/optimized LASSO feature sets underscores the utility of modeling “traditional” linear associations between survey features and ID outcomes. Further, a wide range of algorithms contributed to the ensembles with non-zero super learner weights. Collectively, these findings suggest that (a) a number of different classifiers can be used to predict ID onset from self-report/survey data with an acceptable level of accuracy, even with a selective number of features, and (b) the incremental predictive validity of combining individual algorithms via ensemble learning may be small. Although reasonable to question whether these improvements in AUC warrants the use of all available features and computational intense ensemble procedure such as super learning, any improvement in prediction accuracy is important when the goal is forecasting debilitating outcomes such as IDs. In addition, the differential/incremental performance of individual classifier-feature set combinations and super learning may be more pronounced in more complex data structures (e.g., including neuroimaging, psychophysiological, or audio features).

Several features appeared to have transdiagnostic relevance by being selected in feature sets for IDs, particularly indicators of prior trauma/stress (e.g., number of childhood adversities, sexual assault victimization) and mental disorders/symptoms (e.g., PTSD diagnosis, SF-12v2 Mental Disability). In comparison, subclinical features of some outcomes only were selected in feature sets for that outcome (e.g., subclinical social anxiety fears and social phobia; subclinical elevated mood and mania). These findings are in line with research implicating both distal (childhood trauma/adversity, Carre et al., 2013; Hoppen and Chalder, 2018) and proximal (recent stress, Hammen, 2005; Miloyan et al., 2018) environmental factors as important transdiagnostic predictors of IDs, as well as evidence that experiencing some mental disorders/symptoms (including subthreshold symptoms) increases risk of developing additional disorders/symptoms (Karsten et al., 2011; Kim-Cohen et al., 2003; Merikangas et al., 2003). Similar predictors have been included in previously developed algorithms for ID onset (King et al., 2008; Moreno-Peral et al., 2014; Wang et al., 2014).

Our evaluation of model performance based on AUC is consistent with prior efforts to develop algorithms predicting the onset of depressive (Bellón et al., 2011; King et al., 2013; King et al., 2008; Wang et al., 2014), bipolar (Gan et al., 2011), and anxiety disorders (King et al., 2011; Moreno-Peral et al., 2014). Our CV super learner for DEP achieved a higher AUC than was obtained by the Wang and colleagues algorithm for incident onset of major depression developed using NESARC data and parametric/stepwise regression methods (hold-out sample AUC = 0.7259). Several ID onset prediction models also have been developed through two multi-site cohort studies of primary care patients in Europe and South America; “PredictD” (Bellón et al., 2011; King et al., 2013; King et al., 2008) and “PredictA” (King et al., 2011; Moreno-Peral et al., 2014). CV performance of the super learner ensembles was generally higher than test sample performance of the “PredictD” model for major depression (AUC = 0.728, King et al., 2013) and “PredictA” model for generalized anxiety/panic (AUCs = 0.707 in one sample but 0.811 in another, King et al., 2011).

AUC is limited in that it is a metric of overall prediction accuracy that does not capture performance using a specific high-risk threshold that might be used to make decisions/recommendations for preventive intervention (Wald and Bestwick, 2014). Accordingly, we also evaluated the operating characteristics of various high-risk thresholds. Using Youden’s Index to operationalize high-risk thresholds resulted in the correct classification of over two-thirds of all cases for each outcome. However, this performance (sensitivity) was only 2–3 times better than would be expected by chance because >20% of each sample had predicted probabilities surpassing the Youden’s Index thresholds. In comparison, the top ventile of risk accounted for roughly one-quarter to one-third (up to 7.5 times the expected values) and top decile of risk between one-third and one-half (up to 5.3 times the expected values) of all incident cases of IDs. Whereas the top decile (10%) of super learner risk accounted for 36.97% of all incident cases of DEP (3.69 times the expected value), the top decile of Wang and colleagues (Wang et al., 2014) NESARC algorithm accounted for 33.9% of all cases (3.39 times the expected value). Other prior ID algorithm development studies did not report sensitivity and/or the size of high-risk groups (Bellón et al., 2011; King et al., 2011, 2013; Moreno-Peral et al., 2014), making comparisons difficult (e.g., if 75% of all individuals are classified as high risk, sensitivity of 75% would be poor).

Although additional validation of the current models is needed, there could be several ways to disseminate ID risk algorithms. As has been done for cardiovascular disease (http://static.heart.org/riskcalc/app/index.html#!/baseline-risk), publicly available online risk calculators and preventive intervention recommendations could be made available and accessed independently or in collaboration with healthcare professionals (e.g., during appointments). Utilization of ID algorithms also could be useful during ubiquitously-experienced life stages of stress/risk during which it might be feasible to assess ID risk and provide recommendations for preventive intervention (e.g., during college orientation). Numerous ID preventive interventions could be recommended for individuals predicted to be at highest risk (e.g., exercise, Harvey et al., 2017; self-guided internet prevention Deady et al., 2017; ongoing assessment, psychotherapy/pharmacotherapy referrals). However, the costs and anticipated benefits (e.g., number needed to treat) of the recommended prevention approach would need to be carefully considered. One path toward integrating ID risk algorithms in a cost-effective way could be by using algorithms to identify and recruit individuals to participate in prevention research (cf. recruitment based on family history), and expanding the models to predict who among the highest risk would benefit from a specific prevention approach (precision preventive medicine).

This study has several limitations. The data were exclusively self-report and primarily categorical/dichotomous measures. It is possible that super learner performance, including incremental performance over the individual algorithms, could be improved with information on additional risk factors assessed dimensionally (e.g., severity of subthreshold symptoms) and using other units of analysis (e.g., neurophysiological reactivity, Meyer et al., 2015). Relying on categorical DSM-IV diagnoses as the primary outcome measures also is limited. As has been done in the PTSD algorithm literature (Galatzer-Levy et al., 2014), future research developing ID algorithms should assess symptom severity repeatedly over time with the goal of predicting symptom trajectories (e.g., increasing, chronic, and remitting ID symptoms). Super learning also has limitations; for example, it requires significant computational time, particularly when implemented with CV. Further, although our use of 10-fold CV is a study strength (cf. split sample validation), replication of model performance in independent samples is needed.

Within the context of these limitations, the current study is the first to use ensemble learning to develop algorithms for adult onset IDs. The algorithms achieved acceptable-to-excellent overall prediction accuracy and a high concentration of outcome cases were observed among individuals predicted to be highest risk. As the number of empirically-supported ID preventive interventions continues to grow, further validation, expansion, and dissemination of such algorithms could be of great value for the broader public health goal of reducing the incidence of ID psychopathology.