Dynamic Growth Metrics for Examining Prenatal Exposure Impacts on Child Growth Trajectories: Application to Perfluorooctanoic Acid (PFOA) and Postnatal Weight Gain

Abstract

Background

Epidemiologic studies investigating prenatal exposures in relation to growth typically rely on cumulative growth measures such as weight or BMI. However, less is known about how prenatal exposure may impact other aspects of growth dynamics, including timing and velocity.

Objectives

To describe and apply a nonlinear growth model previously used in other health science fields to characterize postnatal growth trajectories for use in environmental epidemiology studies.

Methods

We used a double logistic function to model child weight trajectories from birth to 5.5 years using data from the Swedish Environmental Longitudinal Mother and Child, Asthma and Allergy (SELMA) study. From this, we approximated several infant growth metrics: 1) duration of time needed to complete 90% of the infant growth spurt (Δt₁), 2) the maximum growth rate in infancy or infant peak growth velocity (PGV), 3) the age at infant PGV (δ₁), a measure of growth tempo, and 4) the weight plateau at the end of the infant growth spurt (α₁). We assessed these metrics in relation to prenatal perfluorooctanoic acid (PFOA) exposure among 1,334 mother-child pairs, and differences between boys and girls.

Results

Average estimated infant PGV and its timing (δ₁) were 0.68 kg/month and 3.4 months, respectively. Mean infant growth spurt duration (Δt₁) was 13 months, ending at an average weight plateau (α₁) of 8.2 kg. Higher prenatal PFOA concentrations were related to a longer duration of infant growth (Δt₁: 0.06; 95% CI=0.01, 0.11). PGV was not impacted, but higher prenatal PFOA concentrations were significantly related to delayed infant PGV (δ₁: 0.58; 95% CI=0.17, 0.99) and a higher post-spurt weight plateau (α₁: 0.81; 95% CI=0.21, 1.41). After adjusting for false discovery, results were only significant for δ₁ and α₁. We observed a significant interaction by sex for the association with δ₁, and stratified analyses revealed the association was only significant among girls.

Conclusion

Model-derived growth metrics were consistent with published growth standards. This novel application of nonlinear growth modeling enabled detection of altered infant growth dynamics in relation to prenatal PFOA exposure. Our results may help describe how PFOA yields lower birthweights, but higher weight later in childhood. Future applications may characterize adolescent growth or additional metrics of biological interest.

1. INTRODUCTION

Human growth patterns in early life provide critical information on individual- and population-level health. Early life growth can serve as a marker of overall health status, or may be an initial indication of developmental abnormalities and be used as a risk factor for health effects in later life (Himes 2009; Regnault and Gillman 2014). The clinical importance of monitoring child growth trajectories is illustrated by the high frequency of well-child visits in the first few years of life (Regnault and Gillman 2014), and by considerable attention by the World Health Organization and Centers for Disease Control and Prevention to developing and updating child growth standards (Kuczmarski et al. 2002; World Health Organization 2009).

In addition to genetics, environmental factors such as nutrition, infection, and social conditions were long acknowledged as determinants of human growth, evidenced by war and famine related changes in stature (Himes 2009). David Barker first proposed that adverse environmental conditions (i.e., famine) during the prenatal period impacted fetal growth and predisposed individuals to cardiovascular diseases later on in life (Barker 2007), inspiring broad research into the Developmental Origins of adult Health and Disease (DOHaD) (Wadhwa et al. 2009). It is now recognized that the prenatal and early postnatal periods are highly sensitive to environmental exposures, including anthropogenic contaminants (Barouki et al. 2012). Although chemical contaminants may only elicit subtle alterations to endocrine signaling and gene expression, these alterations may lead to persistent changes in long term health (Barouki et al. 2012).

Mounting evidence suggests that perfluoroalkyl substances (PFASs) are one such group of chemicals that may impact growth (Bach et al. 2015). Numerous laboratory and epidemiology studies report that reduced fetal growth and lower birth weight are associated with prenatal PFASs exposures such as perfluorooctane sulfonic acid (PFOS) and perfluorooctanoic acid (PFOA) (Marks et al. 2019; Negri et al. 2017). These substances were also reported to alter postnatal growth, including lower weight and BMI among infants and toddlers (Andersen et al. 2010; Gyllenhammar et al. 2018; Maisonet et al. 2012; Shoaff et al. 2018; Yeung et al. 2019), but then eventually leading to higher weight and adiposity later in childhood (Braun et al. 2016; Gyllenhammar et al. 2018; Høyer et al. 2015; Lauritzen et al. 2018; Maisonet et al. 2012). A potential limitation of prior studies is the near exclusive use of cumulative growth measures, such as weight and BMI as the outcome of interest, rather than evaluating growth characteristics and trajectories. To further our understanding of how PFAS may impact postnatal growth, alternative growth metrics are needed.

To address this research gap, we propose implementing a nonlinear model to characterize early postnatal growth, and derive dynamic growth metrics for novel application to environmental epidemiology. Our proposed approach uses two independent steps. First, we describe individual growth curves using a double logistic model. Second, we apply the derived growth indicators in a linear model conditioned on the exposure of interest. Our example application assesses prenatal PFOA exposure in relation to the model-estimated growth indicators using data from the Swedish Environmental Longitudinal Mother and Child, Asthma and Allergy (SELMA) study.

2. METHODS

2.1. Infant Growth Characterization

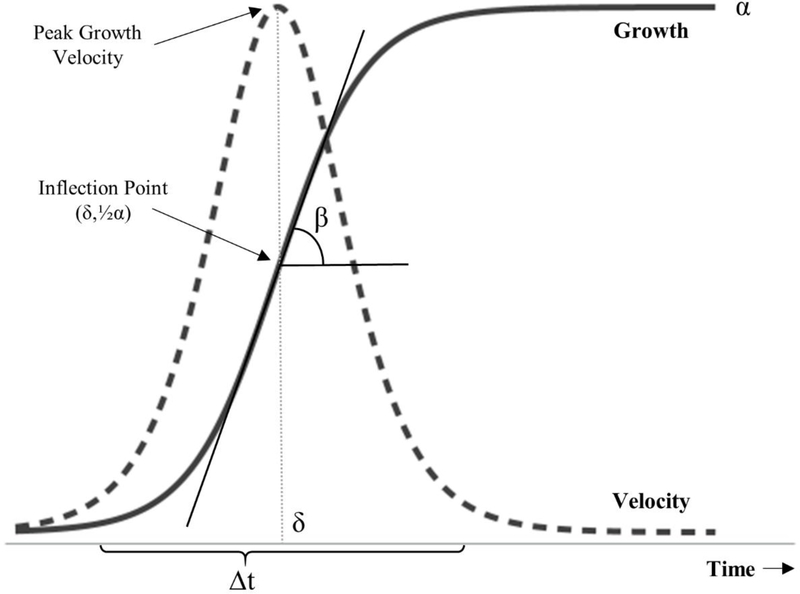
Logistic functions are commonly used to model exponential growth limited by some natural process, producing a characteristic S-shape (Figure 1) (Tsoularis and Wallace 2015). Equation 1 is a single logistic function.

$$\mu (t)=\frac{\alpha }{1+e^{-\beta (t-\delta )}}$$ (1)

In the context of child growth over time, μ(t) is an anthropometric measurement (e.g., height, weight) at time t (e.g., age), α is the asymptotic limit on growth (e.g., final height or weight), β is the slope at the inflection point, and δ is the location in time of the inflection point where concavity flips (Hauspie and Molinari 2009; Molinari and Gasser 2009). Since logistic functions are symmetric about the inflection point, the y-coordinate of the inflection point is defined by Equation 2.

Figure 1. Logistic Growth.

Logistic growth is exponential with an asymptotic limit (α). At the inflection point (δ, ½α), the rate constant is determined by the slope of the tangent line (β). The duration of growth is defined here as the time needed to grow from 10% to 90% of α. Growth velocity is the first derivative of the logistic growth curve, and the peak velocity is reached at time=δ.

$$\mu (\delta )=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\alpha$$ (2)

Growth velocity (Equation 3) is calculated by taking the first derivative of Equation 1 with respect to time.

$$\frac{\partial \mu (t)}{\partial t}=\frac{\alpha \beta e^{-\beta (t-\delta )}}{{(1+e^{-\beta (t-\delta )})}^2}$$ (3)

The maximum growth rate occurs at the inflection point and can be calculated using Equation 4, and is often called Peak Growth Velocity (PGV) (Hauspie and Molinari 2009).

$$\frac{\partial \mu (\delta )}{\partial t}=\frac{\alpha \beta }{4}$$ (4)

Finally, the length of time, i.e. Δt, it takes to grow from 10% to 90% of the final weight or height (α) can be interpreted as the duration of growth. This can be calculated by Equation 5 (Meyer 1994).

$$\mathrm{\Delta }t=\frac{\ln 81}{\beta }$$ (5)

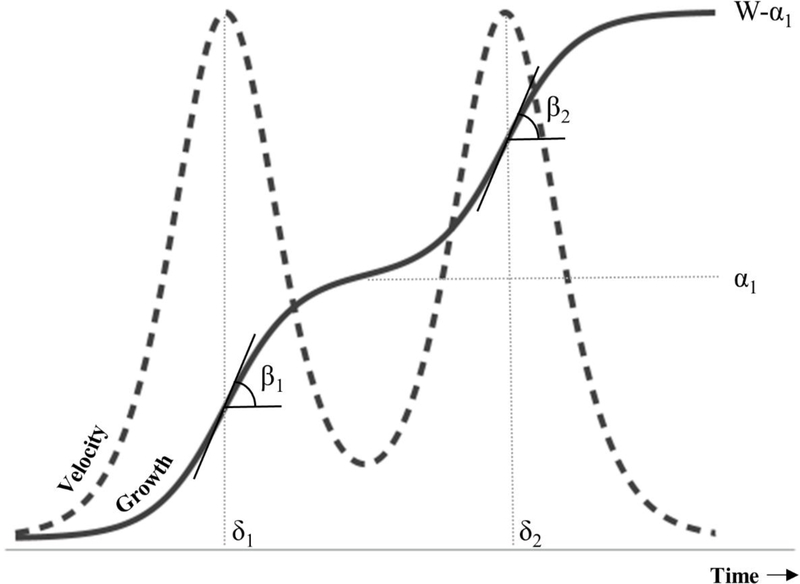
Some growth processes may have multiple pulses (Meyer 1994). In the case of child growth, genetic and environmental factors may produce defined growth spurts which can be described using a double logistic model (Figure 2, Equation 6) (Hauspie and Molinari 2009; Meyer 1994).

$$\mu (t)=\frac{{\alpha }_1}{1+e^{-{\beta }_1\left(t-{\delta }_1\right)}}+\frac{W-{\alpha }_1}{1+e^{-{\beta }_2\left(t-{\delta }_2\right)}}$$ (6)

Here, μ(t) and t are as previously described. The two logistic terms describe two growth spurts with rate constants β₁ and β₂ and inflection point locations at δ₁ and δ₂, respectively. In contrast to the single logistic model with a single asymptote (Equation 1, α), the double logistic model has two asymptotes, α₁ and W. Growth spurts are separated by the α₁ asymptote (an intermediate plateau in height or weight). W is the final asymptote (e.g. final height, weight). Growth velocity over time (Equation 7) can be estimated by taking the first derivative of Equation 6 with respect to time.

Figure 2. Double Logistic Growth.

Double logistic growth describes two growth spurts governed by two logistic functions with slopes β₁ and β₂, and inflection points at δ1 and δ2. The spurts are separated by an intermediate asymptote (α₁).

$$\frac{\partial \mu (t)}{\partial t}=\frac{{\alpha }_1{\beta }_1{e}^{-{\beta }_1\left(t-{\delta }_1\right)}}{{\left(1+e^{-{\beta }_1\left(t-{\delta }_1\right)}\right)}^2}+\frac{{\beta }_2\left(W-{\alpha }_1\right)e^{-{\beta }_2\left(t-{\delta }_2\right)}}{{\left(1+e^{-{\beta }_2\left(t-{\delta }_2\right)}\right)}^2}$$ (7)

Bock (1973) proposed Equation 6 to describe the onset and intensity of pubertal growth where the first and second logistic terms characterized child and adolescent height growth, respectively. Later, a third logistic term was added to describe early- and mid-childhood growth spurts along with adolescent growth (Bock and Thissen 1980). Due to model flexibility and our interest in characterizing weight gain, we propose applying the double logistic model to weight observations in infancy and early childhood. Weight measurements after age two years are subject to greater uncertainty (Bozzola and Meazza 2012), therefore we primarily focus on early growth. In our application the maximum infant growth rate, or infant PGV, corresponds to the first inflection point, δ₁, and can be calculated using Equation 8.

$$\frac{\partial \mu \left({\delta }_1\right)}{\partial t}=\frac{{\alpha }_1{\beta }_1}{4}+\frac{{\beta }_2\left(W-{\alpha }_1\right)e^{-{\beta }_2\left({\delta }_1-{\delta }_2\right)}}{{\left(1+e^{-{\beta }_2\left({\delta }_1-{\delta }_2\right)}\right)}^2}$$ (8)

Meyer (1994) described a taxonomy of double logistic models where growth may be sequential in that the second spurt does not begin until the first spurt finishes, or overlap to some degree. Since infant and child growth spurts may not be clearly defined and vary by individual child (Molinari and Gasser 2009), partial overlap is possible. This overlap may impact infant growth parameter estimates. Therefore, to understand how much the child growth spurt impacted the infant estimates of interest, we calculated the percent saturation S₂ of the second logistic term with respect to W when time was set to δ₁ (Equation 9).

$$S_2=\left(\frac{\left(\mu \left({\delta }_1\right)-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\alpha }_1\right)}{\left(W-{\alpha }_1\right)}\right)\times 100\%$$ (9)

The lower the saturation level, the more sequential the two logistic curves. The higher the saturation level, the more overlap between logistic curves. For sequential growth spurts, parameters for the two logistic terms can be reasonably isolated since the second logistic term will provide negligible information to the first logistic term. Therefore, PGV may be approximated by the first term in Equation 8 (e.g. $\frac{{\alpha }_1{\beta }_1}{4}$), and the duration of the isolated infant growth spurt, Δt₁, can be approximated by Equation 10.

$$\mathrm{\Delta }{t}_1=\frac{\ln 81}{{\beta }_1}$$ (10)

This duration can also be interpreted as the age when 90% of infant growth is attained.

3. APPLICATION

While Bock’s logistic models have been used to evaluate growth metrics in relation to cardiometabolic outcomes (Sun et al. 2014; Sun and Schubert 2009), evaluations of prenatal environmental influences on growth are lacking using this approach. To illustrate the utility of these growth indicators in environmental health, we applied the double logistic growth models to child weight trajectories using participants in the SELMA study. We then assessed prenatal PFOA concentrations in relation to the estimated infant growth indicators.

3.1. Study Population

The SELMA study is a population-based study that recruited more than 2300 pregnant women in the first trimester (median week 10) from prenatal clinics in Värmland county, Sweden, from November 2007 to March 2010. Detailed recruitment and sample collection procedures were described previously (Bornehag et al. 2012, 2015). Participants provided written consent. The study was reviewed and approved by the Regional Ethical Review Board (Uppsala, Sweden).

3.2. Prenatal Blood

Non-fasting blood samples were collected from mothers during their first prenatal visit. Samples were stored at −70°C (serum) at the Laboratory of Occupational and Environmental Medicine (LOEM) at Lund University, Lund, Sweden. Serum was analyzed for PFOA and cotinine, a biomarker of tobacco exposure, using LC-MS/MS (UFLCXR, SHIMADZU Corporation, Kyoto, Japan and QTRAP 5500, AB Sciex, Foster City, CA, USA), with full details provided elsewhere (Lindh et al. 2012; Shu et al. 2018). The limits of detection were 0.02 ng/mL for PFOA and 0.2 ng/mL for cotinine.

3.3. Covariates

At study entry, data on maternal age, parity, and smoking were collected via questionnaires. Mothers were considered smokers if they reported current smoking or had cotinine levels indicative of active smoking (>15 ng/mL) at the first prenatal visit (Shu et al. 2018). Data on gestational age, birthweight, and maternal weight were collected from the Swedish Medical birth register.

3.4. Anthropometric Measurements

Weight measurements and exact age recorded at birth and during well-child visits were obtained from medical records. Up to 15 measurements were available from birth to age 5.5 years (birth; week 2; months 2, 3, 4, 5, 6, 8, 10, and 12; years 1.5, 2.5, 3, 4, 5.5).

In some instances, there were apparent data entry errors for age and weight data, including incorrect units (e.g. years vs. months, g vs. kg). To avoid subjective interpretations of specific values, we systemically cleaned data to eliminate apparent data entry errors and reduce measurement error. This is essential for nonlinear model convergence to a global minima (Molinari and Gasser 2009). Visits that did not meet the following criteria were deleted. First, age and weight must be ≥10% of the overall median age and weight for each visit. Second, age must be ≤3 times, and weight must be ≤10 times the overall median for each visit. Third, individual child age must increase monotonically in each consecutive visit. Fourth, to allow for known weight variability (e.g., diurnal, seasonal) without losing many data points, individual child weight must increase monotonically within a 5% margin of error in each consecutive visit. Finally, we excluded children with fewer than 8 of the 15 possible visits to minimize nonlinear model nonconvergence due to sparse data.

3.5. Statistical Analysis

3.5.1. Child Growth Modeling

We fit individual child weight measurements to the double-logistic model (Equation 6) using PROC NLIN in SAS 9.4 (SAS Institute Inc. 2018). Example code is provided in the Supplemental Material. The final weight for the children (W) was unknown since there is no clear evidence for distinct mid-childhood weight plateau (Molinari and Gasser 2009) and observation numbers varied by child in the SELMA study. Therefore, we set W to 40 kg, a value that exceeded the data range, to reduce computational complexity when there were inadequate data to estimate the plateau of the second curve, avoid arbitrarily choosing an age cutoff, and since the second logistic curve is not of primary interest. We specified a range of starting values based on visual inspection of observed growth trajectories.

For each child, we estimated the infant growth spurt slope (β₁), age at infant PGV (δ₁), and weight plateau (α₁) using nonlinear least squares. As an indicator of fit, we output the sum of squares error (SSE). To quantify the amount of overlap between the two logistic curves, we calculated the percent saturation in the second curve at the time of the first inflection point (S₂). We then calculated the duration of infant growth spurt (Δt₁) and infant PGV assuming sequential growth spurts (saturation ≤10%). We reviewed the distribution of each parameter; to eliminate the need for outlier analysis based on regression residual diagnostics, we deleted study subjects with growth parameter estimates greater than three standard deviations above the mean. We also deleted two study subjects where the approximated δ₁ was less than zero. All growth metrics used in this application to infant weight growth are summarized in Table 1.

Table 1.

Infant Growth Metric Descriptions and Interpretations

Growth Metric	Technical Description	Interpretation	Symbol	Units	Equation
Infant Slope	Slope of the tangent line at the 1st inflection point (a growth rate constant)	Proxy of overall infant growth rate	β1	[kg/months]	6
Infant Peak Growth Velocity	Peak instantaneous velocity on the 1st logistic curve	Peak instantaneous growth rate in infancy	PGV	[kg/months]	8, first terma
Age at Infant PGV	Age at the 1st inflection point and when instantaneous growth rate peaks	Infant growth tempo; how early or late the peak infant growth rate occurs	δ1	[months]	6
Infant Weight Plateau	Asymptote of the 1st logistic curve; an intermediate weight, and starting point for the 2nd logistic curve	Intermediate plateau in weight at the end of the infant growth spurt	α1	[kg]	6
Infant Growth Spurt Duration	Time required to growth from 10% to 90% saturation on the 1st logistic curve (a function of β1)	Time it takes to complete 80% of infant growth; Age when 90% of the infant growth is attained	Δt1	[months]	10a
Curve 2 Saturation	The %saturation of the 2nd logistic curve when the first logistic curve is at 50% saturation (age = δ1)	Measure of how well-defined the infant growth spurt is from the 2nd spurt; we define ≤10% as sequential spurts, >10% as overlapping	S2	[%]	9

^aAssumes sequential growth spurts (S₂≤10%) where the 2^nd logistic term has negligible contribution

3.5.2. Univariate, Bivariate, and Missing Data Analyses

We log-transformed PFOA concentrations, β₁, Δt₁, and SSE to approximate a normal distribution and calculated geometric means (GM) and geometric standard deviations (GSD). We reported descriptive statistics for population characteristics, PFOA, and growth metrics for all children as well as for boys and girls separately. We used the χ² test for homogeneity and t-tests to assess potential differences between boys and girls, as well as those included in the current analysis compared to those excluded due to missing data. We set the statistical significance level to α=0.05.

3.5.3. Linear Regression of Infant Growth Metrics

We assessed prenatal PFOA levels in relation to individual estimates of infant growth ($\widehat{{\beta }_{1\iota }}$, $\widehat{{\delta }_{1\iota }}$, $\widehat{{\alpha }_{1\iota }}$, ${\widehat{\mathrm{\Delta }t}}_{1\iota }$, $\iota nf\widehat{antP}G{V}_{\iota }$) using linear regression. Potential confounders were selected based on prior literature; we adjusted for child sex, preterm birth (gestational age <37 weeks), mother’s age, weight, parity, and smoking (Andersen et al. 2010; Maisonet et al. 2012; Shoaff et al. 2018). We chose to adjust for preterm birth rather than continuous gestational age because bivariate associations with exposure and growth parameters were stronger for the dichotomized variable. Since PFOA may impact boys and girls differently (Andersen et al. 2010; Maisonet et al. 2012), we assessed the interaction of child sex by maternal PFOA concentrations, and also reported sex-stratified results. We set the statistical significance level to α=0.05 and controlled for false discovery using the Benjamini-Hochberg procedure (Benjamini and Hochberg 1995).

3.5.4. Sensitivity Analyses

To evaluate whether associations were driven by preterm and low birthweight babies, we assessed PFOA and infant growth indicators among full term babies with birthweights greater than the International Statistical Classification of Diseases and Related Health Problems low birthweight cut-off of 2,499 g (World Health Organization 2004). To evaluate the impact of overlapping logistic functions, we compared results for children with and without second curve saturation levels (S₂) above 10%. Finally, we reran analyses excluding one child with an extreme value for the double logistic model SSE.

4. RESULTS

4.1. Study Population and Missing Data Analysis

Of the more than 2300 women enrolled in the first trimester of pregnancy, 1,957 children were born into the study, and 245 mother-child pairs were excluded from the current analysis due to incomplete data on key demographic variables (e.g. maternal age, weight, smoking, parity, child sex, gestational age) (Supplemental Figure 1). Of the 1,712 children in the database with 25,680 possible visits, 1,549 children with 18,740 total visits were remaining following data cleaning for age and weight measurements (described in section 3.4). Thirty-eight children were excluded due to outlying estimated growth parameters (section 3.5.1), and another 177 excluded due to missing maternal PFOA measurements. The current analysis included 1,334 mother-child pairs with complete data. Children excluded due to missing data were on average 73 g heavier at birth (p=0.01), and were more likely to have mothers that smoked (11% versus 7%, p<0.01), had prior pregnancies (59% versus 54%, p=0.02), and were 1.7 kg heavier at the first prenatal visit (p=0.02). However, there were no differences in prenatal PFOA levels between those excluded and the current analysis sample. Therefore, adjustment for selection bias was not indicated.

4.2. Maternal and Child Characteristics

At study enrollment mothers had a mean age of 31 years and mean weight of 69 kg (Table 2). Mean maternal parity was 1.8 children (including the current pregnancy), and 46% had no prior pregnancies. GM maternal serum cotinine levels were 0.2 ng/mL, and 7% of women either self-reported smoking or had serum cotinine levels > 15 ng/mL. Mean gestational age at serum sample collection was 10 weeks, and the GM serum PFOA concentrations were 1.6 ng/mL. There were no differences in maternal characteristics by child sex. Fifty-three percent of children were boys. Mean gestational age was 39 weeks (Table 2), and 4% were preterm (<37 weeks gestation). Mean birthweight among all children was 3,617 g and 2.6% were low birthweight (≤2,499 g). The mean number of postnatal weight observations per child was 12. Boys had significantly higher birthweights, with a mean 89 g higher than girls (p<0.01), but there were no other differences in child characteristics by sex.

Table 2.

Maternal and Child Characteristics by Sex (N=1,334 mother-child pairs)

		All Children				Boys (N=701)				Girls (N=633)
Maternal or Child Characteristic		Mean	SD	Min	Max	Mean	SD	Min	Max	Mean	SD	Min	Max	pc
Mother	Age [years]	31	5	18	45	31	5	18	45	31	5	18	45	0.90
	Weight [kg]	69	13	42	147	69	13	45	147	69	1	42	121	0.86
	Parity [count]	1.8	1	1	10	1.8	1	1	6	1.8	1	1	10	0.67
	Serum Cotinine [ng/mL]a	0.2	26	0	366	0.2	27	0	339	0.3	26	0	366	0.37
	Prenatal Sample Collection [weeks]	10	2	4	27	10	2	4	27	10	2	4	18	0.54
	Prenatal PFOAa [ng/mL]	1.6	1.8	0.2	21.2	1.6	1.7	0.2	13.4	1.6	1.8	0.3	21.2	0.48
Child	Birth Weight [g]	3,617	551	960	5695	3659	571	960	5480	3570	524	1650	5695	<0.01
	Gestational Age (weeks)	39	2	28	43	39	2	28	43	40	2	29	43	0.22
	Postnatal Weight Observations [N]b	12	2	8	15	12	2	8	15	12	2	8	15	0.20

^aGeometric mean and standard deviation reported

^bNumber of weight observations available for each child

^cp-value based on t-test for differences between sexes

4.3. Infant Growth Characteristics

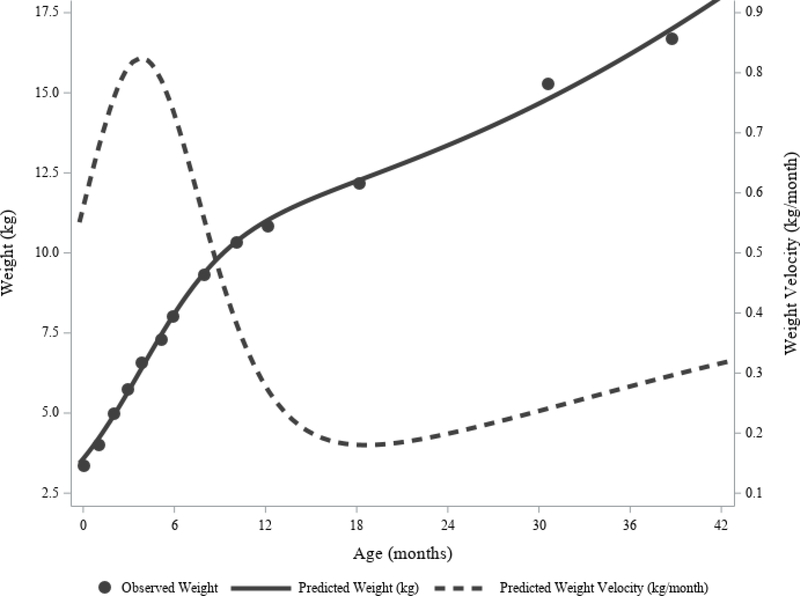
Figure 3 shows the growth trajectory for a child in the SELMA study with near average growth parameters; observed and predicted weight, and predicted weight velocity over time are plotted. Among all children, the mean slope of the inflection point was 0.33 kg/month and the GM infant growth spurt duration was 13.3 months (Table 3). Mean infant PGV was 0.68 kg/month, age of infant PGV was 3.4 months, and the mean infant weight plateau was 8.2 kg. At the first inflection point, the mean saturation of the second logistic curve was 6.3%, indicating growth was approximately sequential and that the second logistic curve could be ignored when approximating information on infant growth. The GM SSE was 0.7, but varied widely with a minimum value rounding to 0 and a maximum value of 95.1. The second highest SSE was only 10.3, indicating that the maximum value was extreme for the distribution. Note that the growth parameters corresponding to the child with an SSE of 95.1 were not outliers and were therefore retained for analysis.

Figure 3. Observed versus Predicated Postnatal Weight and Weight Velocity for an Average Child in the SELMA Study.

This individual child had 13 observations available through 39 months of age (dots), with time between observations increasing with age. Visual inspection shows that the predicted weight estimates (solid line) fit well to the observed weights. The predicted weight velocity curve (dashed line) estimates that the peak velocity occurs at approximately 3.7 months of age.

Table 3.

Infant Growth Characteristics (N=1,334 mother-child pairs)

	All Children				Boys (N=701)		Girls (N=633)
	Mean	SD	Min	Max	Mean	SD	Mean	SD	Pc
Slope (β1)a [kg/months]	0.33	1.60	0.09	1.07	0.35	1.58	0.31	1.62	<0.01
Spurt Duration (Δt1)a [months]	13.3	1.6	4.1	48.4	12.6	1.6	14.1	1.6	<0.01
PGV [kg/months]	0.68	0.22	0.27	1.50	0.74	0.24	0.62	0.20	<0.01
Age of PGV (δ1) [months]	3.4	1.7	0.1	8.8	3.3	1.5	3.7	1.8	<0.01
Weight Plateau (α1) [kg]	8.2	2.4	1.7	15.9	8.4	2.3	8.0	2.5	<0.01
Curve 2 Saturation (S2) [%]	6.3	3.5	0.0	15.0	6.4	3.5	6.2	3.4	0.43
SSEa	0.7	4.1	0.0	95.1	0.8	3.9	0.6	4.3	<0.01

Abbreviations: p, p-value; PGV, peak growth velocity; SD, standard deviation; SSE, sum of squares error

^aGeometric mean and standard deviation reported

^bPGV was approximated using the first term in Equation 8

^cp-value based on t-test for differences between sexes

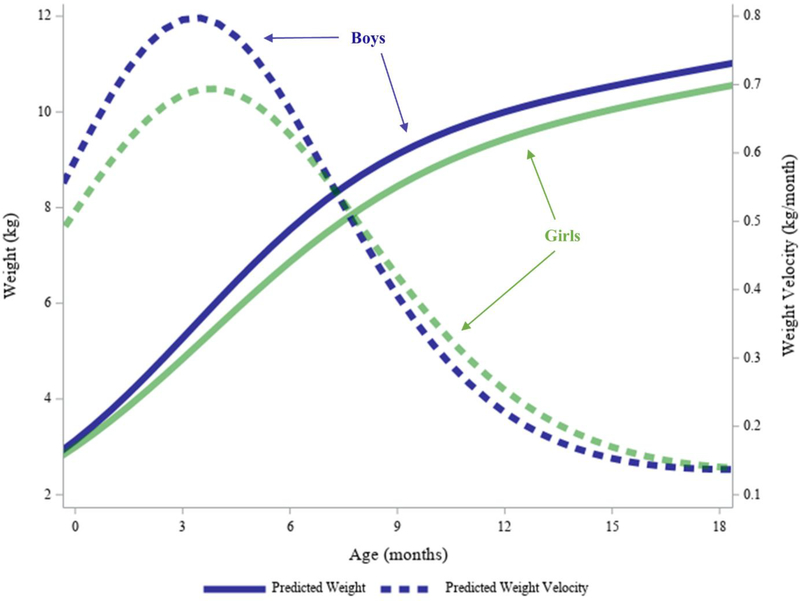
Compared to girls, boys had significantly steeper slopes at the inflection point (β₁: 0.35 versus 0.31 kg/month, p<0.01) and shorter growth spurt durations (Δt₁: 12.6 versus 14.1 months, p<0.01) (Table 3). Boys had significantly higher infant PGV (0.74 versus 0.62 kg/month, p<0.01) that occurred significantly earlier (δ₁: 3.3 versus 3.7 months, p<0.01). The weight plateau was also significantly higher among boys (α₁: 8.4 versus 8.0 kg, p<0.01). Figure 4 shows the average predicted weight and weight velocity for boys versus girls. Note that the infant PGVs in Figure 4 are slightly higher than the approximated PGV in Table 3. This is due to the fact that infant PGV presented in Table 3 was approximated using the first term in Equation 8 for ease of calculation since our focus was on infant growth, and because average growth trajectories were sequential (e.g. second term in Equation 8 negligible). In contrast, the time series plot in Figure 4 necessitates use of both terms in Equation 8.

Figure 4. Average Predicted Weight and Weight Velocity Trajectories from Birth to Age 2 Years by Sex.

Predictions are shown through age 18 months to emphasize differences between girls and boys in infancy. On average, boys weigh more than girls from birth, and this difference increases through the first year of life due to a steeper slope (β₁). Infant PGV is higher and occurs sooner (δ₁) for boys compared to girls. Note that the velocity curve graphed here uses both terms in Equation 8 by necessity.

There were no differences in curve 2 saturation levels by child sex (Table 3), and values indicated that both boys and girls had approximately sequential growth spurts. SSE was significantly higher among boys (0.8 versus 0.6, p<0.01), indicating a poorer fit. This difference between boys and girls remained significant even after excluding a boy with the maximum SSE value.

4.3. Prenatal PFOA Exposure and Infant Growth

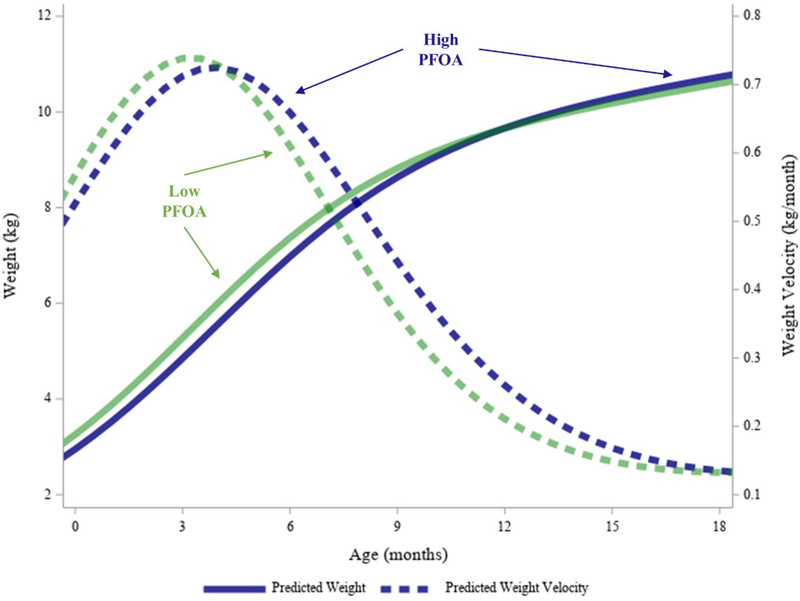
Higher PFOA levels were related to smaller slopes at the first inflection point (β₁: −0.06; 95% CI=−0.11, −0.01), and analogously, a longer duration of infant growth ((Δt₁: 0.06; 95% CI=0.01, 0.11) (Table 4). This change corresponded to a 4% increase in the infant growth spurt duration for an interquartile-range (IQR) change in PFOA levels. However, these associations were not significant after controlling for false discovery. While infant PGV was not impacted, higher prenatal PFOA concentrations were significantly related to PGV occurring later in infancy (δ₁: 0.58; 95% CI=0.17, 0.99). This change corresponds to infant PGV occurring five days later for an IQR change in PFOA levels. Finally, higher PFOA was related to a significantly higher weight plateau (α₁: 0.81; 95% CI=0.21, 1.41). This corresponded to the infant growth spurt stabilizing 255 g higher for an IQR change in PFOA levels. Figure 5 shows the average predicted weight and weight velocities for children with prenatal PFOA exposure levels at the 10^th and 90^th centiles to represent high versus low exposure.

Table 4.

Association between Prenatal log₁₀PFOA Levels (ng/mL) and Growth Characteristics (N=1,334 mother-child pairs)

Sex	Growth Characteristic	Est	SE	LL	UL	p
All Children	Log of Infant Slope (log10β1)	−0.06	0.03	−0.11	−0.01	0.02
Boys		−0.03	0.04	−0.10	0.04	0.37
Girls		−0.09	0.04	−0.16	−0.01	0.02
All Children	Log of Infant Spurt Duration (log10Δt1)	0.06	0.03	0.01	0.11	0.02
Boys		0.03	0.04	−0.04	0.10	0.37
Girls		0.09	0.04	0.01	0.16	0.02
All Children	Log of Infant PGVa	−0.02	0.02	−0.05	0.02	0.35
Boys		−0.02	0.02	−0.07	0.03	0.42
Girls		−0.01	0.02	−0.06	0.04	0.62
All Children	Age of Infant PGV (δ1)	0.58	0.21	0.17	0.99	0.01*
Boys		0.14	0.27	−0.39	0.67	0.60
Girls		1.01	0.32	0.38	1.65	<0.01*
All Children	Infant Weight Plateau (α1)	0.81	0.30	0.21	1.41	0.01*
Boys		0.26	0.41	−0.54	1.06	0.53
Girls		1.37	0.46	0.47	2.27	<0.01*

Abbreviations:

^*statistically significant after Benjamini-Hochberg correction for false discovery

Est, linear regression coefficient estimate; LL, 95% confidence interval lower limit; p, p-value; PGV, peak growth velocity; SE, standard error; UL, 95% confidence interval upper limit

Notes: Models adjusted for sex, preterm birth, mother’s age, weight, parity, and smoking

^aPGV was approximated using the first term in Equation 8

Figure 5. Average Predicted Weight and Weight Velocity Trajectories for High versus Low (10^th versus 90^th Centile) Prenatal PFOA Exposure Levels.

Higher PFOA levels were related to significantly delayed infant PGV and higher infant weight plateau. Higher PFOA levels were also related to nonsignificantly lower slope, and longer infant spurt duration. Note that the velocity curve graphed here uses both terms in Equation 8 by necessity.

In sex-stratified analyses, we observed associations among girls only. An IQR change in prenatal PFOA concentrations was related to a 7% increase in the infant growth spurt duration (Δt₁: 0.09; 95% CI=0.01, 0.16), infant PGV occurring approximately 10 days later (δ₁: 0.58; 95% CI=0.17, 0.99), and stabilizing at a weight 432 g higher (α₁: 1.37; 95% CI=0.47, 2.27) among girls (Table 4). However, only the associations for age at infant PGV (δ₁) and infant weight plateau (α₁) remained significant after controlling for false discovery. In analyses of interaction between prenatal PFOA and child sex, significant differences in PFOA-induced changes in the age at PGV (δ₁) between girls and boys was detected (p=0.02). However, the PFOA-by-sex interaction terms were not statistically significant for any other growth parameters.

4.4. Sensitivity Analysis

After excluding 63 infants whom were classified as preterm (<37 weeks gestation) or low birthweight (≤2499 g) infants, associations between PFOA and infant growth parameters were similar among the remaining 1,271 infants. For example, among all children, prenatal PFOA concentrations were related to smaller slope at the first inflection point (β₁: −0.07; 95% CI=−0.12, −0.01) and infant PGV occurring later (δ₁: 0.62; 95% CI=0.19, 1.04). Among children with sequential double logistic curves (second logistic curve saturation levels less than 10% at time set to δ₁), results were similar to those presented in Table 4. Specifically, prenatal PFOA concentrations were related to a smaller slope at the first inflection point (β₁: −0.06; 95% CI=−0.11, −0.01) and infant PGV occurring later (δ₁: 0.68; 95% CI=0.22, 1.15). In contrast, among children with more superimposed double logistic curves (saturation levels >10%), there was no association between PFOA levels and slope (β₁: 0.01; 95% CI=−0.09, 0.12) or age of infant PGV (δ₁: 0.19; 95% CI=−0.49, 0.86). Excluding the observation with the highest nonlinear model SSE also produced similar results.

5. DISCUSSION

This study evaluated the impact of early prenatal PFOA exposure on postnatal growth among 1,334 mother-child pairs from the Swedish SELMA study. In a novel application to environmental epidemiology, we used time series weight measurements to model growth trajectories and derived several infant growth metrics, including duration of the infant growth spurt, PGV, time at PGV, and the weight plateau at the end of the infant growth spurt. These metrics were then assessed as outcome variables in relation to first trimester PFOA levels. We found that higher PFOA levels were related to significantly delayed age of PGV and a higher infant weight plateau, particularly among girls. Higher PFOA levels were also related to a smaller infant slope and longer infant growth spurt duration, but these results were not significant after controlling for false discovery. PGV itself was not impacted.

Most prior literature evaluating PFASs in relation to child growth used cumulative growth metrics such as birth and postnatal weights. For example, numerous studies reported that prenatal PFOA was related to lower birthweight (Apelberg et al. 2007; Maisonet et al. 2012; Meng et al. 2018; Minatoya et al. 2017; Starling et al. 2017), and lower weight and BMI in early life (Andersen et al. 2010; Shoaff et al. 2018). In the SELMA cohort, an inverse relationship between prenatal PFOA exposure and birthweight was also observed (Wikstrom et al., accepted in Pediatric Research). A drawback of cumulative growth measurements is that they lack information on the dynamic growth processes (Lampl et al. 2015; Molinari and Gasser 2009). While repeated measures analyses of weight has shown that PFOA exposure reduced growth through age three (Yeung et al. 2019), alternative methods are needed to evaluate growth tempo and velocity.

By implementing a double logistic model and approximating additional growth indicators, we detected PFOA-induced changes to growth dynamics. We found that PFOA was associated with the tempo of infant growth spurts, where higher prenatal PFOA exposure was associated with PGV occurring later in infancy and the infant growth spurt ending at a higher weight plateau. The latter finding is consistent with studies reporting associations between prenatal PFOA exposure and higher adiposity and BMI among infants (Starling et al. 2019), older children (Braun et al. 2016; Gyllenhammar et al. 2018; Mora et al. 2017) and adults (Halldorsson et al. 2012). Although results were nonsignificant, we also detected that PFOA exposure may increase the duration of the infant growth spurt. However, PFOA did not influence peak growth velocity in our analysis.

The term ‘catch-up growth’ is defined as above average growth velocity for a particular age (de Wit et al. 2013). In contrast, our results indicated PFOA-related lower birthweight (Wikstrom et al. accepted) preceded a delayed tempo and longer duration of infant growth, rather than higher velocity. This suggests that PFOA impacts on growth operate via different biological pathways than other potential causes of growth restriction, such as undernutrition that characteristically show catch-up growth once alleviated by medical or nutritional intervention (de Wit et al. 2013). While Hales and Barker proposed the thrifty phenotype hypothesis to explain the lifelong adverse health impacts resulting from fetal and infant undernutrition (Hales and Barker 2001), further development is needed to incorporate the role of environmental contaminants. Barker’s work also suggested that catch-up growth through 3 years of age was an important predictor of future health (Dover 2009). In contrast, our analysis focused on infancy because weight measurement data was sparse after 18 months of age. This limited our ability to detect changes during critical growth periods in toddler and early childhood years.

Stratified analyses revealed the association was only significant among girls. We also detected a statistical interaction by sex for age at peak growth velocity. This is consistent with some prior studies that showed stronger associations between PFASs and growth among girls (Chen et al. 2017; Halldorsson et al. 2012; Maisonet et al. 2012; Mora et al. 2017; Yeung et al. 2019). This may indicate an increased susceptibility among female infants to growth mediating pathways. However, we must also note that on average, the double logistic model we used fit the data for girls better than boys, which may have also influenced the results.

Our study estimated several metrics of postnatal weight growth that show consistency with prior literature, adding assurance to model validity. Overall, we observed an increase in weight velocity until 3.5 months where it peaked at 0.82 kg/month, after which weight velocity declined. The peak velocity is similar to standards developed for British children in the 1960s where peak velocities were estimated at 0.85 kg/month (Tanner et al. 1966), but less than median WHO standards of 1 to 1.1 kg/month (World Health Organization 2009). However, both Tanner et al. (1996) and the WHO (2009) estimated peak weight velocity occurring approximately 4 to 6 weeks earlier than we predicted in the SELMA study population. This may be due to difference in estimation methodologies. We may have also estimated later peak velocities than the WHO standards since we only obtained two measurements by one month of age; additional measurements during the first few months of life may have revealed an earlier PGV. We also observed higher velocities among boys during early infancy which is consistent with standards (Tanner et al. 1966; World Health Organization 2009).

The growth modeling approach presented here has several strengths and limitations for future application. Beyond a more complete characterization of infant growth compared to cumulative weight measures, this method can be applied to other measurements (e.g., height, head circumference) and can be characterized beyond infancy. Instantaneous velocities for specific time periods coinciding with ongoing exposures, or a priori critical windows can be estimated. Further analysis of growth acceleration can be achieved by taking the second derivative of the logistic growth curve. The availability of simple, individual child growth metrics also allows flexibility for subsequent regression modeling.

However, adequate reconstruction of growth velocity curves requires serial anthropometric measurements with limited measurement error. This may only be feasible in environmental epidemiology studies with medical record data linkage. The frequency of measurements also affects model-extrapolated growth metrics and nonlinear model choice. The growth metrics presented here should be interpreted as approximations, with further investigation needed to determine clinical relevance. If there were numerous measurements recorded within the first few weeks of life, a triple logistic or other nonlinear model may be required to adequately characterize post-birth weight loss. We modeled the unconditional growth curve of each child individually, implying that shape is determined by weight and age measurements only. In our second step, we evaluated shifts in the curve conditioned on exposure and covariates. While this adds simplicity to the nonlinear modeling step, alternative strategies are available for modeling all children simultaneously, with some able to condition on exposure and demographic variables. These include mixed effects models (Grajeda et al. 2016; Grimm et al. 2011), shape invariant models (Beath 2007; Cole et al. 2010), and Bayesian approaches (Arjas et al. 1997; McKeague et al. 2011). Future studies are needed to compare our approach with alternative strategies.

6. CONCLUSION

We presented a novel application of nonlinear growth models for assessing environmental exposures during pregnancy in relation to childreńs growth. Using a double logistic model, we characterized several aspects of infant growth including the duration and tempo of the infant growth spurt, weight velocity, and the post-spurt infant weight plateau. We found that this method provided insight into how prenatal PFOA exposure may shift child growth trajectories. Specifically, we observed that PFOA-related lower birthweight was followed by a delay in peak growth and a higher infant weight plateau. Follow-up of SELMA participants will help further characterize how prenatal exposures may impact child and adolescent growth trajectories. Future studies are needed to confirm findings presented here and investigate other aspects of postnatal growth in relation to environmental exposures, including height and BMI.

HIGHLIGHTS.

• Child growth trajectory modeling provides insight into individual growth dynamics

• Prenatal PFOA exposure was associated with a delay in infant growth

• Estimated growth metrics may identify mechanistic differences in growth restriction

ABBREVIATIONS

PFOA

perfluorooctanoic acid

PGV

peak growth velocity