A 450 million years long latitudinal gradient in age‐dependent extinction

Abstract

Leigh Van Valen famously stated that under constant conditions extinction probability is independent of species age. To test this 'law of constant extinction', we developed a new method using deep learning to infer age‐dependent extinction and analysed 450 myr of marine life across 21 invertebrate clades. We show that extinction rate significantly decreases with age in > 90% of the cases, indicating that most species died out soon after their appearance while those which survived experienced ever decreasing extinction risk. This age‐dependent extinction pattern is stronger towards the Equator and holds true when the potential effects of mass extinctions and taxonomic inflation are accounted for. These results suggest that the effect of biological interactions on age‐dependent extinction rate is more intense towards the tropics. We propose that the latitudinal diversity gradient and selection at the species level account for this exceptional, yet little recognised, macroevolutionary and macroecological pattern.

We developed a new method using deep learning to infer age‐dependent extinction and analyzed 450 myr of marine life across 21 invertebrate clades. We found that extinction rate significantly decreases with age in > 90% of the cases. We propose that the latitudinal diversity gradient and selection at the species level account for this exceptional, yet little recognized, macroevolutionary and macroecological pattern.

Introduction

Leigh Van Valen’s Law of Constant Extinction (Van Valen 1973) states that under constant ecological conditions the probability for a species to go extinct is independent from its age, that is, the time passed since its origination. This idea has been the focus of a number of paleontological studies providing evidence for increased extinction risk with stratigraphic duration (Pearson 1992), for the opposite (Finnegan et al. 2016), or even giving full support to the law of constant extinction (Quental & Marshall 2013; Alroy 2014). Unfortunately, although the law of constant extinction has enormous implications to understand the evolution of diversity and the mechanisms driving species extinct, testing it empirically is difficult, due to sampling biases (Foote 1994; Wiltshire et al. 2014), scale issues (Barnosky 2010), and because overall fluctuations in the extinction rate occur in time (Quental & Marshall 2013; Marshall 2017).

Here we develop a method to infer age‐dependent extinction (ADE) rates from fossil occurrence data using deep learning within a neural network framework (hereafter ADE‐NN). Differently from previous efforts (Quental & Marshall 2013; Alroy 2014), ADE‐NN evaluates whether the extinction rate changes with species age while accounting for the incompleteness of the fossil record and for the limited temporal resolution characterising the dating of most fossil remains. We used ADE‐NN to classify fossil datasets among five discrete categories of age‐dependent extinction rates representing (1) strongly and (2) moderately decreasing rates with age, (3) stochastically constant rates (i.e. extinction rate independent of age), and (4) moderately or (5) strongly increasing extinction rates with age.

In modern day (Mittelbach et al. 2007; Soria‐Carrasco & Castresana 2012; Pyron & Wiens 2013) as well as in past ecosystems (Crame 2001; Buzas et al. 2002; Allen & Gillooly 2006; Jablonski et al. 2006; Mittelbach et al. 2007; Jablonski et al. 2013), both species diversity and extinction risk have been shown to generally change with latitude. Hence, to account for possible latitudinal effects, we partitioned the record into distinctive clades and then the species within the clades into low‐latitude (within 23° in latitude from the equator), mid‐latitude (from 23° to 46° in latitude from the equator), and high‐latitude (> 46° away from the equator) species, depending on the position of the weighted centre of their geographic distribution on Earth during their existence (Castiglione et al. 2017). This generated 56 subgroups (21 clades x 3 latitudinal bands minus 7 subgroups relative to clades that are not present in the northern latitudinal band). Finally, since mass extinction events represent moments of extremely high extinction rates (Raup 1991; Jablonski 2001), we checked whether the extinction rates differ when comparing species that lived during times of background extinction rate to species lived during the build‐up of a mass extinction.

Material and methods

The fossil record and species ranges

Fossil occurrence data were retrieved from the Paleobiology Database (http://www.paleodb.org) and presented in full in Raia et al. (2016) and Castiglione et al. (2017). The record spans in age from the Late Cambrian to the Late Cretaceous, covering some 450 million years of extinct marine life overall (Fig. S3). Each data point includes the paleocoordinates and the (estimated) minimum and maximum age of the single fossil localities. We treated the records by removing data points lacking a species‐level taxonomic classification (e.g. sp., cf.), or individual localities extending beyond the known fossil record limits of individual clades. After applying these criteria, the final dataset included 14 272 species and 83 183 occurrences. All analyses described below were run at species level.

Modelling age‐dependent extinction

Age‐dependent extinction affects the distribution of species longevities, that is, the time between species origination and their extinction. In particular, if extinction is constant (the null expectation), species longevities are distributed exponentially, following the properties of a random death process. In the presence of ADE, the distribution deviates from the exponential expectation and a Weibull distribution is often used to model longevities in this context (Ezard et al. 2016; Hagen et al. 2017). If extinction is decreasing with species age the shape parameter of the Weibull distribution is smaller than 1, whereas if extinction rate increases with age the shape parameter is greater than 1. Under a shape parameter equal to 1, the Weibull distribution reduces to an exponential, therefore capturing a process of age‐independent extinction. Under this model, the extinction rate μ of a species of age a is:

$$\mu (a)=\frac{k}{s}{\left(\frac{a}{s}\right)}^{k-1}$$ (1)

where k and s are the shape and scale parameters of the Weibull distribution, respectively. Based on the properties of the Weibull distribution, the median of the distribution of longevities is: s(ln 2)1/k.

A recent study (Hagen et al. 2017) described a Bayesian method to infer age‐dependent extinction from fossil occurrence data (hereafter ADE‐Bayes), while explicitly modelling the effects of incomplete sampling determined by the preservation process. The method has been shown to work well under different preservation scenarios but assumes that the age of fossils is known without error. Unfortunately, most fossil occurrences are dated based on the respective stratigraphic ranges, which means that the dates are provided as a range between a minimum and a maximum age. We ran simulations to assess the effect of low temporal resolution in the fossil dates on the performance of the ADE‐Bayes method and found that coarsely dated occurrences tend to bias the results of the ADE‐Bayes model by overestimating the shape parameter of the Weibull distribution (Table S1).

The ADE‐NN method

To tackle the problem of biased ADE estimates in the presence of dating uncertainties, we developed a new method based on neural networks and deep learning (Goodfellow et al. 2016) to detect the presence of age‐dependent extinction (hereafter ADE‐NN) based on fossil occurrences, while accounting for poor temporal resolution of the data. The method, rather than processing the individual fossil occurrences, relies on a set of features designed to describe different properties of the paleontological record, including preservation biases and temporal resolution (see below). We designed ADE‐NN to classify fossil datasets into one of five categories of age‐dependent extinction rate, corresponding to five ranges of values for the shape parameter of a Weibull distribution (Appendix S1). The first category describes a process with strong decrease in extinction rates (strongD) as a function of the species age (i.e. the time since the species appearance in the fossil record), corresponding to species lifespans following a Weibull distribution with shape parameter between 0.2 and 0.6. Under this scenario, young species at the 25% quantile of the distribution of lifespans face an extinction rate ca. 3.7 times higher than older ones at the 50% quantile. Species that survived to reach the 75% quantile of the distribution of lifespans are subject to an extinction rate 10.6 times lower than the initial one. The second category describes a weaker rate decrease associated with age (Weibull shape 0.6–0.8), with a twofold decrease in the rate between the 25% and the 75% quantile of the distribution of lifespans (mild decrease, mildD). The third category represents the null model in which extinction rate is essentially independent of age (Weibull shapes 0.8‐1.2), in keeping with the ‘law of constant extinction’ (constant). The fourth and fifth categories capture scenarios of rate increase with species age with a 30% and a twofold increase in extinction rates between the 25% and the 75% quantile of the distribution of lifespans, respectively (Weibull shapes 1.2–1.4; 1.4–2; mildI, strongI). The relative changes in extinction rates under the different categories are shown in Fig. S1. Although a neural network could be used here to infer the Weibull shape parameter as a continuous value, we preferred a categorical classifier as it allowed us to estimate the probability for a dataset to fall in each category (using the SoftMax function). This in turn allowed us to explicitly quantify the ability of the method to correctly infer or reject ADE scenarios and to establish a probability threshold that yields an arbitrarily low rate of false positives (see Results). Additionally, the five classes are easy to interpret because they offer an immediate view of the ADE process found to accrue to a particular group (either constant, decreasing or increasing extinction rates with age), while the probabilities estimated for each class remain informative of the confidence interval around the shape parameter (e.g. if the true shape parameter is close to the boundary between two categories, the two adjacent categories will likely obtain similar probabilities).

Numerical representation of the fossil data

We implemented four groups of features (totalling 123 features) to describe a fossil dataset, which provide the input for the ADE‐NN method.

1. First, we use a vector counting the species based on the number of sampled occurrences, where the first item in the vector represents the count of species with a single occurrence, the second item is the number of species with two occurrences, etc. The vector is of a fixed size of 101 items, the last one of which includes all species (if any) with more than 100 occurrences. The vector is then normalised so that the items sum up to 1.

2. The next feature is the average temporal bin size which is computed as the mean of the sizes of the temporal ranges across all occurrences in the dataset

3. The third group of features is a vector counting the expected number of species with occurrences found within a single time‐bin, across two time‐bins, and up to 20 time‐bins. This is computed based on the average temporal bin size (see above) and drawing random dates for each occurrence from uniform distributions bounded at the minimum and maximum ages of each fossil occurrence. Any species with samples expected to spread across more than 20 time bins are included in the last item of the vector. The vector is then normalised so that the items sum up to 1.

4. Finally, we use an approximate estimate of the preservation rate, indicating the expected number of fossil occurrences per lineage per myr. This is computed based on a randomisation of the fossil ages as described above, focusing on species with more than one occurrence (i.e. excluding singletons). We resample randomly the ages of the fossil occurrences based on the respective minimum and maximum ages and generate, a vector t of dated occurrences. We then compute an approximate preservation rate q as:

$$q\approx \frac{{\sum }_i^S(N_i-1)}{{\sum }_i^S(max(t_i)-min(t_i))}\text{if}{N}_i>1$$

where S is the number of species and N_i is the number of occurrences for the i ^th species.

Simulated datasets as training, validation and test sets

We generated a total of 130 000 simulated fossil datasets to train, validate and test the ADE‐NN method, under a range of extinction, preservation and time‐binning scenarios. For each simulated dataset we randomly drew the following parameters:

1. The number of total lineages was sampled from a uniform distribution U[50, 1000]. We note that the actual number of sampled lineages will be lower after sampling fossil occurrences as several species might leave no fossil record.

2. The longevity of each lineage was drawn from a Weibull distribution with shape κ and scale λ. To ensure that simulated datasets equally represented all five shape categories (0.2‐0.6, 0.6‐0.8, 0.8‐1.2, 1.2‐1.4, 1.4‐2.0), we randomly selected a category and drew the shape parameter from a uniform distribution within the category’s range. For instance, if the first category was selected, we sampled κ ~ U[0.2, 0.6]. We then sampled the mean longevity of lineages (i.e. the mean of the Weibull) from a uniform distribution l ~ U[1.5, 10] and used it to derive the respective scale [following the procedure introduced in Hagen et al. (2017)]:

   $$\lambda \sim \frac{l}{\mathrm{\Gamma }(1+1/\kappa )}$$

3. The preservation rate was drawn from a uniform distribution U[0.25,1]. As in the simulations described above we then used the preservation rate to sample fossil occurrences based on a Poisson process and on the vector of longevities. Lineages with no fossil records were discarded from the analysis, thus generating the sampling bias expected from empirical data.

4. We binned the age of the fossil occurrences based on time bins of size randomly selected from a uniform distribution U[2, 10].

We then summarised each dataset based on the 123 features described above. We used the first 120 000 datasets as training + validation set and the remaining 10 000 simulations to quantify the test accuracy of the method on independent datasets.

Optimising the neural network configuration and hyper‐parameters

The ADE‐NN method is implemented in Python (v. 3.7) using the TensorFlow (https://www.tensorflow.org) platform via the library Keras (https://keras.io) (Chollet 2018). We trained and validated the neural network based on the 120 000 datasets and tested a number of model configurations to find the settings that maximised the accuracy on the validation set. In all tests, we used a “Glorot normal” kernel initializer, “ReLU” activation function for the hidden layers, and the “SoftMax” function in the output layer to obtain probabilities of the dataset to be included in each class (Goodfellow et al. 2016). In the training phase, we tested batch sizes of 100, 1000 and 10,000 and a number of hidden layers going from 1 to 4 (i.e. 12 different configurations). The number of nodes was set equal to the number of features (123) with the default inclusion of the bias vector (https://keras.io). Under each configuration, we run for up to 10 000 epochs while monitoring the accuracy of the predictions on the validation set (Fig. S1) and replicated the analysis 10 times under different random seeds.

The accuracy obtained from the validation set and averaged across the different numbers of layers was 77.3, 77.6 and 77.7 for batch sizes of 100, 1000 and 10 000, respectively, and we therefore chose to use a batch size of 10 000 in our empirical analyses. Under this setting, the validation accuracy was around 77.7% regardless of the number of hidden layers, but the model with three hidden layers yielded the lowest validation cross‐entropy loss (which measures the distance between predicted and true classification Goodfellow et al. 2016), thus slightly outperforming the other settings (Table S2). The solutions obtained under different seeds were almost identical and the validation accuracies under each setting differed by 0.5–1.9% across replicates.

Analysis of the empirical data

Empirical fossil datasets where transformed into their numerical representation and analysed using ADE‐NN. Since steps 3 and 4 generating the features representing the fossil data involve random draws (see section Numerical representation of the fossil data), we replicated the ADE‐NN 1000 times on each empirical dataset. We then summarised results computing the mean and 95% confidence intervals for the preservation rate q and the probabilities estimated for each category of the Weibull shape (Table S4).

ADE analyses per latitudinal band

We generated subgroups of species for each clade based on their geographic range to assess the effect of latitude on age dependency in extinction rate. In order to attribute individual species to a given latitudinal band, we divided the fossil record into two subsets. The first includes the species with less than five occurrences, whereas the second subset includes remaining species. In the former case, we calculated the geometric centre (the centroid) of the minimum convex polygon including the species occurrences, whereas in the latter we took as the centroid the mean geographic position (i.e. the Central Feature). For each polygon, we chose an adequate geographic projection to better display the species geographical extent. In particular, the total longitudinal extent of considered species ranges from −179 to 179 degrees, whereas the total latitudinal extent ranges from −85 to 80 degrees. Keeping in mind this global extent of the fossil record, we chose three different equal area projection systems to properly compute species’ geographic ranges. Specifically, when a species polygon was comprised within 180 decimal degrees in longitude, we applied the Lambert Azimuthal Equal Area projection. For polygons exceeding 180 decimal degrees and ranging within ± 30 latitudinal degrees, we applied the Mollweide Equal Area projection. Alternatively, if the polygon fell outside the ± 30 decimal degrees of latitude from the equator, we applied the Albers Equal Area projection. Where any of these projections could not be applied, we split the polygons into smaller portions and projected them by using Lambert Azimuthal Equal Area projection. The resulted polygons were, then, intersected with the digitised version of 90 deep past world maps ( https://www.earthbyte.org/paleodem-resource-scotese-and-wright-2018/ ) in order to exclude land portions from marine species geographic extension.

Effects of taxonomic bias and latitudinal band

One potential bias with the fossil record is that species diversity counts might be inflated by unrecognised synonyms and because intraspecific variability is often underestimated (Alroy 2002). This could be problematic because invalid synonyms are most likely present with few occurrences in the record, potentially biasing that extinction rate towards a pattern of rapid decrease over time (i.e. strongD). To account for this, we performed additional analyses after arbitrarily reassigning a number of species occurrences to other species in the record within taxonomic groups (see Supporting Information for more details). The probability of reassignment was inversely proportional to the actual number of fossil occurrences in the record, so that rare species are more likely to be synonymised with abundant species than the other way around. We performed ADE‐NN analyses with three different sub‐sampling schemes, reassigning 10, 20 and 30% of the species occurrences within clades (Tables [Link], [Link], [Link]).

For each ADE‐NN implementation (i.e. full dataset and sub‐sampling schemes), we fitted a generalised linear model (GLM) to the chance of finding strongD as the most appropriate model to describe age‐dependency in extinction rate, using the latitudinal bands as the grouping variable and species diversity (per group per latitudinal band) as the covariate.

Effect of mass extinctions

The law of constant extinction was specifically framed in the context of ‘constant’ ecological conditions as a zero‐sum game of species loss (extinction) and gain (speciation) events. The law has been tested over geological time periods (including Van Valen’s original formulation), always interpreting ecological constancy at the geological time scale. However, during a mass extinction the probability for a species to disappear is statistically higher than during ordinary times (Raup 1991) and potentially unrelated to the species intrinsic capacity for survival (Erwin 2001; Jablonski 2001). Similarly, after a mass extinction the low diversity favours lower extinction rate because of relaxed competition effects on survival (Alroy 2008), which could in turn provide exceptions to any age‐dependent extinction occurring during times of background extinction (Pearson 1992). To account for this, we ran the ADE‐NN models on the 21 clades after removing all the species that lived immediately before or after a mass extinction event. To this aim, we took the last geologic epoch before and the first geologic epoch after each mass extinction event as a reference and removed from the record any species with one or more fossil occurrences falling during these geological horizons. The same was repeated using the last geologic stage before and the first geologic stage after each mass extinction event as a reference. We used the International Chronostratigraphic Chart (v2019/05, Cohen et al. 2013) for stages and epochs boundaries.

Results

Performance of the ADE‐NN method

After optimising the architecture and hyper‐parameters of the neural network based on the validation accuracy and cross‐entropy loss, we evaluated the accuracy of the best ADE‐NN model (batch size of 10 000 and 3 hidden layers) using an independent test set of 10 000 datasets. The test accuracy averaged across 10 random seeds was 78.62% with a test cross‐entropy loss of 0.54. While the error rate is 21.38%, we can use the probabilities assigned to the category corresponding to age‐independent extinction to define a threshold under which we cannot reject the null model even if the highest probability is assigned to one of the other four categories. To do that, we simulated 10 000 additional datasets with settings identical to those use for the training, validation and test sets, except for the shape parameter of the Weibull distribution, which was fixed to 1 (thus yielding age‐independent extinction). The correct category of Weibull shape received the highest probability in 84.02% of the datasets, suggesting a false positive rate around 0.16. However, our simulations indicate that we can reduce the false‐positive error rate if we only reject age‐independent extinction when the respective category receives a probability smaller than a threshold. In particular, rejecting age‐independent extinction when P(0.8 < κ < 1.2) < 0.16 yields a false‐positive rate of 0.047 and this threshold was therefore used in all empirical analyses.

Our simulations showed that the ADE‐NN method strongly outperformed the ADE‐Bayes model in the presence of poor temporal resolution in the fossil data (see also Appendix S1 and Tables S1, S3). The improvement includes lower false‐positive rate and higher true‐positive rate indicating that the ADE‐NN method should be the preferred choice over ADE‐Bayes when the temporal resolution of the data is low (5 myr in our simulations).

Empirical evidence of decreasing age‐dependent extinction rate

We found that species extinction rate significantly decreases with species age in 51 out of 56 subgroups (91.1%, Tables 1, Table S4) when the clade species are partitioned by latitudinal band. In the low‐latitude band, the extinction rate decreases with species stratigraphic duration 21 out of 21 times (16 with strongD; 5 with mildD, Fig. 1). In the mid‐latitude band, the extinction risk decreases with species stratigraphic duration 19 out of 21 times (17 strongD, 2 mildD; Fig. 1) and remains constant into two instances. Finally, in the high‐latitude band the extinction risk decreases with species stratigraphic duration 11 out of 14 times (7 strongD, 4 mildD; Fig. 1), remains constant twice, and weakly increases with age once (Cystoporida bryozoans, Table 1, Table S4).

Figure 1.

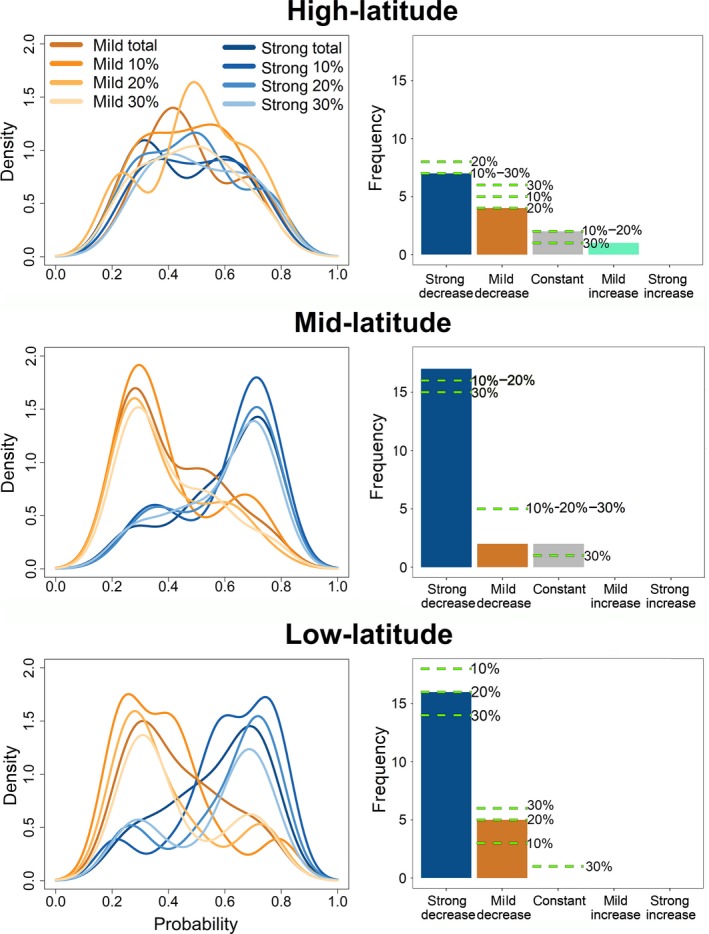
Plots of the probability to find a decrease in extinction rate over time per latitude. Left column: density plots of the probability to find a strong (strongD) or mild (mildD) decrease in extinction rate with species age, across all clades and considering different potential taxonomic biases. The cumulative probability obtained summing strongD and mildD, is close to 1 in most clades. Extinction rates are most strongly decreasing with age at low latitudes, whereas the age dependency weakens (nonetheless remaining the prevalent mode of extinction) at higher latitudes. Tests accounting for potential taxonomic inflation show that the results are robust even if 30% of the species are treated as invalid synonyms. Right column: histograms showing the frequency of each model being the most appropriate per latitudinal band. The horizontal dashed lines represent the same figures under different levels of reassignment of rare species occurrences to other species in the records to account for taxonomic inflation (total = no reassignment, or 10, 20, 30% of reassignments). The only instance for extinction rate increase over time pertains to Cystoporida bryozoans (upper row, light‐green bar).

Table 1.

Most probable model of extinction rate change as a function of species age per taxonomic group and latitudinal band

Clade	Low latitude			Mid latitude			High latitude
	Best model	P_best	P_const	Best model	P_best	P_const	Best model	P_best	P_const
Athyridida	strongD	0.837	0.001	strongD	0.941	0.001	mildD	0.919	0.059
Auloporida	mildD	0.515	0.014	strongD	0.537	0.018	–	–	–
Bellerophontidae	strongD	0.787	0.002	strongD	0.981	0	–	–	–
Cystiphyllida	strongD	0.498	0.026	strongD	0.600	0.035	–	–	–
Cystoporida	mildD	0.602	0.021	strongD	0.886	0.003	mildI	0.493	0.154
Desmoceratidae	strongD	0.625	0.025	strongD	0.958	0.001	strongD	0.587	0.101
Euomphalidae	strongD	0.989	0	mildD	0.764	0.105	–	–	–
Favositida	strongD	0.580	0.011	strongD	0.917	0.002	–	–	–
Fenestrida	strongD	0.988	0	mildD	0.593	0.042	mildD	0.831	0.029
Lophospiridae	strongD	0.996	0	strongD	0.921	0	–	–	–
Orthida	strongD	0.726	0.003	strongD	0.979	0	strongD	0.488	0.027
Orthotetida	strongD	0.938	0	strongD	0.972	0	constant	0.692	0.692
Productida	strongD	0.616	0.001	strongD	0.500	0.002	strongD	0.810	0.001
Proetidae	strongD	0.92	0.003	constant	0.184	0.184	constant	0.347	0.347
Pterineidae	strongD	0.905	0.005	strongD	0.997	0	–	–	–
Rhabdomesida	mildD	0.692	0.033	constant	0.385	0.385	mildD	0.764	0.021
Spiriferida	strongD	0.988	0	strongD	0.666	0.003	strongD	0.855	0.001
Spiriferinida	strongD	0.809	0.001	strongD	0.985	0	strongD	0.530	0.007
Stauriida	strongD	0.897	0.002	strongD	0.765	0.008	strongD	0.603	0.041
Strophomenida	mildD	0.796	0.024	strongD	0.982	0	strongD	0.675	0.008
Trepostomida	mildD	0.763	0.056	strongD	0.623	0.011	mildD	0.790	0.064

The models are classified as strong decrease in the rate over time (strongD), mild decrease in the rate with species age (mildD), constant rate (constant), mild rate increase (mildI). The value P__best represents the probability associated to the most probable model as estimated by the ADE‐NN, while P_{_const} is the probability associated with a model with constant extinction. Rejecting the latter when P_{_const} < 0.16 yields a Type I error rate < 0.05 (see Methods). We found no instance of strong increase in the rate over time.

GLM regression showed that strongD is equally likely to be the most appropriate model at low latitudes as it is at intermediate latitudes (GLM regression slope, P = 0.196) but not at high latitudes (factor latitude, P ≪ 0.001), where indeed we found evidence for weaker age‐dependent extinction (Fig. 1). Species diversity significantly differs per latitudinal band (covariate species diversity, P ≪ 0.001) as the interaction terms (GLM, mid latitude per number of species, P = 0.014; high latitude per number of species, P ≪ 0.001).

Although accounting for strong taxonomic inflation slightly decreased the support for strongD in favour of mildD (Fig. S4), models with extinction rates decreasing with age were found to be the most probable in 53 cases out of 56 (36 strongD, 17 mildD), even when reassigning 30% of the species occurrences. These results indicate that the notion of decreasing extinction rate with stratigraphic duration holds firm and pervasive after accounting for taxonomic inflation (Fig. 1, Tables [Link], [Link], [Link]).

The analysis of entire clades (irrespective of geographic range) show decreasing extinction rate with species age as the dominant mode 21 out of 21 times (Table S8). Among these, strongD is the most probable model in 19 cases. Restricting the analysis to time intervals of background extinction (i.e. after removing either stages or epochs bracketing mass extinctions) did not change considerably these results, with significant evidence for decreasing extinction rate with species age still found across all clades (Table S9). The dominant mode of age dependent extinction remained strongD, which was the preferred mode of extinction in 14 cases. Finally, separate analyses of individual time intervals of background extinction showed that there are no obvious temporal trends in extinction modes, with instances of strongD and mildD extinction similarly scattered across all intervals (Table S10).

Discussion

The prevalence of strongD as the best‐fitting model indicates that most species within clades live short lives (because of the extremely high extinction risk for very young species), whereas those which survive the early stages are likely to experience asymptotically decreasing extinction risk. This observation is consistent with the idea that species behave as units of selection. Under species selection (Jablonski 2008), taxa possessing biotic traits conferring better survival, such as large geographical range or generalist ecological niche, are positively selected, meaning that they endure higher speciation or lower extinction rates, on average, over time (Gilinsky 1986; Jablonski 2008). At high latitudes species tend to be tolerant to climatic variation, a pattern that has been observed even in deep‐time fossil records (Blackburn & Gaston 2003; Zacaï et al. 2018). This greater climatic tolerance, together with the presumably lower intensity of biotic interactions (because of the low diversity) and slower diversification dynamics (Wiens et al. 2006; but see Fortelius et al. 2015 for a counter example), makes high‐latitude areas the least susceptible to species selection. In contrast, the higher standing diversity toward the tropics makes the network of biotic interactions more complex. In an extensive review Schemske et al. (2009) found biotic interactions were never found to be less important at low, as compared to high, latitudes. This result holds true in spite of the fact that the importance of such interactions could be relaxed by ecological specialisation (Safi & Kerth 2004; Raia et al. 2016) and long‐term climatic variability (Rabosky et al. 2018; Rangel et al. 2018) and suggests that species selection is strongest in the tropics. It is thus unsurprising that strongD is more prevalent in the tropics, where species diversity and the potential for intense biotic interactions are higher.

The ubiquity of decreasing age‐dependent extinction rates across the vast majority of clades indicates that decreasing extinction rates throughout species lifespans represent a general rule governing species survival. While finding a definitive explanation for the mechanisms determining this extinction pattern might be unfeasible by using the fossil record, the latitudinal trend towards stronger age dependency and higher species richness towards the low latitude suggests that biotic interactions might play an important role in shaping spatial extinction patterns. Our results are thus not inconsistent with the Red Queen hypothesis, stating that biotic interactions shape the pace of evolution (Van Valen 1973; Quental & Marshall 2013; Žliobaitė et al. 2017). Rather, we argue the effect on survival rates of such interactions is predictably variable across space, being more intense towards the tropics, and generating a temporal pattern of decreasing extinction rate within clades, favoured by the selection of species bearing survival‐related traits.

Software and Data Availability

The ADE‐NN method is implemented in Python v. 3. The code is included in the PyRate open‐source software package (https://github.com/dsilvestro/PyRate, Silvestro et al. 2019). The input files, the pre‐trained neural network, and instructions to reproduce all results shown here are archived in a Zenodo public repository with https://doi.org/10.5281/zenodo.3537888.

Author Information

The authors declare no Competing Financial Interests.

Authorship

P.R. and D.S. conceived the study. S.C., A.M., M.M. and C.S. collected the data. M.D.F., A.M., S. C. and D.S. developed the methods and performed the analyses. All the authors contributed to develop the ideas and writing of the manuscript.

Data Accessibility Statement

Data available from the Dryad Digital Repository: https://doi.org/10.5281/zenodo.3537888.

Supporting information