Comparison of affinity ranking using AutoDock-GPU and MM-GBSA scores for BACE-1 inhibitors in the D3R Grand Challenge 4

Abstract

Molecular docking has been successfully used in computer-aided molecular design projects for the identification of ligand poses within protein binding sites. However, relying on docking scores to rank different ligands with respect to their experimental affinities might not be sufficient. It is believed that the binding scores calculated using molecular mechanics combined with the Poisson-Boltzman surface area (MM-PBSA) or generalized Born surface area (MM-GBSA) can more accurately predict binding affinities. In this perspective, we decided to take part in Stage 2 in the Drug Design Data Resource (D3R) Grand Challenge 4 (GC4) to compare the performance of a quick scoring function, AutoDock4, to that of MM-GBSA in predicting the binding affinities of a set of β-Amyloid Cleaving Enzyme 1 (BACE-1) ligands. Our results show that re-scoring docking poses using MM-GBSA did not improve the correlation with experimental affinities. We further did a retrospective analysis of the results and found that our MM-GBSA protocol is sensitive to details in the protein-ligand system: i) neutral ligands are more adapted to MM-GBSA calculations than charged ligands, ii) predicted binding affinities depend on the initial conformation of the BACE-1 receptor, iii) protonating the aspartyl dyad of BACE-1 correctly results in more accurate binding affinity predictions.

Introduction

Accurate estimation of protein-ligand interactions and the energetic basis of ligand binding are of great importance for successful structure-based drug discovery projects. Much effort has been devoted to develop computational methods for evaluating the binding of a ligand to a protein of interest and the strength of that binding, including docking and scoring approaches [1], virtual screening [1,2], and physics-based free energy methods [3].

Blind community wide-challenges such as the Drug Design Data Resource (D3R) Grand Challenge [4] and the Statistical Assessment of Modeling of Proteins and Ligands (SAMPL) (https://samplchallenges.github.io/) [5] provide an excellent platform for developers to test and validate their computer-aided drug design methodologies against experimental datasets. Moreover, the unbiased setting of these challenges allows the participants to compare the performance of their workflows and techniques to other computational methods in the field, thus highlighting potential areas of enhancement.

Every year, the D3R Grand Challenge organizers release pharmaceutically relevant datasets of protein-ligand complexes for the evaluation of ligand pose prediction and binding affinity protocols. This year, we decided to bring together our expertise in pose prediction and binding free energy calculations to participate in the D3R Grand Challenge 4 (GC4) to rank a set of ligands based on their predicted affinities towards the β-Amyloid Cleaving Enzyme 1 (BACE-1) involved in Alzheimer’s disease [6].

In Stage 1a of D3R GC4, the participants were asked to predict the binding affinities of 154 BACE-1 compounds using any available PDB structure data or binding data. At the end of Stage 1, co-crystal structures of additional 20 ligands were released by the D3R organizers, allowing the participants to use these structures to refine the affinity predictions. In the present work, we describe our participation in Stage 2, where we predicted the binding affinities of the 154 ligands.

Many previous studies have evaluated the ability of molecular mechanics combined with the Poisson-Boltzmann surface area (MM-PBSA) and molecular mechanics combined with generalized Born surface area (MM-GBSA) [7,8] methods to predict ligand binding poses and binding affinities, and compared the accuracy of these predictions to that of docking scores [9–18]. Kaus et al. [9] have reported that MM-GBSA method performs better than standard scoring functions in ranking binding poses. Similarly, Rastelli et al. [15] have shown that both MM-GBSA and MM-PBSA rescoring methodologies improve the affinity ranking estimated by AutoDock scoring function.

On the other hand, participants in past D3R Grand Challenges have reported poor correlations between their estimated MM-GBSA binding scores and experimental affinities [16–18]. In fact, MM-GBSA and MM-PBSA are not always accurate methods for drug design projects because the quality of the results appears to depend on the protein-ligand system, the ligand sets, and details used in the method, such as the interior dielectric constant, the continuum-solvation method, the charges, and the entropies [7].

The ambition of this collaborative report was to evaluate only the binding affinity prediction accuracy of MM-GBSA scores relative to AutoDock4 scores. Therefore, starting with the same binding poses generated using AutoDock-GPU, we compared our predicted affinities with the experimental affinities for the two scoring approaches – AutoDock4 and MM-GBSA. Based on the correlation statistics and performance metrics obtained for both submissions, we found that re-scoring the affinities using MM-GBSA free energy estimates did not improve the correlation with experimental values. During post-analysis, we found that MM-GBSA scores depend on the initial protein conformation, the protonation states of the BACE-1 active site, and the charge of the ligands, and we were able to improve our MM-GBSA-based correlation metrics retrospectively.

Theory and Methods

AutoDock4 energy score

The AutoDock4 scoring function [19] can be described as a classical (additive) force field supplemented with an implicit solvation model and a ligand entropy term. The force field consists of three terms: a 12–6 Lennard-Jones potential, a Coloumb potential with a distance-dependent dielectric constant, and a 12–10 potential for hydrogen bonds. The implicit solvation model is an additive pairwise potential in which the solvent accessibility of each atom is estimated based on the proximity of surrounding atoms [20]. It is an empirical model that depends both on atom type parameters and the partial charges [19]. It accounts for (de)solvation of both the ligand and the receptor. The ligand entropy term accounts for the loss of conformational freedom of the ligand upon binding, adding a penalty that is linearly dependent on the number of rotatable bonds.

Several approximations are employed in AutoDock, in order to make the calculations suitable for rapidly docking large libraries of compounds. Scores are single point evaluations of the scoring function, thus neglecting the majority of entropic contributions. Bond lengths and bond angles are treated as rigid and non-polar hydrogens are omitted. Rotatable bonds are allowed to rotate freely, neglecting rotamer preferences. Partial charges are based on the empirical method from Gasteiger and Marsili [21], and can be considered “lower quality” in comparison to charge assignment methods based on some form of electronic structure calculation, even via semi-empirical methods such as AM1-BCC [22].

MM-GBSA score calculations

MM-GBSA calculations are a widely used tool for estimating protein-ligand binding free energies [7,15,23,24]. Some propose these as a reasonable compromise between fast and inaccurate methods like scoring functions [25] to computationally rigorous but expensive methods like alchemical free energy calculations [26].

MM-GBSA calculations are usually performed on an set of protein-ligand binding conformations generated using a short molecular dynamics (MD) simulation, which can either be in implicit or explicit solvent. MM-GBSA energy values, which provide an estimate of the free energy of binding (ΔG_bind), are then calculated using end-point estimates given in the equation below:

$$\Delta G_{bind}=G_{complex}-G_{receptor}-G_{ligand}$$ (1)

The free energy for each of the complex, receptor and ligand is evaluated using contribution from four different terms

$$G=\langle E_{MM}\rangle +\langle G_{GB}\rangle +\langle G_{SASA}\rangle -T\langle S_{solute}\rangle$$ (2)

where E_MM is the molecular mechanical energy in the gasphase consisting of contributions for electrostatic, van der Waals and internal energies, E_GB is the polar solvation free energy based on the Generalized-Born implicit solvent model, E_SASA is the non-polar solvation term calculated using the solvent accessible surface area (SASA) and TS_solute is the product of the absolute temperature T and the solute entropy S_solute. The solute entropy term can either be ignored (often done for congeneric series) or approximated. The quasiharmonic approximation [27] and normal mode analysis of the vibration frequencies [28] are most commonly used for estimating the solute entropy term.

Here, MM-GBSA scores are reported in units of kcal/mol and are based on end-point free energy estimates. However, they should not be confused with true binding free energy calculations [26], as they involve several additional approximations. Partly as a result, calculated MM-GBSA values are typically much lower (more negative) than experimental binding free energies. The differences arise from the different approximations used to account for the solvation and configurational entropy of the protein and the ligand. Also, water molecules or cavities in the binding pocket are modeled using bulk (continuum) water, which cannot capture the finer details of water-mediated interactions present in explicit water simulations, and in some cases can produce artifactual water placements. Hence in this work, we will be referring the MM-GBSA values as MM-GBSA scores and not MM-GBSA free energies.

Docking protocol

Docking was performed using AutoDock-GPU [29], an OpenCL implementation of AutoDock4 [19]. The search procedure utilizes three types of ligand motion: translation, rotation (of the entire ligand as a rigid body) and rotation of atoms affected by each rotatable bond. The search algorithm is a genetic algorithm (GA) hybridized with ADADELTA [30], a gradient-based optimizer. In every GA generation, all individuals (i.e. poses) are subjected to 500 ADADELTA iterations. The number of GA runs was 100, and each GA performed 10 million score evaluations, totaling 10⁹ score evaluations per docking.

Ligands were prepared using Python scripts that use OpenBabel [31,32] to generate three-dimensional coordinates and to assign AutoDock atom types and Gasteiger-Marsili partial charges [21]. Each ligand was docked to 10 different protein conformations, corresponding to the following PDB IDs (chain): 2B8V (A), 2F3F (C), 2P4J (D), 2WF3 (A), 3L59 (B), 3MSJ (C), 3MSK (A), 4EWO (A), 4FS4 (A) and 4RCF (A). These structures were the selected representatives of different binding pocket conformations. REDUCE [33] added hydrogen atoms while allowing Asn, Gln and His side chains to flip. Then, the standard protocol [34] was used to assign AutoDock4 atom types, partial charges, and determine which bonds are rotatable. After all dockings were performed, the binding pose with the best score, as well as the protein structure it was docked into, constituted the starting structure for the MD simulation and subsequent MM-GBSA calculation.

Macrocycle conformations were explored during the docking by artificially breaking one of the chemical bonds within each macrocycle, generating the corresponding open linear structure which can be modeled as fully flexible during docking. To restore the original bond, and consequently the cyclic structure, a potential is applied to attract the atoms formally bonded to their covalent bond distance. This allows the macrocycle conformation to be fully sampled flexibly during docking.

Nearly all BACE-1 ligands of GC4 share a common substructure that is also found in several PDB structures. This substructure consists of a hydroxyl group attached to a short two-carbon aliphatic chain, followed by an amide. Based on publicly available BACE-1 structures, this substructure has a conserved binding mode, making several hydrogen bonds with the binding pocket. To exploit this information during the docking, we used the ligand in the PDB 4DPF as a template for the position of the common substructure of GC4 ligands. A biasing penalty was applied to three atoms: the hydroxyl oxygen, one of the carbons in the aliphatic chain and the nitrogen in the amide. This penalty increases linearly with the distance from the corresponding atom of the template structure. If this distance is below 1.2 Å, the biasing penalty is zero, and the output score corresponds to the original, unaltered AutoDock4.2 scoring function.

To take advantage of further similarities with BACE-1 ligands in the PDB, we used pose filters to discard docked poses that differ from the binding modes observed in 2F3F, 4DPF and 4K8S. These pose filters act on specific chemical motifs that occur both in GC4 ligands and in these reference structures. The chemical motifs were identified manually by visual inspection, and the filtering process was automated using Python scripts and OpenBabel [35,32].

This docking protocol, including the biasing penalty and pose filters, was used to predict the binding poses of the 20 BACE-1 ligands in Stages 1a and 1b of GC4. In our best performing submissions, which are very similar to the protocol used herein, the binding poses of all 20 ligands were predicted within 2 Å RMSD from the native structure. We describe the performance of variations of this protocol, as well as further details about the methodology in a separate publication [36].

Re-evaluating the binding affinities of the ligands using MM-GBSA scores

We generated a 14ns long MD trajectory for each of the protein-ligand complexes in explicit solvent and then reevaluated the binding scores using end-point MM-GBSA calculations. The MD simulations were performed using the pmemd.cuda module of Amber18 simulation package [37]. We added partial charges to the ligand atoms using the Antechamber program (from Amber 16 package [38]) and AM1-BCC charge model [22]. The simulated system was prepared using tleap (also available in Amber16 package) and used Amberff99sb [39], GAFF version 1.8 [40] and TIP3P water [41] for the protein, ligand and water force field respectively. The protein-ligand complex was placed in a cubic simulation box with 10 Å of water surrounding the complex. We next added Na+ and Cl− ions to neutralize the system and to ensure a salt concentration of 0.1M. The protein heavy atom-hydrogen bonds were constrained using SHAKE. The simulation used a time step of 2 fs. Particle mesh Ewald method was used to evaluate long-range electrostatic interactions with 9.0 Å cutoff for the real space electrostatics and van der Waals forces.

We first minimized the ligand, water, and the ions for 1000 steps with 25 kcal/mol-Ų positional restraints on the protein, followed by another 1000 steps of minimization with the protein restraints reduced to 10 kcal/mol-Ų. Next, the system was heated from 10 K to 300 K in NVT ensemble for 140 ps with 10 kcal/mol-Ų restraints on the protein-ligand complex. We then successively decreased the restraints on the protein-ligand complex for 20 ps to first 5 and then to 2 kcal/mol-Ų, followed by 2 kcal/mol-Ų restraint only on the ligand. We used Langevin thermostat with a collision frequency of 2 ps⁻¹ to maintain the temperature of the system. We simulated the system for 14 ns in NPT ensemble for the production run. Isotropic pressure scaling was used to regulate the pressure with a relaxation time of 2 ps. The first four ns was discarded as equilibration.

We saved the positions of the atoms every 100 ps during MD. The final trajectory used for the MM-GBSA calculations consisted of 100 frames that correspond to the last 10 ns of the production trajectory. MM-GBSA scores were calculated using the MMPBSA.py program [42] in Amber16 at a salt concentration of 0.1 nM and using the GBneck2 model [43]. Quasi-harmonic approximation was used to approximate the solute entropy.

The MD simulation for each protein-ligand complex took about four hours on a NVIDIA GeForce GTX TITAN X GPU (Maxwell architecture). The MM-GBSA calculations ran for about six hours on a single Intel Xeon CPU (E5–2630 v3 2.40 GHz).

Results and Discussions

Our main goal in this work was to see whether re-scoring docked poses with MM-GBSA scores can improve the correlation of predicted binding affinities with experimental values. We used AutoDock4.2 scores and MM-GBSA scores to rank the binding affinities of BACE-1 ligands in Stage 2 in D3R GC4. Our workflow did not involve visual inspection of docked poses. For this reason, the results reported herein are representative of automated approaches.

The performance of docking and MM-GBSA scores in predicting the affinities of the 154 ligands is assessed by the Kendall’s τ and Spearman’s ρ rank correlation coefficients. We also report Pearson’s r and R². We have compiled all these metrics for our predictions in Table 1. Since all metrics lead to the same conclusions, we base our discussion on Kendall’s τ values, which is the first metric reported in the D3R evaluation page.

Table 1.

Correlation coefficients between predicted and experimental affinities. R² is Pearson’s r squared. Standard deviations were calculated from 10000 bootstrap samples.

	All (n=154)
	Kendall’s τ	Pearson’s r	Spearman’s ρ	R2
AutoDock4 a	0.19 ± 0.06	0.30 ± 0.09	0.27 ± 0.08	0.09 ± 0.05
MM-GBSA b	0.20 ± 0.06	0.31 ± 0.08	0.30 ± 0.08	0.10 ± 0.05
	Charge 0 (n=18)
	Kendall’s τ	Pearson’s r	Spearman’s ρ	R2
AutoDock4	0.05 ± 0.23	0.25 ± 0.32	0.06 ± 0.30	0.06 ± 0.14
MM-GBSA	0.44 ± 0.15	0.65 ± 0.11	0.62 ± 0.18	0.42 ± 0.13
	Charge +1 (n=132)
	Kendall’s τ	Pearson’s r	Spearman’s ρ	R2
AutoDock4	0.23 ± 0.06	0.32 ± 0.09	0.31 ± 0.09	0.10 ± 0.06
MM-GBSA	0.19 ± 0.07	0.30 ± 0.09	0.27 ± 0.09	0.09 ± 0.05

^aFig. 2a, submission cq7ug

^bFig. 2b, submission utgv6

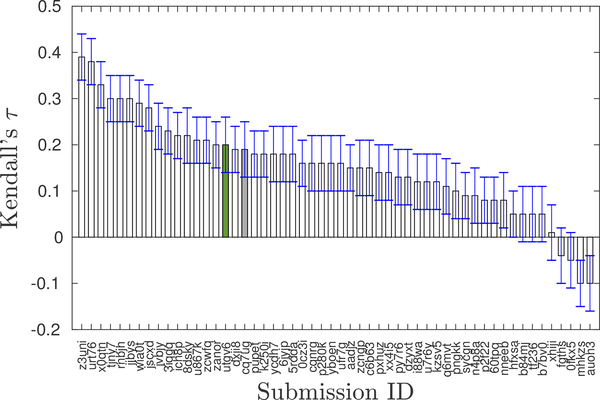
Re-scoring docked poses with MM-GBSA did not improve correlation with experimental values. The Kendall’s τ between experimental pK_d and AutoDock4.2 scores (submission cq7ug) is 0.19 ± 0.06, and that of MM-GBSA scores (submission utgv6) is 0.20 ± 0.06. Thus, the predictive performance of these methods is statistically identical and both of them correlate poorly with the experimental values. Nevertheless, our predictions are statistically better than a random prediction which has an average Kendall tau of zero. In the context of all submissions to Stage 2 of GC4, our predictions ranked in the top third (Fig. 1, rank 16 and 18 out of 54 participants).

Fig. 1. Ranking of our submissions based on Kendall’s τ in the BACE-1 affinity ranking challenge.

The submissions include both structure-based and ligand-based predictions. The gray bar corresponds to the submission with AutoDock score and the green one for the one with re-scored binding affinities using MM-GBSA calculations. There was negligible improvement in the correlations with experiments with the re-scored submission.

MM-GBSA calculations have more detailed representation of the underlying physics at play than docking scores and literature work from other groups suggested they would be more accurate [9,11,13]. So it was perhaps surprising that there was not any improvement in the affinity estimation with the MM-GBSA rescoring. We also saw that there was no correlation between the AutoDock4 scores and MM-GBSA scores (Kendall’s τ equal to −0.06 ± 0.05). These findings prompted us to investigate more about our protocol to check whether any change in the simulation conditions could improve the results.

Ligands with different net charge have different correlation metrics

With the goal of identifying aspects of the MM-GBSA approach that could be improved, we searched for features that are associated with particularly good predictions. Our ligand dataset consisted of both positive and neutral ligands. Previous work by Rastelli et al. [15] has shown that there is a decrease in correlation between predicted and experimental affinities for ligands with different formal charges, which led us to separately analyze ligands with different formal charges (Table 1).

We found that the predicted affinities of ligands modeled in a neutral state (n=18) exhibited better rank correlation (Kendall’s τ of 0.44 ± 0.15) with experiment than those for ligands modeled with a +1 charge (Kendall’s τ of 0.19 ± 0.07). This suggests that neutral ligands are more amenable to MM-GBSA calculations. Sun et al. [10] have reported ligand binding affinity prediction accuracy degrading with net charge of the ligand. Their Pearson’s r degraded from 0.608 ± 0.003 for ligands with net charge zero to 0.564 ± 0.003 for those with net charge one. It is to be noted here, that in our study the sample size for neutral ligands is small (only 18 ligands).

Predictive performance varies with protein conformations

A total of ten protein conformations were considered for docking the ligands. The MM-GBSA calculations were performed using the protein conformation that produced the ligand pose with the best docking score, according to the AutoDock4.2 scoring function. The majority of ligands were simulated in the protein conformations associated with PDBs 4EWO (n=75) and 2WF3 (n=69).

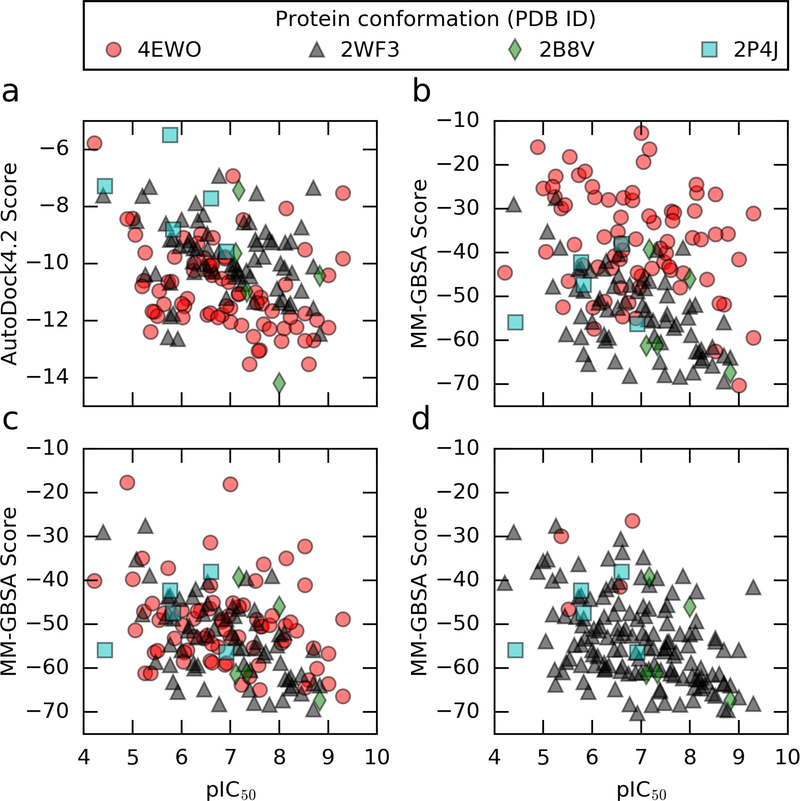
We next decided to investigate whether different protein conformations resulted in different correlation metrics. Table 2 lists the correlation statistics for subsets of ligands docked and simulated in different protein conformations. Fig. 2 plots the predicted MM-GBSA scores against the experimental binding affinities for different protein conformations.

Table 2.

Correlation coefficients between predicted and experimental ligand binding affinities for subsets of BACE-1 ligands modeled in different protein conformations. R² is Pearson’s r squared. The standard deviations do not account for the experimental uncertainty. 4EWO, 2WF3, 2B8V, and 2P4J are the PDB codes of the different protein conformations used. n refers to the total number of ligands in each dataset. For MM-GBSA scores, affinities of ligands modeled in 4EWO have the weakest correlation with the experimental affinities. For AutoDock4, affinities of ligands modeled in different protein conformations have similar correlation coefficients with the experimental values.

	4EWO (n=75)
	Kendall’s τ	Pearson’s r	Spearman’s ρ	R2
AutoDock4	0.26 ± 0.09	0.32 ± 0.14	0.36 ± 0.12	0.10 ± 0.09
MM-GBSA	0.15 ± 0.09	0.27 ± 0.12	0.22 ± 0.12	0.08 ± 0.06
	2WF3 (n=69), 2B8V (n=5) or 2P4J (n=5)
	Kendall’s τ	Pearson’s r	Spearman’s ρ	R2
AutoDock4	0.23 ± 0.09	0.33 ± 0.12	0.29 ± 0.12	0.11 ± 0.07
MM-GBSA	0.36 ± 0.07	0.53 ± 0.09	0.50 ± 0.09	0.28 ± 0.09

Fig. 2.

Plots of predicted scores against the logarithm of experimental binding affinities. a) Docking scores (submission ID cq7ug). b) MM-GBSA scores (submission ID utgv6). AutoDock4 scores and MM-GBSA scores had similiar correlation metrics in our original binding affinity prediction (submissions a and b). c) MM-GBSA scores based on MD simulation in 4EWO were modified to have a single protonated aspartate instead of two. Correlation metrics improved with new protonation state. d) 71 out of 75 ligands originally simulated in 4EWO were simulated in 2WF3 instead. We saw further improvement in correlation metrics with the 2WF3 receptor structures.

The subset of ligands simulated in 4EWO exhibited poorer rank correlation with experiment (Kendall’s τ of 0.15 ± 0.09) for the MM-GBSA scores compared to the other protein structures used - 2WF3, 2B8V, 2P4J (Kendall’s τ of 0.36 ± 0.07). For AutoDock4 scores, we see similar rank correlation coefficients for different protein conformations. Hence in the succeeding work, we looked into the protein structure 4EWO to see whether we modeled it correctly.

Protonation states affect MM-GBSA scores

We noticed while doing post-analysis of our results that the catalytic aspartyl dyad (Asp32, Asp228) of BACE-1 in the prepared protein structure for 4EWO had both aspartates in the protonated form (i.e., Asp32^H, Asp228^H). This is a possible source of error, because in the apo state, Asp32 is protonated and Asp228 is de-protonated in the active pH range (3.5–5.5) of BACE-1 [44]. Although the protonation state of the aspartyl dyad changes in the presence of inhibitors [45, 46], it is a safer choice to model the aspartyl dyad as Asp32 protonated, and Asp228 de-protonated (Asp32^H, Asp228⁻). Hence, we decided to recalculate the MM-GBSA scores of the ligands docked and simulated in 4EWO, but with the Asp32^H, Asp228⁻ protonation state of the 4EWO structure.

The correlation statistics of the 4EWO simulations with the Asp32^H, Asp228⁻ protonation state are reported in Table 3 and the plot of predicted versus experimental affinities is depicted in Fig. 2c. Also, Fig. S1 shows the distribution of the MM-GBSA scores for the two protonation states. Overall, the MM-GBSA scores were lower for the single protonated aspartyl dyad compared to the double protonated, indicating that the binding pose is more stable for the single protonation state. The Kendall τ improved by about one standard deviation, confirming that the Asp32^H, Asp228⁻ form is more adequate than modeling both Asp as protonated.

Table 3.

Correlation coefficients between predicted and experimental ligand binding affinities for the entire BACE-1 ligands set. R² is Pearson’s r squared. The standard deviations do not account for the experimental uncertainty. n refers to the total number of ligands. Ligands originally simulated in 4EWO with a double protonated aspartyl dyad (Asp32^H Asp228^H), were modeled again in 4EWO with a single protonated aspartyl dyad (Asp32^H Asp228⁻) or in 2WF3 structure also with a single protonated aspartyl dyad. Compared to 4EWO with Asp32^H Asp228^H, using 4EWO with Asp32^H Asp228⁻ improved the correlation between predicted and experimental binding affinities. The highest correlation between predicted and experimental affinities was obtained using the MM-GBSA method and 2WF3 structure.

	Retrospective calculations (n=154)
	Kendall’s τ	Pearson’s r	Spearman’s ρ	R2	Modifications to ligands originally simulated in 4EWO
MM-GBSAc	0.25 ± 0.06	0.38 ± 0.08	0.37 ± 0.08	0.15 ± 0.06	4EWO structure modeled as Asp32H Asp228−
MM-GBSAd	0.30 ± 0.05	0.44 ± 0.07	0.44 ± 0.07	0.20 ± 0.06	Ligands docked and simulated in 2WF3 structure
AutoDock4	0.21 ± 0.06	0.29 ± 0.09	0.29 ± 0.08	0.08 ± 0.05	Ligands docked to 2WF3 structure

^cFig. 2c

^dFig. 2d

Moreover, we computed the RMSD of the ligands between the initial docked poses and the final states at the end of the MD simulations for the two protonation states of 4EWO: i) Asp32^H, Asp228^H and ii) Asp32^H, Asp228⁻. We used Chimera [47] to align the active site of each initial BACE-1-ligand complex to the last frame of the corresponding MD trajectory. The alignment of the active site was done within 5 Å of the ligand. Then, we computed the RMSD values with Chimera. Out of 75 ligands, 54 had lower RMSD values when docked and simulated in BACE-1 with the single protonated aspartyl dyad (Asp32^H, Asp228⁻). The RMSD values are reported in the Supplementary Information available on https://github.com/MobleyLab/D3R-2018-AutoDock-MMGBSA/blob/master/RMSD.csv. This result shows that the binding mode of BACE-1 ligands depends on the protonation states of aspartates 32 and 228 and confirms that it is better to model the protonation state of BACE-1 as Asp32^H, Asp228⁻ for the given ligand dataset. Overall, these findings suggest that in large-scale binding affinity calculations, the protonation state of the protein should be treated carefully.

Simulating in 2WF3 instead of 4EWO improves calculated binding affinities

Since the correlation between predicted and experimental affinities was better for the subset of ligands modeled in the structure 2WF3 than in 4EWO (Table 2), we recalculated the docking and MM-GBSA scores for the ligands modeled in 4EWO using the 2WF3 structure instead. The protonation state of the 2WF3 structure was modeled as Asp32^H, Asp228⁻. Then, the correlation coefficients on the entire set were computed using the updated scores (Table 3). The performance of MM-GBSA improved, displaying a Kendall τ equal to 0.30 ± 0.05, while the performance of docking remained constant (Kendall τ equal to 0.21 ± 0.06). This shows that MM-GBSA is potentially better than docking, in agreement with the more accurate physical description, but the results are sensitive to modeling choices, such as protein conformation and protonation state, making it difficult to achieve optimal predictive performance in a prospective context.

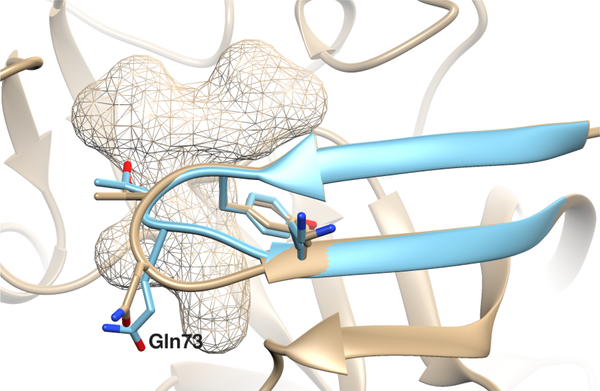
The largest difference between 2WF3 and 4EWO is in the ‘flap’ region (Fig. 3), which interacts extensively with BACE-1 ligands. Interestingly, docking scores are generally lower when docking to 4EWO (Fig. 2a), while MM-GBSA scores are lower when simulated in 2WF3 (Fig. 2b and S2). The exact reasons behind this opposite trend are unknown, but we speculate that none of the 10 protein conformations used for docking was “good enough” to accommodate the 75 ligands that displayed lower (i.e. better) docking scores in 4EWO. Arguably, the docking score was better in 4EWO because the flap is slightly more open, thereby accommodating ligands that could not fit as well in 2WF3. On the other hand, we argue that 2WF3 is more representative of the actual protein-ligand complex, resulting in lower (i.e. better) MM-GBSA scores on average.

Fig. 3.

Differences in the ‘flap’ region formed by the residues 67–75 in the 4EWO (in tan) and 2WF3 (in blue) co-crystal structures of BACE-1. The mesh region is the binding site for the macrocycles in the D3R dataset. The β-hairpin of the ‘flap’ region of 2WF3 is narrower than 4EWO with the Gln73 side-chain being pointed towards the binding site. This results in the binding pocket of 2WF3 being slightly smaller than that of 4EWO.

Overall, these arguments highlight the sensitivity of docking to receptor conformation, and motivate the inclusion of flexibility into the receptor [48], not only for the improvement of docking methodology by itself, but also for providing better docked poses for free energy calculations.

In this study, we looked at two different parameters for the MM-GBSA calculations, namely protonation state and protein conformation during our retrospective analysis. Both of these parameters turned out to have non-trivial impact on the calculated binding affinities. However, they are many more MM-GBSA calculation parameters which can possibly affect the binding affinities which were not explored in the current work.

We performed the MM-GBSA calculations using the GBneck2 model in this work, which has not, to our knowledge, been benchmarked against older GBSA models (GB-HCT, GB-OBC1 and GB-OBC2 [49,50]) for affinity prediction. Protein targets are sensitive to GBSA models [10], hence using older GBSA models might improve the binding affinities.

Another option is to perform MM-PBSA calculations instead, which are physically more accurate and computationally more expensive. In fact, we tried during the early stages of the D3R GC4 to implement the PBSA model utilizing the AMBER package, but we did not get reasonable binding free energy predictions (some binding free energy values were positive). Due to the short timeframe of the challenge, we did not troubleshoot the PBSA implementation and proceeded with the MM-GBSA approach.

Also, both MM-GBSA and MM-PBSA methods strongly depend on a number of parameters such as the force field, the dielectric constant, the radii, the studied protein-ligand system, and the length of the MD simulations [10,24,51]. Thus, we think that with a careful choice of simulation protocol and optimized parameters, we could reach the same prediction accuracy using both MM-GBSA and MM-PBSA methods.

We used the popular ‘single trajectory protocol’ [52] in this work, which involves simulating only the protein-ligand complex and re-purposing the bound conformations of the protein and ligand for the unbound calculations. It is assumed that the protein and the ligand sample similar conformations in the bound and unbound states which might not be always valid. It may be worth trying the ‘multiple trajectory protocol’ in the future since the macrocycles do not have much flexibility in the binding pocket due to their size, and might possibly sample other conformations when simulated in pure solvent.

Other parameters which could be investigated in this context are different entropic approximations, ligand charge models and the solute or interior dielectric constant [14].

Lastly, another avenue worth exploring from a cost-cutting point of view is to use single-point minimized structures for the MM-GBSA calculations, similar to single-point docking score calculations. There are studies present in the literature [15,24] which have shown similar correlations between MM-GBSA scores obtained using single-point structures and those using ensembles of MD generated structures. However, recently published literature suggests that most studies still use multiple conformational snapshots from MD for the MM-GBSA calculations [53–55].

The poor performance of our MM-GBSA protocol is consistent with other studies reporting the participation of other researchers in previous D3R Grand Challenges [16–18]. Different MM-GBSA parameters were used in our work and these previous studies. While Réau et al. [16] performed their MM-GBSA calculations using the OBC1 Generalized model on a single ligand-protein structure after minimization, Salmaso et al. [18] used three replicas of 2 ns of MD simulations for each protein-ligand system. Also, Salmaso et al. used a different GB model developed by Onufriev-Bashford-Case [56] and relied on the MM-GBSA average value of the three replicas in their re-scoring protocol. On the other hand, Ignjatović et al. [17] used the MM-GBSA implementation in the Prime program in the Schrödinger software suite that uses a unique minimized protein-ligand structure and the variable dielectric solvent VSBG 2.0 [57]. They found that the performance of their MM-GBSA approach depends on the ligand set.

By comparing the MM-GBSA protocols described in these different studies, one cannot really suggest a general way to improve the performance of the MM-GBSA method if any such exists. In fact, the performance of the MM-GBSA method is sensitive to many factors such as the charge model, the continuum solvation method, the length of the used trajectory, and the protein-ligand system. Moreover, our estimation of the true performance of the MM-GBSA method is biased since successful MM-GBSA methods are published more often than failures. Therefore, in order to use MM-GBSA methods more reliably in computer-aided drug design projects, benchmark studies evaluating multiple MM-GBSA protocols and parameters on the protein of interest are needed.

Conclusions

There are two components in structure-based affinity prediction challenges – pose prediction and binding score evaluation. Both of these contribute to the accuracy of predicted binding affinities. In order to evaluate only the affinity prediction capability of different scoring methods, the starting protein-ligand binding poses need to be the same, which is rarely the case in D3R Grand Challenges where each participating group has its own pose prediction and binding score evaluation methodology.

To better separate pose prediction from scoring, our two groups decided to collaborate and combine our different areas of expertise in this study – docking and free energy calculations and participate in the structure-based binding affinity prediction challenge for the target BACE-1 in D3R GC4. We used AutoDock-GPU for docking the ligands, employing the AutoDock4 scoring function, and then calculated MM-GBSA binding affinities. MM-GBSA binding energy calculations did not improve the predictive performance with respect to AutoDock4 scores. In a retrospective analysis, we identified two modeling aspects that were detrimental to the quality of MM-GBSA scores, namely the choice of protein conformation and the protonation state of residues in the binding pocket. While it is clear that MM-GBSA can make better predictions than docking scores, making the optimal modeling choices is a non-trivial task that requires knowledge of the system under study and thus is likely difficult in a prospective setting.

Unlike previous D3R Grand Challenge datasets, the BACE-1 ligand dataset consisted of macrocycles. Thus, the binding affinity calculations are very challenging, especially because macrocycles have multiple flexible bonds resulting in a large conformational space. Consequently, a more accurate MM-GBSA protocol may require sampling the complete unbound conformational space visited by the receptor and the ligand, separately.

Our assessment of MM-GBSA performance roughly agrees with that of several previous research groups which participated in previous D3R Grand Challenges [16–18] – specifically, we find that MM-GBSA does not perform particularly well at binding affinity estimation for BACE-1 inhibitors. In order to really determine whether MM-GBSA is valuable in general (and when and what flavor of it), we as a field probably need to exhaustively benchmark it, and the various approaches to it.

These results – not just our own – highlight the importance of blind challenges for the community to evaluate method performance, particularly for drug design projects.