Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2019 Aug 13;34(1):266–275. doi: 10.1111/cobi.13364

Using metapopulation theory for practical conservation of mangrove endemic birds

Ryan Huang 1,✉, Stuart L Pimm 1, Chandra Giri 2
PMCID: PMC7028092  PMID: 31183898

Abstract

As a landscape becomes increasingly fragmented through habitat loss, the individual patches become smaller and more isolated and thus less likely to sustain a local population. Metapopulation theory is appropriate for analyzing fragmented landscapes because it combines empirical landscape features with species‐specific information to produce direct information on population extinction risks. This approach contrasts with descriptions of habitat fragments, which provide only indirect information on risk. Combining a spatially explicit metapopulation model with empirical data on endemic species’ ranges and maps of habitat cover, we calculated the metapopulation capacity—a measure of a landscape's ability to sustain a metapopulation. Mangroves provide an ideal model landscape because they are of conservation concern and their patch boundaries are easily delineated. For 2000–20015, we calculated global metapopulation capacity for 99 metapopulations of 32 different bird species endemic to mangroves. Northern Australia and Southeast Asia had the highest richness of mangrove endemic birds. The Caribbean, Pacific coast of Central America, Madagascar, Borneo, and isolated patches in Southeast Asia in Myanmar and Malaysia had the highest metapopulation losses. Regions with the highest loss of habitat area were not necessarily those with the highest loss of metapopulation capacity. Often, it was not a matter of how much, but how the habitat was lost. Our method can be used by managers to evaluate and prioritize a landscape for metapopulation persistence.

Keywords: colonization, conservation priorities, extinction risk, fragmentation, mangroves, metapopulation, patches, colonización, fragmentación, manglares, metapoblación, parches, prioridades de conservación, riesgo de extinción, 破碎化, 优先保护, 灭绝风险, 定殖, 斑块, 集合种群, 红树林

Short abstract

Article impact statement: Application of metapopulation theory shows where area of habitat loss is highest; metapopulation capacity is not necessarily also the highest.

Introduction

Human actions have endangered many species, not only because they have caused extensive loss of habitat, but also because they have severely fragmented remaining habitat (Haddad et al. 2015). Increased fragmentation and isolation prevent colonizers from arriving and rescuing a foundering population, and therefore habitat fragments lose species and the remaining populations lose fitness (Ferraz et al. 2003; Pimm et al. 2006). At issue, is how one characterizes fragmented landscapes in ways that reflect the extinction risk of their constituent species, and importantly, how it changes over time.

There are familiar descriptive statistics that quantify fragmentation. FRAGSTATS provides a package to calculate these, for example (McGarigal et al. 2012). There are reviews too (Urban et al. 2009; Rayfield et al. 2010) that consider the spatial arrangements of habitat fragments and studies of the efficacy of reconnecting them (Newmark et al. 2017). These studies of structural connectivity are numerous due to their simplicity (Tischendorf & Fahrig 2000), but, as a result, their ecological relevance is questionable (Kupfer 2012; Vimal et al. 2012). Metapopulation models, however, are dynamic. They explicitly consider the presence and absence of a species in a landscape over time. Moreover, they include the ecology of the species and combine the separate influences of patch area and isolation. These metapopulation models directly predict risk of extinction in fragmented systems, and one can parameterize these models with empirical data. Examining questions involving a species’ changing likelihood of persistence as its habitat fragments requires such an approach. Moreover, metapopulation models permit calculation of the changes in risk due to loss or shrinkage of individual patches. Descriptions of habitat metrics—their size and interpatch distances—are only indirect measures of extinction risk (Minor & Urban 2008).

Our method follows from the metapopulation models of Levins (1969), Hanski (1994), and Schnell et al. (2013a). Each patch or fragment of habitat in a landscape potentially contains a transient local population, and the metapopulation is the aggregate of all such interacting populations. The chance of a population persisting in a single fragment relies on 2 opposing forces: extinction rate and colonization rate. Patch area and interpatch distances, respectively, govern these 2 rates. The structure of the landscape thus determines its ability to sustain a metapopulation, a characteristic known as metapopulation capacity (Hanski & Ovaskainen 2000). Metapopulation capacity is a unitless metric that may best be interpreted as the number of patches in a nonspatial metapopulation. It is analogous to effective metapopulation size (Schnell et al. 2013a). Should the metapopulation capacity fall below an extinction threshold determined by the ratio of interpatch immigrations to the extinctions within patches, the species population collapses to zero (in‐depth discussion in Supporting Information). The intuition behind metapopulation capacity is to characterize a given metapopulation's chance of persistence given the landscape's arrangement, thus providing an indicator of extinction risk (Gu et al. 2002).

Previous studies have considered metapopulation risks elsewhere based on these methods (Schnell et al. 2013a, 2013b). Such studies ask whether the International Union for Conservation of Nature (IUCN) Red List classifications for species might change if one includes quantitative estimates of risk from fragmentation and show this to be true. These studies support the need for quantitative estimates of the consequences of fragmentation in species assessments. Other studies have used metapopulation capacity to evaluate the functioning of local landscapes (Hanski & Meyke 2005; Shen et al. 2015; Schnell & Safi 2016). Few studies have done so at regional scales, and those that have applied arbitrary boundaries and were confounded by complexities when scaling to larger landscapes (Larrey‐Lasalle et al. 2018).

To facilitate the conservation need for quantification of the effects of fragmentation, we devised a guide for calculating relative changes in metapopulation capacity over time to evaluate the impact of fragmentation on species’ extinction risk. We wanted our framework to be of practical use in conservation. We used mangrove endemic bird metapopulations as examples of how conservationists may evaluate a changing landscape's capacity to support species.

Mangroves are an ideal habitat to model with a metapopulation approach given their distinct characteristics that make determining patch boundaries simple (Giri et al. 2011). Additionally, they are one of the most rapidly disappearing ecosystems on the planet (Duke et al. 2007), and an estimated 40% of mangrove endemic vertebrates are globally threatened (Luther & Greenberg 2009). Mangroves face a variety of threats, from sea‐level rise, to overconsumption of freshwater upstream, to deforestation for the creation of charcoal or aquaculture. In addition to the loss of ecosystem services, the destruction of mangroves incurs massive economic costs to human development from increased exposure to tropical storms and flooding (Millennium Ecosystem Assessment 2005).

We asked the following questions. Which mangrove endemic bird metapopulations are most quickly losing their chance of persistence and where do they occur? Is measuring habitat loss sufficient to understand a species’ changing risk of extinction over time? It would not be were small losses in habitat associated with substantial increases in extinction risks or vice versa. What are the spatial drivers of changing metapopulation capacity following landscape changes? Is it the loss of large patches versus many small patches? What are the consequences of the breakup of large patches into small patches? Finally, how can a metapopulation approach be used to set conservation priorities when other, strictly spatial methods cannot?

The key components of our method are range maps for species that accurately account for restrictions from land use; new high‐resolution imagery of mangrove distributions that are available at different intervals to permit analysis of long‐term trends; and a model linking metapopulation capacity to habitat fragmentation.

Methods

We aimed to provide a complete recipe for how conservationists may apply metapopulation theory to empirical landscapes and how to interpret the results. Two case studies provide specific examples of what may drive large changes in metapopulation capacity and how conservationists may utilize metapopulation models for prioritization of specific patches. For each species analyzed, the first step established a map of habitat patches of high to moderate quality. Variation in habitat quality requires users to determine a relevant threshold. The goal was to use the maps of habitat to refine species ranges for an accurate description of where individuals may occur. With sufficient care and thought, one could use the results of a species distribution model that produces a binary map of habitat versus nonhabitat. Finally, we input the spatial arrangement of species’ land use into a spatially explicit metapopulation model to generate a summary for the entire landscape.

Spatially Explicit Metapopulation Model

We employed a spatially explicit metapopulation model (Schnell et al. 2013a), a modified version of that by Hanski and Ovaskainen (2000). The only change was the inclusion of a self‐colonization component that weighs the importance of large patches within a system. We set colonization and dispersal as a function of interpatch distance, f(Dij), for which we calculated closest edge‐to‐edge pairwise distances for all patches (i and j) within a system and multiplied this value by the area of the source patch (Aj). The product of the rate of colonization with the inverse of the extinction rate (1/Aix) provided the ratio that described the likelihood a species would occupy a patch or not. We summarized the entire model as a matrix:

Mij=fDijAjAixi≠jAjAixi=j. (1)

The leading eigenvalue (λ) of this matrix, M, provided the metapopulation capacity, analogous to the effective amount of habitat available to a metapopulation (Hanski & Ovaskainen 2000) or effective metapopulation size (Schnell et al. 2013a). Although one could get a basic understanding of the extent of fragmentation of a landscape through 3 main metrics (number of patches, average inter‐patch distance, and total area), λ is related to extinction risk directly due to its relation to the extinction threshold set by the ratio of within‐patch extinction to colonization rates (details on how these metrics independently influence λ are in Supporting Information).

The dispersal function was where species‐specific information is included. This function determined the probability that individuals may move through the interpatch landscape and successfully reach another habitat patch. For our model, we used a log‐sech distribution parameterized with field data on Amazonian passerine birds (van Houtan et al. 2007). This distribution took the following form, where we set the average dispersal distance (α) equal to 317 m and the distribution tail thickness (β) to 1.77:

fDij=2arctanα/Dij1/1β−1πDij≥0. (2)

Unfortunately, the lack of specific information on rates of dispersal for each endemic species forced us to use the same parameters for all avian species. This allowed us to compare the ability of similar landscapes to sustain a species and determine how landscape changes affected species over time.

We ran a sensitivity analysis by calculating the relative change in λ when we varied the α value from 100 m to 5000 m. We based this on work by Martin and Fahrig (2018) who produced an extensive list of average dispersal distances of bird species from North America and the United Kingdom for a wide variety of taxa. To identify impacts of varying α on species with a variety of range sizes, we ran the sensitivity analysis on 3 different species: Mangrove Hummingbird (Amazilia boucardi) (patch number = 405, total habitat area = 351 km2), Blood‐colored Woodpecker (Veniliornis sanguineus) (patch number = 4041, total habitat area = 1357 km2), and a subspecies of the Plain‐bellied Emerald (Amazilia leucogaster leucogaster) (patch number = 12,021, total habitat area = 10,256 km2).

Unlike dispersal, the extinction function was relatively similar across taxa, and most species could be accurately parameterized with a value of 0.5 for x (Gilpin & Diamond 1976; Hanski & Ovaskainen 2000; Schnell et al. 2013a, 2013b).

Identifying Endemic Metapopulations

To identify mangrove endemic bird species, we first selected all avian species that BirdLife International (2017) classified as using mangroves as a major habitat. We defined these species as mangrove specialists. Although the loss of mangrove habitat would assuredly have a significant impact on the long‐term persistence of these species, many of them may also utilize nearby lowland forest and salt marshes. A drawback of our metapopulation approach is that it is based on the assumption that the landscape is binary (habitat and nonhabitat) and that we were modeling the entirety of a metapopulation's patch system. Thus, we further refined the list of mangrove species to those that were obligate mangrove endemics. Starting with the list of specialists, we performed an extensive literature search across a variety of sources, including the Handbook of the Birds of the World and eBird (Luther & Greenberg 2009; Sullivan et al. 2009; del Hoyo et al. 2017). With these various sources, we determined if the species habitat requirements restricted their occurrence to mangrove forests and if they are regularly observed in such areas.

As part of this process, we noticed that many species had some subspecies or populations that were mangrove endemics and some subspecies or populations that were not. Consequently, we determined endemicity based on subspecies classifications rather than limiting ourselves to the species level. Taxonomic opinions on allopatric species and subspecies often change.

The last step was to split the species or subspecies ranges into independent metapopulations. Using van Houtan et al.’s (2007) dispersal function as a guide, we calculated that an individual had a <1% chance of colonizing a patch that was >75 km away. Thus, we delineated independent metapopulations boundaries as a cluster of patches, where every patch was within 75 km of at least one other patch in that cluster. Clusters separated by >75 km (between the 2 nearest patches) were considered distinct metapopulations. If the ranges of 2 or more subspecies were close enough to permit a >1% chance of dispersal between patches, we considered all subspecies involved as a single metapopulation. Given that we delineated metapopulations based on dispersal ability, it is important that users of this method have some confidence that there is little to no exchange of individuals between defined metapopulations, a situation that might not be true for species with large average dispersal distances.

Habitat and Forest Cover Changes

The second required input for a spatially explicit metapopulation model was a detailed map of potential habitat patches. Giri et al. (2011) provided the most current, accurate, and highest resolution map of global mangrove habitat at a 30‐m resolution. Unfortunately, this level of detail was only available globally for the year 2000. To determine how fragmentation changed, we incorporated another source of forest change (Hansen et al. 2013). Thus, to model potential habitat for 2015, we overlaid the mangrove data from 2000 (Giri et al. 2011) with the Hansen's forest‐change data (available through 2017). We removed areas that lost forest from 2000 to 2015. A disadvantage to this approach was that it did not allow us to model potential expansion or reforestation of mangrove habitat since 2000. This approach restricted our results to only decreases in metapopulation capacity. Given the rapid rates of deforestation and the difficulty in accurately identifying mangrove forests from satellite imagery, we believe that this method is the best available at present.

Calculating Metapopulation Capacity and Changes

Once we identified a mangrove‐endemic metapopulation, we then refined its range to the habitat patches determined from the forest‐cover data. The resulting map depicted the total amount of potential habitat available to the metapopulation. We removed all fragments of <1 ha for computational ease. Although these patches are unlikely to sustain a local population, our method could not account for the use of these patches as stepping stones in facilitating dispersal (Boscolo et al. 2008). Using R version 3.4.2 (R Core Team 2018) and the rgdal package (Bivand et al. 2018), we identified the fragment areas and pairwise nearest edge‐to‐edge interpatch distances necessary for the metapopulation model (Eq. 1) for years 2000 and 2015 (sample code in Supporting Information). We calculated the resulting λ and the dominant eigenvector of the same matrix; the latter of which informs us of each patch's contribution to the overall metapopulation capacity.

After calculating the relative change in λ from 2000 to 2015 for each metapopulation, we summarized the data with 2 methods. The first was a simple summation of the relative changes in λ across all overlapping metapopulation ranges, and the second was an average of these changes across the same overlaps. The first method identified which communities of endemic species declined the most in metapopulation capacity, and the second determined which landscapes were the most affected. Each revealed different metapopulation impacts of habitat fragmentation on endemic communities, an approach we did not see in the literature. We then repeated these 2 summary methods for percent habitat area loss across each metapopulation range (except for one Mangrove Robin [Peneonanthe pulverulenta pulverulenta] metapopulation for reasons we explain below) to compare the results of a metapopulation approach to the more traditional area‐only approach.

Results

Mapping Avian‐Mangrove Richness

We classified 106 species as mangrove specialists that together occurred on all continents where there are mangroves. When restricting the list to endemic species, we identified only 32 different species, again found on every tropical continent. Northern Australia had the highest richness of 8 different mangrove endemic species (Fig. 1).

Figure 1.

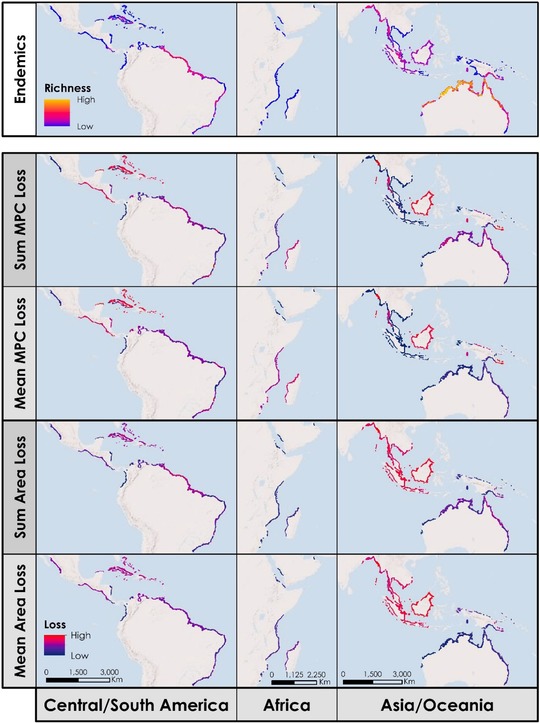
Figure 1

Open in a new tab

Richness of mangrove endemic birds and the relative losses of metapopulation capacity (MPC, λ) and mangrove area from 2000 to 2015. Loss is based on either a sum of declines across all overlapping ranges or average loss across ranges.

Metapopulation Sensitivity to Average Dispersal Distance

As a species’ average dispersal distance increased, the metapopulation capacity also increased, but not considerably. As dispersal distance increased from 100 m to 5000 m, there was a 9.9% increase in λ for A. boucardi (patch number = 405, total habitat area = 351 km2), a 13.7% increase for V. sanguineus (patch number = 4041, total habitat area = 1357 km2), and only a 3.6% increase for A. leucogaster leucogaster (patch number = 12,021, total habitat area = 10,256 km2). The amount of increase in metapopulation capacity depended on the specific spatial arrangement of patches because a larger dispersal distance may only assist individuals in colonizing smaller patches that weakly contribute to the metapopulation capacity.

Changes in Metapopulation Capacity

Across the 32 different endemic species, we identified 99 separate metapopulations (Supporting Information). Of these, 94 experienced declines in mangrove cover from 2000 to 2015 (Supporting Information). Nine metapopulations experienced a small loss in habitat, but no impact on their metapopulation capacities. The remaining 85 metapopulations (86%) saw a decrease in metapopulation capacity. The metapopulation with the largest decline in capacity (34.9%) was the Javan White‐Eye (Zosterops flavus), located along the southern coast of Borneo. Given that the average loss in metapopulation capacity was only 2.17% (σ = 0.06), this was unusually high. It was due to loss of habitat from previously large intact fragments (discussed in more detail below).

When we mapped the loss of metapopulation capacity, certain areas stood out as the major contributors, such as the Caribbean, the Pacific coast of Central America, Madagascar, Borneo, and isolated patches in Southeast Asia in Myanmar and Malaysia (Fig. 1), a pattern consistent when summarizing these results across both sums and averages of loss. Due to its high endemism, metapopulation capacity loss in northern Australia communities differed across the 2 indices. Although there was only a slight change in metapopulation capacity of the landscape on average, every small loss had a large community impact. East Africa showed the opposite trend: metapopulation capacity loss was high per species, but relatively few species were affected.

An important result was the difference in which regions experienced the highest rates of metapopulation capacity loss and those that experienced the most habitat loss. Southeast Asia showed significant mangrove loss across the entire region, yet only Borneo and small patches along Thailand and Myanmar showed corresponding degrees of loss in metapopulation capacity. This mismatch was due to the differing patterns of loss. When a region lost many small patches, individual patches contributed little to the overall metapopulation capacity, but the total area loss added up. By keeping the largest fragments with low extinction risks intact, a species’ likelihood of persistence underwent little change in the face of large‐scale habitat destruction. In contrast, deforesting and fragmenting the largest fragments in a landscape may have disproportionate effects on metapopulation capacity.

Case Study 1 on the Fragmentation of Very Large Patches

Showing one of the largest declines in capacity, the Mangrove Robin metapopulation occurred along the southern half of Papua New Guinea. Although λ decreased by 26.7%, none of the fragmentation metrics (total area loss, interpatch distance, or the number of patches) changed by >3% (Supporting Information). The change in the largest patch in the landscape was responsible for the discrepancy (Fig. 2).

Figure 2.

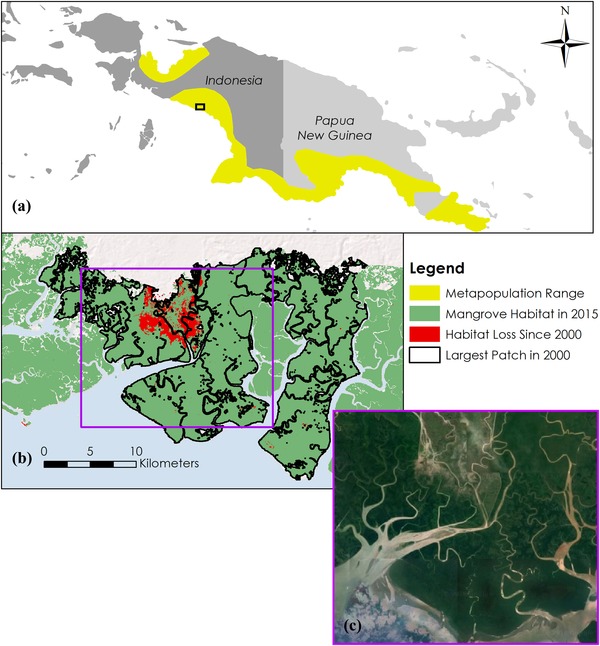
Figure 2

Open in a new tab

(a) Range of a metapopulation of Peneonanthe pulverulenta pulverulenta across coastal Indonesia and Papua New Guinea, (b) fragmentation of the largest mangrove patch since 2000, and (c) satellite imagery of severe flooding of the area outlined by the rectangle in (b).

The largest patch in 2000 in this region was severely fragmented sometime around 2011, potentially due to a flooded river (Table 1 & Fig. 2c). This event destroyed about 5% of the patch's total area and split it into about 50 different fragments. Applying our metapopulation model to just this subset of the whole metapopulation showed that this 5% decrease in the area reduced the metapopulation capacity of the patch by 35%. Area had a compound impact due to both its role in determining local extinction probability and the probability of providing immigrants to nearby patches for rescuing. Even though the entire metapopulation covered roughly 9800 km2 and experienced very little deforestation, the contribution of the largest patch in a system was so great that the effects of its fragmentation dictated the overall metapopulation capacity.

Table 1.

Summary of fragmentation metrics for the entire range of a Peneonanthe pulverulenta pulverulenta metapopulation and for the largest patch within this range in 2000

Metapopulation Largest patch in 2000
2000 patch no. 4312 1
2015 patch no. 4405 50
Δ patch no. +0.02% +50,000%
2000 total area 9851 km2 392 km2
2015 total area 9801 km2 373 km2
Δ total area −0.51% −4.85%
Δλ −26.66%
Open in a new tab

Case Study 2 on Prioritizing Individual Patches

The Sapphire‐bellied Hummingbird (Lepidopyga lilliae) metapopulation in the mangroves east of Barranquilla in northern Colombia exemplified the contributions of individual patches to the overall metapopulation. Patches with the most area were the least likely to contain populations that were extirpated (Fig. 3a). Not surprisingly, connectivity was more important for the central patches than those in the extreme corners (Fig. 3b). Metapopulation theory allowed us to rank the combined effects of area and distance (Fig. 3c).

Figure 3.

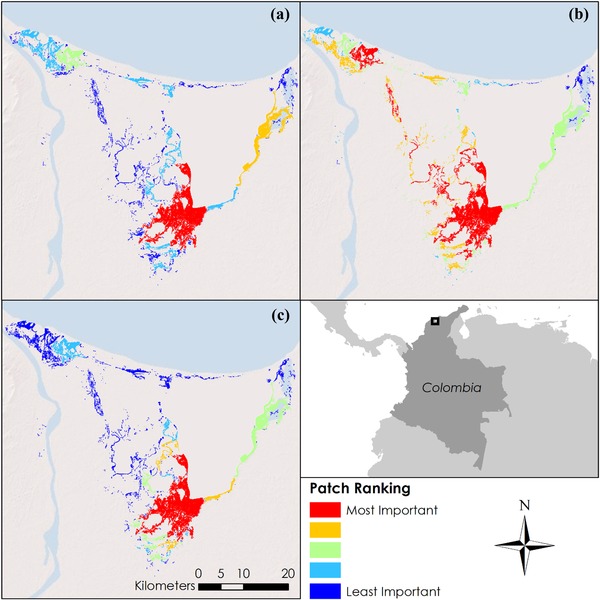
Figure 3

Open in a new tab

Importance of patches of mangroves across the entire metapopulation of Lepidopyga lilliae in northern Colombia in terms of (a) patch area, (b) connectivity to other nearby patches, and (c) area and distance combined as defined by the metapopulation model of Schnell et al. (2013a) (black square, area portrayed in [a–c]).

The metapopulation model results were not a simple summation or product of the effects of area and connectivity. The northwestern corner in Fig. 3 provides an example. Here, there was a patch that was of moderate importance in its area and of major importance in its connectivity to other patches. However, when we combined these in our metapopulation model, its importance to the metapopulation's overall persistence dropped. This change seemed counterintuitive at first. The key laid in the full colonization term of our model. The distance between patches informed us of the probability an individual may travel from one patch to another, but this would only occur if the source patches were occupied. Therefore, we included Aj (area of source patch) in the colonization component. Our example patch decreased in importance because relatively small patches surrounded it; thus, its metapopulation was less likely to be rescued by surrounding patches if it were to be extirpated. Conversely, small patches near the largest patch in the south of the landscape increased in importance when considering the combined metapopulation approach.

Discussion

Metapopulation Capacity Loss across Species and Regions

We found that 86% of metapopulations analyzed lost metapopulation capacity between 2000 and 2015. This was unsurprising because we restricted the analysis to the mangrove extent found in 2000 buffered by only 5 km, which offered little opportunity for reforestation to offset deforestation effects.

The regions with the biggest metapopulation capacity losses were on the island of Borneo, parts of Southeast Asia, the Caribbean, and Central America. In addition to the Mangrove Robin and the Javan White‐Eye, other highly affected species from these regions included the Mangrove Pitta (Pitta megarhyncha), Mexican Sheartail (Doricha eliza), and West Indian Whistling Duck (Dendrocygna arborea). These regions not only experienced losses in mangrove area, but also saw increases in the number of patches and average interpatch distances (Supporting Information), all indicators of increased fragmentation.

Area of Habitat Loss versus Metapopulation Capacity

Deforestation occurred widely in what was once pristine mangrove forests. The causes varied globally, but the most significant drivers were agriculture and aquaculture. Clearing mangroves for shrimp farms has long been a threat (Valiela et al. 2001). Although aquaculture accounted for 30% of mangrove deforestation between 2000 and 2012 in Southeast Asia, conversion for rice and palm oil agriculture were responsible for an additional 38% of mangrove loss (Richards & Friess 2016). Total area lost was an essential factor in determining the persistence of a metapopulation, but not the whole story. Case study 1 exemplifies a small loss of habitat, but a large change in metapopulation capacity. In contrast, some areas of the Malay Peninsula saw an average of 5.52% loss in habitat area, but only a 0.07% loss in metapopulation capacity. Figure 1 shows that the areas of greatest habitat loss did not always match the areas with the largest reduction in metapopulation capacity.

Drivers and Characteristics of Metapopulation Capacity Loss

We identified the important relationships that controlled metapopulation capacity. As we removed area from large patches, the metapopulation capacity decreased dramatically, as evidenced by changes to P. pulverulenta pulverulenta. When nearby small patches depended on these large patches for colonization, this loss in area further compounded the decrease. Thus, slight changes in area could have a disproportionate impact on extinction risk, depending on where area is lost. Conversely, landscapes that lose a lot of area because of the cumulative destruction of small patches (which have low probabilities of local persistence) experienced proportionally smaller changes to metapopulation capacity and extinction risk. Together, this reinforces the result that the regions losing the most mangrove forest were not always the same as those with the highest risk of species extinction, and those experiencing less loss may have created riskier landscapes (Fig. 1).

Using Metapopulation Capacity for Conservation Priorities

Metapopulation models add to how conservation priorities are set at a variety of scales. The criterion of fragmentation is explicit in the rules for the IUCN Red List's categorization of endangerment. The models may provide direct quantification of those risks, something metrics on patches do not do directly. Threats from fragmentation may yield different ranks of the risks that species encounter than those based on the area of habitat alone (Schnell et al. 2013a, 2013b). Although this is true regardless of the level of endemism in a region, areas that have a high number of endemics are particularly sensitive. Fragmentation of a few critical patches may have significant impacts on metapopulation capacity across more species in these species‐rich regions. How one summarizes the fragmentation effects across these communities may result in different priorities. Consider Northern Australia. On average and relative to global loss, it had a low amount of mangrove deforestation (Fig. 1), but the community was rich in mangrove endemics, so fragmentation there affected more species. Thus, each individual species in this region may be a low conservation priority on its own, but the landscape may be a higher priority given its richness.

At a local level, metapopulation models identify the specific individual patches and quantify their contribution to the metapopulation capacity of the landscape. Conservation practitioners can then recognize which patches are essential to a species’ survival and thus avoid future threats or plan potential habitat restorations.

Delineating Range and Estimating Dispersal Distances

There were 2 major limitations in calculating metapopulation capacity: identifying the habitats and parameterizing the models. We assumed that our model included the entire potential habitat; thus, the model is most useful for species with clearly delineated patches. We chose mangroves because we could readily estimate their extent, they contain habitat‐restricted species, and human actions are shrinking them. Similar types of areas with easily delineated boundaries may include marshlands, coral reefs, and clear‐cut forests. Species ranges with clear thresholds such as elevation requirements may also lend themselves to distinct patch boundaries.

Although these models are easy to parameterize, they require detailed species‐specific information on extinction and dispersal. The former is easier. There are direct studies of times to extinction of small populations (e.g., Pimm et al. 1993). These provide necessary insights into the quantitative relationship between patch size and extinction risk.

Dispersal is more difficult. Detecting the movement of individuals between habitat patches is an uncommon event and properly parameterizing such a function for less‐studied species may be challenging. However, uncertainties in the dispersal parameters may not matter greatly if one compares how fragmentation affects a single species through time. For this reason, we used a single dispersal function across species to emphasize the effect of habitat loss and within‐species, relative changes in extinction risk. When comparing species and using the same parameter for each, one assumes that the differences in habitat fragmentation are more important than differences between species dispersal (Schnell et al. 2013a, 2013b). Nonetheless, there may be instances where metapopulation models require dispersal functions to be accurately parameterized. Because dispersal ability is better understood for more species, conservationists may gain more accurate estimates of extinction risk.

Despite these concerns, there are a multitude of potential applications for this method. An obvious extension would be to simulate potential corridor restoration between patches and use of the percent increase in metapopulation capacity as a measure of effectiveness. This method could also account for effort and land prices providing a measure of cost‐effectiveness. Future researchers could also use variants of the metapopulation model to account for nonuniform habitat quality (Hanski 1994). By assigning a quality value to each habitat type or fragment, these modifications may be particularly useful for modeling species that use multiple habitats.

We have presented a practical method of using empirical data available to conservation practitioners and combining it with relevant ecological modeling to evaluate a landscape's capacity to sustain a species over time. One can track the impacts of fragmentation across a species’ entire range as well as at the individual patch level. By using increasingly accurate maps of habitat and land cover, we incorporated the exact manner of habitat loss into our conservation decision making. In doing so, we found that general habitat loss and a species likelihood to persist are not entirely correlated. More accurate conservation decisions can be made if ecological impacts of fragmentation and not just habitat loss are considered.

Supporting information

A detailed description of metapopulation modeling (Appendix S1), analysis of fragmentation metrics on λ (Appendix S2), sample shapefile and code for calculating metapopulation capacity of a single species (Appendix S3), and detailed results of mangrove endemics species (Appendix S4) and changes in metapopulation capacity (Appendix S5) are available online. The authors are solely responsible for the content and functionality of these materials. Queries (other than absence of the material) should be directed to the corresponding author.

Click here for additional data file. (1MB, zip)

Acknowledgments

This material is based on work supported by the National Science Foundation Graduate Research Fellowship under Grant DGE‐1644868 and by the National Aeronautics and Space Administration under grant NNX17AI08G issued through the ROSES‐2015 Program.

Article impact statement: Application of metapopulation theory shows where area of habitat loss is highest; metapopulation capacity is not necessarily also the highest.

Literature Cited

  1. BirdLife International . Data zone . 2017. BirdLife International, Cambridge, United Kingdom.
  2. Bivand R, Keitt T, Rowlingson B. 2018. rgdal: bindings for the ‘geospatial’ data abstraction library. R Package Version 1:3–4. [Google Scholar]
  3. Boscolo D, et al. 2008. Importance of interhabitat gaps and stepping‐stones for Lesser Woodcreepers (Xiphorhynchus fuscus) in the Atlantic Forest, Brazil. Biotropica 40:273–276. [Google Scholar]
  4. del Hoyo J, Elliott A, Sargatal L, Christie DA. Kirwan G, editors. 2017. Handbook of the birds of the world alive. Lynx Edicions, Barcelona. [Google Scholar]
  5. Duke NC, et al. 2007. A world without mangroves? Science 317:41–42. [DOI] [PubMed] [Google Scholar]
  6. Ferraz G, Russell GJ, Stouffer PC, Bierregaard RO, Pimm SL, Lovejoy TE. 2003. Rates of species loss from Amazonian forest fragments. Proceedings of the National Academy of Sciences 100:14069–14073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gilpin ME, Diamond JM. 1976. Calculation of immigration and extinction curves from the species‐area‐distance relation. Proceedings of the National Academy of Sciences 73:4130–4134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Giri C, Ochieng E, Tieszen LL, Zhu Z, Singh A, Loveland T, Masek J, Duke N. 2011. Status and distribution of mangrove forests of the world using earth observation satellite data. Global Ecology and Biogeography 20:154–159. [Google Scholar]
  9. Gu W, Heikkilä, Hanski I. 2002. Estimating the consequences of habitat fragmentation on extinction risk in dynamic landscapes. Landscape Ecology 17:699–710. [Google Scholar]
  10. Haddad NM, et al. 2015. Habitat fragmentation and its lasting impact on Earth's ecosystems. Science Advances 1:e1500052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hansen MC, et al. 2013. High‐resolution global maps of 21st‐century forest cover change. Science 342:850–853. [DOI] [PubMed] [Google Scholar]
  12. Hanski I. 1994. A practical model of metapopulation dynamics. Journal of Animal Ecology 63:151–162. [Google Scholar]
  13. Hanski I, Meyke E. 2005. Large‐scale dynamics of the Glanville fritillary butterfly: landscape structure, population processes, and weather. Annales Zoologici Fennici 42:379–395. [Google Scholar]
  14. Hanski I, Ovaskainen O. 2000. The metapopulation capacity of a fragmented landscape. Nature 404:755–758. [DOI] [PubMed] [Google Scholar]
  15. Kupfer JA. 2012. Landscape ecology and biogeography: rethinking landscape metrics in a post‐FRAGSTATS landscape. Progress in Physical Geography: Earth and Environment 36:400–420. [Google Scholar]
  16. Larrey‐Lasalle P, et al. 2018. A methodology to assess habitat fragmentation effects through regional indexes: illustration with forest biodiversity hotspots. Ecological Indicators 89:543–551. [Google Scholar]
  17. Levins R. 1969. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bulletin of Entomological Society of America 15:237–240. [Google Scholar]
  18. Luther DA, Greenberg R. 2009. Mangroves: a global perspective on the evolution and conservation of their terrestrial vertebrates. BioScience 59:602–612. [Google Scholar]
  19. Martin AE, Fahrig L. 2018. Habitat specialist birds disperse farther and are more migratory than habitat generalist birds. Ecology 99:2058–2066. [DOI] [PubMed] [Google Scholar]
  20. McGarigal K, Cushman SA, Neel MC, Ene E. 2012. FRAGSTATS: spatial pattern analysis program for categorical maps. Version 4. University of Massachusetts, Amherst: Available from https://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed June 2017). [Google Scholar]
  21. Millennium Ecosystem Assessment (MEA) . 2005. Ecosystems and human well‐being: wetlands and water. World Resources Institute, Washington, D.C. [Google Scholar]
  22. Minor ES, Urban DL. 2008. A graph‐theory framework for evaluating landscape connectivity and conservation planning. Conservation Biology 22:297–307. [DOI] [PubMed] [Google Scholar]
  23. Newmark WD, Jenkins CN, Pimm SL, McNeally PB, Halley JM. 2017. Targeted habitat restoration can reduce extinction rates in fragmented forests. Proceedings of the National Academy of Sciences 114:9635–9640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Pimm SL, Diamond J, Reed TM, Russell GJ, Verner J. 1993. Times to extinction for small populations of large birds. Proceedings of the National Academy of Sciences 90:10871–10875. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Pimm SL, Dollar L, Bass OL Jr. 2006. The genetic rescue of the Florida panther. Animal Conservation 9:115–122. [Google Scholar]
  26. R Core Team . 2018. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: Available from http://www.R-project.org/. [Google Scholar]
  27. Rayfield B, Fortin MJ, Fall A. 2010. The sensitivity of least‐cost habitat graphs to relative cost surface values. Landscape Ecology 25:519–532. [Google Scholar]
  28. Richards DR, Friess DA. 2016. Rates and drivers of mangrove deforestation in Southeast Asia, 2000–2012. Proceedings of the National Academy of Sciences 113:344–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Schnell JK, Harris GM, Pimm SL, Russell GJ. 2013a. Estimating extinction risk with metapopulation models of large‐scale fragmentation. Conservation Biology 27:520–530. [DOI] [PubMed] [Google Scholar]
  30. Schnell JK, Harris GM, Pimm SL, Russell GJ. 2013b. Quantitative analysis of forest fragmentation in the Atlantic forest reveals more threatened bird species than the current red list. PLOS ONE 8 (e65357) 10.1371/journal.pone.0065357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Schnell JK, Safi K. 2016. Metapopulation capacity meets evolutionary distinctness: spatial fragmentation complements phylogenetic rarity in prioritization. Biodiversity Conservation and Phylogenetic Systematics 14:319–332. [Google Scholar]
  32. Shen G, et al. 2015. Climate change challenges the current conservation strategy for the giant panda. Biological Conservation 190:43–50. [Google Scholar]
  33. Sullivan BL, Wood CL, Iliff MJ, Bonney RE, Fink D, Kelling S. 2009. eBird: a citizen‐based bird observation network in the biological sciences. Biological Conservation 142:2282–2292. [Google Scholar]
  34. Tischendorf L, Fahrig L. 2000. On the usage and measurement of landscape connectivity. Oikos 90:7–19. [Google Scholar]
  35. Urban DL, Minor ES, Treml EA, Schick RS. 2009. Graph models of habitat mosaics. Ecology Letters 12:260–273. [DOI] [PubMed] [Google Scholar]
  36. Valiela I, Bowen JL, York JK. 2001. Mangrove forests: one of the world's threatened major tropical environments: at least 35% of the area of mangrove forests has been lost in the past two decades, losses that exceed those for tropical rain forests and coral reefs, two other well‐known threatened environments. AIBS Bulletin 51:807–815. [Google Scholar]
  37. van Houtan KS, Pimm SL, Malley JH, Bierregaard RO Jr, Lovejoy TE. 2007. Dispersal of Amazonian birds in continuous and fragmented forest. Ecology Letters 10:219–229. [DOI] [PubMed] [Google Scholar]
  38. Vimal R, Mathevet R, Thompson JD. 2012. The changing landscape of ecological networks. Journal for Nature Conservation 20:49–55. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

A detailed description of metapopulation modeling (Appendix S1), analysis of fragmentation metrics on λ (Appendix S2), sample shapefile and code for calculating metapopulation capacity of a single species (Appendix S3), and detailed results of mangrove endemics species (Appendix S4) and changes in metapopulation capacity (Appendix S5) are available online. The authors are solely responsible for the content and functionality of these materials. Queries (other than absence of the material) should be directed to the corresponding author.

Click here for additional data file. (1MB, zip)

Articles from Conservation Biology are provided here courtesy of Wiley

RESOURCES