Abstract
Cystic fibrosis (CF) is a progressive, genetic disease characterized by frequent, prolonged drops in lung function. Accurately predicting rapid underlying lung‐function decline is essential for clinical decision support and timely intervention. Determining whether an individual is experiencing a period of rapid decline is complicated due to its heterogeneous timing and extent, and error component of the measured lung function. We construct individualized predictive probabilities for “nowcasting” rapid decline. We assume each patient's true longitudinal lung function, S(t), follows a nonlinear, nonstationary stochastic process, and accommodate between‐patient heterogeneity through random effects. Corresponding lung‐function decline at time t is defined as the rate of change, S′(t). We predict S′(t) conditional on observed covariate and measurement history by modeling a measured lung function as a noisy version of S(t). The method is applied to data on 30 879 US CF Registry patients. Results are contrasted with a currently employed decision rule using single‐center data on 212 individuals. Rapid decline is identified earlier using predictive probabilities than the center's currently employed decision rule (mean difference: 0.65 years; 95% confidence interval (CI): 0.41, 0.89). We constructed a bootstrapping algorithm to obtain CIs for predictive probabilities. We illustrate real‐time implementation with R Shiny. Predictive accuracy is investigated using empirical simulations, which suggest this approach more accurately detects peak decline, compared with a uniform threshold of rapid decline. Median area under the ROC curve estimates (Q1‐Q3) were 0.817 (0.814‐0.822) and 0.745 (0.741‐0.747), respectively, implying reasonable accuracy for both. This article demonstrates how individualized rate of change estimates can be coupled with probabilistic predictive inference and implementation for a useful medical‐monitoring approach.
Keywords: longitudinal data analysis, medical monitoring, nonstationary process, nowcasting, predictive probability distributions
1. INTRODUCTION
Cystic fibrosis (CF) is the most common life‐shortening genetic disease in Whites, affecting an estimated 70 000 individuals worldwide.1 Patient registry data have been used for decades to advance therapeutics and care, steadily increasing the life expectancy of individuals with CF.2 However, the clinical course of this chronic disease remains marked by progressive loss of lung function and eventual respiratory failure. Rapid pulmonary decline, which is characterized by an initial drop in lung function, that is, sustained over time, occurs predominantly during adolescence, and early adulthood,3, 4, 5 but typically recurs throughout the lifespan.6, 7 Rapid decline requires immediate clinical intervention to recover lung function, which is measured using FEV1 (forced expiratory volume in 1 second of percentage of predicted). Landmark studies stemming from CF epidemiology and quality improvement have elucidated strong associations of clinical and demographic characteristics with rapid decline8, 9 and care management practices have been improved/modified based on these observations.10 A single‐center study that defined rapid decline as a decrease in FEV1 of more than 10% predicted within the prior 12 months from the maximum observed FEV1 showed that subsequently treating patients according to this decision rule corresponded to mean improvements in overall FEV1. 11 A similar study at another CF center corroborated these findings.12 Early detection of rapid decline or its impending onset would enable early treatment, and potentially prevention. However, statistical methods for medical monitoring to guide the early detection of rapid CF lung‐function decline do not exist.
There are several national CF patient registries across the world, which obtain longitudinal data on key variables including FEV1, and several studies have developed models for FEV1 trajectories over the CF life course.13 Repeated measures of FEV1 are clearly correlated over time within an individual, and a random intercepts model14 has been the most widely used approach to fit longitudinal lung‐function data. Studies of the Danish and US CF registries analyzing longitudinal FEV1 using exponential covariance to model the longitudinal correlation rather than conventional random intercepts alone found improvements in model fit and prediction.7, 15 Subsequently, a systematic review used a weighted analysis, which included parameter estimates and mean trajectories reported from 39 peer‐reviewed articles, to estimate mean FEV1 trajectory over age. The review highlighted the nonlinear, heterogeneous nature of FEV1 decline between individuals and the range of analysis approaches undertaken amongst the studies.16 In another study aimed at clustering trajectories of lung‐function decline into phenotypes, we found that individuals with the highest pulmonary function early in life tended to have rapid decline at a later age than more severe phenotypes; these individuals with the later decline tended to experience the greatest losses over time.5 Although numerous studies shed light on the nonlinear, heterogeneous nature of FEV1 decline, and the opportunities to assess lung function using various patient registries, the results offer explanations—as opposed to predictions—about the clinical course of CF in the individual patient.
The goal of this article is to describe the application of a nonstationary stochastic process model to obtain individual‐level predictions of being in a state of rapid decline in lung function as measured by FEV1. We refer to this as “nowcasting,” and by focusing on the rate of change, we go beyond the typical pointwise prediction of the absolute level of a longitudinal biomarker, which is often inadequate to guide clinical decision making. The notion of modeling uncertainty of predicted values through a target‐based probability rather than a pointwise confidence interval (CI) has existed for decades.17 One example is interim monitoring in clinical trials to compute the predictive probability of success (e.g., a favorable response to treatment) given interim data.18 Previous studies have described approaches using continuous longitudinal biomarkers to predict changes in trajectories based on a binary decision rule that classifies individuals at a given timepoint. Motivated by the need to monitor clinically meaningful changes over time in CD4 count trajectories from HIV patients, Foulkes et al19 proposed two different prediction‐based classification approaches. Their application goal was to predict whether or not CD4 count would exceed a clinically meaningful threshold (e.g., 200 cells/mm3) for each patient over time. For the first approach, they dichotomized CD4 counts according to the threshold and fit a generalized linear mixed effects model on the binary responses; model‐based probabilities were used to generate a receiver‐operating characteristic (ROC) curve. The second approach fit a linear mixed effects model to observed longitudinal CD4 and then used the predicted value and corresponding prediction variance to construct a rule for classification based on a threshold. A more recently described approach, highlighted in a review by Albert, is to fit such two‐stage models simultaneously through shared random parameters, which would alleviate calibration error induced using “plug‐in” estimates of random effects.20 Li and Gatsonis21 combined multiple biomarker trajectories using scores from functional principal components analysis and adjusted for possibility of verification bias, to develop a composite diagnostic marker for classifying patient‐specific diagnosis of cancer recurrence.
Diggle et al22 recently extended predictive probabilities for monitoring renal failure using an estimate of the patient's longitudinal glomerular filtration rate (GFR). They replaced the random slope term in the Gaussian random intercept and slope model with an integrated continuous‐time random walk. They evaluated a predictive probability distribution for the patient‐specific rate of change, to determine the probability that the patient's current rate of decrease in GFR would exceed 5% per year. In this article, we apply the same methodology in the CF context; using FEV1 as the biomarker, we assume the true longitudinal lung function follows a process S(t) with corresponding rate of change S′(t). We construct a noisy version of using a data model consisting of observed longitudinal FEV1, which is our noisy measurement of lung function, and observed (also noisy) covariate information. By conditioning on relevant data, we can create a class of target functions for prediction that is specific to rapid lung‐function decline.
Translating these approaches into point of care is critical to the utility of real‐time prediction models. Monitoring tools have been presented in the clinical literature, but have limited appearances in the statistical literature. A recent clinical study, which was aimed at predicting late seizures after ischemic stroke using Cox proportional hazard modeling, presented a downloadable smart phone app for making predictions with new patients.23 A joint longitudinal‐survival model for prostate cancer recurrence was accompanied by an online risk calculator, providing predictions of up to 3 years in advance.24 We translate the final prediction model for a rapid lung‐function decline into an app in R Shiny. Our app shows how to use this model as a dynamic prognostic tool for CF clinical decision making.
In this novel application tailored to rapid CF disease progression, we construct predictive probabilities specific to underlying rates of change within a given population. We build upon previous work by (i) modifying the target function to generate predictive probabilities of rate of change in the patient‐specific mean response S′(t); (ii) including a bootstrapping algorithm that provides CIs for the predictive probabilities; (iii) providing a prediction model platform in R Shiny that could be integrated into point of care.
The rest of the article is organized as follows. The following section details the motivating CF registry data. Section 3 introduces the linear mixed model setup specific to the CF application and describes the estimation of rapid decline and methods used for assessment of model fit. In Section 4, we define the predictive probability of rapid decline under uniform thresholds and personalized scenarios. We describe the bootstrapping algorithm used to provide CIs for the predictive probabilities and corresponding empirical simulations used to examine predictive performance. Individual patient predictions, the clinical dashboard created with the R Shiny app and comparison to an existing clinical algorithm are described in Section 5. We conclude in Section 6 with a discussion of how the presented approach differs from existing methods, as well as clinical implications and future considerations to further extend the approach and improve utility of the clinical dashboard. Supporting Information for this article include (i) R implementation code in Data S1; (ii) Supporting Information on model diagnostics, held‐out and forecast validation metrics and an overview of the Shiny app in Data S2.
2. CYSTIC FIBROSIS REGISTRY DATA
Data were obtained from the US Cystic Fibrosis Foundation Patient Registry (CFFPR), which has been used to track outcomes for more than 50 years and includes demographic and clinical encounter‐level data obtained from patients at care centers accredited by the Cystic Fibrosis Foundation.25 The analysis cohort used for this prediction modeling study consisted of patients with a valid CF diagnosis who were presumed “at risk” for rapid decline and followed in the CFFPR between January 1, 2003 and December 31, 2015. We considered available data from 2003 onward because most relevant predictors of rapid decline were consistently documented at each clinical encounter—as opposed to annually—beginning in 2003. Patients younger than 6 years of age were excluded because of potentially unreliable pulmonary function testing.
The model development segment of the cohort, which included a random subset of 80% of patients, consisted of 24 704 patients who contributed a total of 896 088 FEV1 observations. Demographic and clinical summaries for the development cohort are shown in Table 1. The median number of observations per patient was 31 and ranged from 1 to 253. Per‐patient duration of follow‐up ranged from 0 to 13 years, with a median of 8.5 and a mean of 7.7. Figure 1 shows representative FEV1 trajectories overage available in the dataset. The example profiles, highlighted as black lines, demonstrate the between‐patient and within‐patient variability commonly observed in longitudinal lung‐function data, as well as the nonlinear, heterogeneous nature of FEV1 decline specific to CF disease progression.
Table 1.
Clinical and demographic composition of the cystic fibrosis data
| Characteristics | Development cohort (n = 24 704) | Validation cohort (n = 6175) |
|---|---|---|
| Birth cohort | ||
| <1981 | 5455 (22.1%) | 1336 (21.6%) |
| 1981 to 1988 | 4886 (19.8%) | 1220 (19.8%) |
| 1989 to 1994 | 4476 (18.1%) | 1090 (17.7%) |
| 1995 to 1998 | 2887 (11.7%) | 727 (11.8%) |
| 1999 to 2005 | 4642 (18.8%) | 1170 (18.9%) |
| >2005 | 2358 (9.5%) | 632 (10.2%) |
| Genotype (F508del mutation type) | ||
| Homozygous | 11 150 (45.1%) | 2851 (46.2%) |
| Heterozygous | 9884 (40%) | 2430 (39.4%) |
| Neither/unknown | 3670 (14.9%) | 894 (14.5%) |
| Male gender | 12 744 (51.6%) | 3211 (52%) |
| Age at baseline, mean; median (min‐max) | 16.6; 12.5 (6.0‐81.8) | 16.5; 12.4 (6.0‐79.0) |
| FEV1 at baseline mean; median (min‐max) | 79.8; 83.8 (9.3‐149.3) | 80.1; 82.9 (8.8‐143.4) |
| Medicaid insurance use | ||
| At baseline | 11 069 (44.8%) | 2759 (44.7%) |
| Ever during follow‐up | 19 032 (77%) | 4789 (77.6%) |
| Microbiology | ||
| Pseudomonas aeruginosa | ||
| At baseline | 6509 (26.3%) | 1646 (26.7%) |
| Ever during follow‐up | 18 434 (74.6%) | 4649 (75.3%) |
| Methicillin‐resistant Staphylococcus aureus | ||
| At baseline | 1774 (7.2%) | 472 (7.6%) |
| Ever during follow‐up | 10 821 (43.8%) | 2639 (42.7%) |
| CF‐related diabetes mellitus | ||
| At baseline | 1961 (7.9%) | 490 (7.9%) |
| Ever during follow‐up | 7525 (30.5%) | 1853 (30%) |
| Alive through follow‐up | 23 692 (95.9%) | 5927 (96%) |
Abbreviations: CF, cystic fibrosis; FEV1, forced expiratory volume in 1 second of percentage of predicted.
Figure 1.
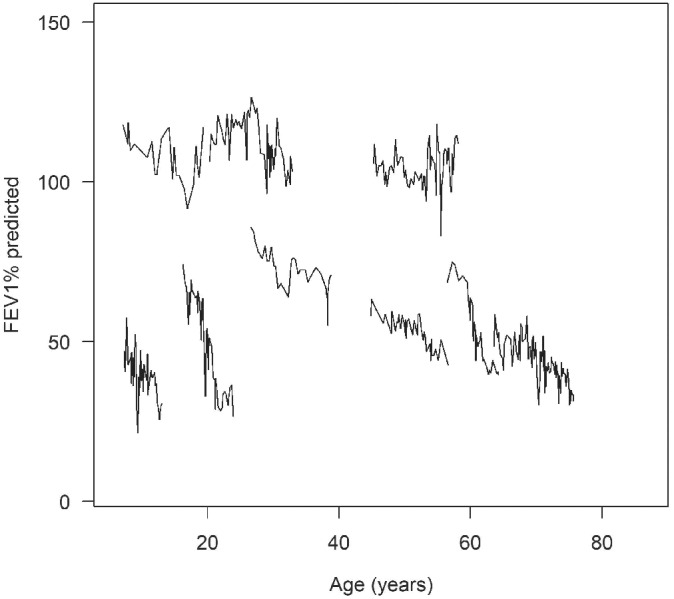
Observed forced expiratory volume in 1 second of percentage of predicted against age at measurement (in years). Five specific patient profiles, illustrating various patterns of rapid decline over the lifespan, are shown as black lines
The dataset also included binary time‐varying measures on Medicaid insurance use, microbiology (infection with Pseudomonas aeruginosa or Methicillin‐resistant Staphylococcus aureus, MRSA) and CF‐related diabetes (CFRD) mellitus. Summary statistics for these additional variables at baseline and across follow‐up are shown in Table 1. There were 1529 patients with missing data on one or more static covariates who were excluded from the analysis cohort (Table S1 in Data S2). Because age was used as the time scale, there was left‐truncation because individuals were included only from 2003. Time since baseline (in years) was included in the modeling. Furthermore, all individuals were censored at their age at the end of 2015, at death or at the first year of receiving a lung transplant if that occurred first. To partially address potential bias due to these design features, the subsequently described models were adjusted for birth cohort (<1981, 1981‐1988, 1989‐1994, 1995‐1998, 1999‐2005, >2005). To account for irregular sampling due to disease severity, we included numbers of acute pulmonary exacerbations and outpatient visits within the year prior to a given clinical encounter as covariates in the longitudinal models described below.
3. MODELING RAPID DISEASE PROGRESSION
In this section, we present the specific form of the nonstationary stochastic process model used to depict age‐related lung‐function decline in the CF cohort and show how this model can be used to assess rapid disease progression in an application. We let Yij be the lung function (FEV1) measurement for the ith patient taken at time point tij, i = 1, …, N; j = 1, …, ni. Herein, tij is patient age, in years. The stochastic model can be expressed as:
| (1) |
where μi(tij) represents the fixed effects of the model in Equation (1). Between‐patient heterogeneity is incorporated in the model with a random intercept term Ui, where Ui ∼ N(0, ω2). The term Wi(tij) denotes realizations from the zero‐mean, continuous‐time integrated Brownian motion process such that , where Bi(v) is the rate of change in lung function at time v depicted as Brownian motion and Bi(0) = 0. The term Zij ∼ N(0, τ2) represents independent, identically distributed measurement error. Expression μi(tij) can be decomposed as:
| (2) |
The design matrix Xi(tij) includes covariates (both static and time‐varying as defined in Section 2) and corresponding parameter vector α. The function f(tij) is the common shape of (nonlinear) FEV1 trajectories at the population level. In an effort to balance regression splines and stochastic covariance, we examined different spline basis functions and knot selections. We selected truncated power splines of cubic degree as defined by Ruppert et al26; using knot locations (ξ1 = 12.7, ξ2 = 19.2, ξ3 = 25.6, ξ4 = 32.1, ξ5 = 38.5) that were determined by the quantile method, similar to a previous study.7 We denote the corresponding coefficients for the global polynomial and truncated spline terms as β0, …, β3 and b1, …, b5, respectively. We use integrated Brownian motion in place of random slopes, conventionally used in CF FEV1 modeling, to capture the nonmonotone variation in each patient's lung‐function trajectory (Figure 1) and provide a stochastic function for predictions involving the rate of change. The random slope model often fits data from short follow‐up sequences well, but is too inflexible to capture the patterns of variation seen in long‐term follow‐up.15 The integrated Brownian motion process follows a normal distribution with covariance function for time points (ages) s and t:
| (3) |
This enables greater flexibility over conventional models, in terms of the shape of realizations, that have been used to characterize changes in FEV1. 27
We can estimate the rate of change in FEV1 by taking the first derivative with respect to age at a given time based on Equation (1) and modeling it as a noisy version of Si(t):
| (4) |
Herein, is the underlying rate of change at current time t for the ith patient, representing this individual's true rate of change in lung function. This function can be estimated by terms in Equation (2) that correspond to overall mean rate of progression fi′(t) and terms involving time‐varying covariates and covariate‐by‐time interactions; Bi(t) represents Brownian motion obtained from differentiating the integrated Brownian motion process Wi(t). Herein, Bi(t) ∼ N(0, σ2t) and has covariance Cov(Bi(s), Bi(t)) = σ2min(s, t).
3.1. Model fitting
A stratified random sampling approach was used to partition the CFFPR analysis cohort data into three nonoverlapping datasets: (i) development; (ii) out‐of‐sample validation; (iii) masked forecasting (Figure S1 in Data S2). We first randomly split the cohort into 80% and 20%, representing datasets (i) and (ii), respectively. To create a dataset (iii), a subset of the cohort from dataset (i) was randomly selected to have the last 2 years of their data masked, to examine forecast accuracy beyond the period included in the model and compare the forecast values to actual data. This scenario corresponds to the typical CF setting in which newly accrued patient data would be used to forecast rapid decline on patients with data already deposited into the registry and part of model fitting/updating.
Maximum likelihood estimates of the model parameters (Table 2) were obtained on dataset (i) using the lmenssp package in R.28 Although our primary goal is the prediction of rapid decline, we examined parameter estimates for model coefficients. After accounting for the nonlinear, population‐level progression of FEV1 through f′(t), we found that being born into a more modern birth cohort corresponded to less rapid FEV1 decline; increased frequency of clinic visits was associated with higher overall FEV1; longer follow‐up, increased frequency of pulmonary exacerbations, being female and having an infection with P aeruginosa were associated with more rapid decline. Having CFRD and using Medicaid insurance were associated with slightly less rapid decline (coefficients were relatively small). MLEs of the covariance parameters indicated large between‐patient heterogeneity and residual variance ; estimated variance of the integrated Brownian motion process was .
Table 2.
Parameter estimates and standard errors for the CF dynamic regression model
| Parameter (context) | Estimate | 95% CI | |
|---|---|---|---|
| Shape, f(t) | β0 (Intercept) | 8.6850 | (3.184, 14.186) |
| β1 (Age) | −1.5997 | (−2.341, −0.858) | |
| β2 (Age2) | 0.5023 | (0.437, 0.567) | |
| β3 (Age3) | −0.0224 | (−0.024, −0.02) | |
| b1 | 0.0458 | (0.043, 0.049) | |
| b2 | −0.0308 | (−0.033, −0.029) | |
| b3 | 0.0089 | (0.007, 0.011) | |
| b4 | −0.0024 | (−0.005, 0) | |
| b5 | 0.0008 | (−0.001, 0.002) | |
| Covariate effects, α | α1 (time since baseline) | −0.2843 | (−0.419, −0.15) |
| Ref: F508del homozygote | α2 (F508del heterozygote) | −1.3377 | (−1.993, −0.683) |
| α3 (F508del neither/unknown) | −3.7539 | (−4.715, −2.793) | |
| α4 (Male) | −2.2355 | (−2.842, −1.629) | |
| Ref: born before 1981 | α5 (born 1981‐1988) | 12.1304 | (7.947, 16.314) |
| α6 (born 1989‐1994) | 11.5799 | (7.195, 15.965) | |
| α7 (born 1995‐1998) | 14.9403 | (10.405, 19.476) | |
| α8 (born 1999‐2005) | 16.8315 | (12.287, 21.376) | |
| α9 (born >2005) | 17.5418 | (12.804, 22.279) | |
| α10 (FEV1 at baseline) | 0.8181 | (0.809, 0.827) | |
| α11 (Enzyme use) | −0.5294 | (−0.634, −0.424) | |
| α9 (Pseudomonas aeruginosa) | 0.6668 | (0.47, 0.864) | |
| α10 (Methicillin‐resistant Staphylococcus aureus) | −0.2329 | (−0.453, −0.013) | |
| α11 (CF‐related diabetes mellitus) | −1.0740 | (−1.32, −0.828) | |
| α11 (Medicaid insurance use) | −0.2293 | (−0.373, −0.085) | |
| α11 (Outpatient visits in last year) | 0.1211 | (0.112, 0.13) | |
| α12 (Acute exacerbations in last year) | −0.7478 | (−0.777, −0.718) | |
| Ref: F508del homozygote | α13 (F508del heterozygote × age) | 0.1615 | (0.071, 0.252) |
| α14 (F508del neither/unknown × age) | 0.3640 | (0.236, 0.492) | |
| α15 (Male × age) | 0.2338 | (0.151, 0.317) | |
| Ref: born before 1981 | α5 (born 1981‐1988 × age) | 1.0893 | (0.872, 1.306) |
| α6 (born 1989‐1994 × age) | 1.5485 | (1.325, 1.772) | |
| α7 (born 1995‐1998 × age) | 1.7227 | (1.486, 1.96) | |
| α8 (born 1999‐2005 × age) | 1.8683 | (1.636, 2.101) | |
| α9 (born >2005 × age) | 1.8638 | (1.557, 2.17) | |
| α11 (Enzyme use × age) | −0.0018 | (−0.007, 0.003) | |
| α19 (Pseudomonas aeruginosa × age) | −0.0259 | (−0.037, −0.015) | |
| α10 (Methicillin‐resistant Staphylococcus aureus × age) | −0.0072 | (−0.018, 0.003) | |
| α20 (CF‐related diabetes mellitus × age) | 0.0185 | (0.009, 0.028) | |
| α11 (Medicaid insurance use × age) | 0.0072 | (0.001, 0.013) | |
| Variance | ω2 (between patient) | 25.2557 | (22.417, 28.094) |
| σ2 (within patient) | 0.8747 | (0.862, 0.888) | |
| τ2 (residual) | 69.9562 | (69.744, 70.169) | |
Abbreviations: CF, cystic fibrosis; FEV1, forced expiratory volume in 1 second of percentage of predicted.
Predictive performance for validation datasets (ii) to (iii) was evaluated for the accuracy of FEV1% predicted. The Metrics used were root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) for FEV1% predicted (Table S2 in Data S2). RMSE was 7.8% predicted for held‐out patients in dataset (ii), suggesting reasonable predictive accuracy for newly accrued CF patients. Horizons of 0.5, 1, and 2 years were examined for masked forecasting with dataset (iii). Respective RMSE values were 5.1%, 5.8%, and 6.5% predicted. As shown in the Supporting Information, MAE and MAPE exhibited similar patterns for both types of validation, suggesting reasonable predictive accuracy for FEV1. Accuracy improved as years of observed follow‐up increased (Figure S2 in Data S2), but was variable with respect to number of follow‐ups (Figure S3 in Data S2).
3.2. Model checking
Diagnostics were examined for standardized empirical residuals, which were computed based on fitted values from the model in Equation (1). Following notation from Diggle et al,22 we let ri = Yi − f(ti) − Xiα be the vector of residuals for the ith patient. The corresponding estimated variance‐covariance matrix for Yi is , where Ji is a ni × ni matrix of ones; Ri is a ni × ni matrix with element (j, k) written as:
and Ii is the identity matrix of size ni. We decomposed using lower triangular matrix Si such that as . Then, we computed the transformed empirical residual vector for each patient (i = 1, …, N).
These standardized residuals were plotted against both the fitted values and age (Figure 2, upper panels). Each plot includes the LOWESS smoother shown in black, which fell on the horizontal line at zero. Residuals plotted against age suggested that the mean of the residuals is about zero; however, the spread of the residuals decreased with age, indicating heteroscedasticity. The residuals exhibited a symmetric bell‐shaped distribution (lower‐left panel), but the quantile‐quantile plot (lower‐right panel) implied heavier tails than the standard normal distribution.
Figure 2.
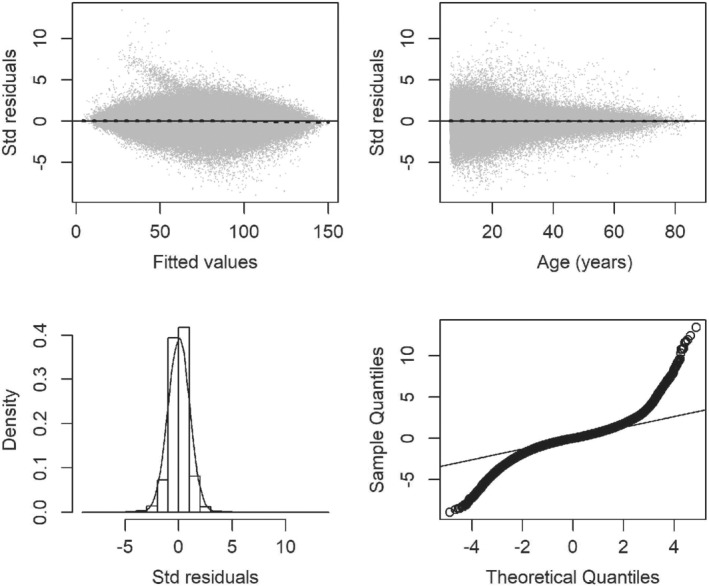
Diagnostics for standardized empirical residuals from the cystic fibrosis dynamic regression model, including residuals vs fitted values (upper‐left panel), residuals vs the time variable, age (upper‐right panel), histogram with standard normal density overlay (lower‐left panel), and quantile‐quantile plot (lower‐right panel)
Covariance assumptions (Figure 3) based on the fitted model were examined using empirical variograms for longitudinal data.29 The variogram for raw residuals ri was calculated using a bin size corresponding to weekly intervals and represents the variance of the difference between residuals within patients at time lags from 0 to 13 years (left panel, gray line). This variogram was used to partition total process variance into three components of variation: between patient (28%), within patient (53.3%), and residual error (18.4%). The smoothed empirical variogram fit (black line) suggests that the correlation between paired lung function measures decreased as separation in time increased. Although this function did not have an asymptote, the shape is similar to what has been shown with longitudinal FEV1 modeling in the Danish CF registry.15 Covariance assumptions were examined using a variogram of the transformed residuals (right panel). Empirical variogram ordinates were obtained using the formulas presented by Diggle et al.22 Random deviation about 1 implies that the model fits well. Ordinates increased up to about lag 0.1, then remained relatively steady, indicating a similar correlation through the range of lags, until a sharp drop around lag 0.5, at which point the function increased.
Figure 3.
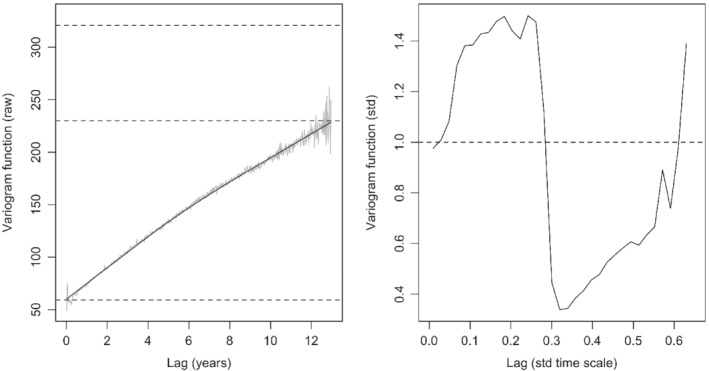
Variogram based on the raw residuals against separation in time, as years (left panel) with the dashed lines representing total process variance (320.61); the smooth black line is the empirical variogram function with upper and lower dashed lines (229.92 and 59.07, respectively) marking partitions for between‐patient variance, within‐patient variance, and residual error. Variogram for transformed residuals against the lag based on the transformed time scale (right panel). Each plot was averaged over bin sizes of 0.017 (corresponding to weekly intervals); bins with fewer than 20 residuals were excluded
Transformations (eg, log) of the response variable were considered to stabilize the variance. Modeling the data only from age 6 to 30 years old avoided presence of fitted values around 50 shown in Figure 2 (upper‐left panel), and similar diagnostic results were found when subsetting the data so that only F508del homozygotes were included. Both alternatives gave otherwise similar results as modeling the primary analysis cohort. Using time since baseline to form the model covariance resulted in a similar model fit and diagnostics. Specifying alternative distributions for the random effects did not impact results. Different numbers and locations of knots were considered, and the presented model had the best fit. More detail on the alternative knot settings and corresponding results are provided in Table S3 in Data S2.
4. PREDICTING RAPID DISEASE PROGRESSION
Conditional distributions from the model were used to form predictions of each patient's true lung function, of which FEV1 is assumed to be an unbiased proxy. These conditional distributions have been shown to be Gaussian given the previously described linear mixed effects model assumptions.22 Forms of these Gaussian distributions are detailed therein (equations 4.8‐4.12).22
4.1. Predictive probabilities of rapid decline
We let the covariate history up to a given time t of each patient be represented as ℋi(t) = {Xi, (tij, yij) : tij ≤ t}. Based on this history, we can construct a predictive probability distribution for S′(tik) (defined in Equation 4) being below a given threshold δ at time tik with estimation of parameter vector :
| (5) |
where is the true underlying rate of change in lung function; δ is the threshold (in % predicted/year) for identifying rapid decline; is the first‐order derivative of μi(tik) with respect to time tik.
By looking at the derivative of an individual's estimated lung‐function trajectory overage, we can see their rate of decline at different ages and hence identify periods of faster decline, the age of peak decline and other clinically relevant target functions. These thresholds can be used to assign a level of rapid decline overall or specific to the individual patient. Figure 4 shows an example with δ = − 1.5 % predicted/year; values below this rate would imply the patient is in rapid decline.
Figure 4.
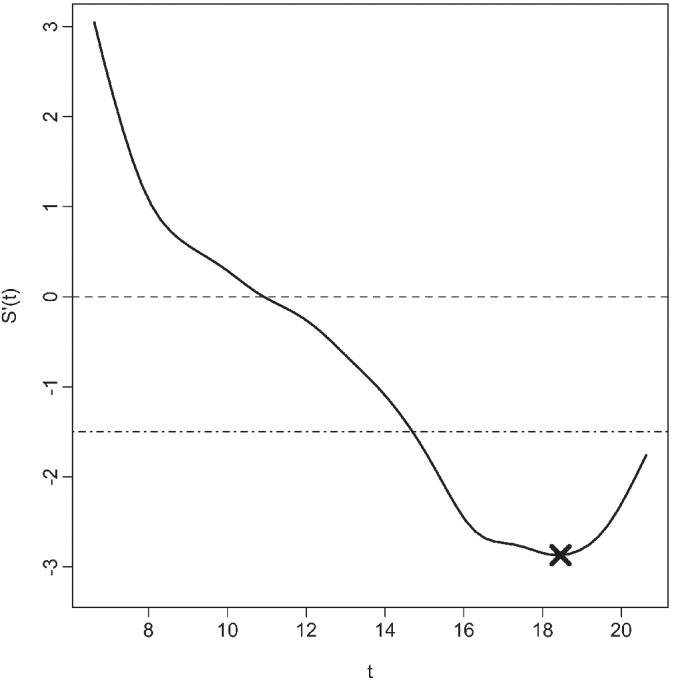
Underlying rate of change in lung function S′(t) from childhood until early adulthood over time t depicted as a smooth curve (black line), indicating periods with a loss of lung function (values below the dashed horizontal line at 0, indicating when the slope is negative) with examples of a uniform threshold of rapid decline (−1.5% predicted/year, dashed‐dotted line) and peak decline (−3% predicted/year, marked as “X”)
Although uniform thresholds (hereafter, denoted as δc) can aid clinicians in evaluating whether a patient is in a period of rapid decline, it may also be desirable to assess the patient's risk of experiencing peak decline at a given time point. Peak decline can be defined based on the derivative of a given patient's lung‐function trajectory as
| (6) |
In application, is the estimate of individualized peak decline obtained by plugging in the model‐based estimates for the parameters and solving for time. For example, Figure 4 shows a lung‐function trajectory with peak decline (−3% predicted/year) occurring ∼18.5 years of age.
4.2. Bootstrapping procedure
We used a simulation‐based bootstrapping algorithm for functions involving complicated derivatives,30 to acquire a 95% CI for the predictive probabilities. Let and denote the mean and covariance matrix for Bi(tik) defined in Section 3, given ℋi(tik). Assume satisfies.
| (7) |
where denotes the vector , which is estimated by from the model. We conducted the bootstrapping process for each patient via the following steps:
Draw independent samples (l = 1, …, L): ∼ where is the estimate of from the model. Compute . In our application, we used L = 100.
For each sample and given time point tik, calculate from Equation (5) using and mean‐squared error as .
Construct the (1 − α) × 100% CI for the predicted probability of rapid decline at time tik as . We used α = 0.05.
5. INDIVIDUAL PATIENT PREDICTIONS
Individual patient predictions from the CF dynamic regression model, along with 95% prediction intervals for longitudinal FEV1 and the corresponding rate of change, are shown for two patients in Figure 5. Row 1 corresponds to a female F508del heterozygous patient. Beginning with the leftmost plot, the gray dots represent her observed FEV1 data overage; the fitted trajectory is the solid black line with 95% CI in gray bands. The Brownian motion nowcast density (middle plot) shows declining lung‐function overage, punctuated by a sharp drop around 12‐years‐old; this plot shows the fluctuating rate of disease progression. The gray portions represent nowcasts of FEV1 and rate of change, while the red fitted curves and prediction intervals provide a short‐term forecast of FEV1 and rate of change assuming the data over the last 2 years were unobserved. Her real‐time predicted probability of rapid decline (rightmost plot) is variable overage and coincides with the predicted rate of progression, with periods of highest risk around 11 to 12 years old and again from 17 to 19 years old. Her forecasted probability of rapid decline, taken with the last 2 years of her data masked, agrees with the nowcasted values that incorporate the observed data.
Figure 5.
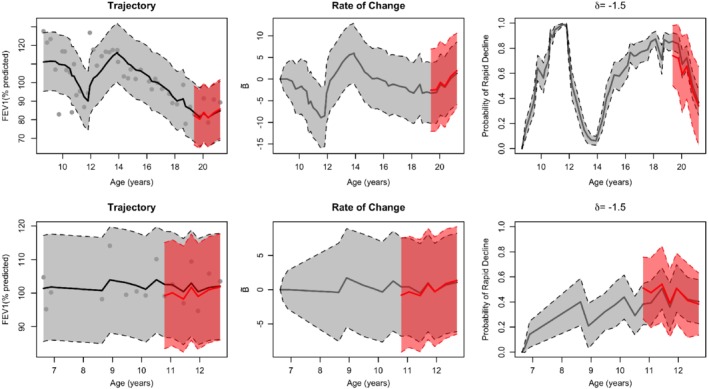
Dynamic predictions for a female F508del heterozygous patient (first row) and a male F508del homozygous patient (second row). Observed FEV1 (black dots) against age is shown for each patient (first column) with estimated lung function S(t) and 95% CI (gray bands) and 2‐year forecasted lung function (red line with prediction bands); underlying rate of change S′(t) estimated by Brownian motion (second column), including prediction intervals and forecasts; predictive probabilities of rapid decline (defined as δ c = −1.5% predicted/year) (third column), including bootstrapped 95% CI and forecasts. CI, confidence interval; FEV1, forced expiratory volume in 1 second of percentage of predicted [Color figure can be viewed at http://wileyonlinelibrary.com]
Another patient (male F508del homozygote) has predictions shown in Row 2 of Figure 5. Compared with the previous patient, his progression is steadier overage. His estimated Brownian motion process was less variable than the female (middle panel). His risk of rapid decline remained low through adolescence based on nowcasted values. The corresponding forecasted risk of rapid decline was slightly higher than nowcasted around age 11 years.
Each row of Figure 6 corresponds to these two patients, showing their real‐time predictive probability of rapid decline defined as δc < −3% predicted/year (first column) and personalized threshold, (second column). Within each patient, predictive probabilities for the target values were similar over time; however, the predictive probability of a given patient reaching peak decline varied over time. Peak decline estimates for displayed female and male patients were = −2.51 and −1.66% predicted/year, respectively.
Figure 6.
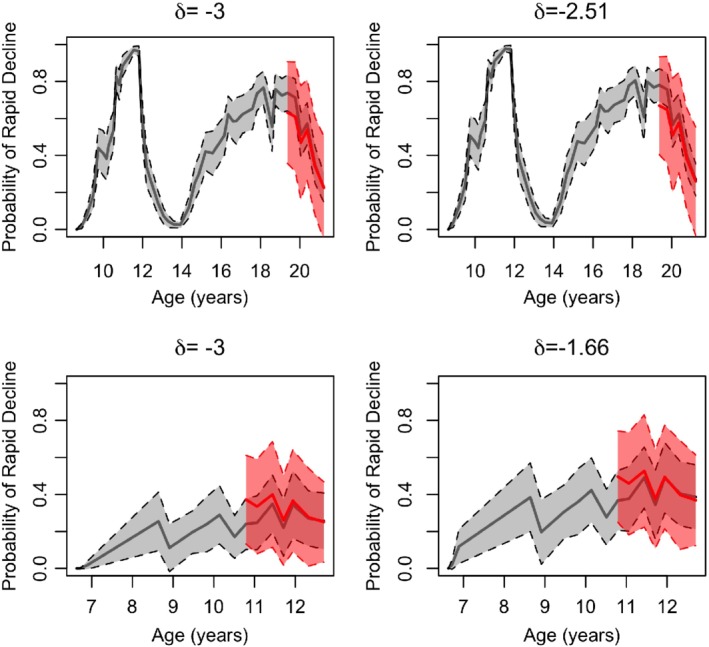
Predictive probabilities of rapid decline (defined as δ c < −3% predicted/year) (first column) corresponding to patients in Figure 5 (first row is the female F508del heterozygote; second row is the male F508del homozygote); personalized threshold δi (ti*) is shown for each patient (second column), including bootstrapped 95% CI and forecasts. CI, confidence interval [Color figure can be viewed at http://wileyonlinelibrary.com]
5.1. Empirical simulations
We investigated properties of the predictive probabilities of rapid decline from the model using simulation studies. We randomly selected 500 patients from the training cohort data; thus, the number of observations varied by patient. We used their covariate information as explanatory values in the simulation study. Random effects Ui, Wi(tij) and Zij were simulated from their corresponding distributions assumed in the model fitting. Parameters were set to their estimated values from Table 2. We performed 150 replications using the covariate information and random effects distributions above, to generate the Yij values. We ran the model on each replication batch of the Yij values. Accuracy of the predictive probabilities for nowcasting rapid decline was assessed using area under the ROC curve (AUC). This can be achieved for a given patient at time tik by defining an indicator function:
| (8) |
Herein, can be evaluated against to yield AUC estimates, where is estimated based on Equation (5).
We examined AUC estimates for uniform thresholds δc = − 1.5% predicted year, −3% predicted/year, and personalized peak decline (Table 3). The impact of not adjusting for extent of follow‐up (incorporated in the model as time since baseline) was examined. Scenarios were considered in which limited data were available per patient by randomly selecting 2‐, 5‐, or 10‐year intervals of data. Adjusting for time since baseline produced the most consistent AUC estimates across slices, which is likely expected given that simulations were generated including this variable. Not adjusting for follow‐up and limiting observation periods to 2 years or less increased AUC estimates; this is likely explained by the choice of the Brownian motion process, which has increasing variation over follow‐up that may not be realized over shorter durations. Using complete data, the uniform thresholds had a lower AUC than the threshold based on the individualized peak decline.
Table 3.
Predictive accuracy as area under the ROC curve (AUC) from empirical simulations
| AUC: 50th percentile (25th, 75th) | |||||
|---|---|---|---|---|---|
| Structure | Threshold for rapid decline, % predicted/year | 2‐year slice | 5‐year slice | 10‐year slice | Complete data |
| Full model | δc = −1.5 | 0.745 (0.740, 0.751) | 0.749 (0.743, 0.752) | 0.746 (0.744, 0.749) | 0.745 (0.741, 0.747) |
| δc = −3.0 | 0.747 (0.742, 0.753) | 0.757 (0.753, 0.761) | 0.755 (0.753, 0.758) | 0.754 (0.751, 0.756) | |
|
|
0.821 (0.816, 0.825) | 0.851 (0.847, 0.856) | 0.827 (0.823, 0.831) | 0.817 (0.814, 0.822) | |
| No adjustment for time since baseline | δc = −1.5 | 0.985 (0.983, 0.987) | 0.754 (0.750, 0.758) | 0.716 (0.713, 0.719) | 0.710 (0.707, 0.713) |
| δc = −3.0 | 0.988 (0.986, 0.989) | 0.780 (0.775, 0.785) | 0.722 (0.719, 0.725) | 0.713 (0.710, 0.716) | |
|
|
0.994 (0.993, 0.996) | 0.843 (0.837, 0.852) | 0.779 (0.774, 0.783) | 0.754 (0.749, 0.758) | |
5.2. Prediction model app
The R Shiny package was used to develop an interactive clinical tool for predictions based on the presented model specific to δc = − 1.5% predicted/year. The latest prototype of the app with individualized predictions for the forecast validation cohort is hosted at http://predictfev1.com. A proof‐of‐principle study describing how this prototype version was developed using clinician feedback has been described elsewhere.31 A still image from the app is shown (Figure 7) for a female patient with no F508del alleles with first available observed FEV1 at age 7.3 years, born during 1995 to 1998, and baseline FEV1 of 96.9% predicted. The patient experienced FEV1 loss that became more severe with age and was at high risk by ∼ 8‐years‐old. Her risk varied over follow‐up, but increased again at 16‐years‐old. The gray shaded area includes data used for training the prediction model, while the red shaded area covers the 2‐year forecast period. This patient had relatively few pulmonary exacerbations (indicated by blue‐green shading on rightmost upper panel) and increased her clinic visit frequency with age. The gray/red dots in the panel correspond to indicator functions for the covariates. She was diagnosed with CFRD, had lower socioeconomic status (use of Medicaid insurance) and experienced infections with P aeruginosa, but not MRSA. A description of the app functionality, including patient selection and generating normative data, and an additional illustration are provided as Supporting Information (Figures S4 and S5 in Data S2).
Figure 7.
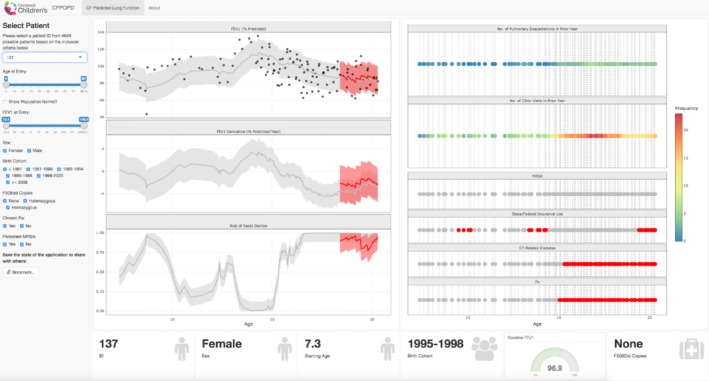
R Shiny app (screenshot) displaying real‐time risk of rapid decline in the individual cystic fibrosis patient (female case with genotype having no F508del alleles). The left panel provides user‐specific selections for patients and demographic/clinical characteristics. The middle panel includes graphs corresponding to lung‐function trajectory, rate of change, and predictive probability of rapid decline (threshold set to δ c = −1.5% predicted/year). The third panel shows heat map of covariates included in the model for rolling numbers of exacerbations and clinic visits in year to each clinical encounter, infection with MRSA, use of state/federal insurance, diagnosis of cystic fibrosis‐related diabetes, and infection with Pseudomonas aeruginosa. MRSA, Methicillin‐resistant Staphylococcus aureus [Color figure can be viewed at http://wileyonlinelibrary.com]
5.3. Center‐level comparison
The prediction model was applied to data collected from patients receiving care between January 4, 2012 and February 27, 2017, at an accredited CF center that currently employs a clinical algorithm to detect time to first rapid decline. Their algorithm defines the rapid decline at a given visit as a drop in FEV1 of at least 10% predicted from the maximum FEV1 observed over the preceding year.32 The model was applied with modifications for the younger age range and more recent birth cohorts present at the center, compared with the entire CFFPR. Rapid decline was defined from the model using δc = − 1.5% predicted/year. Our goal was to compare the center's definition with the model‐based definition of rapid decline developed in this article, to determine the extent to which these two distinct definitions of rapid decline may yield different detection times.
There were 212 patients aged 6 to 22 years old who contributed 3846 observations over the timeframe at the single CF care center (Table S4 in Data S2). The prediction model detected a similar subgroup of patients experiencing a rapid decline to those identified using the center‐level algorithm (sensitivity: 83%), but detected a different subgroup of patients who were classified as not experiencing rapid decline (specificity: 64%). The prediction model identified 120 out of 145 patients whom the center‐level algorithm identified experiencing a rapid decline over the study period. Mean (range) of the timing of rapid decline based on the model and center‐level algorithm were 12.54 (6‐19.5) and 13.19 (6.3‐20.7) years of age, respectively. Therefore, rapid decline was identified roughly 8 months earlier using the model, compared with the clinical algorithm (mean difference: 0.65 years, 95% t‐interval: 0.41‐0.89).
6. DISCUSSION
We have presented a statistical method for monitoring and detecting rapid disease progression depicted by long, irregularly observed time series, tailoring the approach to CF lung disease. This article demonstrates how estimated rate of change in an individual's lung‐function trajectory can be used to establish both clinically meaningful and patient‐specific thresholds that, when coupled with probabilistic predictive inference and translated through an app, provide a useful medical‐monitoring approach. Gaussian linear mixed models with nonstationary stochastic processes provide a natural framework for formulating targets like rapid decline or peak decline in chronic disease settings. The resulting predictive probabilities, which were shown to be well calibrated based on held‐out data, are clinically informative risk measures. Predictions shown were made at once over a 2‐year horizon; however, the approach could be used successively across the horizon as new clinical information is accrued.
This novel application examined over 30 000 patients “at‐risk” for rapid decline and showed the substantial heterogeneity in FEV1 progression among patients and within a given patient's trajectory. For example, the two cases shown in Figures 5 and 6 have distinct lung‐function trajectories and risk profiles for rapid decline. Although previous studies identified early adolescence/adulthood as high risk,3, 8, 9 we found that risk of rapid decline varied considerably between patients and within a given patient during this period. Our approach and application provides a pillar in CF diagnostic medicine by focusing on a modern, comprehensive cohort, and development of a prognostic aid. We have confirmed the attenuated decreases in FEV1 that have been shown previously, further expanded the timeframe to predict risk beyond early adulthood and provided those predictions according to individual patient characteristics. This is the basis on which the presented cases among the 4849 profiles shown in the web application, can differ considerably yet may go unnoticed without real‐time monitoring tools. Our findings suggest that it may be easier, in practice, to predict whether a patient has hit their nadir (peak decline), compared with a specific threshold of decline. This result could be attributed to each patient's trajectory having a nadir, but not everyone may reach the prespecified uniform threshold. It is also possible that uniform thresholds could be of smaller magnitude and generally more difficult to predict within a noisy time series.
Empirical simulations of our model indicate that long‐term follow‐up on some portion of patients in the cohort may be necessary to understand actual predictive performance across targets (uniform or personalized). Predictive probabilities for a target function involving S′(t) cannot be verified for accuracy in real data applications, given the lack of a “gold standard.” Care guidelines recommend quarterly “well” visits for patients with CF.33 Our analysis excluded 4.7% of the overall cohort due to missing covariate data, which consisted primarily of individuals who were older (Table S1 in Data S2). Bias due to irregular “sick” visits is not directly addressed with our approach; however, a recent assessment of various model strategies applied to irregularly sample longitudinal data found that MLEs from mixed effects models had less bias, compared with estimates from other model types.34 Jointly modeling follow‐up in the presented model could further alleviate this issue. Given that the response variable FEV1 has measurement error, it is possible that including baseline FEV1 as a covariate and having Ui as a random intercept induce bias. We examined models, each excluding one of these terms, but found worse model fit and predictive accuracy.
Sensitivity analyses of subcohorts according to genotype and age indicated that the model tended to underestimate FEV1 from individuals with a mild or uncharacteristic CF phenotype, highlighting the difficulty in making predictions about these subpopulations. Regression diagnostics from the CFFPR application also indicated violations to constant variance, which can create problems with model coefficient estimates, standard errors, and assumptions regarding specification of Wi(tij) as integrated Brownian motion. Although lmenssp does not contain direct remedies for this issue with non‐constant variance, it offers extensive selections for random effects to alleviate the issue with covariance specification. We examined alternative (differentiable) specifications and found model fitting and prediction were best using the presented structure based on BIC, AIC, and validation metrics. Furthermore, the formulation of the predictive probabilities wherein Wi(tij) is a stationary process results in a process for Bi(tij) that manifests unrealistic rates of disease progression. Empirical simulations show reasonable nowcasting performance; however, other processes need to be examined for long‐term forecasting due to the increasing variation that Brownian motion exhibits over follow‐up. The decreases in estimated AUC that correspond to longer duration of follow‐up (Table 2) may also be attributable to possible heteroscedasticity from the application of the model (Figure 2).
The integrated random walk specified in our model is locally linear, but has continuously changing slope, which enabled detection of localized, sharp changes in the FEV1 trajectory, facilitating our aim of obtaining real‐time predictive probabilities for monitoring rapid decline. An alternative approach would be to use a segmented linear mixed effects model with random change points, which can also be implemented in R.35 Mixtures of piecewise linear models of this form have been applied to classify CF patients aged 6 to 25 years, according to high‐magnitude changes in the slope of observed longitudinal FEV1. 4 This type of random change‐point model elucidates the age at which maximal FEV1 loss tends to occur in a population or subpopulations of individuals from childhood to early adulthood and seeks to identify this one‐time event (ie, one change point per patient). Extending the approach to encompass possibly multiple random change points per patient to identify one or more bouts of rapid decline, as opposed to a single maximal loss, provides additional localized detection commensurate with our case‐study goals. Despite this flexibility, the approach assumes underlying smoother trajectories than those obtained from integrated Brownian motion, which more reasonably captures the “saw‐tooth” variation found in CF FEV1 (Figure 1). Thus, segmented modeling potentially decreases the sensitivity with which real‐time rapid decline may be detected.
The approach undertaken in our study has important distinctions from past examples aimed at using biomarker trajectories to predict clinically meaningful changes in non‐CF contexts that involve classification‐based solutions. Although Foulkes et al19 also used a Gaussian linear mixed effects model in one of their approaches, they assumed variation in longitudinal trajectories could be described by a random intercept and slope model, where the latter term simplifies to Wi(tij) = bitij rather than integrated Brownian motion as we specified in Equation (1). This simplification may not be reasonable for long sequences of repeated measurements over time,36 especially for a context like CF in which the FEV1 biomarker measurements are correlated for over 15 years.7, 15 The multivariate approach taken by Li and Gatsonis21 could be adapted to the univariate setting in our case study, but additional work would be needed to incorporate covariate information, as this is not included in their current formulation, and clinical interpretation for monitoring purposes may be limited if explanatory (input) variables for predictive probabilities are confined to scores.
Finally, by translating this model and approach into a point‐of‐care tool, there are several implications for clinical care and shared decision making, as well as various strategies for improving the clinical utility of the app. Having a substantial risk of rapid decline (eg, predictive probability >0.80) could serve as a trigger to initiate more frequent clinical visits, assessments for infections or mobile reporting of cough symptoms. The approach could complement methods to monitor patients outside the clinical setting, such as the efforts made to collect at‐home spirometry.37 The web application could be expanded to facilitate shared decision making between the provider and patient, enabling the patient to view her accrued data and risk of rapid decline. Real‐time updating could be accomplished by integrating the application with electronic health record data as it is accrued at the center level. Earlier developments on joint modeling and prostate cancer recurrence were implemented in an online calculator that can be used to assess real‐time risk.24 As modulators become more available which correct the underlying defect of CF, it will be critical to update the model using newer data, accounting for these novel therapies and changes to clinical care. The prognostic utility of the model could be compared with current clinical algorithms for the treatment of rapid decline in a prospective study. As more statisticians translate findings from prediction models into point of care through R Shiny and other technologies, additional work will be needed to communicate risk measures from clinical dashboards to providers and patients.38
FINANCIAL SUPPORT
The authors disclosed receipt of the following financial support for the research, authorship and/or publication of this article: This research was supported by NIH/NHLBI grants K25 HL125954 and R01 HL141286.
ETHICAL APPROVAL
The Institutional Review Board at Cincinnati Children's Hospital Medical Center approved the study design and analytic plan.
CONFLICT OF INTEREST
None declared.
Supporting information
Data S1 Annotated_R_Script
Data S2 Supporting Information
ACKNOWLEDGEMENTS
The authors thank Jane Khoury, PhD, and Maurizio Macaluso, MD, for their presubmission reviews of the article; the Cystic Fibrosis Foundation for the use of Cystic Fibrosis Foundation Patient Registry data to conduct this study; the Registry Committee for their thoughtful feedback and data dispensation; the patients, care providers, and clinic coordinators at cystic fibrosis centers throughout the US for their contributions to the Registry. The authors thank the handling editor and reviewers for their suggestions, which enhanced the content and quality of the article.
Szczesniak RD, Su W, Brokamp C, et al. Dynamic predictive probabilities to monitor rapid cystic fibrosis disease progression. Statistics in Medicine. 2020;39:740–756. 10.1002/sim.8443
Funding information National Heart, Lung, and Blood Institute, K25 HL125954; National Heart, Lung, and Blood Institute, R01 HL141286
DATA AVAILABILITY
The data that support the findings of this study are available from the Cystic Fibrosis Foundation. Restrictions apply to the availability of these data, which were used under license for this study. Requests for data may be sent to datarequests@cff.org.
References
- 1. Farrell PM. The prevalence of cystic fibrosis in the European Union. J Cyst Fibros. 2008;7(5):450‐453. [DOI] [PubMed] [Google Scholar]
- 2. Salvatore D, Buzzetti R, Mastella G. An overview of international literature from cystic fibrosis registries. Part 5: update 2012‐2015 on lung disease. Pediatr Pulmonol. 2016;51(11):1251‐1263. [DOI] [PubMed] [Google Scholar]
- 3. Vandenbranden SL, McMullen A, Schechter MS, et al. Lung function decline from adolescence to young adulthood in cystic fibrosis. Pediatr Pulmonol. 2012;47(2):135‐143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Moss A, Juarez‐Colunga E, Nathoo F, Wagner B, Sagel S. A comparison of change point models with application to longitudinal lung function measurements in children with cystic fibrosis. Stat Med. 2016;35(12):2058‐2073. [DOI] [PubMed] [Google Scholar]
- 5. Szczesniak RD, Li D, Su W, et al. Phenotypes of rapid cystic fibrosis lung disease progression during adolescence and young adulthood. Am J Respir Crit Care Med. 2017;196:471‐478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Liou TG, Adler FR, Cox DR, Cahill BC. Lung transplantation and survival in children with cystic fibrosis. N Engl J Med. 2008;359(5):536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Szczesniak RD, McPhail GL, Duan LL, Macaluso M, Amin RS, Clancy JP. A semiparametric approach to estimate rapid lung function decline in cystic fibrosis. Ann Epidemiol. 2013;23(12):771‐777. [DOI] [PubMed] [Google Scholar]
- 8. Konstan MW, Morgan WJ, Butler SM, et al. Risk factors for rate of decline in forced expiratory volume in one second in children and adolescents with cystic fibrosis. J Pediatr. 2007;151(2):134‐139. [DOI] [PubMed] [Google Scholar]
- 9. Konstan MW, Wagener JS, Vandevanter DR, et al. Risk factors for rate of decline in FEV1 in adults with cystic fibrosis. J Cyst Fibros. 2012;11(5):405‐411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Marshall BC, Nelson EC. Accelerating implementation of biomedical research advances: critical elements of a successful 10 year Cystic Fibrosis Foundation healthcare delivery improvement initiative. BMJ Qual Saf. 2014;23(Suppl 1):i95‐i103. [DOI] [PubMed] [Google Scholar]
- 11. Siracusa CM, Weiland JL, Acton JD, et al. The impact of transforming healthcare delivery on cystic fibrosis outcomes: a decade of quality improvement at Cincinnati Children's hospital. BMJ Qual Saf. 2014;23(Suppl 1):i56‐i63. [DOI] [PubMed] [Google Scholar]
- 12. Schechter M, Schmidt JH, Williams R, Norton R, Taylor D, Molzhon A. Impact of a program ensuring consistent response to acute drops in lung function in children with cystic fibrosis. J Cyst Fibros. 2018;17:769‐778. [DOI] [PubMed] [Google Scholar]
- 13. Jackson AB, Goss CH. Epidemiology of CF: how registries can be used to advance our understanding of the CF population. J Cyst Fibros. 2018;17(3):297‐305. [DOI] [PubMed] [Google Scholar]
- 14. Laird NM, Ware JH. Random‐effects models for longitudinal data. Biometrics. 1982;38(4):963‐974. [PubMed] [Google Scholar]
- 15. Taylor‐Robinson D, Whitehead M, Diderichsen F, et al. Understanding the natural progression in %FEV1 decline in patients with cystic fibrosis: a longitudinal study. Thorax. 2012;67(10):860‐866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Harun SN, Wainwright C, Klein K, Hennig S. A systematic review of studies examining the rate of lung function decline in patients with cystic fibrosis. Paediatr Respir Rev. 2016;20:55‐66. [DOI] [PubMed] [Google Scholar]
- 17. De Finetti B. Theory of Probability. Vol 1 New York, NY: Wiley; 1974. [Google Scholar]
- 18. Dmitrienko A, Wang MD. Bayesian predictive approach to interim monitoring in clinical trials. Stat Med. 2006;25(13):2178‐2195. [DOI] [PubMed] [Google Scholar]
- 19. Foulkes AS, Azzoni L, Li X, et al. Prediction based classification for longitudinal biomarkers. Ann Appl Stat. 2010;4(3):1476‐1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Albert PS. Shared random parameter models: a legacy of the biostatistics program at the National Heart, Lung, and Blood Institute. Stat Med. 2019;38(4):501‐511. [DOI] [PubMed] [Google Scholar]
- 21. Li H, Gatsonis C. Combining biomarker trajectories to improve diagnostic accuracy in prospective cohort studies with verification bias. Stat Med. 2019;38(11):1968‐1990. [DOI] [PubMed] [Google Scholar]
- 22. Diggle PJ, Sousa I, Asar O. Real‐time monitoring of progression towards renal failure in primary care patients. Biostatistics. 2015;16(3):522‐536. [DOI] [PubMed] [Google Scholar]
- 23. Galovic M, Dohler N, Erderlyi‐Canavese B, et al. Prediction of late seizures after ischaemic stroke with a novel prognostic model (the SeLECT score): a multivariable prediction model development and validation study. Lancet Neurol. 2018;17(2):143‐152. [DOI] [PubMed] [Google Scholar]
- 24. Taylor JM, Park Y, Ankerst DP, et al. Real‐time individual predictions of prostate cancer recurrence using joint models. Biometrics. 2013;69(1):206‐213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Knapp EA, Fink AK, Goss CH, et al. The Cystic Fibrosis Foundation Patient Registry. Design and methods of a National Observational Disease Registry. Ann Am Thorac Soc. 2016;13(7):1173‐1179. [DOI] [PubMed] [Google Scholar]
- 26. Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. New York, NY: Cambridge University Press; 2003. [Google Scholar]
- 27. Szczesniak R, Heltshe SL, Stanojevic S, Mayer‐Hamblett N. Use of FEV1 in cystic fibrosis epidemiologic studies and clinical trials: a statistical perspective for the clinical researcher. J Cyst Fibros. 2017;16:318‐326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Asar O, Diggle PJ. Linear mixed effects models with non‐stationary stochastic processes. https://cran.r-project.org/web/packages/lmenssp/lmenssp.pdf. Published 2016. Accessed September 13, 2019.
- 29. Diggle PJ, Heagerty P, Liang K‐Y, Zeger SL. Longitudinal Analysis of Data. 2nd ed. Oxford, UK: Oxford University Press; 2002. [Google Scholar]
- 30. Mandel M. Simulation‐based confidence intervals for functions with complicated derivatives. Am Stat. 2013;67(2):76‐81. [Google Scholar]
- 31. Szczesniak RD, Brokamp C, Su W, McPhail GL, Pestian J, Clancy JP. Improving detection of rapid cystic fibrosis disease progression—early translation of a predictive algorithm into a point‐of‐care tool. IEEE J Transl Eng Health Med. 2018;7:2800108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. McPhail GL, Weiland J, Hoberman AJ, et al. Improving rapid FEV1 decline through quality improvement. Pediatr Pulmonol. 2013;48:394. [Google Scholar]
- 33. Cystic Fibrosis Foundation . Cystic Fibrosis Foundation Patient Registry, Annual Report. Bethesda, MD: Cystic Fibrosis Foundation; 2016. [Google Scholar]
- 34. Neuhaus JM, McCulloch CE, Boylan RD. Analysis of longitudinal data from outcome‐dependent visit processes: failure of proposed methods in realistic settings and potential improvements. Stat Med. 2018;37(29):4457‐4471. [DOI] [PubMed] [Google Scholar]
- 35. Muggeo VMR. Package 'Segmented'. https://cran.r-project.org/web/packages/segmented/segmented.pdf. Published 2019. Accessed September 13, 2019.
- 36. Henderson R, Diggle P, Dobson A. Joint modelling of longitudinal measurements and event time data. Biostatistics. 2000;1(4):465‐480. [DOI] [PubMed] [Google Scholar]
- 37. Lechtzin N, Mayer‐Hamblett N, West NE, et al. Home monitoring in CF to identify and treat acute pulmonary exacerbations: eICE study results. Am J Respir Crit Care Med. 2017;196:1144‐1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Spiegelhalter DJ. Risk and uncertainty communication. Annu Rev Stat Appl. 2017;4:31‐60. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1 Annotated_R_Script
Data S2 Supporting Information
Data Availability Statement
The data that support the findings of this study are available from the Cystic Fibrosis Foundation. Restrictions apply to the availability of these data, which were used under license for this study. Requests for data may be sent to datarequests@cff.org.


