Re-evaluating circuit mechanisms underlying pattern separation

Summary

When animals interact with complex environments their neural circuits must separate overlapping patterns of activity that represent sensory and motor information. Pattern separation is thought to be a key function of several brain regions, including the cerebellar cortex, insect mushroom body and dentate gyrus. However, recent findings have questioned long-held ideas on how these circuits perform this fundamental computation. Here we re-evaluate the functional and structural mechanisms underlying pattern separation. We argue that the dimensionality of the space available for population codes representing sensory and motor information provides a common framework for understanding pattern separation. We then discuss how these three circuits use different strategies to separate activity patterns and facilitate associative learning in the presence of trial-to-trial variability.

Introduction

Imagine you are about to run an experiment in a laboratory, when the phone rings. You leave the lab, and chat on the phone for a few minutes with your colleague. Upon re-entering the lab you quickly realise that something has changed (spot the difference - Figure 1A). Although the change in sensory inputs is small relative to the total sensory information contained in each scene, the difference between the two conditions is immediately apparent. This example illustrates the inherent ability of the brain to distinguish between subtle, but important differences in the detail of the environment.

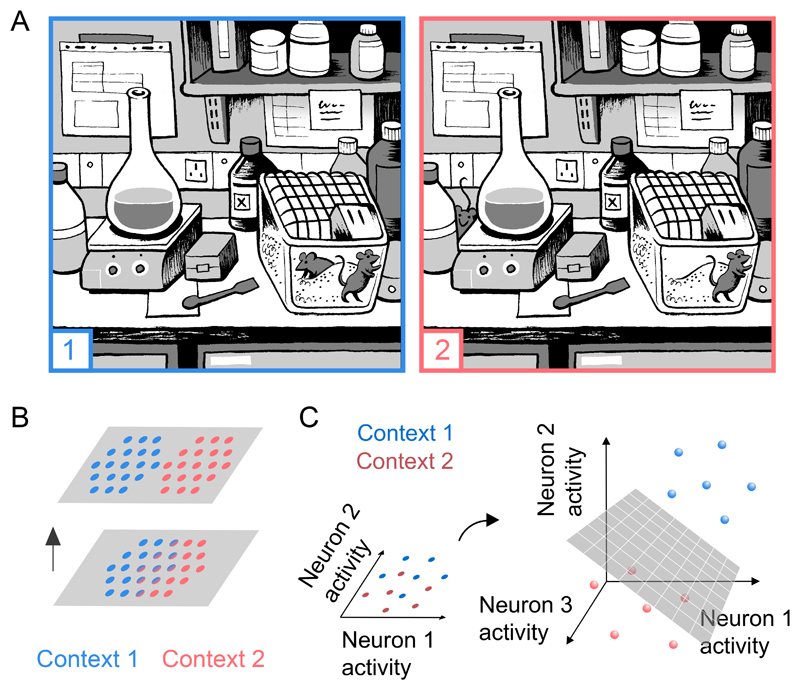
Figure 1. Pattern separation is a fundamental circuit computation.

A Spot the difference. This classic children’s puzzle requires the reader to hunt for small differences between two near-identical images. But in this example, the relocation of the escaped mouse is immediately clear. This demonstrates the brain’s ability to recognize small differences between similar scenes. Illustration by Matteo Farinella.

B Marr hypothesized that neural circuits separate overlapping neural activity patterns by activating distinct ensembles of neurons (Marr, 1969). Neurons that are active under context 1 are shown in blue, and those active under context 2 are shown in red. Grey represents neurons that are silent in both contexts.

C Albus argued that the cerebellar cortex separates patterns in neural activity space by expanding the dimensionality, enabling a downstream decoder neuron to linearly classify them (Albus, 1971). Blue/red represents neural activity patterns in different trials during context 1 or 2. Grey inclined plane indicates hyperplane in activity space that separates the two contexts.

Sensory, proprioceptive, and motor information is represented by the spatiotemporal firing patterns of populations of neurons. To identify subtle changes in the external world, the brain must distinguish between similar patterns of neuronal activity. This can be facilitated by ‘pattern separation’, a process in which neural circuits transform similar input activity patterns into more distinct output patterns. Pattern separation in neural circuits was first formulated by David Marr (Marr, 1969), who was inspired by two generic features of the circuitry of the cerebellar input layer: the extensive divergence from a smaller number of mossy fibre inputs to a much larger number of granule cells, and widespread feedback inhibition that regulates granule cell excitability. Based on these features, Marr hypothesized that the cerebellar input layer projects mossy fibre activity patterns onto a much larger population of sparsely active granule cells, thereby reducing the overlap between activated neurons (Figure 1B).

James Albus independently developed a similar theory based on analogies between the cerebellar cortex and supervised learning algorithms from early artificial intelligence research (Albus, 1971). In this framework, each activity pattern can be considered as a point in activity space, where each dimension corresponds to the activity of a different neuron. Albus argued that the divergent architecture of the cerebellar input layer recodes input patterns in an expanded activity space, thereby increasing their linear separability, (i.e., the ability to separate different groups of input patterns in activity space via a hyperplane; Figure 1C). This enables a downstream decoder, such as a perceptron (Rosenblatt, 1958) or support vector machine (Cortes and Vapnik, 1995), to better classify input patterns into arbitrary associations using supervised learning. In the cerebellar cortex such supervised learning is thought to occur largely in Purkinje cells (Brunel et al., 2004; Ito, 2006; Gao et al., 2012; Ohmae and Medina, 2015; Herzfeld et al, 2018; Raymond and Medina, 2018), where precise sensorimotor associations are formed by learning rules with narrow temporal windows (Suvrathan and Raymond, 2016). However, neural activity exhibits significant trial-to-trial variability due to a variety of factors, including noise from inherently stochastic processes (e.g. neurotransmitter release at synapses), fluctuations in the external stimulus, and changes in the internal state of the animal (e.g. attention). Therefore, a key question for pattern separation is how neural circuits separate overlapping representations in the presence of unwanted variability (Laurent, 2002).

Despite the differing conceptual details between their theories, Marr and Albus both predicted that the divergent feedforward excitation present in the cerebellar input layer implements pattern separation. These concepts (often combined into ‘Marr-Albus theory’) have been extended to other divergent circuits that are upstream from areas involved in associative learning. But, fifty years later, it still remains unclear how different neural circuits separate noisy activity patterns. Indeed, several mechanisms believed to be involved in this fundamental computation have recently been called into question by new experimental and theoretical studies in three brain regions proposed to perform pattern separation: the cerebellar cortex, insect mushroom body, and dentate gyrus. In this review, we re-evaluate classical concepts of Marr-Albus theory of pattern separation in light of these new findings, and discuss recent challenges to how they may be implemented in these circuits.

Three key circuits that perform pattern separation

Cerebellar cortex

The cerebellum is thought to use associative learning to coordinate movements and predict the sensory consequences of active movement (Wolpert et al., 1998; Kennedy et al., 2014; Brooks et al., 2015; Singla et al., 2017). The evolutionarily conserved, highly regular structure of the cerebellar cortex has encouraged much speculation as to how the computations required for these functions are achieved (Figure 2A; Braitenberg, 1961; Eccles et al., 1967; Marr, 1969; Albus, 1971; Fujita, 1982; Pellionisz and Llinas, 1982; Kanerva, 1988; Tyrrell and Willshaw, 1992; Miall et al., 1993; Ito, 2006; Yamazaki and Tanaka, 2007; Dean et al., 2010). Mossy fibres carry sensory and motor information (van Kan et al., 1993; Arenz et al., 2008; Huang et al., 2013; Proville et al., 2014; Powell et al., 2015) to the cerebellar input layer (or granule cell layer’), where they form multiple ‘en passant’ presynaptic boutons. Each large bouton makes glutamatergic synapses onto the short dendrites of multiple granule cells (Eccles et al 1967; Silver et al., 1992). Granule cell axons ascend into the molecular layer, where they bifurcate to form long ‘parallel fibres’ that synapse onto numerous Purkinje cells and interneurons. Granule cells also receive feedforward and feedback inhibition from Golgi cells (Vos et al., 1999; Duguid et al., 2015), which are driven by excitatory inputs from mossy fibres through their basal dendrites (Kanichay and Silver, 2008) and ascending granule cell axons and parallel fibres through their apical dendrites (Dieudonné, 1998; Cesana et al., 2013). Golgi cells are sparsely interconnected via chemical synapses (Hull and Regehr, 2012) and densely connected via electrical synapses (Dugue et al., 2009; Szoboszlay et al., 2016), which enables them to respond to excitatory input in a concerted (Vervaeke et al., 2012) or desynchronized manner (Vervaeke et al., 2010).

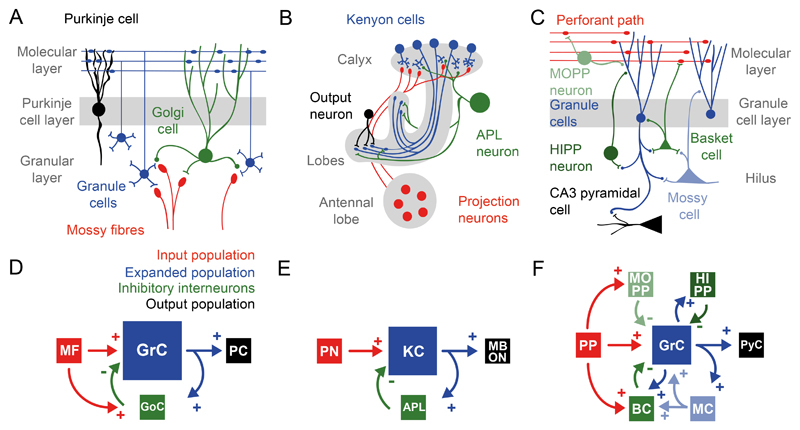
Figure 2. Three circuits that perform pattern separation.

Circuit-level (A-C) and systems-level (D-F) diagrams of the cerebellar cortex, mushroom body, and dentate gyrus. Colour key for all panels: red, excitatory afferents; dark blue, excitatory interneurons (here called the ‘expanded’ population); green, inhibitory interneurons; and black, output neurons. Size of boxes indicates relative expansion.

A,D Cerebellar cortex: Mossy fibres (MF) carry sensorimotor information to the granule cells (GrC), whose axons ascend to the molecular layer and bifurcate, eventually contacting Purkinje cells (PC). Inhhibitory Golgi cells (GoC) receive input from both mossy fibres and parallel fibres and project to granule cells in the granule cell layer, thereby delivering a combination of feedforward and feedback inhibition.

B,E Mushroom body: Projection neurons (PN) in the antennal lobe project to Kenyon cell (KC) dendrites in the mushroom body calyx. Kenyon cell axons extend, forming the peduncle, and bifurcate into the lobes where they contact mushroom body output neurons (MBON). A single GABAergic neuron, called the anterior paired lateral neuron (APL) in flies, receives input from almost all Kenyon cells in the lobes and inhibits almost all Kenyon cells in the calyx.

C,F Dentate gyrus: Perforant path (PP) fibres, originating from entorhinal cortex, project to the distal dendrites of granule cells (GrC). Granule cell axons extend through the hilus, where they contact hilar interneurons, and ultimately project to CA3 pyramidal cells (PyC). Granule cells are embedded in a complex network of multiple inhibitory interneuron subtypes. This includes feedforward and feedback inhibition from molecular layer perforant path interneurons (MOPP), hilar perforant path interneurons (HIPP) and basket cells (BC). A second excitatory dentate cell type, mossy cells (MC), are recurrently connected with both granule cells and local hilar inhibitory neurons such as basket cells.

Two converging lines of thought have led to the hypothesis that the cerebellar input layer separates overlapping input patterns. The first stems from the cerebellum's role in associative learning. Pattern separation is a useful pre-processing step for associative learning, so any circuit that is involved in associative learning is also a key candidate for pattern separation. A classic example is eyeblink conditioning, in which animals are trained to associate a neutral sensory cue (e.g. auditory or visual) with a delayed presentation of an unconditional stimulus (air puff or electric shock; Attwell et al., 2002). Pattern separation could facilitate this form of associative learning by making neural representations of different sensory inputs more distinct, ensuring that the unconditional stimulus is not mistakenly associated with similar, but not identical, cues. This hypothesis is consistent with functional evidence of the cerebellum’s involvement in sensory discrimination (Gao et al., 1996; Parsons et al., 1997; Parsons et al., 2009), but most eyeblink conditioning studies have used a single sensory cue. A recent study found that lesioning cerebellar nuclei affected the ability of mice to discriminate between two tones in a delay eyeblink conditioning task (Sakamoto and Endo, 2013). But lesioned animals were still able to learn a simple eyeblink conditioning task, suggesting that the task was not fully dependent on the cerebellum. Moreover, a patient with cerebellar cortical atrophy was unable to learn to associate two tones with different delays (Fortier et al., 2000). These studies are consistent with the idea that pattern separation plays a role in cerebellar supervised learning by helping discrimination of sensory cues, but direct experimental evidence of cerebellar pattern separation is lacking.

Second, substantial theoretical work based on Marr-Albus theory has shown that the circuitry of the input layer of the cerebellar cortex is well suited for pattern separation (Marr, 1969; Albus, 1971; Kanerva, 1988; Tyrrell and Willshaw, 1992; Billings et al., 2014; Cayco-Gajic et al., 2017; Litwin-Kumar et al., 2017). This relies on three main circuit mechanisms: a large divergence (or ‘expansion’), sparse synaptic connectivity, and broad feedback inhibition. First, the projection from mossy fibres to granule cells is highly divergent, with granule cells greatly outnumbering mossy fibres. Indeed, cerebellar granule cells are the most abundant of all neurons in the vertebrate brain. Second, broad feedback inhibition is provided by Golgi cells, which form electrically coupled syncytia, and have large axonal arbours. Finally, the connectivity structure is sparse, with each granule cell receiving synaptic input from only four mossy fibres on average. These circuit mechanisms are conserved across different cerebellar regions and species (Wittenberg and Wang, 2007), suggesting that the cerebellar cortical circuitry is important for survival.

Together, these studies have built an anatomical and theoretical foundation for cerebellar pattern separation based on Marr-Albus theory. However, direct experimental evidence in the cerebellum is still lacking, due to the technical difficulty of studying populations of densely packed cells in awake animals with conventional multi-unit electrophysiological recordings. Several groups have recently overcome the technical hurdles of recording granule cell population activity by using two-photon imaging and genetically encoded calcium indicators (Giovannucci et al., 2017; Knogler et al., 2017; Wagner et al., 2017; see also Ozden et al., 2012). These studies have challenged several long-held assumptions about the properties of granule cell activity, suggesting that traditional concepts underlying cerebellar function should be re-evaluated (discussed in detail below).

Mushroom body

Early lesion and ablation experiments identified the mushroom body as a centre for olfactory memory and associative learning in insects (de Belle and Heisenberg, 1994; Connolly et al., 1996). The axons of olfactory receptor neurons expressing the same olfactory receptor converge onto specific glomeruli in the antennal lobes, forming a spatial odourant map (Fishilevich and Vosshall, 2005). Projection neurons integrate signals from stereotyped sets of glomeruli, which form random synaptic connections onto Kenyon cells in the mushroom body calyx (Figure 2B) (Masuda-Nakagawa et al., 2005; Murthy et al., 2008; Caron et al., 2013; but see Eichler et al., 2017; Zheng et al., 2018). Like the cerebellar input layer, the mushroom body circuitry is highly divergent, with the number of Kenyon cells far exceeding the number of projection neurons. In Drosophila, the synaptic connectivity is also sparse: Kenyon cells have an average of seven dendritic claws, each of which is innervated by a single projection neuron (Butcher et al., 2012; Caron et al., 2013; Gruntmann and Turner, 2013; but, see Jortner et al., 2007 for a denser connectivity scheme in locust). Global feedback inhibition is provided by a single GABAergic neuron, called the anterior paired lateral (APL) neuron in Drosophila, which is both presynaptic and postsynaptic to virtually all Kenyon cells (Leitch and Laurent, 1996; Liu and Davis, 2009; Papadopoulou et al., 2011), although recent evidence suggests that the APL neuron may also mediate local lateral inhibition (Inada et al., 2017). Kenyon cell axons project out from the calyx to form the lobes, where they converge onto a smaller number of mushroom body output neurons.

The role of the mushroom body in associative olfactory learning, and its broad similarities with the divergent circuitry of the cerebellar cortex (Farris, 2011), led to the idea that the mushroom body performs pattern separation (Laurent, 2002). This concept was directly tested by a study that used whole-cell recordings to determine that average odour-evoked Kenyon cell responses were indeed more separated than those of olfactory receptor neurons (Turner et al., 2008). More recent work has taken advantage of genetically encoded calcium indicators to image populations of Kenyon cells during an olfactory learning task, verifying that the ability of flies to generalise aversive associations to novel odours depends on the level of overlap between the odour-evoked Kenyon cell activity patterns (Campbell et al., 2013). Conversely, the overlap between projection neuron activity patterns could not predict learned discrimination performance in flies (Parnas et al., 2013). In a separate experiment, disruption of the mushroom body circuitry by silencing feedback inhibition resulted in Kenyon cell activity patterns becoming more similar, and flies were unable to learn to distinguish similar odours (Lin et al., 2014). These experimental results suggest that the mushroom body separates odour-evoked activity patterns, and that this function is critical for associative learning and behavioural discrimination of odours.

Dentate gyrus

The overall structure of the hippocampus is classically described as a ‘trisynaptic’ circuit, with information flowing from the entorhinal cortex to the dentate gyrus, followed by areas CA3 and CA1. As the first stage in this pathway, the dentate gyrus is thought to separate entorhinal input patterns prior to memory storage in the hippocampus (Marr, 1971; McNaughton and Morris, 1987; Yassa and Stark, 2011; Schmidt et al., 2012; Knierim and Neunuebel, 2016; Rolls, 2016). Like the cerebellar cortex, the dentate gyrus has a trilaminar structure that is characterised by divergent projections onto a larger population of granule cells, and convergence onto a smaller number of CA3 pyramidal cells (Figure 2C). However, there are substantial differences between these circuits. First, dentate granule cells only modestly outnumber their inputs, whereas in the cerebellum the expansion is much larger. Dentate granule cells also receive thousands of excitatory synaptic inputs from perforant path axons originating in the entorhinal cortex (McNaughton et al., 1991). Another key difference is that dentate granule cells form recurrent loops with a second excitatory cell type: the mossy cells. Granule cell axons descend through the hilus and form boutons that make excitatory synapses on mossy cells, hilar interneurons, CA3 pyramidal cells and CA3 interneurons (Henze et al., 2000). Ascending mossy cell axons project to the molecular layer where they contact granule cell dendrites, while collaterals are thought to innervate local inhibitory interneurons in the hilus (Scharfman, 2016).

While in general cerebellar granule cells only receive inhibition from Golgi cells - with the exception of recently discovered inhibitory feedback (Ankri et al., 2015; Guo et al., 2016) and external broad inhibition (Jaarsma et al., 2018) in specific regions - dentate granule cells are interconnected with multiple inhibitory interneuron subtypes, which are likely to be specialized for distinct functions (Halasy and Somogyi, 1993; Sik et al., 2006; Hosp et al., 2014; Savanthrapadian et al., 2014; Szabo et al., 2017). Of these, one of the most widely studied are basket cells, which receive synaptic input from granule cell axon collaterals, and deliver feedback inhibition to the perisomatic regions of granule cells via their extensive axonal plexus (Ribak, 1992). Granule cells also receive feedforward perisomatic inhibition from basket cells (Ribak, 1992), as well as feedforward dendritic inhibition from molecular layer perforant path associated cells (Han et al., 1993; Li et al., 2013). In addition, recent work has found that parvalbumin-expressing interneurons (which includes some basket cells as well as axo-axonic cells; Hu et al., 2014) establish powerful lateral inhibition between granule cells (Espinoza et al., 2018). Therefore, the general circuit mechanisms of feedforward, feedback, and strong lateral inhibition are present within the complex dentate inhibitory interneuron network.

Direct evidence of pattern separation in the dentate gyrus comes from recent work performing extracellular hippocampal recordings from rats during free exploration. Slight alterations in environmental cues resulted in dentate activity patterns that were less correlated than those in the entorhinal cortex (Neunuebel et al., 2013; Neunuebel and Knierim, 2014). Dentate recordings during exploration of similar environments have also been shown to be less correlated than in CA3 (Leutgeb et al., 2007; Neunuebel and Knierim, 2014) consistent with the hypothesis that the dentate gyrus acts as a pattern separator prior to memory storage in the hippocampus. In humans, a high-resolution functional imaging study found that similar scenes could be decoded with a linear classifier more accurately based on multivoxel patterns in the dentate gyrus than in other hippocampal subfields or the entorhinal cortex (Berron et al., 2016).

Behavioural discrimination tasks are often used as a proxy for pattern separation in the hippocampus. For example, lesion and genetic deletion studies have shown that the dentate gyrus is necessary for the discrimination of similar contexts (Gilbert et al., 2001; McHugh et al., 2007; Hunsaker et al., 2008). Adult-born granule cells have also been implicated in contextual discrimination (Sahay et al., 2011; Nakashiba et al., 2012; Danielson et al., 2016), a result that parallels recent findings that suggest that adult neurogenesis facilitates pattern decorrelation in the olfactory bulb (Li et al., 2018). However, the impact of adult neurogenesis in the hippocampus may be species dependent (Sorrells et al., 2018). Such behavioural assays of pattern separation (sometimes called ‘behavioural pattern separation’) are not necessarily equivalent to the computational process of separating input patterns (Figure 1B) (Santoro, 2013). In this review, we focus on ‘computational’ pattern separation rather than behavioural pattern separation (which has recently been reviewed; Leal and Yassa, 2018). Nevertheless, these behavioural discrimination studies, in combination with electrophysiological and theoretical work, provide strong evidence for pattern separation in the dentate gyrus.

Three circuits, one computation?

We have discussed theoretical, anatomical, functional and behavioural evidence that a key role of the cerebellar input layer, insect mushroom body, and dentate gyrus is to separate activity patterns as a pre-processing step for downstream associative learning and memory formation. These regions share the divergent excitatory projection and feedback inhibition that have been identified by Marr-Albus theory as being beneficial for pattern separation (Figure 2D-F). However, there are significant structural differences between these three circuits, raising the question of how they can each implement pattern separation. We will argue that these circuits use distinct strategies to achieve the same function. To understand how this could be achieved, we will first address the key concepts underlying pattern separation - expansion recoding, sparse coding, decorrelation and dimensionality - and discuss how they are interrelated.

Updating classical concepts of pattern separation

Expansion recoding

A key tenet of Marr-Albus theory is ‘expansion recoding’, in which neural activity space is increased through a random projection of mossy fibre inputs onto a significantly larger population of granule cells (Figure 3A). Expansion recoding is thought to play a key role in pattern separation prior to associative learning. Consistent with this, a study that specifically silenced the synaptic outputs of the majority of cerebellar granule cells found that this intervention affected the acquisition and consolidation of skilled behaviours but not normal motor performance (but concomitant changes in long term plasticity could also contribute to these effects; Galliano et al., 2013). Expansion can be quantified by the ratio of the size of the input population to the expanded layer population. In the cerebellum, individual mossy fibre axons form up to 200 ‘en passant’ boutons (Wu et al., 1999) and the ratio of mossy fibre boutons to cerebellar granule cells is 1:2.9 in rats (Billings et al., 2014), giving an expansion ratio of roughly 1:600 (Eccles et al., 1967). Anatomical estimates of the ratio of projection neurons to Kenyon cells in the mushroom body are roughly 1:40 (Laurent, 2002; Litwin-Kumar et al., 2017). Dentate granule cells also outnumber pyramidal cells in entorhinal cortex, but here the expansion ratio is an order of magnitude smaller (approximately 1:5; Leutgeb et al., 2007). This suggests a divergent architecture of varying degrees in each of these three circuits.

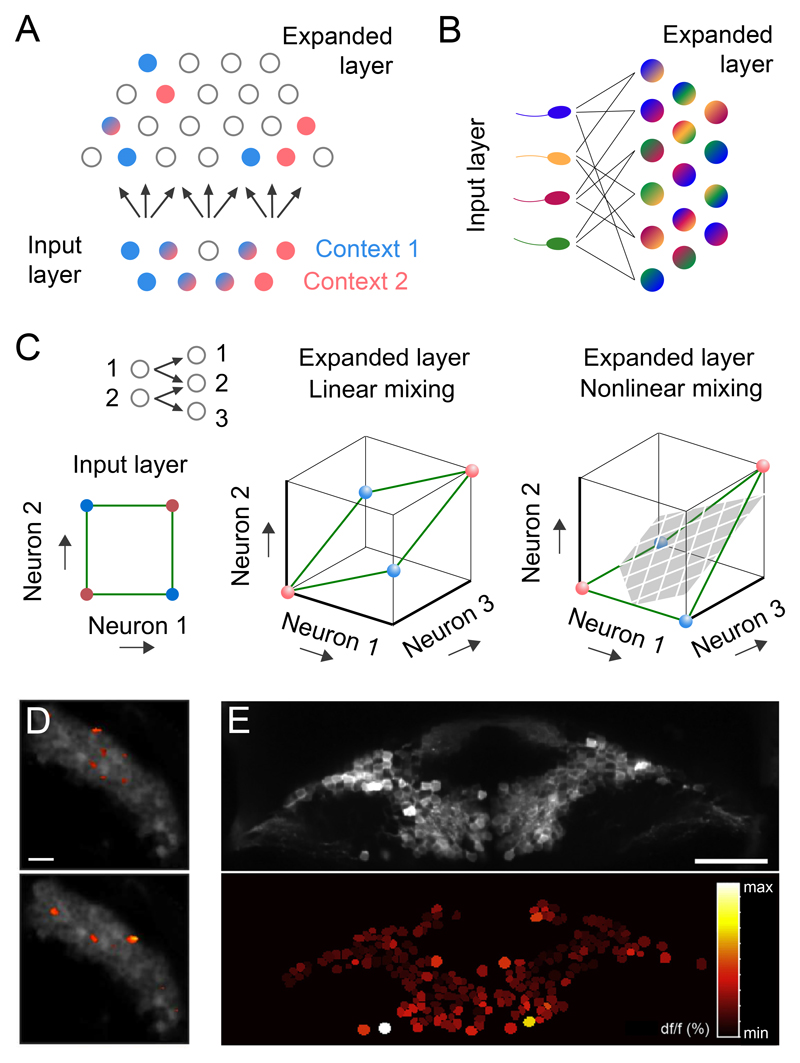
Figure 3. Sparseness and expansion recoding.

A Schematic diagram of expansion recoding and sparsening in feedforward network. Dense, overlapping activity patterns in the input population are projected onto a much larger population of more sparsely active neurons.

B Randomly mixing inputs of different sensory modalities (indicated by different colours) in the expanded population gives rise to a large population of neurons that represent arbitrary input combinations, which can be useful for associative learning.

C Illustration of how expansion and nonlinear mixing increases the linear separability of activity patterns. Left, top: Circuit diagram of two input neurons diverging onto three neurons in the expanded layer. In this example, in the expanded layer, neurons 1 and 3 are selective to single inputs, while neuron 2 mixes both input channels. Left, bottom: Example of input activity patterns representing different contexts (red, blue), which cannot be linearly separated. Middle: If the expanded layer neurons are linear, the activity patterns are still not linearly separable because they fall on the same plane. Right: By adding a thresholding nonlinearity, neuron 2 becomes a coincidence detector for the two input channels. Now as a result of this nonlinear mixing, the activity patterns are linearly separable (demonstrated by the grey hyperplane). Figure inspired by Rigotti et al., 2013.

D Heatmap of Kenyon cell activity for two different odours, overlaid on an anatomical map of mean dF/F activity (colour scale as in E). The few active cells indicates Kenyon cell population coding is sparse. Scale bar, 10 μm. Adapted from Lin et al., 2014 with permission.

E Top: Anatomical map of cerebellar granule cell somata of the larval zebrafish. Bottom: Heatmap of peak dF/F over the same field of view. The large fraction of cells active suggests dense granule cell population activity. Scale bar, 50 μm Adapted from Knogler et al., 2017 with permission.

While divergent circuits are ubiquitous throughout the brain, expansion recoding in Marr-Albus theory is distinguished by the concept of randomly mixing different input channels (Figure 3B). Nonlinear mixing (i.e., combining mixing with a nonlinearity such as a spike threshold) increases the linear separability of activity patterns (Rigotti et al., 2013; Figure 3C). Mixing through random projections has recently been observed in the mushroom body, where anatomical tracing has found that Kenyon cells integrate sensory information from largely random sets of glomeruli (Caron et al., 2013; but recent studies show these projections may not be fully random, see Eichler et al., 2017; Zheng et al., 2018). This includes mixing of glomeruli with different odour tuning (Gruntman and Turner, 2013) or sensory modalities (Yagi et al., 2016; Eichler et al., 2017). This contrasts with other theories that may feature a highly divergent architecture for a different computational role. For example, compressed sensing theories of circuit function feature a similar expansion and sparsening, but the divergent synaptic projection is structured so as to demix specific sparse stimulus features that have been densely encoded in the input population (Ganguli and Sompolinsky, 2012).

In general, however, even Marr-Albus type neural circuits are unlikely to be fully random due to morphological constraints such as dendritic length (Gilmer and Person, 2017). Structured connectivity may also be used to increase the signal-to-noise ratio (SNR) of the circuit, in order to separate activity patterns while constraining noise (Babadi and Sompolinsky, 2014). Nevertheless, for expansion recoding, single neurons in the expanded population should integrate combinations of stimuli across different sources and modalities. In the cerebellar cortex, early studies using whole-cell patch clamp recordings from granule cells suggested that they average inputs with similar receptive field properties (Bengtsson and Jörntell, 2009). But, in the past decade, anatomical (Huang et al., 2013) and physiological evidence (Proville et al., 2014) has accumulated for mixed representations generated through multimodal integration in single granule cells of the cerebellar cortex (Arenz et al., 2008; Chabrol et al., 2015; Ishikawa et al., 2015). Multimodal integration has also been observed in granule cells of the mammalian auditory system (Wigderson et al., 2016) and electrosensory system of weakly electric fish (Sawtell, 2010), which have a ‘cerebellar-like’ circuitry (Oertel and Young, 2004; Bell et al., 2008; Kennedy et al., 2014; Singla et al., 2017). Mixed representations in the dentate gyrus are harder to ascertain, because entorhinal cortical neurons already integrate multisensory cues to generate spatial representations (Campbell et al., 2018). It has been shown that hippocampal projecting neurons in the medial entorhinal cortex are functionally diverse, combining grid cells, head direction cells, and border cells, as well as non-spatial cells (Zhang et al., 2013). In contrast, lateral entorhinal cortex may also encode non-spatial features such as object identity (Deshmukh and Knierim, 2011) and time (Tsao et al., 2018). However, it is not known but seems likely that these functionally distinct sources are integrated in single dentate granule cells.

Sparse coding

Traditional theories of how pattern separation is functionally implemented in neural circuits have often centred on the sparseness of population activity. Neuronal population activity is generally considered to be sparse if few neurons are active within a relevant time window. Population sparseness and expansion recoding are independent properties, as neural populations can be expanded into either a sparse or dense code just by changing the intrinsic excitability of the neurons in the expanded layer. However, these two properties have often been linked through theories of pattern separation, as Marr-Albus theory hypothesized that the cerebellar cortex reduces the overlap between densely coded mossy fibre activity through a combination of expansion recoding and sparsening of activity.

Based on arguments of efficient Purkinje cell learning, Marr originally predicted that <5% of cerebellar granule cells are active at any one time (Marr, 1969). As Marr-Albus theory was extended to other brain regions, such ‘ultra-sparse’ population coding formed the core of our current understanding of pattern separation, associative learning, and memory storage (Marr, 1971; Kanerva, 1988; Tsodyks et al., 1988; Rolls and Treves, 1990; Tyrrell and Willshaw, 1992; Schweighofer et al. 2001; Földiak, 2002; Laurent, 2002). However, it was technically difficult to determine the population sparseness of codes within neuronal circuits until the advent of multisite extracellular electrodes, as it requires recordings from populations of cells simultaneously (in contrast to temporal or lifetime sparseness, a separate property that characterizes the temporal pattern of spiking activity in a single neuron; Willmore and Tolhurst, 2001). Considerable evidence has now accumulated that the mushroom body employs ultra-sparse coding, as studies using a variety of methods, including whole-cell recordings, tetrode recordings, and calcium imaging, all found that only around 5-10% of Kenyon cells were active upon odour presentation (Figure 3D) (Perez-Orive et al., 2002; Wang et al., 2004; Turner et al., 2008; Honegger et al., 2011; Lin et al., 2014). In comparison, odours evoked activity in up to 70% of upstream projection neurons (Perez-Orive et al. 2002; Wilson et al., 2004).

In the dentate gyrus, ultra-sparse granule cell population activity (2-5%) over long timescales was originally inferred from immediate-early gene expression (Chawla et al., 2005; Tashiro et al., 2007; Alme et al., 2010). Tetrode recordings revealed denser activation levels, with reports varying from 12% (Jung and McNaughton, 1993) to over 50% (Shen et al., 1998; Leutgeb et al., 2007). Several studies additionally reported that putative granule cells often had multiple place fields (Jung and McNaughton, 1993; Leutgeb et al., 2007; Alme et al., 2010; Park et al., 2011), further confounding the concept of sparse granule cell coding. One caveat of these studies is that, due to the extremely low firing rates of granule cells during wakefulness (O’Keefe, 1976; Jung and McNaughton, 1993; Neunuebel and Knierim, 2012; Diamantaki et al., 2016), extracellular recordings may underestimate the fraction of “silent” cells. Moreover, histological localisation can be insufficient to identify granule cells, as electrodes in the granule cell layer may pick up signals from large mossy cells in the hilus (Neunuebel and Knierim, 2012). Recently, three studies addressed these limitations by developing classification methods for electrophysiological recordings (GoodSmith et al., 2017; Senzai and Buzsáki, 2017) or using calcium imaging (Danielson et al., 2017) to identify granule cells and mossy cells in awake mice. They found that granule cell activitiy is much sparser than mossy cell activity during behaviour, and that they typically have single (if any) place fields. Therefore, these new studies confirm that dentate granule cells utilize ultra-sparse coding.

In the cerebellum, granule cell activity was long assumed to be ultra-sparse because of predictions from Marr-Albus theory. But this concept has been challenged based on the temporally dense activity of single granule cells recorded in vivo (Chadderton et al., 2004; Jörntell and Ekerot, 2006; Spanne and Jörntell, 2015; Chen et al., 2017). Indeed, granule cells fire in bursts with spontaneous rates of >100 Hz during locomotion and in response to sensory stimuli (Van Beugen et al., 2013; Powell et al., 2015). As a result, the question of sparse coding in the cerebellar cortex has been controversial. Selective expression of high sensitivity genetically encoded calcium indicators has recently made it possible to record from large populations of granule cells in awake animals. Using this approach (or a related approach using a synthetic calcium indicator), several recent studies have reported that granule cell population activity is far denser than had previously been believed, with more than two thirds of imaged granule cells being active concurrently in some cases (Figure 3E) (Ozden et al., 2012; Giovannucci et al., 2017; Knogler et al., 2017; Sylvester et al., 2017). But, there are several caveats of these findings. First, two of these studies were done in larval zebrafish, which may have different circuit dynamics from the adult animal (Knogler et al., 2017; Sylvester et al., 2017). Moreover, calcium imaging can detect subthreshold dendritic events, such as calcium influx though synaptic receptors, as well as spike-generated calcium transients, which may decrease the apparent sparseness observed in imaging studies. Finally, measuring population sparseness requires defining a physiologically relevant timescale for signal integration. Population activity that is sparse on short timescales could appear denser on larger timescales. The kinetics of the calcium indicator used in these studies is slow with a decay of hundreds of milliseconds, an order of magnitude larger than the timescale for synaptic integration of granule cells (D’Angelo et al., 1995; Schwartz et al., 2012; Rothman et al., 2009; Billings et al 2014). Nevertheless, these recent findings cast doubt on ultra-sparse population coding in the cerebellar cortex.

It is puzzling that cerebellar granule cell activation may be denser than the ultra-sparse coding observed in the mushroom body and dentate gyrus. If these three regions all perform the same function, why do they maintain such different activation levels? One possibility is that the cerebellar cortex may use a different strategy for pattern separation that does not rely on ultra-sparse coding. This hypothesis is supported by recent modelling of the cerebellar granule cell layer which found that pattern separation could occur both in sparse and in dense regimes of granule cell activity (Cayco-Gajic et al., 2017). Instead, expansion and decorrelation (discussed in the following section) were more predictive of pattern separation performance than sparseness alone.

One reason for the different levels of population activity exhibited by these circuits could be the trade-off between sparseness and conservation of information (Billings et al., 2014). Overly sparse representations limit the amount of information that can be transmitted. Consistent with this, decreasing the excitability of cerebellar granule cells by increasing inhibition is associated with ataxia in GABA transporter 1 knockout mice (Chiu et al., 2005). The cerebellum may simply need to encode a large amount of information in a short period of time, due to its constant monitoring of sensory, motor, and proprioceptive information for estimation of errors in movements (Ohmae and Medina, 2015; Herzfeld et al., 2018) and in sensory prediction (Wolpert et al., 1998; Roth et al., 2013; Brooks et al., 2015). Indeed, a recent theoretical study has revealed a trade-off between stimulus prediction and sparseness (Chalk et al., 2018). The authors found that model neural ensembles that were trained to predict future stimulus information were significantly less sparse than those that had been trained to recover past information. Thus, the denser activation levels seen in the granule cell layer of the cerebellar cortex may be due to a need for higher throughput for real time motor control and predictive coding. By contrast, the mushroom body and the dentate gyrus may be able to maintain sparser representations, which are more energetically efficient (Attwell and Laughlin, 2001). Several theoretical studies have also shown that the sparseness of output representations controls a precise trade-off between generalization and discrimination of associative learning (Barak et al., 2013). Therefore, differences in sparseness in these regions could reflect differences in coding strategy. These recent studies together offer an intriguing potential explanation for why the cerebellar cortex, whose roles in motor control and sensorimotor prediction are well established, may utilise denser representations than the mushroom body and the dentate gyrus.

Decorrelation

Theoretical work has highlighted the strong impact that correlations in neural activity can have on information processing and population coding in neural circuits (Averbeck et al., 2006; Kohn et al., 2016). Correlated variability can corrupt encoded information, and unlike independent noise, cannot be mitigated by spatial or temporal averaging (Figure 4A). Signal correlations (i.e., correlations reflecting similar stimulus tuning) impede pattern separation by limiting the range of possible neuronal activity patterns. Decorrelation is crucial for associative learning, as correlated input sources can counteract the benefits of sparse coding and expansion recoding (Cayco-Gajic et al., 2017). How then can neural circuits transform activity patterns to form decorrelated population activity?

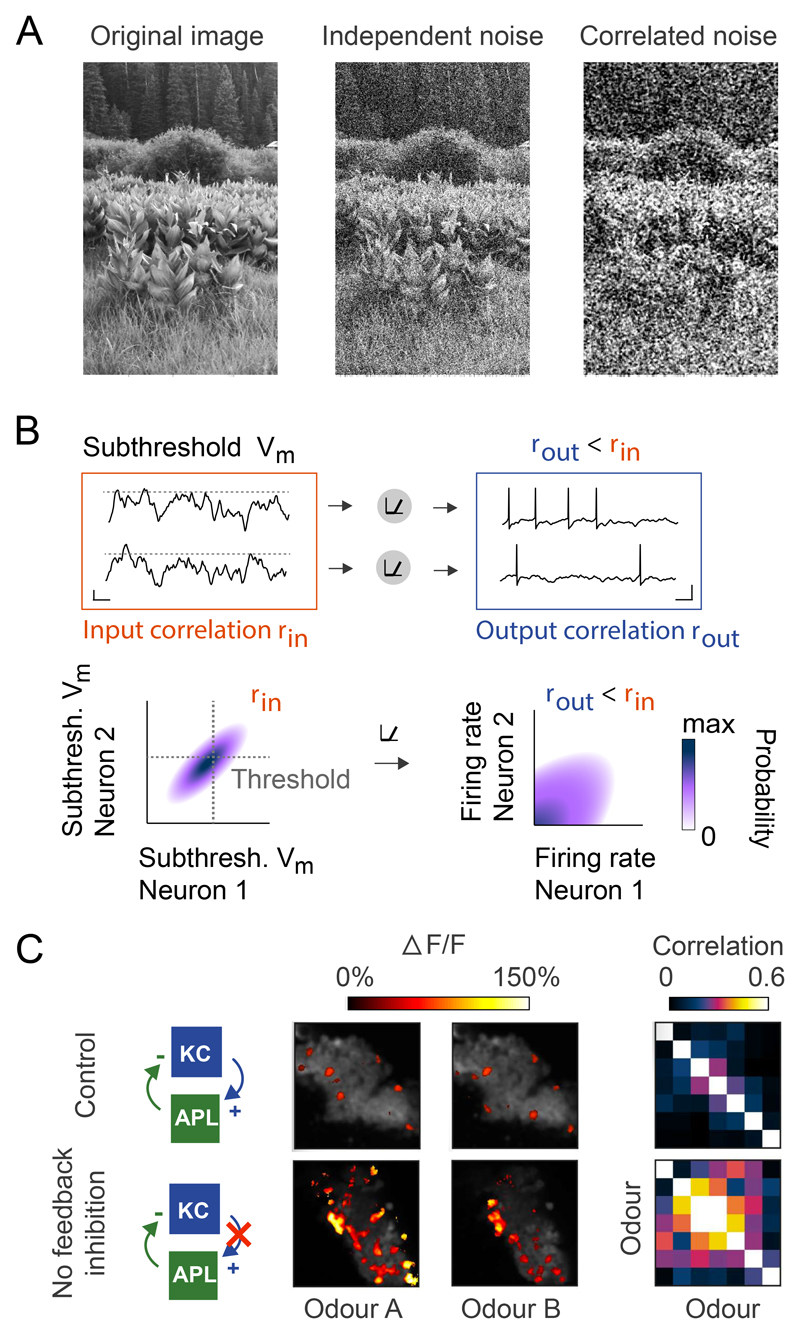
Figure 4. Decorrelation.

A Illustration of the harmful effects that correlated noise can have on information. Left: original image of grass and shrubs. Centre: Image with independent Gaussian noise added to each pixel. Right: Image with spatially-correlated noise added to each pixel, keeping the same variance as used for the independent noise. The addition of spatial correlations destroys fine-resolution information in the image.

B Thresholding can reduce correlations in synaptic input. Top: Schematic of two neurons with correlated subthreshold membrane potentials (left; scale bar indicates 50 ms, 2 mV). Thresholding nonlinearities reduce their output correlations by removing correlated fluctuations in subthreshold membrane potential. As a result, spiking output is less correlated (right; scale bar indicates 50 ms, 10 mV). Bottom: Distribution of correlated subthreshold membrane potentials for two neurons (left). Colour represents the joint probability density of the inputs, and grey lines represent each neuron’s intrinsic threshold. After thresholding, the firing rates of the two neurons are significantly less correlated, because co-varying subthreshold inputs are quenched (right). Figure inspired by de la Rocha et al., 2007.

C Feedback inhibition sparsens and decorrelates population activity patterns. Left: Top, schematic of feedback inhibition onto mushroom body Kenyon cells (KC) via the anterior paired lateral (APL) neuron. Bottom, with feedback inhibition blocked. Centre: Heat map of average Kenyon cell responses to two different odours (cf. Figure 3D). Note the denser activation profiles when feedback inhibition is blocked. Right: Correlation matrices of Kenyon cell activity patterns for seven different odours. Note the stronger cross-correlations between activity patterns representing distinct odours when feedback inhibition is blocked. Adapted from Lin et al., 2014 with permission.

One strategy for counteracting such correlations is to limit common input through sparse synaptic connectivity (Cayco-Gajic et al., 2017; Litwin-Kumar et al., 2017), as observed anatomically in the cerebellar cortex and Drosophila mushroom body. Dense synaptic connectivity increases the amount of shared presynaptic partners, and in the limiting case of all-to-all feedforward connectivity, forms a fully redundant code. Another strategy is to actively decorrelate synaptic inputs through neuronal or circuit mechanisms. For example, thresholding nonlinearities tend to decorrelate input patterns by eliminating correlated subthreshold fluctuations (Figure 4B; de la Rocha et al., 2007; but note that this may not be true for highly non-Gaussian synaptic input). This could explain the low intrinsic excitability of dentate granule cells (Gonzalez et al., 2018). Similarly, the large tonic GABA_A receptor inhibitory conductance present in cerebellar granule cells (Brickley et al., 1996) ensures a high spike threshold (Hamann et al., 2002) that typically requires activation of three of the four mossy fibre inputs (D’Angelo et al., 1995; Jörntell and Ekerot, 2006; Rothman et al., 2009; but see Rancz et al., 2007). Raising the intrinsic excitability of cerebellar granule cells has been shown to impair the consolidation of learning (Seja et al., 2012), consistent with the idea that thresholding nonlinearities play an important role in pattern separation and associative learning.

A similar decorrelating effect can be obtained by broad feedback inhibition, which has been observed in the cerebellar cortex and the mushroom body. A recent study in fly found that blocking feedback inhibition increased correlations between Kenyon cell patterns to distinct odours (Figure 4C), illustrating the importance of feedback inhibition for pattern decorrelation (Lin et al., 2014). Moreover, blocking feedback inhibition significantly impaired the discrimination of similar, but not dissimilar, odours in a fear conditioning task (Lin et al., 2014). Lateral inhibition, as observed in the dentate gyrus, can also decorrelate neural activity by introducing competition between granule cell activity (Giridhar et al., 2011). In practice, it is often difficult to tease apart the effects of decorrelation from sparseness. Inhibition and thresholding, which decorrelate activity patterns, also play key roles in controlling sparseness. Feedback inhibition adaptively regulates excitability (Hamann et al., 2002; Papadopoulou et al., 2011; Gupta and Stopfer 2012; Lin et al., 2014; Temprana et al., 2014; Kee et al., 2015), in part by matching spike threshold to the overall activity level (Mitchell and Silver, 2003; Billings et al. 2014; Tabuchi et al., 2018). However, sparse population activity is not necessarily decorrelated (and vice versa). But because they are linked by common neuronal and circuit mechanisms, sparseness and decorrelation often co-occur despite being distinct properties. Therefore, to comprehensively understand the effects of sparse coding, decorrelation, and expansion on pattern separation, a framework is needed to combine these different factors.

Dimensionality

The dimensionality of a system refers to the number of independent variables that are needed to describe all of its states. For neural circuits, each state is described by the activity of all neurons in the population. The potential number of activity patterns is determined by both the size of the neuronal population, and the dynamic range of the firing rate of each neuron. The maximum dimensionality of a neural circuit is the size of the neural population, because it can be fully described by the activity of each neuron. However, the dimensionality is limited by the fact that many of the vast number of potential activity patterns never occur because of redundancies and dependencies between neurons. For example, a microcircuit of two perfectly anti-correlated neurons is one-dimensional, because the activity of one neuron is sufficient to describe the activity of the full circuit. As a result of these factors, fewer independent variables than the number of neurons in the circuit will typically be needed to describe neural activity.

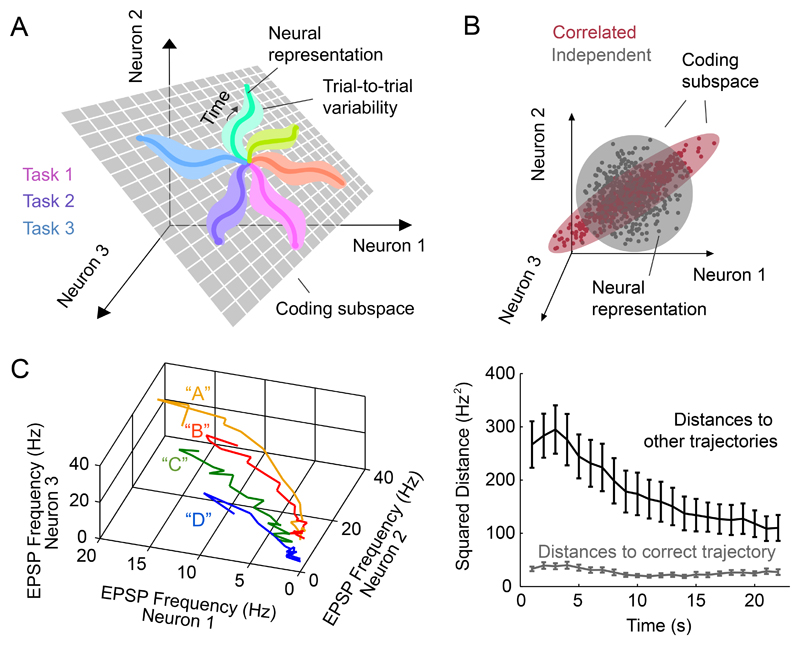
To understand the link between pattern separation and dimensionality, it is useful to separate the concept of the spatiotemporal activity patterns that represents a single or a few stimuli or tasks (sometimes called a ‘neural manifold’; Gallego et al., 2017) from its ‘coding subspace’, which comprises the full set of population representations of all possible stimuli, behaviours, and internal states of the animal, (Figure 5A). The coding subspace is a subset of activity space, which represents all possible neural activity patterns, including ‘non-coding’ subspaces that are observed but that do not represent changes in stimuli or behaviour (Druckmann and Chklovskii, 2012), as well as neural states that never occur. Higher dimensional coding subspaces facilitate the separation of overlapping activity patterns by providing a larger activity space in which those representations are embedded, thereby increasing their linear separability (Cover, 1965; Figure 1C). In contrast, low-dimensional coding subspaces limit the extent of potential representations that can be generated by a neural circuit.

Figure 5. Dimensionality of the coding subspace.

A The coding subspace (grey plane) is the subset of neural activity space in which neural representations (coloured lines) are embedded. Trial-to-trial variability (lighter shaded regions) consumes the space available for distinct neural representations.

B Correlations reduce the dimensionality of the coding subspace. Correlated (red shading) and independent (grey shading) coding subspaces plotted in activity space. Each point represents the neural representation of a distinct stimulus or task.

C Example of spatiotemporal pattern separation in the dentate gyrus. Left: Average EPSP rate trajectories from 3 mossy cells during perforant path stimulation at four different locations. Note that the trajectories remain separated in activity space over time. Right: Average distance of a single-trial EPSP pattern to the correct (black) or incorrect (grey) neural representations (average trajectories), plotted over time. Despite variability between trials, the activity patterns remain closer to their average neural trajectories than to other trajectories. This means the trial-to-trial variability is constrained to limit the overlap between neural representations of different perforant path stimulations. Adapted from Zylberberg et al., 2016 with permission.

An advantage of focusing on the dimensionality of the coding subspace is that it can integrate multiple interrelated factors into the same conceptual framework. Expansion, when combined with nonlinear mixing, increases the dimensionality of the coding subspace (Rigotti et al., 2013; Fusi et al., 2016). In contrast, signal correlations reduce the dimensionality of the coding subspace (as in the two-neuron microcircuit example above) highlighting the need to minimize correlations through sparse synaptic connectivity and decorrelation (Figure 5B; Cayco-Gajic et al., 2017; Litwin-Kumar et al., 2017). Thresholding nonlinearities can increase the dimensionality of the coding subspace by decorrelating activity, but excessive sparsening can ultimately limit the extent of the coding subspace (Barak et al., 2013; Babadi et al., 2014; Billings et al., 2014; Cayco-Gajic et al., 2017; Litwin-Kumar et al., 2017). Importantly, dimensionality is a better indicator of how constrained neural activity is than the average pairwise correlation coefficient because it takes into account the activity of the full population (Recanatesi et al., 2018). Within this framework, trade-offs between different structural and functional properties can be viewed as competing factors controlling dimensionality. Therefore, rather than individually quantifying the impact of expansion, mixed representations, sparse coding, and decorrelation, these interdependent properties can be understood in terms of the dimensionality of coding subspace, providing a more unified view of several determinants of pattern separation.

While high dimensional coding subspaces endow neural circuits with a greater potential capacity for distinct representations, trial-to-trial variability of neuronal responses consumes coding subspace, and in the limiting case could fill it entirely. The presence of variability therefore increases the overlap between activity patterns (Figure 5A). Thus to perform pattern separation neural circuits must increase the effective SNR of their coding subspace (Babadi et al., 2014; Litwin-Kumar et al., 2017). This could be accomplished by either increasing the separation between the mean activity patterns or by reducing their trial-to-trial variability. It is likely that a combination of these strategies is used, but different circuits may be biased towards either strategy depending on the SNR or the correlation structure of trial-to-trial variability in the input population. Thus, even different functional zones or modules within the same brain region may be biased towards either increasing dimensionality of their coding subspace, or noise reduction, to implement pattern separation. This may explain, for example, why some studies of cerebellar granule cells have concluded that they increase the SNR of their inputs by averaging similarly tuned mossy fibres (Ekerot, and Jörntell, 2008; Bengtsson and Jörntell, 2009), while other studies have found evidence of multimodal integration (Arenz et al., 2008; Huang et al., 2013; Chabrol et al., 2015; Ishikawa et al., 2015).

In this view, neural circuits must learn to encode distinct stimuli with separated trajectories with minimal overlap due to noise or variability (Friedrich and Laurent, 2001; Stopfer et al., 2003; Broome et al., 2006; Shen et al., 2013; Zylberberg et al., 2016; Remington et al., 2018). Even within a high-dimensional coding subspace, linear separability depends on the geometry of the variability of neural representations (Chung et al., 2018). In the dentate gyrus, a recent study tested the relationship between signal and noise by intracellularly recording from triplets of mossy cells in vitro while stimulating the perforant path in different locations (Zylberberg et al., 2016). Despite considerable fluctuations in the mossy cell representations, the authors found that this variability was constrained to be near the average trajectory in activity space, so that the representations of different perforant path inputs remained separated (Figure 5C). Shuffling the statistics of the noise reduced the accuracy of a decoder trained to classify the location of stimulation (Zylberberg et al., 2016). This illustrates the importance of characterizing both the coding subspace and the properties of the noise, to determine whether neural circuits use high-dimensional activity to separate activity patterns.

One disadvantage of using dimensionality is that it can be difficult to determine. In principle, measuring dimensionality is as straightforward as recording a population of neurons and using principal component analysis (or a nonlinear dimensionality reduction method) to determine how many components are necessary to capture the majority of the variance (Cunningham and Yu, 2016). However, subsampling of neuronal populations and limited recording times can lead to severe underestimates (Gao and Ganguli, 2015), while measurement noise and nonlinear dynamics can inflate the apparent dimensionality (Cunningham and Yu, 2016). Moreover, recent theoretical work has also demonstrated that the dimensionality of neural representations is necessarily limited by the complexity of the task involved (Gao et al., 2017). Recent imaging of cerebellar granule cell responses to simple visual stimuli and electric shocks in larval zebrafish, which have roughly 6000 granule cells, found only seven-dimensional representations of these stimuli (Knogler et al., 2017). Similarly, a recent study in mice has found low-dimensional granule cell representations during a simple forelimb-movement task (Wagner et al., 2018). Whether these results represent the full extent of the coding subspace, or whether these trajectories are embedded within a higher-dimensional repertoire of potential representations of more complex stimuli and behaviours, is yet to be established. Quantification of the dimensionality of the coding subspace and the representations of different behaviours requires recordings from large numbers of neurons across a very large behavioural repertoire. Towards this end, new high-density electrophysiological probes, such as Neuropixels, have enabled simultaneous large-scale extracellular recordings of spikes from multiple regions (Jun et al., 2017). Several promising new imaging technologies that can record intracellular calcium from large numbers of identified cells have also been recently developed (Grewe et al., 2011; Katona et al., 2011; Froudarakis et al., 2014; Nadella et al., 2016; Sofroniew et al., 2016; Yang et al., 2016; Stringer et al., 2017). Moreover, recent theoretical advances may help estimate the dimensionality from noisy neural data (Machens et al., 2010; Stringer et al., 2018), or based on the local connectivity motifs of neural circuits (Recanatesi et al., 2018). These new techniques will enable us to better quantify the dimensionality of the coding subspace, and characterise the statistical structure of the trial-to-trial variability of the sensory and motor representations embedded within it.

Challenges to traditional circuit mechanisms

So far, we have discussed recent findings that update our understanding of pattern separation in the cerebellar cortex, mushroom body, and dentate gyrus. However, Marr-Albus theory predicts certain circuit properties that have been challenged by recent findings in these circuits. Here we address these challenges to traditional circuit mechanisms underlying pattern separation, and discuss potential solutions.

Feedforward excitation

Marr-Albus theory posits that neural circuits separate overlapping activity patterns through a divergent excitatory feedforward projection (Figure 3A). Local circuits that perform pattern separation have generally been assumed to lack recurrent excitatory connections between neurons in the expanded population, since dense recurrent connections are expected to mix distinct signals and complete similar patterns, rather than separate them (Rolls, 2016). In the cerebellum, the excitatory projection from mossy fibres to granule cells is purely feedforward, and granule cells do not synapse onto each other. However, indirect excitatory feedback could occur through the inhibition of Golgi cells via metabotropic glutamate receptor activated G-protein-coupled inwardly-rectifying potassium (GIRK) channels (Watanabe and Nakanishi, 2003). The presence of such mechanisms could contribute to separating neural trajectories by exploiting the rich dynamics of edge-of-chaos networks (Rossert et al., 2015), in analogy with reservoir computing (Yamazaki and Tanaka, 2007; Buonomano and Maass, 2009; Sussillo and Abbott, 2009). Recent studies have also discovered evidence of long-range sparse feedback projections from deep cerebellar nuclei to the cerebellar input layer (Houck and Person 2014; Ankri et al., 2015; Houck and Person 2015; Gao et al., 2016; Low et al., 2018). These projections could provide feedback excitation or a combination of feedback excitation and inhibition depending on the target cell(s), but it is not clear how such long-range feedback affects pattern separation. One possibility is that feedback projections may have no role in pattern separation, and may simply extend the timescale over which sequences of movements can be learned (Khilkevich et al., 2018). Alternatively, feedback may be beneficial for pattern separation if it is sufficiently sparse (Wiechert et al., 2010). Indeed, recent work in the vertebrate olfactory system has found that removing long-range cortical feedback by inactivating piriform cortex increases the correlation between odour responses in the olfactory bulb (Otazu et al., 2015).

In the mushroom body, the possibility of dense recurrent connections has been raised by the existence of synapses between fibres in the peduncle (Schurmann, 2016). Recent reconstruction of the mushroom body of larval stage Drosophila has found frequent axo-axonic connections between Kenyon cells, which reduce the dimensionality of the coding subspace in a model of the mushroom body circuit (Eichler et al., 2017). However, it is not clear if these recurrent connections occur in the adult animal. These findings highlight the need to better characterise the local microcircuitry of the mushroom body calyx and lobes to determine how the connectivity structure may affect the coding subspace.

Also complicating the feedforward view of pattern separation is the recurrent circuitry within the dentate gyrus. Although dentate granule cells do not synapse onto other granule cells under normal conditions, they synapse onto and receive feedback excitation from mossy cells in the hilus. But the net effect of mossy cells on granule cell excitability has been unclear, as they also recruit hilar interneurons that inhibit granule cells (Scharfman, 2016). Mossy cell deletion studies have also found mixed effects on granule cell activity (Ratzliff et al., 2004; Jinde et al., 2012). A new study using closed-loop optogenetics to selectively modulate mossy cell populations found that mossy cells have a protective, regulatory effect on granule cell excitability, albeit in epileptic mice (Bui et al., 2018). Moreover, recent modelling found that deleting mossy cells in a computational model of the dentate gyrus increased pattern overlap because of the reduced disynaptic feedback inhibition (Chavlis et al., 2017; Danielson et al. 2017). Therefore, rather than contributing to runaway excitation, these studies suggest that mossy cells support feedback inhibition and help to maintain sparse, decorrelated granule cell activity.

Sparse synaptic connectivity

Several recent theoretical studies have shown that sparse synaptic connectivity is optimal for associative learning because it reduces correlations, maximises the dimensionality of the activity patterns, and allows for lossless information transfer (Billings et al., 2014; Cayco-Gajic et al., 2017; Litwin-Kumar et al., 2017). This circuit property is found in the cerebellar input layer, where granule cells receive a narrow range of 2-7 mossy fibre inputs (with an average of four; Eccles et al., 1967), a level of connectivity that has been evolutionarily conserved in the cerebellum since the appearance of fish (Wittenberg and Wang, 2007). Similarly sparse connectivity is also observed in cerebellar-like circuits such as the dorsal cochlear nucleus in the mammalian auditory system (Mugnaini et al., 1980) and the electrosensory system of weakly electric fish (Kennedy et al., 2014). Moreover, in Drosophila mushroom body, each Kenyon cell has only 2-11 dendritic claws (with an average of seven; Butcher et al., 2012; Caron et al., 2013). These results suggest that sparse synaptic connectivity plays a key role in pattern separation in the cerebellar cortex and Drosophila mushroom body.

Unlike their counterparts in fly, Kenyon cells in locust are much more densely innervated, indicating that sparse connectivity is not the only solution for counteracting correlations. Each Kenyon cell is contacted by 400 projection neurons, roughly half of the population (Jortner et al., 2007). How, then, can the locust mushroom body maintain a sparse, decorrelated coding subspace? One possibility is that strong sparsening of activity by high thresholds in locust Kenyon cells may help to compensate for correlations introduced by the dense connectivity (Masse et al., 2009). Another possibility is that odour-evoked oscillations in Kenyon cells, which are present in the locust (Laurent, 2002) but weak in Drosophila (Turner et al., 2008; Masse et al., 2009), play a greater role in pattern separation in these species. Upon odour stimulation, locust projection neurons form transiently synchronized ensembles, creating short integration windows for Kenyon cells and causing them to act as coincidence detectors (Perez-Orive et al., 2002; Gupta et al., 2016). The sparsening conferred by such coincidence detection, in combination with decorrelation of temporally evolving trajectories, can help to separate activity patterns (Laurent, 2002). Pharmacological block of oscillations (but not odour selectivity) in the projection neurons of honey bees impaired discrimination of molecularly similar odours, but did not affect the performance for dissimilar odourants (Stopfer et al., 1997). This suggests that oscillatory synchronization of projection neurons contributes to pattern separation by adding a temporal dimension to encoding, a strategy that is also employed in the mammalian olfactory processing (Friedrich and Laurent, 2001; Margrie and Schaefer, 2003; Poo and Isaacson, 2009). Therefore, a potential explanation for the difference in synaptic connectivity is that the dense innervation observed in locust may be overcome by high thresholding and coincidence detection during oscillatory input activity.

Dense innervation is also observed in the dentate gyrus, where thousands of perforant path inputs converge onto single granule cells (McNaughton et al., 1991). The sheer number of synaptic inputs are likely to convey significant input correlations, which could limit the dimensionality of granule cell responses. Strong lateral inhibition (Espinoza et al., 2018) could compensate for denser synaptic connectivity by implementing winner-takes-all competition between granule cells. The diversity of dentate interneurons is also likely to enable them to closely match excitation and spike threshold and confer precise control over granule cell firing (Halasy and Somogyi, 1993; Sik et al., 2006; Hosp et al., 2014). By adaptively modulating granule cell excitability, dentate circuits may therefore be able to control the trade-off between sparsening activity and conserving information (Billings et al., 2014), maintaining ultra-sparse firing (Dieni et al, 2013), which is effective at decorrelating their inputs. Consistent with this view, immature adult-born granule cells, which receive significantly fewer perforant path inputs (Dieni et al., 2016) receive reduced synaptic inhibition (Li et al., 2012; Marin-Burgin et al., 2012; Dieni et al., 2013). In addition to adaptive inhibition, recent work also suggests that nonlinear dendritic processing contributes to sparse granule cell activity and pattern separation by nonlinear thresholding (Chavlis et al., 2017). Interestingly, dentate granule cells receive bursts of EPSCs and IPSCs, that exhibit coherence in theta and gamma frequency bands, respectively (Pernia-Andrade and Jonas, 2014), raising the possibility that they use synchronous oscillatory activity and coincidence detection to generate sparse decorrelated codes, as in the locust mushroom body. The dentate gyrus may therefore combine dendritic processing, strong inhibition, adaptive control of granule cell excitability, and oscillatory temporal coding to decorrelate their inputs and maintain an ultra-sparse code despite the large convergence of entorhinal inputs on granule cells.

Together, these results suggest different strategies to increase the dimensionality of coding subspace in neural circuits. On one hand, the cerebellar cortex and Drosophila mushroom body use sparse synaptic connectivity to limit the corrupting influence of correlations. However, locust (and possibly honey bee) mushroom body and mammalian dentate gyrus may compensate for their denser synaptic connectivity with increased thresholding and oscillatory coding to maintain sparse representations. Another interesting possibility is that plasticity may compensate for denser innervation levels, as recent theoretical work has shown that dense synaptic connectivity can be advantageous for associative learning if supervised learning extends to the input layer (i.e., the synapses between projection neurons and Kenyon cells; Litwin-Kumar et al., 2017). But whether this mechanism is utilized by the locust mushroom body or the dentate gyrus remains to be seen. Nevertheless, these studies together indicate that, rather than relying on a single solution, these neural circuits appear to utilise several distinct strategies to generate higher-dimensional coding subspaces for pattern separation and associative learning.

Alternative mechanisms for pattern separation

Pattern decorrelation is thought to occur in a wide range of circuits, including those with recurrent synaptic connectivity that are not classically thought to perform pattern separation. Theoretical work has shown that adding random sparse recurrent excitatory or inhibitory connections can amplify threshold-mediated decorrelation by adding high-variance synaptic input that makes neural responses more distinct (Wiechert et al., 2010). Unlike Marr-Albus theory, this recurrent mechanism does not require a large expansion, explaining how pattern decorrelation could occur in regions that lack a divergent feedforward architecture, such as the vertebrate olfactory system (Wiechert et al., 2010).

In the olfactory bulb, mitral cell odour representations have been shown to be more discriminable than those of olfactory sensory neurons (Friedrich and Laurent, 2004), and become increasingly separated over time (Friedrich and Laurent, 2001). In vivo recordings have recently shown that the responses of mitral and tufted cells to different odour mixtures tend to be less correlated than the responses of their inputs (Gschwend et al., 2015). Diverse inhibitory interneurons also mediate a large range of inhibitory mechanisms on mitral cells (Burton, 2017). The most abundant of these are granule cells, which are thought to enhance odour tuning through lateral inhibition (Yokoi et al., 1995; Arevian et al., 2008; Giridhar et al., 2011). But more recent work suggests granule cell inhibition is involved in spike timing (Fukunaga et al., 2014), and feedforward inhibition within the glomerulus regulates slower sniff-coupled odour-evoked inhibition (Fukunaga et al., 2014). Broadly tuned inhibition from parvalbumin-expressing interneurons could also mediate gain control of mitral cell responses (Kato et al., 2013). This overall arrangement of inhibition is consistent with the theory of non-topographical contrast enhancement (Cleland and Sethupathy, 2006), which implements a weak version of a winner-take-all algorithm that is well suited for high dimensional representations that cannot be represented in a smooth topography. Therefore the lack of expansion and mixing in mitral cells within the olfactory bulb circuit represents an alternative strategy to traditional Marr-Albus feedforward networks for decorrelating high dimensional input patterns. Interestingly, mitral cells project to a much larger population of pyramidal cells in piriform cortex (Shepherd, 2004). Moreover, broad inhibition in the piriform cortex (Poo and Isaacson, 2009) contributes to sparsening and decorrelation that is thought to further contribute to separating overlapping odour representations (Stettler and Axel, 2009; Miura et al., 2012). These aspects of the piriform circuit suggest that it may fit better with the Marr-Albus framework of pattern separation, following more targeted decorrelation mechanisms within the olfactory bulb.

The visual system is characterised by a highly divergent projection from lateral geniculate nucleus to primary visual cortex (Stevens, 2001), and this is accompanied by considerable sparsening and decorrelation of activity (Olshausen and Field, 1996; Vinje and Gallant, 2000; Froudarakis et al., 2014). Furthermore, recent evidence from large scale calcium imaging indicates that the V1 coding subspace is as high-dimensional as mathematically possible, while still retaining smooth representations (Stringer et al., 2018). This expansion and sparsening of visual information is consistent with the theory that the successive stages of the visual pathway increase the separability of cortical representations of object identity (DiCarlo et al., 2012). However, rather than the random expansion predicted by Marr-Albus theory, visual cortical neurons receive specific geniculate inputs that contribute to their direction selectivity (Reid and Alonso, 1995; Sun et al., 2016; Lien and Scanziani, 2018). Therefore, the expansion observed in visual cortex appears specialised for feature selection, rather than for general purpose pattern separation.

Conclusion

Pattern separation is a fundamental computation by which neural circuits separate overlapping activity patterns in preparation for downstream associative learning and memory storage. Marr and Albus pioneered the first theories of this circuit computation with their widely influential work on the cerebellar cortex. Marr-Albus theory proposed that neural circuits perform pattern separation by projecting them onto a much larger population of sparsely active neurons. Towards this end, several structural properties and functional mechanisms have been identified that are thought to underlie pattern separation: divergent feedforward excitatory connectivity, sparse random synaptic connectivity, feedback inhibition and sparse population coding. Here, we re-evaluated these mechanisms in light of recent advances in three canonical brain regions widely thought to perform this function: the cerebellar cortex, the mushroom body, and the dentate gyrus.

To address recent challenges to Marr-Albus theory, we argue that the dimensionality of the coding subspace provides a useful way to understand pattern separation in these circuits, as it unifies sparse coding, expansion, mixing and decorrelation into the same conceptual framework. Moreover, we discussed how different circuit mechanisms can be understood as different approaches to projecting neural population representations of stimuli and motor tasks into a higher dimensional coding subspace. For example, pattern separation in the dentate gyrus and mushroom body may be achieved by a combination of expansion, strong thresholding, lateral inhibition and coincidence detection to generate an ultra-sparse, decorrelated coding subspace. However, we propose that the cerebellum requires higher information throughput because of its role in coordinating movements and predicting the sensory consequences of movement. Therefore, rather than utilizing ultra-sparse activity patterns that can limit information content (Billings et al., 2014), it may rely more on expansion and sparse synaptic connectivity to reduce the impact of input correlations (Cayco-Gajic et al., 2017; Litwin-Kumar et al., 2017) and generates a higher-dimensional coding subspace in which activity patterns can be separated effectively.

The trade-offs implicit in these strategies means that quantifying population sparseness, expansion, or the correlation between neurons in isolation may not be sufficient to determine whether a neural circuit performs pattern separation. On the other hand, dimensionality can unify many of the concepts underlying pattern separation, but it can be difficult to quantify, in practice (Gao and Ganguli, 2015). Moreover, pattern separation cannot easily be predicted from neural circuitry without knowing the specific wiring. For example, divergent neural circuits may not necessarily separate patterns (e.g., compressed sensing), and pattern separation may not require divergent circuits (e.g. olfactory bulb or edge-of-chaos recurrent networks). Directly testing pattern separation is challenging because it requires simultaneously measuring the input and expanded layer populations of a circuit, and comparing the activity patterns representing distinct stimuli or tasks within each population. While increasing the dimensionality of the coding subspace allows for a greater capacity for distinct representations, trial-to-trial variability in representations within the coding subspace can increase pattern overlap. It is likely that neural circuits combine an increase in the dimensionality of their coding subspace with noise reduction strategies that are matched to the properties of their inputs. Indeed, the precise statistical structure of correlated neural variability can have a strong impact on the overlap of distinct neural representations (Averbeck et al., 2006; Moreno-Bote et al., 2014). Therefore characterising the dimensionality of the coding subspace and the structure of noise are both needed for a comprehensive picture of pattern separation.

The characteristic properties of the cerebellar input layer, consisting of a sparse synaptic connectivity, large expansion, spike thresholding, multimodal integration, and broad feedback inhibition, suggests that this prototypical Marr-Albus circuit acts as a flexible general-purpose pattern separator. Similarly, the mushroom body, with its large expansion, random synaptic connectivity and global inhibition, appears to utilise a similar mechanism, although different species (i.e., fly vs. locust) seems to rely on different mechanisms to sparsen and decorrelate Kenyon cell activity. In contrast, the rules that govern the well documented pattern separation in the dentate circuit are more enigmatic. The modest expansion, high spike threshold and strong lateral inhibition suggest that the dentate gyrus may use ultra-sparse coding and winner-takes-all competition to make granule cell representations more distinct. It is tempting to speculate that these mechanisms, together with the non-random, specialized subnetworks of inhibitory interneurons, enable the dentate gyrus to separate specific contexts, rather than acting as a generic Marr-Albus pattern separator.

In addition to Marr-Albus theory, Marr is also remembered for his influential proposal that neural systems should be studied at three levels of analysis: computational, algorithmic, and implementational (Marr and Poggio, 1977). At the computational level, the cerebellar input layer, insect mushroom body, and dentate gyrus have been identified as having key roles in pattern separation and associative learning. At the algorithmic level, we have argued that different functional determinants of pattern separation can be unified under the conceptual framework of dimensionality. Finally, at the implementational level, we propose that these regions use distinct structural mechanisms and functional properties to increase the dimensionality of their neural coding subspaces to facilitate pattern separation and associative learning.