On-chip surface acoustic wave and micropipette aspiration techniques to assess cell elastic properties

Abstract

The cytoskeletal mechanics and cell mechanical properties play an important role in cellular behaviors. In this study, in order to provide comprehensive insights into the relationship between different cytoskeletal components and cellular elastic moduli, we built a phase-modulated surface acoustic wave microfluidic device to measure cellular compressibility and a microfluidic micropipette-aspiration device to measure cellular Young's modulus. The microfluidic devices were validated based on experimental data and computational simulations. The contributions of structural cytoskeletal actin filament and microtubule to cellular compressibility and Young's modulus were examined in MCF-7 cells. The compressibility of MCF-7 cells was increased after microtubule disruption, whereas actin disruption had no effect. In contrast, Young's modulus of MCF-7 cells was reduced after actin disruption but unaffected by microtubule disruption. The actin filaments and microtubules were stained to confirm the structural alteration in cytoskeleton. Our findings suggest the dissimilarity in the structural roles of actin filaments and microtubules in terms of cellular compressibility and Young's modulus. Based on the differences in location and structure, actin filaments mainly contribute to tensile Young's modulus and microtubules mainly contribute to compressibility. In addition, different responses to cytoskeletal alterations between acoustophoresis and micropipette aspiration demonstrated that micropipette aspiration was better at detecting the change from actin cortex, while the response to acoustophoresis was governed by microtubule networks.

I. INTRODUCTION

Cells in vivo are subjected to mechanical forces and can mechanically interact with the local microenvironment. Hence, their mechanical properties play an important role in cellular behaviors.^1–3 The mechanical property of a cell is also believed to be governed by its cytoskeleton, comprising of actin filaments, intermediate filaments, and microtubules. The cytoskeleton supports the cell's inner structure and is known to be responsible for cellular processes such as proliferation, migration, and differentiation.^4,5 The cytoskeleton can also be altered by pathological conditions, leading to changes in mechanical properties.^3,6,7 For example, malaria induces the distortion of the cytoskeleton and thereby the alteration in deformability of the infected red blood cell.^8,9 The change in the cytoskeleton from a rigid structure to a more compliant state produces less stiff metastatic cancerous cells as compared with their benign counterparts.^10–12 Hence, it highlights the importance of understanding cytoskeletal mechanics and shows the possibility to exploit cell mechanical properties as a label-free and sensitive biomarker for diagnostic applications.

The cell mechanical property is commonly defined by its stiffness, usually measured by techniques providing a Young's modulus or shear modulus value.¹³ These techniques include atomic force microscopy (AFM),^14,15 optical stretching,¹⁶ magnetic twisting cytometry,¹⁷ micropipette aspiration,^18,19 and acoustic radiation induced deformation.^20–22 Each technique applies a mechanical load on adherent cells or suspension cells, whole-cell or onto the cell surface, statically or dynamically, and in contact or contact-free conditions. These methods examine the reaction of single cells and measure the elastic modulus at the cellular level.²³ For example, AFM locally indents an adherent cell via a cantilever and measures the resisting force as well as the deformation, while the optical stretcher traps and deforms a cell in suspension by dual-beam lasers and examines the whole-cell property in a contact-free manner.

However, a recent study reported that the elastic modulus measurements of MCF-7 breast cancer cells by different techniques can vary 1000-fold, where up to six commonly used techniques were implemented and compared.²⁴ The authors concluded that the measurements are specific to the force profile, the location probed on the cell, and other factors in these different techniques. In addition, there is evidence showing that a single-modulus measurement was unable to reveal cytoskeletal alterations in some cases.^25–27 Even if considering the cell as a homogeneous and isotropic object, at least two of the elastic moduli (Young's modulus, shear modulus, bulk modulus, etc.) are needed to fully describe its elastic property.

These observations suggest the necessity of multi-modulus measurement to better understand cellular mechanical behavior and cytoskeletal mechanics. Some single-modulus measuring studies achieved the second modulus by assuming a Poisson ratio of 0.5, indicating that cells are incompressible. However, there are evidence that the Poisson ratio of a cell could range from 0.37 to 0.45, undermining the validity of the constant assumption.^28–30 On the other hand, a few studies attempted to determine two independent elastic moduli using one mechanical measurement. For example, a custom cytocompression device that compresses cells against a glass slide using a compressing probe was used to characterize compressive stiffness and the apparent Poisson ratio of chondrocytes.³¹ Similarly, Lin et al. applied controlled, uniform hydrostatic pressure on monocytes to measure Young modulus and Poisson ratio.³² However, it is uncertain that these measures of two moduli are truly independent and decoupled, as they are derived from one deformation mode. Furthermore, Nijenhuis et al. applied atomic force microscopy (AFM) and scanning acoustic microscopy in the same study, as two independent techniques, to characterize cell shear modulus and bulk modulus separately and independently and support the discussion of independent contributions of the cytoskeleton on volume change and shape change.¹³ This approach, however, is limited in utility by high equipment cost, time-consuming protocols, and low throughput due to the two microscopic methods.

During the last decade, the emerging microfluidic techniques have been demonstrated with lower cost and higher throughput for cell mechanical measurements, as compared with conventional techniques. In this study, we applied two independent microfluidic techniques to study the cytoskeletal structure and its relationship to the cell mechanical property. A phase-modulated surface acoustic wave (PM-SAW) microfluidic device measuring cellular compressibility (the inverse of the bulk modulus) and a microfluidic micropipette-aspiration (μFMA) device measuring Young's modulus were developed for this purpose. The microfluidic devices were validated based on experiments and computational simulations, thereby facilitating measurement of two independent elastic moduli with minimal prior assumptions. Next, the actin filaments or microtubules of MCF-7 breast cancer cells were disrupted, and the compressibility and Young's modulus were examined by the two techniques, respectively. The actin filaments and microtubules were also visualized by immunofluorescence staining to confirm the structural alteration in the cytoskeleton. In this study, we evaluated the contributions of actin filaments and microtubules to cellular compressibility and Young's modulus and also discussed the capabilities of acoustophoresis and micropipette aspiration to detect different cytoskeletal changes.

II. METHOD

A. Phase-modulated surface acoustic wave (PM-SAW) microfluidic device

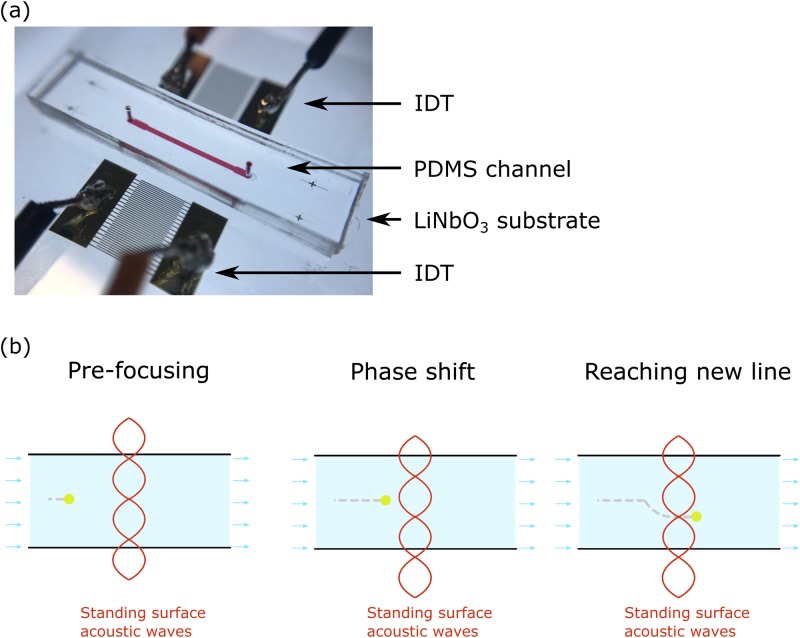
As described in our previous study,³³ the phase-modulated surface acoustic wave (PM-SAW) device consists of a LiNbO₃ piezoelectric substrate with two interdigital transducers (IDTs) at each side and a polydimethylsiloxane (PDMS) microfluidic channel bonded to the middle of the substrate [Fig. 1(a)]. The microfluidic channel is aligned parallel to the IDTs. Two counter-propagating acoustic waves are generated due to the piezoelectric effect of the substrate upon applying two coherent, sinusoidal electrical signals on the IDTs. The acoustic waves travel from the IDTs to the fluidic channel in the form of a Rayleigh wave confined to the substrate surface and enter the fluidic domain, forming a standing acoustic wave and, therefore, pressure interference in the fluid. The particles inside the fluidic channel are pushed by acoustic radiation force and pre-focused at the pressure node that is parallel to the flow [Fig. 1(b)]. Then, the phase of one input signal at the IDT is shifted by 120°, resulting in phase offset and, therefore, translation of the pressure node [Fig. 1(b)]. The pre-focused particles are pushed to the new nodal line, where the lateral motion is governed by the equation defined as below, involving acoustic radiation force F_r and the Stokes drag force F_drag,

$$F_r+F_{drag}=ma,$$ (1)

where F_r denotes the acoustic radiation force, F_drag denotes the Stokes drag force, m denotes the mass of the particle, and a denotes the acceleration.

FIG. 1.

(a) Image of phase-modulated surface acoustic wave (PM-SAW) device with two interdigital transducers (IDTs) on a LiNbO₃ piezoelectric substrate and a polydimethylsiloxane (PDMS) microfluidic channel bonded in the middle. (b) Working mechanism of PM-SAW microfluidic device. The particles are pushed by acoustic radiation force and pre-focused at the pressure node. Then, the phase of one input signal at the IDT is shifted by 120°, resulting in the translation of the pressure node. Following, the pre-focused particles are moved to the new nodal line.

The acoustic radiation force F_r on a compressible spherical particle in standing acoustic fields is defined as³⁴

$$F_r=-{\displaystyle \frac{\pi {\displaystyle \frac{\alpha P_I{\rho }_s{c}_s}{A_w}{V}_p{\beta }_m}}{2\lambda }\times \left({\displaystyle \frac{5{\rho }_P-2{\rho }_m}{2{\rho }_P+{\rho }_m}-{\displaystyle \frac{{\beta }_P}{{\beta }_m}}}\right)\times \sin (2ky),}$$ (2)

where ρ_P, β_P, and V_P denote the density, compressibility, and volume of the particle, respectively; ρ_m and β_m denote the density and compressibility of the medium, respectively; ρ_s and c_s denote the density and acoustic velocity within the substrate, respectively; y denotes the lateral distance away from the pressure node and y = 0 coincides with pressure node; λ and k denote the wavelength and the wavenumber of acoustic wave, respectively; P_I denotes the input power to the IDT; A_w denotes the working area of IDT; and α denotes the energy coefficient.

The well-known Stokes drag force on a sphere is defined as

$$F_{drag}=-6\mu \pi R{v}_{rel},$$ (3)

where μ denotes the dynamic viscosity, R denotes the radius of the particle, and v_rel denotes the particle velocity relative to that of the flow.

The fabrication, dimension, and experimental setup of the PM-SAW device are demonstrated in the supplementary material. 10-μm polystyrene microbeads (Magsphere) were used to calibrate the acoustic intensity of the PM-SAW device by determining the energy coefficient α in Eq. (2). The details of the calibration process can be found in the previous study.³³ Once calibrated, the theoretical trajectory of 10-μm polystyrene microbeads was simulated based on Eqs. (1)–(3) and compared with the experimental one. Subsequently, MCF-7 cells with or without cytoskeletal disruption were tested by the PM-SAW device. Cytochalasin-B, which is known to disrupt actin filaments,³⁵ and 2-methoxyestradiol, which is known to disrupt microtubules,³⁶ were separately added to MCF-7 cell populations for 4 h prior to mechanical characterization. The compressibility of cells is the only unknown parameter that can be estimated by fitting the theoretical trajectory with the experimental trajectory, assuming a constant cell density of 1050 kg m⁻³ based on our previous study and other studies from the literature.^33,37,38 Then, the compressibility of control, actin-disrupted and microtubule-disrupted groups of MCF-7 cells were measured by the PM-SAW device.

B. Microfluidic micropipette-aspiration (μFMA) device

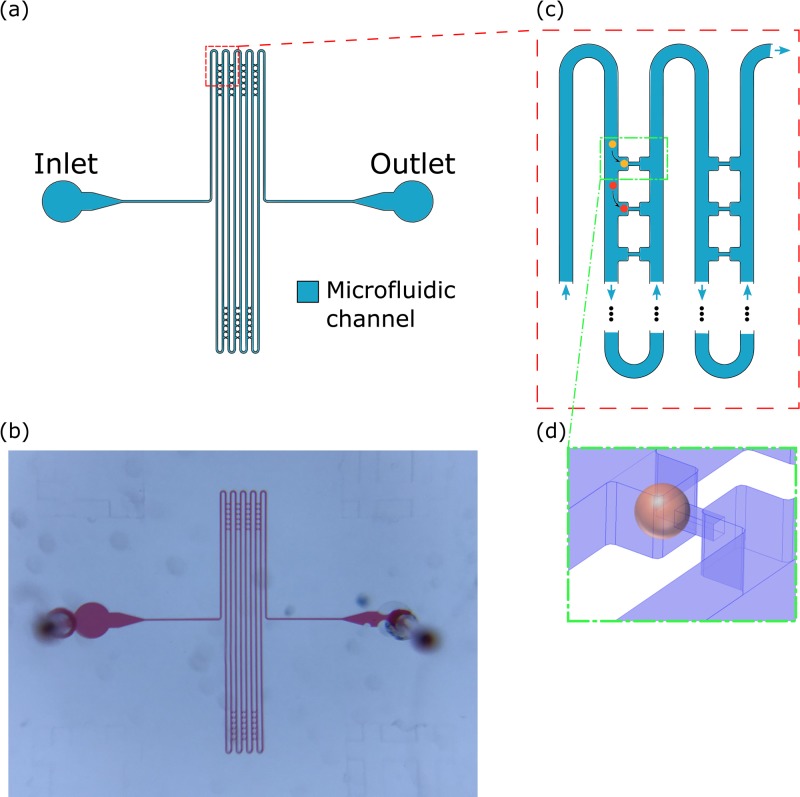
The layout of the microfluidic micropipette-aspiration (μFMA) device is based on a design in the study of Lee et al.³⁹ As shown in Fig. 2, our design consists of a main serpentine microfluidic channel and 42 micropipette-aspiration units, which is fewer than the repeating units in the study of Lee et al. The major advantage is allowing the observation of half of the units in one field of view and, therefore, reducing the number of microscopic scanning positions for the ease of observation. The 42 units are located across two neighboring segments of the main channel and aligned in seven columns, each of which has six units. Each unit is comprised of chambers and a micropipette, where the chamber accommodates the cell to be aspirated and the micropipette is at the center of the chamber sidewall such that the cell remains in suspension while being aspirated by micropipette (Fig. 2).

FIG. 2.

(a) Overall layout and (b) photo of microfluidic micropipette-aspiration (μFMA) device. (c) Zoomed-in schematic of the junction between micropipette-aspiration unit and main channel, where a cell would preferably enter the unit. (d) Zoomed-in schematic of a cell loaded at one micropipette-aspiration unit, where the pressure difference between the two ends is completely exerted on the loaded cell.

The experimental procedures comprise three steps: channel priming, cell loading, and stepwise aspiration. At the beginning of the experiment, the μFMA device is flushed by Tyrode's solution containing 0.25% BSA and 0.3% Pluronic F127 to remove all of the air inside the microfluidic channel. Then, cells are loaded into the μFMA device and trapped in the micropipette-aspiration unit. The loading mechanism of this device is similar to the pipette array in the previous study.³⁹ The rationale is based on the careful design of the flow resistances along the main channel and micropipette. The flow resistance along a rectangular channel is determined by its cross-sectional width and height as well as the path length. Although the micropipette has a smaller cross section than the main channel, the main channel is much longer than the micropipette and, therefore, has a high flow resistance. As a result, a cell at the junction between the micropipette-aspiration unit and the main channel would preferably enter the unit. The design incorporating six repeated units in one column further ensures that the cells enter the chamber of micropipette-aspiration unit instead of traveling along the main channel. Once a cell enters the chamber, the micropipette is completely blocked since cell diameter is greater than that of micropipette, and the following cells would move on to downstream unoccupied units.

After all the micropipette-aspiration units are loaded with cells, the pressure difference between the two ends of micropipette due to pressure drop along the main channel is completely applied to the loaded cells. The pressure difference can be defined by the Darcy–Weisbach equation⁴⁰

$$\mathrm{\Delta }p={\displaystyle \frac{C(\alpha )\mu LQ{(W+H)}^2}{8{(W\times H)}^3},}$$ (4)

where C(α) denotes the laminar friction constant for aspect ratio α and C(α) = 56.91 for α = 1 in our device,⁴¹ μ denotes the dynamic viscosity of the fluid, L denotes the path length between the two ends of micropipette along the main channel, Q denotes the flow rate, and W and H denote the main channel cross-sectional width and height.

The pressure difference is increased stepwise by increasing the flow rate every 2 min, which allows the aspiration length to reach the steady state prior to the next pressure increment. The data series of aspiration length L_p vs the corresponding pressure difference Δp can be used to estimate Young's modulus of the cell via linear regression based on an elastic half-space model,⁴²

$$E={\displaystyle \frac{{\displaystyle \frac{3\mathrm{\Delta }p\mathrm{\Phi }}{2\pi }}}{{\displaystyle \frac{L_p}{R_p}}},}$$ (5)

where E denotes Young's modulus, Φ denotes the geometric constant of micropipette and takes the value of 2.1 in our device given the thickness and the radius of micropipette,^42,43 L_p denotes the aspiration length, and R_p denotes the hydraulic radius of micropipette. Since the micropipette is square in cross section, the equivalent hydraulic radius is half of the side length.^39,44

The fabrication, dimension, and experimental setup of the μFMA device are demonstrated in the supplementary material. To confirm the cell-loading mechanism and the hydrodynamic pressure difference applied on the cells, computational fluid dynamics (CFD) models were built in 3D using COMSOL 4.3a (COMSOL Multiphysics) to study the flow field in the μFMA device. One column of units was modeled to represent the seven repeated columns. The velocity field and pressure field were simulated for cell loading (when micropipette-aspiration units are vacant) and stepwise aspiration (when micropipette-aspiration units are fully occupied) using the laminar flow component.

Similar to the PM-SAW experiment, MCF-7 cells treated with cytochalasin-B and 2-methoxyestradiol were tested by the μFMA device. The loading flow rate was chosen as 10 nl/min, and the cell concentration was ∼1 000 000/ml, ensuring that loaded cells are not subjected to significant suction pressure and the loading can finish within 10 min. The cells experienced stepwise increasing pressure generated by increasing flow rate with the increment of 10 nl/min for every 2 min until 100 nl/min. Young's modulus of control, actin-disrupted, and microtubule-disrupted cells were estimated based on linear regression analysis of the aspiration length vs the corresponding pressure.

C. Cell culture

MCF-7 cells [American Type Culture Collection (ATCC)] were cultured in a complete DMEM medium [containing 10% (v/v) HIFCS, 2 mM l-glutamine, 1% (v/v) non-essential amino acids, 1% (v/v) sodium pyruvate, 0.2% (v/v) sodium bicarbonate, 15 mM HEPES, 100 IU/ml penicillin, and 50 μg/ml streptomycin]. The cells were kept at 37 °C in a humidified atmosphere containing 5% CO₂. The cells were passaged twice weekly by washing confluent cell monolayers twice with PBS and incubating with trypsin (0.12% w/v) for 5 min or until cells were in suspension, followed by centrifugation at 462 × g and resuspended in complete DMEM.

D. Actin and microtubule disruption

Both cytochalasin-B (Sigma) and 2-methoxyestradiol (Steraloids) were initially dissolved in DMSO, then diluted in complete DMEM and added to the cells at 10 μM. The same concentration of DMSO was identically diluted and added to the control group as vehicle control. After adding the drugs, cells were left in the 37 °C incubator with 5% CO₂ for 4 h, washed with PBS, trypsinized, and suspended in the solution prior to the experiment.

E. Immunofluorescence

MCF-7 cell suspension was prepared following the procedures prior to the experiment as described above and fixed in 10% (v/v) neutral buffered formalin (NBF) for 10 min. After PBS washes, the cells were centrifuged onto slides using cytospin (Shandon Cytospin 4, Thermo) at 350 rpm, 10 min. The non-specific binding sites were blocked by incubation with 5% normal goat serum/0.1% Triton X-100 in PBS for 1 h. β-tubulin (9F3) rabbit monoclonal antibody (1:100, No. 2128S, Cell Signaling) was incubated overnight at 4 °C followed by an AlexaFluor-594 conjugated anti-rabbit IgG (H + L) cross-adsorbed secondary antibody (1:500, No. A-11012, Invitrogen). The cells were then stained with Oregon-green 488 (green) phalloidin (1:50, O7466, Invitrogen Molecular Probes) for 20 min. The cell nuclei were stained with DAPI for 10 min. The slides were mounted using the DAKO fluorescent mounting medium (S3023, DAKO) and examined using the Zeiss LSM880 Airyscan Fast Confocal Microscope (Biological Optical Microscopy Platform, University of Melbourne).

III. RESULTS

A. PM-SAW device validation

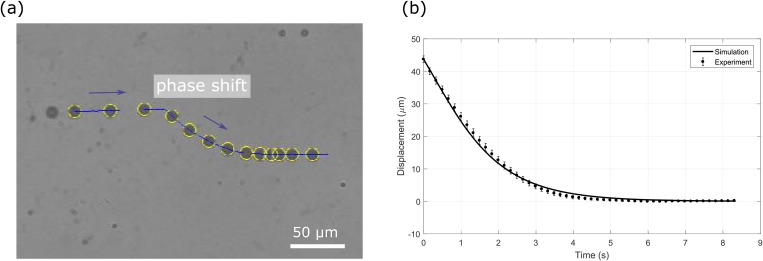
Prior to cell measurement using the PM-SAW device, the device was validated by 10-μm polystyrene microbeads. Once injected into the PM-SAW device, the microbeads were pre-focused at the pressure node of standing acoustic waves. Upon a phase shift by 120°, the microbeads moved to the new pressure nodal line due to phase modulation (Fig. 3). The trajectory of the microbeads being pushed to the new pressure node was captured, represented in displacement vs time and subsequently compared with the theoretical trajectory simulated for the same microbead (Fig. 3). We found that the experimental and simulated trajectories for all microbeads were closely matched and exhibit a fitting residual error of 0.77 μm (defined as the root mean square of the difference between the experimental and the simulated displacement) and a relative error of 1.8% (defined as the ratio of the fitting residual error to the total displacement). Behavior of the PM-SAW device agrees with that reported in our previous study.³³ As further validation, an example of compressibility measurement using the PM-SAW device was provided and compared with literature values in the supplementary material.

FIG. 3.

(a) Overlaid images captured at different stages of a 10-μm polystyrene microbead being pushed toward the new pressure node upon phase-shift in the PM-SAW device. (b) Experimentally captured trajectory and the simulated trajectory of the microbead.

B. μFMA device validation

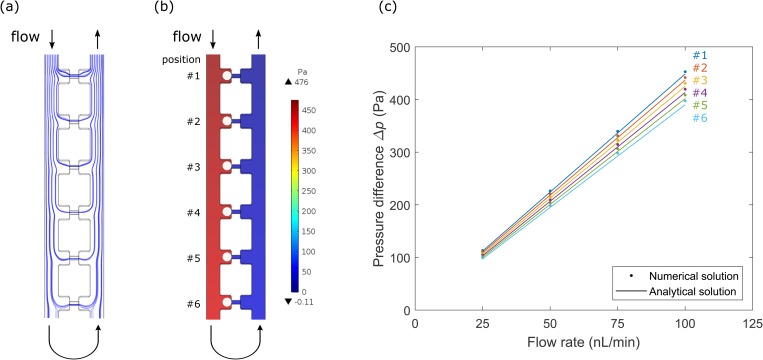
Two three-dimensional CFD models were built to study the mechanism of the μFMA device and to validate the applied pressure. The first CFD model simulated cell loading at a constant flow rate while the micropipette-aspiration units were vacant. The streamlines were plotted in Fig. 4(a) and showed that the majority of fluid flowed into the six units in the column at the junction with the main channel due to the flow resistance design. It suggests a successful cell loading mechanism and agrees with our observation during the experiment.

FIG. 4.

(a) Simulated streamlines for cell loading at a constant flow rate while the micropipette-aspiration units are vacant in the μFMA device. (b) Simulated pressure field at the flow rate of 100 nl/min while cells are loaded in the μFMA device. The six units are labeled as position 1–6 for further illustration. (c) Numerical pressure difference simulated as shown in (b) and analytical pressure difference derived from Eq. (4) vs flow rate, for each position from position 1 to 6.

The second CFD model simulated the pressure field at a certain flow rate during stepwise aspiration and repeated for different flow rates. The pressure field at the flow rate of 100 nl/min was visualized in Fig. 4(b), and the six units were labeled as position 1–6. It was found that the pressure difference between two ends of the unit dropped slightly from position 1 to position 6, due to the reduction in the path length along the main channel. The numerical pressure difference simulated by the CFD model and the analytical one derived from Eq. (4) were plotted with regard to the flow rate, which exhibited a linear relationship [Fig. 4(c)]. The same trend of pressure drop from position 1–6 was observed at different flow rates. Hence, the pressure difference was configured specific to the position of each unit during following measurements. In addition, the analytical solutions matched well with the numerical ones such that the analytical solutions were used in the following for saving computational resources. As further validation, an example of Young's modulus measurement using the μFMA device was provided and compared with literature values in the supplementary material.

C. Compressibility and Young's modulus measurements after actin and microtubule disruption

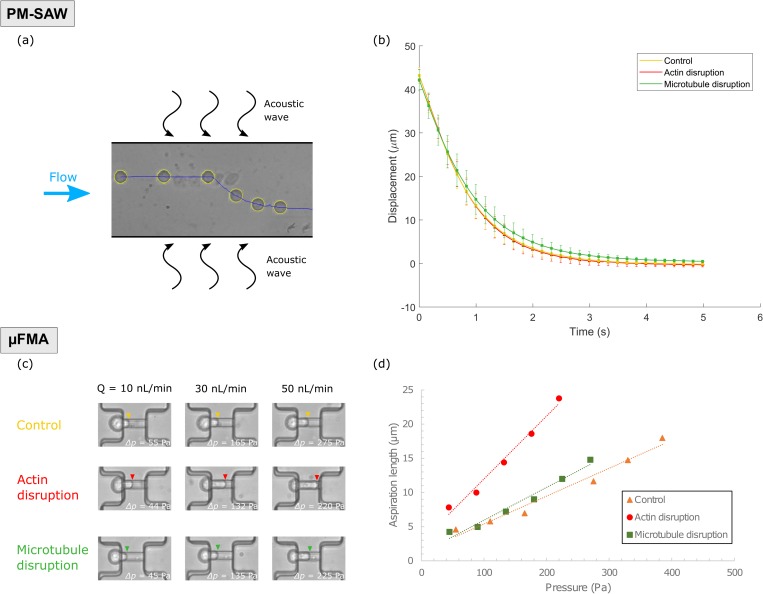
Actin filaments and microtubules are the two major cytoskeletal components that contribute to cell mechanical behavior. In order to discuss the contributions of these two cytoskeletal components to the two elastic moduli of interest and evaluate the capabilities of the two devices to detect cytoskeletal alteration, actin filaments and microtubules of MCF-7 cells were disrupted by drug treatments, respectively. The two disrupted groups as well as the common control group were measured by PM-SAW and μFMA devices.

In the PM-SAW device, as exposed to phase-modulated acoustic waves, MCF-7 cell was pushed from the original pre-focusing pressure node to the new pressure node [Fig. 5(a)]. By plotting the trajectory on which the cell moved to the new nodal line as displacement vs time for the three groups, we noticed that the microtubule-disrupted group moved slower than the control and actin-disrupted group, while no difference was found between the control and actin-disrupted groups [Fig. 5(b)]. The slopes of the trajectories of control and actin-disrupted groups were steeper than that of the microtubule-disrupted group, indicating that the acoustic radiation force was reduced after microtubule disruption but unchanged after actin disruption.

FIG. 5.

(a) Overlaid images captured at different stages of MCF-7 cell being pushed toward the new pressure node upon phase-shift in the PM-SAW device. (b) Average trajectories of control, actin-disrupted, and microtubule-disrupted MCF-7 cells in the PM-SAW device, represented as displacement vs time. (c) Demonstrations of different aspiration lengths of MCF-7 cells with or without actin/microtubule disruption with regard to an increasing flow rate and, therefore, increasing pressure in the μFMA device. (d) Aspiration length vs pressure for control, actin-disrupted, and microtubule-disrupted MCF-7 cells as shown in (c).

In the μFMA device, MCF-7 cells were loaded at the micropipette-aspiration units and aspirated by stepwise increasing pressure. The images of cells being aspirated into micropipette were shown at different flow rates and, therefore, different applied pressure for the three groups [Fig. 5(c)]. The aspiration length of the cell from actin-disrupted group was longer than those from the other two groups at the same flow rate and similar pressure. In addition, in the graph of aspiration length vs pressure for the three cells, the slope of actin-disrupted group was distinguished from the control and microtubule-disrupted groups, while the difference between the control and microtubule-disrupted groups was subtle [Fig. 5(d)]. Considerations should be given to the aspiration length that was constantly measured from the edge of micropipette. Even though the edge of micropipette may not exactly coincide with the starting edge of a cell, only the incremental response will be considered due to the nature of the following linear regression analysis and, therefore, any global offset error will have no impact on the results.

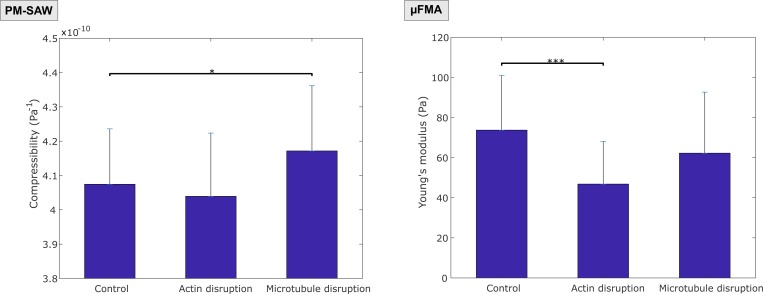
The compressibility and Young's modulus were calculated for the three groups (Fig. 6). The measured compressibility of the control group was 4.07 ± 0.16 × 10⁻¹⁰ Pa⁻¹ (mean ± SD, n = 31); that of the actin-disrupted group was 4.04 ± 0.18 × 10⁻¹⁰ Pa⁻¹ (n = 34); and that of the microtubule-disrupted group was 4.17 ± 0.19 × 10⁻¹⁰ Pa⁻¹ (n = 36). A statistically significant difference in compressibility was found between the control and microtubule-disrupted group (p < 0.05, unpaired t test), while there was no significant difference in compressibility between the control and actin-disrupted group (p = 0.42). The measured Young's modulus of the control group was 73.7 ± 27.3 Pa (mean ± SD, n = 28); that of the actin-disrupted group was 46.8 ± 21.3 Pa (n = 23); and that of the microtubule-disrupted group was 62.3 ± 30.4 Pa (n = 34). A statistically significant difference in Young's modulus was found between the control and actin-disrupted group (p < 0.001, unpaired t test), while there was no significant difference in Young's modulus between the control and microtubule-disrupted (p = 0.12). The alteration of actin filaments was revealed by Young's modulus change using micropipette aspiration rather than compressibility change using acoustic waves, whereas the alteration of microtubules was revealed by increased compressibility.

FIG. 6.

Compressibility (left) and Young's modulus (right) measurements of control (n = 31 for compressibility; n = 28 for Young's modulus), actin-disrupted (n = 34 for compressibility; n = 23 for Young's modulus), and microtubule-disrupted (n = 36 for compressibility; n = 34 for Young's modulus) MCF-7 cells using PM-SAW and μFMA devices, respectively. Please note that * denotes p < 0.05 and *** denotes p < 0.001, using unpaired t-test. Each bar with an error bar represents mean ± SD.

With the independently measured compressibility $\beta$ and Young's modulus E, the Poisson ratio $\nu$ of MCF-7 cells can be then estimated by the well-known elastic modulus conversion formula $\nu =1/2-E\beta /6$, assuming that cells are homogeneous isotropic linear elastic materials. In all groups, the calculated Poisson ratios were close to 0.5, with a deviation less than 5 × 10⁻⁹. The deviations of Poisson's ratios from incompressible limit, 0.5 − $\nu$, were calculated as 5.0 ± 1.9 × 10⁻⁹ (control), 3.2 ± 1.4 × 10⁻⁹ (actin-disrupted), and 4.3 ± 2.1 × 10⁻⁹ (microtubule-disrupted), where the errors were calculated using standard error propagation.

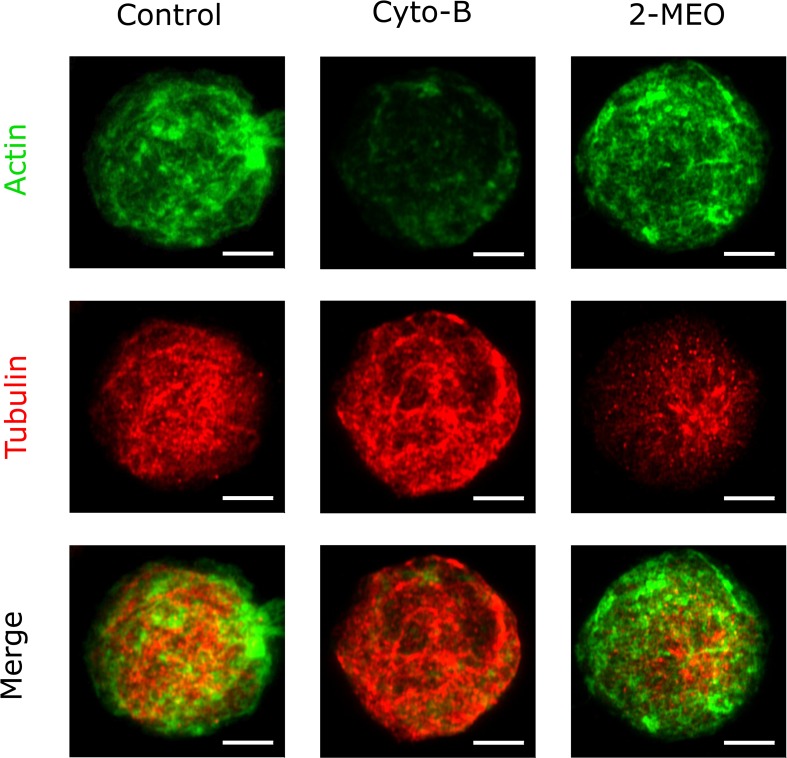
D. Immunofluorescent visualization

In order to confirm the cytoskeletal alterations of MCF-7 cells used in this study, actin filaments and microtubules were stained as described in the Method section. Immunofluorescence imaging showed significant effects of cytochalasin-B and 2-methoxyestradiol on the distributions of actin and microtubule networks (Fig. 7). The actin filaments were distributed as a network at the periphery of the cell. In the control cells, the actin staining exhibited partly clear filamentous interconnections and partly punctate structure as bright spots. Upon treatment of 10 μM cytochalasin-B, there was indiscernible filamentous structure observed in the actin staining and the overall network density was reduced. In contrast, the filamentous networks of actin remain with the treatment of 10 μM 2-methoxyestradiol (Fig. 7).

FIG. 7.

Immunofluorescence images of actin and tubulin of control, 10 μM cytochalasin-B (Cyto-B) treated, and 10 μM 2-methoxyestradiol (2-MEO) treated MCF-7 cells. Scale bar represents 5 μm.

Tubulin was stained to visualize the microtubule networks and found throughout the cell. The fibrous structures of microtubules were clearly observed in the control and cytochalasin-B treated cells. However, the tubulin staining appeared as disjoined and scattering dots at the treatment of 2-methoxyestradiol, indicating that the microtubule network was disrupted (Fig. 7).

IV. DISCUSSION

In this study, micropipette aspiration and acoustic wave were implemented in a microfluidic environment to examine Young's modulus and compressibility of MCF-7 cells. In Young's modulus measurements of this study, MCF-7 cells were found to become softer due to reduction of Young's modulus after actin disruption, while no significant difference was shown after microtubule disruption; in the compressibility measurements, MCF-7 cells became more compressible after microtubule disruption but showed no difference after actin disruption. The immunofluorescence imaging confirmed the cytoskeletal alterations in this study, and the observations of suspension cells with cytoskeletal disruptions were in agreement with the previous studies that similarly immunolabeled suspension cells.^16,27 In addition, the Poisson ratio of MCF-7 cells was estimated based on the measured Young's modulus and compressibility and found to be very close to but slightly less than 0.5, suggesting that the behaviors of MCF-7 cells are close to incompressible due to the major fluidic component in the cytoplasm.

In the literature, several studies reported Young's modulus in response to cytoskeletal alterations including actin disruption and microtubule disruption. For example, Young's modulus of the MCF-10A non-tumorigenic epithelial cell line was found reduced due to actin disruption by latrunculin-A using a similar microfluidic pipette device.³⁹ Human umbilical vein endothelial cells,⁴⁵ platelets,⁴⁶ neutrophils,⁴⁷ and porcine aortic endothelial cells⁴⁸ were aspirated by the conventional micropipette and exhibited higher aspiration length, suggesting lower Young's modulus due to actin disruption by cytochalasin. In addition to measurements using micropipette aspiration, AFM was implemented to reveal that Young's modulus of cells decreased after actin disruption.^13,25 These studies agree with our observation using the μFMA device that the actin disruption of MCF-7 cells caused a reduction of Young's modulus. On the other hand, micropipette aspiration has also been used to show that Young's moduli of human neutrophils⁴⁹ and chondrocytes²⁷ had no significant change after microtubule disruption by colchicine. Other studies using moving probe indentation on chondrocytes²⁶ and AFM on fibroblasts²⁵ showed that no change in Young's modulus was induced by microtubule disruption. These studies agree with our observation using the μFMA device that the microtubule disruption of MCF-7 cells did not induce a significant impact on Young's modulus.

In addition, a few studies measured compressibility (or equivalently bulk modulus) in response to cytoskeletal alterations. As the acoustic wave is a type of compression wave such that acoustic propagation in a material is primarily related to its compressibility, acoustic-based methods were usually applied for cell compressibility measurements. One study examined mouse fibroblasts using scanning acoustic microscopy and reported that disrupting actin filaments left the compressibility (or bulk modulus) unchanged.¹³ On the other hand, it was reported in our previous study that disrupting microtubules increased cell compressibility.³³ In addition to acoustic-based methods, a custom cytocompression device was built to study chondrocytes and showed that the initial compressibility derived from visually measured volume change were increased only at microtubule disruption (represented as decreasing initial apparent Poisson's ratio) and unchanged at actin and intermediate filaments disruptions.³¹ These studies are consistent with our observations using the PM-SAW device that microtubule disruption of MCF-7 cells increased the compressibility and actin disruption had no impact.

In contrast to our observations, there are studies showing the decrease in Young's modulus of microtubule-disrupted endothelial cells⁴⁸ and platelets,⁴⁶ and the increase in Young's modulus and the decrease in compressibility (or the increase in bulk modulus) of microtubule-disrupted fibroblasts.¹³ These discrepancies could be attributed to a number of factors. As pointed out in the study of Wu et al.,²⁴ elastic modulus measurements could vary regarding the force profile and other loading conditions of techniques. For example, in the study of endothelial cells using micropipette aspiration,⁴⁸ a constant pressure instead of stepwise increasing pressure was applied, and the size of micropipette and the aspiration length were smaller than those in our study, which may lead to different elastic modulus measurements. Furthermore, different cell culturing or testing conditions could result in different measured elastic moduli. For example, the hardening of fibroblasts after microtubule disruption was demonstrated using adhered cells and explained as actin polymerization compensating for the microtubule disruption, which may not be pronounced after detaching cells from the substrate.¹⁶

The measurement discrepancies among the literature appear to be caused by mechanical loading and cellular physiological conditions, as well as by the need for a minimum of two elastic moduli to generate a mechanical model, supporting the advantages of two independent techniques to measure the cell mechanics as used in this study. This approach could reduce possible variation due to cell culture differences among laboratories, facilitate comparison between techniques, and obtain elastic moduli independently.¹³ This more comprehensive approach is made easier by lower cost, lesser instrumental requirement, and higher throughput of these microfluidic methods compared with conventional techniques. Although the experiments using two techniques in this study were performed in parallel, it is possible for future work to combine them into one microfluidic device, examining every single cell by applying the two techniques in sequence and performing a paired comparison, as shown in one previous study where acoustophoresis and optical stretching were combined.⁵⁰ The combination of two measurement methods could raise concerns such as SAW-induced structural change of the cell lipid bilayer, which might affect the cell membrane deformation when using micropipette aspiration. However, it was also reported that the transient submicron indentations on lipid bilayer induced by high-frequency (>10 MHz) SAW rapidly recovered upon SAW relaxation.⁵¹ The use of acoustic wave has been considered a non-invasive method with minimal effect on cell viability, proliferation, and differentiation.^52,53 Hence, we anticipate that any SAW-induced temporal effect will not affect the micropipette-aspiration measurement if combined in cascade.

Our observations demonstrate the roles of cytoskeletal components with regard to cellular elastic moduli. The differences in subcellular localization and organization of actin and microtubule networks denote their distinctive structures. Actin filaments are distributed around the cellular cortex beneath the plasma membrane and form a network of cross-linked stress fibers.⁵⁴ Conversely, microtubules form a network throughout cytoplasm originating from centrosome and extending to cell periphery and can be thought of as structural rods.^31,55 Then, the cellular tensegrity model links the cytoskeletal structures to their mechanical roles.^4,5 The model suggests that actin filaments could be deemed as pre-stressed tensional “cables” and are better at resisting tension and shape distortion, so they mainly contribute to tensile Young's modulus which is defined in the elastic regime of uniaxial deformation. Microtubules are presumed to behave as compression-resistant “struts” and showed greater ability to withstand compression, thereby mainly contributing to compressibility which measures the relative volume change in response to uniform compression. For example, one study analyzed an icosahedron tensegrity structure consisting of six struts in the center and 24 cables connecting the ends of struts and reported that its bulk modulus (equivalent to compressibility) was not affected by the cable pre-stress and the resistance to compression was essentially due to the strut stiffness.⁵⁶ In another study, a tensegrity structure with repeating 3-strut (also known as two-stage 3-bar SVD-type tensegrity) showed that its axial stiffness or Young's modulus was increased by the cable pre-stress increase.⁵⁷ Despite more complex interconnection between cytoskeletal networks, these tensegrity structures with cables and struts resemble the actin and microtubule networks as structural analog, and the tensegrity mechanical behaviors are consistent with the results in this study. The consistency suggests that the different roles of cytoskeleton on cellular elastic moduli could be explained by the cellular tensegrity model.

In addition, our results showed that micropipette aspiration showed greater ability in detecting alteration in actin filaments and acoustophoresis exhibited better performance in detecting alteration in microtubules. The different responses of these two techniques could be determined by the relationship between the mechanical loading conditions and cytoskeletal structures. Micropipette aspiration applies localized suction pressure, increasing the load on the actin cortex underlying cell membrane, and hence, causing a change in cell shape. In contrast, acoustic waves propagate by means of compression and decompression throughout the entire spatial cellular structure, and thereby the response may be dominated by the microtubules. For future cell mechanics studies, these observations suggest the need to select a suitable measuring technique based on its mechanical loading conditions and the cellular structure of interest.

V. CONCLUSION

This study established a phase-modulated surface acoustic wave (PM-SAW) microfluidic device for cellular compressibility measurement and a microfluidic micropipette-aspiration (μFMA) device for cellular Young's modulus measurement. It allows independent measurements of two elastic moduli of MCF-7 cells in response to cytoskeletal alterations. Different structural roles of actin filaments and microtubules were found in relation to cellular elastic moduli, where actin filaments mainly contribute to tensile Young's modulus and microtubules mainly contribute to compressibility (or bulk modulus). In addition, micropipette aspiration and acoustophoresis techniques showed the capability in detecting alteration of actin filaments and microtubules, respectively, indicating the necessity for future studies to select a suitable measuring technique according to the cellular structure of interest.

SUPPLEMENTARY MATERIAL

See the supplementary material for details on fabrication, dimension, experimental setup, and validation of the phase-modulated surface acoustic wave (PM-SAW) device and microfluidic micropipette-aspiration (μFMA) device.