Structured gene-environment interaction analysis

Summary:

For the etiology, progression, and treatment of complex diseases, gene-environment (G-E) interactions have important implications beyond the main G and E effects. G-E interaction analysis can be more challenging with the higher dimensionality and need for accommodating the “main effects, interactions” hierarchy. In the recent literature, an array of novel methods, many of which are based on the penalization technique, have been developed. In most of these studies, however, the structures of G measurements, for example the adjacency structure of SNPs (attributable to their physical adjacency on the chromosomes) and network structure of gene expressions (attributable to their coordinated biological functions and correlated measurements), have not been well accommodated. In this study, we develop the structured G-E interaction analysis, where such structures are accommodated using penalization for both the main G effects and interactions. Penalization is also applied for regularized estimation and selection. The proposed structured interaction analysis can be effectively realized. It is shown to have the consistency properties under high dimensional settings. Simulations and the analysis of GENEVA diabetes data with SNP measurements and TCGA melanoma data with gene expression measurements demonstrate its competitive practical performance.

1. Introduction

Beyond the main genetic (G) and environmental (E) effects, gene-environment (G-E) interactions have been shown to be fundamentally important for the etiology, progression, prognosis, and response to treatment of many complex diseases. In the past decade, a long array of statistical methods have been developed for G-E interaction analysis and can be roughly classified as marginal analysis (under which one G measurement is analyzed at a time) and joint analysis (under which a large number of G measurements are analyzed in a single model). Compared to marginal analysis, joint analysis may better describe disease biology (that is, phenotypes and outcomes of complex diseases are associated with the combined effects of multiple genetic factors) and have attracted extensive attention in recent literature.

Joint G-E interaction analysis is challenging with the high data dimensionality. For estimation and also to screen out noises and identify important G-E interactions and main G effects, regularized estimation has been routinely conducted. Among the available techniques, penalization has been popular in recent studies. See Wu and Ma (2018) and references therein. Another challenge comes from the need to respect the “main effects, interactions” hierarchy (Bien et al., 2013; Hao et al., 2018). Under the context of G-E interaction analysis with low-dimensional E variables, this hierarchy postulates that an interaction term cannot be identified, if the corresponding main G effect is not identified. With this hierarchy, “straightforward” penalizations are insufficient. Several penalization techniques have been developed in recent literature to respect this hierarchy (Liu et al., 2013; Wu et al., 2018).

A common limitation shared by many of the existing G-E interaction studies is that the structures of G measurements have not been well accounted for. Consider for example single nucleotide polymorphism (SNP) data. When SNPs are densely measured, those physically close are often in high linkage disequilibrium (LD) and likely have similar biological functions or statistical effects (Reich et al., 2001). Here, there is an adjacency structure which arises from the physical adjacency of SNPs. As another example, consider gene expressions. Recent studies have shown that with coordinated biological functions and correlated measurements, gene expressions can be effectively described using a network structure (Barabasi et al., 2011). Note that for other types of omics measurements, there are also underlying structures, although the construction of such structures may vary across data types.

In the high-dimensional analysis of main G effects, a few structured analysis approaches have been developed to accommodate the underlying structures in estimation and selection. Consider the adjacency structure of SNPs (and other densely measured G factors). Available penalization approaches include the fused lasso (Tibshirani et al., 2005), smooth lasso (Hebiri and van de Geer, 2011), smoothed group lasso (Liu et al., 2012), spline lasso (Guo et al., 2016), and others. When gene expressions (and other G measurements) are described using network structures, network-constrained regularized estimation has been proposed. A popular approach is the network Laplacian-based penalization (Li and Li, 2008). Other network-structured penalization methods include the TLP-based penalty for groups of indicators (Kim et al., 2013), sparse regression incorporating graphical structures among predictors (SRIG) (Yu and Liu, 2016), and others. Extensive investigations have shown that structured analysis can lead to more accurate and more interpretable identification and estimation. It is noted that, with similar spirits, structured analysis can also be conducted based on techniques other than penalization. As penalization is adopted in this study, the above literature review has been focused on this specific technique.

In this study, our goal is to conduct structured G-E interaction analysis, under which the structures of G measurements can be effectively accounted for. This has been well motivated by the success of structured analysis in the study of main G effects and a lack of such analysis in G-E interaction analysis. This study is much more than an extension of the main-G-effect structured analysis. Specifically, in G-E interaction analysis, one G factor manifests multiple effects: its main effect as well as multiple E-interactions. The underlying structures need to be accounted for in the analysis of all these effects. This is further complicated by the “main effects, interactions” hierarchy. Thus, significant computational and statistical developments are needed. Also advancing from some of the existing studies, we accommodate multiple types of underlying structures, especially including the physical adjacency structure of SNPs and network structure of gene expressions, under one framework. This unity significantly benefits methodological and statistical developments. Another advancement is that statistical properties are carefully established, which can provide a more solid ground than some of the existing studies. Overall, this study can provide an alternative and more effective way for conducting G-E interaction analysis.

2. Methods

Consider a dataset with n iid subjects. For the ith subject, let Y_i be the response of interest, and Z_i· = (Z_i1; … , Z_iq) and X_i· = (X_i1; … , X_ip) be the q- and p-dimensional vectors of E and G measurements. First, consider the scenario with a continuous outcome and a linear regression model with the joint effects of all E and G effects and their interactions:

$$Y_i=\sum _{k=1}^q{Z}_{ik}{\alpha }_k+\sum _{j=1}^p{X}_{ij}{\beta }_j+\sum _{k=1}^q\sum _{j=1}^p{Z}_{ik}{X}_{ij}{\eta }_{kj}+{\epsilon }_i,$$ (1)

where α_k’s, β_j’s, and η_kj’s are the regression coefficients for the main E, main G, and their interactions, respectively, and ε_i’s are the random errors. We omit intercept to simplify notation. To respect the “main effects, interactions” hierarchical constraint, we conduct the decomposition of η_kj as η_kj = β_jγkj. Then model (1) can be rewritten as

$$Y_i=\sum _{k=1}^q{Z}_{ik}{\alpha }_k+\sum _{j=1}^p{X}_{ij}{\beta }_j+\sum _{k=1}^q\sum _{j=1}^p{Z}_{ik}{X}_{ij}{\beta }_j{\gamma }_{kj}+{\epsilon }_i={\mathit{Z}}_{i.}\mathit{\alpha }+{\mathit{X}}_{i.}\mathit{\beta }+\sum _{k=1}^q{\mathit{W}}_{i.}^{(k)}\left(\beta \odot {\gamma }_k\right)+{\epsilon }_i,$$

where $\alpha ={\left({\alpha }_1,\cdots ,{\alpha }_q\right)}^{\prime },\beta ={\left({\beta }_1,\cdots ,{\beta }_p\right)}^{\prime },{\gamma }_k={\left({\gamma }_{k1},\cdots ,{\gamma }_{kp}\right)}^{\prime },W_{i\cdot }^{(k)}=\left(Z_{ik}{X}_{i1},\cdots ,Z_{ik}{X}_{ip}\right)$, and ⊙ is the component-wise product. Denote Y as the length-n vector composed of Y_i’s, and Z, X, and W^(k) as the n × q, n × p and n × p design matrices composed of X_i·’s, Z_i·’s, and $W_i^{(k),}s$, respectively.

Consider the penalized objective function

$$Q_n(\theta )=\frac{1}{2n}{\Vert Y-\mathit{Z}\mathit{\alpha }-X\mathit{\beta }-\sum _{k=1}^q{\mathit{W}}^{(k)}\left(\mathit{\beta }\odot {\gamma }_k\right)\Vert }_2^2+\sum _{j=1}^p\rho \left(\left|{\beta }_j\right|;{\text{λ}}_1,r\right)+\sum _{j=1}^p\sum _{k=1}^q\rho \left(\left|{\text{γ}}_{kj}\right|;{\text{λ}}_1,r\right)+\frac{1}{2}{\text{λ}}_2{\mathit{\beta }}^{\prime }\mathit{J}\mathit{\beta }+\frac{1}{2}{\text{λ}}_2\sum _{k=1}^q{\text{γ}}_k^{\prime }\mathit{J}{\text{γ}}_k,$$ (2)

where θ = (α^′, β^′, γ^′)′ = (α^′, β′, γ′₁, … , γ′_q)′, $\Vert \nu {\Vert }_2$ is the L₂ norm of vector $\nu ,\rho \left(|\nu |;{\lambda }_1,r\right)={\lambda }_1{\int }_0^{|\nu |}{\left(1-\frac{x}{{\lambda }_{1}r}\right)}_{+}dx$ is the minimax concave penalty (MCP), λ₁ ≥ 0 and λ₂ ≥ 0 are the tuning parameters, and r > 0 is the regularization parameter. J is the p × p matrix that accommodates the structure of G measurements (more details below). The proposed estimate is defined as the minimizer of (2). The nonzero components of β and β ⊙ γ_k correspond to the important main G effects and interactions that are associated with the response.

In the objective function, the first term is the lack-of-fit. For each of the G factors, penalties are imposed on its main effect as well as interactions. With the decomposition (β_jγ_jk), the proposed penalties guarantee that a G-E interaction is not identified if the corresponding main G effect is not identified. Note that here the setting and hence strategy differ from the pairwise interaction analysis studies such as Choi et al. (2010) and Hao et al. (2018). Specifically, in most G-E interaction analysis, for example as considered in our data examples, the E factors are manually selected based on extensive prior knowledge and have a low dimensionality. As such, there is no need to conduct selection with E effects. In the literature, there are other ways of achieving the hierarchy, for example, the sparse group MCP (Liu et al., 2013). Our exploration suggests that the proposed approach has computational advantages. Accommodating the structures of G measurements In (2), the underlying structures of G measurements are accommodated using the last two penalty terms. Here for interactions, instead of β ⊙ γ_k, we consider the structures of γ_k which can significantly facilitate theoretical and numerical analysis. Our numerical investigation suggests that the two approaches lead to similar results (details omitted). Consider the following two specific examples.

Consider SNP data. Assume that densely measured SNPs have been sorted according to their physical locations. Consider the spline type penalty ${\Sigma }_{j=2}^{p-1}{\left[\left({\beta }_{j+1}-{\beta }_j\right)-\left({\beta }_j-{\beta }_{j-1}\right)\right]}^2$ and ${\Sigma }_{j=2}^{p-1}{\left[\left({\gamma }_{k(j+1)}-{\gamma }_{kj}\right)-\left({\gamma }_{kj}-{\gamma }_{k(j-1)}\right)\right]}^2$ Then, we have J = H′_(p−2)×pH_(p−2)×p with H_jj = H_j(j+2) = 1; H_j(j+1) = −2, and 0 otherwise. For SNPs as well as their interactions with a specific E factor, this penalty promotes smoothness in a similar way as penalizing second order derivatives in spline-based nonparametric estimation. As a result, adjacent SNPs are promoted to have similar main effects (interactions) associated with the response. With main G effects, some alternatives, such as the fused lasso and smooth lasso, promote first-order smoothness, while this penalty promotes second-order smoothness. Guo et al. (2016) shows that the spline type penalty can outperform these alternatives. Another advantage of the spline type penalty is that the quadratic form is computationally more manageable than, for example, the absolute-value-based.

Consider gene expression data. We first construct the adjacency matrix A = (a_jl)_p×p, where $a_{jl}=r_{jl}^{Pcorr}I\left(\left|r_{jl}^{Pcorr}\right|>c^{Pcorr}\right)$ with $r_{jl}^{Pcorr}$ being the Pearson correlation coefficient between gene expressions j and l and c^Pcorr being the cutoff calculated from the Fisher transformation (details in Web Appendix B). We also examine performance of the proposed approach with various values of c^Pcorr in Web Appendix B. It is observed from Web Table 1 that results are similar for c^Pcorr values in a sensible range and the value calculated from the Fisher transformation leads to satisfactory results. Consider J = I − D^−1/2AD^−1/2, where I is the p×p identity matrix and $D=\text{diag}\left({\Sigma }_{l=1}^p\left|a_{1l}\right|,\cdots ,{\Sigma }_{l=1}^p\left|a_{pl}\right|\right)$. With the cutoff c^Pcorr, J is usually a sparse matrix. This penalty encourages the effects of correlated gene expressions to be similar. Several recent studies have established the effectiveness of this Laplacian penalization strategy for the analysis of main G effects. However, its adoption in the context of G-E interaction analysis is still lacking.

The construction of J needs to be adapted to specific settings and may vary across data types. On the other hand, the above definitions can be extended and applied to quite a few other dense and “non-dense” cases, making the proposed analysis broadly applicable. The proposed approach can be extended to other response types/models. For example, in our numerical study, we consider the censored survival outcome and accelerated failure time (AFT) model. Details on this setting are provided in Web Appendix A.

2.1. Computation

With fixed tuning parameters, optimization of (2) can be conducted using an iterative coordinate descent (CD) algorithm. In Web Appendix A, we provide details on the proposed algorithm, a proof of its convergence properties, and the time and space complexity. For the selection of tuning parameters, we set r as 3 to reduce computational cost and choose the values of (λ₁,λ₂) using BIC. Examinations on various values of r and discussions on the approach to produce a parameter path are provided in Web Appendices B and A, respectively. We also examine the values of BIC as a function of λ₁ and λ₂ and parameter paths in Web Figures 1 and 2. Sensible findings are observed.

2.2. Statistical properties

Consider the scenario where the number of G factors increases and the number of E factors is finite as the sample size increases. Let ${\mathit{\theta }}^0={\left({\left({\alpha }^0\right)}^{\prime },{\left({\beta }^0\right)}^{\prime },{\left({\gamma }_1^0\right)}^{\prime },\cdots ,{\left({\gamma }_q^0\right)}^{\prime }\right)}^{\prime }$ be the true parameter values, and ${\Theta }^0={\left({\left({\alpha }^0\right)}^{\prime },{\left({\beta }^0\right)}^{\prime },{\left({\eta }_1^0\right)}^{\prime },\cdots ,{\left({\eta }_q^0\right)}^{\prime }\right)}^{\prime }$ Let ${\mathcal{A}}_1=\left\{j:{\beta }_j^0\ne 0\right\}$, ${\mathcal{A}}_2^k=\left\{j:{\gamma }_{kj}^0\ne 0\text{ and }{\beta }_j^0\ne 0\right\}$, and ${\mathcal{A}}_2={\mathcal{A}}_2^1\cup \cdots \cup {\mathcal{A}}_2^q$. Note that all ${\alpha }_k^{0,}\text{s}$ are nonzero, and the corresponding parameters are not subject to penalization. With the hierarchical constraint, in ${\mathcal{A}}_2^k$, we are only interested in nonzero γ_kj’s for which the corresponding β_j’s are also nonzero. We have j ∈ A₁ if for some k, $j\in {\mathcal{A}}_2^k$. Denote $|\mathcal{A}|$ as the cardinality of set A. Let $s=\left|{\mathcal{A}}_1\right|+\left|{\mathcal{A}}_2^1\right|+\cdots +\left|{\mathcal{A}}_2^q\right|$. For a vector v and index set S, let v_S be the components of v indexed by S. For a matrix M and two index sets S₁ and S₂, denote $M_{{\mathcal{S}}_1}$ and $M_{{\mathcal{S}}_1}$. as the columns and rows of M indexed by S₁, and $M_{{\mathcal{S}}_1,{\mathcal{S}}_2}$ as the submatrix of M indexed by S₁ and S₂.

Denote ${\mathit{\theta }}_{\mathcal{A}}^{*}={\left({\left({\alpha }^{*}\right)}^{\prime },{\left({\beta }_{{\mathcal{A}}_1}^{*}\right)}^{\prime },{\left({\gamma }_{1,{\mathcal{A}}_2^1}^{*}\right)}^{\prime },\cdots ,{\left({\gamma }_{q,{\mathcal{A}}_2^q}^{*}\right)}^{\prime }\right)}^{\prime }$ as the minimizer of ${\tilde{Q}}_n\left({\mathit{\theta }}_{\mathcal{A}}\right)=\frac{1}{2n}\Vert Y-Z\alpha -X_{{\mathcal{A}}_1}{\beta }_{{\mathcal{A}}_1}-\sum _{k=1}^q{W}_{{\mathcal{A}}_2^k}^{(k)}\left({\beta }_{{\mathcal{A}}_2^k}\odot {\gamma }_{k,{\mathcal{A}}_2^k}\right){\Vert }_2^2+\frac{1}{2}{\lambda }_2\left({\beta }_{{\mathcal{A}}_1}^{\prime }{J}_{{\mathcal{A}}_1,{\mathcal{A}}_1}{\beta }_{{\mathcal{A}}_1}+\sum _{k=1}^q{\gamma }_{k,{\mathcal{A}}_2^k}^{\prime }{J}_{{\mathcal{A}}_2^k,{\mathcal{A}}_2^k}{\gamma }_{k,{\mathcal{A}}_2^k}\right)$. In Web Appendix A, we describe the assumed conditions, which are on the property of residual, size of the smallest signal, characteristics of the predictor matrix and J, and orders of λ₁, λ₂, and p. Comparable conditions have been assumed in the literature (Fan and Lv, 2011; Huang et al., 2017). We refer to Web Appendix A for more detailed discussions.

Theorem 1:

Under Conditions (C1)-(C5), there exists a local minimizer ${\mathit{\theta }}_{\mathcal{A}}^{*}$ of ${\tilde{Q}}_n\left({\mathit{\theta }}_{\mathcal{A}}\right)$ such that for any constant E > 0,

$$P\left\{{\Vert {\theta }_{\mathcal{A}}^{*}-{\theta }_{\mathcal{A}}^0\Vert }_2⩽{\delta }_n\right\}>1-\xi ,$$

where ${\delta }_n=\frac{4{\lambda }_2{\Vert {\tilde{J}}_{A,A}{\mathit{\theta }}_A^0\Vert }_2}{\underset{\_}{c}}+E\sqrt{s/n}$ and $\xi =\text{exp}\left(-\frac{{\left[4\sqrt{n/s}{\lambda }_2{\Vert {\tilde{J}}_{A,A}{\mathit{\theta }}_A^0\Vert }_2+E\underset{\_}{c}\right]}^2}{32{\sigma }^2\overline{c}}\right)$ with the definitions of σ˙, $\underset{\_}{c}$, $\overline{c}$, and ${\tilde{J}}_{\mathcal{A},\mathcal{A}}$ provided in Web Appendix A.

Proof is provided in Web Appendix A. With Theorem 1, we have ${\Vert {\mathit{\theta }}_{\mathcal{A}}^{*}-{\mathit{\theta }}_{\mathcal{A}}^0\Vert }_2=O_p(\sqrt{s/n})$ and ${\Vert {\Theta }_{\mathcal{A}}^{*}-{\Theta }_{\mathcal{A}}^0\Vert }_2=O_p(\sqrt{s/n})$, as ${\lambda }_2=O(\sqrt{1/n})(\text{C}4)$ and ${\Vert {\tilde{J}}_{\mathcal{A},\mathcal{A}}{\mathit{\theta }}_{\mathcal{A}}^0\Vert }_2=O(\sqrt{s})(\text{C}5)$. This theorem establishes estimation consistency when the true sparsity structure is known. For the estimation error provided in Theorem 1, we establish the L₂ loss of the oracle estimator. It achieves the order of $\sqrt{s/n}$, which does not depend on log(p) and differs from some existing studies with biased penalties such as lasso (Zhang and Zhang, 2012).

Let ${\mathcal{A}}_1^c=\left\{j:{\beta }_j^0=0\right\}$ and ${\left({\tilde{\mathcal{A}}}_2^k\right)}^c=\left\{j:{\gamma }_{kj}^0=0\text{ and }{\beta }_j^0\ne 0\right\}$. Then ${\left({\tilde{\mathcal{A}}}_2^k\right)}^c\cup {\mathcal{A}}_1^c=\{j:{\eta }_{kj}^0=0\}$.

Theorem 2:

Define $\widehat{\mathit{\theta }}$ as ${\widehat{\mathit{\theta }}}_{\mathcal{A}}={\mathit{\theta }}_{\mathcal{A}}^{*},{\widehat{\beta }}_{{\mathcal{A}}_1^c}=0,{\widehat{\gamma }}_{k,\left({\tilde{\mathcal{A}}}_2^k\right)c}=0$, and ${\widehat{\gamma }}_{k,{\mathcal{A}}_1^c}$ being the minimizer of Q_n(θ) with the other parameters fixed at the values defined above. Then under Conditions (C1)-(C9), with probability tending to 1, $\widehat{\mathit{\theta }}$ is a strict local minimizer of Q_n(θ).

Proof is provided in Web Appendix A. With Theorem 2, we have ${\widehat{\eta }}_{k,{\mathcal{A}}_1^c}=0$ with ${\widehat{\beta }}_{{\mathcal{A}}_1^c}=0$, and ${\widehat{\eta }}_{k,{\left({\tilde{\mathcal{A}}}_2^k\right)}^c}=0$ with ${\widehat{\gamma }}_{k,\left({\tilde{\mathcal{A}}}_2^k\right)c}=0$. Theorem 2 establishes the selection and estimation consistency properties under high-dimensional settings. The definition of $\widehat{\mathit{\theta }}$ is based on the concept of “oracle” (Fan and Lv, 2011; Huang et al., 2017). That is, if there is an oracle informing the true sparsity structure, then the proposed estimator based on (2) would become that in ${\tilde{Q}}_n\left({\mathit{\theta }}_{\mathcal{A}}\right)$ by using this information. Theorem 2 demonstrates that the proposed estimator $\widehat{\mathit{\theta }}$ performs as well as the oracle estimator ${\mathit{\theta }}_{\mathcal{A}}^{*}$, and the estimation consistency of the oracle estimator has been established in Theorem 1.

3. Simulation

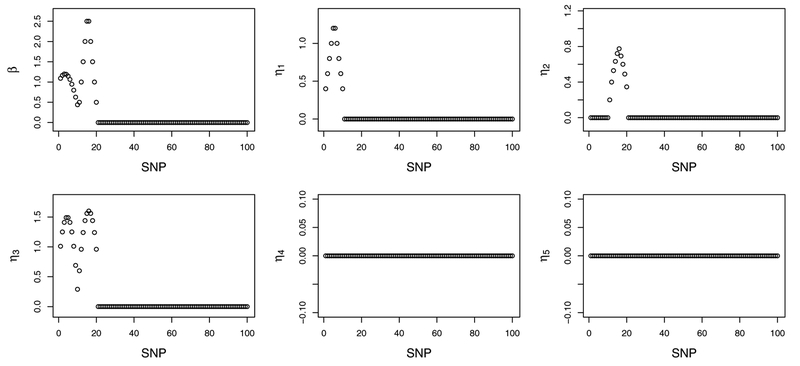
We simulate densely positioned SNP data with an adjacency structure. Specifically, (a) under all scenarios, q = 5 and p = 5; 000. Thus, there are a total of 5,005 main effects and 25,000 interactions. (b) Two approaches, A1 and A2, are adopted to simulate G factors which mimic SNP data coded with three categories (0, 1, 2) for genotypes (aa, Aa, AA). Approach A1 includes two steps, under which we first generate p continuous variables from a multivariate Normal distribution, and then dichotomize the continuous variables at the q₁ and q₂ percentiles to generate 3-level G measurements. In the first step, two correlation structures are considered with different parameters, referred to as AR(0.3), AR(0.5), Band1, and Band2, where AR and Band stand for auto-regressive and banded, respectively. In the second step, q₁ and q₂ are adjusted to generate G factors with different minor allele frequency (MAF) values, referred to as M1 and M2. Under A2, we simulate G factors with the pairwise LD structure. Two pairwise correlations 0.3 and 0.5 are considered, referred to as LD(0.3) and LD(0.5). For MAF, two scenarios similar to those in Step 2 of A1 are considered. We refer to Web Appendix B for details. (c) For E factors, we first generate five continuous variables from a multivariate Normal distribution with marginal mean 0, marginal variance 1, and correlation structure AR(0.3), and then dichotomize two of them at 0 to create two binary variables. There are thus three continuous and two binary E factors. (d) For E factors, their coefficients α_k’s are generated from Uniform (0.8, 1.2). There are 20 main G effects and 40 G-E interactions with nonzero coefficients. Two structures, the “main effects, interactions” hierarchial structure and smoothness structure of SNP effects, are satisfied. A graphical presentation is provided in Figure 1. Detailed values are provided in Web Appendix B. (e) Consider two types of response. The first is a continuous response under model (1). The second is a censored survival response under the AFT model, where the censoring times are generated from an exponential distribution with parameter adjusted to achieve ~ 20% censoring. The random error ε_i follows a standard Normal distribution. (f) Set n = 250 and n = 350 for the continuous and survival settings, respectively. There are a total of 24 scenarios, comprehensively covering a wide spectrum with different types of responses and correlation structures among G factors, and various levels of MAF.

Figure 1.

Simulation: true coefficient values for the main G effects and interactions. To improve presentation, only the first 100 effects are presented. The rest are zero.

We consider the proposed approach with the spline type penalty and the following alternatives. MA, which is a marginal analysis approach that analyzes one G factor along with all E factors and corresponding interactions at a time. P-values of the G factors and interactions are adjusted using the false discovery rate (FDR) approach. This approach has been commonly adopted in published studies. HierMCP, which is the non-structured counterpart of the proposed approach, where the MCP penalty is applied for estimation and selection. Comparing with this approach can reveal the value of incorporating the two structures. SMCP, which is based on model (1) and imposes the MCP and structured penalties on β_j and η_kj without respecting the “main effects, interactions” hierarchy. Comparing with this approach can reveal the value of the special consideration on interactions.

In identification evaluation, measures include the number of true positives and false positives for main effects (M:TP and M:FP) and interactions (I:TP and I:FP), respectively. Estimation performance is assessed using the root sum of squared errors (RSSE) defined as ${\Vert \widehat{\Theta }-{\Theta }^0\Vert }_2$, where $\widehat{\Theta }$ and ${\Theta }^0$ are the estimated and true values of $\Theta ={\left({\alpha }^{\prime },{\beta }^{\prime },{\eta }_1^{\prime },\cdots ,{\eta }_q^{\prime }\right)}^{\prime }$. We also take the underlying structure of SNPs into consideration and compute the root structured error (RSE) $\sqrt{{\left(\widehat{\Theta }-{\Theta }^0\right)}^{\prime }\tilde{J}\left(\widehat{\Theta }-{\Theta }^0\right)}$, where $\tilde{J}=\text{diag}\left(0_{q\times q},J,\cdots ,J\right)$. For evaluating prediction performance, an independent testing set with 100 subjects is generated. We adopt the prediction mean squared error (PMSE) for continuous outcomes and C-statistic (Cstat) for censored survival outcomes. C-statistic is the time-integrated area under the time-dependent ROC framework and measures the overall adequacy of risk prediction for censored survival data, with a larger value indicating better prediction (Uno et al., 2011).

Summary results over 500 replicates under the linear model with M1 and M2 are shown in Tables 1 and 2, respectively. The rest of the results are shown in Web Tables 3 and 4. Across all simulation scenarios, the proposed approach is observed to have superior or similar performance compared to the alternatives. Specifically, it can more accurately identify both the true main effects and interactions while having a small number of false positives. For example in Table 1 with AR(0.3), the proposed approach has (M:TP,M:FP,I:TP,I:FP)=(19.7,0.0,33.8,4.1), compared to (0.1,11.2,2.2,77.9) for MA, (11.7,68.5,3.4,4.2) for HierMCP, and (17.4,2.7,23.4,19.7) for SMCP. Compared to MA and HierMCP, the proposed approach has much better identification performance, which provides a strong support to the structured analysis strategy. It also outperforms SMCP, which suggests the effectiveness of the proposed decomposition strategy for respecting the interaction hierarchy. The advantage of the proposed approach gets more prominent under MAF setting M2. For example in Table 2 with Band1, the proposed approach has (M:TP,M:FP,I:TP,I:FP)=(19.7,1.0,33.3,5.1), compared to (0.1,6.7,1.6,53.6) for MA, (11.7, 64.7,3.9,5.2) for HierMCP, and (16.1,7.0,11.3,74.1) for SMCP. We also observe the superiority of the proposed approach in estimation. For example in Table 1 with LD(0.5), the proposed approach has RSSE=2.95, compared to 16.15 (MA), 17.76 (HierMCP), and 4.93 (SMCP). It also has smaller structured errors. In addition, the proposed approach has satisfactory prediction performance. For example in Table 2 with Band2, the PMSEs are 29.94 (MA), 23.04 (HierMCP), 4.18 (SMCP), and 1.59 (proposed). The observed patterns for data with survival outcomes (Web Tables 3 and 4) are similar.

Table 1.

Simulation results under the linear model with MAF setting M1. In each cell, mean (sd) based on 500 replicates.

	M:TP	M:FP	I:TP	I:FP	RSSE	RSE	PMSE
AR(0.3)
MA	0.1(0.5)	11.2(15.9)	2.2(2.2)	77.9(79.0)	15.03(5.07)	30.32(17.12)	28.36(8.80)
HierMCP	11.7(1.7)	68.5(11.4)	3.4(1.6)	4.2(2.0)	13.29(1.04)	26.48(2.53)	20.45(4.49)
SMCP	17.4(4.1)	2.7(5.2)	23.4(4.8)	19.7(14.3)	5.35(0.94)	2.65(0.67)	2.05(0.39)
Proposed	19.7(0.7)	0.0(0.1)	33.8(3.3)	4.1(2.5)	3.09(0.82)	2.32(0.66)	1.47(0.31)
AR(0.5)
MA	0.4(1.0)	15.0(18.0)	4.8(3.7)	106.9(79.7)	20.15(8.82)	44.63(27.13)	40.81(16.31)
HierMCP	12.5(1.5)	78.1(13.7)	4.1(1.8)	5.3(2.5)	14.54(1.30)	30.51(3.10)	25.42(6.31)
SMCP	19.0(1.4)	3.0(5.2)	23.6(4.7)	20.4(16.5)	5.15(0.88)	2.71(0.67)	2.28(0.70)
Proposed	19.7(0.6)	0.0(0.3)	34.8(2.8)	3.1(2.0)	2.67(0.75)	2.39(0.69)	1.47(0.37)
Band1
MA	0.2(0.8)	10.4(17.0)	1.9(2.3)	75.7(81.1)	13.42(3.38)	24.02(13.53)	24.63(6.17)
HierMCP	11.6(1.6)	70.3(10.5)	3.0(1.8)	4.0(2.0)	13.36(0.97)	26.30(2.41)	20.91(4.06)
SMCP	17.7(3.1)	3.5(5.8)	22.0(4.2)	20.8(15.3)	5.48(0.92)	2.71(0.60)	2.19(0.55)
Proposed	19.6(0.8)	0.0(0.4)	33.4(3.5)	4.3(2.9)	3.24(0.99)	2.40(0.72)	1.55(0.40)
Band2
MA	0.2(0.5)	9.2(14.6)	3.1(3.1)	79.2(80.3)	15.09(4.99)	29.89(17.11)	34.68(10.47)
HierMCP	12.4(1.7)	76.1(14.2)	3.9(1.9)	5.4(2.9)	14.22(1.39)	29.54(3.48)	24.11(6.01)
SMCP	18.8(1.7)	2.2(3.8)	24.4(4.8)	18.8(14.1)	4.93(1.00)	2.72(0.60)	2.17(0.53)
Proposed	19.6(0.6)	0.0(0.0)	34.2(3.6)	3.4(2.2)	2.74(0.92)	2.40(0.77)	1.49(0.41)
LD(0.3)
MA	0.2(0.7)	8.5(13.8)	3.0(2.8)	70.6(75.7)	14.40(4.10)	27.57(13.99)	27.24(7.68)
HierMCP	11.9(1.7)	93.7(10.8)	1.6(1.2)	1.6(1.3)	15.52(1.15)	32.24(2.91)	25.96(5.44)
SMCP	17.3(4.1)	3.0(4.7)	22.9(4.7)	15.4(12.1)	5.42(0.97)	2.68(0.59)	2.23(0.65)
Proposed	19.3(1.0)	0.0(0.1)	33.2(3.8)	3.5(2.6)	3.10(0.98)	2.44(0.73)	1.60(0.44)
LD(0.5)
MA	0.4(1.1)	9.5(16.3)	5.0(3.9)	77.8(73.9)	16.15(5.37)	34.21(16.84)	33.86(10.10)
HierMCP	12.3(1.6)	109.5(14.8)	1.6(1.1)	2.1(1.4)	17.76(1.62)	38.96(4.07)	35.11(9.11)
SMCP	18.6(2.3)	2.4(3.6)	25.3(4.9)	15.7(14.0)	4.93(1.16)	2.61(0.59)	2.20(0.62)
Proposed	19.2(1.1)	0.1(0.4)	33.7(3.8)	2.7(2.6)	2.95(1.10)	2.60(0.89)	1.60(0.50)

Table 2.

Simulation results under the linear model with MAF setting M2. In each cell, mean (sd) based on 500 replicates.

	M:TP	M:FP	I:TP	LFP	RSSE	RSE	PMSE
AR(0.3)
MA	0.1(0.5)	7.1(14.4)	2.0(2.1)	53.9(70.5)	11.20(1.62)	17.58(8.90)	23.30(5.04)
HierMCP	11.9(1.7)	64.4(11.0)	4.2(2.1)	5.7(2.3)	13.09(1.00)	26.28(2.37)	19.38(4.95)
SMCP	16.5(3.3)	6.5(9.9)	12.3(8.3)	68.7(25.9)	7.06(1.51)	3.56(1.05)	5.53(3.43)
Proposed	19.7(0.6)	0.0(0.1)	34.2(3.3)	4.0(2.2)	3.04(0.86)	2.26(0.53)	1.45(0.29)
AR(0.5)
MA	0.3(0.9)	10.3(15.7)	4.0(3.6)	80.0(79.4)	14.89(4.30)	30.05(15.14)	36.06(12.01)
HierMCP	12.5(1.4)	70.2(14.1)	5.0(2.4)	7.3(3.5)	14.02(1.58)	29.43(3.89)	23.00(6.29)
SMCP	17.7(3.1)	4.9(8.1)	17.8(5.9)	54.8(26.8)	6.10(1.12)	3.06(0.83)	4.09(3.23)
Proposed	19.7(0.6)	0.4(2.8)	34.7(2.9)	3.5(2.5)	2.72(0.77)	2.45(0.78)	1.50(0.40)
Band1
MA	0.1(0.8)	6.7(13.3)	1.6(2.1)	53.6(69.2)	10.56(1.14)	14.71(8.46)	22.79(4.91)
HierMCP	11.7(1.5)	64.7(10.1)	3.9(2.2)	5.2(2.7)	13.12(0.96)	25.96(2.44)	19.76(4.25)
SMCP	16.1(3.4)	7.0(10.8)	11.3(7.7)	74.1(23.7)	7.19(1.35)	3.59(0.92)	5.95(3.14)
Proposed	19.7(0.8)	1.0(4.3)	33.3(3.5)	5.1(4.7)	3.24(1.02)	2.51(0.83)	1.58(0.45)
Band2
MA	0.1(0.5)	6.2(13.2)	2.6(2.8)	55.1(70.7)	11.86(2.08)	19.93(10.16)	29.94(7.08)
HierMCP	12.6(1.6)	69.6(17.0)	4.9(2.4)	6.8(2.9)	13.84(1.62)	28.73(3.97)	23.04(6.61)
SMCP	16.9(3.8)	5.2(8.8)	17.8(7.2)	59.3(24.8)	6.18(1.22)	3.09(0.83)	4.18(2.65)
Proposed	19.6(0.7)	1.2(5.7)	33.8(3.6)	4.1(4.0)	2.82(1.02)	2.55(0.92)	1.59(0.57)
LD(0.3)
MA	0.2(0.7)	4.6(11.2)	2.8(2.6)	47.5(65.5)	11.05(1.25)	16.55(7.35)	23.79(5.17)
HierMCP	12.1(1.6)	88.9(10.4)	2.5(1.6)	3.0(1.8)	15.30(1.12)	31.97(2.85)	24.85(5.77)
SMCP	16.1(3.8)	6.7(9.6)	12.0(8.2)	66.5(22.1)	7.13(1.47)	3.58(0.94)	5.85(3.46)
Proposed	19.4(1.0)	0.5(2.0)	33.4(3.8)	3.8(3.4)	3.08(1.02)	2.46(0.72)	1.60(0.45)
LD(0.5)
MA	0.3(1.1)	5.7(14.4)	4.3(3.7)	52.3(69.0)	11.90(1.65)	21.94(7.37)	29.12(6.25)
HierMCP	12.4(1.5)	102.3(16.4)	2.6(1.6)	3.8(1.9)	17.31(1.88)	38.02(4.71)	33.36(9.40)
SMCP	17.0(4.2)	4.8(7.6)	19.1(6.7)	53.2(24.5)	6.03(1.39)	2.97(0.78)	4.11(2.95)
Proposed	19.2(1.2)	0.9(4.5)	33.5(3.8)	3.2(3.8)	3.02(1.16)	2.70(1.01)	1.66(0.60)

For the linear model with MAF setting M1, we simulate three additional scenarios with highly correlated predictors and provide the summary results in Web Table 5. Compared to those in Table 1, the three alternatives identify more true positives but also more false positives. The proposed approach still has favorable performance. For SNP data, we have also examined a few other simulation scenarios, and the observed patterns are similar (details omitted). We have also experimented with continuously distributed G measurements, which mimic gene expression data, and applied the Laplacian type penalty function. Similar superiority of the proposed approach is observed (details omitted).

4. Data analysis

4.1. GENEVA diabetes data (NHS/HPFS)

The Gene Environment Association Studies (GENEVA) consortium is part of the Genes, Environment and Health Initiative (GEI) organized by the NIH. We analyze the GENEVA Type 2 Diabetes data, where the goal is to identify genetic factors that are associated with type 2 diabetes phenotypes, biomarkers, and others. In our analysis, data are downloaded from dbGaP (accession number phs000091.v2.p1). The response variable of interest is body mass index (BMI), which is continuously distributed. BMI level is one of the most important risk factors for type 2 diabetes. Following recent published studies, we take a “loose” definition of E factors. Specifically, E factors considered include age, family history of diabetes among first degree relatives (famdb), total physical activity (act), trans fat intake (trans), cereal fiber intake (ceraf), and heme iron intake (heme), all of which have been suggested to be potentially associated with BMI and diabetes. For G factors, we analyze SNPs on chromosome 4, which plays an important role in many disorders, such as Parkinson’s disease, Huntington’s disease, and others. Preprocessing similar to that in Wu et al. (2014) is conducted, which includes matching subjects, removing SNPs with MAF< 0.05 or deviation from the Hardy-Weinberg equilibrium, and imputing missing data using fastPHASE. Data are available on 2,558 subjects and 40,568 SNPs. As the number of relevant SNPs is not expected to be large, to improve stability, we conduct a marginal screening as follows. First, a p-value is computed for each SNP based on a marginal linear model. With the physical adjacency structure in mind, we select a region as opposed to individual SNPs. Specifically, for each region with 10,000 consecutive SNPs whose physical locations are adjacent to each other, the sum of the p-values is computed. The region including 10,000 consecutive SNPs with the smallest sum is selected for downstream analysis.

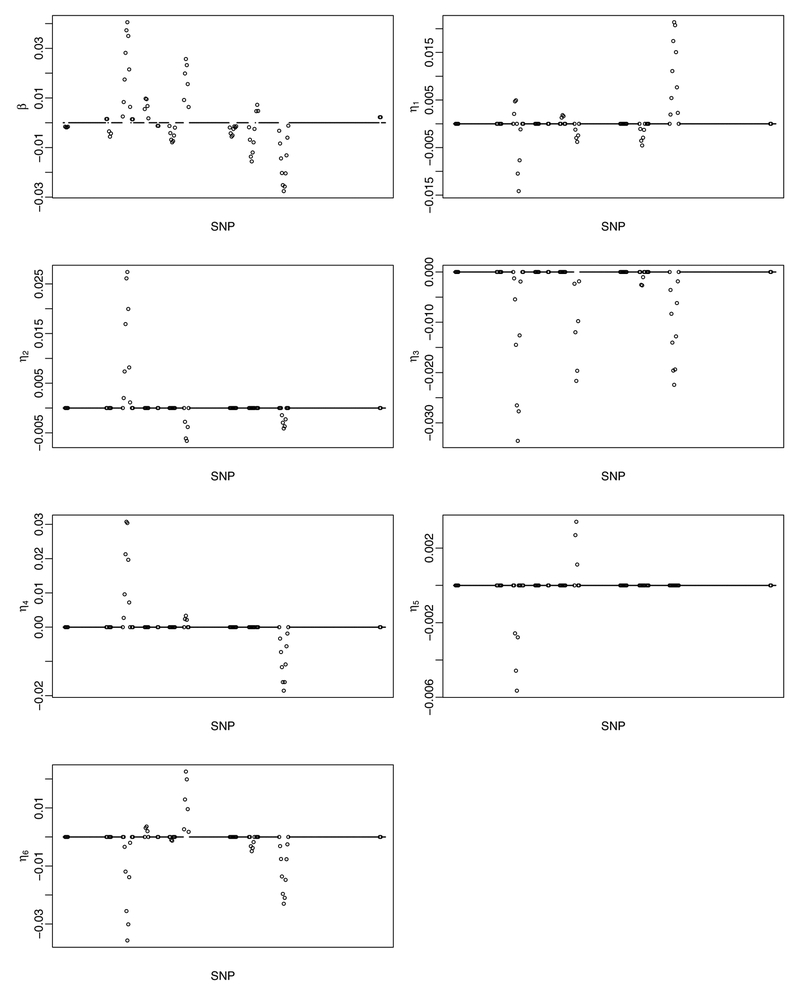
We adopt the linear regression model and spline type penalty. The proposed approach identifies 71 main SNP effects and 128 G-E interactions. The detailed estimation results are provided in Web Table 6 and also presented in Figure 2, where SNPs are sorted according to their physical locations on the chromosome. In terms of main effects, three E factors, age, act, and ceraf, have negative coefficients, and the other three, famdb, trans, and heme, have positive coefficients, which are consistent with findings in the literature. Figure 2 shows that the estimated effects demonstrate a certain degree of smoothness, which fits the design of the proposed approach. Genes that the identified SNPs belong to or are the closest to are also provided in Web Table 6. Literature search suggests that these genes and interactions may have important implications, which may provide support to the validity of the proposed approach. Discussions on biological functionalities are provided in Web Appendix B.

Figure 2.

Analysis of the GENEVA diabetes data (NHS/HPFS) using the proposed approach: identified main G effects and interactions.

Beyond the proposed approach, we also conduct analysis using the alternatives. Detailed estimation results are provided in Web Appendix B. In Table 3, we provide the numbers of main G effects and interactions identified by different approaches and their overlaps as well as the RV coefficients. The RV coefficient measures the degree of overlapping information in two data matrices, with a larger value indicating a higher degree of similarity. It is observed that the proposed approach identifies different main G effects and more significantly different interactions from those with the alternatives. Without reinforcing the interaction hierarchical structure, SMCP identifies the smallest number of main effects but the second largest number of interactions. Both the proposed approach and HierMCP identify a moderate number of main effects and interactions. Measured using the RV coefficients, different sets of identified main effects have relatively high levels of overlapping information, while those of interactions have moderate overlapping information. We also examine the biological similarity of the identified genes based on the Gene Ontology (GO) analysis. Moderate similarity is observed. We refer to Web Appendix B and Web Figure 3 for details.

Table 3.

Data analysis: numbers of main G effects and interactions (diagonal elements) identified by different approaches and their overlaps and RV coefficients (off-diagonal elements).

GENEVA	Main G effects				Interactions
	MA	HierMCP	SMCP	Proposed	MA	HierMCP	SMCP	Proposed
MA	51	10 (0.794)	33 (0.874)	32 (0.851)	57	0 (0.364)	31 (0.514)	0 (0.295)
HierMCP		67	8 (0.786)	6 (0.805)		158	0 (0.615)	5 (0.638)
SMCP			41	30 (0.850)			156	0 (0.527)
Proposed				71				128
SKCM	Main G effects				Interactions
	MA	HierMCP	SMCP	Proposed	MA	HierMCP	SMCP	Proposed
MA	27	3 (0.810)	0 (0.781)	0 (0.792)	21	0 (0.292)	0 (0.274)	0 (0.276)
HierMCP		130	1 (0.815)	1 (0.831)		78	0 (0.442)	0 (0.477)
SMCP			39	15 (0.836)			34	5 (0.477)
Proposed				50				44

With real data, it is difficult to objectively evaluate identification accuracy. To provide support to the identification results, we examine prediction performance and selection stability using a resampling-based approach. Specifically, subjects are randomly split into a training and a testing set. We then estimate parameters using the training set and make prediction for the testing set subjects. With 500 resamplings, we compute the mean PMSEs, which are 15.38 (MA), 17.47 (HierMCP), 13.11 (SMCP), and 13.06 (proposed). The proposed approach has prediction performance comparable to SMCP and better than MA and HierMCP. We further compute the observed occurrence index (OOI) to measure selection stability. It is the probability of a specific main effect or interaction identified in the 500 resamplings. The mean OOI values for the identified main G effects and interactions using the proposed approach is 0.69, compared to 0.47 (MA), 0.39 (HierMCP), and 0.21 (SMCP). The proposed approach has prominent superiority in selection stability.

4.2. TCGA skin cutaneous melanoma data

We consider The Cancer Genome Atlas (TCGA) skin cutaneous melanoma (SKCM) data. TCGA is a collective effort organized by NIH and has published high quality clinical, environmental, and genetic data. We focus on the processed level 3 data, which are downloaded from TCGA Provisional using the R package cgdsr. As in several recent studies, we analyze the (censored) overall survival. The analyzed E factors include age, AJCC nodes pathologic stage (PN), gender, Breslow’s depth, and Clark level, all of which have been extensively studied in the literature. For G factors, we consider the mRNA gene expressions. In TCGA, gene expression measurements are the z-scores, which have been lowess-normalized, log-transformed, and median-centered, and quantify the relative expressions of tumor samples with respect to normals. Data are available on 298 subjects and 18,934 gene expressions. Among the subjects, 152 died during followup. Marginal screening is also conducted, and the 10,000 genes with the smallest p-values are selected for downstream analysis. Here, the distances between genes are not as easy to quantify as for SNPs, and some genes can be far away from each other. As such, the physical location-based region screening in Section 4.1 may not be appropriate. If one wants to accommodate network-based distance, subnetwork detection methods may be needed, which have been demonstrated to be quite complicated and warrant a separate investigation. To avoid excessive complexity, and noting that prescreening is not essential for the proposed analysis, we conduct screening based on p-values directly and select individual genes.

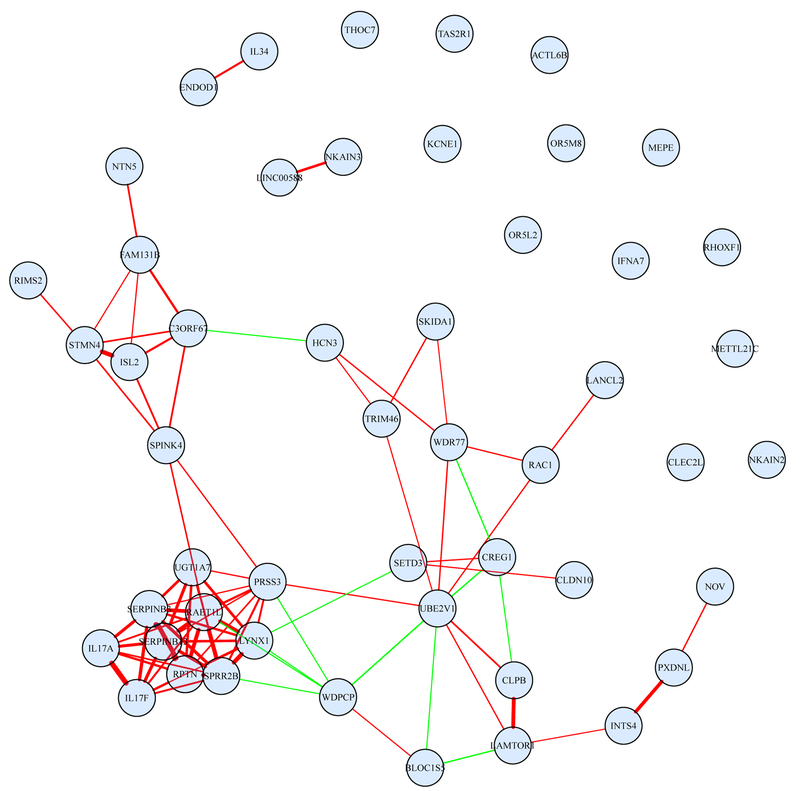
With a censored survival outcome, we adopt the AFT model. Examining the estimation procedure described in Web Appendix A suggests that the proposed computational algorithm can be directly applied. With gene expression measurements, we adopt the Laplacian type penalty. The proposed analysis identifies 50 main G effects and 44 interactions. The detailed estimation results are provided in Web Table 7. All five E factors except for gender have negative coefficients, which match observations in the literature. The identified genes are also presented in Figure 3, where two genes are connected if they have a nonzero adjacency value. For the identified genes, published studies provide independent evidences of their associations with cutaneous melanoma. We refer to Web Appendix B for relevant discussions.

Figure 3.

Analysis of the TCGA SKCM data using the proposed approach: identified main G effects. The edges between genes are defined based on the values of a_jl’s of the adjacency matrix A = (a_jl)_p×p. Positive and negative connections are represented with red and green, respectively. The thickness (strength) of an edge is proportional to |a_jl|. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

Analysis is further conducted using the three alternatives, and the summary comparison results are presented in Table 3. Detailed estimation results are provided in Web Appendix B. As for the previous dataset, the proposed approach identifies different sets of main effects and interactions, and the RV coefficients and GO analysis (Web Appendix B) suggest moderate similarity. We also evaluate prediction performance and selection stability. In prediction evaluation, the mean C-statistics are 0.54 (MA), 0.59 (HierMCP), 0.64 (SMCP), and 0.65 (Proposed). In addition, the average OOI of the proposed approach is 0.87, compared to 0.53 (MA), 0.55 (HierMCP), and 0.77 (SMCP). The proposed approach again has better prediction performance and stability.

5. Discussion

For G-E interaction analysis, in this article, we have developed a new approach which shares similar desirable properties as the existing ones but also advances from them by accommodating the underlying structures of G factors. Although structured analysis has been conducted for main G effects in some recent publications, this study is among the first to conduct structured analysis in the context of G-E interaction analysis. Significant complexity is brought by the multiple effects (coefficients) that correspond to one G factor and the need to respect the “main effects, interactions” hierarchy. We note that in practical data analysis, gene-environment interaction patterns may be more complicated than can be described using the proposed model with hierarchy. For example, pure gene-environment interactions without corresponding main effects have also been suggested in a handful of studies, such as Aschard (2016), Zhou et al. (2019), and others. It has been discussed in Cordell (2009) that whether there are scenarios with interactions but not corresponding main effects is still open to debate and it is also unclear how often they are if they do exist. However, in terms of statistical modeling, statisticians have suggested that models violating the hierarchy may be not sensible, for example, for considering statistical power or postulating a special position for the origin (Bien et al., 2013). Following such studies (Bien et al., 2013; Liu et al., 2013; Wu et al., 2018), we have designed the approach to respect the interaction hierarchy. The proposed approach belongs to the well-established penalization paradigm and has an intuitive definition. Although it has multiple penalty terms, it is computationally much manageable. BIC has been adopted for tuning parameter selection. Besides BIC, cross validation is perhaps also viable. It has been demonstrated that each approach has its shortcomings and cannot perform universally better than the other (Breheny and Huang, 2011). In the interaction analysis conducted by Choi et al. (2010), it has been shown that cross validation performs better in prediction accuracy, whereas BIC outperforms cross validation in variable identification. In this study, it is not our goal to compare and draw conclusions on the relative performance of different tuning parameter selection approaches. We adopt BIC as it has satisfactory performance and lower computational cost. The proposed approach is proved to have the consistency properties, which have not been established for most alternatives and provide a uniquely strong ground for the proposed approach. Extensive numerical studies show the practical superiority. Overall, this study provides a practically useful new way for analyzing G-E interactions.

Although described using the linear regression model for a continuous response as an example, the proposed approach can be extended to other data settings/models. For gene expression data, we have adopted the data-dependent adjacency matrix. We acknowledge that the analysis results may be more dependent on analyzed data compared to those based on data-independent networks, for example, biological networks (protein-protein network, gene regulatory network, etc.). In addition, there may be other adjacency measures. In this study, our goal is to incorporate G factor structures, not compare different adjacency measures. We adopt the proposed one, as it has been a popular choice in the literature (Huang et al., 2011; Shi et al., 2015) and leads to satisfactory numerical performance. It is straightforward to couple with other adjacency measures. The proposed approach can accommodate multiple types of structures, as long as the J matrix satisfies certain mild conditions. We leave it to future research to study the definition and properties of J for other types of omics data. For high dimensional penalization studies, it has been demonstrated in Fan and Lv (2011) that when p > n, it is hard to establish the global optimality for a local solution. In addition, Breheny and Huang (2011) have demonstrated that in high-dimensional settings, global convexity is neither possible nor relevant, and providing that the objective function is convex in a local region that contains the sparse solution is sufficient to a certain extent. The framework of establishing consistency properties based on the local solution is common in published studies, such as Fan and Lv (2011) and Huang et al. (2017). We have studied the local convexity of the objective function on the coordinate subspaces in Web Appendix A. The global optimality can be even more challenging for interaction analysis and is deferred to future investigation.