Skip to main content
PMC home page
Cerebral Cortex (New York, NY) logoLink to Cerebral Cortex (New York, NY)
. 2019 May 2;30(1):215–225. doi: 10.1093/cercor/bhz082

Differential Contribution of Cortical Thickness, Surface Area, and Gyrification to Fluid and Crystallized Intelligence

Ehsan Tadayon 1, Alvaro Pascual-Leone 1, Emiliano Santarnecchi 1,✉
PMCID: PMC7029693  PMID: 31329833

Abstract

Human intelligence can be broadly subdivided into fluid (gf) and crystallized (gc) intelligence, each tapping into distinct cognitive abilities. Although neuroanatomical correlates of intelligence have been previously studied, differential contribution of cortical morphologies to gf and gc has not been fully delineated. Here, we tried to disentangle the contribution of cortical thickness, cortical surface area, and cortical gyrification to gf and gc in a large sample of healthy young subjects (n = 740, Human Connectome Project) with high-resolution MRIs, followed by replication in a separate data set with distinct cognitive measures indexing gf and gc. We found that while gyrification in distributed cortical regions had positive association with both gf and gc, surface area and thickness showed more regional associations. Specifically, higher performance in gf was associated with cortical expansion in regions related to working memory, attention, and visuo-spatial processing, while gc was associated with thinner cortex as well as higher cortical surface area in language-related networks. We discuss the results in a framework where “horizontal” cortical expansion enables higher resource allocation, computational capacity, and functional specificity relevant to gf and gc, while lower cortical thickness possibly reflects cortical pruning facilitating “vertical” intracolumnar efficiency in knowledge-based tasks relevant mostly to gc.

Keywords: cognitive capacity, cortical gyrification, cortical surface area, cortical thickness, human intelligence

Introduction

General intelligence (g) is frequently decomposed into fluid (gf) and crystallized (gc) components (Cattell 1963). While gf is associated with problem solving independent of previous knowledge, gc reflects acquired knowledge and general facts (Deary and Caryl 1997). Although they are correlated, they tap into distinct cognitive abilities and show different trajectory with aging, with gf generally declining with aging, while gc tending to increase with education and age (Horn and Cattell 1967; Manard et al. 2014). Abilities related to gf, such as working memory, attention, and mental manipulation, are generally thought to benefit from a higher number of processing units, allowing for a more flexible allocation of resources during hypothesis testing (Unsworth et al. 2014; Duncan et al. 2017). On the contrary, knowledge-based cognitive performance relies on life-long learning, which is associated with optimization of existing computational schemes, where increased efficiency might be as important as computational power (Wenger et al. 2017a).

Identifying the neuroanatomical correlates of human intelligence has a long history. The initial attempts to relate brain anatomical measurements with intelligence started in the 19th century by relating head size to intelligence (Pearson 1906). These studies found a modest correlation between head size and intelligence, accounting for about 4% of variance (Pietschnig et al. 2015). The advent of neuroimaging techniques made it possible to measure brain volume noninvasively and relate regional cortical gray matter volume to intelligence measures, leading to the formalization of the well-known parieto-frontal integration theory (Jung and Haier 2007). While such evidence has helped localizing pivotal regions supporting g in humans, the exact nature of the contribution provided by specific structural properties of the brain is still unclear. Previous investigations on the association of cortical morphologies and human intelligence have mainly focused on gray matter volume and cortical thickness and have found inconsistent results across studies (Choi et al. 2008; Karama et al. 2011, 2014; Schnack et al. 2015).

Recent studies have shown that cortical gray matter volume can be decomposed into cortical thickness and cortical surface area, which are more biologically plausible morphological measures of cortical architecture (Winkler et al. 2010). Cortical surface area and cortical thickness have distinct developmental trajectories and uncorrelated genetic backgrounds (Panizzon et al. 2009). Cortical thickness is associated with radial neuronal migration and the number of neurons, dendritic arborizations, and glial support in cortical columns. In contrast, cortical surface area is related to tangential neuronal migration and captures the number of mini-columnar units in the cortex (Chenn and Walsh 2003; Rakic 2009; Rakic et al. 2009). Parsing the effect of cortical thickness and surface area on cortical volume has also functional relevance. For instance, cortical surface area and cortical thickness in human early visual cortices have been shown to exert opposite influences on neural population tuning with behavioral consequence for perceptual discrimination (Song et al. 2015). Therefore, in exploring the neural substrate of gf and gc, assessing the contribution of surface area and thickness seems important.

Aside from thickness and surface area, cortical folding, or gyrification, has also been proposed as a candidate neuroanatomical correlate of intelligence. Comparative anatomical studies have shown positive correlation between overall cortical gyrification and cognitive abilities across species (Zilles et al. 2013). Only recently, the regional association between gyrification and intelligence has been carved out, showing higher gyrification in large portions of parietal and frontal regions in subjects with higher g score (Gregory et al. 2016).

Human Positron Emission Tomography (PET) and task-based functional magnetic resonance imaging (fMRI) studies have shown activation of lateral prefrontal as well as parietal regions while subjects perform intelligence tasks. More recently, advances in human resting-state fMRI studies have shown the importance of specific functional networks including the frontoparietal network (FPN), default mode network (DMN), and dorsal attention network (DAN) in explaining individual variability in human intelligence (Colom et al. 2010; Santarnecchi et al. 2017a). The extent to which structural correlates of intelligence correspond to functional correlates of intelligence could offer new insight into structure–function relationship in the neuroscience of human intelligence.

In this study, we tested the hypothesis that gf and gc load on distinct cortical morphologies with different patterns of regional associations. To test this hypothesis, we first used a large sample of young healthy subjects from the Human Connectome Project (HCP, n = 740) (Van Essen et al. 2013) with high-resolution structural T1-weighted MRIs and cognitive tests (identification phase). MRIs were analyzed using FreeSurfer pipeline (Fischl 2012), and a vertex-wise analysis followed by cluster-wise correction was pursued to identify the most significant clusters for each cortical morphology (cortical surface area, cortical thickness, and cortical gyrification). Afterwards, we showed that the structural correlates of intelligence follow the topography of resting-state human brain networks implicated in fluid and crystallized intelligence. Finally, we sought to replicate the findings of the identification phase in a separate data set (NKI-Rockland data set) (Nooner et al. 2012) with different cognitive tests in order to identify the most generalizable clusters linked to gf and gc.

Materials and Methods

Identification Data Set

A total of 740 subjects (age range, 21–35; right-handedness, >40) from the HCP who had 3T structural T1-weighted MRIs as well as neuropsychological data were included for this study.

Behavioral Measures

The standard test for measuring fluid intelligence is the Raven's Standard Progressive Matrices (RSPM), a 60-item multiple-choice test with increasingly difficult pattern-matching tasks. The test assesses abstract reasoning with little dependency on language abilities. In the HCP, gf was measured using an abbreviated version of RSPM called Penn Progressive Matrices (PMAT). PMAT consists of 9-item subset of RSPM, which predicts the original RSPM with great accuracy (Bilker et al. 2012). We used the number of correct responses in the PMAT test for this study (PMAT24_A_CR, ranging from 0 to 9). The PMAT24_A_CR test has also been previously used in functional imaging studies (Finn et al. 2015). Also, a composite gf score (CompGfScore) derived from National Institutes of Health (NIH) toolbox (including the Dimensional Change Card Sort Test, the Flanker Inhibitory Control and Attention Test, the Picture Sequence Memory Test, the List Sorting Working Memory Test, and the Pattern Comparison Processing Speed Test) was tested (Akshoomoff et al. 2013), which gave similar results to PMAT24_A_CR. Here, we only report results for PMAT24_A_CR, which is considered a more direct measure of gf task.

Gc was measured using the NIH toolbox composite scores (Crystallized Cognition Composite), which combines Picture Vocabulary Test and Oral Reading Recognition Test into one score (CompGcScore) (Akshoomoff et al. 2013). The Oral Reading Recognition Test consists of reading and pronouncing either English or Spanish words as accurately as possible. The Picture Vocabulary Test measures receptive vocabulary using a computerized test by asking the subject to identify the correct picture for the audio recording of a word (for detailed description of the HCP behavioral measures, see https://wiki.humanconnectome.org).

MRI Data Acquisition

Structural T1-MRIs in HCP were acquired using a dedicated customized 3-T Connectome Skyra scanner with the following parameters: MPRAGE sequence, TR = 2400 ms, TE = 2.14 ms, and TI = 1000 ms; flip angle = 8 degrees; FOV = 224 × 224 mm; and voxel size = 0.7 mm isotropic.

Image Processing and Statistical Analyses

Structural T1-weighted MRIs were processed with FreeSurfer v6.0 software package to create three-dimensional representations of cortical surface. FreeSurfer pipeline includes automated Talairach transformation, segmentation of subcortical white matter and deep gray matter structures based on intensity and neighbor constraints, intensity normalization, tessellation of gray matter–white matter boundary and gray matter–cerebrospinal fluid boundary, automated topology correction, and reconstruction of cortical surface meshes (Dale et al. 1999). Afterwards, reconstructed white matter surfaces were registered to FreeSurfer template (fsaverage) based on cortical folding patterns using spherical registration implemented in FreeSurfer (mri_surf2surf). Cortical morphologies were then smoothed using a 10 mm full-width-at-half-maximum Gaussian kernel for thickness and surface area and 5 mm for gyrification. Cortical thickness was calculated at each point (vertex) in the cortex by measuring the distance between white and pial surfaces. The vertex-wise cortical surface area was calculated by averaging the area of all faces that meet at a given vertex on the white matter surface. The vertex-wise cortical gyrification was measured by calculating the gyrification index in circular three-dimensional regions of interest (Gregory et al. 2016). This method uses an outer smooth surface tightly wrapping the pial surface and computes the ratio between areas of circular regions on the outer surface and their corresponding circular patches on the pial surface. To make sure that our results are replicable using a different version of FreeSurfer, we also used FreeSurfer processed files provided by the HCP (db.humanconnectome.org) using FreeSurfer v5.3-HCP. In HCP, both T1-weighted and T2-weighted MRIs were used for cortical surface reconstruction. T2-weighted MRIs are mainly used to refine pial surface reconstruction.

In order to find the regional association of cortical morphologies with intelligence measures, a vertex-wise analysis followed by cluster-wise correction was pursued in the identification data set. We devised a method that enables better delineation of most significant vertices in cluster-wise correction and enables more stable cluster visualizations across different cortical morphologies (cortical thickness, surface area, and gyrification). We first split the data into 10-folds (each fold, 740/10, 74 subjects). While holding 1-fold out, we fit a linear regression model to all the remaining folds (9-folds, 666 subjects) at each vertex to test the association between vertex cortical morphometric and gc/gf, controlling for the effects of age, sex, and total brain volume (TBV). The results were then cluster-wise corrected (vertex-wise threshold, 0.01; cluster-wise P value, 0.05). We repeated this step 10 times, each time holding 1-fold out. We then concatenated all the resultant clusters across all iterations. The final map has values between 0 and 10 at each vertex, with 0 indicating that the vertex has not been selected in any of the iterations and 10 indicating that the vertex has been present in all the tested iterations. To show the usefulness of our approach, we also applied vertex-wise thresholding followed by cluster-wise correction on the whole sample (n = 740) and compared the final clusters. To make sure that our findings are not due to chosen vertex-wise threshold, we also performed our analyses using vertex-wise P value of 0.001. The clusters obtained from applying both thresholds are provided as supplementary materials.

Although the effect size is considered small, TBV has been one of the most reliable and consistent predictor of intelligence. Given that it is a matter of controversy whether TBV should be included as a cofactor or not, we ran a follow-up analysis without controlling for TBV. Finally, performance in gc task is correlated with education level by the nature of the tasks, but education is not expected to affect gf. We first checked whether there is an association between education and gf (PMAT) and ran the analyses only on subjects who had at least 13 years of education. Finally, as both gf and gc are correlated with each other, we performed the analyses for gf controlling for gc and vice versa to find the most specific clusters associated with gf and gc.

Overlap with Resting-State fMRI Networks

We tested the overlap between putative resting-state fMRI human networks and regional cortical morphology associated with gf and gc. We used 7 resting-state human networks previously derived from group-level analysis of 1000 subjects (Yeo et al. 2011). Dice coefficient (DC) was used to measure the overlap, defined as:

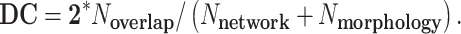graphic file with name M1.gif

N network is the number of vertices in the tested network, Nmorphology is the number of significant vertices in the tested cortical morphology, and Noverlap is the number of vertices in common between the tested network and cortical morphology.

Replication Data Set

To test the generalizability of the structural correlates, we tried to replicate the HCP clusters in the INDI data set, which offer distinct neuroimaging and behavioral measurements. High-quality structural T1-weighted MRIs (3T) for 253 subjects (age range, 21–45) were acquired using a 3-T Siemens MAGNETOM TrioTim with the following parameters: MPRAGE sequence, TR = 1900 ms, TE = 2.52 ms, and TI = 900 ms; flip angle = 9 degrees; FOV = 250 × 250 mm; voxel size = 1 mm isotropic.

Structural T1-MRIs were processed similar to HCP data. gf and gc were measured using the Wechsler Abbreviated Scale of Intelligence, a cognitive battery composed by 4 subtests: vocabulary, similarities, block design, and matrix reasoning. Vocabulary and similarities are combined to index gc, while block design and matrix reasoning are combined to form gf. Similar to identification phase, we first ran a vertex-wise analysis controlling for the effect of age, sex, and TBV. Afterwards, clusters present in at least 7 iterations (arbitrary threshold) from identification phase were tested separately for their corresponding cognitive measures, while controlling for the effects of age, sex, and TBV.

Results

Global Neuroanatomical Correlates of Intelligence

The total cortical surface area and average gyrification showed positive correlations with gf and gc, while average cortical thickness was not correlated with gf or gc (Fig. 1). Given that global neuroanatomical measures might obscure the underlying associations, further testing of regional association of each cortical morphology with gf and gc was conducted.

Figure 1.

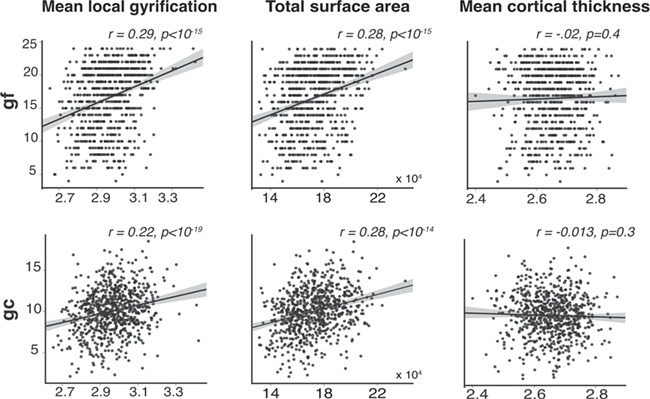
Figure 1

Open in a new tab

Global neuroanatomical correlates of gf and gc. Total surface area and mean gyrification are positively correlated with gf and gc. In contrast, mean cortical thickness showed no statistically significant association with gf or gc.

Structural Correlates of Gf and Gc

Figure 2 shows regional morphological associations with gf and gc. Cortical surface area in left and right superior parietal, left supramarginal, left caudal middle frontal, left pars-opercularis, left inferior temporal, right inferior and middle temporal, right medial orbitofrontal, and right rostral middle frontal were all positively correlated with gf. Cortical gyrification in large portions of left and right frontal, left and right inferior parietal, supramarginal, superior parietal, and superior temporal were positively correlated with gf. Cortical thickness did not show any regional association with gf. Supplementary Figure S1 shows the results for the gf-associated cortical morphologies controlled for gc.

Figure 2.

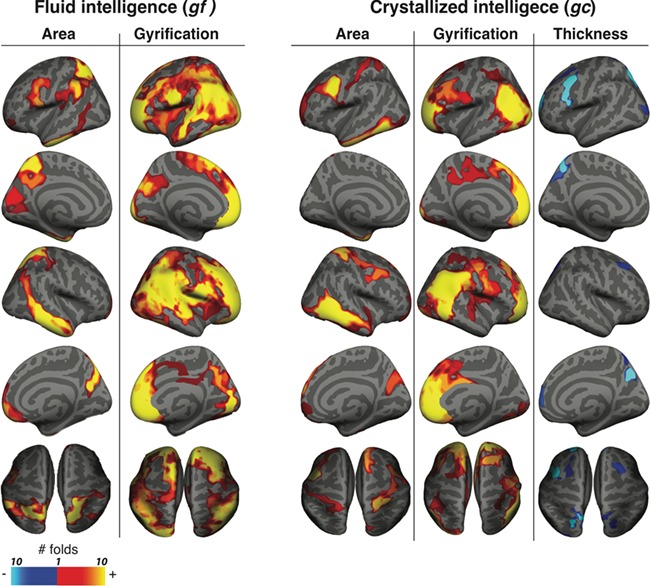
Figure 2

Open in a new tab

Regional morphological correlates of gf and gc. Vertex-wise structural correlates of gf and gc for cortical surface area, gyrification, and thickness. The subjects were divided into 10-folds. Vertex-wise analysis followed by cluster-wise correction was applied to combined subjects from 9-folds, while holding 1-fold out. The procedure was repeated 10 times. The resulting clusters were combined across all the iterations. The color shows the number of iterations that the vertex was within a statistically significant cluster (minimum, 0; maximum, 10). The red-yellow vertices show positive correlation; blue-cyan vertices show negative correlation.

Cortical thickness in left caudal middle frontal, left pars-opercularis, left rostral middle frontal, left superior parietal, and right precuneus were all negatively correlated with gc. Cortical surface area in left and right caudal middle frontal, left inferior temporal, right middle temporal and right postcentral, and right superior frontal were all positively correlated with gc. Cortical gyrification in large portions of left and right frontal, left and right inferior parietal, and right supramarginal were positively correlated with gc. Supplementary Figure S1 shows the results for the gc-associated cortical morphologies controlled for gf.

Excluding TBV as a cofactor in the model did not influence the association between gf/gc and cortical thickness, while the association between gf/gc and cortical surface area and gyrification became statistically more significant with larger clusters (Supplementary Fig. S2).

We found a positive correlation between gf score indexed by PMAT24_A_CR and years of education (Supplementary Fig. S3). We ran the analyses only on subjects who had at least 13 years of education, to minimize the possible confounding effect of education level. The resulting clusters were similar to our original findings (Supplementary Fig. S4).

Clusters obtained from applying vertex-wise thresholding and cluster-wise correction to the whole data set (n = 740) were similar to identical to clusters obtained from splitting the data into 10-folds (Supplementary Fig. S5). However, by splitting the data, we were able to also map the most important vertices within the clusters, providing final weighted cluster maps (Supplementary Fig. S6).

We also performed the analyses using a more stringent vertex-wise threshold of 0.001, with essentially similar results. We have provided the final clusters from applying both vertex-wise thresholds (P = 0.01 and P = 0.001) and the corresponding cluster-wise P value in a supplementary excel file. As a final sanity check, we redid the entire analyses using cortical surfaces reconstructions provided by the HCP and found similar to identical results (Supplementary Fig. S7).

Overlap with Resting-State fMRI Networks

We measured the overlap between resting-state fMRI networks and the regional cortical morphology associations of gf and gc (Fig. 3). Gf-related areas had the largest overlap with the DAN (DC = 0.31) in the left hemisphere and the DMN (DC = 0.34) in the right hemisphere. Gc-related areas had the largest overlap with the limbic (DC = 0.30) in the left hemisphere and the DMN (DC = 0.32) in the right hemisphere. Gc-related thickness had the largest overlap with the FPN (DC = 0.19) in the left hemisphere and the DAN in the right hemisphere (DC = 0.17).

Figure 3.

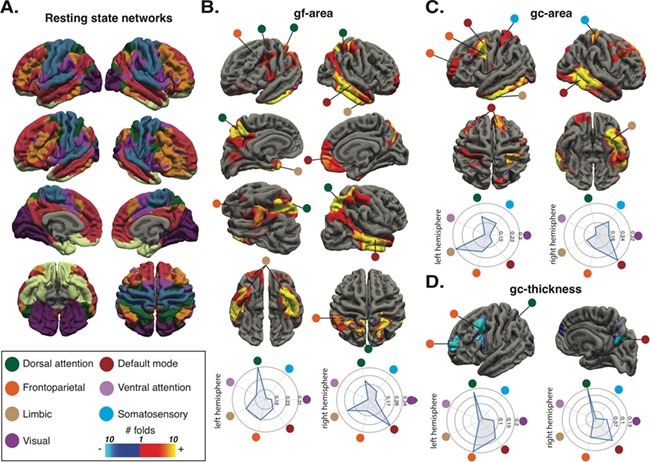
Figure 3

Open in a new tab

Correspondence between structural correlates of intelligence and functional resting-state human networks. Group-average (N = 1000) resting-state human networks by Yeo et al. (2011) (A). gf-cortical surface area associations (B), gc-cortical surface area (C), and gc-cortical thickness associations (D). The radar graphs show the DC for each network. The circles show the correspondent network.

Replication in INDI

Vertex-wise analyses for surface area, thickness, and gyrification were performed for gf and gc in INDI data set. Afterwards, significant clusters from identification phase (HCP) were separately tested in INDI data set for their corresponding cognitive measures. Similar to the identification phase, gf showed strong positive association with surface area in superior parietal, inferior temporal, and inferior frontal gyrus; positive association with gyrification in distributed regions of the cortical ribbon; no association with cortical thickness. Almost all tested clusters from the identification phase had statistically significant association with gf in INDI (Fig. 4A). Unlike gf, gc showed less striking association with cortical morphologies, and few clusters from the identification phase showed statistically significant association with gc (Fig. 4B).

Figure 4.

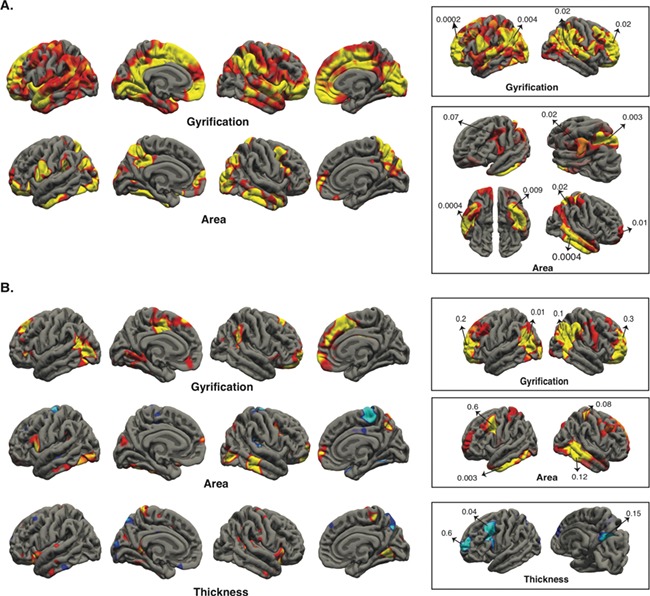
Figure 4

Open in a new tab

Replication of gf and gc clusters in INDI data set. Vertex-wise analysis (P ≤ 0.05) followed by testing the most significant clusters of identification phase in INDI for gf (A) and gc (B). The boxes show the tested HCP clusters in INDI, and the numbers are P values.

Discussion

In this study, we tried to parse the link between different cortical morphologies and individual variability in gf and gc in a large data set of young healthy individuals, with replication in a separate data set using different behavioral measures. We found that while cortical gyrification in distributed regions of parietal, temporal, and frontal lobes displayed a positive correlation with gf and gc, cortical surface area and thickness showed more specific associations, which corresponded with meaningful cortical regions and resting-state fMRI networks. Specifically, gf showed positive association with cortical surface area and no association with cortical thickness. On the other hand, better performance in gc was associated with overall decreased cortical thickness as well as higher cortical surface area. Finally, higher surface area in left inferior temporal and right middle temporal gyri showed positive correlations with both gf and gc, suggesting possible shared structures contributing to both gf and gc.

Computational Power versus Optimized Processing

Gf measures the ability to solve novel problems, which relies on generating, testing, and refuting multiple hypotheses to find the optimal solution to a given task (Fig. 5A). Cognitive factors underlying gf have been matters of study for decades. Importantly, performance in gf is highly correlated with working memory, suggesting that working memory capacity might be an important determinant of gf performance. The link between working memory performance and gf has been attributed to attention control, capacity to maintain goals, subgoals and hypotheses, and long-term memory (Unsworth et al. 2014). Moreover, functional imaging studies have shown that working memory, attention, and gf engage similar networks, suggesting possible shared neural correlates (Gray et al. 2003; Santarnecchi et al. 2017a). In this study, we found that better performance in gf was associated with cortical expansion in brain regions previously attributed to gf, working memory, attention as well as visuo-spatial processing in structural and functional imaging (Gray et al. 2003; Colom et al. 2007; Kravitz et al. 2011, 2011; Petersen and Posner 2012; Constantinidis and Klingberg 2016), cortical morphologies (Deary et al. 2010), and lesion studies (Woolgar et al. 2010; Barbey et al. 2014).

Figure 5.

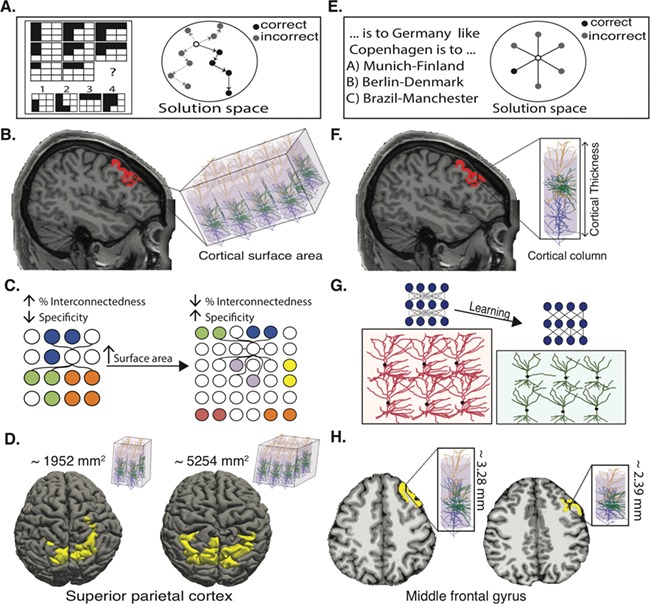
Figure 5

Open in a new tab

Contribution of cortical thickness and surface area to gf and gc. Schematic example of a gf task, which requires navigating the solution space to find the correct answer (A). Cortical surface area is associated with the number of cortical columns (B). Higher cortical surface area can potentially lead to increased capacity by increasing the number of cortical columns (information processing units) as well as to increased functional specificity of cortical columns by reducing fraction of intercolumnar interconnections (C). Cortical surface area in superior parietal cluster morphed back into pial surface for two representative subjects (D). Schematic example of a gc task, which relies on accessing stored knowledge (E). Cortical thickness is associated with thickness of cortical columns determined by dendritic arborizations and glial support (F). Learning can lead to pruning of random connections between neurons, creating a more structured neural network, leading to decreased cortical thickness by reducing dendritic arborizations (G). Cortical thickness in left middle frontal gyrus morphed back into pial surface for two representative subjects (H).

How can regional cortical expansion lead to better performance in gf? Our brain has finite capacity for information processing (Luck and Vogel 1997). While the exact nature of the limited capacity is still not understood, two main models have been proposed. One model claims that there are only a limited number of available slots for holding information, and once filled, new information cannot be added (fixed capacity model) (Fukuda et al. 2010). In contrast, the second model argues that although there is no upper limit for number of representations, the competition between representations for resource allocation leads to information loss as the number of representations grow (flexible resource model) (Franconeri et al. 2013). Recent human psychophysics studies and monkey's electrophysiology have found more evidence in favor of the flexible resource model (Buschman et al. 2011; van den Berg et al. 2012; Miller and Buschman 2015). Regardless of the exact mechanism of capacity limit, higher cortical surface area can lead to increased information processing capacity by providing more cortical columns (Rakic 2008), which are the functional units of the cortex (Mountcastle 1997) (Fig. 5B). Moreover, higher number of cortical columns should be associated with reduced fraction of intercolumnar connections (percent interconnectedness) (Ringo 1991) (Fig. 5C). This has been suggested to increase functional specificity of cortical columns and reduction of overlap in representations, which confer higher capacity to hold information (Ringo 1991). This idea has been recently supported by functional imaging study of neural population tuning in human early visual cortex: higher cortical surface area in early visual cortex is positively associated with sharpness of neural population tuning and better performance in perceptual discrimination (Song et al. 2015). By the same token, cortical expansion in gf-related brain regions can lead to higher information processing capacity and ability to generate (represent), test and refute multiple hypotheses simultaneously, with less interference between generated hypotheses (Franconeri et al. 2013). By parsing cortical volume into thickness and surface area, we were able to show that cortical expansion is the underlying factor for better performance in gf rather than higher cortical thickness (Fig. 5D). These results indicate the importance of studying cortical surface area as a separate entity in future gf studies.

Unlike gf, gc is related to accessing stored knowledge and general facts, which have been accumulated throughout years of learning and education (Deary et al. 2010) (Fig. 5E). In this study, we found that better performance in gc was associated with lower cortical thickness and higher cortical surface area. Previous studies on cortical changes associated with human learning and plasticity have shown increased cortical thickness (and volume, which mainly is driven by change in thickness) shortly after learning. Recently, the expansion–renormalization model has been hypothesized to explain unfeasible endless expansion of cortex (increased cortical thickness) in life-long learning (Wenger et al. 2017a). According to this model, learning-induced increased cortical thickness, brought by many cellular mechanisms including formation of new synapses and dendritic arborizations as well as proliferation of astrocytes, is followed by selection of the most efficient neural circuitries through pruning of inefficient connections (renormalization). The renormalization of cortical changes has been shown in human imaging studies (Wenger et al. 2017b) as well as animal models (Xu et al. 2009). Our findings support and extend the expansion–renormalization model. Repeated learning followed by pruning of unnecessary and weak connections between neurons would lead in long term to more stable and efficient neural circuitry, explaining decreased cortical thickness in the corresponding brain regions (Fig. 5G,H). Furthermore, our results tie in well with positive association of intelligence with both thinner cortex as well as faster rate of cortical pruning during development (Schnack et al. 2015) and less activation and metabolic consumption in individuals with higher cognitive performance (Haier et al. 1992).

Lower cortical thickness and higher cortical surface area in left caudal middle frontal gyrus were the most significant clusters for gc. Cortical thickness in left caudal middle frontal gyrus undergoes changes in cortical thickness in subjects learning new language (Mårtensson et al., 2012; Koyama et al. 2017). Higher cortical surface area accompanied by lower cortical thickness has been associated with better performance in visual perception discrimination and lend support to the proposed model of enlarged cortical surface area and decreased cortical thickness as the most advantageous cortical design for crystallized knowledge (Song et al. 2015).

Shared Neuroanatomical Correlates of gf and gc

Although gf and gc rely on distinct cognitive abilities, individuals with higher gf perform better in gc tasks as well (Deary et al. 2010). This can imply engagement of some shared neural networks in both gf and gc. We specifically found that cortical surface area of anterior temporal lobe (including anterior inferior temporal gyrus) and middle temporal is associated with both gf and gc. Studies on patients with semantic dementia as well as human imaging studies have shown the role of anterior temporal lobe in formation of concepts and semantic knowledge (Ralph et al. 2017). Anterior temporal lobe specifically acts as a modality-invariant hub, which infers higher-order relationships among sensory, motor, verbal, and nonverbal information (Abel et al. 2015), and can play a significant role in both gf and gc.

Our results also show that cortical gyrification in frontal, parietal, and temporal regions was positively correlated with both gf and gc, which is in line with previous studies of regional cortical gyrification association with intelligence (Gregory et al. 2016). This indicates gyrification as a possible shared neuroanatomical correlate of both gf and gc, with less regional specifications but rather global characteristics of the brain.

In this study, we showed results with and without correction for TBV. Correcting for TBV reduced the size and significance level of the clusters for the association between gf/gc and cortical surface area. While cortical thickness shows more or less similar values across subjects with less amount of variability, cortical surface area varies greatly across subjects, which makes it a more prominent factor contributing to TBV. We believe that controlling for TBV more clearly reveals the regional association between cortical surface area and gf/gc, as the results are not contaminated by factors that are correlated with both TBV and intelligence, such as white matter volume.

Brain Structure–Function Relationship and Human Intelligence

A central question in neuroscience is the relation between structure and function in the brain. We found that structural correlates of fluid and crystallized intelligence correspond to brain regions that are active while subjects perform fluid and crystallized intelligence tasks and to well-known human functional networks previously associated with human intelligence. Our results are also in line with the recent meta-analysis of gf-related co-activation maps showing great similarity with resting-state human brain networks including the DAN and the FPN (Santarnecchi et al. 2017b). These findings also provide structural evidence for the network-centric notion of human intelligence resulting from the interaction of multiple brain regions (Barbey 2018).

Limitations of the Study and Future Directions

It is important to mention that metrics reported in this study are indirect measures of cortical morphologies using MRI. Importantly, it has been proposed that cortical thickness can be affected by myelination in deeper layers of the cortex especially during development (Sowell et al. 2001). Higher myelination in the gray matter–white matter boundary can lead to false segmentation of gray matter as white matter, resulting in apparent cortical thinning. Recently, thinning of visual cortex during development has been linked to increased myelination in the visual cortex, rather than pruning (Natu et al. 2018). Future studies using myelination maps combined with diffusion imaging and T1-weighted MRI are needed to determine whether the negative association between cortical thickness and gc can be attributed to pruning or myelination.

Also, subject’s movement during MRI acquisition can lead to underestimation of cortical thickness, which could be a potential confounding factor (Reuter et al. 2015). However, subjects with higher cognitive ability move less compared to subjects with lower cognitive ability (Wylie et al. 2014). This minimizes the possibility of movement as a confounding factor in our study, as the relationship between cortical thickness and gc was found to be negative.

Although we did not find any statistically significant association between cortical thickness and gf, this does not necessarily mean no association exists. Future studies with larger sample sizes are needed to further investigate the potential association between cortical thickness and gf with smaller effect sizes.

In this study, we were able to partially replicate results across two relatively large data sets, specifically for the association between gf, cortical surface area, and gyrification. However, results for the association between cortical morphologies and gc were not fully replicated. This can be partly due to relatively small sample size in the replication data set (INDI) and partly due to very different behavioral and psychological measurement of gc across two data sets. Future studies with larger sample size and more similar behavioral measures will reveal the generalizability of the findings across different data sets.

Conclusion

We tried to disentangle the contribution of different cortical morphologies including cortical thickness, surface area, and gyrification, to individual variability in gf and gc. Our findings suggest a framework where ``horizontal” cortical expansion, indexed by cortical surface area, enables greater resource allocation and computational capacity relevant to gf and gc, whereas decreased cortical thickness possibly reflects cortical pruning processes facilitating ``vertical” intracolumnar efficiency in knowledge-based tasks linked to gc.

Supplementary Material

supplementary_materials_bhz082
Click here for additional data file. (672KB, docx)
clusters_bhz082
Click here for additional data file. (16.9KB, xlsx)

Notes

The content of this paper is solely the responsibility of the authors and does not necessarily represent the official views of Harvard Catalyst, Harvard University and its affiliated academic health care centers, the National Institutes of Health and the Sidney R. Baer Jr. Foundation. Conflict of Interest: None declared.

Funding

Broad Institute at Harvard-MIT (2016P000351 to E.S. and A.P.L.); Defense Advanced Research Projects Agency (HR001117S0030 to E.S. and A.P.L.); Beth Israel Deaconess Medical Center (Chief Academic Officer Grant 2017 to E.S.); Berenson-Allen Foundation (A.P.L.); Sidney R. Baer Jr. Foundation (A.P.L.); National Institutes of Health (R01HD069776, R01NS073601, R21 MH099196, R21 NS082870, R21 NS085491, and R21 HD07616 to A.P.L.); Harvard Catalyst, The Harvard Clinical and Translational Science Center (NCRR and the NCATS NIH, UL1 RR025758 to A.P.L.).

References

  1. Abel TJ, Rhone AE, Nourski KV, Kawasaki H, Oya H, Griffiths TD, Howard MA, Tranel D. 2015. Direct physiologic evidence of a heteromodal convergence region for proper naming in human left anterior temporal lobe. J Neurosci. 35:1513–1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Akshoomoff N, Beaumont JL, Bauer PJ, Dikmen S, Gershon R, Mungas D, Slotkin J, Tulsky D, Weintraub S, Zelazzo P et al. 2013. NIH toolbox cognitive function battery (CFB): composite scores of crystallized, fluid, and overall cognition. Monogr Soc Res Child Dev. 78:119–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barbey AK. 2018. Network neuroscience theory of human intelligence. Trends Cogn Sci. 22:8–20. [DOI] [PubMed] [Google Scholar]
  4. Barbey AK, Colom R, Paul EJ, Grafman J. 2014. Architecture of fluid intelligence and working memory revealed by lesion mapping. Brain Struct Funct. 219:485–494. [DOI] [PubMed] [Google Scholar]
  5. Bilker WB, Hansen JA, Brensinger CM, Richard J, Gur RE, Gur RC. 2012. Development of abbreviated nine-item forms of the Raven’s standard progressive matrices test. Assessment. 19:354–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Buschman TJ, Siegel M, Roy JE, Miller EK. 2011. Neural substrates of cognitive capacity limitations. Proc Natl Acad Sci U S A. 108:11252–11255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cattell RB. 1963. Theory of fluid and crystallized intelligence: a critical experiment. J Educ Psychol. 54:1–22. [DOI] [PubMed] [Google Scholar]
  8. Chenn A, Walsh CA. 2003. Increased neuronal production, enlarged forebrains and cytoarchitectural distortions in beta-catenin overexpressing transgenic mice. Cereb Cortex. 13:599–606. [DOI] [PubMed] [Google Scholar]
  9. Choi YY, Shamosh NA, Cho SH, DeYoung CG, Lee MJ, Lee J-M, Kim SI, Cho Z-H, Kim K, Gray JR et al. 2008. Multiple bases of human intelligence revealed by cortical thickness and neural activation. J Neurosci. 28:10323–10329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Colom R, Jung RE, Haier RJ. 2007. General intelligence and memory span: evidence for a common neuroanatomic framework. Cogn Neuropsychol. 24:867–878. [DOI] [PubMed] [Google Scholar]
  11. Colom R, Karama S, Jung RE, Haier RJ. 2010. Human intelligence and brain networks. Dialogues Clin Neurosci. 12:489–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Constantinidis C, Klingberg T. 2016. The neuroscience of working memory capacity and training. Nat Rev Neurosci. 17:438–449. [DOI] [PubMed] [Google Scholar]
  13. Dale AM, Fischl B, Sereno MI. 1999. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 9:179–194. [DOI] [PubMed] [Google Scholar]
  14. Deary IJ, Caryl PG. 1997. Neuroscience and human intelligence differences. Trends Neurosci. 20:365–371. [DOI] [PubMed] [Google Scholar]
  15. Deary IJ, Penke L, Johnson W. 2010. The neuroscience of human intelligence differences. Nat Rev Neurosci. 11:201–211. [DOI] [PubMed] [Google Scholar]
  16. Duncan J, Chylinski D, Mitchell DJ, Bhandari A. 2017. Complexity and compositionality in fluid intelligence. Proc Natl Acad Sci U S A. 114:5295–5299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, Constable RT. 2015. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat Neurosci. 18:1664–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fischl B. 2012. FreeSurfer. Neuroimage. 62:774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Franconeri SL, Alvarez GA, Cavanagh P. 2013. Flexible cognitive resources: competitive content maps for attention and memory. Trends Cogn Sci. 17:134–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fukuda K, Awh E, Vogel EK. 2010. Discrete capacity limits in visual working memory. Curr Opin Neurobiol. 20:177–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gray JR, Chabris CF, Braver TS. 2003. Neural mechanisms of general fluid intelligence. Nat Neurosci. 6:316–322. [DOI] [PubMed] [Google Scholar]
  22. Gregory MD, Kippenhan JS, Dickinson D, Carrasco J, Mattay VS, Weinberger DR, Berman KF. 2016. Regional variations in brain gyrification are associated with general cognitive ability in humans. Curr Biol. 26:1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Haier RJ, Siegel BV, MacLachlan A, Soderling E, Lottenberg S, Buchsbaum MS. 1992. Regional glucose metabolic changes after learning a complex visuospatial/motor task: a positron emission tomographic study. Brain Res. 570:134–143. [DOI] [PubMed] [Google Scholar]
  24. Horn JL, Cattell RB. 1967. Age differences in fluid and crystallized intelligence. Acta Psychol (Amst). 26:107–129. [DOI] [PubMed] [Google Scholar]
  25. Jung RE, Haier RJ. 2007. The parieto-frontal integration theory (P-FIT) of intelligence: converging neuroimaging evidence. Behav Brain Sci. 30:135–154discussion 154–187. [DOI] [PubMed] [Google Scholar]
  26. Karama S, Bastin ME, Murray C, Royle NA, Penke L, Muñoz Maniega S, Gow AJ, Corley J, Valdés Hernández M, Lewis JD et al. 2014. Childhood cognitive ability accounts for associations between cognitive ability and brain cortical thickness in old age. Mol Psychiatry. 19:555–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Karama S, Colom R, Johnson W, Deary IJ, Haier R, Waber DP, Lepage C, Ganjavi H, Jung R, Evans AC. 2011. Cortical thickness correlates of specific cognitive performance accounted for by the general factor of intelligence in healthy children aged 6 to 18. Neuroimage. 55:1443–1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Koyama MS, O’Connor D, Shehzad Z, Milham MP. 2017. Differential contributions of the middle frontal gyrus functional connectivity to literacy and numeracy. Sci Rep. 7:17548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kravitz DJ, Saleem KS, Baker CI, Mishkin M. 2011. A new neural framework for visuospatial processing. Nat Rev Neurosci. 12:217–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Luck SJ, Vogel EK. 1997. The capacity of visual working memory for features and conjunctions. Nature. 390:279–281. [DOI] [PubMed] [Google Scholar]
  31. Manard M, Carabin D, Jaspar M, Collette F. 2014. Age-related decline in cognitive control: the role of fluid intelligence and processing speed. BMC Neurosci. 15:7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mårtensson J, Eriksson J, Bodammer NC, Lindgren M, Johansson M, Nyberg L, Lövdén M. 2012. Growth of language-related brain areas after foreign language learning. Neuroimage. 63:240–244. [DOI] [PubMed] [Google Scholar]
  33. Miller EK, Buschman TJ. 2015. Working memory capacity: limits on the bandwidth of cognition. Daedalus. 144:112–122. [Google Scholar]
  34. Mountcastle VB. 1997. The columnar organization of the neocortex. Brain J Neurol. 120(Pt 4):701–722. [DOI] [PubMed] [Google Scholar]
  35. Natu VS, Gomez J, Barnett M, Jeska B, Kirilina E, Jaeger C, Zhen Z, Cox S, Weiner KS, Weiskopf N, et al. Forthcoming 2018. Apparent thinning of visual cortex during childhood is associated with myelination, not pruning. bioRxiv. 368274. [DOI] [PMC free article] [PubMed]
  36. Nooner KB, Colcombe SJ, Tobe RH, Mennes M, Benedict MM, Moreno AL, Panek LJ, Brown S, Zavitz ST, Li Q et al. 2012. The NKI-Rockland sample: a model for accelerating the pace of discovery science in psychiatry. Front Neurosci. 6:152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Panizzon MS, Fennema-Notestine C, Eyler LT, Jernigan TL, Prom-Wormley E, Neale M, Jacobson K, Lyons MJ, Grant MD, Franz CE et al. 2009. Distinct genetic influences on cortical surface area and cortical thickness. Cereb Cortex. 19:2728–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pearson K. 1906. On the relationship of intelligence to size and shape of head, and to other physical and mental characters. Biometrika. 5:105–146. [Google Scholar]
  39. Petersen SE, Posner MI. 2012. The attention system of the human brain: 20 years after. Annu Rev Neurosci. 35:73–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Pietschnig J, Penke L, Wicherts JM, Zeiler M, Voracek M. 2015. Meta-analysis of associations between human brain volume and intelligence differences: how strong are they and what do they mean. Neurosci Biobehav Rev. 57:411–432. [DOI] [PubMed] [Google Scholar]
  41. Rakic P. 2008. Confusing cortical columns. Proc Natl Acad Sci U S A. 105:12099–12100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Rakic P. 2009. Evolution of the neocortex: perspective from developmental biology. Nat Rev Neurosci. 10:724–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Rakic P, Ayoub AE, Breunig JJ, Dominguez MH. 2009. Decision by division: making cortical maps. Trends Neurosci. 32:291–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Ralph MAL, Jefferies E, Patterson K, Rogers TT. 2017. The neural and computational bases of semantic cognition. Nat Rev Neurosci. 18:42–55. [DOI] [PubMed] [Google Scholar]
  45. Reuter M, Tisdall MD, Qureshi A, Buckner RL, van der Kouwe AJW, Fischl B. 2015. Head motion during MRI acquisition reduces gray matter volume and thickness estimates. Neuroimage. 107:107–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Ringo JL. 1991. Neuronal interconnection as a function of brain size. Brain Behav Evol. 38:1–6. [DOI] [PubMed] [Google Scholar]
  47. Santarnecchi E, Emmendorfer A, Pascual-Leone A. 2017a. Dissecting the parieto-frontal correlates of fluid intelligence: a comprehensive ALE meta-analysis study. Intelligence. 63:9–28. [Google Scholar]
  48. Santarnecchi E, Emmendorfer A, Tadayon S, Rossi S, Rossi A, Pascual-Leone A. 2017b. Network connectivity correlates of variability in fluid intelligence performance. Intelligence. 65:35–47. [Google Scholar]
  49. Schnack HG, Haren NE, Brouwer RM, Evans A, Durston S, Boomsma DI, Kahn RS, Hulshoff Pol HE . 2015. Changes in thickness and surface area of the human cortex and their relationship with intelligence. Cereb Cortex. 25:1608–1617. [DOI] [PubMed] [Google Scholar]
  50. Song C, Schwarzkopf DS, Kanai R, Rees G. 2015. Neural population tuning links visual cortical anatomy to human visual perception. Neuron. 85:641–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Sowell ER, Thompson PM, Tessner KD, Toga AW. 2001. Mapping continued brain growth and gray matter density reduction in dorsal frontal cortex: Inverse relationships during postadolescent brain maturation. J Neurosci. 21:8819–8829. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Unsworth N, Fukuda K, Awh E, Vogel EK. 2014. Working memory and fluid intelligence: capacity, attention control, and secondary memory retrieval. Cogn Psychol. 71:1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. van den Berg R, Shin H, Chou W-C, George R, Ma WJ. 2012. Variability in encoding precision accounts for visual short-term memory limitations. Proc Natl Acad Sci U S A. 109:8780–8785. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Van Essen DC, Smith SM, Barch DM, TEJ B, Yacoub E, Ugurbil K, WU-Minn HCP Consortium . 2013. The WU-Minn Human Connectome Project: an overview. Neuroimage. 80:62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Wenger E, Brozzoli C, Lindenberger U, Lövdén M. 2017a. Expansion and renormalization of human brain structure during skill acquisition. Trends Cogn Sci. 21:930–939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Wenger E, Kühn S, Verrel J, Mårtensson J, Bodammer NC, Lindenberger U, Lövdén M. 2017b. Repeated structural imaging reveals nonlinear progression of experience-dependent volume changes in human motor cortex. Cereb Cortex. 27:2911–2925. [DOI] [PubMed] [Google Scholar]
  57. Winkler AM, Kochunov P, Blangero J, Almasy L, Zilles K, Fox PT, Duggirala R, Glahn DC. 2010. Cortical thickness or grey matter volume? The importance of selecting the phenotype for imaging genetics studies. Neuroimage. 53:1135–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Woolgar A, Parr A, Cusack R, Thompson R, Nimmo-Smith I, Torralva T, Roca M, Antoun N, Manes F, Duncan J. 2010. Fluid intelligence loss linked to restricted regions of damage within frontal and parietal cortex. Proc Natl Acad Sci U S A. 107:14899–14902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Wylie GR, Genova H, DeLuca J, Chiaravalloti N, Sumowski JF. 2014. Functional magnetic resonance imaging movers and shakers: does subject-movement cause sampling bias. Hum Brain Mapp. 35:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Xu T, Yu X, Perlik AJ, Tobin WF, Zweig JA, Tennant K, Jones T, Zuo Y. 2009. Rapid formation and selective stabilization of synapses for enduring motor memories. Nature. 462:915–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Yeo BTT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zöllei L, Polimeni JR et al. 2011. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol. 106:1125–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Zilles K, Palomero-Gallagher N, Amunts K. 2013. Development of cortical folding during evolution and ontogeny. Trends Neurosci. 36:275–284. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supplementary_materials_bhz082
Click here for additional data file. (672KB, docx)
clusters_bhz082
Click here for additional data file. (16.9KB, xlsx)

Articles from Cerebral Cortex (New York, NY) are provided here courtesy of Oxford University Press

RESOURCES