Associations between Neighborhood SES and Functional Brain Network Development

Abstract

Higher socioeconomic status (SES) in childhood is associated with stronger cognitive abilities, higher academic achievement, and lower incidence of mental illness later in development. While prior work has mapped the associations between neighborhood SES and brain structure, little is known about the relationship between SES and intrinsic neural dynamics. Here, we capitalize upon a large cross-sectional community-based sample (Philadelphia Neurodevelopmental Cohort, ages 8–22 years, n = 1012) to examine associations between age, SES, and functional brain network topology. We characterize this topology using a local measure of network segregation known as the clustering coefficient and find that it accounts for a greater degree of SES-associated variance than mesoscale segregation captured by modularity. High-SES youth displayed stronger positive associations between age and clustering than low-SES youth, and this effect was most pronounced for regions in the limbic, somatomotor, and ventral attention systems. The moderating effect of SES on positive associations between age and clustering was strongest for connections of intermediate length and was consistent with a stronger negative relationship between age and local connectivity in these regions in low-SES youth. Our findings suggest that, in late childhood and adolescence, neighborhood SES is associated with variation in the development of functional network structure in the human brain.

Introduction

Higher socioeconomic status (SES) during youth is associated with lower risk for psychiatric disorders (Duncan et al. 1994; Evans and Cassells 2014), higher executive function (Noble et al. 2007), higher levels of educational attainment and income (McLoysd 1998; Ryan et al. 2006; Duncan et al. 2012), and better physical health (Cohen et al. 2010; Evans 2016). SES is also associated with cortical development as early as infancy (Hanson et al. 2013; Tomalski et al. 2013; Betancourt et al. 2016; Brito et al. 2016; Farah 2017; Jha et al. 2018). Notably, emerging evidence points to a pattern of accelerated structural brain development in low-SES individuals (Piccolo et al. 2016; LeWinn et al. 2017), suggesting that SES may moderate the associations between age and structural brain development. Yet whether such moderating relationships also exist in functional brain development remains unknown. Findings of more protracted structural brain development in high-SES youth are at odds with the overall impression of findings from studies of brain function, which have been performed at specific ages but infrequently over a large developmental age range. These studies, on the whole, suggest potentially faster functional brain development in high-SES children and adults, including increased functional specialization in language regions in high-SES kindergartners (Raizada et al. 2008), more mature frontal gamma power in high-SES infants (Tomalski et al. 2013), and increased resting-state functional connectivity in high-SES children and adults (Sripada et al. 2014; Smith et al. 2015; Barch et al. 2016; Marshall et al. 2018) (although whether this is indicative of greater maturation is unclear). This apparent paradox motivates a thorough investigation into whether and how SES relates to functional brain network development in youth.

Cortical networks become increasingly specialized and segregated with age (Fair et al. 2009; Stevens et al. 2009b; Stiles and Jernigan 2010; Satterthwaite et al. 2013b; Grayson and Fair 2017). Increasing evidence suggests that this age-dependent pattern of cortical segregation supports the normative maturation of cognitive function (Gu et al. 2015; Baum et al. 2017; Wig 2017). Yet, explicit studies of regional specialization and circuit segregation have traditionally been hampered by the dearth of computational techniques and methodological approaches that are appropriate for the study of spatially distributed interconnected systems. Recent advances in network neuroscience have met this need by drawing on mathematics, physics, and computer science to formalize a model of the brain as a network of interacting elements (Bassett and Sporns 2017).

Recent work has suggested that SES may be associated with variation in intrinsic neural dynamics across the lifespan. The network approach was recently used to examine the relationship between SES and functional brain networks in aging (Chan et al. 2018). SES was found to moderate age-related differences in functional network segregation across the lifespan, such that lower SES individuals showed reduced functional network segregation in middle age, consistent with a hypothesis of faster brain aging in low-SES individuals (although we note that this was a cross-sectional study that could not address this interpretation directly). Although links between SES and network segregation could reflect genetic differences rather than environmental influences, a recent twin study of adolescents showed that the heritability estimate for the clustering coefficient, a statistic that measures the potential for information segregation, is low and, therefore, that it might be especially sensitive to environmental influences (van den Heuvel et al. 2013). Variation in functional connectivity associated with environmental rather than genetic influences might result from stress-induced alterations in neuroendocrine pathways (Sripada et al. 2014), changes in synapse number or morphology associated with environmental complexity (Diamond et al. 2004; Markham and Greenough 2005), or reduced white matter integrity associated with systemic inflammation (Gianaros et al. 2013; Porter et al. 2018). Taken together, these studies suggest that environmental exposures associated with low SES might also be associated with age-related differences in network dynamics, but nothing is yet known about how SES relates to network segregation during development.

Across the majority of these studies, SES has been examined at the household level, comprising household characteristics such as income or education. Other studies have used neighborhood SES, which captures the availability of social and community resources. Although above we use the term SES broadly to refer to studies examining household characteristics as well as those investigating aspects of neighborhood SES, both neighborhood and household SES are multifaceted constructs that may have differing associations with brain development (Ursache and Noble 2016). Both are commonly examined as composite metrics, comprising variation in multiple aspects of the early environment (Farah 2017). To characterize SES in this work, we focus on neighborhood SES. Notably, though neighborhood SES is highly correlated with household-level SES (operationalized here as maternal education), here we focus solely on the effect of neighborhood SES (above and beyond household-level SES, see Supplementary Section 2). Neighborhood SES captures additional variance in the types of experiences children encounter and has been shown to be associated with developmental outcomes above and beyond household-level SES (Chen et al. 2015; Chetty et al. 2016; Marshall et al. 2018). Neighborhood SES may become increasingly salient as children mature (Leventhal and Brooks-Gunn 2000); in this particular sample, neighborhood SES is more predictive of cognitive performance than parental characteristics such as education, race, or age (Moore et al. 2016).

While previous studies lay important groundwork, a key gap remains. Namely, we have not yet probed the associations between neighborhood SES and the development of functional brain network segregation during childhood and adolescence. In the present report, we address this gap by leveraging the extensive cross-sectional neuroimaging data of the Philadelphia Neurodevelopmental Cohort (PNC), a community-based sample of youth between the ages of 8 years and 22 years (Satterthwaite et al. 2016). In a total of n = 1012 youth, we examine blood oxygen level–dependent (BOLD) signal in functional magnetic resonance images (fMRI) acquired as participants rested inside the scanner. We estimate interregional correlations in spontaneous, low-frequency BOLD timeseries, and we represent the interregional correlation matrix as a network, in which nodes represent brain regions and edges represent correlation values (Fig. 1b). Next, we employ computational tools from network neuroscience to examine the effect of SES on functional brain network topology as a function of age. To parse topology, we focus on metrics of local-scale and mesoscale segregation that have been shown to change over development (Satterthwaite et al. 2013b; Wu et al. 2013; Betzel et al. 2014; Gu et al. 2015; Baum et al. 2017): the clustering coefficient (Watts and Strogatz 1998) (Fig. 2a) and the modularity quality index (Newman 2006), respectively. We note here that, in accordance with the wording in these studies, we use the word “change” to describe associations between age and the outcome measure of interest. However, in the context of a cross-sectional study, these terms cannot be used to draw conclusions about developmental trajectories.

Figure 1.

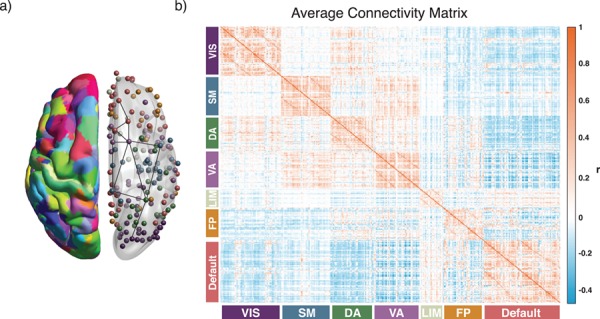
Schematic of approach. (a) A total of N = 360 regions of interest in a multimodal cortical parcellation (Glasser et al. 2016). From each region, we estimated the mean BOLD timeseries, and then we calculated the functional connectivity between any two regions using the Pearson correlation coefficient. For each subject, we collated all functional connectivity estimates into a single N × N adjacency matrix. The left hemisphere depicts the parcellation, while the right hemisphere depicts regions represented as network nodes and colored by their association to putative cognitive systems (Yeo et al. 2011). (b) The average functional connectivity matrix across subjects, ordered by putative cognitive systems. VIS: visual; SM: somatomotor; DA: dorsal attention; VA: ventral attention; LIM: limbic; FP: frontoparietal.

Figure 2.

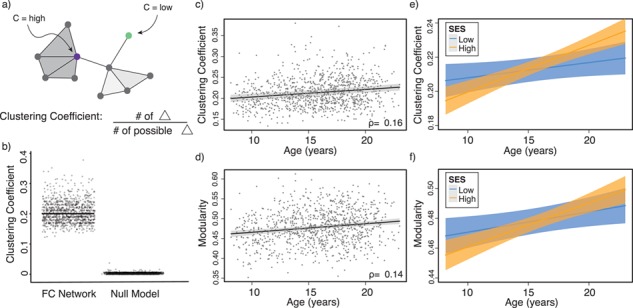
Variation in age and SES is associated with whole-brain functional network topology at rest. (a) The clustering coefficient can be used to assess the degree to which neighboring nodes in a graph tend to cluster together. In a binary graph, such as that illustrated here, the clustering coefficient measures the fraction of triangles around a node; the purple node has a high clustering coefficient, and the green node has a low clustering coefficient. In our study, we use an extension of this measure that is appropriate for signed, weighted networks. (b) The average clustering coefficient is significantly higher in the observed functional brain networks than in random network null models in which the average edge weight, degree distribution, and strength distribution have been preserved (p < 1 × 10^-15). (c) Older age is associated with higher average clustering coefficient, controlling for sex, race, head motion, and mean edge weight. Note that the values that are plotted are partial residuals. Partial correlation between age and the average clustering coefficient is shown (Spearman’s ρ, P < 1 × 10⁻⁶). (d) The value of the modularity quality index obtained by maximizing a modularity quality function (see Materials and Methods) is also positively associated with age, controlling for sex, race, head motion, and mean edge weight. Note again that the values that are plotted are partial residuals. Partial correlation between age and the modularity quality index is shown (Spearman’s ρ, P < 1 × 10⁻⁵). (e) High-SES youth display a stronger positive relationship between age and the average clustering coefficient of functional brain networks at rest than low-SES youth over this developmental period. (f) High-SES youth also display a trend towards a stronger positive relationship between age and the modularity quality index of functional brain networks at rest than low-SES youth over this developmental period.

We take an explicitly hierarchical approach to the question of how functional brain network topology in development is associated with neighborhood SES. At the coarsest level of the hierarchy, we examine interactions between age and SES on whole-brain summary measures of network topology. At a median level of the hierarchy, we perform higher-resolution analysis at the level of putative functional systems including the default mode, frontoparietal, attention, and limbic systems, among others. At the lowest level of the hierarchy, we perform fine-grained analysis at the level of individual brain regions. In light of prior work, we hypothesized that both the modularity quality index and the clustering coefficient would be positively associated with age (Satterthwaite et al. 2013b; Wu et al. 2013; Gu et al. 2015) (although see also Supekar et al. 2009). Moreover, based on recent evidence for decreased resting-state connectivity in low- as opposed to high-SES children and adults (Sripada et al. 2014; Barch et al. 2016), we hypothesized that low-SES youth would exhibit either lower segregation on average or a weaker positive association between segregation and age than high-SES youth. After testing these hypotheses, we investigate several potential explanatory factors, including regional homogeneity (ReHo) of the BOLD signal as well as interregional Euclidean distance. The latter factor was motivated by recent work demonstrating that many advantageous properties of brain networks, such as their robustness to perturbation and capacity for information processing, entail a trade-off between wiring cost of anatomical connections between neurons and the emergence of these adaptive topological patterns (Bullmore and Sporns 2012); we hypothesized that metabolic constraints associated with variation in the environment might shift this trade-off towards less costly short-distance connections over mid- or long-distance connections. Finally, to further confirm our results, we perform sensitivity analyses in a smaller sample (n = 883) that excluded participants currently using psychoactive medication as well as participants with a history of psychiatric hospitalization. As a whole, our study presents evidence for associations between SES and the development of functional network topology, providing greater insight into possible neural manifestations of early environmental influences.

Materials and Methods

Participant Sample

The PNC is a large community-based sample of youth between the ages of 8 years and 22 years, a subset of which participated in an extensive neuroimaging protocol (n = 1601) (Calkins et al. 2015). After excluding youth with abnormalities in brain structure or a history of medical problems that could impact brain function (n = 154), poor imaging data that did not pass quality assurance protocols (described in detail below, n = 432), or inadequate coverage of some brain regions in our parcellation (n = 3), we selected a subsample of 1012 children and adolescents (nf = 552 female, mean age = 15.78 years) with neuroimaging data. Participants excluded for abnormalities in brain structure or a history of medical problems were not significantly older than our analysis sample (mean age of included participants = 14.89 years, mean age of excluded participants = 15.21 years; Student’s t-test P = 0.05); SES did not significantly differ between the groups (included participants: mean percent in poverty = 17%, mean percent married = 44%, mean median family income = $72 334; excluded participants: mean percent in poverty = 15%, mean percent married = 47%, mean median family income = $77 102; P = 0.08). Participants excluded due to poor quality imaging data were significantly younger (mean age of included participants = 15.78, mean age of excluded participants = 12.77; P < 1 × 10⁻¹⁵) and from lower SES backgrounds than our analysis sample (included participants: mean percent in poverty = 16%, mean percent married = 45%, mean median family income = $74 684; excluded participants: mean percent in poverty = 19%, mean percent married = 43%, mean median family income = $66 845; P < 0.001). Sex was significantly associated with mean edge weight (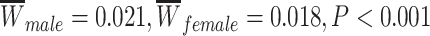) and was not significantly associated with motion (P > 0.11). Demographic information was collected by participant report, including sex, race (coded as White, Black/African-American, or Other; Other includes Asian, Native American, Hawaiian Pacific Islander, and Multi-Racial), and home address.

Measurement of SES

To represent participant neighborhood SES, composed of census-level data of the census block of each participant, we studied a factor score previously derived from this data set (Moore et al. 2016). This factor summarized the observed variance across multiple features including percent of residents married, percent of residents in poverty, median family income, percent of residents with a high school education, population density, and percent of residents employed. In the main text, we present several analyses with a median split of high and low neighborhood SES groups for ease of visualization and interpretation (see Supplementary 2B and 2C for all analyses conducted with SES as a continuous variable, results are qualitatively similar). In the high neighborhood SES group, the mean percent in poverty was 5%, mean percent married was 60%, and mean median family income was $107 039; in the low neighborhood SES group, the mean percent in poverty was 27%, mean percent married was 30%, and mean median family income was $41 946. The high and low neighborhood SES groups were not significantly different in age (P > 0.22) or sex (P > 0.28, see Supplementary Table 1 for bivariate relationships between predictors).

Imaging Data Acquisition

All imaging data were acquired on the same 3T Siemens Tim Trio scanner with 32-channel head coil at the Hospital of the University of Pennsylvania. BOLD signal was measured using a whole-brain, single-shot, multi-slice, gradient-echo (GE) echoplanar sequence with the following parameters: 124 volumes; time repetition (TR) = 3000 ms; time echo (TE) = 32 ms; flip angle = 90 degrees, field of view (FoV) = 192 × 192 mm, matrix = 64 × 64, slice thickness = 3 mm, slice gap = 0 mm, and effective voxel resolution = 3 × 3 × 3 mm. During the resting-state scan, subjects were instructed to keep their eyes open and fixate on a white crosshair presented against a dark background. Prior to the resting-state acquisition, a magnetization-prepared rapid acquisition GE T1-weighted image was acquired to aid spatial normalization to standard atlas space, using the following parameters: TR = 1810 ms, TE = 3.51 ms, FOV = 180 × 240 mm, matrix = 256 × 192, 160 slices, time to inversion = 1100 ms, flip angle = 9 degrees, and effective voxel resolution of 0.9 × 0.9 × 1 mm. Further study procedures and design are described in detail elsewhere (Satterthwaite et al. 2014a).

Imaging Data Preprocessing

Whole-head T1 images were registered to a custom population template created with advanced normalization tools (ANTs) (Avants et al. 2011) using the top-performing diffeomorphic SyN registration (Klein et al. 2009). Preprocessing of resting-state timeseries was conducted using a validated confound regression procedure that has been optimized to reduce the influence of subject motion (Satterthwaite et al. 2013a; Ciric et al. 2017); preprocessing was implemented in XCP engine, a multimodal toolkit that deploys processing instruments from frequently used software libraries, including FSL (Jenkinson et al. 2012) and AFNI (Cox 1996). Further documentation is available at https://pipedocs.github.io/intro.html and https://github.com/PennBBL/xcpEngine. Following distortion correction using a B0 map, the first 4 volumes of the functional timeseries were removed to allow signal stabilization, leaving 120 volumes for subsequent analysis. Functional timeseries were band-pass filtered to retain frequencies between 0.01 Hz and 0.08 Hz. Functional images were realigned using MCFLIRT (Jenkinson et al. 2002) and skull-stripped using BET (Smith 2002). Data were demeaned, and linear and quadratic trends were removed. Intensity outliers were removed and interpolated over using AFNI’s 3dDespike utility. Confound regression was performed using a 36-parameter model; confounds included global signal, 6 motion parameters as well as their temporal derivatives, quadratic terms, and the temporal derivatives of the quadratic terms (Satterthwaite et al., 2013a). Global signal regression has been shown to be among the most effective methods for reducing the influence of motion on estimates of the BOLD signal (Ciric et al. 2017; Power et al. 2017a; Power et al. 2017b; Parkes et al. 2018). Prior to confound regression, all confound parameters were band-pass filtered in a fashion identical to that applied to the original timeseries data, ensuring comparability of the signals in frequency content (Hallquist et al. 2013). Subjects that displayed high levels of motion (mean relative root mean squared (RMS) displacement greater than 0.20 mm or more than 20 frames with over 0.25 mm of motion) or poor signal coverage were excluded from all analysis. Functional images were coregistered to the T1 image using boundary-based registration (Greve and Fischl 2009) and aligned to template space using ANTs, as described above; all transforms were concatenated, and thus only one interpolation was performed.

Network Construction

We extracted time-varying mean BOLD signal from N = 360 regions of interest, which collectively comprised a multimodal parcellation of the cerebral cortex (Glasser et al. 2016). We estimated the functional connectivity (Friston 2011) between any two brain regions (region i and region j) by calculating the Pearson correlation coefficient (Zalesky et al. 2012a) between the mean activity timeseries of region i and the mean activity timeseries of region j (Biswal et al. 1995). We represented the N × N functional connectivity matrix as a graph or network in which regions were encoded as network nodes and in which the functional connectivity between region i and region j was encoded as the weight of the network edge between node i and node j. We used this encoding of the data as a network to produce an undirected, signed adjacency matrix A. Additionally, to evaluate whether our results were dependent on specific node definitions, we examined an alternative network constructed by applying a gradient- and similarity-based parcellation of the cerebral cortex (Schaefer et al. 2017; see Supplementary Section 3 and Supplementary Figure 6).

Original efforts in the emerging field of network neuroscience (Bassett and Sporns 2017) began by studying binary graphs, where edges were assigned weights of either 1 or 0 (Scannell et al. 1995; Sporns et al. 2005; Kaiser and Hilgetag 2006). In the context of functional brain networks, these early studies thresholded the functional connectivity matrices, often based on statistical testing of significance (Achard et al. 2006). Edges with original weights greater than the threshold were maintained as edges with a new weight of 1, while edges with original weights less than the threshold were assigned a new weight of 0 (Bassett et al. 2006; Stam et al. 2007; Rubinov et al. 2009). However, recent evidence has demonstrated that the maintenance of edge weights is critical for an accurate understanding of the underlying biology of neural systems (Bassett and Bullmore 2017). Simultaneously, recent evidence in applied mathematics has demonstrated that graph-related calculations are markedly more robust in weighted graphs than in binary graphs (Good et al. 2010). In light of these two strands of evidence from the application domain and from mathematics, we maintained all edge weights without thresholding and studied the full graph including both positive and negative correlations.

In the construction of these functional brain networks, we noticed that some participants did not have adequate coverage of all 360 brain regions. Because graph statistics tend to be heavily biased by the size of the graph, we ensured that the number of brain regions was consistent across participants. Specifically, we observed that 23 participants did not have adequate coverage (<50% brain tissue in functional space) of the right area 52 parcel, which is the smallest parcel in the multimodal parcellation used in this work. Accordingly, we excluded this parcel across all participants, leaving 359 nodes for subsequent analysis. Three participants had inadequate coverage of parcel V3B (left V3B, n = 2; right V3B, n = 1); we excluded these participants from further analysis (see Participant Sample).

Network Statistics

In the course of our investigation, we sought to assess the effects of SES on both local and mesoscale architecture in functional brain networks estimated from fMRI BOLD measurements acquired at rest. To assess local network architecture, we used the most commonly studied graph measure of local connectivity—the clustering coefficient—that is commonly interpreted as reflecting the capacity of the system for processing within the immediate neighborhood of a given network node (Achard et al. 2006; Bartolomei et al. 2006; Bassett et al. 2006; Xu et al. 2016). This measure of local connectivity is often interpreted as a measure of local segregation in arbitrary network systems including the brain (Sporns 2010; Garcia-Ramos et al. 2016; Ciullo et al. 2018), although the field still lacks definitive studies linking the clustering coefficient of functional connectivity patterns to segregation of information in finely resolved circuit-level data acquired invasively in nonhuman animals. While mesoscale network architecture comes in several forms (Betzel et al. 2018), we considered the most commonly studied mesoscale organization—assortative community structure—that is commonly assessed by maximizing a modularity quality function (Porter et al. 2009; Fortunato 2010). Together, these two measures allow us to distinguish between effects of SES that are differentially located within immediate or extended neighborhoods of the functional brain network.

Clustering Coefficient

While the clustering coefficient has been defined in several different ways, it is generally considered to be a measure of local network segregation that quantifies the amount of connectivity in a node’s immediate neighborhood. Intuitively, a node has a high clustering coefficient when a high proportion of its neighbors are also neighbors of each other. We specifically used a formulation that was recently generalized to signed weighted networks (Zhang and Horvath 2005; Costantini and Perugini 2014). This version is sensitive to nonredundancy in path information based on edge sign as well as edge weight and importantly distinguishes between positive triangles and negative triangles, which have distinct meanings in networks constructed from correlation matrices.

To present the formal definition of the clustering coefficient, we begin by representing the functional connectivity network of a single participant as the graph G = (V,E), where V and E are the vertex and edge sets, respectively. Let 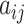be the weight associated with the edge (i,j)∈V, and define the weighted adjacency matrix of G as 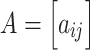. The clustering coefficient of node i with neighbors j and q is given by

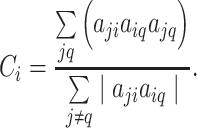(1)

The clustering coefficient of the entire network was calculated as the average of the clustering coefficient across all nodes as follows:

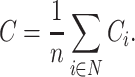(2)

In this way, we obtained estimates of the regional and global clustering coefficient for each subject in the sample.

When examining analyses conducted on thresholded networks containing only positive weights, a formulation of the clustering coefficient suitable for fully weighted networks was used (Zhang and Horvath 2005), analogous to that presented above (see Supplementary Section 4).

Modularity Quality Index

As with the clustering coefficient, there are many different statistics that have been defined to quantify the modular structure of a network. Yet, many of them have in common the fact that they have been constructed to assess the extent to which a network’s nodes can be subdivided into groups or modules characterized by strong, dense intramodular connectivity and weak, sparse intermodular connectivity. Our approach is built on the modularity quality function originally defined by Newman (Newman 2006) and subsequently extended to weighted and signed networks by various groups.

Specifically, we follow Rubinov and Sporns (2011) by first letting the weight of a positive connection between nodes i and j be given by 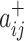, the weight of a negative connection between nodes i and j be given by 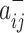, and the strength of a node i, 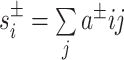, be given by the sum of the positive or negative connection weights of i. We denote the chance expected within-module connection weights as 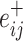for positive weights and 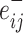for negative weights, where 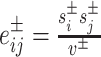. We let the total weight, 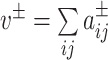, be the sum of all positive or negative connection weights in the network. Then the asymmetric generalization of the modularity quality index is given by

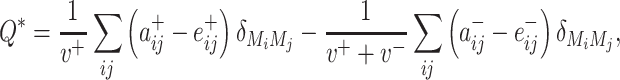(3)

where 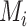is the community to which node i is assigned, and 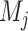is the community to which node j is assigned. We use a Louvain-like locally greedy algorithm as a heuristic to maximize this modularity quality index subject to a partition M of nodes into communities.

Network Null Models

To explicitly test whether the topological properties of functional brain networks were significantly different from those that would be expected by chance, we conducted comparisons with two distinct random network null models that differed in their level of stringency. To define these null models, we first note that a node’s degree is given by the number of edges emanating from it or leading to it, and the strength of a node is the average weight of the edges emanating from it or leading to it. Our first, and least stringent null model, was one in which the empirical network topology is destroyed by permuting the location of edges uniformly at random while maintaining the degree distribution. This null model is commonly used in the literature, but may be better suited to the study of binary networks where the degree distribution is an important feature than it is to the study of weighted networks where the strength distribution may also be an important feature of the topology (Rubinov and Sporns 2011; Bassett and Bullmore 2017). To be conservative, therefore, we also employed a null model that preserved both the degree and strength distributions, suitable for use in complex functional brain networks. This model preserves both the sign and approximate weight of connections when permuting edges. We generated a total of 100 instantiations of each null model per participant.

ReHo

To gain a fuller understanding of the neural mechanisms underlying associations between age and functional network topology, we also considered the local organization of the BOLD signal within each region of interest. Specifically, we estimated voxelwise ReHo using Kendall’s coefficient of concordance computed over the BOLD timeseries in each voxel’s local neighborhood, defined to include the 26 voxels adjoining its faces, edges, and vertices (Zang et al. 2004). Preprocessing steps were identical to those described above. We then computed the mean ReHo of each of the N = 360 cortical regions of interest.

Statistical Modeling and Testing

The relationship between various markers of brain development and age is sometimes nonlinear (Shaw et al. 2006), as is the relationship between these same markers and SES (Piccolo et al. 2016). Thus, we first examined our data for the presence of nonlinear relationships between the clustering coefficient and age. Flexible nonlinear functions were estimated using generalized additive models with the mgcv package in R (Wood 2011; Satterthwaite et al. 2014b). The penalty parameters for the nonlinear spline terms were fit as random effects and tested using restricted likelihood ratio tests (RLRTs) with RLRsim (Scheipl et al. 2008). Note that these tests of nonlinearity are constructed so as to test for nonlinear effects over and above any linear effects that may be present.

After confirming the absence of any significant nonlinear relationships, we proceeded with linear models. Specifically, we modeled the linear effect of age and the age × SES interaction on network topology while controlling for sex, race, head motion (mean relative RMS displacement over the whole timeseries), and average edge weight in the functional brain network. The choice to include the average edge weight as a covariate of noninterest ensures that subsequent results reflect changes in network topology rather than global differences in connectivity strength (Van Wijk et al. 2010; Ginestet et al. 2011; Yan et al. 2013). We used multiple ordinary least squares linear regression with the lm() command in R to fit the following general equation:

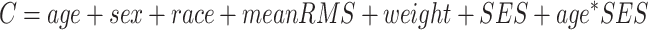(4)

where C is the global clustering coefficient. Analyses examining the main effect of age or SES on network topology omitted the interaction term. All β values reported are standardized coefficients. We used the R package visreg to calculate 95% confidence intervals around fitted lines and to generate partial residuals.

We used an identical model when estimating age and age × SES effects on network statistics of individual brain regions (Fig. 3). For all analyses performed at the node level, we controlled for multiple comparisons using the false discovery rate (q < 0.05) (Benjamini and Hochberg 1995). We tested for significant differences between nested models when appropriate using likelihood ratio tests.

Figure 3.

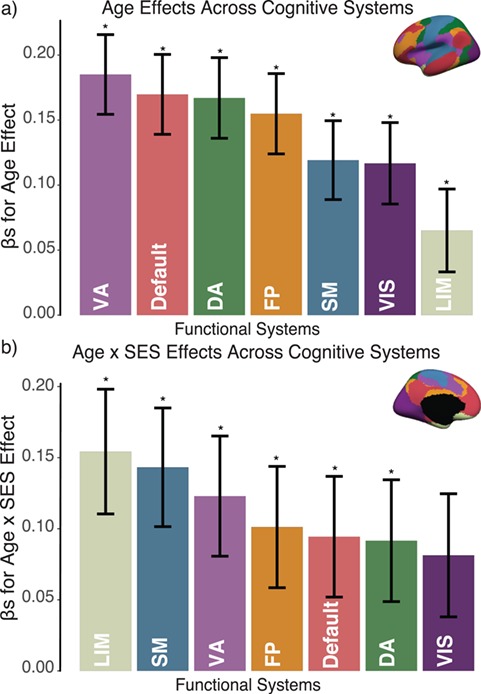
Variation in age and SES is associated with system-level functional network topology at rest. (a) Older age is associated with higher clustering coefficient most strongly in the default mode, ventral attention, and dorsal attention systems. (b) SES effects on associations between age and the clustering coefficient were strongest in the limbic, somatomotor, and ventral attention systems. Error bars depict standard error of the mean (SEM), and asterisks indicate p_FDR < 0.05. VA: ventral attention; DA: dorsal attention; SM: somatomotor; LIM: limbic; FP: frontoparietal; VIS: visual.

To examine associations between SES and development within putative functional networks, we assigned each node to 1 of 7 large-scale functional systems defined a priori (Yeo et al. 2011). We then calculated the average clustering coefficient across nodes within each system and examined the linear effect of age and the age × SES interaction for each system separately. To examine whether the age × SES interaction differed across cognitive systems, we examined the fit of a model including a 3-way interaction (age × SES × cognitive system) compared with a restricted model including only the age × SES interaction. As an additional test, we estimated the similarity between the system partition and the distribution of the effect estimates. Specifically, in this analysis, we first normalized and discretized the effect estimates, and then we calculated the z-score of the Rand coefficient between the discretized interaction effects across nodes and the partition of nodes into systems (Traud et al. 2011). We assessed statistical significance using a non-parametric permutation test; we permuted the distribution of interaction estimates uniformly at random 10 000× and, for each permutation, calculated the z-score of the Rand coefficient between the interaction estimates and the Yeo system partition. Then, we rank-ordered the z-scores of the Rand coefficient on permuted data and compared the true value of the z-score of the Rand coefficient with that of the null distribution. Observing higher effect estimates in a specific cognitive system suggests that the variable of interest (age or age × SES) is more strongly associated with the variation in the clustering coefficient in that system.

To examine the relationship between ReHo and the clustering coefficient, we examined pairwise partial correlations between the 2 metrics across regions, controlling for all covariates specified in Equation 4 above. To examine age and age × SES effects on the clustering coefficient above and beyond the effects of ReHo, we regressed the regional ReHo out of the regional clustering coefficient and used the residuals of this regression as the variable of interest in Equation 4 in place of the raw clustering coefficient to again assess effects across cortical areas.

To examine the effect of physical distance on our findings, we follow Betzel and Bassett (2018) by thresholding each network by distance in bins, ranging from the top 10% of shortest edges to the bottom 10% of longest edges. We then calculated the clustering coefficient on these sparse networks and estimated the age × SES effect within each distance bin. The physical distance of an edge was estimated as the Euclidean distance between the centroids of 2 regions of interest in the template space. Although Euclidean distance is an imperfect proxy for anatomical connection distance, previous work has shown it to be comparable to measures of wiring distance based on diffusion imaging data (Supekar et al. 2009). We assessed statistical significance using null network models that permuted the distribution of edge weights uniformly at random within subgraphs. We calculated the clustering coefficient on these null network models, and we compared the age × SES effect observed in the null models with that observed in the empirical data.

We used non-parametric permutation tests to assess the significance of the differences in strength of age × SES effects across edges. We permuted the distribution of edge weights uniformly at random and calculated standardized coefficients for the age × SES effect, averaged for 1) edges between nodes that demonstrated a significant node-level effect, 2) edges between these nodes and the rest of the brain, and 3) edges connecting nodes that did not show a significant node-level effect. We then compared the true differences in standardized coefficients with the differences calculated from permuted distributions of edge weights.

We conducted all analyses in R (R Core Team 2013) and MATLAB using custom code as well as functions from the Brain Connectivity Toolbox (Rubinov and Sporns 2010). The data reported in this paper have been deposited in the database of Genotypes and Phenotypes under accession number dbGaP:phs000607.v2.p2 (https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v2.p2). Code for analyses presented here is available at www.github.com/utooley/rsfmri_envi_networks.

Results

Variation in Age and SES Is Associated With Whole-Brain Functional Network Topology at Rest

We sought to understand how functional brain network topology at rest related to age and SES by first considering a metric of local segregation. We found that age significantly predicted the average clustering coefficient, with older children displaying higher average clustering coefficients than younger children (Fig. 2c, β = 0.17, 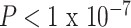). Sex (higher in females, β = 0.10, P = 0.001), mean edge weight (β = 0.17, 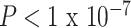), and in-scanner motion (β = −0.16, P < 1 × 10⁻⁷) were also significant predictors of average clustering coefficient. The main effect of SES was not significant (β = 0.03, P = 0.5; full model: F(7,1004) = 16.07, 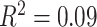, 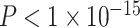). We observed no significant nonlinear relationship between the average clustering coefficient and age (RLRT = 0.39, P > 0.15) or network weight (P > 0.2).

Notably, we observed a significant interaction between SES and age, such that high-SES youth demonstrate a stronger positive association between age and average clustering coefficient than low-SES youth (Fig. 2e, P = 0.004). Mean edge weight (β = 0.16, 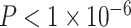) and motion (β = −0.17, 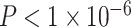) were also significant predictors of clustering coefficient in this model (full model: F(8,1003) = 15.18, 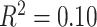, 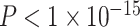). We observed similar results when controlling for maternal education but do not find similar results when using maternal education in lieu of neighborhood SES (see Supplementary Section 1). In a final conservative test, we observed no significant effects of age or age × SES interactions in random network null models that 1) preserved degree distribution or 2) preserved mean edge weight, degree distribution, and strength distribution (all P values greater than 0.33). We also pursued an extensive set of supplementary analyses to ensure that our results were not due to specific methodological choices (See Sensitivity Analyses and Supplementary Sections 2–4). To ensure that our results were not specific to the multimodal parcellation used in the main analyses, we reanalyzed the data using an alternative parcellation scheme. Notably, we observed qualitatively similar results when employing a parcellation generated from gradients and similarity of intrinsic functional connectivity patterns (Schaefer et al. 2017). Age was positively associated with the average clustering coefficient (β = 0.13, 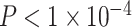), and we observed a significant interaction between SES and age, such that high-SES youth demonstrate a stronger positive association between age and average clustering coefficient than low-SES youth (P = 0.002; see Supplementary Section 3 and Supplementary Fig. 6 for full models).

Next, using a metric of mesoscale segregation, we conducted a set of parallel analyses to determine the relations between age and SES and the modularity quality index. We observed that older age was associated with a higher modularity quality index (Fig. 2d, β = 0.16, 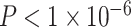). Sex (higher in females, β = 0.10, P = 0.001), mean edge weight (β = −0.21, 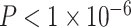), and in-scanner motion (β = −0.07, P = 0.02) were all significant predictors of the modularity quality index; the main effect of SES was not significant (β = −0.01, P = 0.8; full model: F(7,1004) = 16.78, 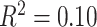, 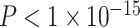). Notably, a model including the interaction of age and SES was significant [F(8,1003) = 15.22, 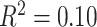,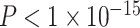]; the age-by-SES interaction was marginally significant (Fig. 2f, P = 0.05).

Intuitively, modules are composed of strong clusters. Thus, the trending significance of SES moderating the positive association between modularity and age could possibly be driven by the strength of the effect on the clustering coefficient. Statistically, we observed that the modularity quality index is significantly correlated with the average clustering coefficient (Spearman’s ϱ = 0.78, 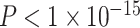). To determine which effect was driving the observed results, we included both the average clustering coefficient and the modularity quality index in a single model. Even when thus controlling for modularity, we found that SES significantly moderated the positive association between age and the average clustering coefficient (age × SES interaction, P = 0.03). Interestingly, the reverse was not the case; when controlling for the average clustering coefficient, the moderating effect of SES on the association between age and modularity was not significant (age × SES interaction, P = 0.5). Thus, we cannot claim that changes in modularity are an important marker of the moderating effect of SES on associations between age and network topology but rather conclude that the fundamental driver is the clustering coefficient and associated variation in local network topology.

Variation in Age and SES Is Associated With System-Level Functional Network Topology at Rest

We next asked whether age-by-SES interaction effects might be particularly strong in one or more putative cognitive systems. To address this question, we assigned each brain region to 1 of 7 systems defined a priori (Yeo et al. 2011), and we estimated the effect of age and SES on that system’s regional clustering coefficients (Fig. 3). We observed that the strength of the association between age and the clustering coefficient varied across cognitive systems, with strongest associations in the default mode (β = 0.17,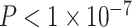), ventral attention (β = 0.19, 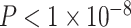), and dorsal attention (β = 0.17, 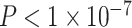) systems. We observed a significant interaction between cognitive system and age, such that the effect of age on regional clustering coefficient varied by system (P = 0.002). We also observed that the effect of SES on the association between the clustering coefficient and age varied, with a significant 3-way interaction between age, SES, and cognitive system (P < 1 × 10⁻⁶), indicating that age-by-SES interactions are distinct across cognitive systems. The strongest age × SES interaction effects were located in the somatomotor (β = 0.14, P < 0.001), limbic (β = 0.15, P < 0.001), and ventral attention (β = 0.09, P = 0.03) systems (see Supplementary. Fig. 2 for full interaction plots by system). Finally, we calculated the z-score of the Rand coefficient between the vector of regional interaction β’s and the vector of regional system assignments and found that the 2 were significantly more similar than would be expected by chance (permutation testing, P < 0.0001). Together, these data indicate that age-by-SES interactions are distinct across cognitive systems.

Variation in Age and SES Is Associated With Region-Level Functional Network Topology at Rest

We next asked whether age-by-SES interactions might differ even within cognitive systems, at the level of single brain regions. To address this question, we first noted that the clustering coefficient was highest in the bilateral posterior cingulate and precuneus, bilateral middle temporal gyrus, and bilateral insular cortex (Fig. 4a). Older age was associated with higher clustering coefficient most strongly in bilateral orbitofrontal cortex and anterior cingulate, bilateral insular cortex, right precuneus, and bilateral inferior parietal lobe (all 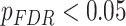; Fig. 4b). The moderating effect of SES on associations between age and the clustering coefficient was strongest in bilateral anterior and right posterior cingulate, bilateral orbitofrontal cortex, bilateral somatomotor areas including precentral and postcentral gyri, and bilateral paracentral lobule (all age × SES effects 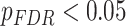; Fig. 4c). In these regions, high-SES youth display a stronger association between age and the clustering coefficient than low-SES youth (Fig. 4d).

Figure 4.

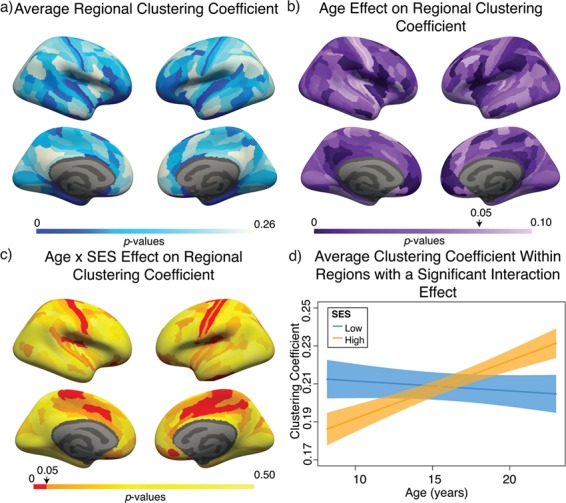
Variation in age and SES is associated with region-level functional network topology at rest. (a) On average, values of the clustering coefficient are largest in the precuneus, middle temporal gyrus, and inferior frontal gyrus. (b) Regional P values for the effect of age on the clustering coefficient. By visually comparing panel (b) with panel (a), we observe that regions with high clustering coefficient tend to show positive associations between clustering coefficient and age. (c) Regional P values for the effect of SES on associations between age and the clustering coefficient. Significant age-by-SES interactions are located in the limbic, somatomotor, and ventral attention systems. Image is thresholded to control for multiple comparisons using a false discovery rate of q < 0.05; significant regions are shown in red. (d) SES effects on the positive relationship between age and the clustering coefficient, extracted from only nodes that show a significant age-by-SES interaction.

ReHo

To better understand these regional effects, we considered an even finer-grained measure of the neurophysiology: ReHo, which assesses the similarity of the BOLD time course within a voxel to that of its neighboring voxels. ReHo is thought to reflect the strength of local or short-distance connectivity (Jiang and Zuo 2016); we employ it here to capture variation associated with intraregional as opposed to interregional functional connectivity. We note that ReHo is calculated at the voxel level and averaged across voxels within each region separately, in contrast to the clustering coefficient that is calculated from edge weights reflecting functional connectivity between regions. Thus, ReHo and clustering coefficient are mathematically independent quantities, and any observed relation between them is not an artifact of the analysis but rather could be indicative of underlying biological processes (Alexander-Bloch et al. 2010; Zalesky et al. 2012b; Lee and Xue 2017). We observed that across participants, ReHo measurements averaged over the whole brain were not significantly correlated with the average clustering coefficient (P = 0.17, controlling for subject-level covariates of age, sex, race, and in-scanner motion). Notably, we found that older age was associated with lower ReHo (β = −0.14, ), but the main effect of SES was not significant (P > 0.5, see Supplementary 5 for full models). In a model including the age-by-SES interaction, the interaction was not significant (P > 0.33). Additionally, controlling for ReHo does not affect the estimated significance of the age-by-SES interaction on the whole-brain clustering coefficient (age-by-SES interaction P = 0.002).

In contrast to the whole-brain effects, we found that across regions, mean ReHo measurements were significantly correlated with the mean nodal clustering coefficient (r = 0.59, ), a relation that held even after controlling for subject-level covariates (all _; see Supplementary Fig. 7). We examined region-level measurements of ReHo for age (Fig. 5b) and age-by-SES effects (Fig. 5c). We found that approximately one-fifth of brain regions showed an SES effect on associations between age and ReHo (59 of 359 regions, age-by-SES interaction 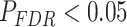). In these regions, high-SES youth show initially lower ReHo and a weaker negative relationship between age and ReHo (Fig. 5d, see Supplementary Section 5 for full whole-brain models). Although the slope of the age effect on ReHo is reversed compared with that of the clustering coefficient (average ReHo β = −0.23), the directionality of the age-by-SES interaction is similar.

Figure 5.

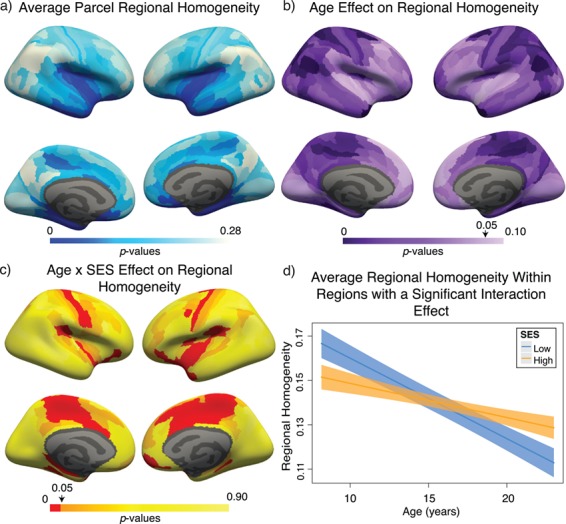
Variation in age and SES is associated with ReHo of functional brain networks at rest. (a) On average, values of ReHo are the largest in the inferior parietal lobe, precuneus, and posterior cingulate. (b) Regional P values for the effect of age on ReHo. Negative associations between age and ReHo were widespread and were strongest in the precuneus, inferior parietal lobe, and premotor cortex. (c) Regional P values for the effect of SES on associations between ReHo and age. Image is thresholded to control for multiple comparisons using the false discovery rate (q < 0.05); significant regions are shown in red. (d) SES effects on the associations between ReHo and age, extracted from only nodes that show a significant age-by-SES interaction.

It is interesting to note that while ReHo does not explain the whole-brain effect of SES on associations between the clustering coefficient and age (see above), it might at least partially explain the regional effects: low-SES youth display a stronger negative relationship between ReHo and age, which might lead to decreased edge weight due to reduced signal amplitude and thus weaker clustering of edges forming triangles connecting functionally related areas. By visually comparing Figure 3c to Figure 5c, we observe that regions with a significant age-by-SES interaction on the clustering coefficient are similar with those demonstrating an age-by-SES interaction on ReHo. Thus, we next regressed the regional effect of ReHo out of the clustering coefficient and found that this procedure eliminates the age-by-SES interaction in predicting the clustering coefficient (all regional age × SES P values greater than 0.05). These results indeed suggest that ReHo partially explains regional moderating effects of SES on positive associations between age and the clustering coefficient.

Spatial Embedding of the Associations Between Age and SES and Functional Network Topology at Rest

The fact that the moderating effects of SES on associations between age and the clustering coefficient are not fully explained by local homogeneity of connectivity as measured by ReHo suggests the presence of a second explanation dependent on nonlocal or spatially distributed processes. To probe this possibility, we separated edges into 10 equal-sized bins based on their physical length, as estimated by the Euclidean distance between regional centroids (mean edge length for bins: 24.7 mm, 40.9 mm, 51.5 mm, 60.5 mm, 68.9 mm, 76.9 mm, 84.8 mm, 93.2 mm, 103.2 mm, 120.4 mm). For each distance bin, we constructed a subgraph of the full network that was only composed of the edges whose physical distances were located within that bin, and we estimated the clustering coefficient on that subgraph. We observed the strongest effect of SES on associations between age and the clustering coefficient in subgraphs composed of middle-length connections (Fig. 6), consistent with the notion that these spatially distributed circuits are associated with SES. The moderating effect of SES on associations between the clustering coefficient and age were significantly greater in middling-length connections than expected in permutation-based null models (; see Materials and Methods).

Figure 6.

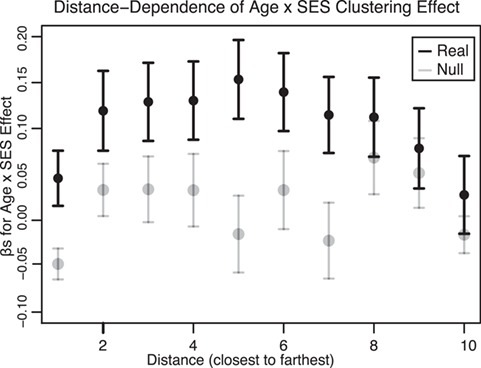
Dependence of age-by-SES interactions on the length of functional connections. We observed the strongest moderating effect of SES on associations between age and the clustering coefficient in subgraphs of the whole-brain functional network that were composed of middling-length connections. Here we show β values from the original model, calculated on subgraphs of the whole-brain functional network that are composed of edges of different lengths. Error bars depict SEM. The β values from models calculated on randomized null models of subgraphs are shown in gray. For simplicity, we segregated edges into 10 bins according to their lengths.

One possible corollary of this finding is that these middling-length edges could preferentially connect regions that show significant moderating effects of SES. Visual inspection of Figure 3c reveals that these regions are at short to middling distances from each other. To determine whether this was indeed the case, we estimated the age-by-SES effect on each edge separately and conducted permutation tests on the distribution of age-by-SES effects across 3 groups of edges: 1) edges between nodes that demonstrated a significant node-level effect on the clustering coefficient (shown in red in Fig. 3c), 2) edges between these nodes and the rest of the brain, and 3) edges connecting nodes that did not show a significant node-level effect on the clustering coefficient (shown in orange and yellow in Fig. 3c; see Materials and Methods). We observed that the effect of SES on associations between age and edge strength was significantly stronger on edges between nodes that showed a significant age-by-SES effect on the regional clustering coefficient (β = 0.0460) than on edges connecting those nodes to the rest of the network (β = 0.0055, P < 0.0001) or on edges connecting nodes that did not show an age-by-SES effect (β = 0.0012, P < 0.0001). This observation supports the intuitive conclusion of our initial findings; the edges that show a stronger association between clustering coefficient and age in high-SES youth than low-SES youth are in fact the edges forming triangles connecting regions that show a significant age-by-SES effect.

Sensitivity Analyses

We conducted an extensive set of supplementary analyses to ensure that our results were not sensitive to specific methodological choices (see Supplementary Sections 2–4 and Supplementary Figs 3–6). We conducted sensitivity analyses with a smaller sample (n = 883), excluding participants that were currently taking psychoactive medication or who had a history of psychiatric hospitalization. Excluded participants were significantly older (mean age of included participants = 15.65 years, mean age of excluded participants = 16.58 years; Student’s t-test P = 0.002) and have higher SES than those included in the restricted sample (included participants: mean percent in poverty = 16%, mean percent married = 44%, mean median family income = $73 103; excluded participants: mean percent in poverty = 14%, mean percent married = 48%, mean median family income = $85 471; P = 0.01). Results were qualitatively similar to those found in the full sample (see Supplementary Sections 2A and 2C and Supplementary Fig. 3). We observed that older age was associated with a higher whole-brain clustering coefficient (β = 0.17, 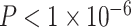, full model: F(7,875) = 12.43, 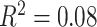, 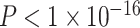). We also observed a significant interaction between SES and age, such that higher-SES youth displayed a stronger positive relationship between mean clustering coefficient and age than low-SES youth (P = 0.004; full model: F(8,874) = 12.01, 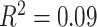, 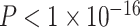). We observed qualitatively similar results when examining SES as a continuous variable in this smaller sample (see Supplementary 2B and 2C). Notably, we observed a high level of correspondence between results in various sensitivity analyses (see Supplementary Table 3). Correlations between the regional extent of age × SES interactions in different samples or with different methodological choices were high (r’s = 0.75–0.92, Ps < 0.001; see also Supplementary 2D and Supplementary Table 3 ).

We also explored potential interactions between psychoactive medication use (or previous psychiatric hospitalization) and our effects of interest (age and age × SES interactions) in the full sample (n = 1012). Neither the main effect of psychiatric history nor the age × psychiatric history interaction was significant predictors of the whole-brain clustering coefficient (Ps > 0.68). Additionally, the age × SES × psychiatric history interaction was not a significant predictor of the whole-brain clustering coefficient (P > 0.17).

Discussion

Here we examined the relationship between neighborhood SES and the development of functional brain network topology at rest. We took an explicitly multilevel approach, hierarchically investigating whole-brain summary measures of network topology, followed by higher-resolution analysis of functional systems and individual brain regions, as well as conducting analyses of metrics at several scales, from the mesoscale metric of the modularity quality index to the finer-grained metric of ReHo. In a large community-based sample of 1012 youth, we uncovered evidence that older age is associated with greater local segregation of the network, as operationalized in a commonly studied metric in graph theory known as the clustering coefficient. Youth in high-SES neighborhoods had lower initial levels of local segregation and displayed stronger positive relationships between local segregation and age than youth in low-SES neighborhoods. Local segregation was associated with age most strongly in the ventral attention, default mode, and dorsal attention systems, and SES moderated with the relationship between age and local segregation most strongly in the limbic, somatomotor, and ventral attention systems. Importantly, the effect of SES on associations between the clustering coefficient and age is partially explained by spatially distributed circuitry indicated by middling-length connections and partially explained by intraregional connectivity in the form of ReHo in the BOLD time course. Collectively, our results provide insight into the relationship between intrinsic functional brain network topology and age and how the environment might relate to these associations with development.

In youth ages 8 years to 22 years, we found that older age was associated with higher local segregation as assessed by the clustering coefficient. This is, to our knowledge, the largest study to date to address associations between local segregation and age in this age range and clarifies previous literature reporting both no change in local segregation with age (Fair et al. 2009; Supekar et al. 2009) and increases in local segregation with age (Wu et al. 2013) in functional brain networks. In our study, the observed relationship between local segregation and age was strongest in regions in the ventral attention and default mode systems, including areas of the frontal cortex, anterior cingulate, insular cortex, precuneus, and inferior parietal lobe. Increased network segregation with development has been widely reported in both structural and functional brain networks (Fair et al. 2009; Stevens et al. 2009b; Satterthwaite et al. 2013b; Baum et al. 2017) and is believed to reflect the increasing segregation and refinement of modular network architecture with age (Grayson and Fair 2017), a process that has been found to begin in infancy (Gao et al. 2015b) and continue through childhood and adolescence (Gu et al. 2015). There is increasing evidence that network segregation is advantageous for functional specialization, adaptability to task demands, and the reduction of interference across disparate functions (Fornito et al. 2012; Wig 2017), and thus these neurodevelopmental changes in local network organization could contribute to supporting maturation of cognitive functions through childhood and adolescence (Baum et al. 2017).

We found that neighborhood SES moderated associations between age and local segregation, such that high-SES youth had a stronger positive association with age than low-SES youth, a pattern suggestive of faster functional brain development in the high-SES population, though we note that we cannot address this hypothesis in this cross-sectional study. Previous work in a similar age range has suggested that high household SES is linked to a more protracted trajectory of structural brain development (Piccolo et al. 2016; LeWinn et al. 2017), though both this work and our own employ cross-sectional samples. In light of our findings, this evidence suggests that SES might be differentially associated with functional and structural brain development, such that high-SES youth have a more protracted trajectory of structural brain development but faster functional brain development. An important future direction will be to investigate how structural metrics relate to functional measures over the course of development. Alternatively, our findings might not be at odds with findings of protracted structural development in high-SES children, as high-SES youth might initially show lower levels of local segregation in late childhood due to increased synaptogenesis and widespread connectivity early in development. This putative mechanism is also supported by findings of greater gray matter volume and faster growth trajectories in high-SES infants and children (Hanson et al. 2013), which would then rapidly develop into a more segregated network architecture as synapse elimination and pruning continues into adulthood (Innocenti and Price 2005; Huttenlocher 2009).

Our findings relate to a recent report that SES moderates negative associations between age and functional network segregation, such that high-SES older adults show attenuated declines in segregation with age (Chan et al. 2018). However, it should be noted that there were many differences between this study and the current report. In Chan et al. (2018), the authors used global system segregation as their measure of network segregation and examined this measure in older and aging adults in relation to household-level SES, quantified as a composite of individual education and occupation. In their report, the authors found that when controlling for childhood SES as a covariate, SES-related differences in functional network segregation in midlife remained significant. We examined several higher-level measures of network segregation (see Supplementary Section 6), including this metric of system segregation, and did not find relationships with SES or interactions between SES and age. Chan et al. (2018) did not examine local segregation or mesoscale segregation in their report. Additionally, the system segregation measure used in their work is inherently dependent on an assigned community partition, while the metrics examined in this report are largely independent of any community partition. Our findings suggest that the moderating effect of neighborhood SES on associations between age and functional network segregation in our sample operates primarily at the local and mesoscale level rather than globally. We speculate that the effect of SES on brain function may follow a progression from local to global across the lifespan.

Another possibility is that neighborhood SES might have relationships with brain development that are distinct from those of household SES, as we do not find a similar pattern of effects when using maternal education in lieu of neighborhood SES (Whittle et al. 2017; Marshall et al. 2018). Although some previous work has employed maternal education as the sole measure of household SES (Stevens et al. 2009a; Gianaros et al. 2011), the use of only one indicator limits our ability to comprehensively model this construct; this fact may have reduced our sensitivity to detect effects of household SES on functional network segregation. Our results add depth to previous findings of alterations in connectivity that report both higher (Marshall et al. 2018) and lower (Sripada et al. 2014; Gao et al. 2015a; Barch et al. 2016) resting-state functional connectivity in low-SES populations. Our results are also in keeping with recent evidence of increased modularity in structural covariance networks of men from affluent neighborhoods as compared with deprived neighborhoods (Krishnadas et al. 2013); we also found that high-SES youth had a stronger association between age and modularity than low-SES youth, although this effect was less strong than that on local segregation.

High functional local segregation indicates that a given node is connected with a group of densely interconnected local clusters (Bullmore and Sporns 2009). Many advantageous topological properties of brain networks entail a tradeoff between these properties and wiring cost (Bullmore and Sporns 2012). If the regions in which we see higher functional local segregation were spatially confined, this increase would be parsimonious in the sense of physical wiring cost over shorter axonal distances (Henderson and Robinson 2011). In contrast, we observe that the moderating effect of neighborhood SES on associations between age and the clustering coefficient were strongest at midrange connection lengths. Increases in clustering between more distant regions entail a higher biological cost (van den Heuvel and Sporns 2011), and this might suggest that neighborhood SES entails a metabolic or environmental constraint on the more costly connections in the brain. The limbic system is particularly sensitive to experiences of adversity during development (Cameron et al. 2017), and in accordance with others’ findings (Gianaros et al. 2011; Hanson et al. 2012), we find that prefrontal areas of the limbic system show strong moderating effects of neighborhood SES on associations between local segregation and age. (Note, however, that early adversity and neighborhood SES are overlapping but distinct constructs.) We also found a strong moderating effect of SES on the positive association between age and local clustering in the somatomotor network, especially in primary motor cortex, reminiscent of other evidence for the effects of SES on functional brain network development in somatomotor regions present as early as infancy (Gao et al. 2015a). These regions undergo earlier maturation (Deoni et al. 2012; Miller et al. 2012), perhaps contributing to our ability to detect associations with the environment in childhood and adolescence, and are situated at the far end of the sensorimotor-transmodal gradient of functional cortical organization (Margulies et al. 2016; Huntenburg et al. 2018).

We examined intraregional local connectivity (ReHo), an even finer measure of the local neurophysiology than local segregation, as a potential factor influencing our results (Jiang and Zuo 2016). Zalesky et al. (2012b) found that reductions in ReHo were associated with a reduction in the strength of edges connecting those regions, potentially due to reduced signal coherence and amplitude. In a similar vein, we found that local homogeneity of connectivity is correlated with local segregation across regions (Alexander-Bloch et al. 2010; Lee and Xue 2017). Moreover, we found that controlling for ReHo accounts for the age-by-SES interaction effects on regional local segregation. Primary sensory networks including the somatomotor network have high interindividual variability in ReHo (Jiang and Zuo 2016), which might contribute to the moderating effect of SES seen on the negative association between age and ReHo in somatomotor areas. Developmental changes in intra-regional homogeneity and network segregation have both been posited to be due to pruning of local connections (Supekar et al. 2009; Lopez-Larson et al. 2011; Huang et al. 2015; Jiang et al. 2015; Lim et al. 2015). However, we note that the direction of the relationship between age and intra-regional homogeneity is unlike that of local segregation, as in this age range older youth show lower levels of the former and higher levels of the latter. Though not the focus of this paper, we speculate that this might represent a developmental shift from local connectivity to the segregated midrange connections required for distributed cognitive operations (Fair et al. 2009; Petersen and Sporns 2015; Cohen and D’Esposito 2016).

More broadly, we speculate that the relationship between environmental measures and the brain may not be constant across the lifespan. It is possible that brain structure is influenced early in development, contributing to our ability to detect early environmental effects on brain structure throughout the lifespan (i.e., Staff et al. 2012; Holz et al. 2015; Chan et al. 2018), while environmental influences on brain function may be ongoing and changing across the lifespan. We capture only a small window of these associations in this study, and controlling for childhood SES may not change results stemming from ongoing influences of the environment on brain function. Disentangling these complex relationships will require longitudinal samples with many measures, characterizing both the early and current environment of the participants. A complementary hypothesis is that environmental influences on the brain may be primarily visible during periods of rapid change such as aging or development. Such a hypothesis would imply that in this work, we capture only a small extent of environmental impacts on the brain that would be detectable during development, as at 8 years or 9 years of age (the low end of our sample age range), children have already undergone a considerable amount of developmental change.

Methodological Considerations

Several limitations inherent to this study are worth mentioning. First, this is a cross-sectional sample, with which we have limited power to examine developmental processes (Kraemer et al. 2000). As we have noted previously, longitudinal studies examining relationships between the environment and the development of functional brain network topology will be necessary to further validate our results. Second, results with developmental samples have recently been shown to be disproportionately affected by head motion (Satterthwaite et al. 2012; Roalf et al. 2016; Byrge and Kennedy 2018). To mitigate the impact of motion-related artifacts on our results, we applied current best practices in motion correction (Ciric et al. 2017) and controlled for motion in all of our analyses. Additionally, emerging evidence suggests that longer resting-state acquisitions are more optimal and improve reliability (Birn et al. 2013; Noble et al. 2017), and in this work, we collected only 6.2 min of neuroimaging data at rest. Third, low SES is associated with a number of biological factors across the lifespan that we did not assess and thus were unable to control for in our analyses, including birth outcomes (Blumenshine et al. 2010), health disparities (Cohen et al. 2010; Singh et al. 2010), and variation in neuroendocrine and cardiometabolic pathways (Evans and Kim 2007; Goodman et al. 2007; Gianaros et al. 2013, 2017). These factors have been posited as potential mechanisms underlying observed associations between childhood SES and brain outcomes; for example, work by Evans and Kim (2007) suggests that one potential mediator of changes in cardiometabolic pathways associated with disadvantage in childhood is nurturing parenting (Evans et al. 2007; Miller et al. 2014), which has also been associated with structural brain development in adolescents (Brody et al. 2017). An important direction for future work is to assess these factors and examine how each contributes singularly and in combination to observed associations between SES and brain development. Fourth, we examined neighborhood-level SES as a composite factor tied to U.S. Census data by geocoding, an approach that aligns with the few studies that examine neighborhood SES and brain development (Krishnadas et al. 2013; Whittle et al. 2017). We examined maternal education as a proxy for household-level SES and found associations between neighborhood SES and functional brain network development above and beyond the associations with household-level SES. However, maternal education reflects only one aspect of household-level SES, and thus these findings might reflect a lack of complete characterization of household SES—future data with more comprehensive characterization of aspects of the early environment will be needed to investigate this question. Additionally, SES is a multi-faceted construct with various components that might have differing associations with brain network organization, and thus a major goal for future research is to assess different specific components of both neighborhood and household SES and their independent contributions to effects on brain development (Ursache and Noble 2016; Farah 2017). Fifth, we employed null network models to examine whether functional network topology differed significantly from that expected by chance in a random network of equivalent weight and degree distribution (Rubinov and Sporns 2011), an approach with limitations when applied to correlation networks (Zalesky et al. 2012a). The development of alternative null models that more closely approximate the architecture of correlation networks commonly found in biological data is an important area for future research (Barabási and Oltvai 2004; Bazzi et al. 2016).

Conclusion

In this work, we presented evidence of an association between neighborhood SES and resting-state functional brain network topology in developing youth. We found that associations between local segregation and age are moderated by variation in neighborhood SES, in a direction consistent with an interpretation of faster functional brain development in youth from high-SES neighborhoods. Neighborhood effects on brain development have been found above and beyond household-level effects (Whittle et al. 2017; Marshall et al. 2018) and may be tied to inequalities in resource distribution, perceived safety and cohesion of the neighborhood (Sampson et al. 1997; Diez Roux and Mair 2010), school quality (Aikens and Barbarin 2008), crime (Sampson et al. 1997), or other factors such as noise pollution or green space (Estabrooks et al. 2003; Casey et al. 2017). Our findings add to the growing body of literature emphasizing the importance of the neighborhood environment during development and suggest that neighborhood-level interventions for low-SES communities hold promise for promoting healthy brain development.

Funding

John D. and Catherine T. MacArthur Foundation (to D.S.B.); Alfred P. Sloan Foundation (to D.S.B.), ISI Foundation (to D.S.B.); Paul Allen Foundation (to D.S.B.); Army Research Laboratory (W911NF-10-2-0022 to D.S.B.), Army Research Office (Bassett-W911NF-14-1-0679, Grafton-W911NF-16-1-0474, DCIST-W911NF-17-2-0181 to D.S.B.); Office of Naval Research (to D.S.B.); National Institute of Mental Health (2-R01-DC-009209-11, R01-MH112847, R01-MH107235, R21-M MH-106799 to D.S.B.); National Institute of Child Health and Human Development (1R01HD086888-01 to D.S.B.); National Institute of Neurological Disorders and Stroke (R01 NS099348 to D.S.B.); National Science Foundation (BCS-1441502, BCS-1430087, NSF PHY-1554488, BCS-1631550 to D.S.B. and Graduate Research Fellowship to U.A.T.); R01MH113550 (to T.D.S. and D.S.B.); R01MH107703 (T.D.S.); R21MH106799 (D.S.B. and T.D.S.); R01MH107235 (R.C.G.); Penn/CHOP Lifespan Brain Institute.

Notes

The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies. Conflict of Interest: None declared.