Estimates for energy expenditure in free-living animals using acceleration proxies; a reappraisal

Abstract

1. It is fundamentally important for many animal ecologists to quantify the costs of animal activities, although it is not straightforward to do so. The recording of triaxial acceleration by animal-attached devices has been proposed as a way forward for this, with the specific suggestion that dynamic body acceleration (DBA) be used as a proxy for movement-based power.

2. DBA has now been validated frequently, both in the laboratory and in the field, although the literature still shows that some aspects of DBA theory and practice are misunderstood. Here we examine the theory behind DBA and employ modelling approaches to assess factors that affect the link between DBA and energy expenditure, from the deployment of the tag, through to the calibration of DBA with energy use in laboratory and field settings.

3. Using data from a range of species and movement modes, we illustrate that vectorial and additive DBA metrics are proportional to each-other. Either can be used as a proxy for energy, and summed to estimate total energy expended over a given period, or divided by time to give a proxy for movement-related metabolic power. Nonetheless, we highlight how the ability of DBA to predict metabolic rate declines as the contribution of non-movement related factors, such as heat production, increases.

4. Overall, DBA seems to be a substantive proxy for movement-based power but consideration of other movement-related metrics, such as the Static Body Acceleration and the rate of change of body pitch and roll, may enable researchers to refine movement-based metabolic costs, particularly in animals where movement is not characterized by marked changes in body acceleration.

1. Background

No organism lives without expending energy. Energy is primarily used in supporting internal metabolism and heat production (resting metabolic rate [RMR] and specific dynamic action) and physical activity. Of these, physical activity can cause the greatest variation in the rate of energy expenditure. Extreme examples include cheetahs Acinonyx jubatus, which may expend up to 100 W/kg during a sprint (Wilson, Lowe, et al. 2013) or auks (Alcidae), which fly using 146 W/kg (Elliott, Ricklefs, et al. 2013), although even habitual costs of travel for animals are appreciable (cf. Alexander 2005). Given that animals must always engage in some behavior, even if this is inactivity, the associated variation in energy expenditure is a key link between behavior and overall fitness (Grémillet et al. 2018).

Precise measurement of energy expenditure is, however, not trivial, even within the tightly controlled conditions of a laboratory (Elia & Livesey 1992) and although the doubly-labelled water method (Schoeller & Van Santen 1982; Speakman 1997) enables estimates of field metabolic rate of wild animals between two defined times (Nagy, Girard & Brown 1999), the idea that it might be possible to determine the metabolic costs of activities of wild animals is challenging (Butler et al. 2004). Nonetheless, a number of proxies for energy expenditure in free-living animals have been proposed, most notably heart rate and, more recently, acceleration-based metrics such as dynamic body acceleration (DBA). There is extensive literature detailing the pros and cons of the heart rate method (Green 2011) which was first considered over a century ago (Henderson & Prince 1914) and used fairly extensively by the 1950s and 60s on humans (LeBlanc 1957; Booyens & Hervey 1960) and animals (Webster 1967). Similarly, decades ago, Meijer et al. (Meijer, Westerterp & Koper 1989) inter alia, considered that some aspects of acceleration might be useful as a proxy for energy expenditure in humans, although the concept was only formalized within the framework of DBA, and tested in Great cormorants Phalacrocorax carbo, in 2006 (Wilson et al. 2006). There has been a rapid uptake of this method by animal ecologists (Curry 2014) in the 12 years since the first publication and early demonstrations that DBA could predict the costs of movement for terrestrial, aquatic and even aerial locomotion over fine scales and at the level of individual animals (Halsey et al. 2009; Elliott, Le Vaillant, et al. 2013).

This study revisits the theoretical basis for DBA and the utility of these metrics for studying the energetics of wild animals, drawing, in part, upon an extensive new database of acceleration data. Specifically, we assess factors that affect the utility of DBA as a proxy for energy expenditure, from the logistics of device attachment, to the way that DBA is calibrated in laboratory and field settings, and the relevance with respect to specific life-history traits. It is hoped that this will address some of the confusion surrounding the use of DBA, as is manifest in the literature, as well as catalyse work considering improvements for the future.

2. Results and Discussion

Linking animal-generated acceleration and energy expenditure

Central to the use of acceleration as a proxy for the rate of energy expenditure (or power; nominally measured in watts), is that the major part of energy expenditure by animals above resting metabolic rate is due to movement (King & Farner 1961). Processes such as specific dynamic action (McCue 2006) and thermoregulation (Karasov 1992) cannot be quantified using acceleration metrics unless at least some part of them changes the acceleration of the animal body (such as shivering - and even then, this may be a small fraction of the process’s whole power allocation). Simply put, as the fraction of non-movement-based power increases, so the predictive power for overall power use by an animal using acceleration decreases.

The derivation of dynamic body acceleration and its link to energy expenditure is both precise and vague (Gleiss, Wilson & Shepard 2011). Precisely, vertebrates move by contracting muscles, causing limbs to move, accelerating and decelerating as they do so within their normal movement cycle. Newton’s second law tells us that the acceleration is equal to the force divided by the mass. In this case, the mass is constant and the force is provided by the muscles. Newton also tells us that the work done (J) is given by the force multiplied by the distance over which this force is applied and that the rate of doing work (or the rate of energy expenditure, in J/s or W) is given by the work done divided by the time over which it is done. This is relatively easy to apply for any pair of muscles performing opposite functions on a single limb extension and flexion. However, animals move by using a large suite of muscles, many of which act tangentially to others for limb stability (Zajac, Neptune & Kautz 2003) so the dynamic body acceleration to power link becomes generalised to a summation of the forces involved in movement, manifest by the acceleration of the trunk, the major body-mass part (see Gleiss, Wilson & Shepard 2011). In other words, the concept of DBA nominally (see below) relies on the summation of acceleration vectors (in all three dimensional axes) with temporal integration, representing the forces acting on the animal’s body-mass, thereby linking it to work and power.

How, therefore, should acceleration metrics be best treated to act as proxies for power use, given (a) the complexities of tangential muscle contraction, and (b) that the accelerations recorded by an accelerometer attached to an animal’s trunk are due to both the motion of the trunk and acceleration caused by the Earth’s force of gravitation? A triaxial sensor recording acceleration on the three orthogonal axes in a tag attached to an immobile animal’s body will only record gravitational acceleration which will be variously allocated to one of the three measurement axes according to tag orientation (cf. Shepard, Wilson, Quintana, et al. 2008). Since acceleration is a vectorial quantity, having direction as well as magnitude, the total gravitational acceleration (A_gravitation) is given by the vectorial sum of the three axis components;

$${\text{A}}_{\text{gravitation}}={({\text{Ax}}^2+{\text{Ay}}^2+{\text{Az}}^2)}^{0.5}$$ (1)

where the A term denotes the acceleration and the x, y and z, refer to the three orthogonal axes. In an immobile tag, the total acceleration will always have a vectorial sum of 1 g (the value of the Earth’s gravitational field). When the animal moves, the acceleration recorded by the three axis accelerometers will be superimposed on the values given by the Earth’s gravitational field, resulting in higher or lower values at any one time in each of the three axes depending on the movement of the animal. It is specifically the difference between the recorded acceleration from each of the axes and the Earth’s gravitational acceleration that can be allocated to movement produced by the animal. The conventional method to access the Earth’s gravitational field component is to use a lowpass filter (Sato et al. 2003; Simon, Johnson & Madsen 2012) or smoothing window (of about two seconds (Shepard, Wilson, Halsey, et al. 2008)). Subtraction of the smoothed (or filtered) data from the raw data in each axis provides an estimate of the acceleration perceived by the tag as it is produced by the movement of the animal (Gleiss, Wilson & Shepard 2011). Normally, the vectorial sum of the smoothed data (see equation 1) should equate to 1 g. During rapid turning, however, particularly where it occurs over extended periods, such as banking by a falcon or turning by a cheetah, the vectorial sum of smoothed data may exceed 1 g by some considerable amount (Wilson, Mills, et al. 2013). Similarly, an animal in freefall is expected to have a vectorial sum of the smoothed data of around 0 g. The significance of this will be discussed below.

Derivation of DBA – VeDBA and ODBA

Having removed the Earth’s gravitational field from each of the recorded acceleration axes, these should now be summed to provide a measure of DBA. Mathematically, this follows the approach given in equation 1 where the vectorial sum (Vectorial sum of the Dynamic Body Acceleration, VeDBA) is;

$$\text{VeDBA}={({\text{DAx}}^2+{\text{DAy}}^2+{\text{DAz}}^2)}^{0.5}$$ (2)

where the ‘D’ term refers to the dynamic acceleration stemming from the subtraction of the smoothed acceleration data from the raw. This expression for DBA has been tested against rate of oxygen consumption $\left(\dot{\text{V}}{\text{O}}_2\right)$ on numerous occasions across taxa (e.g. Wright et al. 2014; Bidder et al. 2017) and found to be a powerful predictor. However, its formulation is at odds with the first proposition for DBA, that of Overall Dynamic Body Acceleration (ODBA – Wilson et al. 2006) which was simply based on the non-vectorial sum of the absolute dynamic acceleration values from the three acceleration axes following;

$$\text{ODBA}=\left|\text{DAx}\right|+\left|\text{DAy}\right|+\left|\text{DAz}\right|$$ (3)

Strictly speaking, this is mathematically incorrect, but its formulation recognises that limb-, and therefore body-, movement is brought about by multiple muscles, many of which act tangentially to each other for limb stability (see above). The object was to find the best possible predictor of oxygen consumption appreciating that in the F = ma formulation, if mass (m - e.g. animal or muscle mass) is constant, the force (F) directly equates to acceleration (a). As such, a good physiological starting point is to recognize that $\dot{\text{V}}{\text{O}}_2$ is proportional to the force exerted by the muscle (Taylor et al. 1980; Alexander 2003; Praagman et al. 2006) so that the forces developed by any two-muscle pair (denoted by subscripted m) acting together; F_m1 and F_m2 will be proportional to $\dot{\text{V}}{\text{O}}_2$ via;

$${\text{F}}_{\text{m}1}={\text{k}}_{1·}{\dot{\text{V}}\text{O}}_{2\text{m}1}$$ (4)

and

$${\text{F}}_{\text{m}2}={\text{k}}_{2·}{\dot{\text{V}}\text{O}}_{2\text{m}2}$$ (5)

where the numbers of the subscripts refer to the two muscles and k-values are constants of proportionality. It is now reasonable to try and find a force/acceleration metric that recognizes that the total oxygen being consumed by the two-muscle system described above $\left(\dot{\text{V}}{\text{O}}_{2\text{total}}\right)$ will be;

$${\dot{\text{V}}\text{O}}_{2\text{total}}={\dot{\text{V}}\text{O}}_{2\text{m}1}+{\dot{\text{V}}\text{O}}_{2\text{m}2}$$ (6)

which is a scalar sum, not a vectorial solution (Qasem et al. 2012). However, reverting back to the force vectors for each muscle, we have;

$${\text{F}}_{\text{m}1}={({{\text{Fx}}_{\text{m}1}}^2+{{\text{Fy}}_{\text{m}1}}^2+{{\text{Fz}}_{\text{m}1}}^2)}^{0.5}$$ (7)

where x, y and z refer to the orthogonal measurement axes, and

$${\text{F}}_{\text{m}2}={({\text{F}{\text{x}}_{\text{m}2}}^2+{\text{F}{\text{y}}_{\text{m}2}}^2+{\text{F}{\text{z}}_{\text{m}2}}^2)}^{0.5}$$ (8)

so that the force magnitude resulting from two muscles acting perpendicular (the situation would be more complex if the muscles were not perpendicular) at the same point would be;

$${\text{F}}_{\text{magnitude}}={({[{({\text{F}{\text{x}}_{\text{m}1}}^2+{\text{F}{\text{y}}_{\text{m}1}}^2+{\text{F}{\text{z}}_{\text{m}1}}^2)}^{0.5}]}^2+{[{({\text{F}{\text{x}}_{\text{m}2}}^2+{\text{F}{\text{y}}_{\text{m}2}}^2+{\text{F}{\text{z}}_{\text{m}2}}^2)}^{0.5}]}^2)}^{0.5}$$ (9)

while the oxygen consumption is expected to be given by eqn (6) or, substituting eqns (4) and (5);

$$\dot{\text{V}}{O}_{2\text{total}}={\text{F}}_{\text{m}1}/{\text{k}}_1+{\text{F}}_{\text{m}2}/{\text{k}}_2$$ (10)

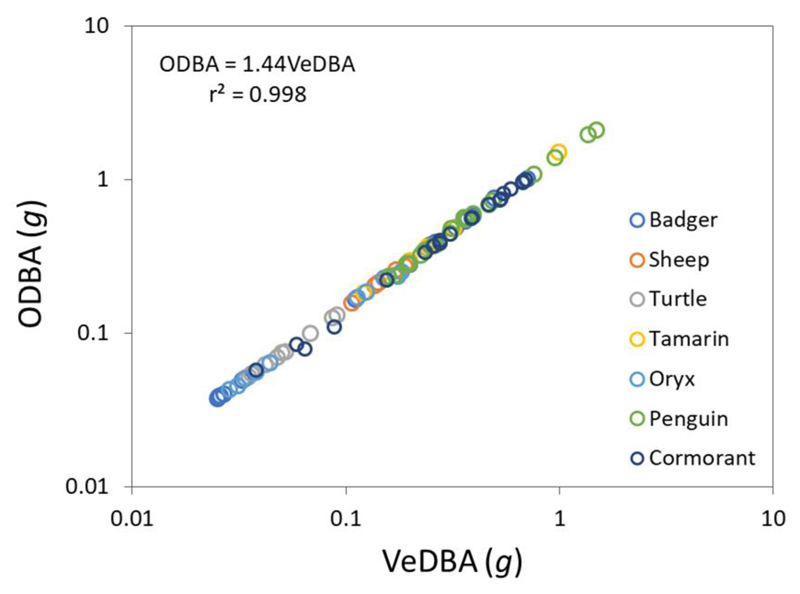
The fundamental difference between eqns (9) and (10) reflects either a vectorial or scalar sum expression, respectively, based on the resultant forces of the two muscles (cf. eqn 3), and represents the two different forms of DBA (eqns (2) and (3), respectively). Notably, acceleration can effectively be substituted for force in eqns (9) and eqn (10) (see above) by removing the constants of proportionality. This then, in part, explains the discrepancy between ODBA and VeDBA and highlights why both terms have merit in their own way (Qasem et al. 2012). In fact, proper comparisons of one against the other for their predictive capacity for $\dot{\text{V}}{\text{O}}_2$ are rare. However, where they do occur, ODBA is statistically marginally better (Qasem et al. 2012; Bidder et al. 2017) although there are cases where there seems no significant difference between the two (Wright et al. 2014). There are also some curious findings regarding the difference between ODBA and VeDBA, such as ODBA varying statistically significantly with (human) movement over surface type while VeDBA does not (Bidder et al. 2017). Unsurprisingly, the two metrics are very closely linked. Qasem et al. (Qasem et al. 2012) noted, for running humans, a linear relationship between ODBA and VeDBA and a r² of 0.987. In fact, a regression of VeDBA against ODBA across multiple disparate species engaged in a large variety of activities (Fig. 1) shows that the data essentially all fit along one tight line with a gradient of 1.42.

Figure 1.

Mean ODBA versus mean VeDBA values for a variety of animals equipped with tri-axial accelerometers (dots show values from individuals) engaged in activities ranging from resting to walking, swimming, flying, and feeding (see supplementary information 1).

This is extremely convenient since it means that workers wishing to compare data sets can convert between metrics. Given that there is little to choose between ODBA and VeDBA, we suggest that researchers use the term DBA generally, but be specific about its derivation at the outset. Those requiring the absolute best fit between DBA and $\dot{\text{V}}{\text{O}}_2$ may prefer to use ODBA while those seeking to describe animal motion without the energetic component may prefer VeDBA. We would however, suggest that workers standardize terminology to avoid confusion (cf. Duriez et al. 2014).

Factors affecting DBA metrics

Tag position

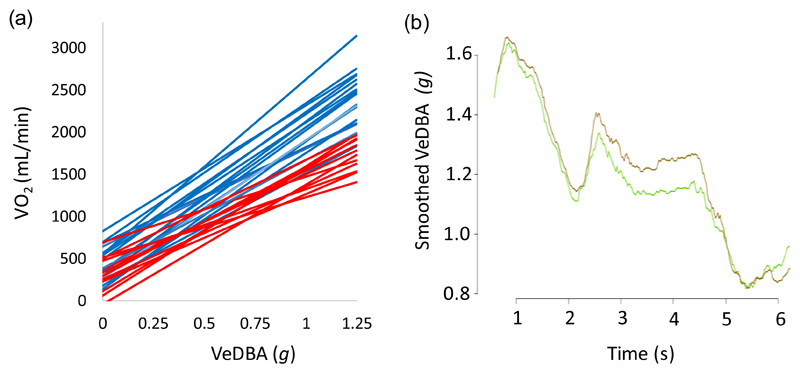
What turn out to be niceties in differences between ODBA and VeDBA as predictive metrics of $\dot{\text{V}}{\text{O}}_2,$ are, in fact, overshadowed by a number of other factors which profoundly affect DBA metrics and which are often not considered. Perhaps the most pertinent of these is tag position on the animal. It is generally possible to orientate a tag on an animal so that the tag’s orthogonal axes concur with the major body axes of the animal and thereby obviate any concerns about angular inadequacies of the ODBA metric (Qasem et al. 2012). This also dovetails with worker aims when using acceleration data to determine animal behaviour (Shepard, Wilson, Quintana, et al. 2008). But, just as a tag located at different positions along a limb produces different acceleration signals (Liu, Inoue & Shibata 2009), variation in within-body tag positionings produces substantial differences in DBA (Figure 2). This therefore also changes the different relationship between $\dot{\text{V}}{\text{O}}_2$ and DBA (the example between back- and waist-mounted tags for 15 humans running at various speeds shows highly statistically significant differences in both intercept (supplementary information 2 (t = 5.04, df = 14, P < 0.001) and slope (t = 3.36, df = 14, P < 0.004)). Clearly therefore, the relationship between DBA and $\dot{\text{V}}{\text{O}}_2$ for one tag position cannot then be used to extrapolate to $\dot{\text{V}}{\text{O}}_2$ from another tag position (Fig. 2b). So where should the tag be placed? Actually, ideally at the centre of gravity, which is generally impossible for external tag attachments since it is in the centre of the animal’s trunk. However, as long as the accelerometer is placed on main mass of the animal, it probably does not matter much, provided that the position is held constant between individuals.

Figure 2.

The variation in VeDBA according to the logger position. (a) The best fit relationships between (mean) VeDBA and oxygen consumption for 15 humans moving on a treadmill at various speeds. DBA metrics were either calculated from an accelerometer mounted on the upper-back (blue lines) or waist (red lines). Each line shows fits from one individual derived from >10 speeds (see supplementary information 2). (b) The difference in smoothed VeDBA (over 0.5 s) for a pigeon taking flight equipped with two tri-axial accelerometers, one on the upper back (green line) and one on the lower back (brown line). The difference between the signals varies with the flight phase (see supplementary information 3).

Tag stability

In a manner similar to physical positioning of a tag to an animal, tag stability on the body can also make a profound difference to the DBA signal. Thus, tags on collars that are not standardized to neck diameter can be expected to move differently to those that are fitted snugly, with looser collars tending to rotate more. This can be a problem if devices are attached for long periods and the target animal’s body mass also changes substantially (Hilderbrand et al. 1999). Nonetheless, this might be obviated through the use of glue as an alternative method of attaching tags, a practice that is often employed by pinniped researchers (e.g. Rosen, Gerlinsky & Trites 2018). Unsurprisingly, tags attached to birds using tape (Wilson & Wilson 1989) are also subject to wobble more if not fixed carefully. Indeed, even within a single deployment, birds may carry accelerometers that produce an increasingly dynamic signal under defined behaviours, if the study animal is prone to removing the tags, with consequences for DBA metrics.

Environmental DBA

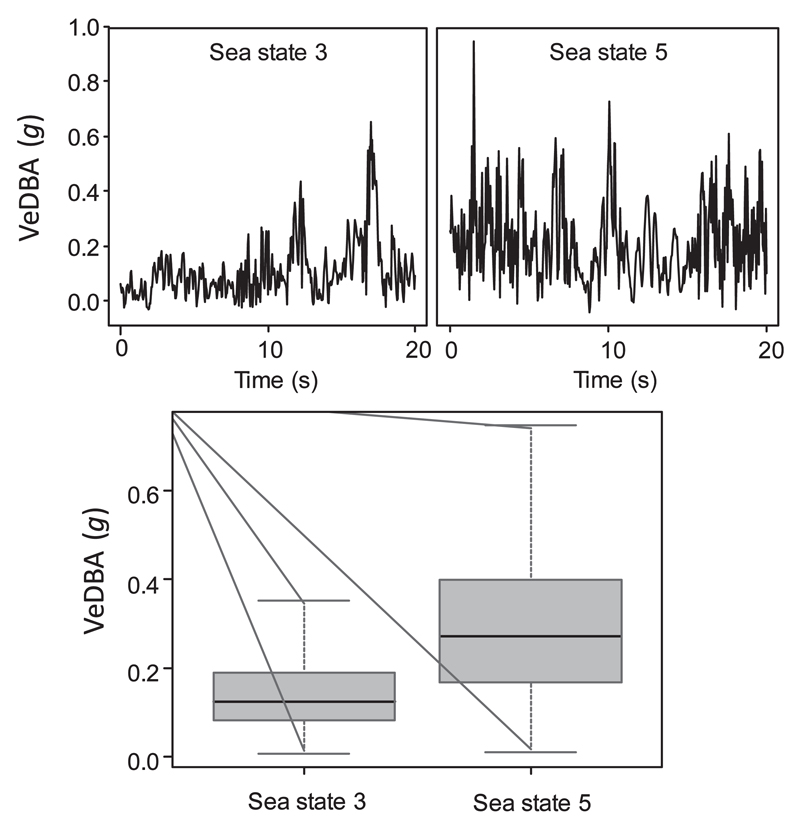
A central tenet behind the use of DBA is that the acceleration must be derived from the muscle-powered movement of the animal. Animal bodies can, however, be subject to substantive environmental acceleration, most notably caused by flow in fluid media, such as turbulence or variation in wind strength in air or wave action in water. For example, an Imperial cormorant Phalacrocorax atriceps resting on land has a mean ODBA of 0.075 g (Gómez-Laich et al. 2011), which equates to about 15 W/kg (Gómez-Laich et al. 2011), and this power use is expected to be similar to birds resting at the surface between dives.

However, sea state can profoundly change the DBA value so that, for example, an Imperial cormorant resting between dives during Beaufort sea states 3 and 5 has predicted mean ODBA values of 0.17 and 0.40 g (after conversion of VeDBA values of 0.12 and 0.28 g, respectively (see above)) (Fig. 3) which, using the power versus ODBA relationship in Gomez-Laich et al. (2011) translates to 19.1 and 28.6 W/kg.

Figure 3.

Environmental DBA, recorded by tags on Imperial Cormorants Phalacrocorax atriceps resting at sea in Patagonia. The upper two panes show the change in VeDBA over time for two different Beaufort sea states (ascertained by examining video footage from the birds (Gómez-Laich et al. 2015). The lower pane shows a box Whisker plot of the data (see supplementary information 4).

The nature of the general relationship between mean DBA and $\dot{\text{V}}{\text{O}}_2$

Regressions of DBA versus $\dot{\text{V}}{\text{O}}_2$ for humans walking and running are essentially linear (cf. Halsey et al. 2009; Wright et al. 2014; Bidder et al. 2017) and this general relationship of;

$$\dot{\text{V}}{\text{O}}_2=\text{kDBA}+\text{c}$$ (11)

where c = RMR (where the DBA value is typically around zero) and k is the gradient of the line, also holds for all species tested thus far. This includes shellfish (Robson et al. 2012), fish (Wright et al. 2014), amphibia (Halsey & White 2010), reptiles (Halsey, Jones, et al. 2011), mammals and birds (Halsey et al. 2009). The generality of this relationship means that it should be possible to couple activity-specific metabolic rate measured within one context (e.g. Allers & Culik 1997) to DBA-specific activities from another study (Graf et al. 2016) (see e.g. Fig. 4). Furthermore, determination of both the intercept and the gradient of the $\dot{\text{V}}{\text{O}}_2$ versus DBA line, with error bars, should allow workers to approximate the metabolic costs of other activities using just DBA metrics. Although the method will not be perfect (e.g. see Gómez-Laich et al. (2011) and Elliot et al. (2013) for consideration of the effects of movement by different muscle groups and in variable media may affect the relationship), it will be more informed than having no measure to link DBA with metabolic rate, and will also capitalize on the extensive work undertaken by all relevant studies.

Figure 4.

The relationship between DBA and $\dot{\text{V}}{\text{O}}_2$ (± SD) in Eurasian beavers Castor fiber, estimated by combining data from different studies; two of which quantified DBA during swimming and resting (PMG & FR unpublished data, n = 7, and (Graf et al. 2015), n=12) and one which quantified $\dot{\text{V}}{\text{O}}_2$ for the same activities (Allers & Culik 1997, n = 6). Although imperfect, the points and the spread around them show the general expected relationship between ODBA and $\dot{\text{V}}{\text{O}}_2$, following the standardized y = mx + c linear model found to date across taxa (see text).

Linking DBA and $\dot{\text{V}}{\text{O}}_2$ over variable timescales; (i) laboratory tests

There is general acceptance that DBA is a powerful proxy for movement-based metabolic rate but little discussion of the shortest period of time over which this might be valid. A standard method used to calibrate DBA (as well as heart rate), is indirect respirometry, measuring oxygen consumption (and/or carbon dioxide production) for laboratory animals moving at a number of constant velocities (e.g. on a treadmill), each for at least 3 minutes of steady-state motion (Halsey, Shepard & Wilson 2011). The three minute time imposition allows oxygen deficits, incurred due to mechanical movement, to be translated out of the muscles, through the blood stream and into the inhaled air (Barstow, Casaburi & Wasserman 1993). It also allows time for the respirometry system to move sampled air into the gas analyser (although this can be calibrated). However, there is no reason why this 3 minute resolution should be mandated on DBA metrics. As explained above, the link between movement-based DBA and energy expenditure should be precisely linked in time.

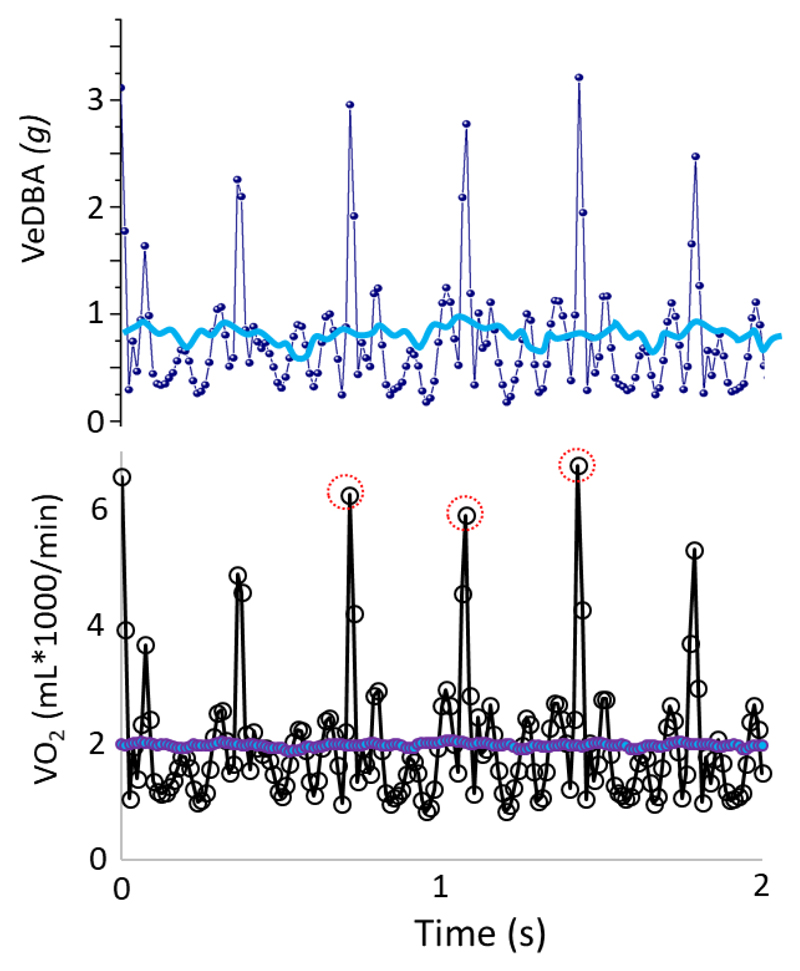
How much, therefore, can be said about the costs of movement over periods of less than 3 minutes? In the simplest case of an animal engaging in repetitive motion, such as striding at a constant frequency at gaseous equilibrium in a respirometry chamber, the mean DBA can be equated to the mean $\dot{\text{V}}{\text{O}}_2$ (Wilson et al. 2006). Theoretically, the mean DBA can also be equated to the mean $\dot{\text{V}}{\text{O}}_2$ over one second, not least because when $\dot{\text{V}}{\text{O}}_2$ is converted to power (cf. Randall et al. 2002), it is expressed in joules per second. Indeed, given this, it is logical that the cost of single strides can also be calculated by dividing oxygen consumption over a defined period by the number of strides. Importantly though, within stride variation in DBA reflects a suite of processes that are not all based on muscular contraction forces directly, such as recovery of elastic energy stored temporarily within tendons (Alexander 2002) (Fig. 5). This restricts the time scale over which DBA metrics can be used to derive $\dot{\text{V}}{\text{O}}_2$, as sub-stride variation in DBA should not be translated linearly into a $\dot{\text{V}}{\text{O}}_2$ estimate (Fig. 5). Nonetheless, it should be possible to estimate the costs of movement above individual strides (and perhaps even single strides) following appropriate smoothing of the acceleration data, coupled with $\dot{\text{V}}{\text{O}}_2$ collected over an appropriate 3 minute steady-state calibration period.

Figure 5.

Upper pane; instantaneous DBA over 2 s for a human on a treadmill travelling at 10 km/h (dark blue line) as well as the DBA smoothed over 1 s (light blue line). Note the peaks in the instantaneous signal showing the impact of the foot hitting the floor. The lower pane shows the direct conversion of both into oxygen consumption following standard (3 min) calibration (see text, cf. Fig. 2). Note how conversion of the instantaneous signal results in impossibly high $\dot{\text{V}}{\text{O}}_2$ values (circled), but how the smoothed signal eliminates this.

Interestingly, detailed examination of the practice of determining $\dot{\text{V}}{\text{O}}_2$ and DBA of subjects on treadmills reveals variation that is problematic to explain, and rarely highlighted. A fundamental concept behind the use of treadmills is that they should allow perfectly steady-state locomotion, particularly in humans, who can be instructed to adhere most to those conditions, so that both DBA and $\dot{\text{V}}{\text{O}}_2$ metrics should be constant at any given speed. This is not the case for either (Fig. 6). The variation in $\dot{\text{V}}{\text{O}}_2$ (Fig. 6b) may be partly due to variation in DBA (Fig. 6a), albeit with an unknown and presumably varying time-lag, but why DBA, even smoothed, should vary to the extent that it does, is unclear. Further work is needed to clarify this because the consequences for DBA metrics and their relation to $\dot{\text{V}}{\text{O}}_2$ are appreciable (Fig. 6).

Figure 6.

Variation in measured rate of oxygen consumption (upper panel) and VeDBA (smoothed over 2 s) (lower panel) for a human with a waist-mounted tag running on a treadmill at a series of constant speeds that increased stepwise by 1 km/h between 3 and 11 km/h (after an initial period at 0 km/h). $\dot{\text{V}}{\text{O}}_2$ was measured using mask respirometry on a breath-by-breath basis but averaged over 5 s (Oxygon Pro [Jaeger Oxygon Manual Version 4.5]). Note the lag in response of the oxygen consumption (see text) but also considerable variability in both this and the smoothed VeDBA, even within one speed (the large step in DBA corresponds to the gait changing from walking to jogging).

Linking DBA and $\dot{\text{V}}{\text{O}}_2$ over variable timescales; (ii) Free-living options

Conceptually, DBA can be likened to energy, where the acceleration metric is equivalent to joules (see eqns 4-10), and so can be summed over time to give overall energy expenditure. However, division of this summed energy equivalent (∑DBA) by time should also provide a power equivalent. Exactly this approach was adopted by Elliott et al. (2013), who used doubly labelled water and accelerometers on auks to find high correlation coefficients between daily energy expenditure (i.e. energy use per unit time) and mean DBA for birds that engaged in diving, swimming, flying and time on land, indicating the precise link between DBA and MR. To make this directly comparable to gas respirometry studies, the daily energy expenditure should be converted into a mean expenditure per second (power). This then makes it conform to the standard DBA versus MR equation (see eqn 11), which can be used for identified activities to derive movement-based energetic costs for highly specific activities.

The use of time-corrected values for DBA and energy expenditure has been flagged up as important by Halsey (2017) because summed values of energy expended over time regressed against summed values for DBA will tend to produce a correlation anyway because the time is the same on both axes: an issue that was termed the “time trap”. Halsey’s work, based on simulations assuming no correlation between DBA and $\dot{\text{V}}{\text{O}}_2$, noted that r² values between summed DBA and summed energy could be as high as 0.4 due to the time correlation alone. In fact, in our own work, where we replicate Halsey’s approach, but additionally include varying genuine correlations between DBA and MR (supplementary information 6), we show rapidly increasing r²-values with increasing genuine correlations (well above 0.4). Regressions of summed values against each other therefore need not be dismissed out of hand. We also note that (i) the use of a single mean value for one metric against a cumulative value for the other dismisses the time issue and (ii) DBA does not scale linearly with time across activities. For example, the standard regression relating DBA to $\dot{\text{V}}{\text{O}}_2$ (eqn 11) has an intercept, where DBA is around 0, which generally corresponds to resting, which incurs no increment in DBA with time.

When DBA metrics for MR fail

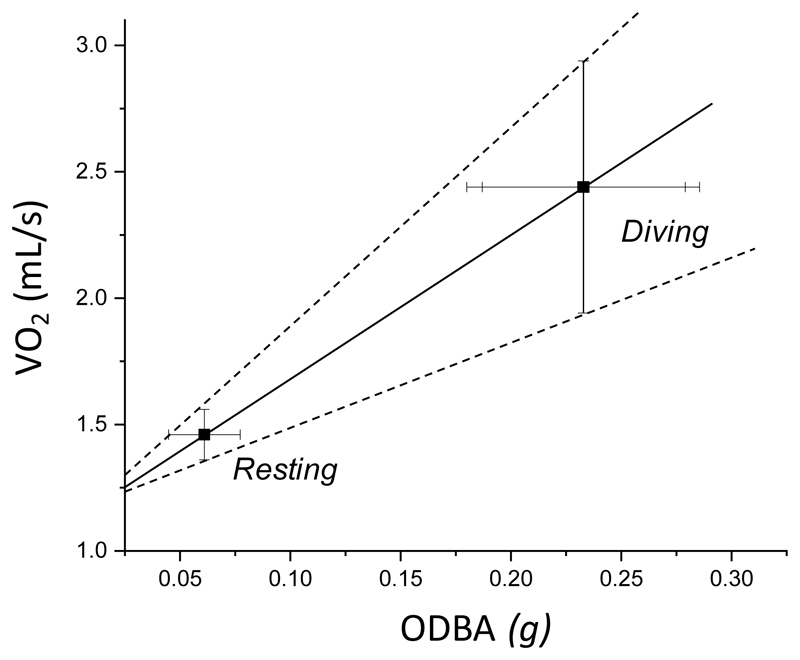
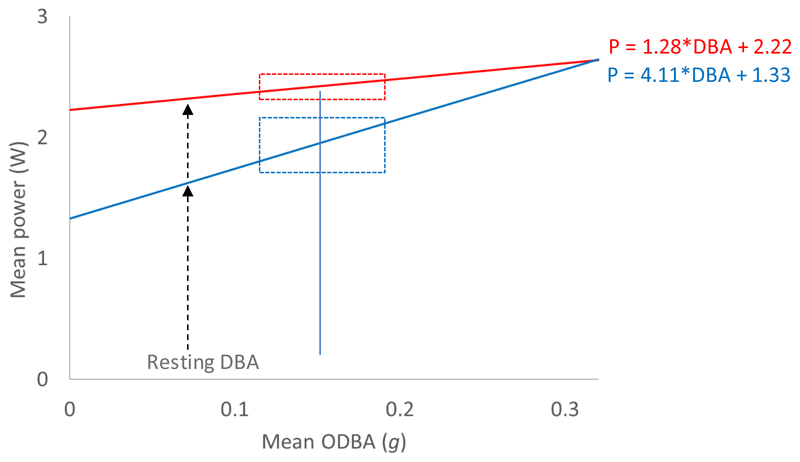
DBA may not, however, be the prime driver of metabolic rate. For example, Ladds et al. (Ladds et al. 2017) found no correlation between mean DBA and mean $\dot{\text{V}}{\text{O}}_2$ in captive, swimming fur seals and sea lions (using gas respirometry), or indeed any correlation between $\dot{\text{V}}{\text{O}}_2$ and swimming stroke rate. Put simply, their protocol could not show that it was more costly to swim than to rest. Why? We can examine potential reasons for this by a simple modelling exercise. Here, individuals spend time in only two activities. Each individual has some (random) time spent in one activity (e.g. rest) and some (random) time spent in another activity (e.g. swimming), with specific values of DBA corresponding to each of those two activities, with specific $\dot{\text{V}}{\text{O}}_2$ costs. Both DBA and $\dot{\text{V}}{\text{O}}_2$ values are identical between the individuals for each activity. Regression of the mean $\dot{\text{V}}{\text{O}}_2$ against the mean DBA, as advocated above, leads to production of the standard DBA versus MR equation (see eqn 11) (Fig. 7). However, this situation does not account for any non-DBA-related metabolic costs.

Figure 7.

Theoretical calculations for relationships between mean power and mean DBA for a time period during which a study animal, here a beaver, can spend time spent engaged in either ‘inactivity’ or ‘activity’. Both have defined power costs (from Allers & Culik (1997) cf. Fig. 4) with randomly allocated lengths of times to both conditions. The blue line shows the situation where DBA is the only modulator of power, whereas the red line shows how the slope of the regression decreases dramatically if thermoregulation costs (also given in Allers & Culik 1997) are included. Since it is extremely unlikely that the study animals will have engaged in only one activity, the real spread of mean power and mean DBA values will be compromised accordingly (the inserted box shows the 95% CI for the grand mean of ODBA measurements on 14 wild beavers (data from Graf et al. 2016)), to which system errors and individual variation (cf. Fig. 2a) must be added. All this dramatically decreases the ability of the researcher to ascertain any relationship between DBA and power.

If we remodel the situation, as above, introducing metabolic costs such as thermoregulation (which imposes a proportionately much greater metabolic rate on resting than on moving due to thermal substitution (cf. Lovvorn 2007)), we can immediately see the susceptibility of this protocol to non-DBA-linked perturbation (Fig. 7). Specifically, with increasing thermoregulatory costs, the regression of mean $\dot{\text{V}}{\text{O}}_2$ to mean DBA increasingly deviates from the simple mean $\dot{\text{V}}{\text{O}}_2$ to mean DBA without a thermoregulatory element (Fig. 7). Indeed, if thermoregulatory costs equaled swimming costs, there would be no gradient in the mean $\dot{\text{V}}{\text{O}}_2$ to mean DBA regression at all. On top of this, by the time we substitute ideal model values with real values, which include inter-animal variation and errors in the methodology (including, for free-living animals) working close to the time limits of doubly labelled water usage of twice the half-life (Speakman 1997)), it is clear that this approach will have little capacity to resolve the relationship between $\dot{\text{V}}{\text{O}}_2$ and DBA. This will be particularly apparent if animals within the sample all adopt roughly similar distributions of activities, which will limit the spread of values in the DBA axis across a correlation gradient that is already reduced (Fig. 7).

A potential solution, in this case, is to have animals at rest in the water to determine RMR_water, before beginning swimming trials and correcting accordingly. Certainly, it is unlikely to be coincidence that the two notable studies that found no relationship between $\dot{\text{V}}{\text{O}}_2$ and DBA were conducted in cold water on homeotherms that operate both in the water and in air (Halsey, White, et al. 2011; Ladds et al. 2017), especially given that RMR_water of aquatic homeotherms that are active in both water and air is substantially more than RMR_air, and approaches that of swimming (e.g. Luna-Jorquera & Culik 2000) but see Fahlman et al. (Fahlman et al. 2005). The process is simply that such homeotherms resting in cold water have to increase metabolic rate to counteract the increased heat loss over that in air (Hind & Gurney 1997). However, as they become more active, they can increasingly substitute the heat increment associated with this activity for this nominal heat loss until the metabolic costs more than compensate (Lovvorn 2007). This thermal substitution explains the non-linear nature of MR with activity in homeotherms exhibiting activities around resting (Ciancio et al. 2016) and is an important consideration in DBA studies.

This case highlights what was said at the outset, that DBA does not cover non-movement-based metabolic rates, and workers need to be aware of other issues that may have a similar effect, including specific dynamic action, the costs of heating cold food (a factor important when persuading lab animals to engage in protocols with food rewards) (Wilson & Culik 1993), isometric muscle contraction and stress (McCue 2006). Indeed, if researchers are interested in comprehensive energy budgets, then any estimates of energy use derived from DBA need to be combined with model estimates of these other costs, which will vary in importance according to the animal and study system. Nonetheless, DBA remains the ideal method with which to examine the energetic implications of animal-decision making in a wide range of systems, and how this might be modulated by individual experience, state and the abiotic/ biotic environment.

Beyond DBA

The above makes it clear that DBA metrics are imperfect, most particularly when non-movement related changes in metabolic rate are appreciable. But neither does DBA capture all of the animal-generated acceleration associated with movement. For example, animals can ‘pull g’ in fast maneuvers such as cornering by cheetahs (Wilson, Mills, et al. 2013). Here, animal experience increased inertial acceleration in additional to the force of gravity, and the vectorial sum of the smoothed channels may not equal 1 (1 corresponds to the Earth’s gravitation field). Any difference between the recorded value and 1 is driven by forces generated by the animal that are not incorporated within DBA (ignoring free-fall-type maneuvers where the value tends towards 0). Therefore VeSBA (the vectorial sum of the static acceleration) should be most informative in these cases. To date, there has been no attempt to link this to power, although we should be doing so.

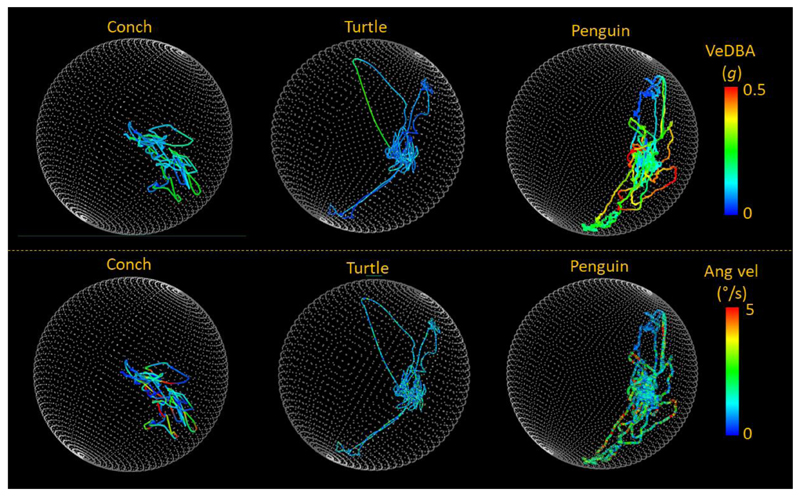
At the other end of the spectrum, slowly moving animals such as many invertebrates and some ectotherms may generate a negligible DBA signal. In such instances, movement may be better represented by rates of change of body pitch, roll or yaw which, although not accelerations, may code for metabolic rate since the animal is still exerting forces to move the body (Fig. 8).

Figure 8.

Five minutes of general activity of three different species (the Giant spider conch Lambis truncata, Loggerhead turtle Caretta caretta and Magellanic penguin Spheniscus magellanicus) manifest on ‘g-spheres’ (which show the extent to which the body pitches and rolls [if the whole sphere were covered, the animal would have adopted all pitch and roll combinations] (Wilson et al. 2016)). Lines are colour-coded by metrics which may be useful as a proxy for rate of energy expenditure. Note how the DBA signal (VeDBA smoothed over 2 s) is most extensive in the penguin, as the animal that shows the most dynamism, but how body angular velocity is appreciable in all three species.

The future

DBA metrics have been demonstrably good predictors for power use for an extraordinary wide spectrum of animals, and this has helped us to move out of the laboratory to allude to the costs of activities of free-ranging animals, particularly because the same acceleration-based technology can be used to determine behaviour so effectively (Shepard, Wilson, Quintana, et al. 2008). But we can do better. Bead-string models (cf. Underhill & Doyle 2006) of animals could provide an explicit calculation of the work done to move between any two configurations: Joints and limbs can be modelled with terms that consider extensive, rotary and torsion motions. Indeed, this, and cognisance of the potential in other movement-based metrics (see above), together with new ideas such as thermal imaging to estimate heat flux (Willis & Horning 2005) and recognition of where acceleration is likely to be less sound, should make the future at once more informed and more exciting. DBA-based metrics themselves can also go further: A next-generation of implantable biosensor (Oliveira et al. 2015) may inform other aspects of animal metabolism, complimentary to DBA, including the signalling mechanisms involved in response, as well as glucose respiration. When combined with mathematical models (Bisker et al. 2015; Lee et al. 2016) of animal physiology, such sensors may provide a connection between DBA and other physiological states, and a vital link between internal state and body action (Nathan et al. 2008).

Acceleration based proxies for energy expenditure have already been used to provide new insight across a range of fields; from animal behavior e.g. in optimal foraging (Shepard et al. 2009) and the age-related costs of migration (Rotics et al. 2016), to ecological and even evolutionary contexts. For instance, Grémillet et al. (2018) demonstrated a link between DBA and the relative breeding performance of individual seabirds. This concept of “energetic fitness” is likely to be a key area of future research, as it not only offers a means of comparing individual differences, but also how different levels of organization, from individuals to populations, may respond to global change (Grémillet et al. 2018).