Direct List Mode Parametric Reconstruction for Dynamic Cardiac SPECT

Abstract

Recently introduced stationary dedicated cardiac SPECT scanners provide new opportunities to quantify myocardial blood flow (MBF) using dynamic SPECT. However, comparing to PET, the low sensitivity of SPECT scanners affects MBF quantification due to the high noise level, especially for ²⁰¹Thallium (²⁰¹Tl) due to its typically low injected dose. The conventional indirect method for generating parametric images typically starts by reconstructing a time series of frame images followed by fitting the time-activity curve (TAC) for each voxel or segment with an appropriate kinetic model. The indirect method is simple and easy to implement; however, it usually suffers from substantial image noise that could also lead to bias. In this paper, we developed a list mode direct parametric image reconstruction algorithm to substantially reduce noise in MBF quantification using dynamic SPECT and allow for patient radiation dose reduction. GPU-based parallel computing was used to achieve more than 2000-fold acceleration. The proposed method was evaluated in both simulation and in vivo canine studies. Compared with the indirect method, the proposed direct method achieved substantially lower image noise and variability, particularly at large number of iterations and at low-count levels.

I. Introduction

THE noninvasive quantification of absolute myocardial blood flow (MBF) with dynamic PET or SPECT provides an important nuclear medicine approach for evaluating and managing coronary artery disease, particularly for multi-vessel diseases [1, 2]. The non-invasive quantification of MBF and the coronary flow reserve (CFR) calculated based on the rest and peak stress MBFs provide an objective assessment of the physiological severity and functional consequences of coronary stenosis. MBF is usually measured using PET with radiotracers such as [¹³N]NH₃, ¹⁵O-water, or ⁸²Rb [3–8]. However, PET MBF is not broadly available due to the relatively small installation base and the need for an onsite cyclotron (for [¹³N] NH₃ and ¹⁵O-water) to produce tracers, and the relatively high scan cost. SPECT scanners, with a much larger installation base and convenient cost-effective long half-life tracers, have the potential to provide absolute MBF quantification to benefit a much larger patient population.

The current indirect data processing pipeline for MBF quantification typically using PET, or sometimes SPECT, is to reconstruct individual dynamic frames and fit each voxel’s or segment’s time activity curve (TAC) with a kinetic model [9, 10]. This conventional approach, however, is subject to several factors that limit the quantification accuracy and precision: 1) it requires selection of the duration of each frame, involving a choice between collecting longer frames with better counting statistics but poor temporal resolution, or shorter frames that are noisier [11]; 2) It requires an accurate model of the noise distribution in each voxel of the reconstructed image, which is a significant challenge as the noise in reconstructed images is space-variant, object dependent, and complicated by inter-voxel correlations [12, 13]; and 3) Within-frame subject’s respiratory and cardiac motions should be corrected. Alternatively, many direct approaches have been proposed [14–22] to produce parametric images from emission raw data without the reconstruction and analysis of individual frames.

Using direct reconstruction to estimate parametric images has been extensively studied for PET [17–20, 23–29]. Due to the slow gantry rotation of conventional SPECT scanners, potentially leading to inconsistent projection data, existing SPECT direct parametric reconstruction methods either estimate TACs based on splines [30, 31] or factor analysis [22, 31] and later require compartmental model fitting as a second-step or only estimate kinetic parameters for specific ROIs [21, 31]. No voxel-by-voxel based reconstruction that directly estimate kinetic parameters from list mode data has been explored to date. A voxel-by-voxel direct parametric reconstruction has the potential to perform high-resolution parametric imaging so that small perfusion defects might be better detected.

^99mTc-sestamibi, ^99mTc-tetrofosmin and ²⁰¹Tl are the three most widely used perfusion tracers in cardiac SPECT studies. ^99mTc-sestamibi and ^99mTc-tetrofosmin both have relatively low extraction fractions (EFs) at high flow rates, while ²⁰¹Tl has a more ideal higher EF. However, ²⁰¹Tl has a long half-life (73 hours) so that clinically, this tracer is used with low injected dose (<2 mCi) to minimize patient radiation exposure. Comparing to ^99mTc-labeled tracers, this leads to increased image noise and reduced image quality, in particular for dynamic ²⁰¹Tl SPECT. While the above mentioned conventional indirect parametric imaging method will amplify image noise, the direct parametric reconstruction approach is expected to reduce image noise and improve the quantification accuracy for all three SPECT tracers, particularly for ²⁰¹Tl.

In this paper, we developed and evaluated a GPU-based list mode direct reconstruction method that produces parametric images directly from SPECT list mode data for a dedicated cardiac stationary SPECT with 19 pinhole collimators and CZT detectors (GE Healthcare NM 530c/570c). The initial investigation was first presented in [32]. This paper is organized as follows. Section II describes the algorithm development, including static list mode reconstruction validation, kinetic 1-tissue (1T) model and derivation of the direct list mode reconstruction algorithm. Algorithm evaluation methods for simulation and in vivo canine data are described in Section III and the results are shown in Section IV. Discussion and conclusions follow in Sections V and VI.

II. Algorithm Development

A. Static List Mode Reconstruction

We first implemented static list mode reconstruction for validation purpose. The list mode EM update equation [33] is:

$${\lambda }_j^{(n+1)}=\frac{{\lambda }_j^{(n)}}{Q_j}{\sum }_k\frac{c_{kj}{A}_k{L}_k{w}_k}{T{\sum }_{j^{\prime }}{c}_{k{j}^{\prime }}{A}_k{L}_k{\lambda }_{j^{\prime }}^{(n)}+T{S}_k}$$ (1)

where λ_j is the count rate at voxel j (counts/s/cm³), n is iteration number; k ∈ (i, t) is the index of each event, which includes the information about event location on detector i at time t; system matrix element c_kj is the contribution of voxel j to event k; A_k is the attenuation of event k; L_k is the decay correction factor at time t, which is defined as L_t = e^{−t·log2/t_1/2} where t_1/2 is the half-life of the tracer; w_k is each event’s uniformity correction value; T is the duration of the scan; S_k is the scatter rate estimation for detector bin i for the scan duration; Q_j is the voxel sensitivity, which is calculated as Q_j = ∑_i c_ijA_iL_t .

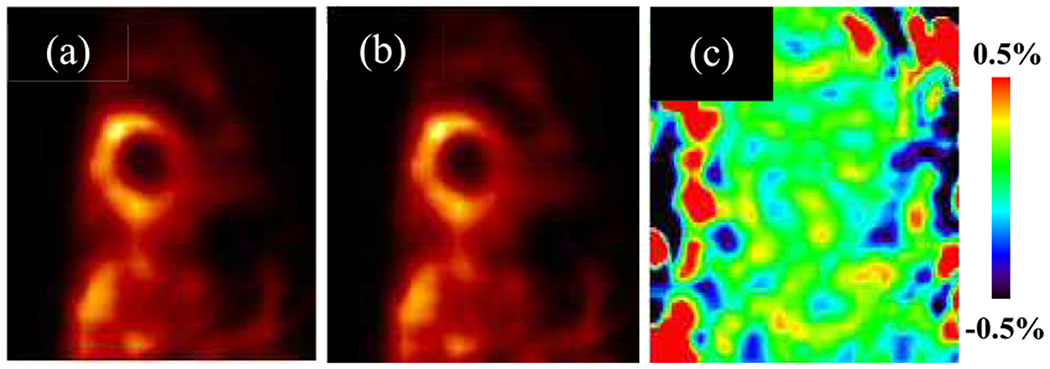
Scatter was first estimated in projection domain for all indirectly reconstructed dynamic frames using Fan’s method [34] to compensate for the low-energy tail of CZT detectors. The estimated scatter projections in each dynamic frame were then divided by the frame duration to obtain the scatter rate estimation. About 1% of the detector pixels were bad pixels, which did not record any counts but the locations of the bad pixels were recorded and known. For projection-based reconstruction, bad pixel count values were interpolated using neighboring pixels. For list mode reconstruction, based on the projection-based interpolation, the corresponding number of events in bad pixels were appended to the list mode data randomly before reconstruction. We validated our list mode reconstruction implementation against currently used projection-based reconstruction, prior to the implementation of list mode direct reconstruction. As a sample 20-min static ²⁰¹Tl canine scan shown in Fig 1, the static list mode reconstruction obtained nearly identical results as the projection-based reconstruction.

Fig. 1.

(a) Projection-based reconstruction; (b) List mode reconstruction; (c) difference image by percentage, for a sample 20-min static ²⁰¹Tl canine scan. Corrections for attenuation, scatter, bad-pixel and decay were applied for both methods.

B. Kinetic Model for ²⁰¹Tl SPECT

In this paper we used the 1T compartmental model because this model has been shown to provide accurate MBF estimation for ²⁰¹Tl [9, 10]. The 1T compartment model was used to describe the time-varying signal in the myocardium C_M(t) = C_L(t) ⊗ K₁e^−k₂t, where C_M(t) (counts/s/cm³) is the myocardium signal, C_L(t) (counts/s/mL) is the left ventricle (LV) input function, K₁ is tracer influx rate (mL·min⁻¹·cm⁻³), k₂ is tracer efflux rate (min⁻¹), and is the convolution operator. To account for blood volume and spillover from LV into the myocardium caused by partial volume and motion, the TAC derived from SPECT image is modeled as

$$\begin{gathered} C_{\text{T}}(t)=(1-V_{\text{L}})C_{\text{M}}(t)+V_{\text{L}}{C}_{\text{L}}(t) \\ =(1-V_{\text{L}})K_1{C}_{\text{L}}(t)\otimes e^{-k_{2}t}+V_{\text{L}}{C}_{\text{L}}(t) \end{gathered}$$ (2)

where V_L is the LV blood volume fraction term. The term (1 − V_L) K₁ is estimated as a lumped uncorrected quantity referred to as K_1,uncorr. Based on these two terms, the partial volume, motion and blood volume corrected K₁ can be computed as:

$$K_1=K_{1,\mathrm{uncorr}}/(1-V_{\text{L}})$$ (3)

C. Direct Parametric Reconstruction Algorithm

For the expectation-maximization (EM) direct reconstruction of the kinetic parameters in section II.B, a non-homogeneous Poisson-distributed complete data space X_ijtτr was defined [25, 26] as the counts collected at detector bin i in time bin t emitted from voxel j from “sub- region” r and where the tracer input that produced that event was delivered at time τ. For the 1T model, this random variable is :

$$X_{ijt\tau r}\sim Poission(\Delta t{c}_{ij}{A}_i{L}_t{\theta }_{rj}{F}_{rjt\tau })$$ (4)

where the argument in the parenthesis is the mean of the Poisson process for the complete data X_ijtτr. Δt is the duration of time bin (1 ms in our implementation). The linear “region” index r can take 2 values (0, 1) to account for contributions from myocardium and LV blood pool to the signal, such that θ_rj = [K_{1,uncorr, j}, V_{L, j}] and F_rjtτ = [C_L(τ)e^{−k_{2, j}(t−τ)}, C_L(t)], where θ_0j = K_{1,uncorr, j}, θ_1j = V_{L, j}, F_0jtτ = C_L(τ)e^{−k_2,j(t−τ)} and F_1jtτ = C_L(t). The corresponding complete data log-likelihood for this Poisson random variable (omitting constant terms) is given by:

$$\log f(x|\theta ,k_2)={\sum }_{ijt\tau r}{x}_{ijt\tau r}\log (\Delta t{c}_{ij}{A}_i{L}_t{\theta }_{rj}{F}_{rjt\tau })-\Delta t{c}_{ij}{A}_i{L}_t{\theta }_{rj}{F}_{rjt\tau }$$ (5)

where x_ijtτr denotes a realization of random variable X_ijtτr. The E-step calculates the complete data expectation at iteration n, given the measured data Y, the current parameter estimates θ⁽ⁿ⁾ and $k_2^{(n)}$ and the estimated scatter rate S:

$$\begin{gathered} E\left[X_{ijt\tau r}|Y_{it},{\theta }_{r,j}^{(n)},k_{2,j}^{(n)},S_{it}\right]=y_{it}\frac{\Delta t{c}_{ij}{A}_i{L}_t{\theta }_{rj}^{(n)}{F}_{rjt\tau }^{(n)}}{{\sum }_{r^{\prime }{j}^{\prime }{\tau }^{\prime }}\Delta t{c}_{i{j}^{\prime }}{A}_i{L}_t{\theta }_{r^{\prime }{j}^{\prime }}^{(n)}{F}_{r^{\prime }{j}^{\prime }t{\tau }^{\prime }}^{(n)}+\Delta t{S}_{it}} \\ =M_{ijt\tau r}^{(n)} \end{gathered}$$ (6)

where y_it is the number of counts detected from detector bin i in time bin t. Replacing x_ijtτr in (5) by the complete data expectation, we have the expectation of the complete data log-likelihood, conditional on the current parameter estimates for each voxel:

$$E\left[\log f(X|\theta ,k_2)|Y,{\theta }^{(n)},k_2^{(n)},S\right]={\sum }_{ijt\tau r}{M}_{ijt\tau r}^{(n)}\log (\Delta t{c}_{ij}{A}_i{L}_t{\theta }_{rj}{F}_{rjt\tau })-\Delta t{c}_{ij}{A}_i{L}_t{\theta }_{rj}{F}_{rjt\tau }$$ (7)

which is what M-step is maximizing. Taking partial derivatives with respect to θ:

$$\frac{\partial }{\partial {\theta }_{r,j}}E\left[\log f(X|\theta ,k_2)|Y,{\theta }^{(n)},k_2^{(n)},S\right]={\sum }_{it\tau }\frac{M_{ijt\tau r}^{(n)}}{{\theta }_{rj}}-\Delta t{c}_{ij}{A}_i{L}_t{F}_{rjt\tau }$$ (8)

and setting them to zero, the update equations for θ can be obtained:

$${\theta }_{r,j}^{(n+1)}=\frac{{\sum }_{it\tau }{M}_{ijt\tau r}^{(n)}}{\Delta t{\sum }_{it\tau }{c}_{ij}{A}_i{L}_t{F}_{rjt\tau }^{(n+1)}}$$ (9)

where θ_0j = K_{1,uncorr, j}, and θ_1j = V_{L, j}. Taking partial derivatives with respect to k₂ and setting to zero

$$\frac{\partial }{\partial k_{2,j}}E[\log f(X|\theta ,k_2)|Y,{\theta }^{(n)},k_2^{(n)},S]={\sum }_{it\tau }\{(t-\tau )\Delta t{c}_{ij}{A}_i{L}_t{K}_{1,\text{uncorr},j}{C}_{\text{L}}(\tau )e^{-k_{2,j}(t-\tau )}-(t-\tau )M_{ijt\tau 0}^{(n)}\}=0.$$ (10)

Inserting the K_{1,uncorr, j} update (9) into (10) yields

$$\frac{{\sum }_{t\tau }(t-\tau )L_t{C}_{\text{L}}(\tau )e^{-k_{2,j}(t-\tau )}}{{\sum }_{t\tau }{L}_t{C}_{\text{L}}(\tau )e^{-k_{2,j}(t-\tau )}}=\frac{{\sum }_{it\tau }(t-\tau )M_{ijt\tau 0}^{(n)}}{{\sum }_{it\tau }{M}_{ijt\tau 0}^{(n)}}$$ (11)

The right-hand side of (11) is dependent on the measured data Y, the current parameter estimates θ⁽ⁿ⁾ and $k_2^{(n)}$ and the estimated scatter rate S. The left-hand of the equation is defined as H(k₂) and is a function of k₂ and the input function. Since H(k₂) is independent of the measured data, it can be pre-computed from the known input function for a range of k₂ values. Note that H(k₂) is a monotonically decreasing function [25], and k₂ can be updated by

$$k_{2,j}^{(n+1)}=H^{-1}\left(\frac{{\sum }_{it\tau }(t-\tau )M_{ijt\tau 0}^{(n)}}{{\sum }_{it\tau }{M}_{ijt\tau 0}^{(n)}}\right)$$ (12)

where the inverse function was fitted by a fifth-order polynomial function [24] in our studies. More details on solving for k₂ can be found in [24]. In this implementation, 500 k₂ values uniformly sampled ranging from 0.001 to 0.6 min⁻¹ were used and fitted to build the pre-computed table. The k₂ range was selected based on the indirect results of the canine studies. Note that other studies, e.g., with different tracers, may have different k₂ ranges. In those cases, different k₂ ranges should be selected accordingly.

Scatter estimation and bad pixel correction were applied in both direct and indirect parametric reconstructions. For the indirect method, the list mode data were first rebinned into multiple dynamic frame projections. Scatter estimation and bad pixel correction were applied to each dynamic frame. For the direct method, scatter rate estimation was obtained by dividing the scatter projection estimates by the frame duration for each dynamic frame; bad pixel events were also estimated and appended to the list mode data for each dynamic frame in the same way as for the static reconstructions described in section II.A.

D. GPU Acceleration

The system matrix in this work was pre-computed with the collimator-detector response functions incorporated. The size of the system matrix was 245000 × 27648 for reconstruction of image size 70 × 70 × 50 with 32 × 32 × 27 detector projection entries. However, the system matrix size is relatively large and was stored in sparse matrix format (25GB in dense matrix format compared to 165MB in Compressed Sparse Column (CSC) format). For projection-based reconstruction, forward and back projection only need to be performed once in each iteration, and can be performed by matrix multiplication easily in Matlab. However, list mode reconstruction requires frequently accessing elements from the system matrix, and is extremely time consuming so that the total computation time was not clinically feasible in Matlab. For acceleration, the reconstruction code was written in C++ and a linear algebra library (Armadillo) was used for general sparse/dense vector and matrix operations. In (8) and (10), the kinetic forward projection terms, ${\sum }_{it\tau }(t-\tau )M_{ijt\tau r}^{(n)}$ and ${\sum }_{it\tau }{M}_{ijt\tau r}^{(n)},$, involve a large number of sparse vector summations (K, the number of events, typically around 10 Million in our studies), with the length of the sparse vector equal to the number of pixels, which is 245000 in this study. To reduce the computation time to an acceptable level, GPU-based parallel computing was implemented with the help of NVIDIA CUDA Sparse Matrix library (cuSPARSE), using a GeForce GTX 1080Ti GPU card. This GPU implementation combined with various sparse matrix libraries achieved an over 2000-fold acceleration compared to the previous CPU implementation, leading to a computation time of ~9 min per iteration for a 10 Million count study.

III. Algorithm Evaluation

A. Evaluation with Simulated Canine Data

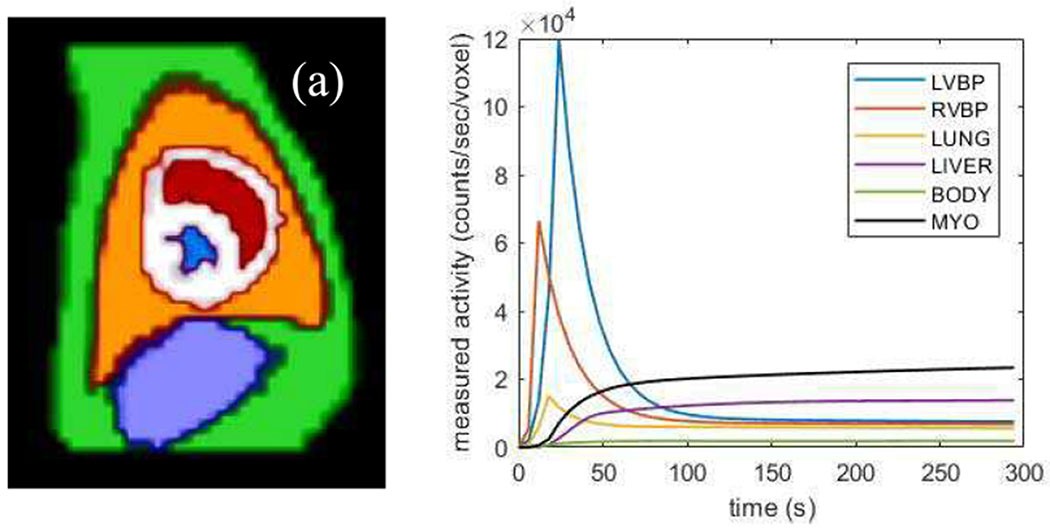
The proposed method was evaluated using a realistic 4D dynamic simulation based on dog anatomy. Six regions were included in the simulation, including myocardium (MYO), left ventricle blood pool (LVBP), right ventricle blood pool (RVBP), lung, liver, and body. The six regions were manually segmented from the contrast-enhanced CT images of a beagle dog (about 10kg weight) described in Section III.B, and then down-sampled to match SPECT voxel size (4 mm³), as shown in Fig. 2(a). The tracer dynamics for all the regions except for MYO were measured and fitted based on a 20 min ²⁰¹Tl SPECT study of the same dog, which are partially shown (the first 300 s) in Fig. 2(b). The 1-Tissue (1T) model was used to describe the kinetics in the myocardium, with K₁, k₂ and V_L set to 0.4 mL·min⁻¹, 0.1 min⁻¹ and 0.2, respectively. The time activity curve of LVBP was used as the plasma input function.

Fig. 2.

(a) The six body regions’ segmentation in SPECT resolution. Red: LVBP; blue: RVBP; white: myocardium; orange: lung; purple: liver; green: body. (b) The ²⁰¹Tl tracer dynamics for the five body parts used in the simulation.

The simulation was based on the geometry of a dedicated cardiac stationary SPECT (GE Healthcare NM 530c/570c) with a pre-computed system matrix. A 20-min list mode dataset was created by forward projecting the 4D phantom to acquire the mean of projection counts for each detector bin (DB) at each time point (sampled every 6 s), then the corresponding number of events for that DB and time bin (TB) were generated and appended to the list mode data in a randomized order. In this quasi-noise-free simulation, the mean count in each DB was rounded to the closest integer prior to the conversion of list mode data. For each sampling time point, the time tags of all the events for a DB were simulated as uniformly distributed within that 6-s time bin. In addition to the quasi-noise-free simulation, full-count and 25% low-count noisy data were also simulated. To generate noisy list mode data, Poisson random variables were generated based on the mean projections of each DB before appending the corresponding events to the list mode data. The 25% low-count list mode data were generated by uniformly down-sampling the full-count noisy list mode data by a factor of 1/4 in the order of event arrival time. Ten noisy replicates were generated for both full-count and 25% low-count noisy simulations. The total number of counts was about 14 million for the full-count simulation. The effects of scatter and motion were not included in the simulations in order to isolate the evaluation of the reconstruction algorithm.

The proposed direct method was compared with the indirect approach following 3D MLEM image reconstruction of each dynamic frame (6×10 s, 2×120 s, 3×300 s). For the indirect method, the basis function approach [35] was used to compute the parametric maps with weighted least squares (WLS) fitting, where 800 basis functions corresponding to k₂ values ranging from .001 to 0.6 min⁻¹ were used. Thus, the indirect method is not susceptible to local minimum within that range of k₂ values since an exhaustive search was performed for the only nonlinear parameter of this model. For the noise-free simulation, uniform weights were used. For the noisy simulations, weights were calculated as [36]: $w_f=L_f^2∕(N_f\times DC{F}^2)$, where L_f is the f^th frame duration, N_f is the count number for the f^th frame and DCF is the decay correction factor. For the direct method, uniform initialization was used and the initial values of K_1,uncorr, k₂ and V_L were set to 0.3 mL·min⁻¹·cm⁻³, 0.1 min⁻¹ and 0.2, respectively. For the indirect method, we initialized the MLEM-based frame reconstructions with a uniform map (1 counts/s/voxel), as in our routine use.

For quantitative analysis, percent bias and coefficient of variation (CoV) were evaluated for both direct and indirect methods. The percent bias per voxel was calculated as ${\text{Bias}}_{{\theta }_j}=({\stackrel{‒}{\theta }}_j-{\theta }_j^{\text{true}})∕{\theta }_j^{\text{true}}\times 100\%$, where ${\theta }_j^{\text{true}}$ is the ground truth parameter (θ can be K₁, K_1,uncorr, k₂ or V_L) value in voxel j and ${\stackrel{‒}{\theta }}_j=({\Sigma }_{rep}{\theta }_{j,rep})∕N_{rep}$ is the mean parameter estimate across replicates, where rep is the replicate index and N_rep is the number of replicates. Voxel-wise CoV per parameter was calculated across replicates as: ${\text{CoV}}_{{\theta }_j}={\sigma }_j∕{\theta }_j^{\text{true}}\times 100\%$, where ${\sigma }_j=\sqrt{\frac{{\sum }_r{({\theta }_{rep,j}-{\overline{\theta }}_j)}^2}{N_{rep}-1}}$ is the standard deviation (STD) across replicates at voxel j. Two volumes of interest (VOI) were considered for simulated data: the whole LV myocardium (of 706 voxels) and the LV myocardium excluding the septum (LV_ES) wall (of 385 voxels), since septum wall can be more prone to the model mismatch error propagated from RVBP. The voxel-wise percent bias and CoV were averaged over the voxels within each VOI to obtain mean bias and mean CoV for each parameter: $B\overline{i}as\theta =({\sum }_{j\in \mathrm{VOI}}{\mathrm{Bias}}_{{\theta }_j})/N_{\mathrm{VOI}}$ and $C\overline{o}{V}_{\theta }=({\sum }_{j\in \mathrm{VOI}}{\mathrm{CoV}}_{{\theta }_j})/N_{\mathrm{VOI}},$, where N_VOI is the number of voxels in the VOI.

B. Evaluation with in vivo Canine Data

Four dynamic SPECT studies were performed on 2 beagles, each scanned twice with at least 1 month between the two scans, using ~2mCi injection of ²⁰¹Tl and a GE Discovery NM/CT 570c hybrid SPECT/CT system. Three studies were rest scans and the other one was a rest scan obtained 30 min after adenosine administration. The scan duration was 20 min, and 11.2±1.7 million events within the energy window 71± 5% keV were recorded. The direct method was compared with the indirect method at full-count level and 25% low-count level. Low-count data were generated by uniformly down-sampling the original high-count data. Four low-count replicates were generated for each study. For the indirect method, 11 frames (6×10 s, 2×120 s, 3×300 s) were reconstructed and WLS was used to estimate each voxel’s parameters with data weighted as described above. Both methods applied CT-based attenuation correction, scatter correction, bad pixel and decay corrections. The direct and indirect results from iteration 80 were compared in the in vivo studies, since 80th iteration is typically used for perfusion studies in clinical settings, and our simulation studies (Fig. 4) showed that both direct and indirect methods resulted in similar K₁ parameter convergence trends. For both direct and indirect methods, the same initialization schemes as in the simulation studies were used, which were described in section III. A.

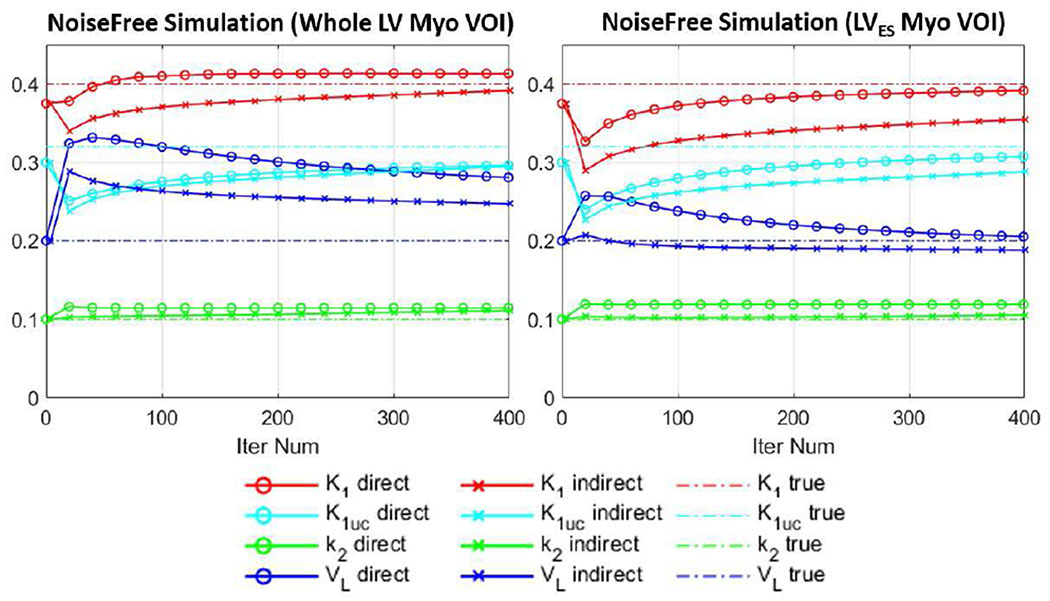
Fig. 4.

Plots of measured K₁, K_1,uncorr (K_1uc), k₂ and V_L parameters vs. iteration in two VOIs (whole LV myocardium and LV_ES myocardium) for the simulation study. The results were shown every 20 iterations for 400 iterations. Direct (circled lines) and indirect (crossed lines) methods were compared. Ground truth values were given by dashed lines.

To estimate the input functions for both methods, the average values in the LV blood pool VOI (of 69 ± 16 voxels for the four canine images) applied to the 11 frame-based reconstructions were used. The measured data points after the peak were fitted with a two-exponential function for smoothing purpose, and the data points before the peak were linearly interpolated (see Fig. 2(b) for an example of the processed curve). The fitted input function curves were then resampled every 6 s to obtain the discrete input functions for both direct and indirect methods.

The reconstructed parametric images were evaluated with the whole LV myocardium VOI (of 342±103 voxels for the four canine studies), and the results are given in Section IV. For 100%-count studies, the mean parameters within the VOIs were calculated as $\overline{\theta }=({\sum }_{j\in \mathrm{VOI}}{\theta }_j)/N_{VOI}$. For each dog’s low-count studieŝ the VOI average of the 4 replicates’ mean parameter $\overline{\overline{\theta }}=({\sum }_{j\in VOI}{\overline{\theta }}_j)/N_{VOI}$ and CoV parameter $C\overline{o}{V}_{\theta }=({\sum }_{j\in \mathrm{VOI}}{\mathrm{CoV}}_{{\theta }_j})/N_{VOI},$ were calculated to evaluate bias and noise, where ${\stackrel{‒}{\theta }}_j=({\Sigma }_{rep}{\theta }_{j,rep})∕N_{rep}$, ${\text{CoV}}_{{\theta }_j}={\sigma }_j∕{\stackrel{‒}{\theta }}_j\times 100\%$, and ${\sigma }_j=\sqrt{\frac{{\Sigma }_{rep}{({\theta }_{rep,j}-{\stackrel{‒}{\theta }}_j)}^2}{N_{rep}-1}}$. We also evaluated the impact of low-dose input functions on both direct and indirect results. For 25%-count studies, input functions estimated from both 100%-count study and their own 25%-count studies were used and compared.

IV. Results

A. Results for Simulated Canine Data

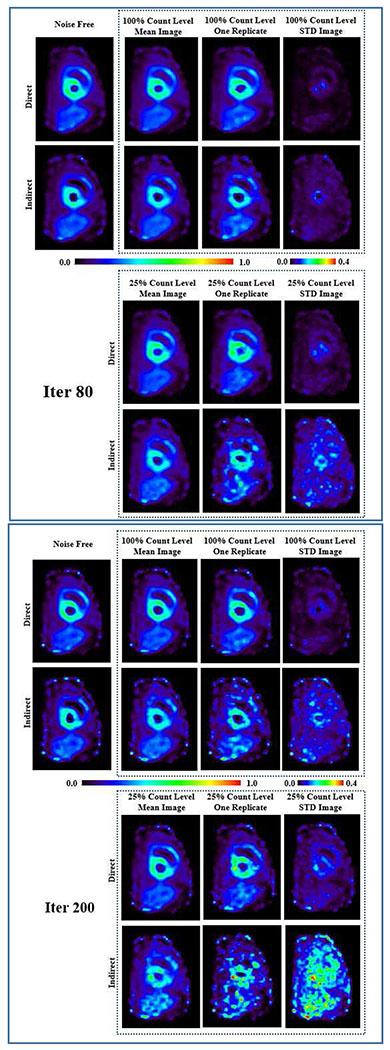
Fig. 3 shows the K₁ parametric images generated by direct and indirect methods for the three groups: noise free, 100% full-count and 25% low-count noisy group. The k₂ parametric images can be found in Fig. S1 in the supplementary materials (available in the supplementary files /multimedia tab). For the two noisy groups, one noisy replicate sample image, the mean image and the STD images of the 10 replicates are given. The images were compared at iteration 80 and iteration 200. It can be observed that at lower count levels and higher iterations, the indirect results are severely corrupted by noise, and the shape of myocardium can no longer be well identified. In contrast, the direct results provided much lower image noise. Note that the direct results at iteration 200 even have lower noise compared to the indirect results at iteration 80.

Fig. 3.

K₁ parametric images generated from simulated canine data by direct and indirect methods for the three groups: noise free, 100%-count and 25%-count noisy simulations. For the two noisy groups, one replicate sample image, the mean image and the STD images of the 10 replicates are given. The images were compared at iteration 80 and iteration 200.

Fig. 4 shows the K₁, K_1,uncorr, k₂ and V_L values as a function of iteration for both direct and indirect methods in the noise-free simulation. The values were measured as the average within the VOI on the parametric images. It can be seen from Fig. 4 (a) that in the whole LV myocardium, even though the V_L term for the direct method was higher compared with that of the indirect method, the K₁ values of both methods were close to the ground truth of 0.4 mL·min⁻¹·cm⁻³. For the LV_ES myocardium VOI, the V_L term for both direct and indirect methods were closer to the ground truth of 0.2, and direct method’s K₁ results were closer to the ground truth compared to the indirect method. The parameter percent biases at 400 iterations are given in Table I, where bias was calculated as (θ^iter400 − θ^true)/θ^true × 100%.

TABLE I.

Comparison of parameter percent biases at iteration 400 between direct and indirect results for the noise-free canine simulation. K₁, K_1,uncorr, k₂ and V_L values were measured as the average within two VOIS: whole LV myocardium and LV_ES myocardium.

Bias @ Iter 400		K1	K1,uncorr	k2	VL
Whole LV Myo	Direct	3.3%	−7.5%	15.0%	40.5%
	Indirect	−2.3%	−7.8%	11.0%	23.5%
LVES Myo	Direct	−2.3%	−3.8%	19.0%	3.0%
	Indirect	−11.3%	−10.0%	6.0%	−6.0%

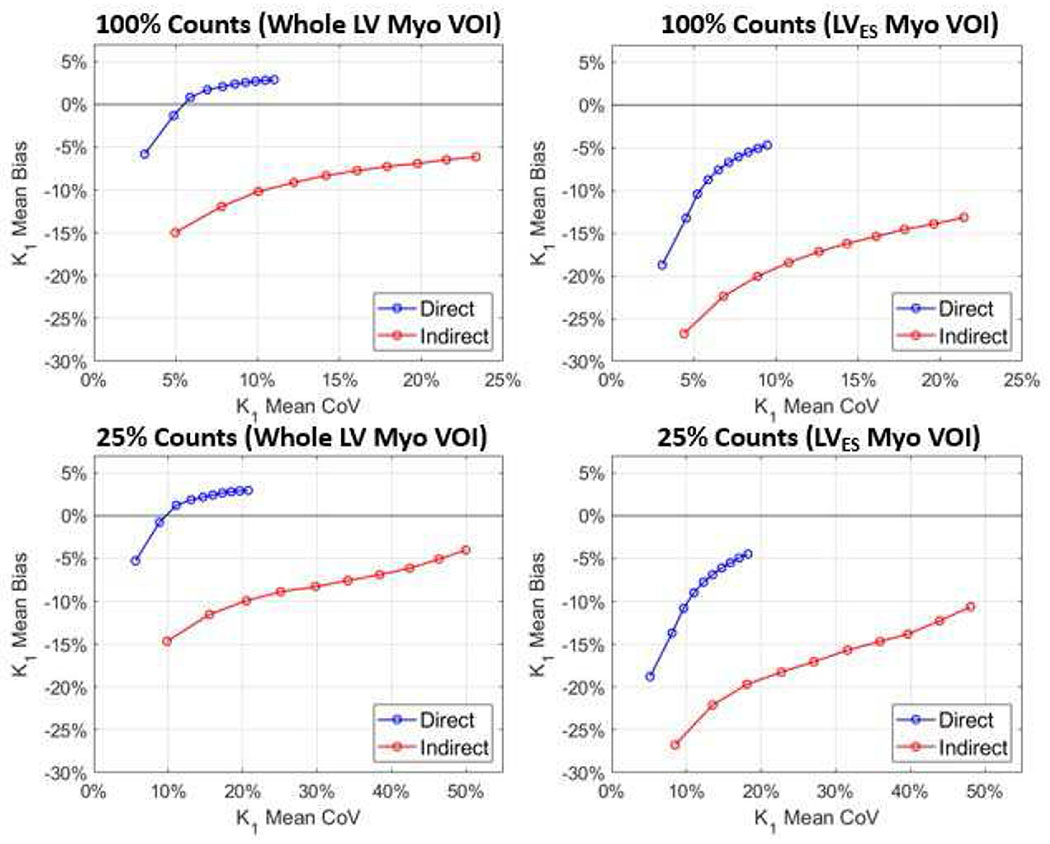
Fig. 5 shows the measured K₁ results for the full-count and 25%-count noisy simulations, where the mean bias (y-axis) vs. mean CoV (x-axis) plots were given. It can be observed that for both simulations and both VOIs, the direct method obtained smaller bias and smaller CoV as compared to the indirect method.

Fig. 5.

Plots of mean bias as a function of mean CoV for two VOIs. For both 100%-count and 25%-count simulations, direct and indirect methods were compared. Circled lines are the mean curves of the 10 replicates. The intervals between circles represent every 20 iterations, starting from iteration 20 at the lower-left corner, to iteration 200 at the top-right corner.

B. Results for in vivo Canine Data

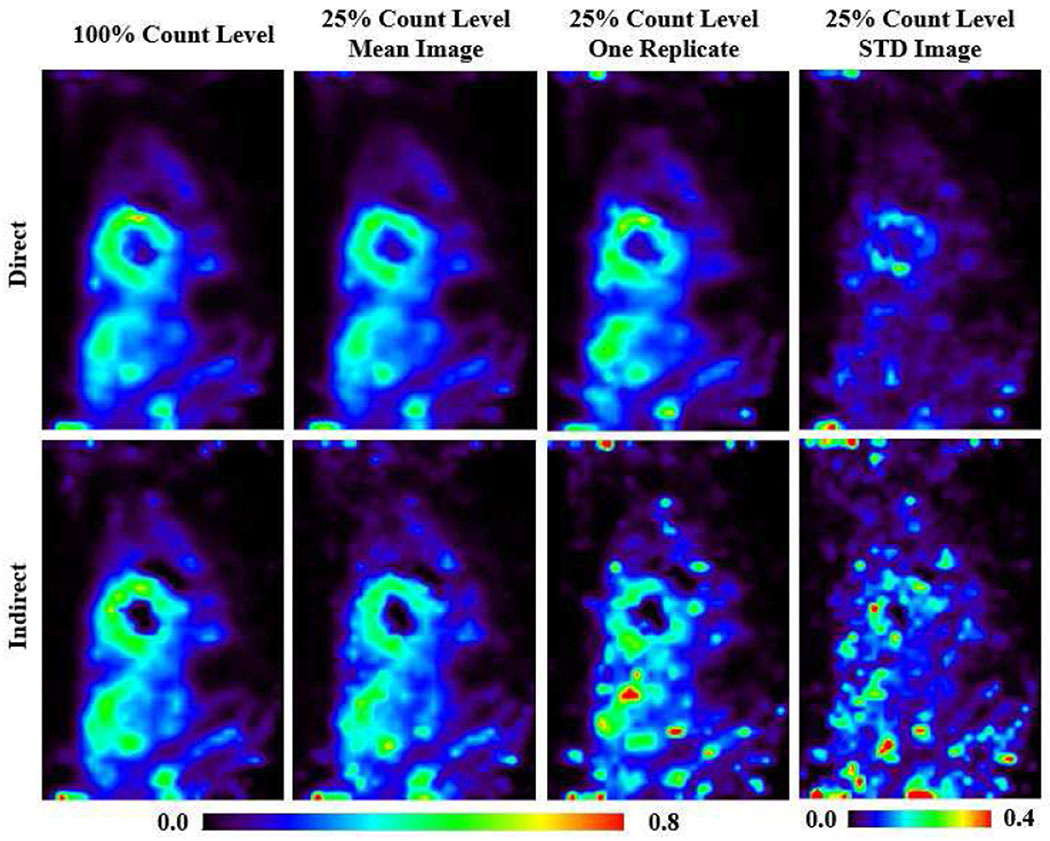
Fig. 6 shows the K₁ parametric images (the k₂ parametric images can be found in Fig. S2 in the supplementary materials that are available in the supplementary files /multimedia tab) of one canine study (Canine Study 4 in Table II) generated by direct and indirect methods for 100% and 25%-count levels. For 25%-count studies, the four replicates’ mean and STD images, and one replicate’s sample images are shown. The images were compared at iteration 80. At both 100% and 25%-count levels using input functions obtained from LV VOI quantification using corresponding dynamic frames, the direct method yielded less noisy results compared to the indirect method.

Fig. 6.

K₁ parametric images of one canine study generated by direct and indirect methods for 100% and 25% count levels. For 25% count studies, the four replicates’ mean and STD images (2^nd and 4^th column), and one replicate’s sample images (3^rd column) are given. The images were compared at iteration 80.

TABLE II.

Results from all four canine studies. K₁ results were measured within whole LV myocardium VOI.

K1 (whole LV myocardium VOI)		Canine Study 1 (baseline)		Canine Study 2 (baseline)		Canine Study 3 (post-adenosine)		Canine Study 4 (baseline)
		Direct	Indirect	Direct	Indirect	Direct	Indirect	Direct	Indirect
100% counts	$\text{Mean}\stackrel{‒}{\theta }(\text{mL}\cdot {\text{min}}^{-1}\cdot {\text{cm}}^{-3})$	0.414	0.383	0.357	0.344	1.504	1.311	0.379	0.397
25% counts w. 25% IF	$\text{Mean}\overline{\overline{\theta }}(\text{mL}\cdot {\text{min}}^{-1}\cdot {\text{cm}}^{-3})$	0.406	0.375	0.354	0.351	1.422	1.282	0.381	0.358
	$(\overline{\overline{\theta }}-\stackrel{‒}{\theta })∕\stackrel{‒}{\theta }\times 100\%$	−1.9%	−2.1%	−0.8%	2.0%	−5.4%	−2.2%	0.5%	−9.8%
	${\overline{\text{CoV}}}_{\theta }$	27.3%	34.3%	31.4%	35.5%	30.4%	35.6%	25.7%	30.2%
25% counts w. 100% IF	$\text{Mean}\overline{\overline{\theta }}(\text{mL}\cdot {\text{min}}^{-1}\cdot {\text{cm}}^{-3})$	0.424	0.396	0.358	0.353	1.526	1.358	0.384	0.406
	$(\overline{\overline{\theta }}-\stackrel{‒}{\theta })∕\stackrel{‒}{\theta }\times 100\%$	−2.4%	3.4%	−0.3%	2.6%	1.5%	3.6%	1.3%	2.3%
	${\overline{\text{CoV}}}_{\theta }$	22.0%	30.8%	29.8%	33.9%	14.4%	29.5%	22.8%	29.1%

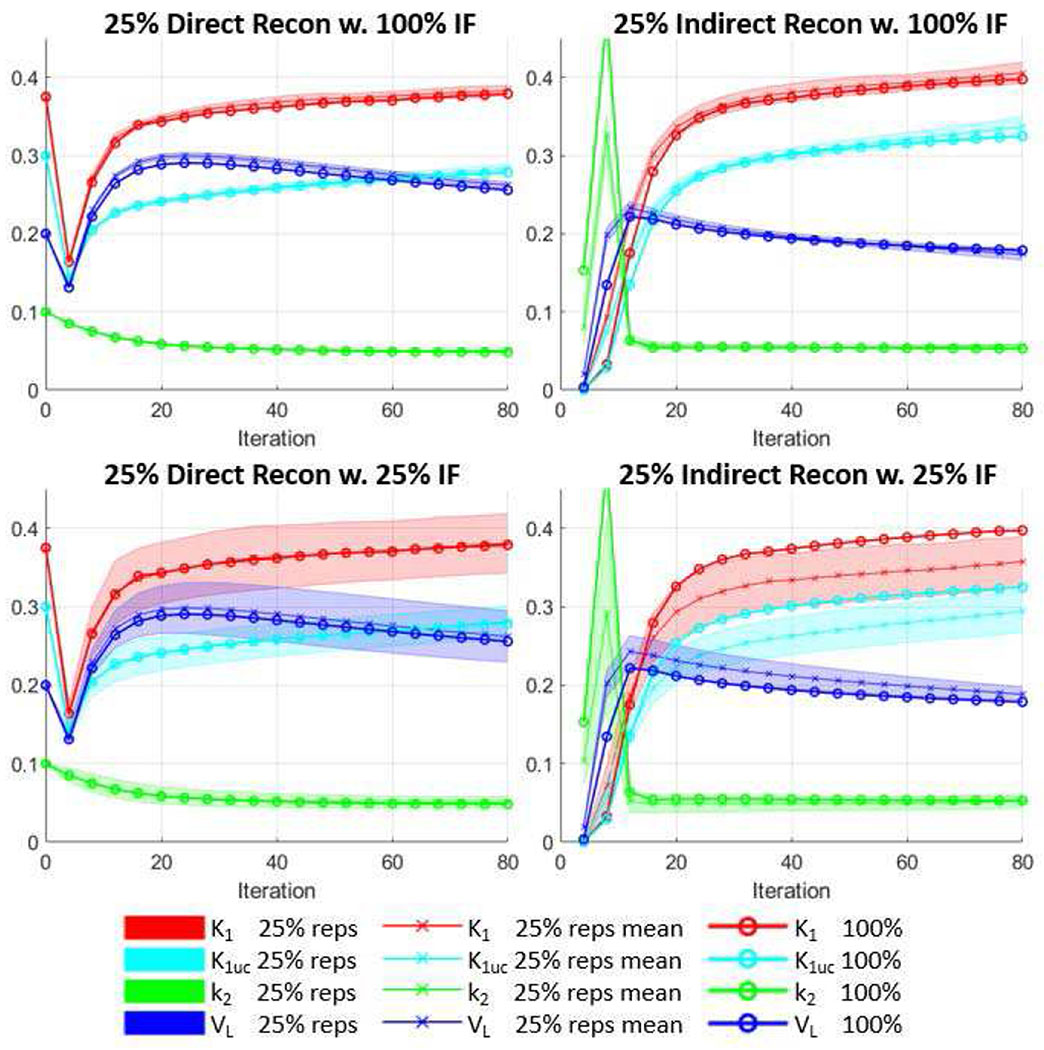
Fig. 7 shows the VOI-based parameters measurements at various iterations for a sample canine study (Canine Study 4 in Table II) for both direct and indirect methods. The first row in Fig. 7 shows the 25%-count results using an input function estimated from the 100% study. It can be seen that for both direct and indirect methods, the mean of the low-count replicates was close to that of the 100%-count result, with minor variations as shown by the shaded area. The second row shows the results using input functions estimated from the 25%-count studies themselves. The broader spread of shaded area indicates that the cross-replicates variability became larger due to the variability of input functions derived from noisy 25%-count data. In this study, bias was observed for the indirect method in the second row, as the mean plots of the replicates deviated from that of the 100%-count study. In contrast, for the direct method the mean plots of low-count replicates aligned well with the 100%-count results.

Fig. 7.

Plots of measured parameters (K_1uc stands for K_1,uncorr) vs. iteration for a in vivo canine study at two count levels. The results were shown every 4 iterations for 80 iterations. The parameters were measured as the average within the whole LV myocardium VOIs. The direct and indirect methods were compared. For the low-count studies, using 100% input function and 25% input functions were also compared. Crossed lines show the mean values of 4 low-count replicates, whereas shaded area shows the standard deviation of the replicates. Circled lines are the results from the 100% count study used as standard.

A summary of all the four canine studies is shown in Table II. Only K₁ values are given since these values are the most important parameter for the assessment of flow with this tracer. The values were averaged over the whole LV myocardium VOI. The definition of all the values were given in Section III. B. For the 100%-count studies, the direct results from 3 out of the 4 canine studies showed slightly higher averaged K₁ over VOI compared with the indirect results, which is consistent with the simulation results in Section IV.A. From the $C\stackrel{‒}{o}{V}_{\theta }$ values, it can be seen that the direct results had lower noise as compared to that of the indirect results. In the 25% low count studies with both direct and indirect methods, using input functions obtained from 100%-count studies resulted in lower parameter estimation variability, as indicated by the reduction in $C\stackrel{‒}{o}{V}_{\theta }$. We observed in one direct result (Canine Study 3) and one indirect result (Canine Study 4) that using input functions obtained from 100%-count studies resulted in parameter mean values $\overline{\overline{\theta }}$ substantially closer to the mean values $\stackrel{‒}{\theta }$ from the 100%-count results, when compared with using input functions obtained from the 25%-count studies. This can be seen in reviewing the percent difference values $(\overline{\overline{\theta }}-\stackrel{‒}{\theta })∕\stackrel{‒}{\theta }\times 100\%$. For the rest of the studies, the parameter mean values $\overline{\overline{\theta }}$ were very close to the mean values $\stackrel{‒}{\theta }$ derived from the 100%-count results. Note that the K₁ value from Canine Study 3 is much higher than the other three canine studies, probably due to persistent vasodilation following administration of adenosine. This suggests that our implementation with precomputed k₂ range is applicable to both rest and stress studies of the ²⁰¹Tl tracer.

V. Discussion

In this work, we developed a direct parametric image reconstruction method for a stationary cardiac SPECT scanner based on the 1T compartment model. unique aspects of this work include the development of the first event-by-event voxel-by-voxel based direct parametric reconstruction for SPECT, the creation and assessment of realistic simulations, and the in vivo canine imaging studies with ²⁰¹Tl, a myocardial perfusion tracer. Motion correction was not included in this paper, but event-by-event motion correction can be incorporated in the future, based on the current framework.

A. Initialization for direct method

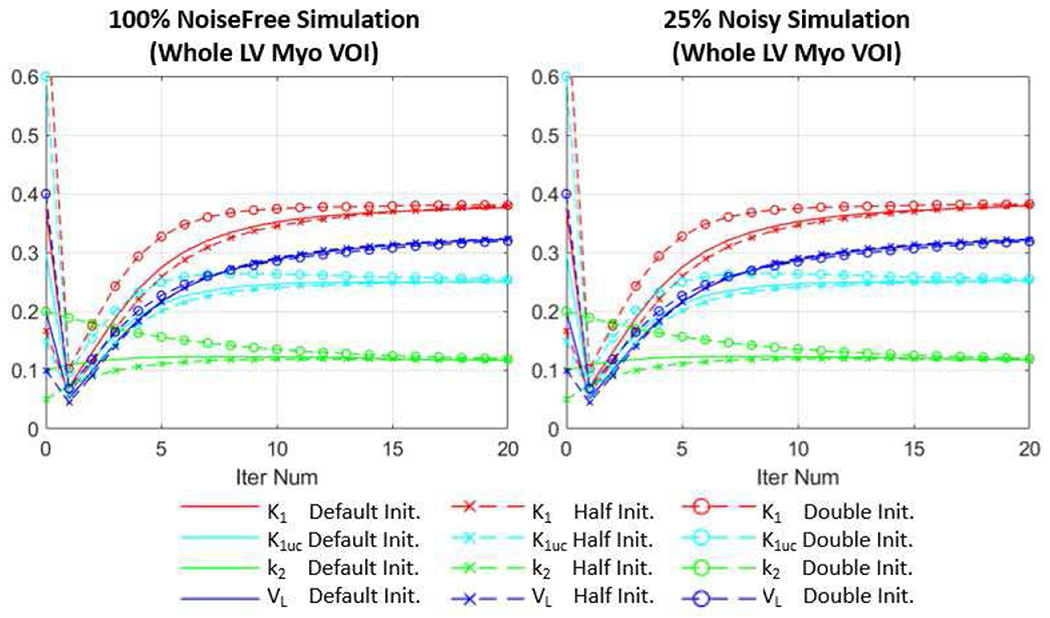
In the simulation study for the direct method, we used the initialization values close to the true values. Actually, for both simulation and in vivo studies in this paper, we chose the initialization values for the direct method such that they represent the typical population-averaged values based on the indirect canine study results. Since we used uniform initialization, the parametric images will re-distribute at the 1^st iteration no matter what initial values we use, and then start to converge. To further investigate the impact of initial values on the convergence of our direct reconstruction, we used halved and doubled initialization values for K_1,uncorr, k₂ and V_L in the simulation study. As can be seen in Fig. 8, even with different initialization values, the parameters converged to almost the same values within 20 iterations (smaller than 2.2% VOI mean value difference for all the parameters). At 80 iteration (not shown in the plots), the VOI mean value differences of all parameters using different initialization values are smaller than 0.7%. Therefore, we believe it is fair to use this set of initialization values since we only look at the parameters after 80 iterations.

Fig. 8.

Comparison of using different initialization values (uniform initialization) for the direct method for the simulation study. The first 20 iteration results are shown for both 100% count noise free simulation and 25% count noisy simulation (one replicate). The parameters were measured as the average within the whole LV myocardium VOIs. The default initialization (Default Init.) values for K_1,uncorr (K_1uc), k₂ and V_L were set to 0.3 min⁻¹cm⁻³, 0.1 min⁻¹ and 0.2, respectively, the same as used in the simulation and in vivo studies. For comparison, results with halved (Half Init.) and doubled (Double Init.) default initialization values are also shown.

B. Relative performance of direct and indirect methods

In the canine simulations we found that at 100% and 25%-count levels, the direct method achieved lower bias for K₁ estimation as compared with the indirect method at matched iterations. Direct method also produced less noisy K₁ images, especially at 25%-count level. In the 25%-count canine simulations (with ground truth input function), direct results had about 50% and 60% lower noise, in terms of $C\stackrel{‒}{o}{V}_{\theta }$ measured in the whole LV myocardium, compared to the indirect results at iterations 80 and 200, respectively. In the 25% count in vivo canine studies, direct results (with input functions obtained from 100%-count studies) had about 30% lower $C\stackrel{‒}{o}{V}_{\theta }$ compared to indirect results at the iteration 80.

Nonetheless, we found higher V_L for the direct results in the whole myocardium region compared to those in the LV_ES myocardium region, as shown in Fig. 4 and Table I. This could be caused by the model mismatch error propagated from RVBP to the myocardium septum region, since the current model does not include the RV blood volume term. The RV term will be included in our model [26] in the next-step development.

We also found that direct results showed reduced contrast particularly in some high-contrast regions (e.g. the boundaries between myocardium and LV/RV cavities. We think this is due to the slower convergence of direct method compared to the indirect method, since the direct method solves a global optimization problem and the voxels are correlated, while in the indirect method each voxel is fitted independently. Some example plots of the log-likelihood functions for the direct method can be found in Fig. S4 in the supplementary materials (available in the supplementary files /multimedia tab). The slower convergence of direct method was also observed in the PET applications [26], where it was reported that the convergence was slower for the direct method than the conventional indirect algorithm, particularly when initializing the direct algorithm with uniform parametric images. Alternatively, using early-iteration indirect results as the initialization for the direct method achieved the true contrast from early iterations, and was relatively stable over iterations. For our SPECT studies, accelerating the convergence and increasing the image contrast of the direct method using the alternate initialization scheme will be explored in the future studies.

In the simulation studies, a large k₂ bias was observed for the direct method compared to the indirect method, even in the LV_ES VOI (Table I). This could be due to the residual model mismatch error propagated from organs other than the heart, including the nearby lung, liver and body regions. In addition, this scanner has a small focused field-of-view (FOV) of approximately 19 cm in diameter [37], which means that the out-of-FOV artifacts could also propagate into the myocardium region and affect the direct method. Interestingly, the direct method produced more accurate K₁ estimation but less accurate k₂ estimation in this case. In a simulation study (Fig. S3 and Table S1 in the supplementary materials, which are available in the supplementary files /multimedia tab) with a uniform cylinder phantom (with diameter 12 cm and height 12 cm) which can fit into the focused FOV and was created based on 1T model, both direct and indirect methods produced very small K₁ biases (2.4% for the direct method, 2.2% for the indirect method) and k₂ biases (1.3% for direct method, 0.9% for indirect method), indicating that in an ideal scenario without the effect of kinetic model mismatch, error propagation and partial volume, the direct method can provide accurate parameter estimation. In this paper we focus on K₁ bias and noise evaluation, since K₁ is clinically more relevant for this myocardial flow tracer. A more detailed evaluation of k₂ parametric images is included in the supplemental materials (available in the supplementary files /multimedia tab).

C. ^K1 vs. ^K_1,uncorr

As shown in equation (3), to correct for partial volume effects, K_1,uncorr was divided by (1 − V_L) to obtain K₁. K_1,uncorr values are less noisy (shown in Fig. 7, the shaded area of the K_1,uncorr plots were narrower than the K₁ plots) and are considered more useful for perfusion defect identification, and K₁ estimates are more accurate for absolute myocardial flow quantification [26]. In PET imaging, it has been reported [26] that K₁ images are more prone to outliers than K_1,uncorr because of the possibility of dividing by a small quantity if V_L is close to 1. Only voxels where 1 − V_L > 0.01 were considered in their implementation to limit the influence of very large outliers. In SPECT imaging, however, such small threshold did not apply well. Due to stronger partial volume effect in SPECT imaging, in the regions close to the blood pool-myocardium interface, V_L will be under-estimated and K_1,uncorr will be over-estimated. Note that it is in the LV blood pool where V_L is mostly close to 1. In SPECT imaging due to partial volume effect, it is common to find V_L much smaller than 0.99, such that the threshold of 0.01 does not work. Dividing an overestimated K_1,uncorr over a small V_L in the blood pool will strongly boost the K₁ in the blood pool regions that are close to the myocardium. In our implementation, the threshold of 0.4 was empirically set and was found to be working well. Since V_L rarely exceeds 0.6 in the myocardium, quantification of K₁ in myocardium can be considered safe with the threshold of 0.4.

D. Input Function

In this work, the image-derived input functions can be inaccurate especially in low-count data, since blood pool activities were measured from dynamic frames, making input functions sensitive to noise induced bias in short-frame reconstructions. In the in vivo canine studies, we have shown that input functions estimated from full-count studies produced results with smaller bias and better reproducibility for both direct and indirect methods, as compared with using the input functions estimated from low-count studies. Further improving input function estimation quality will be investigated in the future, including simultaneously estimating the input function during direct reconstruction [27].

E. Computation Time

In our current implementation, it takes about 9 min per iteration for a study with 10 million counts. For a typical in vivo study, 80 iterations would cost 12 hours, which is still too slow for clinical application. The main obstacle to accelerating our implementation is the system matrix. As mentioned in Section II.D, the system matrix is too large to store in dense matrix format (25GB for reconstruction image size of 70 × 70 × 50). While we were developing the proposed method, we only had 20 GB RAM memory on our computer and the system matrix could not be loaded into our RAM memory, therefore we had to use the system matrix in sparse matrix format. Matrix and vector operations are much slower with sparse matrix format compared to using dense matrix format, since pre-decoding is required before accessing elements from a sparse matrix. Even with GPU acceleration, the current implementation is still not fast enough. We are considering using a larger RAM memory (e.g. 64 GB) in our next-step development, so that the system matrix can be pre-loaded into the memory as dense matrix format, and the computation speed is expected to be significantly boosted to meet clinical need.

It has been reported [37] that for clinical studies with high extracardiac activity using this SPECT/CT scanner, a larger system matrix of 600×600 × 600mm³(150 × 150 × 150 voxels) that incorporates a CT derived body contour in the reconstruction could improve quantitative accuracy within the FOV. The size of this larger system matrix is 348 GB in dense matrix format, and 443 MB in sparse matrix format. When reconstructing a larger FOV, loading the larger system matrix into the RAM is not a viable option since most computers are not equipped with more than 348 GB RAM. In such a case, we would still need to rely on the sparse system matrix framework presented in this work.

F. Motion Correction

One of the advantages of using list-mode reconstruction is its potential to perform optimal motion correction in an event-by-event manner, which has been well demonstrated in PET, for both static and dynamic [25, 26, 38] reconstructions. Motion impact on the dynamic imaging, including both direct and indirect parametric imaging, is more complicated and less predictable than the static imaging, depending on the combination of motion magnitude and timing. Both under- and over-estimation of kinetic parameters can occur due to respiratory pattern change [39] and body motion [38]. Therefore, motion correction is critical in dynamic imaging. Specifically, for SPECT cardiac imaging, respiratory and voluntary body motion are of interest to be corrected [40], and both motions for the heart can be estimated as rigid motion locally. Respiratory motion can be estimated using INTEX (internal-external correlation) technique [41–43] while the body motion can be estimated using multi-frame-acquisition technique [38, 44]. To correct for the motions, prior to reconstruction, we can transform the coordinate of the detector to a new position according to the motion estimation. In other words, the original-space detector coordinate is mapped back to the position in the reference space, where the CT-based attenuation map was acquired [43]. Although motion correction has not yet been implemented in this paper, the list-mode event-by-event reconstruction framework established here can readily incorporate the event-by-event motion correction in the future work.

VI. Conclusion

In this paper, we developed a list mode direct parametric reconstruction framework for dynamic SPECT based on 1T compartment model. GPU-based parallel computing was implemented to achieve more than 2000-fold acceleration. Left-ventricle blood volume fraction term was incorporated to correct for partial volume effect, motion-induced crosstalk from blood pool to myocardium and blood volume. Evaluation using both simulation and in vivo canine studies showed that comparing to the indirect method, the direct method can achieve lower bias and variability, as well as lower noise for MBF estimation. The developed list mode implementation framework is ideal for incorporating event-by-event motion correction directly into the reconstruction. Future work will include incorporating right-ventricle (RV) blood volume term to improve estimation in septum regions, improving input function estimation and optimizing our framework to further decrease the computation time.