Effect of Osmolytes on Conformational Behavior of Intrinsically Disordered Protein α-Synuclein

Abstract

α-Synuclein is an intrinsically disordered protein whose function in a healthy brain is poorly understood. It is genetically and neuropathologically linked to Parkinson’s disease (PD). PD is manifested after the accumulation of plaques of α-synuclein aggregates in the brain cells. Aggregates of α-synuclein are very toxic and lead to the disruption of cellular homeostasis and neuronal death. α-Synuclein can also contribute to disease propagation as it may exert noxious effects on neighboring cells. Understanding the mechanism of α-synuclein aggregation will facilitate the problem of dealing with neurodegenerative diseases in general and that of PD in particular. Here, we have used molecular dynamics simulations to investigate the behavior of α-synuclein at various temperatures and in different concentrations of urea and trimethyl amine oxide. The residue region from 61 to 95 of α-synuclein is experimentally known as amyloidogenic. In our study, we have identified some other regions, which also have the propensity to form an aggregate besides this known sequence. Urea being a denaturant interacts more with these regions of α-synuclein through hydrogen bond formation and inhibits the β-sheet formation, whereas trimethyl amine oxide itself does not interact much with the protein and stabilizes the protein by preferentially distributing water molecules on the surface of the protein.

Significance

The significance of this work lies, in particular, in understanding the pathophysiology of Parkinson’s disease caused by α-synuclein protein and, in general, in understanding the mechanism of protein aggregation in the presence of osmolytes.

Introduction

α-Synuclein is a small (14 kDa) intrinsically disordered protein. It is a highly conserved presynaptic protein that is generously found in various regions of the brain (1, 2, 3) and is closely associated with Parkinson’s disease (PD). PD arises because of abnormal aggregation of α-synuclein, and these aggregates are dominantly found in Lewy bodies as the hallmark of PD (4) and other synucleinopathies, such as multiple system atrophy and dementia with Lewy bodies. Patients diagnosed with Alzheimer’s disease have α-synuclein and coaggregates with amyloid-β (Aβ) in the brain tissue (5). In vitro, α-synuclein form fibrils that have characteristics and morphologies similar to those obtained from a disease-affected brain (6, 7, 8, 9, 10, 11). Patients with PD essentially have aggregates of α-synuclein, which suggests a central role of this protein in a sporadic disorder. However, the normal function of α-synuclein remains poorly understood (12). Proteins are biologically active in their three-dimensional structures, and their biological activity is questioned because of the presence of a natively unfolded structure.

Human α-synuclein protein has 140 amino acid residues and consists of three distinct regions, which includes an amphipathic N-terminal domain (residue 1–60), a central hydrophobic region, the non-Aβ component (residue 61–95), and a highly acidic C-terminal domain (residue 96–140). Monomeric form of α-synuclein is responsible for the formation of aggregates (mainly the non-Aβ component region, which accumulates at a high level in plaques) (12) and play an important role in PD pathogenesis; therefore, the structural analysis of monomeric form of α-synuclein has become very crucial to understand the conformational changes taking place during aggregate formation.

Proteins are marginally stable, and the stability of the protein can easily be altered by changing the thermodynamic environment of the protein or by the addition of small molecules, such as cosolvent or crowding agents (13) and osmolytes (14). Osmolytes are naturally occurring compounds, which may either cause a protein unfolding (termed as denaturant mainly urea) or may result in protein folding into stable native conformations, which, in this case, is an intrinsically disordered conformation of α-synuclein (protectants that include trimethylamine N-oxide) (15). Urea is a small organic compound responsible for the denaturation of the protein (16), and TMAO is a small molecule responsible for the stabilization of the protein (17). Various studies have been performed to explore the effect of two contrasting osmolytes urea and TMAO on the conformations of peptides. Standard molecular dynamics (MD) simulation of deca-alanine peptide has been performed by Kokubo et al. (18) to investigate the nature of denaturing osmolyte urea and protecting osmolyte TMAO. Their result shows different behavior in two osmolytes due to the van der Waals and electrostatic interactions. Mondal et al. (19) also performed a MD simulation on a 32-bead polymer chain in the presence of 7 M urea and 1 M TMAO and found that both osmolytes affect the conformations of the polymer chain in a significantly different manner. Their results showed that urea leads to the formation of an extended conformation, and TMAO suppressed the extended conformation of the polymer chain. MD simulation studies have been widely performed on an intrinsically disordered protein, such as Aβ protein, human amylin, tau protein, α-synuclein, etc. The effect of urea and TMAO on the conformation of tau protein has also been explored earlier (20), which resulted in a population shift in the monomeric form.

Although numerous studies are reported exploring the conformational behavior of proteins in the presence of osmolytes, further investigations are required to explore the mechanistic insights of osmolyte-induced protein compaction and unfolding. Many experimental studies reported earlier show that conformational changes in the monomeric form of α-synuclein induces/sets off fibrillar aggregate formation, which is responsible for PD (4,21); therefore, understanding the conformations of the monomeric form of α-synuclein in the presence of osmolytes becomes essential.

In this study, we have explored the thermal effect and the effect of urea and TMAO in regulating the conformational properties of the monomeric form of α-synuclein, which is intrinsically disordered. Standard MD simulations of 1.8 μs have been performed in explicit water and osmolytes. Remarkable differences have been observed on the α-synuclein conformation by changing temperature, denaturant urea, and protectant TMAO. An increase in temperature leads to the formation of more β-sheets, and urea enhances the formation of extended structure, whereas TMAO results in the formation of compact conformations.

Methods

The crystal structure of intrinsically disordered protein α-synuclein was taken from RCSB Protein Data Bank with PDB: 1XQ8. GROMACS 5.1.4 (22) software package was used to perform the simulations with GROMOS96 53a6 force field. The protein was placed in a triclinic box of length 7 × 17 × 6 nm³, which was filled with single-point charge water model (23), and periodic boundary conditions were used. MD simulations of the protein were performed at three different temperatures, 300, 350 and 400 K, in the presence of water only and at 300 K in the presence of urea and trimethyl amine oxide (TMAO) at various concentrations. An osmolytes box was built before these simulations and equilibrated using the method as described by Rocco et al. (24). The topology for urea and TMAO was built from Automated Topology Builder (ATB) (25). The parameters generated from ATB are found to be reliable and is extensively used in a number of current studies (26, 27, 28, 29, 30, 31). However, to justify the effectiveness of ATB parameters, we have calculated the thermodynamic property (i.e., density), transport property (self-diffusion coefficient), and structural property (RDF and number of hydrogen bonds) of a 3 M TMAO box and compared our result with the shea force field and united atom force field (generated from ATB) of TMAO as a benchmark test (32), which is provided in the Supporting Materials and Methods. Sodium ions were added to neutralize the system. A similar simulation protocol was used as reported earlier (33). A total of nine standard MD simulations were performed with each at a timescale of 200 ns and a total simulation time of 1.8 μs (Table 1). All the systems were simulated under isothermal-isobaric ensemble (NPT; constant number of atoms, pressure, and temperature).

Table 1.

Parameters Used for the MD Simulations of α-Synuclein in Water and Osmolytes

S. Number	Temperature (K)	Osmolytes (M)	Number of Osmolytes	Number of Water Molecules	MD Time (ns)
1	300	–	–	19,396	200
2	350	–	–	19,396	200
3	400	–	–	19,396	200
4	300	Urea 3 M	686	10,118	200
5	300	Urea 5 M	1249	10,032	200
6	300	Urea 8 M	1934	7952	200
7	300	TMAO 3 M	780	12,274	200
8	300	TMAO 5 M	912	11,395	200
9	300	TMAO 8 M	1040	10,899	200

After MD simulations, the last 90 ns of the trajectory was analyzed, discarding the initial 110 ns after the convergence analysis of the trajectories (Fig. S1; Table S1). The overall dynamics of the protein was determined through principal component analysis (PCA), which gives the significant motion of protein. To analyze the stability of the protein at various temperatures and in the presence of osmolytes, the RMSD of the backbone atoms with respect to the initial structures were investigated using gmx rmsdist command. Hydrogen bonds were calculated with a cutoff of 2.5 Å using gmx hbond, distribution of water and osmolytes around protein were calculated using gmx rdf (radial distribution function (RDFs)) command, residue level conformational changes in the protein was carried out using gmx rmsf (root mean-square fluctuation) command, and the interaction energy between osmolytes and protein was calculated using gmx energy command. The percentage of α-helical and β-sheet contents of protein was determined using DSSP program (34). Native contacts were calculated between all the Cα atoms of the protein using VMD (35) software.

There are two main sources of errors/limitations in standard MD simulations, sampling time due to limited computational resources and approximations in the force field. We have established the convergence of trajectories based on the number of cluster and cluster entropy calculation, which clearly shows that the time of sampling is sufficient to give an equilibrated trajectory. Based on convergence criteria, we discarded the initial unequilibrated trajectory and analyzed the latter part of the trajectory to get an equilibrated ensemble of conformations. As far as the second bias of force field is concerned, although the GROMOS force field used is more biased toward β-sheet, in this case, we have shown that the content of the secondary structure as well as other physical parameters are within the variable limit of different experimental observations. This makes our result robust and convincing.

Principal component analysis

Intrinsic properties of macromolecules can be determined by its correlated motion. Proteins are complex in nature, and though the conformational space available to the protein is decided by the large number of degree of freedom, extracting the dynamics of the protein from these large conformational spaces is difficult. Hence, the dominant motions that are basically involved in the function can be characterized by a small number of degrees of freedom or principal components (36). PCA is one of the methods that are capable of extracting the principal modes of motion by diagonalizing the 3N × 3N (N is the number of Cα, C, N, and O atoms) covariance matrix of Cartesian displacements. PCA analysis can provide a brief picture of the motions of macromolecules by applying the dimensionality reduction method (36,37). PCA is based on the calculation and diagonalization of the covariance matrix. Covariance matrix C is calculated as follows:

$$\text{C}=\langle \left(x\left(t\right)-\langle x\rangle \right){\left(x\left(t\right)-\langle x\rangle \right)}^T\rangle ,$$ (1)

where, x(t) shows the coordinates at time “t,” <x> indicates the average position, and <> indicates the ensemble average.

The covariance matrix “C” is then diagonalized to obtain eigenvalues and eigenvectors, as follows:

$$\complement =\text{T}\text{D}{\text{T}}^{\text{T}},$$ (2)

where D is the diagonalized matrix of eigenvalues, and T contains the eigenvectors.

Along with PCA, free energy landscape (FEL) plots were also established by calculating the normalized probability distribution based on the set of ordered parameters. The free energy can be defined based on the probability distribution (P) by using the following relation: F = −RTlnP. The reaction coordinates used here are native contacts (Nc) and RMSD.

Preferential interaction coefficient

The chemical potential of the protein system, generally protein equilibria and reaction kinetics, can be perturbed by the addition of cosolvent to the aqueous protein solution. Cosolvent can interact more strongly or more weakly with the protein than water and thus alters the protein chemical potential. This phenomenon is called “preferential binding” (38), and it governs the physical and chemical properties of the protein.

The cosolvent interactions with the protein can be evaluated by measuring the preferential interaction coefficient and is defined as follows:

$${\text{Γ}}_{\text{XP}}=-{\left(\frac{\partial {\mu }_P}{\partial {\mu }_X}\right)}_{m_P,T,P}={\left(\frac{\partial m_X}{\partial m_P}\right)}_{{\mu }_X,T,P},$$ (3)

where μ and m denotes the chemical potential and concentration, respectively, and the subscripts X and P indicates the cosolvent and the protein, respectively (39).

The thermodynamic way of defining the interaction of cosolvent with the protein is preferential interaction coefficient. The preferential interaction coefficient is defined as the measure of the excess number of cosolvent molecules in the local domain of the protein per protein molecule. Statistical mechanics provide the relationship between thermodynamic definition and spontaneous approach of binding (i.e., excess number of water or osmolyte molecules in the local domain) (40,41), and it can be calculated as follows:

$${\Gamma }_{\text{XP}}=\langle {\text{N}}_X^{local}-\left(\frac{{\text{N}}_X^{bulk}}{{\text{N}}_W^{bulk}}\right){\text{N}}_W^{local}\rangle ,$$ (4)

where N indicates the number of the specific type of molecule (X denotes cosolvent, and W denotes water) in a particular domain, and the angle bracket shows average ensemble. If the value of Γ_XP is greater than zero, then the cosolvent molecule accumulating in the vicinity of the protein is observed showing a net favorable interaction. A denaturant like urea exhibits this type of binding behavior. Conversely, if the value of Γ_XP is smaller than zero, it shows net unfavorable interactions with the protein surface because of the exclusion of cosolvent from the local domain of the protein (42). Such type of behavior is exhibited by protecting osmolytes like TMAO. Eq. 4 is used for calculating the preferential interaction coefficient directly from all atom MD simulations (43). The preferential interaction coefficient (Γ_XP) was calculated as the function of distance from the surface of the protein, and the appropriate cutoff based on RDF was applied.

Diffusion coefficient

Diffusion coefficient for water and osmolyte (urea and TMAO) molecules were calculated to see the extent of translational mobility under different conditions using the Einstein equation:

$$D_w=\underset{t\to \infty }{\lim }\langle {\left|r\left(t\right)-r\left(0\right)\right|}^2\rangle /6t,$$ (5)

where r (t) and r (0) represent the position vectors of the center of mass of molecules at time t and 0. We have taken the average for every molecule after every 10 ps as the time origin. The diffusion coefficients were calculated from the slope of the mean-square displacements versus time plot using the above equation.

Interaction energy between protein and osmolyte

The Coulombic and Lennard-Jones contributions to the total protein-urea and protein-TMAO interaction energy at various concentrations were calculated using the gmx energy command of GROMACS utility.

Tetrahedral order parameter

Orientational tetrahedral order parameter is the most widely used ordered parameter to investigate the structural ordering among the nearby water molecules, and it is defined as follows (44):

$$q=1-\frac{3}{8}\sum _{i=1}^3{\sum _{j=i+1}^4\left(\cos {\theta }_{ij}+\frac{1}{3}\right)}^2,$$ (6)

where θ_ij is the angle subtended by the central oxygen atom of water with its i_th and j_th neighbors. The tetrahedral order parameter measures the extent of the tetrahedral arrangement of central water molecules with its four neighbors. “q” is the mean value and is averaged over a large number of molecular configurations. For a perfect tetrahedral crystal, the value of q is 1 and is 0 for the system with a random distribution of angles (ideal gas limit) (45).

Results and Discussion

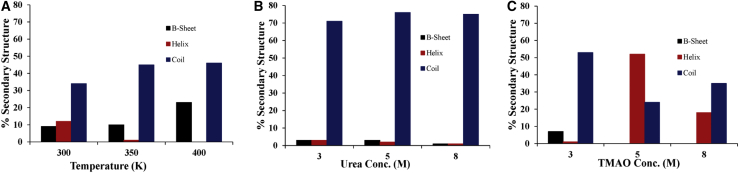
The conformational properties in two contrasting osmolytes and water show significantly differing behavior. In the crystal structure, α-synuclein contains 59% of α-helical, 19% random coil, and 0% β-sheet content. The change in the secondary structural conformation of the protein was obtained using the DSSP program. The percentages of secondary structure content of α-synuclein at different temperatures in water and in different concentrations of urea (3, 5, and 8 M) and TMAO (3, 5, and 8 M) at 300 K are shown in Fig. 1.

Figure 1.

Average secondary structure content of α-synuclein during the last 90 ns of the MD simulation (A) at 300, 350, and 400 K, (B) at 300 K in urea (3, 5, and 8 M), and (C) at 300 K in TMAO (3, 5, and 8 M). To see this figure in color, go online.

In the absence of osmolytes, the formation of the β-sheet takes place at the expense of the α-helical content and increases with increase in temperature (Fig. 1 A). These results indicate that the aggregation propensity of α-synuclein increases with an increase in temperature. This could be because the hydrophobicity of α-synuclein is expected to increase with an increase in temperature, as reported earlier (46). However, another study shows a decrease in fibrillation with an increase in temperature (47). At 300 K, the overall α-helix, coil, and β-sheet content at the end of the protein simulation in water as shown in Fig. 1 A are 12, 38, and 9%, respectively. The corresponding experimental values are within the range of 10–40%, 17–41%, and 0–20%, respectively, depending upon the measurement conditions and techniques employed (48, 49, 50, 51, 52, 53, 54, 55). Thus, the simulation results are qualitatively consistent and quantitatively within range with the experimental results.

In the presence of urea, the formation of β-sheet content is relatively low in comparison with water and decreases with an increase in concentration; this shows the decreased tendency of α-synuclein to form aggregates in the presence of urea (Fig. 1 B). As TMAO is known as a protein-stabilizing osmolyte, the percentage of helical content goes on increasing with an increase in concentration, but this increase is higher at a moderate concentration. At 5 M TMAO concentration, 88% of the α-synuclein remains in its native state (i.e., initially disordered state even after a 200-ns MD simulation) (Fig. 1 C). This observation indicates that TMAO can stabilize the α-synuclein at a moderate concentration.

Additionally, we have also examined the effect of osmolytes (urea 5 M and TMAO 5 M) at higher temperatures, 350 and 400 K, and observed that urea, which inhibits the formation of β-sheets at 300 K, will no longer remain as a β-sheet inhibitor; rather, more β-sheets are formed at a higher temperature in the presence of 5 M urea. However, at 5 M TMAO, the condition is totally reversed; α-synuclein, which was in its initial conformation at 300 K, loses α-helical content at a higher temperature (Table S2). These observations clearly indicate a more pronounced influence of temperature on the protein conformation.

FEL

The FEL may provide information about the pathway of the protein folding and unfolding (56, 57, 58). The two-dimensional FEL profile of Cα root mean-square deviation (RMSD) and number of native contacts show remarkable changes in the protein conformations at different temperatures in the absence of osmolytes and at various concentrations in the presence of osmolytes at 300 K (Fig. 2). α-Synuclein in water forms a β-sheet conformation with an increase in temperature characterized by wider energy basins having a lower value of native contact (Nc ∼0.60–0.78) and lower RMSD (0.20–0.44 nm) at various temperatures (Fig. 2 A). However, α-synuclein in urea shows heterogeneity in sampled conformations characterized by wider basins in which α-synuclein explored a number of intermediates with an energy barrier of 1.0–2.0 kJ/mol (Fig. 2 B). The unfolding of α-synuclein is observed, and it adopts an extended conformation with a lesser number of native contacts (Nc ∼0.60–0.56) and higher RMSD (0.80–1.20 nm), consistent with the unfolding of α-synuclein with an increase in urea concentration (Fig. 2 B). However, α-synuclein in TMAO is represented by smaller basins with energy minima shifted slightly to a lower RMSD value and higher native contacts indicating the stabilization of α-synuclein with an increase in TMAO concentration, but this stabilization is higher at 5 M TMAO because at this concentration, α-synuclein resembles the native conformation with 90% of the native contact of the protein. At 3 M TMAO, extended conformations were adopted by the protein with a higher fluctuation from their initial conformation as indicated by a large RMSD and small native contact value. A higher RMSD value may be assigned because of a larger fluctuation of the coil conformation at a lower TMAO concentration, whereas a higher native contact value could be assigned to the gain of the native-like conformation of the secondary structure at a higher TMAO concentration. The structure corresponding to the energy minima of the FEL plot is shown in the respective inset (Fig. 2). Experimental analysis was also carried out by Ferreon et al. on monomeric α-synuclein in the presence of urea and TMAO; it was observed that TMAO counteracts the effect of urea, and with an increase in TMAO concentration, more compact conformations were formed (59). Our results also indicate that with an increase in TMAO concentration, a more compact conformation was adopted by the protein, which is in agreement with the experimental results. Hence, the stabilizing nature of TMAO is concentration dependent, and it can retain the initial conformation of α-synuclein at 5 M TMAO concentration, which is in agreement with the DSSP result (Fig. 1 C).

Figure 2.

FEL plot of α-synuclein as a function of native contacts and RMSD of Cα atoms of α-synuclein at (A) 300, 350, and 400 K in the absence of osmolyte, (B) 300 K in the presence of urea 3, 5, and 8 M, and (C) 300 K in the presence of TMAO 3, 5, and 8 M. To see this figure in color, go online.

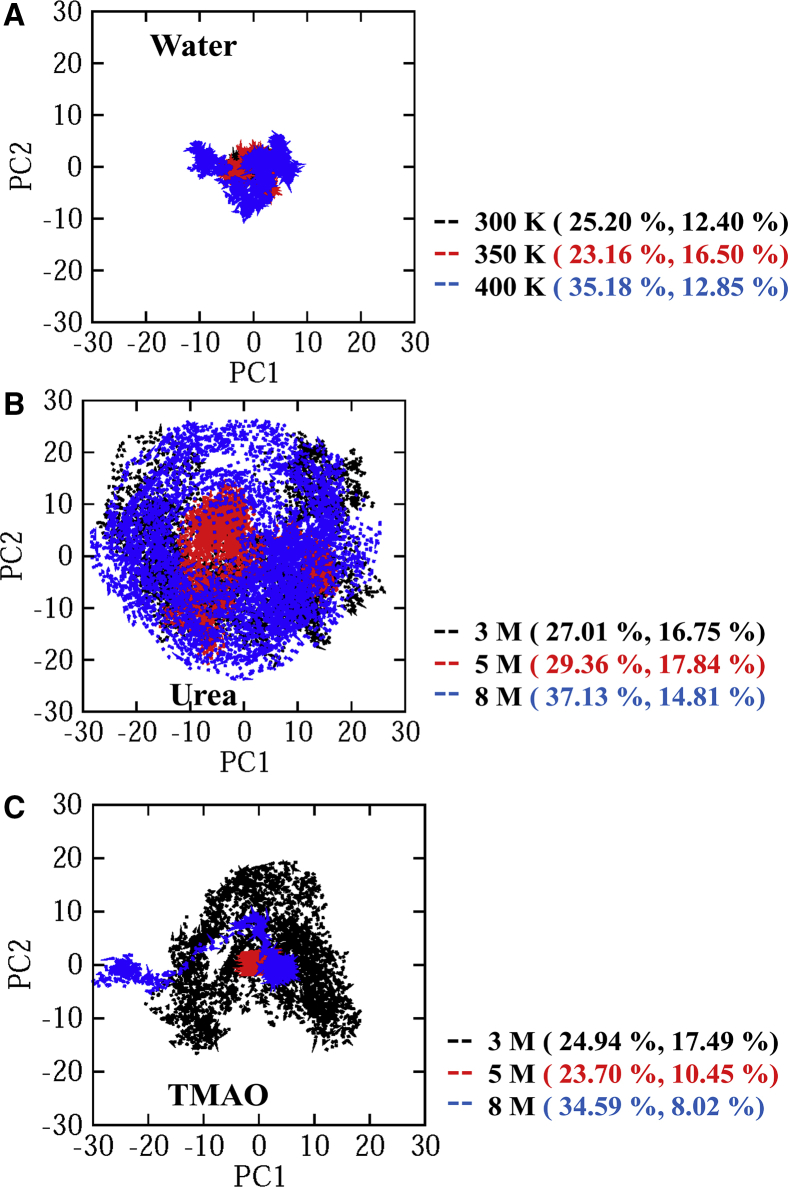
PCA

Principal modes of motion of α-synuclein in osmolytes and in water at different temperatures can be determined through PCA analysis of the MD trajectory data. Fig. 3 shows the projection of the structures of the Cα atoms of α-synuclein in the MD trajectory onto the first two eigenvectors defined by PC1 and PC2, which allows for visualizing the different conformational spaces projected during the MD simulations. Each point in Fig. 3 represents one conformation of α-synuclein that is attained during the MD simulation, and the density of points indicates the population of the conformations sampled during the MD run. It is observed from the results that α-synuclein in water has well-defined clusters as compared to α-synuclein in urea and TMAO. α-Synuclein in urea covered a large region of the conformational space along the PC1 and PC2 than in water (Fig. 3, A and B). This difference in the concerted motion of α-synuclein could be because of the fluctuation of the coil as the formation of the extended structure takes place in urea with increasing urea concentration (Fig. 2 B) than in water as more β-sheets are formed with an increase in temperature (Fig. 2 A). However, the motion of α-synuclein in the presence of TMAO shows nonuniform behavior. At 3 M TMAO, α-synuclein explored a large conformational space along PC1 and PC2, which is different from water solvent simulation at 300 K (Fig. 3, A and C). With a further increase in TMAO concentration, the α-synuclein explored more confined ranges of PC1 and PC2 as the formation of a more compact conformation is observed (Fig. 2 C). At a moderate concentration of TMAO, the α-synuclein explores a very small region of PC1 and PC2 because at this concentration, it remains almost in its initial conformation (Fig. 2 C). TMAO being a stabilizing osmolyte is expected to resist changes in the native state with an increasing concentration; however, we observed a 5 M TMAO concentration to be a better protectant of native structure than 8 M, in which 88% of native structure is retained (Fig. 1). These results suggest that α-synuclein occupies comparatively less space in the phase space at 5 M TMAO than at any other concentration, which shows that TMAO stabilizes the protein in a concentration-dependent manner. This result is also in agreement with the FEL results (Fig. 2 C).

Figure 3.

Projection of the structure of Cα atoms of α-synuclein in MD trajectories onto the first two eigenvectors PC1 and PC2, along with their percentage of contribution in (A) water, (B) urea, and (C) TMAO. To see this figure in color, go online.

Further insights on the conformational dynamics of α-synuclein were obtained using different analytical utility options of GROMACS. In PCA and FEL, only two reaction coordinates are used that alone are not sufficient to justify the extent of the aggregation propensity of the protein. One needs to examine various other properties, which could provide significant information differentiating native and non-native conformations of proteins.

In this context, to validate our previous results, we have calculated various properties, number of native contacts and number of water and osmolyte molecules within the first hydration shell of the protein to see the hydration property, number of hydrogen bonds formed between the protein side chain with water molecules and osmolytes, the interaction energy of the protein and osmolytes, preferential interaction coefficient, and the average tetrahedral order parameter of water molecule.

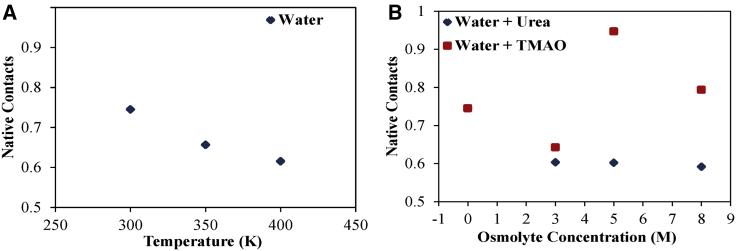
We have monitored the retention of the native conformation of α-synuclein in terms of native contacts. Native contact is defined when two Cα atoms are within 0.7 nm to each other in the conformation of interest as well as in the native state (60). The average value of the fraction of the native contact as a function of temperature and osmolytes (urea and TMAO) concentration between Cα atoms of α-synuclein has been calculated in the presence and absence of osmolytes for the last 90 ns of the trajectory (Fig. 4; Table S3). The average fraction of the native contact in the absence of osmolytes decreases with an increase in temperature during the last 90 ns of the simulation time. In the presence of urea, the fraction of native contact decreases with an increase in urea concentration, which indicates a significant departure from the native state and, hence, results in an extended conformation of the protein. Because at 3 M urea, α-synuclein adopts an ∼80% extended conformation, with a further increase in concentration, no major shift in native contact value is observed. The loss of native contact in the case of TMAO is less as compared to urea, and this loss shows a nonmonotonous behavior with over 90% of the native contact being retained at 5 M TMAO. As expected at 5 M TMAO concentration, the protein conformation resembles the native conformation.

Figure 4.

A fraction of native contacts of Cα atoms of α-synuclein as a function of (A) the temperature (in the absence of osmolytes) and (B) the osmolytes concentration (urea and TMAO). To see this figure in color, go online.

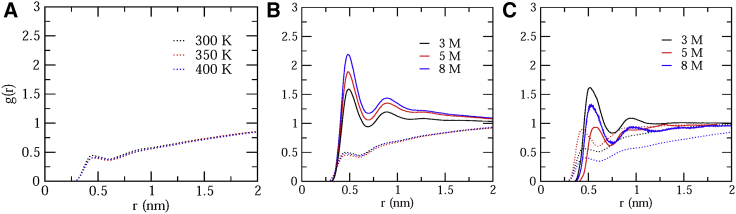
The interaction of the urea and TMAO molecules with α-synuclein requires the calculation of RDFs of water and osmolyte molecules around the α-synuclein. The comparison between RDFs of the urea and TMAO molecules at various concentrations is shown in Fig. 5. The RDFs are calculated from the surface of the protein. The peaks in RDFs are located at the shortest distance from the protein surface, and it indicates the closest interaction of osmolytes and water with the protein. RDFs of water molecules do not show any significant changes at different temperatures and at different concentrations of urea in protein-water and protein-urea simulations, respectively (Fig. 5, A and B). However, in TMAO, RDFs of water molecules shows nonuniform changes as TMAO interact with the protein in nonmonotonic fashion (Fig. 5 C). A small peak in the case of TMAO signifies exclusion of TMAO molecules from the local domain of the protein in comparison with the urea. As seen from Fig. 5 B, it contains two distinct peaks up to 1 nm distant of the protein surface. The first peak around 0.5 nm indicates that more urea molecules are present around the protein and is found to be increasing gradually with an increase in urea concentrations (Fig. 5 B). However, in the case of TMAO, similar to native contacts, RDFs too show a nonmonotonic decrease with a maximal decrease at a 5-M concentration (Fig. 5 C). This suggests that in comparison with urea, the TMAO molecule moves away from the first hydration layer of the α-synuclein. This result indicates that the preferential solvation of α-synuclein is by urea molecules than by TMAO.

Figure 5.

RDFs of (A) water molecules at different temperatures and (B) urea and water molecules and (C) TMAO and water molecules at different concentrations from the surface of the protein (solid line corresponds to osmolytes, and dotted lines correspond to water, respectively). To see this figure in color, go online.

Preferential interaction coefficient

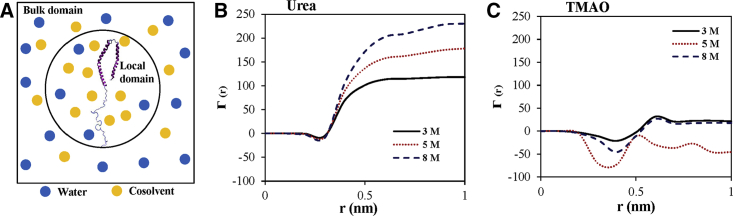
The preferential solvation of α-synuclein in the presence of urea and TMAO can be further studied by the calculation of the preferential interaction coefficient. We plot the preferential interaction coefficient of the urea and TMAO with the protein as a function of the distance “r” from the surface of the protein (i.e., local domain) in urea and TMAO solutions with increasing urea and TMAO concentrations (Fig. 6; (61)).

Figure 6.

(A) Schematic illustration of the local and bulk domain of the protein. (B) The preferential interaction coefficient of urea and (C) TMAO with protein as a function of the distance “r” from the surface of the protein (local domain) is shown. To see this figure in color, go online.

The preferential solvation of the protein with urea has been observed with an increase in concentration of urea, signifying the accumulation of urea in the local domain of the protein. We observed that the preferential interaction includes direct and indirect solvent-mediated interactions between α-synuclein and solvent molecules (urea, TMAO, and water). In contrast, a decrease in protein-TMAO preferential interaction has been observed with an increase in TMAO concentration, which shows the exclusion of TMAO molecules from the local domain of the protein surface, hence reducing the protein-TMAO preferential interaction. The decrease in the value of the preferential interaction coefficient is larger at 5 M TMAO concentration, which is also in agreement with the above results.

Hydration behavior of α-synuclein containing urea and TMAO

To explain the α-synuclein hydration of the systems containing urea and TMAO, the average number of water and osmolyte molecules within first the hydration shell (i.e., 0.5 nm of the protein surface) was calculated at 300 K (Table 2). A fraction of the average number of water and osmolyte molecules was also calculated. In urea, a significant decrease in the number of water molecules is observed in comparison with α-synuclein-water simulation in which the average number of water molecule is 2497 in the first hydration shell. This decrease in the number of water molecules shows that urea molecules preferentially bind to the protein, leading to the exclusion of water molecules from the protein surface. A decrease in the number of water molecules from 2497 to smaller values in the case of TMAO at various concentrations was also observed, but this decrease is smaller than in the case of urea. This indicates that a lesser number of TMAO molecules can bind to the protein surface, resulting in a water to TMAO ratio of 8.6, 13.6, and 11.5 at 3, 5, and 8 M TMAO, respectively, whereas in the case of urea, the water to urea ratio was found to be 6.2, 3.5, and 2.1 at 3, 5, and 8 M urea, respectively. The results obtained here indicate that urea shows an enhanced interaction with the protein surface than TMAO. The dehydration pattern of α-synuclein protein can be clearly seen by the N_W/N_o ratio of Table 2, which indicates prominent protein dehydration in the case of urea and moderate protein dehydration in the case of TMAO. The dehydration pattern can also be seen from Fig. S2, in which the number of water molecules in the first hydration shell is found to be larger in TMAO than in the case of urea. This shows that urea molecules have a high tendency to bind more closely to the protein surface compared to TMAO. A similar type of peptide dehydration was also observed by Sarma and Paul (62) in the case of the S-peptide analog, in which the ratio of N_w/N_u is found to be smaller than N_w/N_t, which shows greater peptide dehydration in the presence of urea compared to TMAO.

Table 2.

Number of Water and Osmolyte Molecules Found within the 0.5 nm of α-Synuclein Surface for All the Systems—Synuclein-Water, Synuclein-Urea (3, 5, and 8 M), and Synuclein-TMAO (3, 5, and 8 M)

Solvent + Osmolytes	Number of Osmolytes(No)	Number of Water (Nw)	Nw/No
Water	0	2497	Not applicable
Water + Urea 3 M	155	968	6.2
Water + Urea 5 M	240	836	3.5
Water + Urea 8 M	351	722	2.1
Water + TMAO 3 M	129	1115	8.6
Water + TMAO 5 M	104	1411	13.6
Water + TMAO 8 M	112	1290	11.5

Hydrogen bond analysis

The interaction mechanism of urea and TMAO with α-synuclein can also be determined by calculating the number of hydrogen bonds formed between the protein side chain with the water molecules at different temperatures in the absence of osmolytes and with osmolytes at 300 K at various concentrations. We have also calculated the interaction energy between the protein and osmolytes at various concentrations at 300 K.

In the absence of osmolytes, the number of hydrogen bonds between the side chain and water were calculated at 300, 350, and 400 K (Fig. 7). It was observed that the number of hydrogen bonds between the side chain and water decreases with an increase in temperature over the course of the simulation time. The formation of more and more antiparallel β-sheets takes place with an increase in temperature as the antiparallel alignment is energetically more favorable because of the perfect alignment of hydrophilic and hydrophobic amino acid residues. Because of this, the number of hydrogen bonds formed between the water and side chain of the protein decreases, which is in good agreement with the FEL results.

Figure 7.

Number of hydrogen bonds formed between the side chain of α-synuclein with water (A) in water at 300, 350, and 400 K, (B) in urea (3, 5, and 8 M), and (C) in TMAO (3, 5, and 8 M) at 300 K. To see this figure in color, go online.

Urea molecules tend to interact more preferentially with the side chain of α-synuclein because the protein side chain forms more energetically favorable bonds with the nearby urea molecules instead of finding a corresponding amino acid residue of the protein (61). This results in the decreased number of hydrogen bonds between the side chains of α-synuclein with the water molecule in the presence of urea at various concentrations (Fig. 7 B), which leads to the extended conformation of the protein. The number of hydrogen bonds between the side chain of the protein with urea was also calculated (Fig. S3), and it was observed that number of hydrogen bonds increases with an increase in the concentration of urea. However, the mechanism of the interaction of TMAO with the protein side chain is entirely different from urea. The TMAO molecule did not interact much with the side chain of the protein (Fig. S3). This lesser number of interactions of TMAO with the side chain of the protein may be due to entropically unfavorable interactions with the amide NH of the protein, as reported by Cho et al. (63). Hydrogen bonds formed between the water and side chain of α-synuclein in the presence of TMAO shows nonmonotonous behavior and shows a larger number of hydrogen bonds at 5 M TMAO because at this concentration, α-synuclein resists the change in its initial conformation (Fig. 7 C).

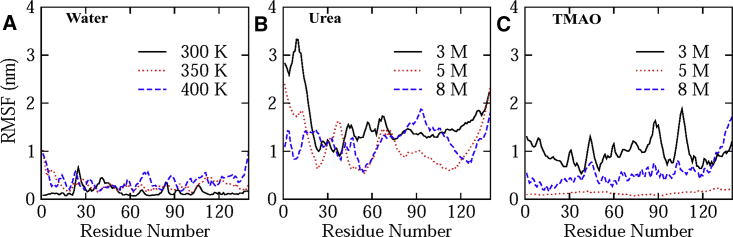
Further analysis of the change in the conformations of α-synuclein was carried out at residue level by plotting root mean-square fluctuations (RMSF) of Cα atoms of α-synuclein averaged over the last 90 ns of the simulation (Fig. 8). Experimentally, it has been known that the core region of α-synuclein, which is involved in fibril formation, and aggregation is residues 61–95 (64) as it leads to the formation of cross β-structure (65). It can be seen from the RMSF plot that in water, along with experimentally known regions, there are some other regions that are also involved in aggregate formation, and this can also be confirmed from DSSP plots in water at various temperatures (Fig. S4).

Figure 8.

RMSFs of Cα atoms of each residue of α-synuclein averaged over last 90 ns in (A) water (300, 350, and 400 K), (B) urea (3, 5, and 8 M), and (C) TMAO (3, 5, and 8 M). To see this figure in color, go online.

With an increase in temperature, the formation of more aggregates takes place as confirmed from DSSP results; therefore, fluctuation in the residues of α-synuclein is smaller in comparison with urea and TMAO. However, in urea, a larger fluctuation in RMSF is observed as an extended conformation is adopted by the protein. It can be seen that the residues that show more fluctuations are 5–27, 28–45, and 60–120 (Fig. 8 B). As urea leads to the formation of an extended structure (i.e., opening of α-helix), hence, more fluctuation in the RMSF value of Cα atoms is seen in comparison with the formation of β-sheet in water (Fig. 8 A). The further addition of TMAO to the system decreases the flexibility of these regions in a concentration-dependent manner (Fig. 8 C). It can be seen that at 5 M TMAO concentration, very little fluctuation in the Cα atom of residues is observed (almost negligible) as at this concentration, α-synuclein remains in its native conformation, which is explained earlier by DSSP results. Thus, TMAO stabilizes and prevents the α-synuclein from forming the β-sheet in a concentration-dependent manner.

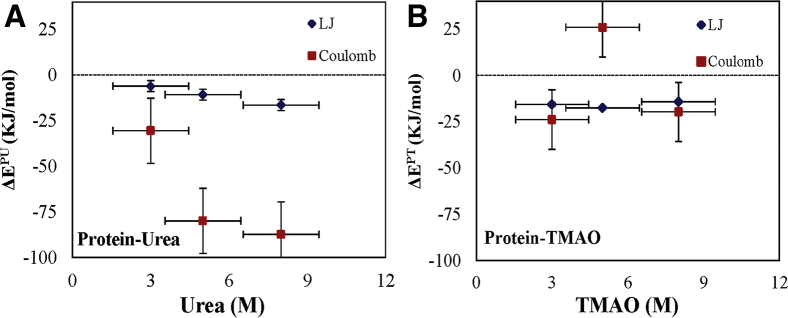
To explore the driving force of protein-osmolyte interactions, nonbonded interaction energy (i.e., both Lennard-Jones (LJ) and Coulomb (CB) energies) was calculated. To do this, we have calculated the interaction energy (E) of the protein with its local solvent located in the first solvation shell (FSS, defined based on the RDF 0.5 nm) (i.e., both with urea (E^PU) and TMAO (E^PT)). Then, the difference upon unfolding (i.e., ΔE^FSS) has been calculated, and the relative contribution of LJ and CB interactions has been examined (66). The calculation was done using Eqs. 7 and 8:

$${\text{Ε}}^{FSS}={\text{Ε}}^{PX}={\text{Ε}}_{LJ}^{PX}+{\text{Ε}}_{CB}^{PX},$$ (7)

$$\Delta {\text{Ε}}^{FSS}={\text{Ε}}_{unfolded}^{FSS}-{\text{Ε}}_{folded}^{FSS},$$ (8)

where folded and unfolded configurations are defined based on the probability distribution of C_α RMSD (67) of the protein with a cutoff value of 1.11 nm, and X = urea (U) or TMAO (T), respectively.

It was observed that, at all concentrations of osmolytes, Coulombic interaction dominates the protein-osmolyte association more than the respective Lennard-Jones interaction. More negative is the value of interaction energy, greater will be the interaction of osmolytes with protein. In the case of urea, Coulomb and Lennard-Jones interaction energy increases with an increase in the concentration of urea (Fig. 9 A). However, in the case of TMAO, Coulombic interaction energy decreases with an increase in the concentration of TMAO, but this decrease is more at a 5 M TMAO concentration, and Lennard-Jones interaction energy is higher at this concentration, which shows the nonuniform behavior of TMAO and is in agreement with the above results (Fig. 9 B). It has also been known from the previous studies that the protecting/stabilizing osmolytes have less direct interaction with the proteins and increases the structural stability of the protein by accumulating in the hydrophobic regions of the proteins (39,68,69). The interaction between protein backbone and TMAO is highly unfavorable (70). It has also been confirmed from the energy results. However, in the case of urea, a strong Coulombic interaction with a protein can be a major reason for the denaturing effect. In urea, the Lennard-Jones interaction energy is higher than TMAO, which is the hallmark of urea, which causes the protein to be denatured by creating a hydrophobic environment, and this is also illustrated in earlier studies (71, 72, 73).

Figure 9.

Changes in Lennard-Jones and Coulombic interaction energy along with the SD of the protein with (A) urea and (B) TMAO at different concentrations. To see this figure in color, go online.

Monitoring the structural and dynamic characteristic of water

Besides direct protein-osmolytes interaction, we also investigated the tendency of osmolytes (specifically, urea and TMAO) to interact with the water molecule and, in turn, modulate the structural and dynamical properties of water molecules. This change in water dynamics might influence the protein conformation.

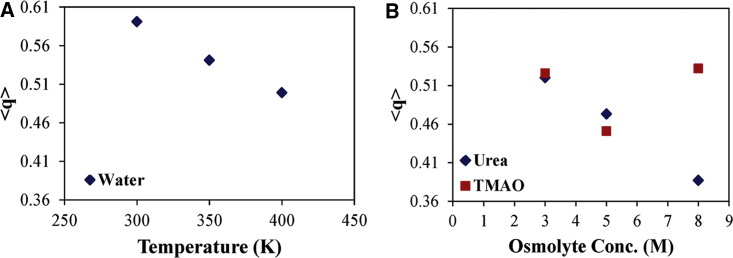
The distribution of orientational tetrahedral order parameter (q) for bulk water molecules at different temperatures and at different concentrations of osmolytes (urea and TMAO) were calculated (Fig. 10). The value of “q” goes on decreasing with an increase in temperature. The value of q is high at 300 K because at this temperature, water attains its maximal orientational order, and the hydrogen bond network is most structured at this temperature. The value of q for pure water is also calculated at 300 K, and its value is found to be 0.597, which is closer to the value obtained at 300 K in the presence of α-synuclein, which shows that the ordered parameter of the water molecule is retained around aggregation-causing proteins (33). A further increase in the temperature leads to the compression of water molecules, which resulted in a decreased value of q. The “q” value also decreases with an increase in the concentration of urea. This result is inconsistent with the prior experimental results obtained from the techniques such as Raman scattering, NMR (74,75), neutron diffraction (76, 77, 78), and many simulation studies (45) for the osmolytes-water system. Because TMAO is known as a protein-stabilizing osmolyte, it therefore has little impact on the hydrogen bonding network of water molecules as compared with other osmolytes (17). The tetrahedral order parameter of water in the case of TMAO first decreases from 0.526 to 0.451 at 3 and 5 M concentration and then increases to 0.532 at 8 M TMAO concentration, which shows the nonuniform behavior of TMAO at 5 M concentration. At 5 M TMAO concentration, the number of hydrogen bonds formed by side chain water is larger than that at any other concentration (Fig. 7 C); therefore, the q value at this concentration decreases as TMAO prefers to interact with water molecules rather than the protein side chain (70), and α-synuclein remains in its native state at 5 M TMAO, which is in good agreement with the above results. Several studies suggest that TMAO can stabilize the folded state of the protein indirectly by enhancing the bulk water structure around the protein. As reported earlier, TMAO stabilizes the protein by strengthening the protein-water interaction (17,79, 80, 81). Even after so many studies, the exact mechanism of action of TMAO on protein stability and on solvent structure remains controversial. The perturbation in the q value is slightly higher in the case of urea because urea leads to a complete unfolding of α-synuclein. This result is in agreement with the previously known result in which perturbation in the q value of water molecules is slightly higher in the case of the unfolded system (60).

Figure 10.

Average tetrahedral order parameter of bulk water molecules at (A) different temperatures (300, 350, and 400 K) in water and (B) 300 K in different osmolytes concentrations—urea (3, 5, and 8 M) and TMAO (3, 5, and 8 M), respectively. To see this figure in color, go online.

The effect of the temperature and osmolytes (urea and TMAO) on the surrounding matrix and the diffusion coefficient of water at 300, 350, and 400 K in the absence of osmolytes (Table 3) and of water and osmolytes (urea and TMAO) at 300 K were calculated (Table 4). The diffusion coefficient of water in the absence of osmolytes is 4.351 × 10⁻⁵ cm² s⁻¹ at 300 K, which is in good agreement with the data obtained from NMR experiments (82).

Table 3.

Diffusion Coefficient of Water Molecules at Different Temperatures in the Absence of Osmolytes

Temperature (K)	Diffusion Coefficient of Water (cm2 s−1) × 10−5
300	4.351
350	8.610
400	15.423

Table 4.

Diffusion Coefficient of Water and Osmolytes (i.e., Urea and TMAO) at Various Concentrations at 300 K

Osmolytes Concentration (M)	Diffusion Coefficient of Water (cm2 s−1) × 10−5	Diffusion Coefficient of Osmolytes (cm2 s−1) × 10−5
Urea 3 M	3.762	1.913
Urea 5 M	3.516	1.853
Urea 8 M	3.190	1.597
TMAO 3 M	2.041	0.778
TMAO 5 M	0.010	0.001
TMAO 8 M	2.323	0.904

The value of the diffusion coefficient increases with the increasing temperature in the absence of osmolytes (Table 3). However, at 300 K, there is significant slowing down of water dynamics in the presence of urea and TMAO at various concentrations as observed from the diffusion coefficient calculations (Table 4). Retardation in dynamics of osmolytes (urea and TMAO) also occurs, and it is higher than those of water. The average number of the hydrogen bond formed between water and osmolytes is found to be increasing with an increase in the concentration of osmolytes (Fig. S5). The variation of diffusivity with the concentration could be explained in terms of bulk viscosity, number of hydrogen bonds between water and osmolytes, and the accumulation of osmolytes around the protein. It is known from the experiments that the diffusivity of the water molecule is slowed down with an increase in osmolyte (urea and TMAO) concentration. Mostly, the rate of the diffusion of the water molecule is the same as that of osmolytes because of the formation of a stronger hydrogen bond between water and osmolytes (83). In the case of TMAO, the observed concentration-dependent diffusivity of the water molecule might be because of the bulk liquid viscosity (83). However, at the lowest diffusivity at 5 M TMAO, a nonmonotonous behavior can be explained in terms of the largest number of the hydrogen bond formed between TMAO and water. Because of a strong interaction between water and TMAO, retardation in the dynamics of the water molecule is more at this concentration than at any other concentration. With a further increase in the TMAO concentration, the diffusion of the water molecule increases as the accumulation of the TMAO molecule around the protein is observed (32) (Fig. 5 C), and also, the number of the hydrogen bonds between water and TMAO decreases (Fig. S5 B), which supports the above results. Contrary to the experimental decrease of the diffusion coefficient at lower concentrations, we observed an increase in the diffusion coefficient value at a significantly higher 8 M concentration.

Conclusion

In this study, we have explored the behavior of α-synuclein in the presence of urea and TMAO at different concentrations. A remarkably distinct conformation of α-synuclein was observed in the presence of both osmolytes. PD linked α-synuclein, which is an intrinsically disordered protein, adopted an extended and compact conformation in the presence of urea and TMAO, respectively. The formation of α-synuclein aggregates and insoluble fibrils linked to PD may be prevented in the presence of urea and TMAO. The unfolding pathway of α-synuclein remains invariant of urea, which is confirmed from the PCA together with FEL analysis that shows the direction of motion of the protein. The stabilizing nature of TMAO is observed in a concentration-dependent manner. A resistance of change in the native conformation of α-synuclein is observed at moderate concentrations in the presence of TMAO. Urea leads to an extended conformation of protein by directly interacting with the side chain of α-synuclein, whereas TMAO itself does not interact much with the α-synuclein and stabilizes the α-synuclein by preferentially distributing the water molecules around the protein surface as observed from hydrogen bond analysis. The hydration behavior of α-synuclein was also studied, and it was observed that urea displaces the water molecule from the surface of protein, whereas displacement of the water molecule from the surface of protein is lesser in the case of TMAO. This study could provide a detailed role of osmolytes (i.e., urea and TMAO) on the conformation behavior of α-synuclein and gives a better understanding of the aggregation behavior of α-synuclein, which is associated with PD.

Author Contributions

I.J. and S.M.N. designed the experiments. I.J. performed the analysis. S.M.N. analyzed the data. Both the authors contributed to the writing of the manuscript.

Editor: Markus Buehler.