Mechanics of Allostery: Contrasting the Induced Fit and Population Shift Scenarios

Abstract

In allosteric proteins, binding a ligand can affect function at a distant location, for example, by changing the binding affinity of a substrate at the active site. The induced fit and population shift models, which differ by the assumed number of stable configurations, explain such cooperative binding from a thermodynamic viewpoint. Yet, understanding what mechanical principles constrain these models remains a challenge. Here, we provide an empirical study on 34 proteins supporting the idea that allosteric conformational change generally occurs along a soft elastic mode presenting extended regions of high shear. We argue, based on a detailed analysis of how the energy profile along such a mode depends on binding, that in the induced fit scenario, there is an optimal stiffness $k_a^{\ast }$ ∼ 1/N for cooperative binding, where N is the number of residues. We find that the population shift scenario is more robust to mutations affecting stiffness because binding becomes more and more cooperative with stiffness up to the same characteristic value $k_a^{\ast }$, beyond which cooperativity saturates instead of decaying. We numerically confirm these findings in a nonlinear mechanical model. Dynamical considerations suggest that a stiffness of order $k_a^{\ast }$ is favorable in that scenario as well, supporting that for proper function, proteins must evolve a functional elastic mode that is softer as their size increases. In consistency with this view, we find a fair anticorrelation between the stiffness of the allosteric response and protein size in our data set.

Significance

Many proteins are allosteric: binding a ligand affects their activity at a distant site. Understanding the principles allowing for such an action at a distance is both of fundamental and practical importance. From the thermodynamic viewpoint, two models have been proposed, according to which binding creates a new stable configuration or instead shifts the thermal equilibrium between existing states. We perform a mechanical analysis of these models and show that they are not equally robust to mutations. We argue that in both cases, function can most properly occur along a soft elastic mode, whose stiffness decreases rapidly with protein size. We show data on 34 proteins substantiating this result, supporting a, to our knowledge, new principle for allosteric design.

Introduction

Many proteins are allosteric: binding a ligand at one or several allosteric sites can regulate function at a distant site, a long-range communication often accompanied by large conformational changes (1,2). There is a considerable interest in predicting the amino acids involved in this communication, or “allosteric pathway,” from structure or sequence data (3,4) because they can be used as targets for drug design (5). Yet, understanding the physical principles underlying such action at a distance in proteins remains a challenge (6,7). From a thermodynamic standpoint, two distinct views have been proposed. In the induced fit scenario, exemplified by the Koshland-Némethy-Filmer model (8), the protein essentially lies in one single state. The latter changes as binding occurs, leading to a conformational change. In an energy landscape picture such as that of Fig. 1 B, it corresponds to a displacement of the energy minimum upon binding. By contrast, in the population shift model exemplified by the Monod-Wyman-Changeux (MWC) model (9), two states are always present. Their relative stability can change sign upon binding, leading to an average conformational change. Although each of these models presumably applies to various proteins, they do not specify which designs allow for efficient action at a distance and how robust these designs are to mutations (10).

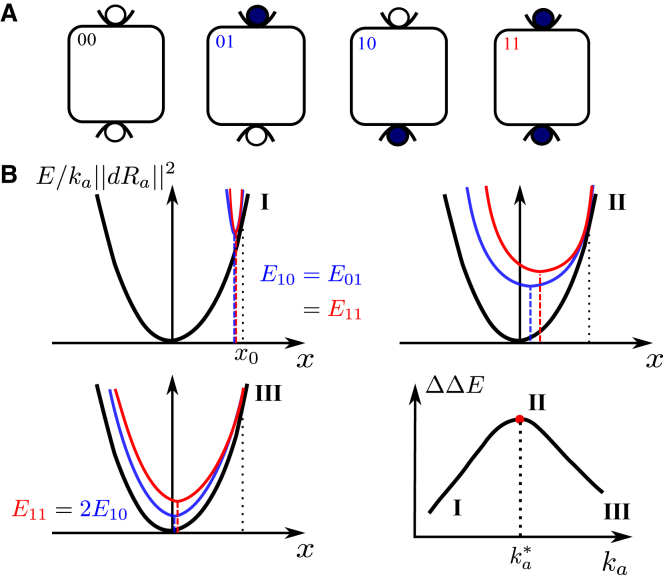
Figure 1.

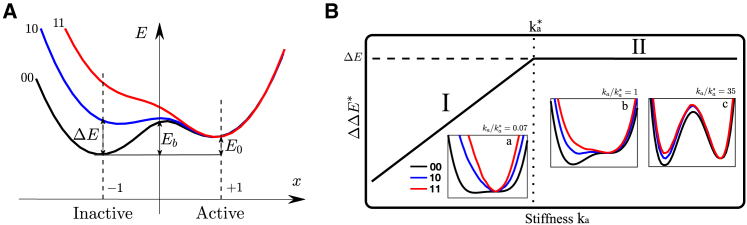
(A) A protein with two binding sites can be unbound “00,” bound to a single ligand “01” (or “10”), or doubly bound “11.” (B) The induced fit scenario is shown. Elastic energy of the unbound state E₀₀(x)/k_a (in black) rescaled for visibility by the soft mode stiffness k_a, singly bound state E₀₁(x)/k_a (in blue), and doubly bound state E₁₁(x)/k_a (in red) as a function of the imposed motion x along its soft mode is shown. E₀₀, E₁₀, and E₁₁ correspond to the minima of the black, blue, and red curves, respectively. In this sketch, we have assumed that for a motion x₀, the protein shape can accommodate perfectly both ligands without deforming; thus, the three energy profiles are identical at that point. Three cases are sketched, depending on the magnitude of the characteristic stiffness of the mode k_a. To see this figure in color, go online.

In several proteins—see below for a systematic study—it has been observed that the allosteric response induced by binding occurs predominantly along one or few vibrational modes (11, 12, 13, 14, 15). This result supports that in at least some proteins, elasticity—possibly nonlinear—is an appropriate language to describe allostery (in contrast to intrinsically disordered proteins that may be considered more as liquids than solids, for which the analysis proposed here would not hold). Very recently, there has been a considerable effort to use in silico evolution (16,17) to study how linear elastic materials can evolve to accomplish an allosteric task (18, 19, 20, 21, 22, 23, 24, 25, 26). In general, binding a ligand locally distorts the protein, which is modeled by imposing local displacements at some site, generating an extended elastic response that in turn determines fitness (chosen specifically to accomplish a given task). These models fall into the induced fit scenario because in the framework of linear elasticity, there is always a single minimum of energy. A particularly key allosteric function within proteins is the amount of cooperative binding, defined as the change of binding energy of a substrate at the active site caused by binding a ligand at the allosteric site. Materials optimized to display such a cooperativity over long distances develop a single extended “mechanism”—a soft elastic mode like the motion of closing scissors—connecting the two binding sites (21). It is found that the stiffness k_a (i.e., the curvature of the energy) of this mode cannot be too large nor too small for cooperativity to occur and that optimal design corresponds to $k_a^{\ast }$ ∼ 1/N, where N is the number of particles in the system. If proteins are nearly optimal, mutations stiffening that mode should thus diminish cooperativity. Yet, these predictions are restricted to strictly linear elasticity, an approximation that presumably does not hold in the regime in which most proteins operate—certainly not in the population shift scenario.

In this work, we show that the population shift and the induced fit models are very different from a mechanical perspective. In the former case as well, function can be achieved by developing a mechanism or soft elastic mode, but cooperativity, instead of steadily decreasing, saturates to a constant value once the mode stiffness passes some characteristic value, whose scaling with N is $k_a^{\ast }$ ∼ 1/N. We confirm this prediction in a nonlinear elastic model of allostery. This result implies that cooperativity is more robust toward mutations increasing stiffness in the population shift scenario. Yet, displaying a stiffness much larger than $k_a^{\ast }$ implies a very long transition time between the two states and is presumably prohibited, suggesting the hypothesis that allosteric proteins function with modes presenting a stiffness near the characteristic value $k_a^{\ast }$ in both cases. We test this proposition systematically using x-ray crystallographic data of 34 allosteric proteins. We first confirm that one or a few vibrational modes contribute to the allosteric response and introduce a, to our knowledge, new observable establishing that this response presents unusually extended regions of large shear, as found previously for three proteins (27). Next, we confirm that the characteristic mode stiffness tends to decrease with the propagation length, as we expect from the predicted scaling of $k_a^{\ast }$. Finally, we suggest systematic mutational studies to further test how mechanics constrains allostery.

Methods

Allosteric response

We identify a set of 34 allosteric proteins in the Protein Data Bank for which both the active (ligand bound at the allosteric site) and inactive (no ligand bound at the allosteric site) crystalline x-ray structures are available. Their Protein Data Bank identifiers are taken from (27,28) and reported in Supporting Materials and Methods. The set is diverse in functionality and includes enzymes (13), G-proteins (10), kinases (3), response regulators (3), DNA-binding proteins (4), and the human serum albumin, among which 12 protein complexes are present. We can thus estimate the allosteric response $|d{R}_a\rangle$ as the displacement field between the inactive and active structures (after having aligned them via the software Pymol 2.1.1 (29)). Here, we focus on the motion of the N amino acids, located by the position of their α-carbon. As an illustration, the allosteric response of a given protein (the elongation factor Tu) is shown in black arrows in Fig. 5 A. From the allosteric response $|d{R}_a\rangle$, one can readily estimate 1) the magnitude of the displacement ||dR_a||²; 2) the fraction of the protein involved in the response. For any displacement field, this fraction is usually estimated via the participation ratio (30),

$$P=\frac{{\Vert d{R}_a\Vert }^2}{N{\sum }_{i=1}^N{\Vert d{R}_a\left(i\right)\Vert }^4};$$ (1)

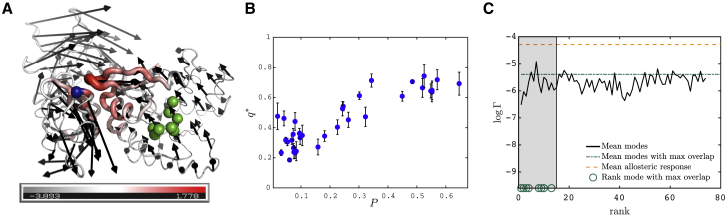
3) A measure of how much relative displacement takes place around atom i. Following (27), we consider the shear pseudoenergy E_sh(i) quantifying the amount of strain—essentially a measure of the relative displacement between adjacent atoms—at residue i, whose precise definition is given in the Supporting Materials and Methods. E_sh(i) = 0 indicates that the protein moves as a rigid body near atom i and, by contrast, is large when atoms slide rapidly past each other. E_sh(i) is shown in color in Fig. 5 A for the protein Tu, illustrating that two parts of the protein are rigidly moving (and counter-rotate), whereas the central region displays significant pseudoenergy E_sh(i), which is reminiscent of a hinge design.

Figure 5.

(A) Allosteric response (black arrows) of elongation factor Tu corresponding to the displacement between the inactive state (where GDP is bound at the allosteric site) and active state (where GTP is bound at the allosteric site and the aminoacyl-tRNA can bind at the active site). The phosphate binding loop (allosteric site) is highlighted in green, while the active site is at the interface between the GDP binding domain and the two other domains, one residue of which is highlighted in blue (35). The shear is encoded in both the color and the thickness of the structure in a logarithmic scale, red corresponds to large shear. The allosteric response is similar to that of a hinge. (B) Maximal overlap q^∗ as function of the participation ratio P is shown. (C) The observable logΓ is shown, quantifying how modes are both extended and present large shear energy (see main text for definition), averaged over the proteins with overlap larger than 45%, as function of the mode rank for 1) the allosteric response, 2) the modes with largest overlap, and 3) the first 75 modes (having subtracted the one with largest overlap) as indicated in legend. The green circles correspond to the rank of the mode with largest overlap. The shaded region highlights the range where these modes fall. The error bars represent the standard deviation associated to the distribution of ${\text{q}}^{\ast }$resulted from the different values of $R_c$∈$\left[8-12\right]$Å considered for each protein. To see this figure in color, go online.

Elastic networks analysis

To estimate protein elasticity, we use the elastic network model (ENM) (31), in which harmonic springs of identical stiffness are placed between all N α-carbons laying below a chosen cutoff radius R_c ∈ [8–12] Å. The ENM is obviously a crude approximation of real atomic interactions. Yet, its simplicity allows for the systematic study of various proteins, and it has been successful in capturing normal modes relevant for the function of some proteins. The dependence of the results on the value of R_c are indicated by error bars in Fig. 5 B and discussed in Supporting Materials and Methods for Fig. 6 B. This procedure defines an elastic energy from which the matrix of the second derivatives, i.e., the Hessian matrix H, can be computed. From H, one can readily estimate the stiffness k_a of the allosteric response as the curvature of the elastic energy in that direction:

$$k_a=\frac{\langle d{R}_a\left|H\right|d{R}_a\rangle }{{\Vert d{R}_a\Vert }^2}.$$ (2)

Figure 6.

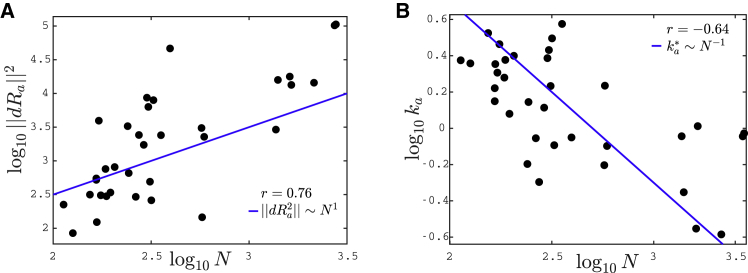
(A) Logarithm of the square of the norm of the allosteric response, ||dR_a||², is shown as function of the logarithm of the number of residues, N. The solid line corresponds to $\Vert d{R}_a^2\Vert$ ∼ N. (B) The logarithm of the stiffness k_a as a function of the logarithm of the number of residues N is given. The solid line represents the theoretical prediction $k_a^{\ast }$ ∼ 1/N. In both plots, r indicates the Pearson coefficient. To see this figure in color, go online.

Finally, the eigenvectors of H define the 3N vibrational modes of the protein ${\left\{|v_i\rangle \right\}}_{i=1\dots 3N}$. Following (11, 12, 13, 14, 15), the overlap q_i between the allosteric response and mode i characterizes their similarity (q_i = 1 implies that they are identical):

$$q_i=\frac{\left|\langle d{R}_a|v_i\rangle \right|}{\sqrt{\langle d{R}_a|d{R}_a\rangle \langle v_i|v_i\rangle }}.$$ (3)

Results and Discussion

Geometrical interpretation of mechanical constraints in induced fit allostery

As sketched in Fig. 1 A, a protein with two binding sites can be unbound (labeled “00”), bound to a single ligand (labeled “01” or “10”), or doubly bound (labeled “11”). We define by E₀₀, E₁₀, E₀₁, E₁₁ the energy of the protein in these four situations (corresponding to the minimal energy of their energy landscape) and choose E₀₀ = 0 as the reference energy. Cooperativity is then defined as

$$\mathit{\Delta \Delta }E=E_{10}+E_{01}-E_{11}.$$ (4)

To simplify notation below, we assume a symmetry between the states 01 and 10, in particular E₁₀ = E₀₁. Our qualitative conclusions below, however, remain valid even if this symmetry does not hold.

Consider a protein displaying cooperativity thanks to the presence of a soft elastic mode. Let us denote by x a variable indicating the motion along that mode (see our numerical model below for a concrete example in the context of a shear design), which varies from zero to unity as the protein undergoes its allosteric response. The energy profile E₀₀(x) of the unbound state follows

$$E_{00}\left(x\right)=k_a{\Vert d{R}_a\Vert }^{2}f\left(x\right),$$ (5)

where ${\Vert d{R}_a\Vert }^2=\sum _{i=\mathrm{1...}N}{\Vert d{\overrightarrow{R}}_i\Vert }^2$ is the norm of the allosteric response $|d{R}_a⟩\equiv \left\{d{\overrightarrow{R}}_a\left(i\right)\right\}$ and $d{\overrightarrow{R}}_a\left(i\right)$ is the vector displacement of the amino acid i. We expect that if the protein has N residues, ||dR_a||² is on the order of Na², where a is the interatomic distance. We will confirm empirically the dependence of ||dR_a||² with N below. k_a is the mode stiffness and f(x) some function of order unity such that f″(x = 0) = 1. For a purely linear elastic material, f(x) = x²/2. More generally, for the induced fit scenario, f(x) presents a single minimum, as illustrated in Fig. 1 B. In (21), it was argued that if linear elasticity applies, then there is an optimal stiffness $k_a^{\ast }$ for cooperativity. We present a geometrical interpretation of this result that extends it to the induced fit scenario in general and will be useful to explain why the population shift scenario behaves differently. Local chemical interactions that lead to identical binding energies for the inactive and active states do not affect cooperativity and thus need not be considered here. For concreteness, we assume that after some motion x₀ = 1 along that mode, the protein shape can accommodate perfectly both ligands without deforming. It implies that the energy profiles of the bound states E₁₀(x) and E₁₁(x) satisfy E₁₀(x₀) = E₁₁(x₀) = E₀₀(x₀), as pictured in Fig. 1 B. However as x departs from x₀, the protein shape does not match the ligands, imposing an elastic strain at the binding sites and leading to an increase of elastic energy in the protein that will trigger motion along other elastic modes. Assuming that the ligands are rigid and that each binding site involves on the order of n₀ atoms that move by a distance a as the protein undergoes its allosteric response, we have E₀₁(x) − E₀₀(x) = n₀ka²g(x − x₀), where k characterizes the stiffness of interatomic interactions and is large in comparison with the one of soft modes, i.e., k $\gg$ k_a. Here, g is some dimensionless function vanishing quadratically in zero but possibly nonlinear at large arguments.

E₁₁, E₀₁ can be computed as the minimum of the curves E₁₁(x) and E₀₁(x), respectively, from which the cooperativity ΔΔE is readily computed. Two extreme cases occur, illustrated in Fig. 1 B:

• 1)If k_aN $\ll$ n_ok (Fig. 1 B.I), as x moves away from x₀, the elastic energy induced by binding n₀ka²g(x − x₀) is very significant in comparison to the mode energy E₀₀(x) ∼ k_aNa²f(x). Thus, both E₁₀(x) and E₁₁(x) have a sharp minimum near x₀, with E₁₁ ≈ E₁₀ ≈ k_a||δR_a||²f(1). Thus, ΔΔE = E₁₀ + E₀₁ − E₁₁ ≈ E₁₀ ≈ k_a||δR_a||²f(1), which vanishes as k_a → 0.
• 2)If k_aN $\gg$ n₀k is very large (Fig. 1 B.III), n_oka²g(x − x₀) is small in comparison to E₀₀(x): E₀₀(x), E₁₁(x), and E₀₁(x) are very close to each other and must thus all present a minimum near x = 0. Thus, binding does not trigger motion along the soft mode, whose presence is useless. No extended modes couples the two binding sites, and E₁₁ ≈ E₀₁ + E₁₀, leading to ΔΔE → 0 as k_a → ∞.
• 3)Optimal cooperativity is thus found at some intermediary $k_a^{\ast }$ ∼ n_ok/N, corresponding to Fig. 1 B.II. Note that this argument for an optimal $k_a^{\ast }$ does not require the energy profile f(x) to be an exact parabola as long as it is monotonically growing in both directions around its minimum.

Mechanical aspects of the population shift model

MWC model

We recall some aspects of the MWC model. To simplify notation, we consider that the protein displays two symmetric binding sites as illustrated in Fig. 1 A. The protein is assumed to lie in two possible distinct configurations, “inactive” (In) and “active” (Ac). In the absence of binding, we take the energy of the inactive state as our reference (i.e., $E_{00}^{In}=0$) and denote the energy of the active state $E_{00}^{Ac}$ = E₀. We assume that the active configuration has a well-suited geometry to bind each ligand; thus, no elastic energy is spent for binding, and $E_{10}^{Ac}=E_{01}^{Ac}=E_{11}^{Ac}$ = E₀. By contrast, we assume that in the inactive state, binding costs some energy ΔE, leading to $E_{10}^{In}=E_{01}^{In}$ = ΔE and $E_{11}^{In}$= 2ΔE. The last assumption of additivity of binding energies within a given configuration, i.e., for a frozen mode amplitude, is expected to be accurate if the two binding sites are distant enough because no elastic coupling between them is expected in that case.

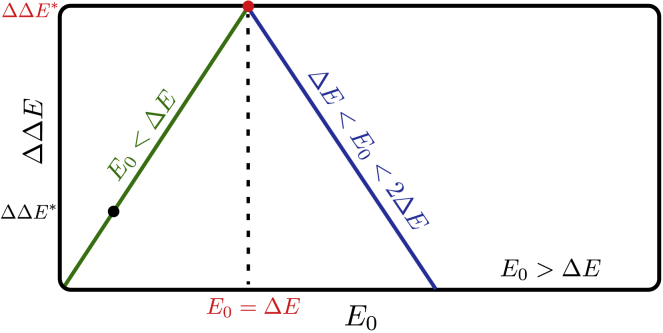
For each binding situation, the configuration (inactive or active) chosen is the one with the smallest energy, e.g., E₀₁ = min$\left(E_{01}^{In},E_{01}^{Ac}\right)$. Computing the cooperativity, one finds three different cases:

• 1)if E₀ < ΔE, then the binding of one ligand is sufficient to drive the system in the active state, implying E₁₀ = E₁₁ = E₀ and ΔΔE = E₀;
• 2)if ΔE < E₀ < 2ΔE, then the binding of one ligand is not sufficient, and two ligands have to bind to drive the system in the active state. Consequently, ΔΔE = 2ΔE − E₀;
• 3)if E₀ > 2ΔE, then ΔΔE = 0 because the system stays in the inactive state even if two ligands are bound. The sketch of this behavior is shown in Fig. 2, illustrating that the maximal cooperativity is found for E₀ = ΔE.

Figure 2.

Cooperative energy ΔΔE as function of the energy cost of binding a ligand E₀ is sketched for the MWC model. The maximal cooperative energy that the system can reach is ΔΔE^∗. To see this figure in color, go online.

Mechanical consideration in the MWC model

Our observations (see the empirical section below) indicate that a significant fraction of allosteric proteins operate mainly along one normal mode of the elastic energy, supporting the idea that in these cases, a favored path connects the inactive and active configurations. We expand the energy (in the absence of ligand) in terms of the motion x along that path (in this two-states case, it is more convenient to choose a coordinate x varying between −1 and +1 as the protein undergoes its allosteric response). Note that if nonlinearities are present, this path is not along a single linear mode but bends in phase space. Our analysis below holds independently of such bending. We keep the minimal number of nonlinear terms that allow displaying two states (a polynomial of four degrees has five parameters; three of them can be fixed by redefining the reference energy and changing the definition of x by both a multiplicative and additive constants):

$$E_{00}\left(x\right)=k_a{\Vert d{R}_a\Vert }^2\left(\frac{1}{8}{x}^4-\frac{1}{4}{x}^2+xb\right),$$ (6)

where b is a parameter reflecting how the energy profile is tilted toward the inactive state, k_a characterizes the stiffness of the mode, and ||dR_a||² is the square norm of the allosteric response.

A typical profile following Eq. 6 is shown in Fig. 3 A. We denote by inactive the lowest of the two minima and the other one by active. Note that 1) in the case b = 0, Eq. 6 describes two identical minima at x = ±1 of stiffness k_a, separated by an energy barrier E_b = k_a ||δR_a||²/8. 2) When the parameter b is positive, we have E_Ac > E_In up to b = b_c = 1/$\left(3\sqrt{3}\right)$ where the active state becomes unstable and only a single stable state is left. 3) At fixed k_a, the energy difference between the two states E₀ is maximal at b = b_c, where one finds E₀ = $\frac{3}{8}$k_a ||dR_a||². 4) For small b, E₀ $\simeq$2k_a ||dR_a||²b. In what follows, we focus on the case b < b_c, where the population shift model lies.

Figure 3.

(A) Sketch of the energy profiles E₀₀(x) (black), E₁₀(x) (blue), and E₁₁(x) (red) between two states, active (Ac) and inactive (In), as a function of the motion x along the path connecting them. The energy difference E₀ between the inactive and active unbound state, the energy cost of binding one ligand ΔE, and the height of the energy barrier E_b are highlighted. (B) Maximal cooperative energy ΔΔE^∗ as function of the stiffness of the allosteric response k_a is given, showing (I) linear growth and (II) a plateau. Energy profiles for k_a$\ll k_a^{\ast }$, k_a ∼ $k_a^{\ast }$, and k_a$\gg k_a^{\ast }$ are shown in inset. There are obtained from the nonlinear elastic model of allostery described below. To see this figure in color, go online.

Next, we assume that the active configuration matches the shape of both ligands so that binding events in that state cost no energy. However, by moving away from the configuration, the shapes of the protein and ligands do not match anymore, and the protein needs to deform elastically near the binding site. Again, assuming that each binding site involves on the order of n₀ atoms, which move by a distance of order a from the active to the inactive state, we have a binding energy E₁₀(x) − E₀₀(x) = n₀ka²g(x − x_Ac), where x_Ac ≈ 1 is the location of the active state along the path. This energy is exemplified by the difference between the blue and black curves in Fig. 3 A. Thus, the binding energy in the inactive state follows ΔE = n₀ka²g(x_In − x_Ac) ≈ 4n₀ka², which is independent of the protein size and mode stiffness k_a. As explained before, if the two binding sites are distant enough, for a given mode amplitude, the elastic costs of binding will simply add up: E₁₁(x) − E₀₀(x) = 2n₀ka²g(x − x_Ac), as shown in red in Fig. 3 A.

How the mode stiffness constrains cooperativity

To quantify this constraint we define the maximal cooperativity over all possible tilts b given k_a: ΔΔE^∗ $\equiv$ max_b{ΔΔE(k_a, b)}. We find two regimes:

• 1)If Nk_a $\ll$ n₀k, then the elastic costs associated with binding are very large compared to E₀. Both E₁₀(x) and E₁₁(x) are peaked close to x_Ac, as illustrated in Fig. 3 B.a. Thus, E₀ < ΔE, implying ΔΔE = E₀ according to Fig. 2, which is maximized at b = b_c leading to ΔΔE = $\left(3/8\right)$ k_a||dR_a||² ∼ k_aNa². Thus, ΔΔE vanishes linearly at small k_a, as illustrated in Fig. 3 B. This result is qualitatively similar to the induced fit case, for which ΔΔE also vanishes linearly as shown in Fig. 1 B.
• 2)If Nk_a $\gg$ n₀k, then the elastic cost is very small in comparison to E₀: E₀₀(x), E₁₀(x), and E₁₁(x) are almost identical as illustrated in Fig. 3 B.c. In that regime, cooperativity is optimized by choosing a small tilt fixing E₀ to ΔE according to Fig. 2, implying ΔΔE = ΔE ∼ n₀ka², which is independent of k_a. This plateau behavior is represented in Fig. 3 B and appears at $k_a^{\ast }$ ∼ n₀k/N.

This result represents a fundamental difference with the induced fit case, for which a large stiffness destroys cooperativity. Indeed, in the induced fit scenario, a large stiffness implies that the minimal energy is always found for x ≈ 0 as illustrated in Fig. 1 B.III, implying that binding does not move the protein along that mode, which is thus useless. This state of affairs is ultimately a geometric necessity stemming from the fact that the three curves E₀₀(x), E₁₀(x), and E₁₁(x) must be very close to each other in that regime, and each must present a single minimum. Consequently, the positions of these minima must be very similar in the three cases, leading to x ≈ 0 independently of binding ligands or not. This geometric necessity vanishes as soon as two minima are present.

Note that although ΔΔE asymptotes to a constant for k_a $\gg k_a^{\ast }$, the barrier E_b between the inactive and active states grows linearly with k_a in that limit. Large barriers would lead to undesirably slow transition rate between states; thus, we expect that in practice, k_a lies reasonably close to $k_a^{\ast }$.

A mechanical model for population shift allostery

We seek to model that 1) the allosteric response often takes place mainly along a single vibrational mode. 2) Various architectures can lead to allostery, including the well-known shear (27,32) or hinge (13) designs and others not falling in these categories (33,34). Such a diversity is also found in in silico evolution schemes (21). Yet, such synthetic architectures always present soft extended regions in which most of the strain (i.e., relative motion) is located. Such an observation was made in a few proteins (27) and will be generalized below. For proteins presenting two stable configurations, we expect these regions to present two possible ways of locally stacking amino acids well.

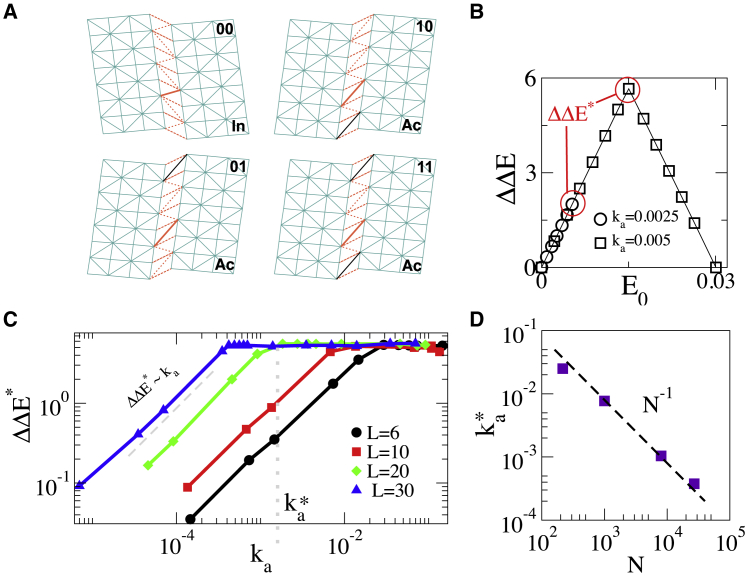
As an illustration, we consider the shear design in which the protein presents two three-dimensional rigid regions connected by a soft planar layer that can easily deform. The rigid regions consist of harmonic springs of stiffness k, shown in blue in Fig. 4 A. The soft layer consists of anharmonic springs (shown in red in Fig. 4 A), whose energy versus extension curve is nonlinear, chosen to have the same form as Eq. 6. These nonlinear springs have a characteristic stiffness k_w and present two stable extensions at which they exert no force, whose relative energy is controlled by some bias b_w. These stable extensions are chosen such that two states of the protein as a whole, the inactive and active states shown in Fig. 4 A, present no contact forces by construction and are thus local minima of the energy. Finally, the protein presents two binding sites at its top and bottom. At each site, binding imposes that the distance between two nodes (indicated by black lines in Fig. 4 A) equals the distance it naturally presents in the active state, thus favoring it. The details about the construction of the microscopic model are discussed in Supporting Materials and Methods.

Figure 4.

(A) Sliced view of our three-dimensional mechanical model for population shift allostery. In blue: rigid elastic regions made of harmonic springs of stiffness k, separated by a weak nonlinear region made of nonlinear springs (in red) of stiffness k_w with k_w$\ll$k. The inactive state (In) favors short springs, whereas the active state (Ac) favors long springs, as exemplified by a solid orange spring in the weak band. The location of the binding sites are represented by a solid black spring. (B) ΔΔE as function of E₀ for different values of k_a for a linear length L = 20 is shown, where L³ = N. (C) Maximal cooperative energy ΔΔE^∗ as function of k_a for L = 6, 10, 20, and 30 is shown. The kink in these curves define the crossover stiffness $k_a^{\ast }$. (D) $k_a^{\ast }$ versus number of nodes in the model N, supporting $k_a^{\ast }$ ∼ N⁻¹. To see this figure in color, go online.

We can now numerically compute the energy profiles E₀₀(x), E₀₁(x), and E₁₁(x) as a function of the motion along the shear mode x by imposing a shear displacement (i.e., a value of x) and letting the entire elastic energy of the material relax except for that mode. The insets of Fig. 4 show our results. The value of the mode stiffness k_a can be extracted from fitting Eq. 6 to E₀₀(x) and measuring the displacement norm ||dR_a|| and can be increased by increasing k_w. From E₀₀(x), one readily computes the energy difference E₀ between the inactive and active states, which can be increased by monitoring the microscopic bias b_w. From the minima of E₀₀(x), E₀₁(x), and E₁₁(x), one immediately extracts the binding costs ΔE and ΔΔE.

Fig. 4 B shows ΔΔE for two values of k_a as the energy difference E₀ is increased. For large k_a, ΔΔE passes through a maximal ΔΔE^∗ = ΔE, whereas for small k_a, ΔΔE is smaller, and its maximum is fixed by the maximal achievable energy difference E₀. ΔΔE^∗ as a function of k_a is shown for different system sizes N in Fig. 4 C, confirming the presence of two regimes with a crossover at some $k_a^{\ast }$ ∼ 1/N as shown in Fig. 4 D. Overall, these observations validate our theoretical predictions on the dependence of $k_a^{\ast }$ with the number of residues and on how the stiffness k_a qualitatively affects cooperativity.

Empirical study of 34 allosteric proteins

Geometry of the allosteric response

Fig. 5 B reports the maximal overlap q^∗ $\equiv$ max_iq_i as a function of the participation ratio P. Our observation indicate that q^∗ is in general large (in half of the cases, larger than 0.45), supporting further that allostery indeed occurs mainly along one mode (11, 12, 13, 14, 15). Interestingly, this effect is stronger when most sites of the protein are involved in the allosteric response (P large). Interestingly, some protein complexes (for example, ATCase; see the values of q^∗ in Table S1) also display a large projection of their allosteric response on a single mode, supporting that mechanical considerations can be valuable in such cases as well.

We now provide systematic data supporting that the allosteric response presents extended regions of large shear energy (27). More specifically, we argue that while some vibrational modes can present significant shear (e.g., localized modes capturing the motion of dandling loops) and other can be extended (such as plane-wave-like modes), the allosteric response is unique in presenting both aspects, thus revealing a specific design principle. To quantify this effect, we introduce the quantity, which can be defined on any displacement field:

$$\log \mathit{\Gamma }\equiv \left[\gamma {\log }_{10}\left(\text{P}\right)+{\log }_{10}\left(\Vert E_{sh}\Vert \right)\right],$$ (7)

where ||E_sh|| is the total magnitude of the shear energy, i.e., ||E_sh|| = ${\left(\sum _i{E}_{sh}{\left(i\right)}^2\right)}^{1/2}$. LogΓ is large if the displacement is extended and if the shear energy is large. The factor γ characterizes the trade-off between these two features. Here, we choose γ = 3.5, reflecting the fact that for vibrational modes, we find that P varies ∼3.5 times less in relative terms than ||E_sh||, as shown in the Supporting Materials and Methods. Thus, for γ = 3.5, the spatial extension and the amount of shear equally affect logΓ. Fig. 5 C shows logΓ averaged over the 17 proteins with q^∗ > 45% for the allosteric response (yellow line), the mode with maximal overlap (blue line), and the first 75 vibrational modes (having subtracted the one with largest overlap) as function of the mode rank. We find that Γ is typically 160 times larger for the allosteric response than for vibrational modes, a very significant difference underlying the specific geometry of the allosteric response.

Scaling of response stiffness k_a with protein size

We can now test our conjecture that the allosteric stiffness k_a is close to $k_a^{\ast }$ ∼ 1/N where cooperativity saturates, which implies in particular an anticorrelation between k_a and protein size. In our theoretical estimate of $k_a^{\ast }$, we have assumed that the allosteric response magnitude is linear in the protein size, i.e., ||dR_a||² ∼ N. It is a natural assumption because the larger the protein, the more likely its response involves many residues. The relationship between these two quantities is tested in 34 proteins in Fig. 6 A. We indeed find a strong correlation between the logarithms of ||dR_a|| and N (Pearson coefficient r = 0.76 with p-value p = 1.64 × 10⁻⁷. Pearson coefficients are computed on the logarithmic values via the MATLAB R2017b (The MathWorks, Natick, MA) function corr). Overall, data are consistent with our assumption of proportionality.

Finally, we plot the allosteric response stiffness k_a measured according to Eq. 2 in terms of N for all proteins in Fig. 6 B. A key finding is the fair anticorrelation between the logarithms of these two quantities (Pearson coefficient r = −0.64 with p-value p = 4.00 × 10⁻⁵), supporting the idea that larger allosteric proteins need to evolve a softer elastic mode to accomplish function, as expected from our analysis. The signal that we observe is encouraging, especially given the possible sources of noise in the analysis, among which, in particular, is the use of the ENM to build the Hessian matrix.

Conclusions

We have provided systematic evidence that the allosteric response occurs along one soft elastic mode, and we have introduced a, to our knowledge, novel observable Γ to establish that this response generally displays unusually extended regions of high shear strain. These observations support that for many proteins, elasticity is a useful starting point to describe allostery. We have revisited the two classical thermodynamic models of allostery from this perspective and provided a detailed study of how the energy profile along the soft mode evolves with binding. We find that induced fit and population shift models qualitatively differ. In the induced fit model, there is an optimal stiffness $k_a^{\ast }$ ∼ 1/N associated to that mode beyond which the cooperative binding energy eventually decreases to zero. The population shift model is more robust to mutations affecting stiffness, and $k_a^{\ast }$ ∼ 1/N simply marks a crossover beyond which cooperativity saturates and the transition time between configurations rapidly explodes. We introduced a, to our knowledge, novel nonlinear elastic model for allostery supporting these views. Our key result is that proper function is achieved if proteins evolve an elastic mode whose softness must rapidly decrease with size, a prediction supported by the anticorrelation observed between these quantities.

Systematic mutation scan on one single protein, in which binding assays to measure cooperativity are combined with single molecule experiments or ultrafast laser pulses to estimate the stiffness of the allosteric response, would be extremely useful to test the predicted relationship between these quantities. Molecular dynamics experiments could further test how the energy profile along the soft elastic mode evolves with binding. Elucidating such an interplay between thermodynamics and mechanics in proteins would be valuable in a variety of tasks, including de novo protein design and the discovery of novel allosteric pathways.

Author Contributions

R.R., C.B., L.Y., and M.W. conceived the project, and M.W. supervised research. R.R., S.M.F., and S.Z. developed the tools for the empirical data analysis. L.Y., C.B., and R.R. performed computations and developed the numerical methods for the network model. L.Y. and M.W. developed the theory. All authors analyzed the results and wrote the final manuscript.

Editor: Amedeo Caflisch.