Abstract
Recent mathematical results for the noisy Kuramoto model on a 2-community network may explain some phenomena observed in the functioning of the suprachiasmatic nucleus (SCN). Specifically, these findings might explain the types of transitions to a state of the SCN in which 2 components are dissociated in phase, for example, in phase splitting. In contrast to previous studies, which required additional time-delayed coupling or large variation in the coupling strengths and other variations in the 2-community model to exhibit the phase-split state, this model requires only the 2-community structure of the SCN to be present. Our model shows that a change in the communication strengths within and between the communities due to external conditions, which changes the excitation-inhibition (E/I) balance of the SCN, may result in the SCN entering an unstable state. With this altered E/I balance, the SCN would try to find a new stable state, which might in some circumstances be the split state. This shows that the 2-community noisy Kuramoto model can help understand the mechanisms of the SCN and explain differences in behavior based on actual E/I balance.
Keywords: suprachiasmatic nucleus, Kuramoto model, community networks, bifurcation point, E/I balance, splitting behavior
All life on earth is adapted to the external 24-h light-dark cycle, in which mammals normally have one bout of activity each cycle and one bout of sleep. However, when hamsters are placed in constant light conditions, this regular pattern of sleep and wakefulness is disturbed, and splitting of the activity bout may occur. In this case, the single period of activity is dissociated into 2 components that ultimately settle in antiphase, effectively producing sleep-wake cycles of approximately 12 h (Pittendrigh and Daan, 1976). It has been shown that this behavioral phase splitting in hamsters and mice has its origin in the suprachiasmatic nucleus (SCN), which is the location of the master clock that regulates the 24-h rhythms in physiology and behavior (de la Iglesia et al., 2000). The SCN is a bilaterally paired nucleus, in which splitting of the behavioral rhythm, caused by exposure to continuous light conditions, induces the left and right nucleus to activate in antiphase (de la Iglesia et al., 2000; Mendoza and Challet, 2009).
Between species, there are differences in phase-splitting behavior. Hamsters show splitting when put in constant light conditions (Pittendrigh and Daan, 1976; de la Iglesia et al., 2000). In a mutant mouse strain, called the CS mouse, rhythm splitting occurs in constant darkness (Abe et al., 1999). Rats and mice can also show split behaviour when subjected to so-called forced desynchrony protocols (Campuzano et al., 1999; de la Iglesia et al., 2004; Casiraghi et al., 2012). Rats were subjected to a 22-h light-dark cycle and mice to a chronic jet lag protocol. It was shown that in the forced desynchrony protocol, the dissociation arises between the ventral and the dorsal part of the SCN. Here, the ventral part follows the external light-dark cycle, and the dorsal part has a period close to the endogenous free-running period of the animal. It is unknown whether these different types of phase dissociation, being a dissociation in phase of the left and right SCN or of the ventral and dorsal SCN, have different underlying mechanisms.
The interaction within the ventral part is mainly based on the neurotransmitter vasoactive intestinal polypeptide, which is excitatory. In the dorsal SCN, the interaction mainly occurs through arganine vasopressin, which is also excitatory in nature. The communication between the ventral and dorsal part of the SCN occurs predominantly through γ-aminobutyric acid (GABA), which can be inhibitory but in the SCN also excitatory (Choi et al., 2008; Farajnia et al., 2014; Olde Engberink et al., 2018). For the left-right distinction, less is known about the communication mechanisms, let alone whether these are excitatory or inhibitory (Michel et al., 2013).
Recently, a variety of models has been proposed to explain why the phase-split state of the SCN occurs. These models have typically tried to modify the standard 2-oscillator models for the SCN by including time delays in the coupling (Indic et al., 2008), assuming large variation in the coupling strengths (Schroder et al., 2012) or taking the intracommunity coupling to be negative (Oda and Friesen, 2002). The model proposed by Oda and Friesen (2002) models each community of the SCN as a single oscillator and connects these using coupled Pittendrigh-Pavlidis equations. They consider coupled identical oscillators as well as nonidentical oscillators, making a distinction between morning and evening oscillators. Indic et al. (2008) considered a model most similar to the one we will consider. They included the possibility of a delay in the interaction between oscillators and also observed that a nonuniform network structure, which has at least 2 communities, is essential to realize the phase-split state. Their work included analysis of the stability of the phase-split state. The article by Schroder et al. (2012) used a model proposed by Leloup et al. (1999) and Gonze and Goldbeter (2006) and applied this to 2 groups of 100 oscillators. The results were based on numerical simulations and showed that the split state can arise without a change in the structure or strength of the interactions between oscillators but rather by a change in the circadian properties of individual oscillators. Only Schroder et al. (2012) addressed different transitions to the phase-split state, but they did this by looking at the interplay between light intensity and the interaction strength parameters of the individual oscillators. We use a different model, more similar to the model used in Indic et al. (2008). In our model, the external driving is implicit in the change of interaction strength parameters. This model allows us, for the first time, to fully identify the phase diagram to show which transitions are possible for which parameter values.
In this article, we interpret recent findings on the phase diagram of the noisy Kuramoto model on a 2-community network (Meylahn, 2019) in the context of the phase-split SCN, in which the left and right SCN, or the ventral and dorsal part of the SCN, dissociate into 2 antiphasic neuronal communities, instead of using a 2-oscillator model. In contrast to previous studies, in which additional parameters were necessary to obtain a phase-split state, here only the 2-community structure of the network is required. This enriches the model significantly in comparison with the original 1-community version. This is a surprising finding in itself, as the modification to consider the model on a 2-community network seems almost trivial a priori. Not only does this model exhibit the phase-split state, but it also exhibits a bifurcation point in the possible states it can take (shown as separate lines in the phase diagram in Fig. 1), which determines the existence of a nonsymmetrically synchronized state. This might explain the different transitions to the phase-split state observed in the experiments. We investigate the stability properties of the various states by using simulations of the system and find that the system might have to pass through the nonsymmetrically synchronized solution when it is above the bifurcation point.
Figure 1.
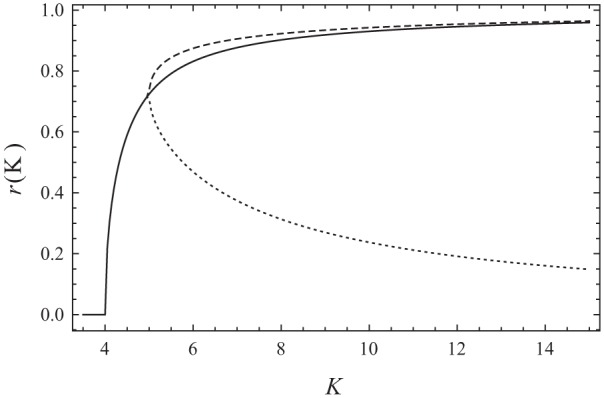
Solutions of the self-consistency equations (5) and (6) for different values of K while and the phase difference is 0. The solid line indicates the symmetric solution, and the dashed lines indicate the nonsymmetric solutions.
Model
To model the SCN, we modified the noisy Kuramoto model by placing it on a 2-community network structure. Each community consists of N oscillators, which correspond to neurons in the SCN. Oscillators in the same community interact with a strength , and oscillators in different communities interact with strength . We will take to be positive (attractive) and will allow to be both positive and negative (attractive or repulsive). We will also simplify the system by taking all oscillators to have the same natural frequency, namely, zero. This seems unrealistic, but since any constant frequency can be rotated out by changing the frame of reference for the system, any constant average natural frequency can be chosen.
We will denote the phase of the oscillators (which can be between 0 and 2π) in the first community by with and the phase of the oscillators in the second community by with . Note that in the current model, both communities contain the same number of oscillatory neurons, . Each angle represents a state of the neuron. The equations governing their evolution are then
| (1) |
and
| (2) |
Here, and are white-noise terms. These can be understood as the effect of the thermal environment in which the SCN resides (i.e., external noise) or as time-dependent variations in the natural frequencies of individual oscillators. The noise has a destabilizing effect on the stationary states, as mentioned in Indic et al. (2008). In our case, for example, the critical conditions and stability of the stationary states depend on the noise intensity. However, since we are considering a whole range of coupling strength parameters and typically the effect of the noise is in relation to these, the phase diagram will not change qualitatively by changing the intensity of the noise. As in the standard Kuramoto model, we define order parameters to measure the amount of synchronization and the average phase in each community:
| (3) |
| (4) |
The synchronization levels and can take values between and , with meaning that the relevant community is completely unsynchronized and being completely synchronized. The average phases and can take values between and 2π. Note that in the unsynchronized state, it is not meaningful to talk about the difference between aligned and anti-aligned, because for a totally unsynchronized community, the mean phase is random and will not evolve in a smooth way (i.e., it is meaningless in this case).
When taking the limit of the number of oscillators going to infinity, we see that the system can be described by a probability distribution in each community, namely, and , giving the probability of finding an oscillator with a given phase at a given time in community 1 and 2, respectively. These distributions depend on all of the order parameters.
Note in this respect that in the circadian field, the synchronization term is often treated differently. Where mathematical phase indicates the state of one oscillator at a specified time point, in the circadian field, the time of a certain state is taken for each oscillator, such as peak time. Thus, synchronization in the mathematical sense indicates a synchronization in oscillator state, while in the circadian sense, it indicates a synchronization of the oscillators in time. Thus, we define the circadian synchronization here as time synchronization.
In the long-time limit, the distributions reach a steady state (a state in which the order parameters are stationary) that can be described analytically (see Meylahn, 2019). Which values the order parameters , and can take in the steady-state distributions are determined by a system of self-consistency equations:
| (5) |
| (6) |
| (7) |
| (8) |
Because of the invariance of the system under rotations, one of the average phases can be set to zero (i.e., ). This ensures that Eq. (7) is satisfied. In Meylahn (2019,) it is proved that the only values , which now also represents the phase difference () between the 2 communities, can take are and π. Simultaneously solving Eq. (5) and (6) for , , while fixing or and , gives a stationary point for the dynamics of the system. Consider first the case in which the average phases are aligned so that their phase difference is (i.e., ). The system assumes only synchronized solutions when the critical condition is met, which is . When this is the case, the system can always be in the symmetrically synchronized state where (which is stable) or in the unsynchronized state, . Here, is the synchronization in the mean-field Kuramoto model with interaction strength . The system, however, also displays a bifurcation point. Consider fixing . Then we can plot the possible solutions for and as a function of , as in Figure 1. We see that at , the symmetrically synchronized state appears. At about , however, nonsymmetric solutions appear, where r1≠ r2. Since both communities are the same in our analysis, both can be in either one of the dashed-line solutions. The other community is then forced to take on the opposite solution (i.e., the system can be in the states upper dashed line, lower dashed line; upper dashed line, lower dashed line or solid line.)
The point at which the nonsymmetric solution bifurcates from the symmetric solutions gives a line in the phase diagram. In Figure 2, we plot the phase diagram given that the average phases are aligned (i.e., ) and given that the phases are anti-aligned (i.e., ). In this figure, we see the area labeled as ) (red online) in which the oscillators in both communities are completely unsynchronized. If the circadian system is in the area labeled (green online), the system can be in a state in which both communities are synchronized in the same phase or both communities are completely unsynchronized. In the area labeled (blue online) the same holds true, but there is also another possible state, namely, the nonsymmetrically synchronized state, in which one community is more synchronized than the other (r1≠ r2).
Figure 2.
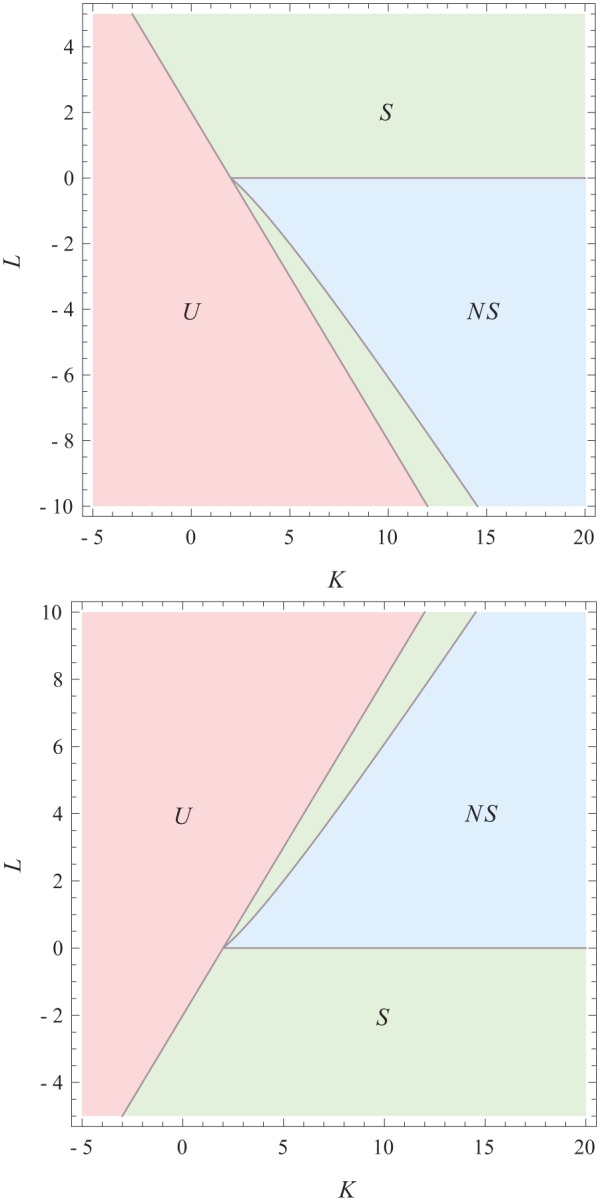
Phase diagram in which the average phases are aligned (top) and in which they are anti-aligned (bottom). In the region labeled (red online), there are only unsynchronized solutions. In the region labeled (green online), there are 2 solutions: the unsynchronized solution and the symmetrically synchronized solution. In the region labeled (blue online), there are three solutions: the unsynchronized, the symmetrically synchronized, and a nonsymmetrically synchronized solution.
Note that, depending on external conditions, the circadian system can move through this phase diagram since the interaction strength parameters might change because of extreme external conditions. Because of the conjecture in Meylahn (2019) about the possible phase differences in the steady state, we assume that these are the only 2 phase diagrams for the steady state.
The analysis done in Meylahn (2019) and summarized here concerns the stationary points of the system of Eqs. (5) to (8) for the order parameters, in which each solution corresponds to a pair of stationary distribution profiles, and . It does not give information about the stability of these stationary points. Stability is a delicate issue to treat mathematically and is an open problem. The link between the symmetric solution and the solution of the mean-field Kuramoto model suggests that this solution is stable while the unsynchronized solution () should be unstable above the critical condition. In the next section, we will present the results of simulations of the system and interpret them in the context of these stability questions.
Simulations
We can simulate the system to investigate the stability properties of the various solutions. We summarize the observed stability properties in Table 1. What is meant by metastable here is that the system can, if prepared correctly, stay in this state for a long time but will eventually move to a stable stationary state (it does not refer to the mathematical definition of metastability). Intuitively, this table makes sense. If the interaction between communities is positive, we can, roughly speaking, say that the 2 communities attract one another. If the system is in a state in which the average phases are anti-aligned, with both communities sufficiently synchronized, it can stay there for a while but would ultimately prefer to be in a state with the phases being aligned. This is because the mean-field Kuramoto model corresponding to the aligned state has interaction strength parameter , which is greater than the one corresponding to the anti-aligned state, . (In the mean-field model, greater interaction strength implies a larger synchronization level.) Examples are given in Figure 3.
Table 1.
Stability of possible solutions when . Here, .
| Solution | Unsynchronized | Synchronized, | Synchronized, | Nonsymmetrically Synchronized |
|---|---|---|---|---|
| Unstable | Metastable | Stable | Unstable | |
| Unstable | Stable | Metastable | Unstable |
Figure 3.
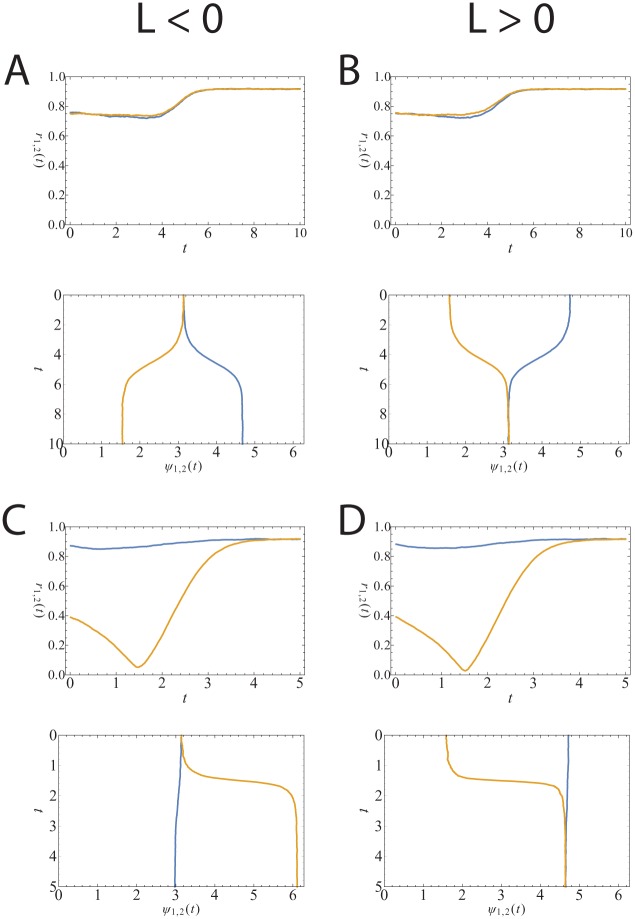
Simulation of 10,000 oscillators per community with (A and C) or (B and D) and (A and B) or (C and D). The time step is set at . The top images show the synchronization levels ( and ) and the bottom the average phases ( and ). The phases are plotted in a way that the different communities can be seen as the 2 components of activity in the suprachiasmatic nucleus. The time on the y-axis can be regarded as consecutive days. (A) and (B) show the case in which and are the same, whereas (C) and (D) show the case in which they differ at first but both approach 1 when the stable state is reached.
The simulations are of 10,000 oscillators per community. In the first simulations (Fig. 3A), we initialize the 2 communities to have approximately the same synchronization level (upper frame) and with the average phases of the 2 communities aligned (lower frame). We take and . In this situation, we expect the aligned state to be metastable since oscillators in different communities repel one another. In the simulation, we see that the system indeed stays in the aligned state for some time before moving to the anti-aligned state. The synchronization level in each community increases during this transition. In Figure 3B, a similar example is shown for . Here, the metastable state is the anti-aligned state (see Table 1).
In the second simulation (Fig. 3C), we again initialize the average phases to be aligned, but this time, one community is more synchronized than the other (upper frame). We take and . Again, the system would like to be in the phase-split state, but this time, the transition occurs by one community having to move to a much lower level of synchrony before the average phases can move apart and assume the higher level of synchrony of the phase-split state. Figure 3D shows a similar situation for . Here, the metastable state is the anti-aligned state (see Table 1).
Discussion
The metastable anti-aligned state discussed in the previous section might be the state observed in hamsters displaying 2 periods of activity in a single 24-h cycle (Pittendrigh and Daan, 1976).
The underlying cause of the dissociation in phase, both phase splitting of the left and right SCN as well as through forced desynchronization of the ventral and dorsal SCN, seems to be that a 2-community structure must be present in the SCN. As these communities interact with each other, in normal circumstances they remain synchronized. However, in particular conditions, these 2 communities can arrive in the metastable anti-aligned state. This state is, as described, metastable, so after some time, it will return to the stable synchronized state. However, it appears that when keeping animals in a forced desynchronization protocol, this metastable state can be maintained, even though the SCN is inclined to return to the stable synchronized state.
Apparently, according to Figure 2, the circadian system of animals is normally either in the green () or blue area () of the state space, which means that the coupling strengths within and between the communities added together are always larger than 2. In different conditions, the parameters and , which signify the strengths in the communication within one community and between both communities, can change, thereby changing the excitation-inhibition (E/I) balance of the SCN as a whole. It has been shown, for example, that in long photoperiods, there is more excitatory GABAergic coupling than there is in short photoperiods (Farajnia et al., 2014; Olde Engberink et al., 2018). Thus, the strengths of these coupling parameters can shift the circadian system through this phase diagram, enabling other possible states to arise, such as the split state or even a desynchronized state.
Changes in external conditions may affect the ability to synchronize by changing the interaction strength , for example. If decreases and the system is usually in the situation in which and , then after the shift, the system could be in the negative region. Figure 3A corresponds to the system being in the aligned state (upper image in Fig. 4) right after the parameter L has been changed, due to an external input, to be negative. In this situation, the aligned state is a solution to the self-consistency equations, but the state is not stable. The system would then want to move to a new stable state for the new balance between and . It finds this new stable state in the phase-split state or the anti-aligned state (lower image in Fig. 4) and in this case does so by the average phases moving apart (lower image in Fig. 3A) while increasing the synchronization levels in both communities simultaneously (upper image in Fig. 3A). This transition can be imagined as a path between the upper and lower images in Figure 4. Alternatively, the system could respond to the change in L by having one community’s average phase move away from the other (lower image of Fig. 3C) while temporarily decreasing its synchronization level (upper image of Fig. 3C). Which transition to the anti-aligned state occurs could depend on the initial change in L, which causes the transition. If it was shifted in the first phase diagram to a point in the blue () region, the system might be forced through the nonsymmetrically synchronized state before being able to move to the symmetrically synchronized anti-aligned state (see Fig. 3C), while it might be able to move directly to this state when it is shifted into the green (S) region that is between the blue () region and the red () region, meaning that the synchronization levels in both communities increase as they move to the phase-split state (as depicted in Fig. 3A). Figure 3B and D show the situation in which the transition occurs in the opposite direction (from anti-aligned to aligned).
Figure 4.
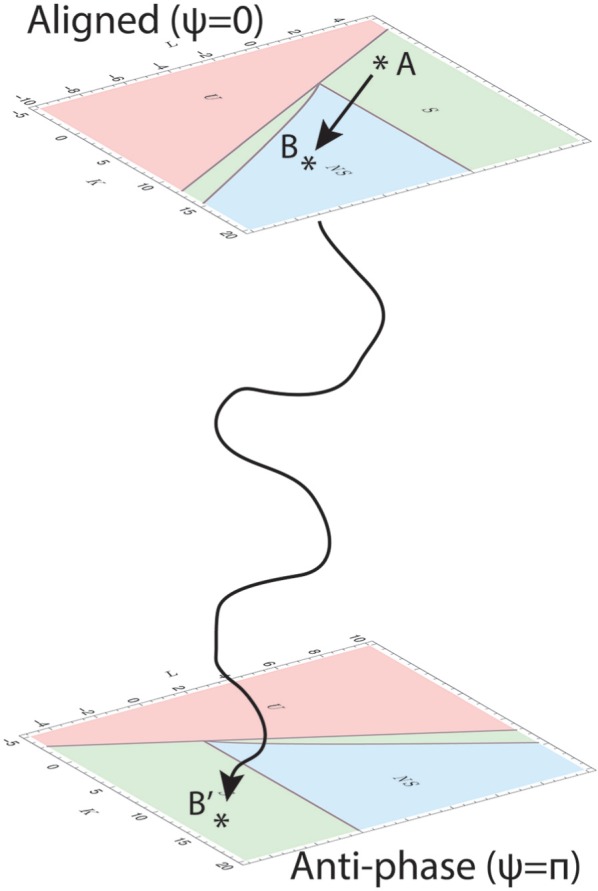
Mechanism of the suprachiasmatic nucleus changing states. A disturbance in the external conditions changes the excitation-inhibition (E/I) balance of the system, meaning that the parameters and/or are changed. This causes the system to go from stable state A to an unstable state B. The system will then be forced to find a new stable state corresponding to the new E/I balance, which could be found in the stable state B′, which lies in the plane in which both communities are in anti-phase.
Phillips et al. (2019) recently showed that there are interindividual differences in light sensitivity between subjects, which may affect sleep and circadian timing. These interindividual differences in light sensitivity may also be the reason that not all animals will arrive in the split state when subjected to constant light or a forced desynchrony protocol. The mechanism that we describe here may explain why some animals do end up in the split situation while others do not. The interindividual differences may cause the change in E/I balance to be a little different among different animals. Thus, each animal would arrive in a different location B in the aligned space in Figure 4. Some of these locations may be stable, while others may be unstable. When an animal arrives in an unstable state, there is a good chance it will end up going to the antiphase plane. Gaining a better understanding of the influence of external light on the E/I balance of individual animals will provide more details on the state space by which the animals are governed.
Studying the dynamics of the system between the various states mathematically is difficult. Simulations of the system give an impression for what might be typical behavior, and they might be relevant for understanding the unpredictable response of the SCN to the different transitions to and from the phase-split state when animals are exposed to constant light or forced desynchronization protocols. To better study the trajectories that the system may take, jet lag studies may be employed to collect data on single cells and review the dynamics between the ventral and dorsal communities. In jet lag experiments, a dissociation between the ventral and dorsal SCN is also observed. Albus et al. (2005) showed that when a phase shift is applied to the SCN, the ventral SCN shifts immediately with the new light-dark cycle, while the dorsal SCN lags behind. The dissociation observed between both communities is dissolved after 6 days (Rohling et al., 2011). Using the jet lag protocol, the dynamics of both communities could be studied in subsequent days.
Conclusion
This article is novel in the fact that it points out the existence of the bifurcation point in the 2-community noisy Kuramoto model and notes that this might be the reason for the observation of different transitions to the phase-split state of the SCN. To prove this is mathematically challenging, since that would require studying the dynamics between different states of the 2-community noisy Kuramoto model. There is also no experimental work measuring the activity of individual neurons in the phase-split state or during the transition into it to which one could compare the simulations done here. The conclusion of this article is then that the 2-community noisy Kuramoto model has more to offer in terms of explaining the behavior of the SCN.
The table predicts that the stable state of the system is the anti-aligned state when . This would mean that, in the case of the ventral-dorsal communities, when GABA is mainly inhibitory, the system would prefer a split state over the aligned state. However, experimental research clearly shows that this is not the case: in normal circumstances, the ventral and dorsal communities are aligned. This may be because we used the simplest model possible, in which both communities are the same and have the same number of neurons and where the interaction strengths within both communities are also the same as the interaction parameters between both communities. A more realistic model would have a different number of neurons for each community, an and (Rohling et al., 2011). Also, the communication strengths of vasoactive intestinal polypeptide in the ventral SCN and arganine vasopressin in the dorsal SCN would not be the same ( and ), and the communication between both communities would not be symmetrical ( and ; Albus et al., 2005). Finally, the natural variation in the frequencies of the neurons firing could be included by adding a term drawn from a distribution in Eq. (1) and a term drawn from a distribution in Eq. (2). These changes make the mathematical analysis significantly more difficult. To decide which mathematical generalizations are worth pursuing, more experimental information is needed regarding the relative numbers of versus , versus , and versus as well as the distribution of natural frequencies in the 2 communities. What is clear is that although the mechanism remains unchallenged, the actual stability diagrams would change, possibly finding stable solutions for an aligned state even when the GABAergic communication is inhibitory.
This does not invalidate the current model, however, as the main message we want to bring forward is that a change in external circumstances brings about a change in the coupling variables within and between 2 communities, thus changing the E/I balance of the system. This change in E/I balance may move the system into an unstable or metastable state, and the system will search through its state space for a stable state based on the changed E/I balance.
Acknowledgments
We thank Stephan Michel for valuable comments on earlier versions of the article. This work was supported by Velux Foundation, project grant 1029. J. M. Meylahn is supported by NWO Gravitation Grant 024.002.003 NETWORKS.
Footnotes
Conflict of Interest Statement: The authors have no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
ORCID iDs: Jos H. T. Rohling  https://orcid.org/0000-0001-5721-2715
https://orcid.org/0000-0001-5721-2715
Janusz M. Meylahn  https://orcid.org/0000-0002-4388-805X
https://orcid.org/0000-0002-4388-805X
References
- Abe H, Honma S, Honma K, Suzuki T, Ebihara S. (1999) Functional diversities of two activity components of circadian rhythm in genetical splitting mice (CS strain). J Comp Physiol A 184(3):243-251. [DOI] [PubMed] [Google Scholar]
- Albus H, Vansteensel MJ, Michel S, Block GD, Meijer JH. (2005) A GABAergic mechanism is necessary for coupling dissociable ventral and dorsal regional oscillators within the circadian clock. Curr Biol 15(10):886-893. [DOI] [PubMed] [Google Scholar]
- Campuzano A, Cambras T, Vilaplana J, Canal MM, Carulla M, Díez-Noguera A. (1999) Period length of the light-dark cycle influences the growth rate and food intake in mice. Physiol Behav 67(5):791-797. [DOI] [PubMed] [Google Scholar]
- Casiraghi LP, Oda GA, Chiesa JJ, Friesen WO, Golombek DA. (2012) Forced desynchronization of activity rhythms in a model of chronic jet lag in mice. J Biol Rhythms 27(1):59-69. [DOI] [PubMed] [Google Scholar]
- Choi HJ, Lee CJ, Schroeder A, Kim YS, Jung SH, Kim JS, Kim DY, Son EJ, Han HC, Hong SK, et al. (2008) Excitatory actions of GABA in the suprachiasmatic nucleus. J Neurosci 28(21):5450-5459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farajnia S, van Westering TL, Meijer JH, Michel S. (2014) Seasonal induction of GABAergic excitation in the central mammalian clock. Proc Natl Acad Sci U S A 111(26):9627-9632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonze D, Goldbeter A. (2006) Circadian rhythms and molecular noise. Chaos 16(2):026110. [DOI] [PubMed] [Google Scholar]
- de la Iglesia HO, Meyer J, Carpino A, Jr, Schwartz WJ. (2000) Antiphase oscillation of the left and right suprachiasmatic nuclei. Science 290(5492):799-801. [DOI] [PubMed] [Google Scholar]
- de la Iglesia HO, Cambras T, Schwartz WJ, Díez-Noguera A. (2004) Forced desynchronization of dual circadian oscillators within the rat suprachiasmatic nucleus. Curr Biol 14(9):796-800. [DOI] [PubMed] [Google Scholar]
- Indic P, Schwartz WJ, Paydarfar D. (2008) Design principles for phase-splitting behaviour of coupled cellular oscillators: clues from hamsters with ‘split’ circadian rhythms. J R Soc Interface 5(25):873-883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leloup JC, Gonze D, Goldbeter A. (1999) Limit cycle models for circadian rhythms based on transcriptional regulation in Drosophila and Neurospora. J Biol Rhythms 14(6):433-448. [DOI] [PubMed] [Google Scholar]
- Mendoza J, Challet E. (2009) Brain clocks: from the suprachiasmatic nuclei to a cerebral network. Neuroscientist 15(5):477-488. [DOI] [PubMed] [Google Scholar]
- Meylahn JM. (2019) Two-community noisy Kuramoto model. Nonlinearity. Available at: arXiv:1812.05896 [Google Scholar]
- Michel S, Marek R, Vanderleest HT, Vansteensel MJ, Schwartz WJ, Colwell CS, Meijer JH. (2013) Mechanism of bilateral communication in the suprachiasmatic nucleus. Eur J Neurosci 37(6):964-971. [DOI] [PubMed] [Google Scholar]
- Oda GA, Friesen WO. (2002) A model for “splitting” of running-wheel activity in hamsters. J Biol Rhythms 17(1):76-88. [DOI] [PubMed] [Google Scholar]
- Olde Engberink AHO, Meijer JH, Michel S. (2018) Chloride cotransporter KCC2 is essential for GABAergic inhibition in the SCN. Neuropharmacology 138:80-86. [DOI] [PubMed] [Google Scholar]
- Phillips AJK, Vidafar P, Burns AC, McGlashan EM, Anderson C, Rajaratnam SMW, Lockley SW, Cain SW. (2019) High sensitivity and interindividual variability in the response of the human circadian system to evening light. Proc Natl Acad Sci U S A 116(24):12019-12024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pittendrigh CS, Daan S. (1976) A functional analysis of circadian pacemakers in nocturnal rodents. J Comp Physiol 106:333-355. [Google Scholar]
- Rohling JHT, van der Leest HT, Michel1 S, Vansteensel MJ, Meijer JH. (2011) Phase resetting of the mammalian circadian clock relies on a rapid shift of a small population of pacemaker neurons. PLoS One 6(9):e25437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroder S, Herzog ED, Kiss IZ. (2012) Transcription-based oscillator model for light-induced splitting as antiphase circadian gene expression in the suprachiasmatic nuclei. J Biol Rhythms 2012;27(1):79-90. [DOI] [PubMed] [Google Scholar]