Uncovering the Role of Key Active-Site Side Chains in Catalysis: An Extended Brønsted Relationship for Substrate Deprotonation Catalyzed by Wild-Type and Variants of Triosephosphate Isomerase

Abstract

We report results of detailed empirical valence bond simulations that model the effect of several amino acid substitutions on the thermodynamic (ΔG°) and kinetic activation (ΔG^⧧) barriers to deprotonation of dihydroxyacetone phosphate (DHAP) and d-glyceraldehyde 3-phosphate (GAP) bound to wild-type triosephosphate isomerase (TIM), as well as to the K12G, E97A, E97D, E97Q, K12G/E97A, I170A, L230A, I170A/L230A, and P166A variants of this enzyme. The EVB simulations model the observed effect of the P166A mutation on protein structure. The E97A, E97Q, and E97D mutations of the conserved E97 side chain result in ≤1.0 kcal mol^–1 decreases in the activation barrier for substrate deprotonation. The agreement between experimental and computed activation barriers is within ±1 kcal mol^–1, with a strong linear correlation between ΔG^⧧ and ΔG° for all 11 variants, with slopes β = 0.73 (R² = 0.994) and β = 0.74 (R² = 0.995) for the deprotonation of DHAP and GAP, respectively. These Brønsted-type correlations show that the amino acid side chains examined in this study function to reduce the standard-state Gibbs free energy of reaction for deprotonation of the weak α-carbonyl carbon acid substrate to form the enediolate phosphate reaction intermediate. TIM utilizes the cationic side chain of K12 to provide direct electrostatic stabilization of the enolate oxyanion, and the nonpolar side chains of P166, I170, and L230 are utilized for the construction of an active-site cavity that provides optimal stabilization of the enediolate phosphate intermediate relative to the carbon acid substrate.

Introduction

Triosephosphate isomerase (TIM) catalyzes the isomerization of d-glyceraldehyde 3-phosphate to form dihydroxyacetone phosphate, by a proton transfer reaction mechanism through an enediolate reaction intermediate (Scheme 1).¹⁻¹³ Proton transfer at carbon is ubiquitous in biology and sets enzymes the difficult problem of reducing the large thermodynamic barriers to formation of carbanion intermediates of nonenzymatic reactions.¹⁴⁻¹⁶ This problem was solved by TIM approximately 3 × 10⁹ years ago,¹⁷ through evolution of a catalyst that satisfies two criteria of perfection, as outlined by Knowles,¹⁸ and which uses the TIM-barrel protein fold present in ca. 10% of all enzymes.¹⁹ These observations have placed TIM at the forefront of enzymes targeted for mechanistic studies, because of the strong possibility that the results of studies on TIM will lead to conclusions that are broadly generalizable to other protein catalysts.²⁰

Scheme 1. Mechanism of TIM-Catalyzed Isomerization of d-Glyceraldehyde 3-Phosphate (GAP) To Form Dihydroxyacetone Phosphate (DHAP).

Computational studies on TIM have been pursued vigorously,^{3−6,8−10,13,21−37} because of their potential to provide a description of the events at the enzyme active site not accessible to examination by experimental studies. The many X-ray crystal structures for TIM from various organisms, and with a variety of ligands bound,³⁸ provide valuable starting points for computational studies that model the experimental activation barrier for conversion of enzyme-bound substrate to product. It is important to test these models with larger bodies of experimental data in order to advance toward computational models that are able to fully reproduce the operation of TIM and other highly proficient enzymes. We have therefore challenged the empirical valence bond (EVB)³⁹ approach to model the results of recent mutagenesis studies on TIM,^16,40−44 with a focus on substitutions of the amino acid side chains shown in Figure 1 (using yeast yTIM numbering throughout this work).

Figure 1.

X-ray crystal structure of the closed complex between yeast TIM (yTIM) and DHAP (PDB ID: 1NEY(45)), which shows the positions of the following active-site side chains relative to the substrate DHAP: K12, E97, E165, P166, I170, and L230. In this study, we have examined single and/or double amino acid substitutions at each of these positions.

The residues of interest in this work are, specifically, as follows:

(1) The side chain cation of K12, which is positioned to interact with both the substrate phosphodianion and the partial negative charge that develops at the substrate carbonyl group at the transition state for substrate deprotonation (Scheme 1).^41,46,47 The K12G substitution affects mainly the electrostatic stabilization of the anionic transition state⁴⁶ and thus should be modeled with precision by EVB simulations.

(2) The highly conserved second-shell amino acid side chain anion of E97,⁴⁸ which forms an ion pair to the cationic K12 side chain.^{44,46,47,49,50} The E97A substitution examines the modeling of replacement of a residue on the second sphere of side chains at the enzyme active site.⁵¹

(3) The side chain of P166, which clashes with the carbonyl oxygen of G209 in loop 7 during the ligand-driven movement of the loop from its unliganded open to its ligand-bound closed conformation. This steric clash results in movement of the E165 carboxylate from an initial “swung-out” position to a “swung-in” orientation that points into the TIM active site, where it is poised to deprotonate the enzyme-bound substrate.⁵²⁻⁵⁴ The P166A substitution eliminates this steric clash so that the E165 side chain remains in the swung-out position in the closed form of TIM.⁴⁰ This amino acid substitution tests the precision of EVB simulations in modeling the effect of an amino acid perturbation that results in a defined change in protein structure.

(4) The side chains of I170 and L230, which fold over the catalytic carboxylate side chain of E165 at the closed form of TIM and displace to the bulk aqueous solvent four of six water molecules that lie within 6 Å of this side chain.^{15,42,43,54,55} We previously reported the results of simulations to model the effect of I170A, L230A, and I170A/L230A substitutions on the activation barrier for deprotonation of d-glyceraldehyde 3-phosphate (GAP) and dihydroxyacetone phosphate (DHAP) bound to yeast TIM (yTIM),¹³ but report here slightly modified barriers obtained by the improved computational methods used in the present work. The I170A and L230A substitutions examine the precision of the EVB method in modeling the effect of a change in the polarity of the enzyme active site through replacement of hydrophobic side chains by solvent water.⁴³

The EVB simulations do an excellent job of modeling the experimental effect of substitution of both the polar side chains of K12 and E97 and of the substitution of the nonpolar side chains of P166, I170, and L230, on the activation barriers (ΔG^⧧) for deprotonation of enzyme-bound DHAP and GAP by the carboxylate side chain of E165. These simulations also provide values of ΔG° for proton transfer from the bound substrate to TIM to give the enediolate phosphate intermediate and the protonated carboxylic acid side chain, which cannot be determined by experiment. We report here a large extension of previously reported linear free energy relationships between the activation barriers ΔG^⧧ and Gibbs free energy change, ΔG°, for TIM-catalyzed deprotonation of enzyme-bound DHAP and GAP, to form the corresponding enediolate reaction intermediates,¹³ with Brønsted slopes of β = 0.73 (R² = 0.994) and β = 0.74 (R² = 0.995) for the deprotonation of DHAP and GAP, respectively. This extended Brønsted relationship shows that the substituted polar and nonpolar side chains act cooperatively for the common purpose of reducing the standard-state Gibbs free energy of reaction for proton transfer from substrate to TIM and that 70% of the change in the driving force for the reaction in water is expressed at the transition state for proton transfer. This change in reaction driving force is obtained through the direct stabilization of the enediolate phosphate by interaction with the cationic K12 side chain and through the precise placement of the nonpolar P166, I170, and L230 side chains at a substrate cage, engineered by Nature in order to minimize the standard-state Gibbs free energy of reaction for deprotonation of the enzyme-bound substrate.

Methodology

The empirical valence bond approach³⁹ was used in this work to model the TIM-catalyzed deprotonation of substrates DHAP and GAP, in wild-type and substituted TIM variants. We selected this approach based on our previous successes when using this model to capture the catalytic effect of wild-type TIM as well as of key active-site substitutions on the rate-limiting deprotonation of these substrates.^13,34,36,37 All simulations in this study were performed using the OPLS-AA force field⁵⁶ as implemented in the Q6 version of the Q simulation package,^57,58 following the protocol outlined in detail in our previous studies.^13,36 Our starting point for all EVB simulations was the crystal structure of wild-type yeast TIM (yTIM) in complex with DHAP (PDB ID: 1NEY(45,59)). In the case of the TIM variants studied in this work, all glycine and alanine substitutions were generated by simple truncation of the appropriate side chains, whereas in the case of the E97D and E97Q substitutions, the rotamers for the aspartate and glutamine side chains, respectively, were selected from the Dunbrack 2010 backbone-independent rotamer library,⁶⁰ as implemented into Chimera.⁶¹ Simulations were performed on wild-type TIM, as well as on the K12G, E97A, K12G/E97A, E97D, E97Q, P166A, I170A, L230A, and I170A/L230A variants.

All starting structures were then solvated in a 24 Å spherical droplet of TIP3P water molecules,⁶² centered on the C1 atom of bound DHAP or GAP (see ref (13) for atom numbering), described using the Surface Constrained All Atom Solvent (SCAAS) approach.⁶³ All residues within the inner 85% of this sphere were fully mobile, whereas those in the outer 15% were subjected to a 10 kcal mol^–1 Å^–2 harmonic positional restraint to restrain them to their original crystallographic positions, and all residues outside the droplet were essentially fixed to their crystallographic positions using a 200 kcal mol^–1 Å^–2 restraint, as described in previous work.^13,34,36,37 All residues within the mobile region were kept in their expected ionization states at physiological pH, assigned based on a combination of analysis using PROPKA 3.1⁶⁴ and visual inspection, and residues outside the mobile region were kept in their neutral form, as is standard practice in such simulations in order to avoid system instabilities introduced due to the presence of charges outside the explicit simulation sphere. For a full list of ionized residues and histidine protonation states in our simulations, see Table S1.

Each enzyme–substrate system was then subjected to six initial equilibration runs of 40 ns at 300 K with different initial velocities, heating from 0 to 300 K as described in refs (13) and (36) (Figures S1 and S2). This was then followed by five EVB simulations per equilibration run, performed using 51 mapping frames of 200 ps in length each, resulting in a total of 30 individual EVB trajectories for each system and 600 EVB trajectories over all systems. The starting points for the EVB simulations were generated by assigning new random seeds at the end point of the preceding equilibration run and performing a further 110 ps of equilibration to generate the new starting structures for the EVB simulations. All equilibration and EVB simulations were performed at the transition state for the proton transfer reaction, based on the valence bond states shown in Figure S3, as described in our previous work,¹³ in order to enable simultaneous propagation of EVB trajectories downhill toward the reactant and the product state. All simulations were performed using a 1 fs time step, to a total equilibration time of 240 ns per system (4.80 μs over all systems) and a total EVB simulation time of 306 ns per system (6.12 μs over all systems). Note that we used the same EVB parameters (H_ij and α) as in our prior studies to describe the deprotonation of substrates DHAP and GAP. These parameters can be found in Table S2. For a description of these parameters, see refs (39) and (65), and for a description of how the EVB fitting was performed for these reactions see ref (13). All EVB parameters used in this work can be found in the Supporting Information of ref (13), and full protocols and simulation details can be found in our previous work on TIM.^13,36

All energy analysis in this study was performed using the QCalc module of the Q simulation package. VMD version 1.9.1⁶⁶ was used to perform all structural analysis. Representative structures at various stationary points for the TIM-catalyzed deprotonation of DHAP and GAP in wild-type and P166A TIM were obtained by performing clustering analysis, using the method of Daura et al.⁶⁷ as implemented in GROMACS version 4.6.5.⁶⁸ A cutoff distance of 0.5 Å was used for the analysis, which was based on structures sampled every 2 ps of the simulation time. All structural figures were generated using the PyMOL version 2.2.3 visualization package.⁶⁹

Results

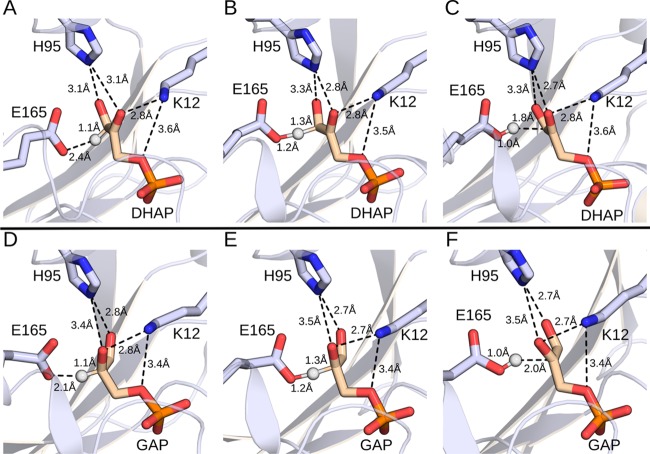
Figure 2 shows representative structures of the Michaelis complexes, transition states, and enediolate phosphate intermediates for the deprotonation of substrates DHAP and GAP by wild-type yTIM during our EVB simulations. These simulations are performed starting with the high-resolution structure of yTIM (PDB ID: 1NEY(45,59)), and we therefore use the numbering for yTIM for all amino acid side chains. Table 1 summarizes the activation barriers and reaction free energies for the deprotonation of substrates DHAP and GAP to form enediolate phosphate intermediates (Scheme 1) catalyzed by the wild-type and substituted variants of TIM that were calculated in EVB simulations and comparisons between calculated activation barriers and activation barriers determined by experiment. The bar graphs from Figure 3 compare the calculated and experimental activation barriers. We note that, in several cases, calculated activation barriers are compared to experimental values obtained using enzyme kinetic parameters determined for amino acid substituted variants of TbbTIM (from Trypanosoma bruceibrucei). There is strong evidence that the active-site catalytic side chains at TIMs from different organisms afford a similar stabilization of the isomerization transition state: (A) The active sites determined by X-ray crystallographic analysis of TIMs with as little as 50% sequence homology are superimposable.⁷⁰ (B) The similar kinetic parameters determined for wild-type TIMs from Trypanosomes,⁷⁰ yeast,^41,71 rabbit muscle,⁷⁰ and chicken muscle⁷² show that these enzymes provide a similar (±1 kcal mol^–1) total stabilization of the rate-determining transition states for isomerization of GAP and DHAP. These results predict similar effects of side chain substitutions on the activation barrier.

Figure 2.

Representative structures of wild-type TIM at various stationary points. (A, D) Michaelis complexes, (B, E) transition states, and (C, F) intermediate states for the deprotonation of substrates (A–C) DHAP and (D–F) GAP. Shown here are the (donor–hydrogen and acceptor–hydrogen) distances involved in the proton transfer step, as well as distances between the side chains of the key active-site residues H95 and K12 and the substrate. All distances annotated on this figure are averages over the entire simulation trajectory. The corresponding average distances for wild-type TIM and all the variants included in this study are presented in Tables S3 to S5.

Table 1. Activation Barriers and Reaction Free Energies for the Deprotonation of DHAP and GAP by Different TIM Variants, To Form Enediolate Phosphate Reaction Intermediates^a.

substrate	catalyst	ΔGexp⧧	ΔGcalc⧧	ΔGTIM⧧ – ΔGnon	ΔGWT⧧ – ΔGmut	ΔGcalc‡ – ΔGexp	ΔG°calc	ΔG°TIM – ΔG°non
DHAP	CH3CH2CO2–		25.4 ± 0.03				19.0 ± 0.03
	WT-TIM	13.7b,c	15.0 ± 0.4	–10.4		1.3	5.2 ± 0.4	–13.8
	I170A	15.8b	15.6 ± 0.5	–9.8	–0.6	–0.2	5.8 ± 0.7	–13.2
	L230A	16.6b	15.8 ± 0.3	–9.6	–0.8	–0.8	7.0 ± 0.4	–12.0
	I170A/L230A	17.4b	16.8 ± 0.2	–8.6	–1.8	–0.6	7.5 ± 0.3	–11.5
	K12G		18.7 ± 0.3	–6.7	–3.7		10.5 ± 0.5	–8.5
	E97A	13.9b (14.1c)	14.8 ± 0.4	–10.6	0.2	–0.9	4.8 ± 0.5	–14.2
	K12G/E97A		18.9 ± 0.3	–6.5	–3.9		10.6 ± 0.4	–8.4
	E97D	13.9b,c	14.9 ± 0.3	–10.5	0.1	1.0	4.0 ± 0.3	–15.0
	E97Q	14.1b (14.5c)	14.9 ± 0.3	–10.5	0.1	0.8	5.2 ± 0.6	–13.8
	P166A	16.3b	17.2 ± 0.3	–8.2	–2.2	0.1	8.5 ± 0.3	–10.5
GAP	CH3CH2CO2–		24.0 ± 0.03				16.0 ± 0.04
	WT-TIM	12.9b (12.5d)	13.7 ± 0.5	–10.3		0.8	2.6 ± 0.6	–13.4
	I170A	16.0b	15.5 ± 0.7	–8.5	–1.8	–0.5	4.1 ± 0.7	–11.9
	L230A	14.2b	14.4 ± 0.3	–9.6	–0.7	0.2	3.3 ± 0.4	–12.7
	I170A/L230A	16.3b	15.2 ± 0.3	–8.8	–1.5	–1.1	4.3 ± 0.5	–11.6
	K12G	17.7c	16.2 ± 0.4	–7.8	–2.5	–1.5	6.0 ± 0.4	–10.0
	E97A		13.7 ± 0.7	–10.3	0.0		1.7 ± 0.7	–14.3
	K12G/E97A		16.5 ± 0.4	–7.5	–2.8		6.5 ± 0.4	–9.5
	E97D	15.2d	13.0 ± 0.4	–11.0	0.7	–2.2	1.5 ± 0.6	–14.5
	E97Q	17.4d	14.4 ± 0.4	–9.6	–0.7	–3.0	3.4 ± 0.4	–12.6
	P166A	15.6b	16.4 ± 0.4	–7.6	–2.7	0.1	5.4 ± 0.4	–10.6

^aAll energies are shown in kcal mol^–1. Calculated energies are averages and standard error of the mean over 30 individual EVB trajectories, as described in the Methodology section. Shown here are both the values calculated in aqueous solution (CH₃CH₂CO₂^– as the general base) and those in different TIM variants. The corresponding experimental values are based on kinetic data for different TIM variants.

^bData from TbbTIM.

^cData from yTIM.

^dData from PfTIM, where available, as presented in refs (16), (40)–⁴⁴, (50), and (70). ΔG^⧧_calc and ΔG^⧧_exp denote the calculated and experimental activation free energies, respectively, ΔG⁰_calc denotes the calculated reaction free energy, ΔG^⧧_TIM – ΔG^⧧_non denotes the difference between the activation free energy calculated for the TIM-catalyzed reaction and for the background reaction in aqueous solution, ΔG^⧧_WT – ΔG^⧧_mut denotes the difference between the activation free energy calculated for wild-type TIM and for the different TIM variants considered in this work, ΔG^⧧_calc – ΔG^⧧_exp denotes the difference between the calculated and experimental activation free energies for wild-type TIM and the different TIM variants considered in this work, and ΔG⁰_TIM – ΔG⁰_non denotes the difference between the reaction free energy calculated for different TIM variants and for the background reaction in aqueous solution.

Figure 3.

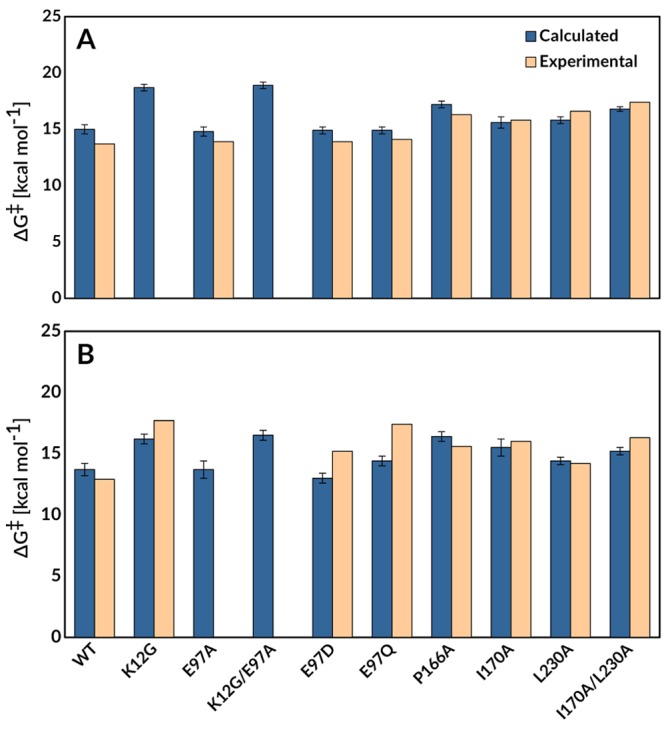
Comparison of the activation free energies determined by EVB simulations (blue) and from experimental kinetic parameters (based on experimental kinetic measurements performed on TbbTIM, yTIM, and PfTIM,^{16,40−44,70} tan), for TIM-catalyzed deprotonation of substrates (A) DHAP and (B) GAP to form enediolate reaction intermediates. The raw data for this figure are presented in Table 1.

Discussion

The activation barriers reported in Table 1 and Figure 3 were obtained from EVB simulations performed starting with the high-resolution structure of yTIM (PDB ID: 1NEY(45,59)). The overall agreement between the experimental and computed activation barriers is generally within ±1 kcal mol^–1 and is similar to the previously published agreement between experimentally and computationally determined effects, respectively, of I170A, L230A, and I170A/L230A substitutions on the activation barriers for TbbTIM- and yTIM-catalyzed deprotonation of GAP and DHAP.¹³ We have increased the radius of the water droplet/mobile region in our EVB simulations from 20 Å in our previous computational studies of TIM and its variants^13,36 to 24 Å in the present work, as was also done in ref (37). This improves the description of TIM flexibility through the use of a larger mobile region, but comes with a greater computational cost associated with the increased size of the water droplet. The 4 Å increase in the radius of the water droplet (and thus also the size of the mobile region in the EVB simulations) in the present study results in up to a 0.8 kcal mol^–1 higher calculated activation barriers for the deprotonation of both DHAP and GAP. However, there is no discernible improvement in the agreement between the experimental and calculated activation barriers for wild-type TIM and the I170A, L230A, and I170A/L230A variants that were previously modeled using a 20 Å radius for the water droplet/mobile region.¹³ This is consistent with a diminishing return in computational precision for these EVB simulations, from the increasing computational cost associated with increases in the radius of the water droplet/mobile region to >20 Å.

Protein Variants

K12 and E97 Substitutions

The K12M/G15A variant of TIM showed no detectable activity for catalysis of isomerization,⁴⁶ and the X-ray crystal structure for this variant revealed that the interaction between the K12 side chain and the substrate phosphodianion is required to observe substrate bound to the crystalline protein.⁷³ The K12G variant of yTIM is active, but the amino acid substitution results in a 7.8 kcal mol^–1 increase in the activation barrier to k_cat/K_M for TIM-catalyzed isomerization,⁴¹ and much of the lost catalytic activity may be rescued by alkyl ammonium cations.⁴⁷ The interaction between GAP and K12G yTIM is too weak to provide clear evidence for saturation.⁴¹ However, the K12G substitution results in a 2.4 kcal mol^–1 destabilization of the complex to the intermediate analogue phosphoglycolate (PGA), which is consistent with a 2.4 kcal mol^–1 destabilization of the Michaelis complex to GAP and a 7.8 – 2.4 = 5.4 kcal mol^–1 increase in the barrier for conversion of this complex to the isomerization transition state.⁴¹

Our EVB simulations predict increases in the activation barrier to substrate deprotonation (ΔΔG^⧧_wt→mut) of 3.7 kcal mol^–1 for substrate DHAP and 2.5 kcal mol^–1 for substrate GAP, compared to wild-type TIM, upon truncation of the K12 side chain to a glycine. By comparison, we obtain similar −3.9 and −2.9 kcal mol^–1 electrostatic contributions to the calculated activation free energies for the deprotonation of substrates DHAP and GAP, respectively, by wild-type TIM (Figure 4), evaluated by applying the linear response approximation (LRA)^74,75 to the corresponding EVB trajectories.^13,36 The calculated 3 to 4 kcal mol^–1 effect of the K12G substitution on the activation barrier to substrate deprotonation is smaller than the estimated 5.4 kcal mol^–1 effect of this substitution on the activation barrier to isomerization of enzyme-bound GAP. However, there is a large uncertainty in the partitioning of the overall 7.8 kcal mol^–1 increase in the experimental activation barrier into effects on k_cat and K_M.

Figure 4.

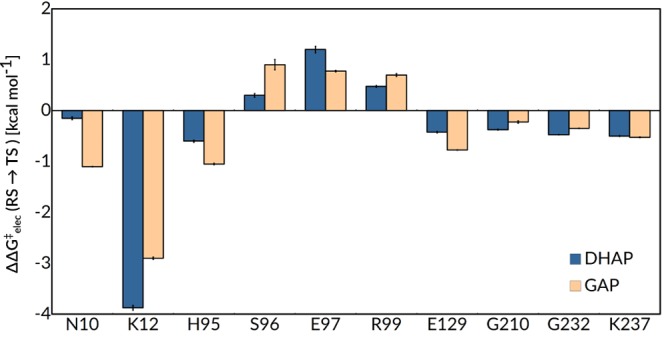
Electrostatic contributions of individual residues to the calculated activation free energies (ΔG^⧧_elec) for the deprotonation of DHAP and GAP by wild-type TIM. As in our previous work,^13,36 all values were calculated by applying the linear response approximation^74,75 to the calculated EVB trajectories and scaled assuming a dielectric constant of 4 for the active site. All values shown are averages over 30 independent trajectories, and the error bars represent the standard error of the mean. The corresponding raw data for this figure are shown in Table S6.

The K12 side chain runs across the surface of TIM, and the side chain cation interacts with substrate bound beneath the protein surface.^41,46,47,73 The E97 side chain lies in the second shell of active-site side chains and forms an anchoring ion pair to the first shell K12 side chain cation (Figure 1). This side chain is conserved at the active sites of all TIMs.⁴⁸ We have carried out EVB simulations to model the effects of amino acid substitutions of E97, in order to examine the functional role that mandates conservation of anchoring the K12•E97 ion pair at TIM.

The E97A, E97D, and E97Q substitutions of yTIM each result in ≤0.7 kcal mol^–1 changes in the calculated activation barriers for wild-type TIM-catalyzed deprotonation of DHAP and GAP (Table 1). These changes are within the uncertainty of these simulations and represent increases in the activation barrier, except for the 0.7 kcal mol^–1 transition state stabilization calculated for the E97D variant of yTIM. There is good agreement between the calculated effect of these three substitutions on the activation barrier for catalysis by wild-type yTIM and the experimental activation barrier (where available) for catalysis by TbbTIM (Figure 3).⁴⁴ The LRA simulations (Figure 4) are consistent with a ∼1 kcal mol^–1 destabilizing contribution to the activation barrier for TIM-catalyzed deprotonation of DHAP and GAP from interactions between the side chain anion of E97 and the distant anionic transition state.

The experimental and computational results show that the contribution of the anchoring K12•E97 ion pair to the enzymatic rate acceleration is <1 kcal mol^–1. EVB simulations likewise show that the E97A substitution of K12G TIM to give the double K12G/E97A substitutions results in a ≤0.3 kcal mol^–1 increase in the calculated activation barriers for the K12G yTIM-catalyzed deprotonation of DHAP and GAP and that the effect of the K12G substitution on the activation barrier for catalysis by the E97A variant lies within 0.3 kcal mol^–1 of the effect of the K12G substitution on the activation barrier for catalysis by wild-type yTIM. We conclude that the role of the E97 side chain in preorganization of the K12 side chain at a K12•E97 salt bridge⁷⁶⁻⁷⁸ does not provide for strong stabilization of the isomerization transition state. This is consistent with the conclusion that the evolutionary pressure to optimize the activity of TIM, which plays a critical metabolic role in cellular energy production by glycolysis,⁷⁹ is so strong that the E97 side chain is strictly conserved in order to obtain a ca. 1 kcal mol^–1 stabilization of the rate-determining transition state. The E97 carboxylate anion is hydrogen bonded to the T75 side chain at the second subunit of TIM.⁸⁰ The placement of this side chain in the middle of a network of hydrogen bonds that spans the K12 and T75 side chains at neighboring protein subunits implies an additional role for E97 in maintaining the dimeric structure for TIM, which merits investigation.

Finally, we note the curious result that E97D and E97Q substitutions at TIM from Plasmodium falciparum (PfTIM) result in 100- and 4000-fold decreases in k_cat for PfTIM-catalyzed isomerization of GAP, which are not modeled by our simulations of yTIM.⁵⁰ Schwans and co-workers have proposed an explanation for this organismal dependence in the measured kinetics, based on small differences in the structures of TbbTIM and PfTIM, for the larger effect of E97D and E97Q substitutions on k_cat for catalysis by PfTIM compared with TbbTIM.⁴⁴

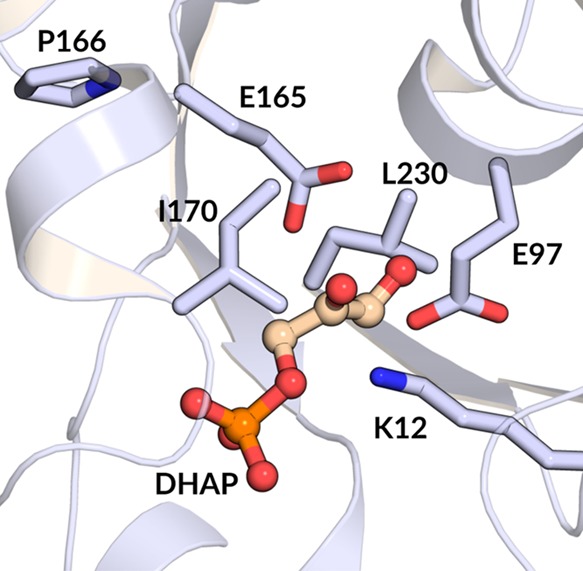
Substitution of P166

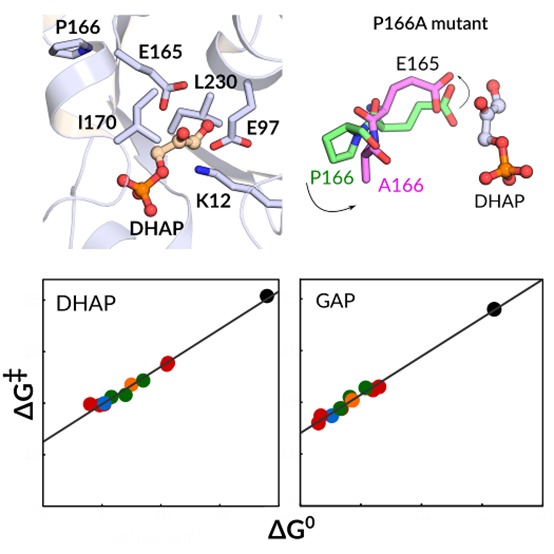
The triad of nonpolar side chains of P166, I170, and L230 line the active-site cavity of TIM. The observation of falloffs in catalytic activity for P166A,^40,81 I170A,^15,42 L230A,⁵⁵ and I170A/L230A⁴³ variants of TIM shows that these side chains play a structural role in the enhancement of the reactivity of the carboxylate side chain of E165 for deprotonation of enzyme-bound substrate. The effects of I170A, L230A, and I170A/L230A substitutions on the reaction activation barrier reflect global changes in the interactions between polar active-site groups and the enediolate-like transition state observed upon substitution of the hydrophobic side chains of I170A and L230A by water at the variant enzymes.⁴³ We have previously used the EVB method successfully to model the effects of I170A, L230A, and I170A/L230A substitutions.¹³

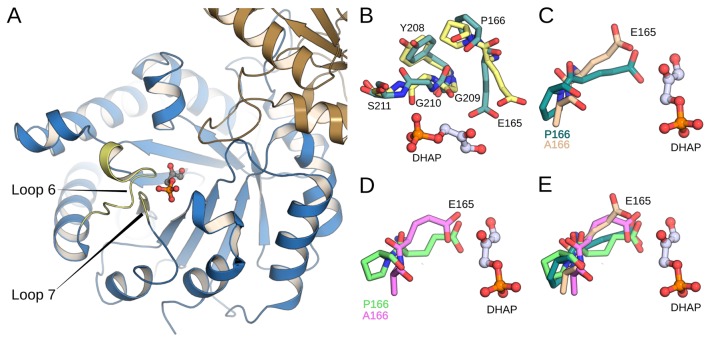
Wierenga and co-workers have provided a detailed description of the role of the P166 side chain in driving the carboxylate side chain of E165 into a hydrophobic cage, where it is flanked by the hydrophobic side chains of I170 and L230 and lies proximal to the carbon acid substrate.⁸² They showed that the X-ray crystal structure of the P166A variant complexed to phosphoglycolate (PDB ID: 2J24(40,59)) is essentially superimposable on the wild-type complex to DHAP (PDB ID: 1NEY(5,59)), except that relief of the steric clash between the carbonyl oxygen of G209 and the pyrolidine side chain of P166 at the P166A variant allows the carboxylate side chain of E165 to relax to the “swung-out” position observed for unliganded TIM (Figure 5).⁴⁰ This small structural change observed in the P166A variant is associated with ca. 50-fold decreases in k_cat and 2-fold decreases in K_m for the turnover of GAP and DHAP.⁸¹

Figure 5.

(A) Close-up view of the tertiary structure of yeast TIM (yTIM) complexed to DHAP (PDB ID: 1NEY(5,59)). (B) Overlay of X-ray structures of loop 7 in TIM structures with closed (PDB ID: 1NEY(5,59) dark green) and open (PDB ID: 1YPI,^59,83 yellow) conformations of loop 6. (C) Overlay of X-ray structures showing the “swung in” and “swung out” conformations of E165 in wild-type yTIM (PDB ID: 1NEY,^5,59 dark green) and the complex of P166A TbbTIM (PDB ID: 2J27,^40,59 tan). (D) Overlay of E165 in representative structures from our EVB simulations (obtained from clustering analysis as described in the Methodology section) at the Michaelis complexes wild-type (light green) and P166A TIM (pink). (E) Overlay of all structures shown in panels (C) and (D).

EVB simulations of the P166A variant were carried out, starting with the crystal structure of the yTIM•DHAP complex (PDB ID: 1NEY(45,59)) and substituting a −CH₃ group for the P166 side chain. The carboxylate side chain of E165 lies initially in the “swung-in” position for wild-type TIM, but, despite starting with the wild-type crystal structure, these simulations remarkably show a similar relaxation in the position of this side chain to the “swung-out” position observed for the crystal structure of the P166A variant complexed to PGA (Figure 5).⁴⁰ These changes in structure result in small increases in the enzyme–substrate donor–acceptor distance from 3.0 Å for the complexes between wild-type TIM and DHAP or GAP to 3.3 and 3.1 Å for complexes between the P166A variant of TIM and DHAP (Table S3) or GAP (Table S4), respectively.

The EVB simulations of the P166A variant of yTIM give 2.7 and 2.2 kcal mol^–1 increases in the activation barrier for deprotonation of GAP and DHAP, respectively, that are in good agreement with the 2.6 and 2.3 kcal mol^–1 increases in activation barriers determined from the effect of the substitution on k_cat for isomerization reactions catalyzed by TbbTIM.⁸¹ We conclude that these simulations model the effect of the P166A substitution both on the structure of the enzyme–ligand complex and on the activation barrier for TIM-catalyzed deprotonation of enzyme-bound substrate.

Linear Free Energy Relationships

We have reported good linear correlation between the kinetic (activation free energy, ΔG^⧧) and thermodynamic (reaction free energy, ΔG°) barriers for the deprotonation of substrates DHAP and GAP by propionate ion from solvent, wild-type TIM, and the I170A, L230A, and I170A/L230A variants.¹³Figure 6 shows large extensions of these linear free energy relationships (LFER) to include all 10 enzyme variants studied in this work. These LFER define strong linear correlations between the kinetic and thermodynamic reaction barriers, with slopes of β = 0.73 ± 0.03 (R² = 0.994) and β = 0.74 ± 0.02 (R² = 0.995) for the deprotonation of DHAP and GAP, respectively. By comparison, Brønsted correlations that include only data for the enzymatic reactions give β = 0.66 ± 0.04 (R² = 0.983) and β = 0.70 ± 0.06 (R² = 0.972) for the deprotonation of DHAP and GAP, respectively. The small differences between the slopes determined when data for the nonenzymatic reaction is omitted or included in these fits are consistent with a similar transition state structure for nonenzymatic and TIM-catalyzed deprotonation of DHAP and GAP.

Figure 6.

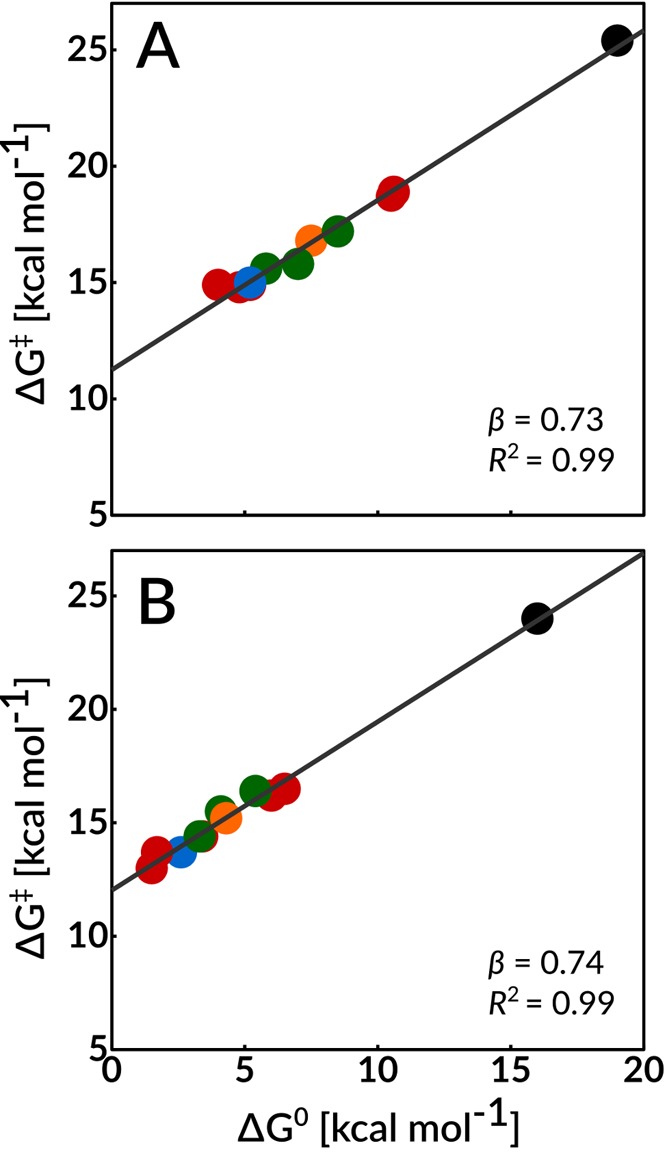
Linear free energy relationships between the activation free energies, ΔG^⧧, and the reaction free energies, ΔG°, determined in this work using EVB simulations, for the deprotonation of DHAP and GAP catalyzed by wild-type TIM and all TIM variants described in this study. The correlation coefficients were calculated using regression analysis to be 0.994 and 0.995 for the deprotonation of substrates DHAP and GAP, respectively. In this figure, the black circles correspond to the nonenzymatic reaction in aqueous solution, the blue circles correspond to the wild-type enzyme, the red circles correspond to single substitutions of polar side chains (K12G and E97A), the green circles correspond to single substitutions of nonpolar side chains (P166A, I170A, and L230A), and finally, the orange circle corresponds to double substitutions of nonpolar side chains (I170A/L230A). The raw data used for this figure are provided in Table 1.

On a methodological note, we refer the reader to detailed analysis and validation of the molecular origins of LFER within a valence bond (VB) framework, such as that presented in refs (84) and (85). In particular, as illustrated in, for example, Figure 2 of ref (85), within such a framework, there are two ways in which a catalyst can reduce the barrier for a chemical reaction. One is by shifting the minima of the VB parabolas relative to each other (an example of the Hammond postulate,⁸⁶ which would give rise to an LFER such as those shown in Figure 6). The alternative involves altering the reorganization energy of the reaction, thus shifting the relative positions of the two diabatic states (an example of the Principle of Least Nuclear Motion;⁸⁷ for more detailed discussion we refer the reader to ref (85)), without necessarily any accompanying change in the overall reaction driving force. Hence, one would expect that EVB calculations should detect LFER (Figure 6) in other cases where there is a strong imperative for stabilization of an enzyme-bound reaction intermediate relative to the intermediate in water. Breakdowns of these LFER might be observed for amino acid substitutions that cause increases in the reaction activation barrier ΔG^⧧, without affecting the reaction driving force ΔG°. For example, amino acid substitutions that cause significant increases in the distance separating the enzymic base from the bound carbon acid substrate may cause increases in ΔG^⧧ without changing the relative stability of the enzyme-bound substrate and reaction intermediate. In such a situation, the EVB simulations would still pick up the impact of these substitutions on the catalytic effect of the enzyme, without producing an LFER. Therefore, an LFER is not necessarily the expected outcome from performing EVB simulations.

Following from this, the LFER shown in Figure 6 provides evidence of the maturity of computational approaches and their power to operate alongside experimental studies in moving toward a comprehensive explanation of the catalytic rate acceleration for TIM and other enzymes. It has been proposed that the prime imperative for enzymatic catalysis of deprotonation of weak carbon acids is that protein catalysts operate on the bound substrates to reduce that standard-state Gibbs free energy for deprotonation of carbon.⁸⁸⁻⁹²Figure 6 supports the existence of this imperative, and the LFER provide support for a simple and self-consistent model to rationalize the contribution of individual amino acid side chains to the enzymatic rate acceleration.

The amino acid side chains whose variants satisfy the Brønsted relationship from Figure 6 play the common role in catalysis of isomerization of stabilizing the enzyme-bound enediolate phosphate relative to bound substrate. The action of two types of side chains is modeled by this figure. First, the polar side chain cation of K12 favors substrate deprotonation by E165 through direct stabilization of negative charge at the enediolate oxygen of the reaction intermediate. EVB simulations (Table 1) predict that the K12G substitution chain results in a 3.7 kcal mol^–1 increase in ΔG^⧧ for deprotonation of DHAP and a smaller 2.5 kcal mol^–1 increase in ΔG^⧧ for deprotonation of GAP, because the side chain lies closer to the O-2 compared to the O-1 oxyanions formed by deprotonation of DHAP and GAP, respectively (Figure 2). The substitution results in larger 5.3 and 3.4 kcal mol^–1 increases in ΔG° for deprotonation of enzyme-bound DHAP and GAP, respectively, because O-2 and O-1 now bear a full negative charge at the enediolate products.

Second, the nonpolar side chains of P166, I170, and L230 favor substrate deprotonation to form the enediolate phosphate trianion through either enhancement of stabilizing interactions between the polar amino acid side chains and negative charge at the enediolate oxygen of this reaction intermediate or through enhancement of the basicity of E165. There is evidence that the changes in ΔG° and ΔG^⧧ reflect both types of effects.

The estimated electrostatic contributions from both protein and solvent to the calculated activation free energies for the deprotonation of DHAP and GAP were reported in a previous computational study of the wild-type and I170A, L230A, and I170A/L230A variants of TIM, where the changes in the total electrostatic interactions are the sum of many small changes in individual interactions, including the electrostatic contributions from N10, K12, H95, S96, and E129.¹³ These computational results are consistent with a small weakening in the electrostatic interactions for these enzyme variants.

The P166A and I170A substitutions result in 0.7 and 2.3 unit decreases, respectively, in the pK_a for the carboxylic acid side chain of E165 at the complex between TIM and the enediolate phosphate analogue PGA.^15,16 These decreases in pK_a are proposed to result from change in the solvation of the carboxylate discussed above, which favors the calculated increases in ΔG° for proton transfer at these TIM variants (Figure 6).

Enzymatic Rate Acceleration

The chemical reaction mechanism for TIM-catalyzed deprotonation of the α-carbonyl carbon is not significantly different from that for the nonenzymatic deprotonation of carbon in water,^12,93 except that the catalytic side chains are tethered at a protein binding pocket that is complementary to the transition state for carbon deprotonation.⁹⁴ These side chains are activated in some way for catalysis at the enzyme active site, compared with water: this activation results from the utilization of the phosphodianion binding energy to drive conversion of the flexible open enzyme to the reactive caged enzyme–substrate complex.^{12,20,95−97} The results from EVB calculations show that cage formation provides a global thermodynamic activation for substrate deprotonation that corresponds to 13.8 and 13.4 kcal mol^–1 increases, respectively, in the driving force for proton transfer from bound DHAP and GAP and that ca. 75% of this thermodynamic activation (10.4 and 10.3 kcal mol^–1, respectively) is expressed at the transition state for substrate deprotonation (Table 1). Figure 6 shows that a large number of active-site side chains at TIM play a common role in catalysis of the isomerization reactions of DHAP and GAP of stabilizing the enzyme-bound enediolate phosphate relative to bound substrate.

The side chains examined in our studies make two distinct contributions to the thermodynamic/kinetic activation of TIM for deprotonation of bound substrate. First, the transition state for proton transfer is stabilized by 3.7 and 2.5 kcal mol^–1 for deprotonation of DHAP and GAP, respectively, through interactions with the cationic side chain of K12. These cations provide no significant stabilization of the transition state for proton transfer in water at pH ≥ 7, where there is no significant catalysis of deprotonation of GAP or DHAP by tertiary ammonium cations.⁹³ Second, the hydrophobic side chains of P166, I170, and L230 occupy positions that minimize the thermodynamic and kinetic barriers to substrate deprotonation. There is good experimental evidence, described above, that the effect on the reaction driving force is due mainly to the enhancement of the basicity of the carboxylate side chain of E165 at TIM compared to aqueous solution.^15,16 The effects of the P166A, I170A, and L230A substitutions on the activation barriers for deprotonation sum to 3.6 and 6.1 kcal mol^–1, respectively, for deprotonation of DHAP and GAP. This serves as an upper limit for the contribution of these side chains to catalysis in the event that the effects of these mutations are additive.

There is additional stabilization of the transition state for formation of the enediolate phosphate oxyanion by interactions with other polar side chains and backbone amides at the enzyme active site, most prominently the imidazole side chain of H95^98,99 and the amide side chain of N10.⁸⁰ These interactions were evaluated as −0.6 (DHAP) and −1.1 kcal mol^–1 (GAP) for H95 and −0.2 (DHAP) and −1.1 kcal mol^–1 (GAP) for N10, obtained by applying the linear response approximation^74,75 to calculated EVB trajectories for the deprotonation of these substrates by wild-type TIM (Figure 4 and Table S6 in the Supporting Information). By comparison, the H95Q mutation results in a ca. 3 kcal mol^–1 increase in the activation barrier for TIM-catalyzed isomerization.¹⁰⁰

In conclusion, the results of experimental and computational studies are converging to provide a clear rationale for the 10 kcal mol^–1 stabilization of the transition state for deprotonation of TIM-bound substrate (Table 1). The total transition-state stabilization represents the combined contributions of many different side chains. The precision in their placement^78,101 at the TIM active site is the end product of the evolution of a catalytic protein–substrate cage that effects a large reduction in the standard-state Gibbs free energy of reaction for proton transfer to the carboxylate side chain of E165^15,16 and which is strongly stabilized by interactions with the substrate dianion.²⁰

Concluding Remarks

We present the results of the most extensive computational study of the effect of substitution of key active-site residues on the activity of triosephosphate isomerase reported to date. These data provide biochemical insight into the mode of enzyme action, while probing the limits of the EVB approach in modeling this deceptively simple proton transfer reaction. The EVB simulations reproduce both the changes in enzyme structure determined for the P166A,⁴⁰ I170A,⁴³ and L230A⁴³ TIM variants and the changes in the experimental activation free energies for the broad range of protein variants reported in Table 1. In addition, the simulations provide thermodynamic barriers to substrate deprotonation that were used in the construction of linear free energy relationships with excellent linear correlations between the kinetic and thermodynamic barriers for the deprotonation of substrates DHAP and GAP over a 10.4 and 14.9 kcal mol^–1 range in activation and reaction free energies, respectively. This extended LFER (Figure 6) shows that the evolution of the remarkable catalytic proficiency of TIM was driven by the selection of caged enzyme–substrate active-site structures that minimize the thermodynamic barrier for the highly unfavorable substrate deprotonation.

The activation barrier for nonenzymatic reactions, which proceed though unstable carbocation (e.g., isopentenyl pyrophosphate isomerase¹⁰² or diterpene synthase¹⁰³) or carbanion^90,104 reaction intermediates, is composed mainly of the thermodynamic barrier to formation of the intermediate.^92,105,106 We propose that the rate acceleration for these enzymes is achieved by reducing this thermodynamic barrier through a mechanism similar to that documented for TIM, where the substrate binds to an open form of the protein catalyst, which then undergoes a ligand-gated conformational change to create a protein–substrate cage. Substrate ionization at this cage is promoted by positioning relevant amino acid side chains so as to provide optimal stabilization of the charged reaction intermediate, relative to the neutral substrate, through electrostatic interactions with catalytic side chains and backbone amides of opposite polarity.⁷⁸ The enzymatic reaction may also be promoted through creation of interactions that destabilize the ground state and which are relieved at the transition state, such as desolvation of the carboxylate side chain of E165, which enhances the basicity of this side chain. This model defines the contribution of participating side chains to catalysis as the effect of the active-site side chains forming this catalytic cage on the equilibrium constant for conversion of enzyme-bound substrate to the reaction intermediate (Figure 6) and posits that the enzymatic rate accelerations are due mainly to preorganization of polar active-site side chains into positions that provide for optimal stabilization of the enzymatic transition state.^78,107

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b08713.

• Additional simulation analysis (RMSD plots, key distances, analysis of electrostatic interactions and water molecules in the active site), as well as relevant empirical valence bond parameters necessary to reproduce our simulations (PDF)

The authors declare no competing financial interest.