Maximal Clique Method for the Automated Analysis of NMR TOCSY Spectra of Complex Mixtures

Abstract

Characterization of the chemical components of complex mixtures in solution is important in many areas of biochemistry and chemical biology, including metabolomics. The use of 2D NMR total correlation spectroscopy (TOCSY) experiments has proven very useful for the identification of known metabolites as well as for the characterization of metababolites that are unknown by taking advantage of the good resolution and high sensitivity of this homonuclear experiment. Due to the complexity of the resulting spectra, automation is critical to facilitate and speed-up their analysis and enable high-throughput applications. To better meet these emerging needs, an automated spin-system identification algorithm of TOCSY spectra is introduced that represents the cross-peaks and their connectivities as a mathematical graph, for which all subgraphs are determined that are maximal cliques. Each maximal clique can be assigned to an individual spin system thereby providing a robust deconvolution of the original spectrum for the easy extraction of critical spin system information. The approach is demonstrated for a complex metabolite mixture consisting of 20 compounds and for an E. coli cell lysate.

Introduction

Because of its spectral resolution, high-field nuclear magnetic resonance (NMR) is an excellent tool for complex mixture analysis without the need for prior physical separation into individual components (Markley et al. 2017). For relatively simple mixtures or spectral regions with little overlap, 1D NMR is often sufficient provided that the spectra of the mixture components are available in a spectral database. For more complex mixtures, 2D experiments, such as ¹³C-¹H HSQC spectra at ¹³C natural abundance (Bodenhausen and Ruben 1980), can be queried in a similar fashion against NMR databases (Robinette et al. 2008; Ulrich et al. 2008; Wishart et al. 2013; Wishart et al. 2007) benefiting from the higher resolution afforded by the indirect ¹³C dimension. For metabolites that have concentrations that are too low to be detected in HSQC spectra, the use of homonuclear 2D ¹H-¹H TOCSY experiments (Braunschweiler and Ernst 1983) is a viable alternative (Bingol and Brüschweiler 2014; Fan and Lane 2016; Gowda and Raftery 2015) as they yield complete spin-connectivity information for the reconstruction of molecular spin systems (Zhang and Brüschweiler 2007). This information does not only allow the robust querying of sets of chemical shifts belonging to the same spin system against customized TOCSY databases of known compounds (Bingol et al. 2014), but also helps characterize unknown mixture components toward the elucidation of their structure.

For many molecular spin systems, 2D ¹H-¹H TOCSY spectra recorded at sufficiently long mixing times (>80 ms) typically connect each resonance of a spin system with each other by a cross-peak. Together this amounts to a significant amount of redundant information (Figure 1). Such redundancy is helpful for the robust spectral interpretation in the case of highly complex spectra, such as those encountered in metabolomics, where peak overlap is very common. This property makes TOCSY spectra also suitable for computer-based analysis. Several different algorithms have been proposed for the automated extraction of spin system information from 2D TOCSY spectra both for poteins (Bartels et al. 1996; Eccles et al. 1991) and complex mixtures (Bingol and Brüschweiler 2011; Zhang and Brüschweiler 2007).

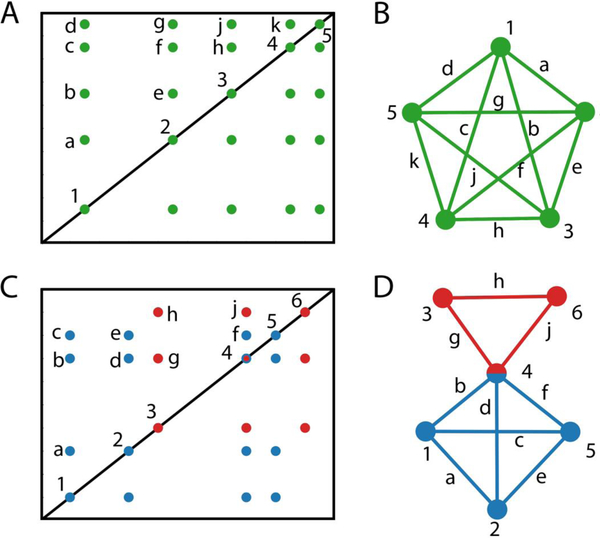
Figure 1.

Schematic illustration how a 2D TOCSY spectrum can be converted to a mathematical graph and interpreted in terms of maximal cliques. A. 2D TOCSY spectrum of a 5-spin system. B. Representation of connectivity information (cross-peaks) of A) as a maximal clique graph where the different spins correspond to nodes and cross-peaks to edges. C. 2D TOCSY spectrum of a mixture of a 4-spin system (blue) and a 3-spin system (red) where resonance 4 belongs to two overlapping resonances from each of the spin systems. D. Maximal clique analysis of TOCSY spectrum of C. The two maximal clique graphs (red and blue subgraphs), which are connected at node 4 due to spectral overlap, each belong to a separate spin system.

In this work, we describe a new strategy for the identification of individual spin systems of mixtures from a 2D TOCSY spectrum based on maximal cliques. It uses information gained from a highly redundant set of cross-peaks that are picked automatically via a standard peak picker. This information is converted into a mathematical graph where each cross-peak represents an edge connecting a pair of diagonal peaks represented by nodes. The resulting graph is then subjected to maximal clique analysis to extract the desired spin system information. A clique represents a complete subgraph, i.e. all of its nodes are connected to each other by an edge (Gross and Yellen 2006). A maximal clique is the largest possible clique, i.e. it is not a subgraph of any other clique. We demonstrate how this method can be extended in an automated and robust manner to real-world TOCSY spectra of complex mixtures. Such spectra typically display cross-peak shapes with multiplet patterns along both dimensions, which frequently lead to the representation of the same cross-peak by multiple cross-peak entries in the peak list.

Graph theoretical analysis of NOESY- and TOCSY-type NMR spectra has been proposed previously for proteins (Oschkinat et al. 1991; van Geeresteinujah et al. 1995; Xu et al. 1994) and complex mixtures (Bingol et al. 2012a; Zhang et al. 2010). Maximal cliques have been used in chemistry and NMR for the computer-assisted chemical structure elucidation to identify and match common parts of 2D and 3D molecular substructures (Koichi et al. 2014; Raymond and Willett 2002). Previous work focused on the maximal clique analysis of individual molecules rather than chemical mixtures, which is the focus of this study.

Materials and Methods

Sample preparation.

A 20-compound mixture was prepared containing 19 typical metabolites, namely adenosine, arginine, ascorbic acid, aspartic acid, citrulline, glutamine, isoleucine, leucine, lysine, methionine, nicotinamide, ornithine, proline, aminobutyric acid, threonine, trigonelline, valine, taurine, glutathione, and glutamic acid as well as DSS (4,4-dimethyl-4-silapentane-1-sulfonic acid) for chemical shift referencing. The final concentration of each metabolite was 1 mM and 0.5 mM for DSS in 600 μL D₂O with 20 mM phosphate buffer.

E. coli BL21(DE3) cells were cultured at 37 °C with shaking at 250 rpm in M9 minimum medium with glucose (natural abundance, 5 g/L) added as the sole carbon source. One liter of culture at OD 1 was centrifuged at 5000g for 20 min at 4 °C, and the cell pellet was resuspended in 50 mL of 50 mM phosphate buffer at pH 7.0. Cell suspension was then subjected to centrifugation for cell pellet collection. The cell pellet was resuspended in 10 mL of ice-cold water and exposed to freeze-thaw procedure three times. The sample was centrifuged at 20,000g at 4 °C for 15 min to remove the cell debris. Pre-chilled methanol and chloroform were sequentially added to the supernatant under vigorous vortexing at an H₂O/methanol/chloroform ratio of 1:1:1 (v/v/v). The mixture was then left at −20 °C overnight for phase separation. Next, it was centrifuged at 4000g for 20 min at 4 °C, and the clear top hydrophilic phase was collected and subjected to rotary evaporation to reduce the methanol content. Finally, the sample was lyophilized. The NMR sample was prepared by dissolving the dry sample in 200 μL of D₂O with 20 mM phosphate buffer and 0.5 mM DSS (4,4-dimethyl-4-silapentane-1-sulfonic acid) for chemical shift referencing.

NMR experiments and data processing.

2D ¹H-¹H TOCSY NMR spectra of both the 20-compound model mixture and E. coli cell lysate were collected. All NMR spectra were collected on a Bruker AVANCE solution state NMR spectrometer equipped with a cryogenically cooled TCI probe at 850 MHz proton frequency at 298 K. The spectral width along both dimensions was set to 10204.1 Hz and the transmitter frequency offset was 4.7 ppm along both dimensions. For TOCSY mixing the DIPSI-2 mixing sequence was used for 90 ms and 120 ms for the 20-compound model mixture and the E. coli cell lysate, respectively. All the data were zero-filled, Fourier transformed, and phase and baseline corrected using NMRPipe (Delaglio et al. 1995). All spectra were converted to MATLAB format for maximal clique analysis. The spectra were then subjected to peak-picking using an in-house 2D peak-picker that identifies local maxima in the 2D spectra that are above an intensity threshold, which is defined as eight times the median absolute deviation of the noise floor. A 9-point 2^nd order polynomial was used to fit to the shape of each cross-peak to obtain sub-pixel resolution for the positions of the peak maxima.

Results

Maximal cliques of TOCSY spectra.

In a 2D ¹H-¹H TOCSY spectrum, each diagonal peak represents a proton spin and each pair of cross-peaks, which are placed symmetrically with respect to the diagonal, establishes that the two spins exchanged magnetization during the TOCSY mixing time and therefore belong to the same spin-system (Figure 1A). Such spin-spin connectivity information from all cross-peaks can be translated into an undirected graph where each node (1, 2, …, 5) represents a spin and pairs of spins that have a common cross-peak are connected by an edge (a, b, …, k) as is illustrated in Figure 1B.

Generally, for a spin system that contains N (non-degenerate) proton resonances, the TOCSY spectrum will display N diagonal peaks and N(N-1)/2 cross-peaks on each side of the diagonal. Its representation by a complete graph will then consist of N nodes where each node is connected to each other by an edge. In the case of resonance overlap within a spin system, the resulting graph is still complete but will contain < N nodes. The occurrence of resonance overlap between two different spin systems (Figure 1C) is somewhat more tricky, since the resulting graph is not any longer complete (Figure 1D). In order to identify each spin system, all maximal cliques need to be identified, which are subgraphs that are complete in themselves and that have maximal size. Identification of all maximal cliques from the experimental TOCSY raw data of the mixture provides access to the underlying spin systems even in the presence of significant peak overlap as described in the following.

Since the diagonal region of a TOCSY spectrum of a complex mixture tends to be crowded, it makes peak-picking along the diagonal difficult. This is illustrated in Figure 2A for a diagonal region of an experimental 2D TOCSY spectrum of a model mixture consisting of 20 different compounds. Instead of trying to accurately identify the peak positions along the diagonal, we define diagonal peak positions (nodes) indirectly from the frequency coordinates of each pair of symmetrically placed TOCSY cross-peaks with respect to the diagonal. Since multiple cross-peaks often belong to the same diagonal peak, some diagonal peaks identified in this way can have very similar or identical chemical shifts. The same applies to cross-peaks that belong to two different spin systems that share an overlapping resonance. Therefore, diagonal peaks determined in this manner may or may not belong to the same spin. Importantly, at this step of the analysis, all diagonal peaks are treated as separate spins and will be assessed for reconciliation later based on the output of the maximal clique analysis. In a 2D ¹H-¹H TOCSY experiment, homonuclear scalar J-couplings will cause multiple maxima for each expected cross-peak. Although a human peak picker can quite easily detect cross-peak centers in order to simplify the connectivity analysis, for an automated peak picker this task is less straightforward, especially in the presence of cross-peak overlap, noise or spectral artifacts.

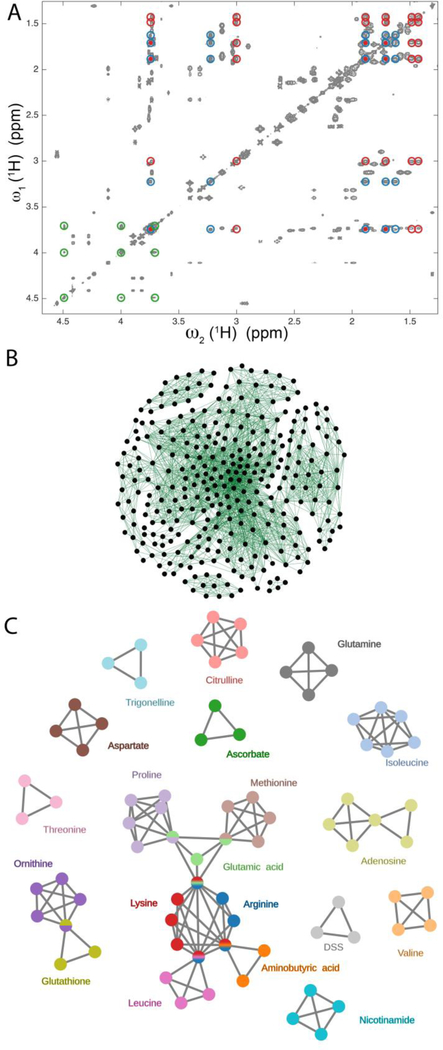
Figure 2.

Illustration of maximal clique method for the extraction of spin systems from redundant cross-peak information of a 2D TOCSY spectrum. A. Region of a 2D ¹H-¹H TOCSY spectrum of a 20-compound model mixture consisting of 19 metabolites and DSS. The red, blue, and green circles belong to lysine, arginine, and ascorbate, respectively, with lysine and arginine showing overlaps of three of their resonances. B. Representation of the 804 cross-peaks picked in the 2D TOCSY spectrum as a graph consisting of a total of 2600 edges and 306 nodes after removing all maximal cliques of size 2 (two nodes connected by an edge). C. Analysis of the graph of Panel B by the maximal clique method produces a non-redundant set of connected and disconnected maximal cliques that can be directly assigned to all spin systems of the mixture components that contain > 2 spins.

Next, the spin connectivity information obtained from the 2D cross-peaks is converted to a mathematical graph, which can be defined by a connectivity matrix that is a square matrix containing zeros and ones. All elements are zero, except when a pair of diagonal elements (nodes) becomes connected by an edge, which is the case when corresponding cross-peaks are present on both sides of the diagonal and within a 0.01 ppm frequency cutoff of their expected locations. Once the entire graph has been constructed, the maximal clique problem is solved using the Bron–Kerbosch algorithm with pivoting, which is a recursive back-tracking algorithm presently considered to be the most efficient maximal clique algorithm for general types of graphs (Bron and Kerbosch 1973). This algorithm deterministically identifies all maximal cliques of the TOCSY connectivity graph.

Each maximal clique is then inspected with respect to the similarity of its nodes. If any two nodes have their chemical shifts within a given cutoff (0.02 ppm), they are merged into a single node reducing the size of the clique by one. In this way the total number of nodes of the graph can be substantially reduced. Next, all maximal cliques are compared with each other to further eliminate redundancy. If all chemical shift differences of the cross peaks of two maximal cliques are smaller than the cutoff (0.02 ppm), the two maximal cliques are considered to represent the same spin system and are combined into the same maximal clique. This leads to the merging of duplicate maximal cliques that represent different multiplet components of the same cross-peaks. Also, maximal cliques whose nodes correspond to a subset of another maximal clique are absorbed in this way. In this step, nodes are merged that belong to the same spin but which were distinct as they were originally derived from different cross-peaks or different multiplet components of the same cross-peak.

These two steps by and large also solve the diagonal peak overlap problem mentioned above: two diagonal peaks with very similar chemical shifts are assigned to the same spin only if they always belong to the same maximal clique, whereas they are assigned to two different spins (whose resonances overlap) if they belong to different maximal cliques.

An important property of this procedure is its robustness with respect to the absence of a TOCSY cross-peak. For a spin system with N spins, a missing cross-peak causes the disappearance of an edge in a maximal clique and the emergence of two new maximal cliques, both of size N-1, where the two cliques are identical except that each lacks one of the two nodes that would be connected by the missing edge, i.e. the two new maximal cliques share N-2 nodes. Computer-based comparison of all maximal cliques with each other readily identifies those maximal cliques that are nearly identical, including those that are caused by a missing cross-peak. Projection of these cliques onto the 2D TOCSY spectrum permits the user to rapidly validate whether a cross-peak was missed during the initial peak-picking. However, in cases where such cross-peaks cannot be identified the TOCSY spectrum simply does not provide sufficient information to unambiguously address whether the two maximal cliques belong to the same spin system or to distinct spin systems with strongly overlapping resonances. Our algorithm is generally more reliable for larger spin systems (N > 3) as their TOCSY spectra contain more redundant connectivity information with the number of cross peaks growing with O(N²). By contrast, the occurrence of small cliques that are false, e.g. with just two nodes, is more likely as there is little redundancy in the spectrum.

After standard 2D FT processing of the 2D TOCSY data, peak-picking and the other analysis steps described above were fully automated, which makes this approach amenable to high-throughput analysis. The computer returns all identified maximal cliques and merges similar cliques that share most of their nodes. The final result of the analysis can be inspected first or, alternatively, be used directly for downstream analysis, such as database query, without prior human intervention.

Application to 20-component mixture.

A region of the 2D ¹H-¹H TOCSY spectrum of the 20-component mixture (19 metabolites plus DSS, Experimental Section) is shown in Figure 2A. Information of 804 automatically picked cross-peaks was converted to a graph consisting of 306 nodes and 2600 edges (Figure 2B), after maximal cliques with only two vertices and one edge had been removed. The resulting graph is inordinately complex for the human eye, but it can be dramatically simplified when subjected to the maximal clique analysis described above. This leads to the graph shown in Figure 2C, which has only 75 nodes and 135 edges, after five false maximal cliques with 3 nodes each were removed by visual inspection based on peak shapes and t₁-noise. This corresponds to a reduction of a factor 4 in the number of nodes extracted from the raw data and a factor of 19 in the number of edges. The colored subgraphs shown in Figure 2C depict the output of the maximal clique method (the only exception is adenosine, vide infra). The spin systems of 16 of the 20 compounds are directly represented by maximal cliques. These include both small spin systems, such as ascorbate and threonine with three nodes each, and larger spin systems, such as citrulline and ornithine with five nodes each. In the case of ornithine, one node is shared with glutathione because of peak overlap (within the cutoff used here of 0.01 ppm). Since the maximal clique information returned by the algorithm is equivalent to the assignment of colors to the separate spin systems, this does not pose any ambiguities in the identification of the spin systems. Similarly, arginine is a maximal clique that is embedded in a larger graph because of peak overlaps with 3 other compounds, namely glutamic acid, leucine, and aminobutyric acid.

Both lysine and isoleucine form nearly complete maximal cliques with only one missing edge (i.e. cross-peak pair). For lysine, one cross-peak (and its symmetric counter part) is missing (at 1.43/1.48 ppm). This is because of its close vicinity to the diagonal, which makes identification by an automated peak picker challenging, whereas the same task is rather straightforward for manual peak-picking. In this case, the superposition of the maximal clique results on the original 2D spectrum allowed the identification of the missing cross-peak and the joining of two maximal cliques that both represented 5 of the 6 distinct resonances (nodes) of this metabolite. For isoleucine, one pair of cross-peaks (at 3.66/1.46 ppm) is very weak and, hence, was not picked by the automated peak picker. Again, the superposition of the maximal clique results on the original spectrum easily revealed the missing link and allowed the joining of the two maximal cliques to a single maximal clique. Proline forms a nearly complete maximal clique, but two of the expected edges are missing, since two cross-peaks (one at 3.32/4.11 ppm and one at 3.41/4.11 ppm) are very weak. Again, visual inspection permits the identification of the two cross-peaks and the establishment of the maximal clique that corresponds to the full proline spin system. The only spin system that eluded a representation by a single maximal clique is the ribose moiety of adenosine (yellow-green subgraph), since more than half of the expected cross-peaks were either missing or were very weak. It led to the representation of this spin system by two maximal cliques, one with 4 and the other with 3 nodes that could be mistakenly assigned to two different spin systems that share an overlapping resonance.

For the purpose of visual validation, the maximal cliques can be mapped onto the original TOCSY spectrum, which is shown in Figure 2A for the three metabolites arginine, lysine, and ascorbate. Ascorbate (green) exemplifies a well-isolated three-spin system. By contrast, lysine (red) and arginine (blue) have three resonances that overlap with respect to each other (within the 0.01 ppm cutoff used).

Application to E. coli.

Application of the maximal clique method to a 2D ¹H-¹H TOCSY spectrum of a lysate of E. coli is illustrated in Figure 3. Because of the high complexity of the spectrum, a very large number of maximal cliques can be identified. In regions with severe peak overlaps, especially in the carbohydrate region (3 – 5 pm), many of the returned cliques belong to false spin systems. For such regions, higher resolution is required as afforded by 3D NMR experiments (see below). By contrast, if a maximal clique falls in a less crowded region, or at least some of the cross-sections are in less crowded regions, the confidence in the correctness of the returned spin system is high. Figure 3 shows examples of maximal cliques returned by the algorithm for E. coli lysate, including some colored ones that mostly belong to known metabolites (i.e. they are contained in the COLMAR TOCCATA database (Bingol et al. 2014; Bingol et al. 2012b)). We could identify ten maximal cliques that represent with high probability spin systems of “unknown” metabolites, including the ones depicted in Figure 3. They are being further analyzed in our lab using the hybrid mass spectrometry-NMR approach SUMMIT MS/NMR (Bingol et al. 2015).

Figure 3.

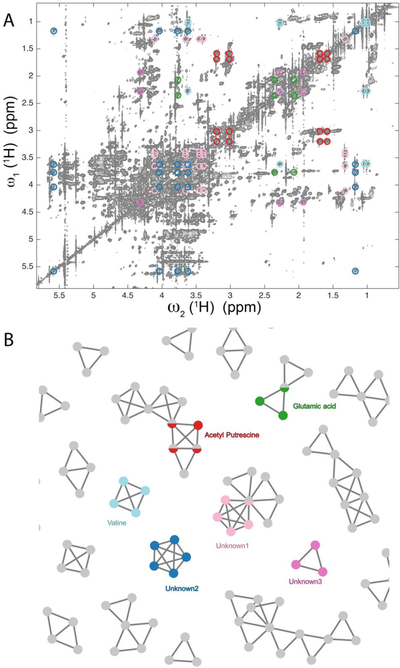
Illustration of maximal clique method for 2D TOCSY spectrum of E. coli cell lysate. A. Region of the 2D ¹H-¹H TOCSY spectrum of E. coli cell lysate. Selected spin systems extracted by the maximal clique method and their cross-peaks are indicated in different colors. B. Depiction of selected maximal cliques corresponding to individual spin systems, including those that belong to the colored cross- and diagonal peaks in A. Besides known compounds, some of these maximal cliques belong to unknowns. Other known metabolites identified by the maximal clique method that are not indicated in the figure include: Aminobutyrate, Arginine, Citrulline, Glutamate, Isoleucine, Leucine, Lysine, N-acetyl-glutamate, Nicotinic acid, Phenylalanine, Proline, Threonine, and Tryptophan. Metabolites that contain only two-spin systems and carbohydrates were not included because of their reduced accuracy (due to the lack of redundant cross-peak connectivity information) and strong cross-peak overlaps, respectively. Since the metabolite concentrations vary widely, the depicted spectrum is plotted at a very low contour level.

As the E. coli spectrum exemplifies, for metabolomics samples of the complexity of an entire cell lysate (or similarly for a tissue sample or a complex biofluid, such as urine) the maximal clique method of 2D TOCSY should, whenever possible, be complemented by additional experiments, such as 2D ¹³C-¹H HSQC and 2D ¹³C-¹H HSQC-TOCSY spectra (Bingol et al. 2016). When using this pair of experiments, the 2D HSQC cross-peaks correspond to the nodes and the cross-peaks seen in the 2D HSQC-TOCSY, but which are not present in the 2D HSQC, correspond to the edges of a graph that can be subjected to maximal clique analysis in full analogy to the 2D TOCSY case. The 2D HSQC and HSQC-TOCSY spectra benefit from higher resolution along the indirect ¹³C dimension at the expense of lower sensitivity when measured at natural ¹³C abundance. Also, since there are no diagonal peaks, the challenge with cross-peaks close to the diagonal encountered in 2D TOCSY is alleviated. For very crowded regions and strongly overlapping compounds, such as carbohydrates, the use of 3D NMR experiments becomes mandatory as is the case for the application of NMR to larger proteins. The use of 3D ¹³C-¹H HSQC-TOCSY experiments to complex mixtures, at ¹³C natural abundance or after ¹³C labeling, permits the application of a maximal clique strategy analogous to the one presented here for homonuclear 2D TOCSY experiments. The 3D ¹³C-¹H HSQC-TOCSY experiment offers additional spectral resolution at the cost of prolonged experiment times, whereby nodes are defined by cross-peaks in a 2D ¹³C-¹H HSQC experiment and edges are defined by 3D HSQC-TOCSY cross-peaks in a way that is analogous to the 2D TOCSY case described above.

Discussion and Conclusion

The maximal clique problem belongs to the class of NP-hard problems, which means that it becomes computationally intractable for very large graphs (Garey and Johnson 1979). Fortunately, for a typical graph in a TOCSY application with less than 2000 nodes, it takes only between several minutes and an hour on a modern desktop computer with a single core. If needed, the problem can be parallelized using a CPU with multiple cores or a high-performance computer cluster. There also exist faster algorithms (Feige 2004) that offer approximate solutions to the maximal clique problem, which is an option for the treatment of larger graphs. For NMR TOCSY spectra of complex mixtures encountered in our lab, the size of the generated graphs can be well managed with modern computers.

The performance of our algorithm also depends on the quality of peak-picking. False peaks caused by thermal noise, t₁-noise, imperfect phase correction or apodization artifacts can introduce false maximal cliques. The projection of the returned cliques on the original spectrum (Figures 2A and 3A), e.g. using the web server tools recently introduced for COLMARm (Bingol et al. 2016), can be used for visual quality control of the returned maximal cliques, a task that can be performed efficiently by a spectroscopist.

Although 2D TOCSY is commonly used for metabolite identification in metabolomics studies, the lack of automated analysis tools of these types of spectra has made the use of 2D HSQC the primary choice, whereby 2D TOCSY spectra are mostly used for validation of the top hits, such as those identified by 2D HSQC (Bingol et al. 2016). However, this complementary use of these experiments does not take advantage of the higher sensitivity of TOCSY vs. HSQC. Homonuclear 2D experiments, such as TOCSY and COSY, can help identify metabolites in biological samples with concentrations that are too low for detection by HSQC, thereby increasing the number of measurable metabolites, which is important for the identification of metabolic pathways.

We presented a graph theoretical method to analyze 2D TOCSY data sets of complex mixtures. The maximal clique method thereby acts as a smart filter on a raw cross-peak list, which can be redundant and large, and accurately produces a small set of non-redundant maximal cliques that correspond to the underlying spin systems without the need for any spectral database information. The robust nature of the method makes it well suited for full automation. A test of our algorithm for a 20-compound model mixture shows that it is capable of identifying all spin systems irrespective of the presence of spectral overlap and t₁-noise. The method is directly applicable for the analysis of TOCSY spectra of a wide range of complex organic mixtures in solution, including ones encountered in metabolomics, consisting of both known and unknown metabolites.