Abstract
Additive manufacturing or, as also called, three-dimensional (3D) printing is considered as a game-changer in replacing traditional processing methods in numerous applications; yet, it has one intrinsic potential weakness related to bonding of layers formed during the printing process. Prior to finding solutions for improvement, a thorough quantitative understanding of the mechanical properties of the interface is needed. Here, a quantitative analysis of the nanomechanical properties in 3D printed photopolymers formed by digital light processing (DLP) stereolithography (SLA) is shown. Mapping of the contact Young’s modulus across the layered structure is performed by atomic force microscopy (AFM) with a submicrometer resolution. The peakforce quantitative nanomechanical mapping (PF-QNM) mode was employed in the AFM experiments. The layered specimens were obtained from an acrylate-based resin (PR48, Autodesk), containing also a light-absorbing dye. We observed local depressions with values up to 30% of the maximum stiffness at the interface between the consecutively deposited layers, indicating local depletion of molecular cross-link density. The thickness values of the interfacial layers were approximately 11 μm, which corresponds to ∼22% of the total layer thickness (50 μm). We attribute this to heterogeneities of the photopolymerization reaction, related to (1) atmospheric oxygen inhibition and (2) molecular diffusion across the interface. Additionally, a pronounced stiffness decay was observed across each individual layer with a skewed profile. This behavior was rationalized by a spatial variation of the polymer cross-link density related to the variations of light absorption within the layers. This is caused by the presence of light absorbers in the printed material, resulting in a spatial decay of light intensity during photopolymerization.
Keywords: additive manufacturing, stereolithography, interface, photopolymer, AFM, elastic modulus
1. Introduction
Three-dimensional printing (3D printing) of photopolymers by digital light processing (DLP) stereolithography (SLA) is a fast, precise, and relatively cheap manufacturing tool, which enables one to convert liquid polymer resins to multifunctional objects with complex, designed shapes.1,2 The DLP-SLA technique involves layer-by-layer processing, in which the resin is light-irradiated and cured, thus allowing an object to be built without masks, molds, and heavy machining.3−5 Microporous platforms with complex shapes and without using specific tools have been obtained, allowing for personalized scaffold manufacturing, e.g., for biomedical applications.6 Many other examples for fabricating implants and devices for tissue engineering for replacement, repair, or regeneration of the human tissue, blood vessels, bones, and muscles (also as an alternative to transplantation) have been described.1,7−9 In addition, SLA is also the subject of distinguished attention in the manufacturing of sophisticated objects made of polymer composites,10 conductive,11,12 or magnetic13 polymers, as well as porous constructs, where the elastic response of the material can be precisely controlled.14,15
In DLP-SLA, the so-called bottom-up printing configuration is typically used16,17 (Scheme 1). This process encompasses curing of the resin by subsequent discreet exposure flashes of light controlled by a projection system, typically consisting of micromirrors (digital mirror device). The light is then directed to the polymer resin through a window in the bottom of the vat holding the resin to be processed. The object under construction is being moved (utilizing programmed step heights to obtain the desired layer thickness) during processing. To prevent resin adherence to the light-transmitting window, a material, for instance, polydimethylsiloxane (PDMS), can be used for its manufacturing that has oxygen permeability that can contain higher amounts of dissolved gas and “reoxygenate” the bottom layer of the resin, thus ensuring partial cure in the bottom part of the solidified layer. During printing, no strong bonding can form between the object and the window, which enables the displacement of the article processed.18 In essence, an oxygen-inhibited photopolymerization takes place at the bottom of the vat, which leads to a layered, inhomogeneous structure across the printed slices that are formed flash by flash.19−21 An important variant of the bottom-up configuration includes the continues liquid interface production (CLIP) technology, where the access of oxygen through the bottom window is strictly controlled to allow continuous operation of the building platform, and thus speeds up the printing process.22
Scheme 1. Schematic Representation of Layer-by-Layer Photopolymer Printing in the Bottom-Up Configuration.
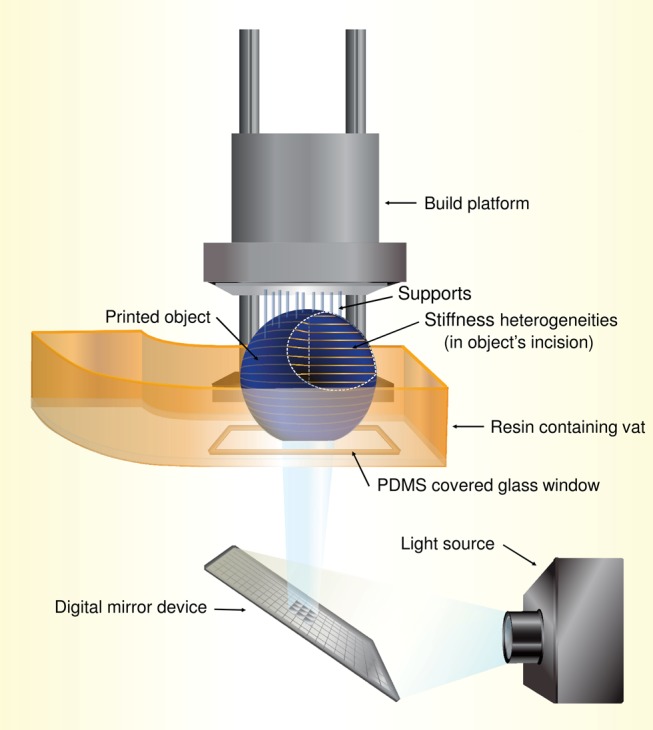
The bottom-up configuration is frequently used, basically because it needs less material to fill up the resin-containing vat, thus enabling the design of relatively small printers.1,16 However, the way an object is printed in the bottom-up configuration has some consequences, namely: (1) it incorporates structural heterogeneities in layers of the 3D printed polymers due to the stepwise build-up processing and (2) a light blocker (an absorbing dye) is usually introduced to control the light-penetration depth, DP. The Dp value is defined as the depth at which the penetrating light intensity falls to 1/e of the maximal light intensity.23,24 Together with the critical irradiation dosage required to initiate the photopolymerization, Ec (usually in mJ/cm2), both Ec and Dp are key parameters in the photopolymerization process and have constant values for individual resin compositions.25,26 Knowing the values of Ec and Dp, one can determine the required optimum settings of the light irradiation dosage, E0, the cure depth, Cd, and the step height, z, for each processing cycle. An expression that connects irradiation dosages and depths can be written as27
| 1 |
The value of Cd is associated with the gel point for the photopolymerized resin and thus with the formation of a three-dimensional network providing shape stability.1,24
Considering the properties of the 3D printed objects, one must target high bonding strength between the layers. This necessitates the use of layers with sufficient depth, i.e., Cd > z, because the stiffness of a polymer at the gel point is too low to endure the printing process.28 However, the scenario when Cd ≫ z should not occur to retain the designed architecture by remaining space-filling features uncured, for example, porous inclusions.1,2,26 Additionally, if Cd ≳ z, printing failure may occur due to poor attachment of the sequentially printed layers.
Stiffness (modulus of elasticity) of the interface between the consecutively printed layers is an important parameter in applications of 3D printed objects.19,21 Hence, achieving good interlayer joints that provide decent dimensional stability during use is the focus of great interest.1,19 If further progress is to be made in this manufacturing field, then the interfacial layers, including their mechanical performance, must be quantitatively characterized to allow one to optimize processing under the best attainable stereolithographic performance.3,5,17,29
Unfortunately, a detailed quantitative characterization of the mechanical property profiles, particularly at the interface, is still in its infancy due to the limited availability of experimental methods and tools that can be used in situ. Initial work by Hofstetter et al. employed a combination of a rheometer, a UV curing system, and a Fourier transform infrared spectrometer (FTIR) to measure the double-bond conversion and the storage modulus simultaneously at the time of curing at the middle section of the individual layers formed (testing depth: 100 μm, cure depth: 200 μm).23 Although this method shows great potential in local (within a plane at given layer depths) and averaged (macroscopic plate in the rheometer) mechanical characterizations, it cannot provide elastic modulus profiles across printed polymer objects at the nano- and micrometer length scales. Very recently, Yin and co-workers proposed orthogonal programming of the matrix stiffness and geometry via controlled oxygen inhibition-assisted stereolithography.30 The effect of the inhibitors on the surface stiffness profiles during the polymerization was analyzed, among others, by atomic force microscopy (AFM) utilizing colloidal probes of 10 μm polystyrene spheres attached to a cantilever. This study shows that the variation in the cross-linking density can be analyzed by quantitative AFM imaging. We expect that AFM-assisted quantitative mechanical characterization would provide novel information on the mechanical performance of the bridging layer, would yield an understanding of the layer-forming photopolymerization process, and elucidate the molecular-level characteristics of the features at the interface as well if performed with sufficiently high resolution.
To this end, here, we analyzed and described the mechanical performance of cross sections by AFM for a commercial photopolymer (PR48, Autodesk) obtained by DLP-SLA in the bottom-up configuration. The printed specimens were cryo-fractured, thus exposing the bulk of printed objects to the surface of the specimens investigated. The AFM studies were performed by systematic force measurements to unveil the contact elastic modulus (hereinafter called Young’s modulus), dissipated energy, and adhesion force maps.
2. Materials and Methods
2.1. 3D Printing
Specimens were printed using an Autodesk Ember 3D printer, which employs a 405 nm light source, in a bottom-up configuration (see Scheme 1). The resin employed (PR48, Autodesk) was placed on a poly(dimethylsiloxane) (PDMS)-covered glass tray (with a PDMS thickness of 2 mm) and cured layer by layer. The light intensity used was 18 mW/cm2 with an exposure time of 2.2 s for each layer; thus, the light irradiation dosage, E0, was 39.6 mJ/cm2 per one layer. The Ec and Dp values were 6.3 mJ/cm2 and 53 μm, respectively.25 Thus, based on eq 1, the cure depth, Cd, had a value of 97 μm. The programmed thickness of layers was 50 μm (the chosen build platform step value, z); thus, the manufacturing of consecutive layers occurred not only below the Cd value but also slightly below the Dp distance. The shape of the samples was designed by a commercial surface modeling software Rhinoceros 4 (Robert McNeel & Associates). The dimensions were as follows: length, 5 cm; width, 3 mm; and thickness, 0.6 mm.
The PR48 resin is composed of tetrafunctional alkoxylated pentaerythritol acrylate (Sartomer SR 494 LM, Arkema), in ∼40% by weight, ∼40% aliphatic urethane acrylate (Ebecryl 8210, Allnex; OH-functionalized urethane acrylate for dual cure application), and ∼20% monofunctional urethane acrylate (Genomer 1122, Rahn). All acrylates have a cross-linkable functional group but the Genomer 1122 works also as a diluent. The content of the photoinitiator (PL-TPO, Esstech) and UV blocker (OB plus, Mayzo) in the resin was ∼0.5% by weight in total. The exact resin composition, glass transition temperature of its components, as well as spectroscopic studies (FTIR, NMR) conducted for Ebecryl 8210 are shown in the Supporting Information. After printing, isopropanol was used to gently wash the samples to remove the remaining resin from the sample surface. Then, the samples were left for 2 days to complete the polymerization of unreacted double bonds.
2.2. Sample Preparation for AFM Imaging
To expose the bulk surface, samples were immersed in liquid nitrogen for 10 min and fractured using nippers. Thereafter, specimens were adhesive-fastened to an AFM sample holder using a two-component epoxy glue (RS 132-605 Structural Adhesive, RS Components, Ltd., U.K.) and left for 2 h to cure the adhesive. The quality of the sample surface was checked by optical microscopy (Olympus BX60, Japan).
2.3. AFM Quantitative Imaging
A Multimode 8 AFM retrofitted with a NanoScope V controller and a JV vertical engage scanner was used in this study (Bruker). Image processing and data analysis were conducted with the NanoScope (version 8.15) and NanoScope Analysis software (version 1.8), respectively. Measurements were performed in air at controlled temperatures (21 °C) and relative humidity (∼40%).
The peakforce quantitative nanomechanical mapping (PF-QNM) mode was used to quantitatively determine the surface distribution of Young’s modulus, dissipated energy, and adhesion forces using cantilevers with nominal spring constants of 42 N/m and a nominal tip apex radius of 8 nm (model NCH, NanoWorld, Switzerland).31 The PF-QNM mode enables capturing images essentially in the absence of lateral (shear) forces. The right choice of cantilever stiffness values was relevant to detect and capture both the cantilever deflection and the sample surface deformation to quantitatively determine the values of Young’s modulus and dissipated energy at each imaging pixel during raster scanning. The sensitivity of the AFM optical system was measured on silicon wafers as a rigid reference. Prior to sensitivity determination, the silicon wafers were ultrasonicated for 10 min in an acetone bath to remove particles and then treated by Piranha solution (20 min) to remove organic residues. The cantilever spring constant was determined by the thermal tune method.32,33 Values ranging from 26.3 to 30.5 N/m were obtained. Young’s modulus, dissipated energy, and adhesion force mapping were obtained by processing and evaluating force–distance curves collected pixel by pixel (256 pixels in 256 lines) following a sine-wave sample–tip trajectory with a frequency of 2 kHz and a peak-force amplitude value of 150 nm. The ScanAsyst panel was set to “individual” and then controlled by the AFM operator to minimize the influence of software auto-optimization (the feedback gain, the scan rate, and the z-scale range) on the data collected. Imaging settings were kept constant during one particular experiment. The typical feedback gain and peak-force setpoint values ranged between 20–25 and 50–500 nN, respectively. The raster scanning was made slow, i.e., the tip was raster scanned (while vibrating) over the sample surface at speeds less than 10 μm/s with the z-scale fixed at 5.6 μm.
Two approaches, including the Derjaguin, Muller, and Toporov (DMT) model of contact mechanics and the “relative modulus determination method,” were employed to quantify the surface stiffness.34−36 As a reference, we used polystyrene (PS; Aldrich, Mw ∼ 280 kg/mol) thin films. Reference samples were prepared by spin-coating (2000 rpm) of PS solutions (20 wt %, diluted in toluene) on Piranha-cleaned silicon wafer supports. For calibration, Young’s modulus value of PS was set at 2.7 GPa.37,38 The calibrated AFM is then used for imaging samples with unknown Young’s moduli. Scanning of the samples was conducted at similar indentation depths to keep the tip–sample contact area constant. The adhesion force was calculated as a difference between the baseline (no force acting part of the force–distance curve) and the snap-off point (the minimal point in the force–distance curve). The dissipated energy was determined by integrating the area between the “approach” and “withdrawal” sections of the force–distance curves. Corresponding dissipated energy values address the energy required to withdraw the tip from the surface (work of adhesion) as well as the energy that is lost during nonelastic deformations (e.g., viscoelasticity) when contact is established and broken.
3. Results and Discussion
3.1. Interface Morphology and Properties
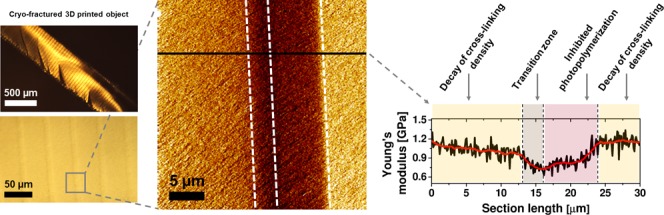
Optical microscopy imaging of the cryo-fractured samples reveals a flat rupture surface with some features attributed to traces of crack propagation formed during specimen preparation (see Figure 1a). Images at higher magnifications show striped features that depict the individual layers formed during printing (Figure 1b,c), as indicated. The distance between the stripes is approximately 50 μm, which is equal to the predetermined thickness value of the printed layers. The black square in Figure 1c represents the projected area studied by AFM and captured in Figure 1d–f. The arrow in Figure 1c indicates the direction of the light illumination in the 3D printing process.
Figure 1.
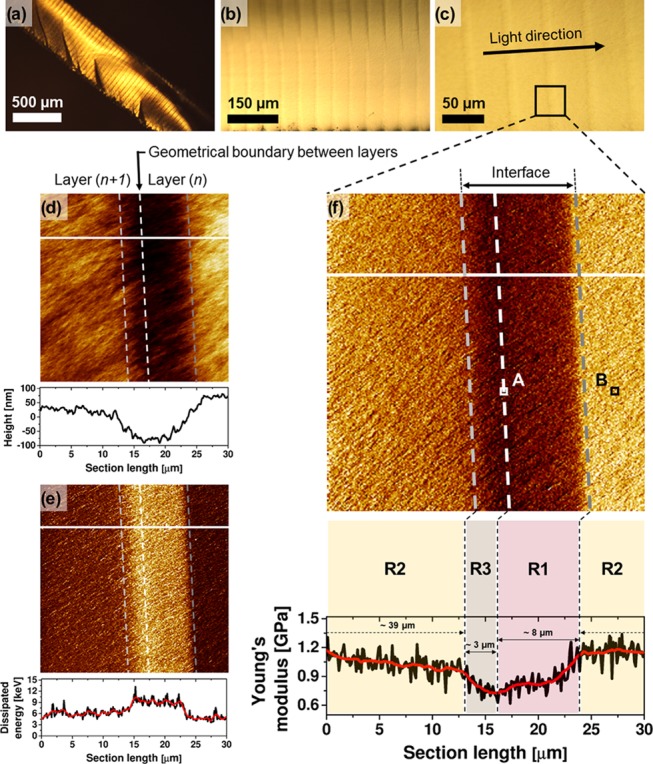
(a–c) Optical microscopy images of DLP-SLA cryo-fractured samples at different magnifications. The black square in (c) indicates the projected area in AFM analysis: quantitative AFM imaging of (d) height (color contrast encoded from 0 to 300 nm), (e) dissipated energy (color contrast encoded from 3 to 15 eV), and (f) Young’s modulus (color contrast encoded from 0.5 to 1.5 GPa) maps of the interface and its vicinity. The AFM cross sections are taken along the white lines and plotted below the maps; two profiles are smoothened (red curve) by the Savitzky–Golay method (points of window: 30, polynomial order: 2).39 The areas in AFM images are divided into three regions: R1, R2, and R3. The R1 and R3 regions form the interface. The R1/R3 borderline (white, dashed) represents a geometrical boundary at which the layer (n) starts to be cured, as the first, and the layer (n + 1) is completed and attached to the layer (n), as the next. The squares marked as A and B (in f) indicate the projected area for high-resolution quantitative AFM imaging shown in Figure 2. The indentation depth map, related to (f), is shown in the Supporting Information.
Quantitative AFM images of height, dissipated energy, and Young’s modulus values are shown in Figures 1d–f with the corresponding cross-section plots. Auxiliary analyses performed in the PF-QNM mode but also in a tapping mode AFM are presented in the Supporting Information, along with the results of the swelling test.
For the discussion, we divided the areas in the AFM images (Figure 1d–f) into three regions, R1, R2, and R3, encompassing domains of different mechanical properties. The R1 and R3 regions define the interface formed in consecutive layer printing, being a part of the layer (n) and a part of the layer (n + 1), as indicated in Figure 1d,f. The step height, z, of the printed object is associated with the R1/R3 borderline. Simply, this is a geometrical boundary where the layer (n) starts to be cured, whereas the layer (n + 1) is attached to it, when curing of the layer (n + 1) is completed.
In all images, the interface is clearly visible, manifested by nearly vertical stripes with an intense, contrasted color. The height profile (cross-section plot in Figure 1d) shows a depression up to ∼150 nm at the interface. The uneven cross section arises from the way samples are prepared during cryo-fracturing. A heterogeneous stress distribution is generated arising from the dissimilar thermal expansion of the layers with different cross-link density (thus different stiffness) values. Once the sample was brought to room temperature after cryo-fracturing, stress is released, which results in the observed cross-sectional profile.
Energy dissipation maps (Figure 1e) clearly show a steep change at the interface, i.e., a 50–60% increase in energy loss. This change indicates variations in the work of adhesion and viscoelastic energy loss.
In the Young’s modulus map, the regions reveal a characteristic trend of the elasticity, i.e., R1—a moderate increase, R2—a smooth decay, and R3—a moderate decrease. For the subsequent discussion, let us first focus on the R1 region, which is light-illuminated in the printing process as first. Although the samples were printed in the bottom-up configuration, where the access of atmospheric oxygen is much limited compared to the top-down configuration, the PDMS-containing vat widow (in the printer used) is a noticeable source of oxygen.40,41 Prior to printing, PDMS is saturated with oxygen according to its solubility. Thereafter, the PDMS serves an oxygen reservoir that can pump the oxygen into a resin. The concentration of the oxygen in the 2 mm-thick PDMS is high enough to prevent printed layers from being stacked to the window. Zhao et al. have shown that the oxygen concentration at the PDMS surface, [O2]0, can be as high as 1 mM.19 During printing, when dissolved oxygen is being consumed, PDMS is “reoxygenated” through the diffusion of oxygen from the resin into the window. The printing process is slow enough (approx. 10 seconds from one layer to another; approx. 2.5 h for a sample) for the oxygen molecules from the resin to be diffused in the PDMS (the oxygen diffusion coefficient is 3.4 × 10–9 m2/s).19,42 This means that the oxygen in the PDMS can be refilled efficiently during the layer printing time. As a result, inhibited photopolymerization leads to an undercured and tacky surface of the printed layer.18,43 This feature is actually beneficial for the interfacial bridging of layer-to-layer structures, and thus for the building process, because a defined layer provides tacky lubrication to a next layer.
Inhibited photopolymerization takes place in a defined space of the layer. The size effects in photopolymers, where the inhibited photocuring occurs, have been of scientific interest both in experiments and in modeling studies.19,20,30,44,45 For instance, O’Brien and Bowman modeled a system of 50-μm-thick diacrylate-based cured films that were exposed to oxygen (at [O2]0 = 1 mM) at the top surface.20 They showed that the top 15 μm of the film revealed negligible double-bond conversion (below ∼ 0.1). Importantly, for further penetration into the film beyond the 15 μm of the thickness, the double-bond conversion showed a sharp transition as a function of the film depth to possess values above ∼0.6, resulting in material solidification.46 Similar results were shown recently by Yin et al. in the SLA manufacturing of diacrylate-based resin in an oxygen-controlled setup.30 For instance, for the light irradiation dosage of 44 mJ/m2, the authors demonstrated that the value of the double-bond conversion drops from ∼0.4 to below ∼0.1 at the top 10 μm of the layer thickness. Also, these authors used a PDMS film as the source of oxygen ([O2]0 = 0.35 mM).
Within the R1 region, Young’s modulus shows a moderate increase; thereafter, it gains a stable value on crossing the R1/R2 borderline. We associate these features, observed in Young’s modulus profile, with the inhibited photopolymerization that occurs in the initial part of the defined layer and estimated the R1 region thickness to be ∼8 μm, as indicated in the cross-section plot. One should realize also that Young’s modulus analysis is conducted on a part of a sample that, in fact, received several light irradiation flashes. Practically, however, only two illumination shots were able to cure the R1 region, namely, the light irradiation dosage projected directly to the defined layer and the light irradiation dosage projected thereafter on the next layer. The third light irradiation dosage is rather not able to cure in R1 region, since the cure depth, Cd, is 97 μm, whereas the layer thickness, z, is 50 μm. By the same token, regions R2 and R3 were also irradiated (effectively) twice.
In the R2 region, Young’s modulus decays smoothly across the layer (for the full layer thickness, see Figure S6 in the Supporting Information). The light irradiation intensity decays as it passes through the layer in which it is absorbed, leading to a variation in the curing effect (cross-linking density).1,23 Across the length of the R2 region, i.e., ∼39 μm, Young’s modulus decreases from ∼1.2 MPa (R1/R2 borderline) to ∼1.0 MPa (R2/R3 borderline), corresponding to ∼17%.
The moderate decrease of Young’s modulus observed in the R3 region is relevant for building the interfacial strength. The R3 region represents a “transition” zone between the highly cured R2 region and the R1 region that experienced “weaker” curing. Along the relatively low thickness (∼3 μm) of the R3 region, the modulus drops by about ∼25% (1.0–0.75 MPa) (Figure 1f). After the light irradiation is completed, the platform built is withdrawn (and glided aside) from the PDMS surface to allow the resin to fill up space and flow underneath the solidified layer. When the resin is brought in contact with the layer, the unreacted double bonds of the layer can act as bridging sites (contribution to interfacial reactions). Moreover, the photoinitiator can also diffuse from the resin into the R1 region of the layer to further support its curing (acceleration of the double-bond conversion).19 Once the next light illumination flash is provided, the previously and subsequently obtained layers form a stable junction with a stiffness gradient, as this can be observed in Young’s modulus cross-section profile.
To study the R3 region in more detail, we analyzed its structure–property relationships in the vicinity of the minimum surface stiffness (white square—location A in Figure 1f) as shown in Figure 2a,c. For comparison, we also show and discuss data collected at the maximum of the surface stiffness (black square—location B in Figure 1f) in Figure 2b,d.
Figure 2.
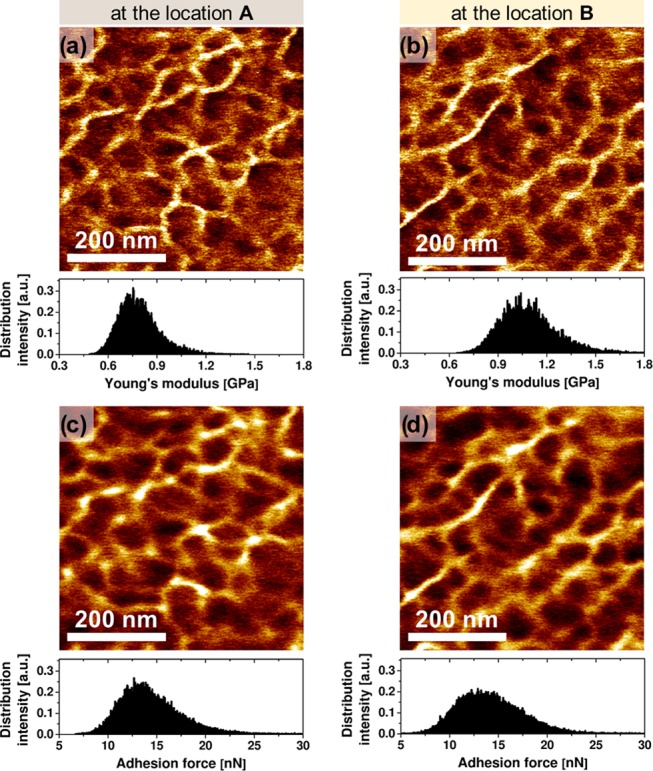
Quantitative AFM imaging: (a, b) Young’s modulus and (c, d) adhesion force maps at location A (a, c) and location B (b, d), as indicated in Figure 1f. The corresponding distributions of Young’s moduli and adhesion force (per image) are shown as histograms. The indentation depth maps, related to (a) and (b), are shown in the Supporting Information.
3.2. Structure and Mechanical Performance at the Nanoscale
One of the strongest advantages of the PF-QNM imaging is the possibility to image structure and morphology with nanoscale resolution, and it also simultaneously determines the mechanical performance of the features imaged.35,36 In our case, the printed material studied possesses a complex molecular architecture due to the presence of three acrylates. Additionally, two acrylate components are urethane based (Ebecryl 8210, Genomer 1122).
Figure 2 shows high-resolution Young’s modulus and adhesion force maps collected near the softest point at the interface, and in the stiff, bulk layer part, respectively (locations A and B shown in Figure 1f). Both surfaces unveil similar features in stiffness and adherence maps. To ensure that the surface profile variation has a limited effect on the observed morphology and measured mechanical properties, we performed a cross-correlation analysis (Supporting Information). The similarities of the nanoscale morphology indicate that while there are quantitative differences in the modulus values in all regions (R1, R2, and R3) related to differences in illumination times and cross-link characteristics, the molecular structure of the cross-linked network essentially remains the same.
The arithmetic averages of moduli values are 0.8 ± 0.1 and 1.1 ± 0.2 GPa for the maps collected at the locations A and B, respectively (Figure 2a,b). The arithmetic averages of adhesion force values are 14.3 ± 2.9 and 14.1 ± 3.1 nN for the maps collected at the same A and B locations, respectively. Again, one may conclude that since adhesion force remains constant across the surface regions imaged, the surface chemical composition essentially does not vary (constant submicron phase morphology). Thus, we can formulate a very important statement that the variation of cross-link density, causing local stiffness variations, is the main factor determining the nanomechanics of the interface and its vicinity.
4. Conclusions
Three-dimensional printed photopolymer interfaces between consecutively prepared layers were studied by AFM PeakForce Quantitative Nanomechanical Mapping from submicron to micrometer length scales. Cross-sectional maps of the Young’s modulus values unveil variations in mechanical performance between successively printed layers, attributed to differences in network cross-link density. The interface reveals changes in the elastic properties originating from oxygen-inhibited photopolymerization and bridging between the consecutive layers. The samples show smooth variations between regions of different stiffness but with the same chemical composition. Our work presents additional insights in the field of 3D printing in the bottom-up configuration because it quantifies the loss of Young’s modulus at the interface and its vicinity for objects obtained using optimum printing parameters. Our results provide a route to derive essential design parameters and show how interface performance should be quantitatively analyzed at the nanoscale to achieve better product performance. At this point, to improve the mechanical stability of the 3D printed objects, we would suggest to limit the oxygen concentration at the PDMS surface to reduce the width of the R1 region. We focused in this work on the relative differences in the contact elasticity across the interface. However, to improve the estimation of the values of Young’s modulus, a standardized methodology in AFM quantitative imaging based on the SNAP protocol can also be considered.47
Acknowledgments
All authors acknowledge the University of Twente for funding. H.G. and W.G. acknowledge support from the Polish Ministry of Science and Higher Education. H.G. acknowledges the Polish National Science Centre for support within the program Miniatura no. 2017/01/X/ST5/00374.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.9b22272.
Chemical structures of the resin and its composition; experimental data: (1) DSC (resin and its individual polymer components), (2) NMR and FTIR of the Ebecryl 8210, (3) swelling test in five solvents, (4) AFM PF-QNM mode indentation depth maps, (5) AFM tapping mode image of the interface and its vicinity, (6) AFM PF-QNM mode height images and cross-correlation analysis (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Melchels F. P.; Feijen J.; Grijpma D. W. A Review on Stereolithography and Its Applications in Biomedical Engineering. Biomaterials 2010, 31, 6121–6130. 10.1016/j.biomaterials.2010.04.050. [DOI] [PubMed] [Google Scholar]
- Schüller-Ravoo S.; Feijen J.; Grijpma D. W. Preparation of Flexible and Elastic Poly(Trimethylene Carbonate) Structures by Stereolithography. Macromol. Biosci. 2011, 11, 1662–1671. 10.1002/mabi.201100203. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Xiao P. 3D Printing of Photopolymers. Polym. Chem. 2018, 9, 1530–1540. 10.1039/C8PY00157J. [DOI] [Google Scholar]
- Truby R. L.; Lewis J. A. Printing Soft Matter in Three Dimensions. Nature 2016, 540, 371–378. 10.1038/nature21003. [DOI] [PubMed] [Google Scholar]
- Stansbury J. W.; Idacavage M. J. 3D Printing with Polymers: Challenges among Expanding Options and Opportunities. Dent. Mater. 2016, 32, 54–64. 10.1016/j.dental.2015.09.018. [DOI] [PubMed] [Google Scholar]
- Bose S.; Vahabzadeh S.; Bandyopadhyay A. Bone Tissue Engineering Using 3D Printing. Mater. Today 2013, 16, 496–504. 10.1016/j.mattod.2013.11.017. [DOI] [Google Scholar]
- Guvendiren M.; Molde J.; Soares R. M. D.; Kohn J. Designing Biomaterials for 3D Printing. ACS Biomater. Sci. Eng. 2016, 2, 1679–1693. 10.1021/acsbiomaterials.6b00121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do A. V.; Khorsand B.; Geary S. M.; Salem A. K. 3D Printing of Scaffolds for Tissue Regeneration Applications. Adv. Healthcare Mater. 2015, 4, 1742–1762. 10.1002/adhm.201500168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi J. W.; Kim N. Clinical Application of Three-Dimensional Printing Technology in Craniofacial Plastic Surgery. Arch. Plast. Surg. 2015, 42, 267–277. 10.5999/aps.2015.42.3.267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X.; Jiang M.; Zhou Z.; Gou J.; Hui D. 3D Printing of Polymer Matrix Composites: A Review and Prospective. Composites, Part B 2017, 110, 442–458. 10.1016/j.compositesb.2016.11.034. [DOI] [Google Scholar]
- Postiglione G.; Natale G.; Griffini G.; Levi M.; Turri S. Conductive 3D Microstructures by Direct 3D Printing of Polymer/Carbon Nanotube Nanocomposites via Liquid Deposition Modeling. Composites, Part A 2015, 76, 110–114. 10.1016/j.compositesa.2015.05.014. [DOI] [Google Scholar]
- Espalin D.; Muse D. W.; MacDonald E.; Wicker R. B. 3D Printing Multifunctionality: Structures with Electronics. Int. J. Adv. Manuf. Technol. 2014, 72, 963–978. 10.1007/s00170-014-5717-7. [DOI] [Google Scholar]
- Huber C.; Abert C.; Bruckner F.; Groenefeld M.; Muthsam O.; Schuschnigg S.; Sirak K.; Thanhoffer R.; Teliban I.; Vogler C.; Windl R.; Suess D. 3D Print of Polymer Bonded Rare-Earth Magnets, and 3D Magnetic Field Scanning with an End-User 3D Printer. Appl. Phys. Lett. 2016, 109, 162401 10.1063/1.4964856. [DOI] [Google Scholar]
- Lin C. Y.; Kikuchi N.; Hollister S. J. A Novel Method for Biomaterial Scaffold Internal Architecture Design to Match Bone Elastic Properties with Desired Porosity. J. Biomech. 2004, 37, 623–636. 10.1016/j.jbiomech.2003.09.029. [DOI] [PubMed] [Google Scholar]
- Melchels F. P. W.; Bertoldi K.; Gabbrielli R.; Velders A. H.; Feijen J.; Grijpma D. W. Mathematically Defined Tissue Engineering Scaffold Architectures Prepared by Stereolithography. Biomaterials 2010, 31, 6909–6916. 10.1016/j.biomaterials.2010.05.068. [DOI] [PubMed] [Google Scholar]
- Santoliquido O.; Colombo P.; Ortona A. Additive Manufacturing of Ceramic Components by Digital Light Processing: A Comparison between the “Bottom-up” and the “Top-Down” Approaches. J. Eur. Ceram. Soc. 2019, 39, 2140–2148. 10.1016/j.jeurceramsoc.2019.01.044. [DOI] [Google Scholar]
- Mondschein R. J.; Kanitkar A.; Williams C. B.; Verbridge S. S.; Long T. E. Polymer Structure-Property Requirements for Stereolithographic 3D Printing of Soft Tissue Engineering Scaffolds. Biomaterials 2017, 140, 170–188. 10.1016/j.biomaterials.2017.06.005. [DOI] [PubMed] [Google Scholar]
- Ligon S. C.; Husár B.; Wutzel H.; Holman R.; Liska R. Strategies to Reduce Oxygen Inhibition in Photoinduced Polymerization. Chem. Rev. 2014, 114, 557–589. 10.1021/cr3005197. [DOI] [PubMed] [Google Scholar]
- Zhao Z.; Mu X.; Wu J.; Qi H. J.; Fang D. Effects of Oxygen on Interfacial Strength of Incremental Forming of Materials by Photopolymerization. Extreme Mech. Lett. 2016, 9, 108–118. 10.1016/j.eml.2016.05.012. [DOI] [Google Scholar]
- O’Brien A. K.; Bowman C. N. Modeling the Effect of Oxygen on Photopolymerization Kinetics. Macromol. Theory Simul. 2006, 15, 176–182. 10.1002/mats.200500056. [DOI] [Google Scholar]
- Jariwala A. S.; Ding F.; Boddapati A.; Breedveld V.; Grover M. A.; Henderson C. L.; Rosen D. W. Modeling Effects of Oxygen Inhibition in Mask-Based Stereolithography. Rapid Prototyping J. 2011, 17, 168–175. 10.1108/13552541111124734. [DOI] [Google Scholar]
- Tumbleston J. R.; Shirvanyants D.; Ermoshkin N.; Janusziewicz R.; Johnson A. R.; Kelly D.; Chen K.; Pinschmidt R.; Rolland J. P.; Ermoshkin A.; Samulski E. T.; DeSimone J. M. Continuous Liquid Interface Production of 3D Objects. Science 2015, 347, 1349–1352. 10.1126/science.aaa2397. [DOI] [PubMed] [Google Scholar]
- Hofstetter C.; Orman S.; Baudis S.; Stampfl J. Combining Cure Depth and Cure Degree, a New Way to Fully Characterize Novel Photopolymers. Addit. Manuf. 2018, 24, 166–172. 10.1016/j.addma.2018.09.025. [DOI] [Google Scholar]
- Ligon S. C.; Liska R.; Stampfl J.; Gurr M.; Mülhaupt R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. 10.1021/acs.chemrev.7b00074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett J. Measuring UV Curing Parameters of Commercial Photopolymers Used in Additive Manufacturing. Addit. Manuf. 2017, 18, 203–212. 10.1016/j.addma.2017.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Bochove B.; Hannink G.; Buma P.; Grijpma D. W. Preparation of Designed Poly(Trimethylene Carbonate) Meniscus Implants by Stereolithography: Challenges in Stereolithography. Macromol. Biosci. 2016, 16, 1853–1863. 10.1002/mabi.201600290. [DOI] [PubMed] [Google Scholar]
- Jacobs P. F.; Reid D. T.. Rapid Prototyping & Manufacturing: Fundamentals of Stereolithography; Society of Manufacturing Engineers, 1992. [Google Scholar]
- Gebhardt A.Rapid Prototyping; Hanser Publishers, 2003. [Google Scholar]
- Ligon-Auer S. C.; Schwentenwein M.; Gorsche C.; Stampfl J.; Liska R. Toughening of Photo-Curable Polymer Networks: A Review. Polym. Chem. 2016, 7, 257–286. 10.1039/C5PY01631B. [DOI] [Google Scholar]
- Yin H.; Ding Y.; Zhai Y.; Tan W.; Yin X. Orthogonal Programming of Heterogeneous Micro-Mechano-Environments and Geometries in Three-Dimensional Bio-Stereolithography. Nat. Commun. 2018, 9, 4096 10.1038/s41467-018-06685-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruker Peakforce QNM User Guide, version 004-1036-000; 2011.
- Hutter J. L.; Bechhoefer J. Calibration of Atomic-Force Microscope Tips. Rev. Sci. Instrum. 1993, 64, 1868–1873. 10.1063/1.1143970. [DOI] [Google Scholar]
- Sader J. E.; Larson I.; Mulvaney P.; White L. R. Method for the Calibration of Atomic Force Microscope Cantilevers. Rev. Sci. Instrum. 1995, 66, 3789–3798. 10.1063/1.1145439. [DOI] [Google Scholar]
- Derjaguin B. V.; Muller V. M.; Toporov Y. P. Effect of Contact Deformations on the Adhesion of Particles. J. Colloid Interface Sci. 1975, 53, 314–326. 10.1016/0021-9797(75)90018-1. [DOI] [Google Scholar]
- Gojzewski H.; Imre B.; Check C.; Chartoff R.; Vancso G. J. Mechanical Mapping and Morphology across the Length Scales Unveil Structure–Property Relationships in Polycaprolactone Based Polyurethanes. J. Polym. Sci., Part B: Polym. Phys. 2016, 54, 2298–2310. 10.1002/polb.24140. [DOI] [Google Scholar]
- Gojzewski H.; Obszarska J.; Harlay A.; Hempenius M. A.; Vancso G. J. Designer Poly(Urea-Siloxane) Microspheres with Controlled Modulus and Size: Synthesis, Morphology, and Nanoscale Stiffness by AFM. Polymer 2018, 150, 289–300. 10.1016/j.polymer.2018.07.034. [DOI] [Google Scholar]
- Kocun M.; Labuda A.; Meinhold W.; Revenko I.; Proksch R. Fast, High Resolution, and Wide Modulus Range Nanomechanical Mapping with Bimodal Tapping Mode. ACS Nano 2017, 11, 10097–10105. 10.1021/acsnano.7b04530. [DOI] [PubMed] [Google Scholar]
- Miyake K.; Satomi N.; Sasaki S. Elastic Modulus of Polystyrene Film from near Surface to Bulk Measured by Nanoindentation Using Atomic Force Microscopy. Appl. Phys. Lett. 2006, 89, 031925 10.1063/1.2234648. [DOI] [Google Scholar]
- Luo J.; Ying K.; Bai J. Savitzky–Golay Smoothing and Differentiation Filter for Even Number Data. Signal Process. 2005, 85, 1429–1434. 10.1016/j.sigpro.2005.02.002. [DOI] [Google Scholar]
- Dendukuri D.; Panda P.; Haghgooie R.; Kim J. M.; Hatton T. A.; Doyle P. S. Modeling of Oxygen-Inhibited Free Radical Photopolymerization in a PDMS Microfluidic Device. Macromolecules 2008, 41, 8547–8556. 10.1021/ma801219w. [DOI] [Google Scholar]
- Jeong H. E.; Suh K. Y. On the Role of Oxygen in Fabricating Microfluidic Channels with Ultraviolet Curable Materials. Lab Chip 2008, 8, 1787–1792. 10.1039/b810348h. [DOI] [PubMed] [Google Scholar]
- Merkel T. C.; Bondar V. I.; Nagai K.; Freeman B. D.; Pinnau I. Gas Sorption, Diffusion, and Permeation in Poly(Dimethylsiloxane). J. Polym. Sci. B 2000, 38, 415–434. . [DOI] [Google Scholar]
- Decker C. Kinetic Study and New Applications of UV Radiation Curing. Macromol. Rapid Commun. 2002, 23, 1067–1093. 10.1002/marc.200290014. [DOI] [Google Scholar]
- O’Brien A. K.; Bowman C. N. Impact of Oxygen on Photopolymerization Kinetics and Polymer Structure. Macromolecules 2006, 39, 2501–2506. 10.1021/ma051863l. [DOI] [Google Scholar]
- Shim T. S.; Yang S. M.; Kim S. H. Dynamic Designing of Microstructures by Chemical Gradient-Mediated Growth. Nat. Commun. 2015, 6, 6584 10.1038/ncomms7584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boddapati A.; Rahane S. B.; Slopek R. P.; Breedveld V.; Henderson C. L.; Grover M. A. Gel Time Prediction of Multifunctional Acrylates Using a Kinetics Model. Polymer 2011, 52, 866–873. 10.1016/j.polymer.2010.12.024. [DOI] [Google Scholar]
- Schillers H.; Rianna C.; Schäpe J.; Luque T.; Doschke H.; Wälte M.; Uriarte J. J.; Campillo N.; Michanetzis G. P. A.; Bobrowska J.; Dumitru A.; Herruzo E. T.; Bovio S.; Parot P.; Galluzzi M.; Podestà A.; Puricelli L.; Scheuring S.; Missirlis Y.; Garcia R.; Odorico M.; Teulon J. M.; Lafont F.; Lekka M.; Rico F.; Rigato A.; Pellequer J. L.; Oberleithner H.; Navajas D.; Radmacher M. Standardized Nanomechanical Atomic Force Microscopy Procedure (SNAP) for Measuring Soft and Biological Samples. Sci. Rep. 2017, 7, 5117 10.1038/s41598-017-05383-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


