Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Feb 10;5(6):2718–2724. doi: 10.1021/acsomega.9b03287

Detachment Behavior of Single-Curved/NonCurved Particles from Ultrasound-Assisted Oscillation Bubbles

Guangxi Ma 1, Wencheng Xia 1,*
PMCID: PMC7033661  PMID: 32095695

Abstract

graphic file with name ao9b03287_0009.jpg

Detachment behavior of single glass particle with the same mass but different shapes from an oscillation bubble driven by the ultrasound energy was investigated. The maximum acceleration of particle motion was calculated based on the oscillation of the bubble bottom point. The maximum acceleration increases with the increasing ultrasonic amplitude. Curved (cylindrical and sphere) particles attach onto the bubble mostly by the curved surface, while noncurved (cube and triangular prism) particles attach onto the bubble mostly by the plane surface. The detachment of noncurved particles requires a larger ultrasonic amplitude than that of the curved particles, whereas a larger ultrasonic amplitude means a larger driving force for the oscillation of the bubble. The detachment force of noncurved particles from the bubble is higher than that of curved particles because of the presence of larger contact areas between noncurved particles and the bubble as well as the sharp edge of noncurved particles, which provides the stable attachment.

1. Introduction

Flotation is a method for upgrading the fine ore and plays an important role in mineral processing. The capture of mineral particles by rising bubbles is a prerequisite for the flotation process. Moreover, the stability of bubble-particle aggregates also plays a significant role in the flotation efficiency. Flotation is a complex process and affected by many parameters.1 The properties of floating particles, flotation devices, and work conditions are the main factors affecting flotation efficiency. The surface morphology of particles, including the size, shape, roughness, crystal structure, and functional group, is the essence to determine its floatability. Several studies have reported that the particle shape characteristic of various minerals plays an important role in the flotation process (Table 1). In general, sharp edges contribute to the quick thinning and rupturing of the water film between the particle and bubble.2 Therefore, mineral particles with irregular shapes generally have higher flotation recovery and flotation rates in comparison with regularly shaped particles. It is noted that most ground or crushed minerals are irregular particles. It is challenging to investigate the influence of particle shape on flotation independently because of the angular shapes and roughness of irregular particles. It is vital to investigate the effect of regular-shaped particles, such as sphere, quadrate, ellipse, triangle, and others on the flotation, especially for the ideal attachment and detachment between the regular shaped particle and the bubble.3 Szczerkowska4 used regular-shaped particles (circular, equilateral triangular, and square platelets), which were stamped from the 1 mm thick polystyrene sheet, to study the influence of particle shape on the flotation. It was found that the flotation kinetics was the slowest for circular platelets.

Table 1. Effect of Particle Shape on Flotation.

type of mineral methods of producing the shaped particles effect on flotation behavior references
coal crusher and roll mills the particle with a larger elongation ratio had a higher flotation recovery (5)
  anthracite coal with the same ash content particles with higher roundness floated slower (6)
magnetite rod and ball mills flotation recovery increased with the increase of elongation ratio (7)
glass beads ball, rod, and autogenous mills elongated and smooth particles had lower wettability characteristics values and more hydrophobicity (8)
  rod and ball mills particles with higher elongation indicated a higher floatability (9)
  rod mills and spherical ballotini ground ballotini generally had higher flotation rates than spherical ballotini (2)
  micron-milled glass fibres and glass beads particles with a larger elongation ratio had the larger contact line and area (10)
  ceramic ball mills and spherical glass particles sharp edges of ground particles trigger film rupture and shorten the attachment time (11)
  ground particles and spherical glass beads larger detachment forces were needed for ground quartz particles than spherical glass beads (12)
  high-speed universal grinder and spherical glass beads the BPA of glass fragments was larger than that of glass beads (13)
polystyrene platelets circular, square and triangular stamped from the PS sheet the flotation kinetics was the slowest for circular platelets, and then increased with a decrease in the surface ratio (4)
plastic six types of granulated plastics Lamellar particles exhibited better floatability than round ones (14)
ink spherical or disc-shaped ink particles the irregularly shaped ink particles did not attach to bubbles as readily as spherical particles (15)
Open in a new tab

Coarse particles usually have high collision efficiency in the flotation. However, the flotation recovery of coarse particles is poor, which is mainly caused by the easier detachment of coarse particles from bubbles.16−18 Therefore, the detachment is important in mineral flotation, especially for the flotation of coarse particles. After the collision and attachment, the bubble-particle aggregate is formed. Yoon and Mao19 pointed out that the particle detached from the bubble when the kinetic energy is larger than the work of adhesion and the energy barrier. Goel20 observed the behavior of particle-laden bubbles in the turbulent shear flow near a rotating impeller in a flotation cell. The results showed that fractional detachment of particles was related to the mechanical energy dissipation rate in the region of the impeller. In the flotation process, the attachment force, including the capillary force, buoyancy force of the particle, and pressure force on the particle, maintains the stability of bubble-particle aggregates. The detaching force, including the weight of particle and external force, tends to detach the particle from the bubble surface.21 The ratio of inertial force to the capillary force was expressed as the Bond number (Bo) to evaluate the stability of bubble particle aggregates, which was only used to describe the two-phase system. The modified Bond number (Bo*) proposed by Schulze, the ratio of the magnitude of all the detaching force to all of the attaching force, to commonly describe the stability of bubble-particle aggregates in the multiphase flotation system.22 If Bo* > 1, the particle will detach from the bubble surface. Otherwise, if Bo* < 1, the bubble-particle aggregate will remain stable.

The detachment of particles forming bubbles in a turbulent vortex was observed by Wang.23 The bubble-particle aggregate was forced to make a centrifugal movement. When the radial centripetal force induced by the rotation is sufficiently high, the particle detached from the bubble surface. Oscillation of bubble-particle aggregate caused by acoustic vibration was studied by Holtham and Cheng.24 They found that the amplitude of oscillations played a vital role in the detachment. The detachment of coarse particles from oscillating bubbles was studied by Xu12 and Awatey.25 The detachment force is mainly determined by the dynamic contact angle. The larger detachment forces were observed for the irregular quartz particles compared to that of the spherical glass beads. This method assumed that the movement of the bubble was the same as that of the loudspeaker. However, the deformation and the elasticity of the bubble should also be considered. In our previous work, the projected area of a fixed unloaded bubble under ultrasonic treatment is similar to a harmonic wave. The irregular glass fragments have a larger bubble-particle attachment angle and higher cumulative flotation recovery than that of spherical glass beads.

In this study, to investigate the detachment of a single regular-shaped particle from the bubble, regular-shaped glass particles (cube, triangular prism, cylindrical, and sphere) were designed and manufactured. Moreover, combined with the ultrasonic treatment, the effect of particle shape on the detachment behavior of a single glass particle under ultrasound-assisted oscillation forces was investigated.

2. Results and Discussion

2.1. Movement of Bubble Bottom under Ultrasonic-Assisted Treatment

Ultrasonic waves are longitudinal waves and rely on the vibration of the surrounding medium to propagate. In the water cell, the bubble is treated by the vibration of the surrounding water to oscillate. The single particle attaches onto the bubble bottom and moves with the bubble bottom. Therefore, the motion of the bubble bottom point is chosen to analyze first. The outline profile of the bubble is determined by the built-in Canny edge detection method supported by the edge function in the Image Analysis Toolbox of MATLAB software. As shown in Figure 1, the motion of the bubble bottom point could be described as a simple harmonic motion under ultrasound-assisted treatment. Furthermore, the larger oscillation amplitude of the bubble bottom point was obtained under the larger amplitude of ultrasound. The motion results of the bubble bottom point were fitted by MATLAB software and given by eq 1. There are some clear asymmetry parts in the motion of the bubble bottom. This asymmetry is the response of an anchored bubble where the effect of the needle will always be there. Therefore, the determination coefficient (R2) of fit all was more than 0.80, which was acceptable.

2.1. 1

where the A is the oscillation amplitude of the bubble bottom, ω is the angular frequency, ω is the time, and δ is the phase of the oscillation.

Figure 1.

Figure 1

Open in a new tab

Motion of the bubble bottom point with different ultrasonic amplitudes (a), ultrasonic amplitude of 22.8 μm; (b) ultrasonic amplitude of 34.2 μm; (c) ultrasonic amplitude of 45.6 μm; (d) ultrasonic amplitude of 57.0 μm; (e) ultrasonic amplitude of 68.4 μm).

The calculated results of eq 1 are shown in Table 2. The oscillation amplitude (A) of the bubble bottom increased significantly with the increasing ultrasonic amplitude. Besides, oscillation frequency (f = ω/2π) and angular frequency (ω) were maintained at a particular value accompanied by some fluctuations. The fluctuations of bubble oscillation frequency occurred at a constant ultrasonic frequency of 20 kHz because of the effect of the needle on the anchored bubble.

Table 2. Calculated Results of eq 1 under Different Ultrasonic Amplitudes.

amplitude at prove tip (μm) A (mm) ω (rad/ms) δ R2
22.8 0.046 1.549 0.0269 0.9319
34.2 0.115 1.708 0.3659 0.8689
45.6 0.181 1.669 –0.2336 0.8036
57.0 0.242 1.664 0.2479 0.8485
68.4 0.366 1.644 0.0168 0.8651
Open in a new tab

The acceleration of oscillation and the maximum acceleration of oscillation could be described by eqs 2 and 3, respectively.

2.1. 2
2.1. 3

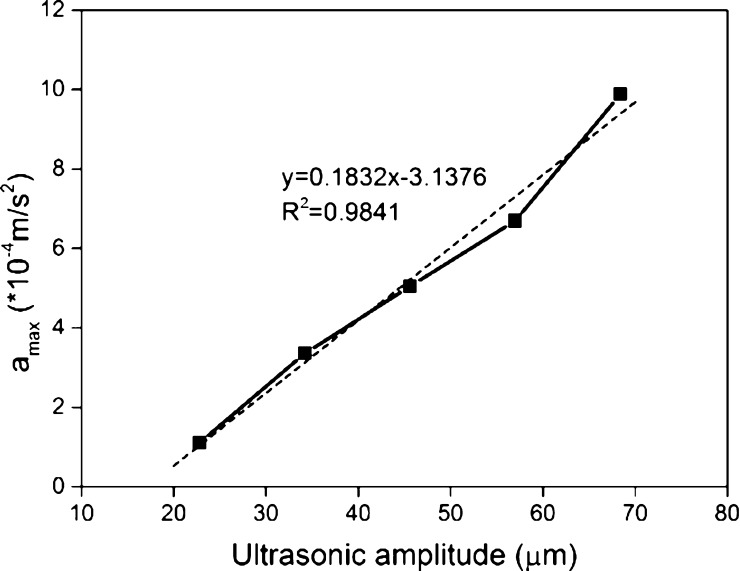
Figure 2 illustrates the maximum acceleration of the oscillation of the bubble bottom point under different ultrasonic amplitudes. The maximum acceleration of oscillation increased with the increasing ultrasonic amplitude. Moreover, there was a linear relationship between maximum acceleration and ultrasonic amplitude. In addition, when the ultrasonic amplitude was beyond 68.4 μm, the bubble would collapse because of excessive oscillation intensity. In general, a larger ultrasonic amplitude means a larger driving force for the oscillation of the bubble.

Figure 2.

Figure 2

Open in a new tab

Maximum acceleration of oscillation of bubble bottom under different ultrasonic amplitudes.

2.2. Detachment Behavior of the Single Particle from the Bubble

As can be seen from Figure 3, the contact line and area between the bubble and single particle with different shapes could be obtained (only the representative pictures were shown). The contact line of the cube, triangular prism, and the cylindrical particle is larger than that of the sphere particle. Besides, the side surface of the cylindrical is curved. Therefore, compare with the plane surfaces of the cube and triangular prism particle, the contact area of the cylindrical particle is also relatively smaller.

Figure 3.

Figure 3

Open in a new tab

Images of contact line between the bubble and particle.

Typical images are chosen in Figure 4 to illustrate the behavior of differently shaped particles detaching from a fixed bubble. In the beginning, the contact area of the bubble and the particle is mainly the plane surface or the curved surface of the particle. The addition of the ultrasound-assisted treatment drives the partly plane surface or the curved surface of the particle away from the bubble. With the more surface of particle detaching from the bubble, the contact area between the bubble and particle changed from the plane surface to the edge or vertex of particle. After this, the particle detaches from the bubble surface easily. Therefore, the energy and force driving the particle bubble contacting surface becoming zero is the energy barrier of bubble-particle detachment.

Figure 4.

Figure 4

Open in a new tab

Detachment behavior of the particle from the bubble.

2.3. Required Ultrasonic Amplitude for Glass Particle Detachment

Figure 5 illustrates the results of the required ultrasonic amplitude for glass-particle detachment with or without the addition of the collector. As shown in Figure 5a, without the addition of the collector, the average required ultrasonic amplitude of cube and triangular prism particles was 35.3 and 30.8 μm, respectively. However, the possibility of cylindrical and sphere particles detaching from the bubble under 22.8 μm ultrasonic amplitude was 100%, which indicated that the required detachment force of cylindrical and sphere particles from the bubble surface was smaller than that of cube and triangular prism particles. Therefore, the average required ultrasonic amplitude of cylindrical and sphere particles was considered as 22.8 μm.

Figure 5.

Figure 5

Open in a new tab

Required ultrasonic amplitude for detachment of particle from the bubble surface.

The addition of the collector improved the floatability of the glass particles, increasing the bubble-particle attachment strength. Figure 5b,c indicates that the required ultrasonic amplitude for the detachment of particles from the bubble surface increased with the increasing usage of the collector.

In the presence of 10–5 mol/L DAH, the average required ultrasonic amplitude for detachment of cube and triangular prism particles was 49.0 and 39.9 μm, respectively. Moreover, the average required ultrasonic amplitude for detachment of cube and triangular prism particles increased by 14.7 and 9.1 μm, respectively, compared with that without the collector. However, the average required ultrasonic amplitude for detachment of cylindrical and sphere particles was still not larger than 22.8 μm. Compare with cylindrical and sphere particles, cube and triangular prism particles have a larger contact surface area. On the one hand, the larger contact surface area of cube and triangular prism particles could enhance the attachment strength. On the other hand, the broader contact surface area could adsorb more collector agents, which was beneficial for the improvement of the particle floatability and attachment force.

In the presence of 10–4 mol/L DAH, all the average required ultrasonic amplitude for detachment of glass particles with differently shaped particles increased obviously. In addition, the detachment of cube and triangular prism particles still required a larger ultrasonic amplitude than that of cylindrical and sphere particles. However, it is noted that the gap of the required ultrasonic amplitude for detachment between glass particles with different shapes became small. It means that the average required ultrasonic amplitude for detachment of glass sphere and cylindrical particles seems close to that of cube and triangular prism particles at a higher collector dosage.

If it is assumed that the moving of single particle attached to the bubble bottom follows the moving of bubble bottom point, the maximum detachment force of the single particle may be calculated by eq 4(12)

2.3. 4

where Fv,max is the maximum force acting on the particle when the particle follows the bottom of the bubble (Fv,max = mamax), and Fg′ is the particle immersed weight (Fg = v(ρp – ρl)g).

The detachment force of particle under ultrasonic-assisted treatment is presented in Figure 6. Because particles with different shapes have the same mass, the detachment force presented a similar trend with the required ultrasonic amplitude. The detachment force of the noncurved particles (cube and triangular prism particle) was larger than that of curved particles (sphere and cylindrical particle), which was constant with the results of Xu.12 With the addition of 10–5 mol/L DAH, the detachment force of noncurved particles increased obviously, while the detachment force of curved particles was still unchanged, which is because of the limit of the ultrasonic amplitude. With more addition of collector, the floatability of all glass particles was improved significantly. Therefore, the detachment force of all shaped particles increased. The detachment force of sphere and cylindrical particles increased significantly, and the gap of the detachment force between curved particles and noncurved particles became small. The larger dosage of the collector weakened the role of the shape in the floatability, which was consistent with the results of Xia13 that the effect of particle shape on the bubble-particle attachment angle and flotation recovery.

Figure 6.

Figure 6

Open in a new tab

Detachment force of particle under ultrasonic treatment.

As shown in Figure 4, noncurved particles (cube and triangular prism particle) attached to the bubble at the edge of the particle surface. During the oscillation of bubble-particle aggregate, the three-phase contact line was significantly pinned at the edge of the noncurved particle surface. Also, the contact angle varied within a certain range because of the contact angle hysteresis. The detachment of the particle from the bubble surface is like that the detachment of the particle from the air–water interface (the size of the bubble is considered infinite).17 When a particle is pulled away from the air–water interface by the disruptive force, the capillary force is considered critical to supporting the particle at the air–water interface. In addition, the capillary force depends on the surface tension force and contact angle.26 The pining of the contact line, the contact line fixes at the edge of the particle surface, leads to an increase in contact angle compared with the static contact angle and an increase in the capillary force correspondingly. Therefore, the particle with a sharp edge requires a larger force than that with rounded cross-sections, when the particle detaches from the air–water interface.27,28 Similarly, the pining performance also occurs in the edge of the noncurved particle surface when particle detaches from the bubble in the water. Compared with curved particles (cylindrical and sphere particle), noncurved particles required a larger detachment force. These results are constant with the results of the detachment of the particle at the air–water interface.

3. Experimental Section

3.1. Minerals

In order to study the detachment behavior of the regular-shaped particle, the cube, triangular prism, and cylindrical particles with the same mass of 0.5 mm glass bead were chosen as the samples. The cube, triangular prism, and cylindrical particles were cut out from a 0.4 mm thick glass plate. The model of shaped glass particles is shown in Figure 7, and the size and shape factors of investigated glass particles are listed in Table 3. The volume and mass of shaped particles are the same, while the surface area, edge length, and the number of vertex of particles are different. The surface area and edge length of noncurved particles (cube and triangular prism particle) are larger than that of curved particles (cylindrical and sphere particle). In addition, there is no vertex on the curved particles, while several vertexes exist on the noncurved particles.

Figure 7.

Figure 7

Open in a new tab

Different shaped glass particles.

Table 3. Size and Shape Factors of Investigated Particles.

shape volume/mm3 surface area/mm2 edge-length/mm number of vertex
cube 0.064 0.96 4.80 8
triangular prism 0.064 1.05 4.86 6
cylindrical 0.064 0.88 2.83 0
sphere 0.065 0.79 0.00 0
Open in a new tab

3.2. Bubble-Particle Detachment Tests

Figure 8 illustrates an experimental apparatus for studying the bubble-particle detachment behavior under ultrasound-assisted treatment. A high-speed camera and a computer in the experiment were used to record the detachment behavior. The water cell was made of polymethyl methacrylate and separated into right and left water cells by a removable plate. An ultrasound probe was fixed in the right water cell to create the ultrasonic wave. The syringe and the needle capillary (internal diameter 2 mm) were fixed in the left water cell to produce a fixed bubble. The horizontal distance between the ultrasound probe and the bubble was about 50 mm.

Figure 8.

Figure 8

Open in a new tab

Design of experimental apparatus for observing bubble particle detachment.

In this study, the detachment behavior of bubble and single particle with different shapes was investigated. First, a fixed bubble was generated by the syringe in the left water cell with de-ionized water at a pH of 10. Second, a glass particle was put on the upper part of the bubble by the thin-tipped tweezers. The particle slid to the bottom of the bubble and attached onto the bubble. After the preattachment process, the ultrasound probe was turned on and lasted for 3 s to drive the bubble-particle aggregate to oscillate. The bubble-particle aggregate was affected by ultrasound-assisted treatment and would tend to detachment. If the bubble-particle detachment behavior did not happen, the ultrasound probe was turned on again with a larger ultrasonic amplitude. During each ultrasound-assisted treatment, the behavior of bubble-particle aggregate was recorded by the high-speed camera with the frame rate of 4000 frames/s. Besides, the detachment test of each kind of shape particle was conducted five times. The required ultrasonic amplitude for the detachment of the particle from the bubble surface was the average value of five tests.

The frequency of the ultrasound probe used in this study (VCX800, SONICS) is 20 kHz, and the smallest ultrasonic amplitude of the ultrasound probe is 22.8 μm.

4. Conclusions

This paper observed the unloaded bubble oscillation and the detachment behavior of single glass particle with different shapes under ultrasound-assisted treatment. The motion of the bubble bottom point could be described as a simple harmonic motion. With an increase in ultrasonic amplitude, the oscillation amplitude (A) of the bubble bottom point increased. Curved particles attached onto the bubble mainly by the curved surface while noncurved solids attached onto the bubble mainly by the plane surface. Because of the larger contact area and presence of the sharp edge of the particle, the detachment of noncurved particle required a larger amplitude of ultrasound than that of the curved particle. In other words, the detachment of noncurved particles from the bubble required a relatively larger detachment force. In addition, the more addition of collector weakened the role of the shape in the floatability of particles.

Acknowledgments

This work was supported by Outstanding Innovation Scholarship for Doctoral Candidate of “Double First Class” Construction Disciplines of CUMT.

The authors declare no competing financial interest.

References

  1. Wills B. A., Finch J.. Wills’ mineral processing technology: an introduction to the practical aspects of ore treatment and mineral recovery; Butterworth-Heinemann, 2015. [Google Scholar]
  2. Koh P. T. L.; Hao F. P.; Smith L. K.; Chau T. T.; Bruckard W. J. The effect of particle shape and hydrophobicity in flotation. Int. J. Miner. Process. 2009, 93, 128–134. 10.1016/j.minpro.2009.07.007. [DOI] [Google Scholar]
  3. Xia W. Role of particle shape in the floatability of mineral particle: An overview of recent advances. Powder Technol. 2017, 317, 104–116. 10.1016/j.powtec.2017.04.050. [DOI] [Google Scholar]
  4. Szczerkowska S.; Wiertel-Pochopien A.; Zawala J.; Larsen E.; Kowalczuk P. B. Kinetics of froth flotation of naturally hydrophobic solids with different shapes. Miner. Eng. 2018, 121, 90–99. 10.1016/j.mineng.2018.03.006. [DOI] [Google Scholar]
  5. Ma G.; Xia W.; Xie G. Effect of particle shape on the flotation kinetics of fine coking coal. J. Clean. Prod. 2018, 195, 470–475. 10.1016/j.jclepro.2018.05.230. [DOI] [Google Scholar]
  6. Wen B.; Xia W. Effect of particle shape on coal flotation. Energy Sources, Part A Recovery, Util. Environ. Eff. 2017, 39, 1390–1394. 10.1080/15567036.2017.1332697. [DOI] [Google Scholar]
  7. Dehghani F.; Rahimi M.; Rezai B. Influence of particle shape on the flotation of magnetite, alone and in the presence of quartz particles. J. South. Afr. Inst. Min. Metall. 2013, 113, 905–911. [Google Scholar]
  8. Ulusoy U.; Yekeler M.; Hiçyılmaz C. Determination of the shape, morphological and wettability properties of quartz and their correlations. Miner. Eng. 2003, 16, 951–964. 10.1016/j.mineng.2003.07.002. [DOI] [Google Scholar]
  9. Rahimi M.; Dehghani F. Influenceoftheroughnessandshapeofquartzparticlesontheirflotationkinetics. Int. J. Miner., Metall. Mater. 2012, 19, 284–289. 10.1007/s12613-012-0552-z. [DOI] [Google Scholar]
  10. Lecrivain G.; Petrucci G.; Rudolph M.; Hampel U.; Yamamoto R. Attachment of solid elongated particles on the surface of a stationary gas bubble. Int. J. Multiphase Flow 2015, 71, 83–93. 10.1016/j.ijmultiphaseflow.2015.01.002. [DOI] [Google Scholar]
  11. Hassas B. V.; Caliskan H.; Guven O.; Karakas F.; Cinar M.; Celik M. S. Effect of roughness and shape factor on flotation characteristics of glass beads. Colloid. Surface. Physicochem. Eng. Aspect. 2016, 492, 88–99. 10.1016/j.colsurfa.2015.12.025. [DOI] [Google Scholar]
  12. Xu D.; Ametov I.; Grano S. R. Detachment of coarse particles from oscillating bubbles—The effect of particle contact angle, shape and medium viscosity. Int. J. Miner. Process. 2011, 101, 50–57. 10.1016/j.minpro.2011.07.003. [DOI] [Google Scholar]
  13. Xia W.; Ma G.; Bu X.; Peng Y. Effect of particle shape on bubble-particle attachment angle and flotation behavior of glass beads and fragments. Powder Technol. 2018, 338, 168–172. 10.1016/j.powtec.2018.07.024. [DOI] [Google Scholar]
  14. Pita F.; Castilho A. Separation of plastics by froth flotation. The role of size, shape and density of the particles. Waste Manag. 2017, 60, 91. 10.1016/j.wasman.2016.07.041. [DOI] [PubMed] [Google Scholar]
  15. Schmidt D. C., Berg J. C.. Selective removal of toner particles from repulped slurries by flotation; Canadian Pulp & Paper Assoc: MONTREAL, (CAN), 1995; pp 227–230. [Google Scholar]
  16. Jameson G. J. Advances in Fine and Coarse Particle Flotation. Can. Metall. Q. 2010, 49, 325–330. 10.1179/cmq.2010.49.4.325. [DOI] [Google Scholar]
  17. Hubbard A. Colloidal science of flotation. J. Colloid Interface Sci. 2004, 273, 343. 10.1016/j.jcis.2004.02.003. [DOI] [Google Scholar]
  18. Wang G.; Evans G. M.; Jameson G. J. Experiments on the detachment of particles from bubbles in a turbulent vortex. Powder Technol. 2016, 302, 196–207. 10.1016/j.powtec.2016.07.025. [DOI] [Google Scholar]
  19. Yoon R. H.; Mao L. Application of Extended DLVO Theory, IV. J. Colloid Interface Sci. 1996, 181, 613. 10.1006/jcis.1996.0419. [DOI] [Google Scholar]
  20. Goel S.; Jameson G. J. Detachment of particles from bubbles in an agitated vessel. Miner. Eng. 2012, 36–38, 324–330. 10.1016/j.mineng.2012.08.001. [DOI] [Google Scholar]
  21. Nguyen A., Schulze H. J.. Colloidal science of flotation; CRC Press, 2003. [Google Scholar]
  22. Schulze H. J. Dimensionless number and approximate calculation of the upper particle size of floatability in flotation machines. Int. J. Miner. Process. 1982, 9, 321–328. 10.1016/0301-7516(82)90038-2. [DOI] [Google Scholar]
  23. Wang G.; Evans G. M.; Jameson G. J. Bubble–particle detachment in a turbulent vortex I: Experimental. Miner. Eng. 2016, 92, 196–206. 10.1016/j.mineng.2016.03.011. [DOI] [Google Scholar]
  24. Cheng T.-W.; Holtham P. N. The particle detachment process in flotation. Miner. Eng. 1995, 8, 883–891. 10.1016/0892-6875(95)00050-z. [DOI] [Google Scholar]
  25. Awatey B.; Thanasekaran H.; Kohmuench J. N.; Skinner W.; Zanin M. Critical contact angle for coarse sphalerite flotation in a fluidised-bed separator vs. a mechanically agitated cell. Miner. Eng. 2014, 60, 51–59. 10.1016/j.mineng.2014.02.009. [DOI] [Google Scholar]
  26. Feng D.-x.; Nguyen A. V. Effect of contact angle and contact angle hysteresis on the floatability of spheres at the air-water interface. Adv. Colloid Interface Sci. 2017, 248, 69–84. 10.1016/j.cis.2017.07.031. [DOI] [PubMed] [Google Scholar]
  27. Feng D.-x.; Nguyen A. V. How does the Gibbs inequality condition affect the stability and detachment of floating spheres from the free surface of water?. Langmuir 2016, 32, 1988–1995. 10.1021/acs.langmuir.5b04098. [DOI] [PubMed] [Google Scholar]
  28. Chatterjee N.; Lapin S.; Flury M. Capillary forces between sediment particles and an air–water interface. Environ. Sci. Technol. 2012, 46, 4411–4418. 10.1021/es2038933. [DOI] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES