Additive manufacturing of cellulose-based materials with continuous, multidirectional stiffness gradients

We combine materials engineering and digital processing to design and print cellulose-based continuous stiffness gradients.

Abstract

Functionally graded materials (FGMs) enable applications in fields such as biomedicine and architecture, but their fabrication suffers from shortcomings in gradient continuity, interfacial bonding, and directional freedom. In addition, most commercial design software fail to incorporate property gradient data, hindering explorations of the design space of FGMs. Here, we leveraged a combined approach of materials engineering and digital processing to enable extrusion-based multimaterial additive manufacturing of cellulose-based tunable viscoelastic materials with continuous, high-contrast, and multidirectional stiffness gradients. A method to engineer sets of cellulose-based materials with similar compositions, yet distinct mechanical and rheological properties, was established. In parallel, a digital workflow was developed to embed gradient information into design models with integrated fabrication path planning. The payoff of integrating these physical and digital tools is the ability to achieve the same stiffness gradient in multiple ways, opening design possibilities previously limited by the rigid coupling of material and geometry.

INTRODUCTION

Functionally graded material (FGM) has gradual change of composition or structure in either a continuous or a stepwise manner, giving rise to a corresponding change in the property of the material (1). Its principle is similar to that of many natural materials: The concentration of a specific functional component or the distribution of a particular structural arrangement changes gradually across space, often adapting to the functions at multiple locations of a single organism (2, 3). This adaptability of composition and structures at the local scale endows FGM with the capability to fulfill multiple, sometimes conflicting, design requirements and promises applications in diverse fields, such as thin films (4), coatings, biomedical engineering (5, 6), and architecture (7). A typical class of FGMs is materials with stiffness gradients; they can better distribute stress at interfaces (3, 8–10), program deformation of soft actuators (11–15), and influence the speed of cell migration (16).

Materials with functional stiffness gradients can be fabricated by constructive processes, where requisite material parts are directly stacked together to form gradients, or mass transport processes, where physical processes, such as molecular diffusion or fluidic flows, create the gradients (1). Multimaterial additive manufacturing (MMAM) (17), a type of constructive process, enables simultaneous geometric and compositional variations during fabrication (18, 19), producing less waste than direct coupling of materials, layering, or subtractive manufacturing (20–22). Among the several methods of MMAM that offer various tradeoffs among complexity, printing resolutions, scalability, and material types, the extrusion-based method is noted for its simplicity, low cost, scalability, and wide range of material choices (18, 23, 24). Despite these advantages, extrusion-based methods suffer from low gradient resolution and weak bonding between dissimilar materials (17). An additional challenge for all MMAM methods is how to incorporate continuous material gradients throughout the design-to-manufacturing workflow in which the gradient design is no longer restricted by the traditional boundary representation of common computer-aided design (CAD) software (17, 25). Specifically, although voxel-based software, such as Monolith (26), enables complex material arrangement, it lacks automatic distribution of materials based on performance requirements and strong integration between design and manufacturing processes for the fabrication of objects with continuous material gradient (25).

Here, we show an FGM manufacturing method that combines materials engineering and digital processing and uses both constructive and mass transport processes in creating continuous gradients (Fig. 1). Specifically, the solutions of a cellulose derivative were engineered to give tunable viscoelastic properties that enabled controlled extrusion (Fig. 1A), and a digital workflow was developed to embed gradient information in the designs and generate custom G-code to control the three-dimensional (3D) printer and syringe pumps (extrusion and positioning systems in Fig. 1B). Filaments of varying compositions and/or cross sections were extruded in a solution phase to facilitate molecular diffusion across filament boundaries in creating continuous gradients (Fig. 1C). To highlight the relevance of combining materials engineering with custom manufacturing strategies, this research uses a biopolymer-based fabrication material that is environmentally friendly and abundant, with diverse applications from tissue engineering (16) to the construction industry (27). The synthesis of these physical and digital tools is the ability to create multidirectional, continuous stiffness gradients in a variety of ways, expanding design possibilities for FGMs.

Fig. 1. Schematics of the fabrication process for printing continuous gradients.

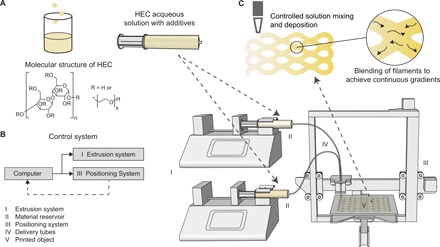
(A) Schematic of the preparation of printing solutions. Hydroxyethyl cellulose (HEC) in powder form is dissolved in water and mixed with additives in a beaker before being transferred into a syringe. (B) Diagram of the control system and schematics of the 3D printing system. The diagram (left) shows the communication workflow that synchronizes the (I) extrusion system and (III) positioning system through a feedback loop. The 3D printing system (right) consists of (I) an extrusion system (one or two syringe pumps), (II) the reservoirs (syringes), and (III) a positioning system (customized low-cost 3D printer TEVO Tarantula i3). Delivery tubes (IV) are equipped with extruding tips and transport the printing solutions and deposit filaments of the solutions on the printing platform (V). (C) Illustration showing the blending of filaments after deposition. Neighboring filaments blend into each other through the diffusion at the molecular scale, thus creating seamless objects and continuous gradients.

RESULTS

Printing materials with tunable rheological and mechanical properties

Our approach to engineer a printing material combines the preparation of a base material solution that provides tunable rheological properties for extrusion printing and the addition of mixable additives that extend the range of properties and property gradients of the final printed material (table S1). Hydroxyethyl cellulose (HEC), a thickening and gelling agent in various applications in the food and cosmetics industry (28), was chosen as the base material. HEC is a derivative of cellulose, the most abundant biopolymer on Earth, and it is nontoxic, biodegradable (29), and environmentally friendly (30). Its solution exhibits shear thinning properties (31) and pH-dependent gelation time, which allows extrusion-based printing and further adjustment with additives. We have selected and tested five different nontoxic additives compatible with HEC base solutions that vary the rheological and mechanical properties (table S1).

The gelation point of HEC, marking its transition from an aqueous solution to a solid hydrogel, was experimentally determined to occur at 96 min (Fig. 2A), and the associated increases in solution viscosity during gelation challenged the syringe pumps’ ability to successfully and consistently deliver the fluids, limiting the printing time window. We studied solution parameters such as HEC molecular weight (fig. S1A), HEC content by weight (fig. S1B), and choice of acidifying agent (fig. S1C) to minimize the rate of increase in solution viscosity. We observe the following general trends: Increases in HEC molecular weight (near pH ~2) and decreases in HEC weight content led to decreases in the gelation rate, and for acidic solutions of the same starting pH (2 to 3.5 region), citric acid (CA) is more effective than hydrochloric acid (HCl) in decreasing the rate. Adding CA to the solution to reach a pH of 3.0 proved to slow the gelation rate the most, as shown in Fig. 2B, extending the gelation point to around 261 min (172% increase) and enabling satisfactory extrusion consistency.

Fig. 2. Rheological properties of the printing solution.

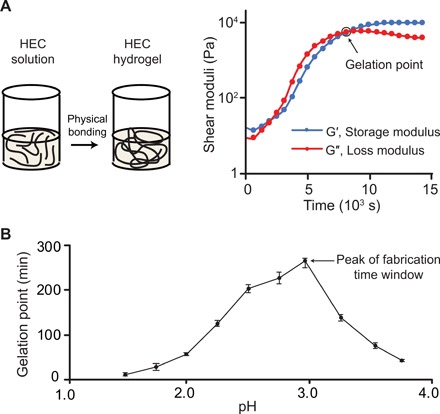
(A) A schematic on the left shows the gelation of the printing solution as a result of physical bonding. The plot of shear moduli versus time on the right shows the gelation point occurring at ~5800 s. By convention, the gelation point is defined as the point in time at which the storage modulus G′ becomes greater than loss modulus G″ after the initial dissolution of HEC species. (B) A plot showing the dependence of gelation time as a function of the pH of the printing solutions. The pH was adjusted by the addition of varying amounts of CA. Error bars denote the SD of three trials. The plot reveals that the highest gelation point, and therefore the longest printing time window, occurs at a pH of ~3.0.

Figure 3A shows the characterization of the printed material and the effect of additives. The addition of lignin increased the stiffness (Fig. 3B) and tensile strength (Fig. 3C) the most, while the inclusion of CA decreased these mechanical properties the most. The former result is due to the fact that lignin is a natural reinforcer to cellulose in Nature, serving as a binder that cross-links polysaccharides to confer strength. The CA was most effective in decreasing the mechanical properties because the HEC hydrogel is formed via physical cross-linking of hydrogen bonds. The presence of sufficient H⁺ ions in the acidic solution perhaps disrupts the hydrogen bonding between the HEC polymer chains and is replaced by bonding between HEC and CA. This would result in a less strong polymer network. These lignin- and CA-differentiated solutions served to provide a range of mechanical properties from which objects with property gradients could be printed, either by sequential deposition of each printing material or in situ mixing (see “Design-to-fabrication workflow” section). Another interesting kind of property variation that was noted was the decrease in stiffness (fig. S2A) and increase in size (fig. S2B) and weight (fig. S2C) of printed samples, with increasing relative humidity due to the hygroscopic nature of cellulose, which could be explored for other applications involving shape-changing structures (32) or temporary, water-soluble objects (see movie S1). Varying the viscosity of the printing solution was equally important to achieving stiffness gradients, as the viscosity determined the cross section of the deposited filaments, providing stiffness modulation through geometric variation. Figure 3D shows the attained viscosity range, as well as the substantial shear thinning properties that are activated by the choice of HEC at the calculated fabrication shear rate of 28.7 s⁻¹. Solutions of high [10 weight % (wt %)] bulk HEC content with added microfibrillated cellulose (MFC; a high-viscosity additive) served as the most viscous mixture with a viscosity of 14.0 Pa·s that resulted in maximal filament cross section, while minimizing the weight ratio of bulk HEC to 2 wt % without any additives produced more fluidic filaments with a viscosity of 1.9 Pa·s. The exact methods of achieving stiffness gradients through these printing solutions modified in terms of E modulus and/or viscosity are expounded in the “Stiffness gradient patterning and applications” section.

Fig. 3. Modulation of the printing material’s mechanical and rheological properties.

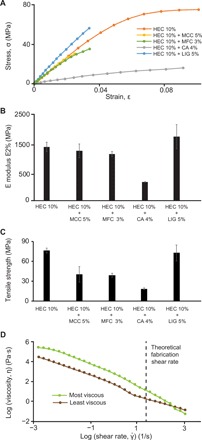
(A) A stress-strain plot showing the mechanical behavior of the base HEC material (10 wt %) as well as with various amounts of different constituent additives (denoted after the additive abbreviation as in table S1). The weight concentration of each additive was selected by maximizing the additive concentration while still ensuring printability of the solution and testability of the samples. (B) A plot comparing the E modulus of the base material and the various modified solutions. Error bars show SDs of three samples. These test results show that CA and lignin had the most impact on stiffness and could be used in the production of stiffness gradients. (C) A plot comparing the tensile modulus of the base material and the modified solutions. Error bars show SDs of three samples. (D) A plot demonstrating the shear thinning properties of the most and the least viscous solutions that can be printed. The calculated shear rate of 28.7 s⁻¹ that the printing solutions experience during extrusion is marked by a dotted line.

Design-to-fabrication workflow

The design-to-fabrication workflow (Fig. 4A and fig. S3) allows users to combine geometric models with gradient data to create FGM data and to generate fabrication code. Grasshopper, a visual programing interface inside the 3D modeling software Rhinoceros 3D (fig. S4), serves as the platform for this workflow. Implementing the workflow within a heuristic software environment creates a seamless data flow between design and fabrication, allowing fabrication parameters to be advantageously exploited during the design process to create diverse gradient properties. In particular, the fabrication parameters of (i) deposition sequence, (ii) deposition rate, and (iii) deposition ratio are used to correspondingly enable the creation of graded objects through (i) superposing layers, (ii) varying material amount, and (iii) varying material composition.

Fig. 4. Design-to-fabrication workflow of graded samples.

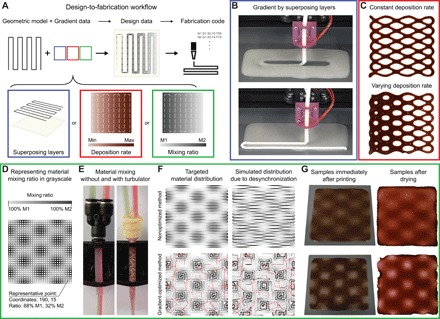
(A) Schematics of the design-to-fabrication workflow. In addition to the geometry, designers have control over material distribution and material composition, enabling the generation of gradient design by three different means: combining multiple layers of varied materials (bottom left), tuning deposition rate (ml/mm) (bottom center), and tuning material ratio (bottom right). (B) Pictures of the fabrication of a multilayer material gradient. A printing solution with low viscosity (top) is deposited first and creates a continuous material layer. A second printing solution with high viscosity (bottom) is extruded on top of the first layer, creating stiffening ribs. The diffusion process between the different layers creates seamless gradients after sample drying. (C) Photos of samples printed with different material deposition rates. Extrusion rate (mL/s) and printer speed (mm/s) parameters are embedded in the design data and tuned to control the material deposition rate (mL/mm). Samples with the same deposition path vary in geometry due to a constant (top) or varying (bottom) deposition rate. (D) Representing material gradients with a grayscale image. A grayscale image is evaluated at different locations according to its brightness and is discretized into a series of points containing information on fabrication parameters such as position and material ratio. (E) Pictures of an extruding tip without (left) and with (right) a turbulator. The turbulator enhances the mixing of the two incoming solutions and increases the homogeneity of deposited filaments. (F) Diagrams showing expected material distribution in a synchronized (left column) and desynchronized (right column) fabrication system through a nonoptimized approach (top row) and gradient-optimized approach (bottom row) to deposition path generation. The gradient-optimized method balances path continuity with material variation rate and makes the printed gradient less sensitive to the desynchronizations between positioning and extrusion systems. The tradeoff is increased path discontinuities, shown in red. (G) Printed samples with continuous material gradients right after deposition (left column) and final gradient result (right column). The samples with nonoptimized deposition paths (top row) show less material contrast than the samples with gradient-optimized deposition paths (bottom row) (photo credit: Pedro A. G. S. Giachini, University of Stuttgart).

First, deposition sequence is explored to develop a superposing layer strategy (Fig. 4B) for stiffness gradient fabrication. In this process, geometric data are associated with layers representing sequential deposition procedures with contrasting mechanical properties. The fluidic characteristic of materials with lower viscosity provides object continuity, while more viscous mixtures are used to discretely alter stiffness. Diffusion between contrasting materials guaranteed interlayer continuity and enabled the production of continuous and pliable sheets of material with patterned reinforcements (see “Stiffness gradient patterning” section).

The second strategy, the deposition rate strategy (Fig. 4C), generated stiffness gradients by varying the rate of the deposition, which resulted in varying amounts of materials along the deposition paths. The deposition rate (ml/mm) depends on the extrusion rate of the syringe pumps (ml/s) and the printer’s nozzle speed (mm/s). These fabrication parameters can be embedded in the geometric data through design layers or functions that determine deposition rate values and behaviors. These data are then translated into fabrication commands that coordinate the distribution of material, exploring material flow as a mean to efficiently permeate infill regions and to enable equal deposition paths to manufacture objects with varied geometric stiffness (see movie S2).

The third strategy generated gradients by varying material mixing ratios (Fig. 4, D to G). An additional data layer is used to store the mixing ratio of the materials being deposited. In this data layer, local composition is defined either by material distribution functions (25) or a graphical method that uses grayscale to represent mixing ratios (Fig. 4D). These design data of mixing ratios are translated into fabrication codes that modified the extrusion rate of the corresponding syringe pumps.

In this scenario, where materials are dynamically mixed during the printing process, a turbulator is used at the merging point of the two delivery tubes to disrupt the laminar flow that results in the extrusion of heterogeneous mixtures (Fig. 4E and movie S3). This approach, although enhancing fluidic mixing, results in an increase in materials’ travel time in the tube before reaching the deposition nozzle and brings both digital and physical challenges to the process. On the digital side, it creates a temporal discrepancy between the positioning and the extrusion systems because the increase in materials’ travel time needs to be accounted for in the fabrication code in order for the positioning system to synchronize with the extrusion system (see Material and Methods). On the physical side, diffusion between sequential mixtures occurs in the turbulator and reduces material contrast, an effect proportional to the dissimilarity between sequential materials’ mixing ratio. In addition, changes in the extrusion rate of a syringe pump require a nonzero time step to coincide with the extrusion rate of the solution at the other end of the delivery tube. For example, in a fabrication scenario where the extrusion speed was abruptly changed from 0 to 0.2 ml/s, delays as long as 8.1 s between the positioning and extrusion systems were recorded; this physical delay has a direct impact on the material composition accuracy.

To address these challenges, we developed a computational strategy to optimize the deposition path (Fig. 4F). This strategy is based on the intuition that minimizing the dissimilarity between sequential material mixing ratios during deposition would reduce errors introduced by the delay due to the materials' travel time and by the diffusion between adjacent material mixtures in the extrusion tube (Fig. 4F). It analyzed the position and the material data of all deposition points and created a gradient-optimized deposition path that balances between path continuity and mixing ratio continuity (see movie S4). Figure 4G compares the same material gradient printed through the nonoptimized and gradient-optimized deposition path methods. As expected, the sample fabricated using the gradient-optimized path method exhibits higher material contrast immediately after deposition and after the postdeposition diffusion that occurs during the drying process.

Stiffness gradient patterning and applications

As described in the previous sections, combining materials engineering and manufacturing developments enables the fabrication of systems that present custom stiffness gradation by controlling both the geometric and material aspects of the printed object. Through the developed strategies, gradients can be tuned at the local and global scales (Fig. 5). At the local scale, geometric stiffness can be tuned by material parameters such as viscosity and solid weight content. Figure 5A shows that solutions with a higher solid weight content dry into comparative higher cross sections, since a larger amount of material is left behind after solvent evaporation. Similarly, as shown in Fig. 5B, solutions with higher viscosities result in higher cross sections after the drying process, as higher viscosities reduce the deposited material’s spread. In addition to the geometric stiffness approaches, local stiffness can also be tuned according to the material mixture’s Young’s modulus (Fig. 5C). These parameters are combined at the global scale to control material distribution, local cross-sectional height, and local Young’s modulus, influencing how an object deforms (see movie S5). As an example, Fig. 5D exhibits cellulose sheets of similar appearance but with varying stiffness gradients being submitted to external forces (stiffness gradient measured in fig. S5). As shown, by distributing stiffness along specific directions or patterns, it is possible to achieve distinct deformation behaviors.

Fig. 5. Strategies for varying stiffness at the local scale and patterning stiffness at the global scale.

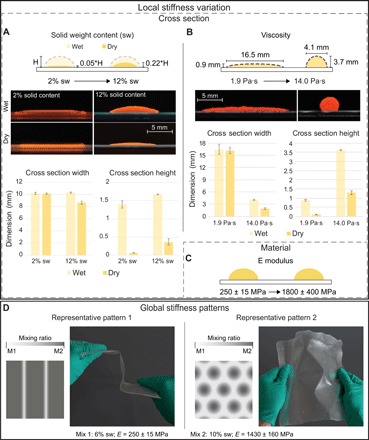
(A) Diagrams and photos of the cross sections of the extruded filaments showing the effect of solid-weight content after solvent evaporation. Printing solutions with lower cellulose concentrations produce filaments with thinner cross sections (left) than filaments printed with the same volume of a high-concentration printing solution (right). (B) Diagrams and photos of the cross sections of the extruded filaments from mixtures of varied viscosity. Printing solutions with lower viscosity produce layers of thinner cross sections (left), whereas printing solutions with higher viscosity results in filaments with thicker cross sections (right). Viscosity values corresponds to the shear rate of 25.1 rad/s. (C) Range of material’s E modulus achieved by altering the cellulose solutions with additives. (D) Patterning local material compositions and cross-sectional characteristics is used to achieve samples with anisotropic stiffness at the global scale. Directionality was patterned by aligning less stiff regions of material, resulting in samples that show bending resistance in one direction and programmable hinge-like behavior in another direction (left). Similarly, this effect was reproduced in multiple directions by patterning more rigid patches of material varying in distribution and shape (right) (photo credit: Pedro A. G. S. Giachini, University of Stuttgart).

Figure 6 shows how stiffness gradients can be used to guide an object’s deformation. By exploring the Young’s modulus range of the different cellulose mixtures (Fig. 6A), it is possible to print visually similar samples with the same cross-sectional thickness that exhibit distinct deformation behavior and end geometry due to their unique programmed stiffness patterns (Fig. 6, B to E). This approach of using an external force to generate the final shape of an initially flat object allows designers to leverage simplified 2D manufacturing strategies, avoiding more complex 3D processes. Applications range from industrial design products (33) to architectural design systems that explore elastic bending of planar objects to achieve form and structural integrity (34, 35).

Fig. 6. Samples showing programmable deformation due to patterned stiffness variation.

(A) A schematic showing stiffness gradients represented by a grayscale image. Mixture 1 has 10 wt % base mixture, and mixture 2 has 10 wt % base mixture and 4 wt % CA. (B to E) Thin cellulose strips of identical size were printed with various stiffness gradient profiles along their length and exhibit different curvature profiles when subjected to the same external displacement. (B) Photograph showing that homogenous stiffness (no gradient) resulted in a symmetric curvature profile. (C) Photograph showing that discrete regions of the weaker mixture resulted in hinge-like behavior that distorted this strip’s curvature profile from the nongraded symmetric curve. (D) Photograph showing a gradual sinusoidal gradient resulted in a curvature profile approximating a circle. (E) Photograph showing that the desired closed end form of this strip was achieved through the printed stiffness gradient, where the weaker regions bent more readily than the stiffer regions. (F and G) Series of photographs of flexible graded sheets that transferred load in the transversal direction to large body deformation in the longitudinal direction for a programmed folding effect. These identical programmed behaviors were achieved by different methods as described in the “Stiffness gradient patterning and applications” section. (F) Sample exhibiting geometric stiffness differentiation through directional placement of reinforcing ribs of higher cross section. (G) Sample exhibiting E modulus differentiation achieved by using a mixture of higher CA content in the regions that were meant to fold. (H) A digital mesh model of the sheet featured in part (G). A fine gradation of E modulus values was applied to approximate the sheet’s continuous gradient. (I) Series of snapshots of the FEM simulation that was developed to predict the programmed folding behavior under a pair of applied forces, represented by the blue block arrows (photo credit: Sachin S. Gupta, University of Stuttgart).

In addition to guiding deformation processes, stiffness patterns also have applications in the development of compliant mechanisms and soft robotics (36, 37). In this scenario, stiffness gradients are designed to create objects that may exhibit complex deformation behavior and redistribution of forces in response to actuation forces. Exemplifying this application, Fig. 6 (F and G) shows the deformation of cellulose samples exhibiting similar stiffness gradients that were patterned using different fabrication strategies. The sequence shown in Fig. 6F exhibits a sample with geometric stiffness differentiation through directional placement of reinforcing ribs of higher cross section, while the sequence shown in Fig. 6G exhibits a sample with E modulus differentiation achieved by using a CA concentration gradient that lowers stiffness in the regions that were meant to fold. Because of lower stiffness regions that resemble common curve-fold hinges, the samples present a curved deformation pattern perpendicular to the direction of the applied force. A finite element method (FEM) simulation was performed to verify the observed deformation behavior of the sample exhibited in Fig. 6G (Fig. 6H). The sample’s fabrication stiffness gradient input was used to create a mesh with a fine Young’s modulus gradient that approximates the continuous stiffness gradient of the physical object. As observed, the simulated mesh showed similar deformation behavior under the application of forces that mirrored the handling of the physical prototype, providing feedback on the distribution of stresses in the deformed sample (Fig. 6I).

DISCUSSION

In summary, this work leveraged a combined approach of materials engineering and digital processing to control material mixing and deposition and to enable extrusion-based MMAM of tunable viscoelastic materials with continuous, high-contrast, and multidirectional stiffness gradients. A method was established to engineer a base solution into a catalog of fluidic, cellulose-based materials with distinct mechanical and rheological properties. This provided the physical foundation for achieving stiffness gradients. In parallel, a digital workflow was developed that allowed the embedding of gradient information into design models, with integrated deposition path planning that considered mechanical property profiles to better distribute materials. The deposited filaments, being in solution state, were then able to seamlessly blend and diffuse, creating a single, coherent graded object upon solidification and drying. The payoff of integrating these physical and digital tools is the ability to achieve the same stiffness gradient in an object in multiple ways, opening design possibilities that were previously limited by the rigid coupling of material and geometry. In addition, the flexibility of the developed setup and software provides a scalable and adaptable process that can be applied to other gradient fabrication scenarios.

The developed method has several limitations. First, this method generally relies on physical bonding of chemically compatible and miscible materials to achieve a solid object, meaning that dissimilar materials or materials that are not chemically compatible or immiscible in a single solution state would not be suitable for this method. Second, our setup currently only allowed for a maximum of two materials to be simultaneously mixed and extruded; a more elaborate fluid delivery system with a higher number of extrusion channels would be required to add an increased number of material combinations. Third, the long drying time and low viscosity of the initially as-deposited filament so far restricted the extension of this method to multilayer printing of above two layers. Last, the maximum force of the syringe pump used in this work posed a limitation on the maximum viscosity of the solutions that could be mixed and extruded, which, in turn, affected the range of the property gradients. For example, the Young’s modulus range of 248 to 1786 MPa was primarily determined by how the responsible additives affected the printability of the polymer solution, with the lignin substantially increasing the viscosity of the solution and the CA considerably increasing the gelation rate at high concentrations.

In the light of these limitations, this work offers the following opportunities for further research. First, for digital processing workflow, optimization of the path planning could be further developed by fine-tuning penalties related to path discontinuities and large differences in material variation rates, potentially increasing the production efficiency of this printing process. Second, for the development of materials, the range of material stiffness can be further extended, and alternative viscous materials could be used, such as other polymer gels, resins, or even materials used in large-scale industries, assuming an appropriate hardware setup is introduced. Third, the main concept of this work could be extended to current large-scale printing technologies (38, 39) to create buildings in which geometry and material continuously change to balance between structural and architectural requirements or even to create adaptable mechanisms (22) to introduce soft hinges or directional bending. Fourth, at the other end of the size spectrum, it would be interesting to test the effectiveness of the established method at small scales, where the natural diffusion of the material may overtake the distribution specified by the fabrication paths, which would be crucial for applications sensitive to small changes in material properties, such as tissue engineering. Fifth, this work can be extended to gradients other than stiffness gradients, such as optical properties, thermal conductivity, electrical conductivity, or even cell nutrient concentration. Last, the implementation of fast-curing liquids, molds, or viscous support materials (40) could even push the current work’s capabilities of printing 2D or 2.5D objects to create fully fledged 3D objects with these internal functional property gradients.

MATERIALS AND METHODS

Printing material preparation and testing

HEC (molecular weights of 90,000, 250,000, 720,000, and 1,300,000 g/mol), lignin, microcrystalline cellulose, CA, HCl, and sodium hydroxide were purchased from Sigma-Aldrich. MFC was graciously donated by Daicel FineChem and Weidmann Fiber Technology.

The multistep procedure for preparing the printing materials is as follows. First, a small quantity (~0.5 to 2.5 wt %) of HEC and/or MFC was added to distilled water and mixed thoroughly using an overhead laboratory mixer to attain the approximate desired viscosity of the printing solution. Next, a predetermined quantity of CA (~0.1 wt %) was added to and dissolved in the solution to make the pH of the solution around 3.0. The third step was the addition of lignin (up to ~5.0 wt %) or a second addition of CA (up to ~4.0 wt %), which was then thoroughly mixed. The final step was the addition of a quantity of HEC that makes up the bulk solid content of the printing material (~10.0 wt %). After a last round of mixing, the finalized printing material was then loaded into a syringe by pouring and was ready for fabrication.

Flow shear rate sweep rheological measurements were conducted in a shear rate range of 10⁻³ to 10³ s⁻¹ with 20-mm 2.013° cone plate geometry. One microliter of samples of the polymer solution was scooped using a spoon and placed on the test stage with a 50-μm gap. Oscillation time sweep rheological measurements were conducted at 4% strain and a frequency of 10 rad/s and 40-mm parallel plate geometry. One microliter of samples of the polymer solution was scooped using a spoon and placed on the test stage with a 50-μm gap.

Tensile tests were performed to characterize the mechanical properties of the engineered materials. The following methods were carried out to identify three main parameters: Young’s modulus (E modulus), tensile strength, and elongation at break. All samples were prepared by pouring 25 ml of material at room temperature on dogbone-shaped molds that were laser cut out of Plexiglass. All samples were tested under constant ambient temperature (around 20°C) and in their dry state after being stored in a dry chamber until their weight approached the initial solid content weight of their mix. Initial tests with strain rates varying across two orders of magnitude (5 to 500 mm/min) were performed to identify an appropriate test parameter, and a strain rate of 40 mm/min was chosen for characterization since it provided similar stiffness results when compared with the strain rate of 500 mm/min while allowing for longer sample observation during the test. Sample width and thickness were measured across three different sections for each sample, and mean values were used as test input. Following literature recommendations for tensile testing of polymers, stiffness values were characterized as the Secant E modulus measured at 2% strain.

As stated in the “Creating printing material with tunable rheological and mechanical properties” section, studies of various solution parameters were conducted to determine which parameters minimized the gelation rate. Where gelation point was not directly measured using a rheometer, the quantity “thickening time” used to indicate the gelation rate was defined as the time it took for the stir bar to be unable to spin continuously due to the solution’s increase in viscosity during gelation. HEC of molecular weights 90,000, 250,000, 720,000, and 1,300,000 g/mol were all tested by preparing base 10 wt % solutions of various pH and allowing them to mix using a stir bar at ambient temperature. Figure S1A shows the general trend that the highest molecular weight (1,300,000 g/mol) led to the slowest thickening time and was therefore the molecular weight of choice for all solution preparations. It was hypothesized that longer average chain lengths of HEC meant more potential binding sites at which the polymer chains could cross-link before the entire chain movement was restricted and a solid gel was formed. The same procedure was conducted to test the effect of HEC weight content on gelation rate (fig. S1B), with concentrations of 2, 5, and 10 wt % at a range of pH values. It shows that the lower the weight concentration, the slower the thickening time. Decrease in weight content reduces the number of HEC polymer chains in solution, which slows the ability of a cross-linked polymer network to form throughout the volume. Last, the test of choice of acidifying agent between HCl and CA (fig. S1C) in creating 10 wt % solutions of various pH was conducted, with HCl proving less effective than CA in increasing the gelation point. CA was more effective because it is a weak acid and acts as a buffer at around pH 3 (pKa1 = 3.1).

One important material property that was noted during this research was the ability of the cellulose samples to absorb water due to their hygroscopic properties. It was apparent that printed samples of cellulose transitioned from stiff to soft and rubber-like upon exposure to humidity, absorbing the water and swelling. The use of a rheometer equipped with a humidity and temperature control chamber enabled the monitoring of the stiffness property of the material from its high moisture content condition to dry state (fig. S3A). In this couple of explorative tests, samples in their humid state were tested while varying the environment’s relative humidity from 95 to 0%. This was possible due to an adaptive behavior of the equipment during the dynamic mechanical analysis that adapted the gap between samples as the material dried and shrank. The range of stiffness values measured from the humid to the dry state of the material span two orders of magnitude, and, interestingly, results show that the stiffness of the material does not seem to vary linearly between the humid and dry states, but rather the stiffness curve exhibits two steep regions where the material experiences a rapid change in stiffness between regions of slow variation. In addition, the increases in size (fig. S3B) and weight (fig. S3C) were also measured. To standardize sample thickness and exposed surface, samples were prepared with a total initial weight of 60 g and poured into large petri dishes. A closed container was used to control environmental conditions. Temperature was kept constant at around 20°C, while relative humidity varied according to the intended drying or swelling cycle. Drying was stimulated by providing a constant flow of pressurized dry air with lower than 3% relative humidity. Humidity was provided by a potassium sulfate salt solution placed inside the container, which stabilizes ambient relative humidity at approximately 94%. After preparation, samples were placed in the container under dry conditions. Two orthogonal lines were marked along the diameter of each sample, indicating the position where measurements were to be taken. Weight and dimensional variations during the drying process were measured until values became constant. The swelling cycle was stimulated next by shutting off the dry air supply to the chamber and introducing a container with a potassium sulfate solution. Again, variations in both weight and dimension were measured until values became constant.

An extension to the hygroscopic properties is the ability of the printed samples to swell to the point of returning to a weakened gel state when saturated with water. Currently, the printed samples do not undergo any chemical cross-linking process to prevent this regression to the gel state. However, dissolution of these swollen, gel-like samples in water actually enables the creation of a new polymer solution with identical solid constituents to the dissolved samples, albeit with less homogenous distribution of solids as in the original printing mixture, according to qualitative observations. Preliminary tests have demonstrated that this new polymer solution can indeed be used to print once again. Thus, in addition to being biodegradable due to its cellulosic material composition (29), the printing material can be recycled (see movie S1).

Geometric input and gradient patterning

Conventional 3D printing procedures use the CAD software to create the desired geometry, which is then exported to a computer-aided manufacturing (CAM) software, where the geometry gets rationalized into fabrication code (G-code). Because of the experimental nature of the project, where new processes had to be developed, it was chosen that the design and fabrication workflow would be developed within Grasshopper, a visual programming plugin for Rhinoceros 3D modeling software that allows the development of custom tools through programming.

To enable the fabrication of material graded samples, and since traditional CAD software does not support assigning heterogeneous material properties to geometries, alternative strategies were investigated to store material data in the virtual geometry for fabrication. The simplest strategy consists of (i) discretizing every geometry input into a series of points and evaluating these points according to a function, allowing the material ratio of each point to be assigned according to, i.e., its position in space or within the curve domain. This method, despite being convenient for assigning complex material pattern data, requires from the user the ability to translate design needs into functions and does not enable an instinctive design process. A second strategy included (ii) visual feedback during the design phase by adopting a graphic design software to create grayscale images with brightness gradients corresponding to the desired material ratio. The brightness evaluation returns a number between 0 and 1 that determines the concentration proportion of two different materials for each point of a 2D surface. To account for a higher number of materials, other evaluating methods based on image data, such as RGB (red, green, and blue) values, could be implemented.

Fabrication setup, communication, and synchronization

An extrusion-based method was chosen due to its hardware flexibility, which allows for easy adaptation of low-cost 3D printers and vast material possibility, since the method can use liquid- or paste-like materials at different scales. The positioning system consists of an adapted fused deposition modeling 3D printer. The usual extrusion nozzle was replaced by a 3D-printed piece capable of holding multiple delivery tubes. Two syringe pumps that control the printing material delivery were used as the extrusion system. Varied printing nozzles were used for material deposition. The choice for a specific printing nozzle depends on the required print duration and resolution, as well as the ability of combining multiple materials or not. A personal computer was used as the input and control system, using USB (universal serial bus) communication ports for the coordination of both the extruding and positioning systems.

A custom fabrication code consisting of a commands list for both printer and syringe pumps was structured in accordance to the hardware’s communication protocols. Tasks of both systems were grouped in a single command line, which was parsed accordingly to each protocol at the time of execution. To establish continuous movements, G-code was sent to be buffered in the 3D printer at a faster rate than the fabrication speed. Because the syringe pumps were not controlled by the 3D printer’s controller board, the Repetier open-source firmware installed in the 3D printer was modified to supply current action feedback when requested. The feedback consisted of adding supplementary G-code functionalities that triggered the printer to send a feedback signal indicating that it had finished processing the last positioning command sent, thus allowing synchronization between printer and extrusion system.

The printing of multiple samples with varied patterned gradients and material properties allowed us to identify that parameters such as material viscosity and gelation time also have an impact on print accuracy. Through observation during printing, we identified that low-viscosity materials were more likely to flow outward of their deposited position, mixing with neighboring materials and decreasing print precision, an issue that can be minimized by assigning a deposition rate coherent with the spacing between deposited filaments. In relation to the gelation time, image comparison of recently concluded prints and images taken during the gelation process and of the final sample shows that the color contrast and sharpness between neighboring materials are lower during the drying process due to diffusion between the materials with differing concentrations in their viscous state.

Printing process

Printing of samples started by preparing the ink solution with appropriate cellulose and additive concentrations and tuning its viscosity. The different inks were then loaded in the extrusion system, with their delivery tubes connected to a custom extruding tip for printing graded samples that contains a turbulator to enhance the mixing of both materials. The cellulose solutions were extruded on top of a polyvinyl chloride (PVC) plate fixed to the printer’s printing bed. After the print was concluded, the PVC plate was removed from the printer, and the print material was left to complete gelation and air dry.

Extrusion nozzle diameters were chosen according to ink viscosity, desired resolution, and print duration. Extrusion nozzles with inner diameter ranging from 0.55-mm needles to 4-mm tubes were tested, which could print solutions within 1.9 and 14.0 Pa·s viscosity. Manufacturing with the printing material was possible due to its shear thinning behavior during extrusion. These theoretical viscosity values were calculated using conditions similar to the ones experienced during fabrication, with a flow rate of 0.18 ml/s in a 3-mm inner diameter tube. A series of initial experiments varying material viscosity, extrusion rate (ml/s), and printing speed (mm/s) were studied to determine the possible width range of printed filaments. The procedure consisted of extruding ink solutions with varying viscosities at a series of deposition rates (ml/mm) and recording the resulting filament width.

Stiffness gradient measurement

The measurements to demonstrate gradient properties of a sample sheet were performed on a customized setup (fig. S2). The setup was built on an inverted optical microscope (Axio Observer A1, Zeiss). The indentation force was measured by a sensitive load cell (GSO-25 and -1 K, Transducer Techniques) mounted on a computer-controlled high-precision piezo motion stage (LPS-65 2″, Physik Instrumente GmbH & Co. KG) in the z direction, with a resolution of 5 nm and a maximum velocity of 10 mm·s⁻¹. Fine positioning in the x and y directions was done by a manual xy stage (NFP-2462CC, Positionierungstechnik Dr. Meierling), and tilt correction was adjusted by two goniometers (M-GON65-U, Newport). The motion control of the piezo stages and the data acquisition were performed by a customized Linux code (Ubuntu, Canonical Ltd.). The program allowed control over preload, velocity, displacement in the x and z directions, and contact time. The load cell was linked to the computer via a signal conditioner (BNC-2110, National Instruments), and the voltage signal from the force measurement was transferred through a data acquisition board (PCIe-6259, National Instruments). The samples were intentionally curved in an arch form, and the measurements were done along the top of the arch to avoid any substrate effect (fig. S2C). For each data point, indentation stopped when the force of 0.02 N was reached. Young’s moduli were estimated according the Hertz theory

$$F=\frac{3}{4}\frac{E}{1-{\nu }^2}{R}^{\frac{1}{2}}{d}^{\frac{3}{2}}$$

where F is the force, E is the Young’s modulus, R is the radius of the force probe, and d is the indentation distance.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/8/eaay0929/DC1

Fig. S1. Effect of different mixture parameters on rheological properties.

Fig. S2. Hygroscopic properties on HEC samples.

Fig. S3. Digital fabrication workflow.

Fig. S4. Visual programming interface.

Fig. S5. Measurements of gradient mechanical properties.

Table S1. Printing materials and additives.

Movie S1. Dissolution in water.

Movie S2. Tunable deposition rate.

Movie S3. Material mixing.

Movie S4. Gradient-optimized print.

Movie S5. Programmable folding prototypes.