On the collision of rods in a quiescent fluid

Abstract

Rods settling under gravity in a quiescent fluid can overcome the bottleneck associated with aggregation of equal-size spheres because they collide by virtue of their orientation-dependent settling velocity. We find the corresponding collision kernel ${\mathrm{\Gamma }}_{\text{rods}}=l{\beta }_1\mathrm{\Delta }\rho V_{\text{rod}}g/\left(16A\mu \right)$, where $l$, $A$, and $V_{\text{rod}}$ are the rods’ length, aspect ratio (length divided by width), and volume, respectively, $\mathrm{\Delta }\rho$ is the density difference between rods and fluid, $\mu$ is the fluid’s dynamic viscosity, $g$ is the gravitational acceleration, and ${\beta }_1\left(A\right)$ is a geometrical parameter. We apply this formula to marine snow formation following a phytoplankton bloom. Over a broad range of aspect ratios, the formula predicts a similar or higher encounter rate between rods as compared to the encounter rate between (equal volume) spheres aggregating either by differential settling or due to turbulence. Since many phytoplankton species are elongated, these results suggest that collisions induced by the orientation-dependent settling velocity can contribute significantly to marine snow formation, and that marine snow composed of elongated phytoplankton cells can form at high rates also in the absence of turbulence.

Coagulation of small particles suspended in a fluid drives formation of a variety of aggregates, from flocs in papermaking (1) to raindrops in clouds (2) to marine snow in the ocean (3). Physical mechanisms generating coagulation include diffusion (4, 5), gravitational settling (2, 6), and turbulence (2, 6, 7). Here, we bring forward an additional mechanism, the collisions between identical rods settling under gravity in a quiescent fluid. In contrast to equal-size spheres, which all settle at the same velocity, rods can collide with each other because their settling velocity is a function of their orientation, which is, in general, variable within an ensemble.

The rate of coagulation is often limited by the bottleneck associated with equal-size particles (2, 3). In a quiescent fluid, identical spherical particles coagulate slowly because the particles settle at the same rate. For this reason, in clouds, the condensation–coalescence transition from micron-size to millimeter-size raindrops would take many hours, were it not for the effects of turbulence (2). Similarly, the formation of marine snow particles in the ocean is often ascribed to turbulence driving encounters between dead or senescent phytoplankton cells (3). These encounters are often modeled as occurring between spherical particles, yet most phytoplankton in the ocean are elongated (8). Here, we show that elongated particles can collide frequently even in the absence of turbulence, by virtue of their orientation-dependent settling velocity.

In a quiescent fluid, the settling velocity of an elongated ellipsoid (“rod”) pointing along the unit vector $p$ reads (9)

$$u\left(p\right)=\frac{1}{8\pi \mu l}\left({\beta }_{0}I+{\beta }_{1}pp\right)\cdot f,$$ [1]

where the gravity force is $f=\mathrm{\Delta }\rho V_{\text{rod}}g$ and the dimensionless functions ${\beta }_0$ and ${\beta }_1$ are given by ($A>1$) ${\beta }_0=A^2/\left(A^2-1\right)+\left(2A^3-3A\right){\xi }_{+}$, ${\beta }_1=-3A^2/\left(A^2-1\right)+2A{\xi }_{+}+\left(A-2A^3\right){\xi }_{-}$, where ${\xi }_{\pm }=\ln \left[A\pm {\left(A^2-1\right)}^{1/2}\right]/{\left(A^2-1\right)}^{3/2}$ (9). Eq. 1 predicts that a rod settles fastest (slowest) when its long side is aligned with (perpendicular to) gravity; the ratio between the two extremes is $\left({\beta }_0+{\beta }_1\right)/{\beta }_0$. An oblique orientation gives an intermediate settling rate, and the direction of motion is then at an oblique angle to gravity. For phytoplankton, typical aspect ratio is $A\approx 5$ [${\beta }_0=5.6$, ${\beta }_1=1.8,\left({\beta }_0+{\beta }_1\right)/{\beta }_0=1.3$], and values up to $A\approx 50$ [${\beta }_0=10.2$, ${\beta }_1=6.2,\left({\beta }_0+{\beta }_1\right)/{\beta }_0=1.6$] are not uncommon; diatom chains can have even larger aspect ratios (8). For example, chains of Skeletonema costatum or filaments of Trichodesmium are typically several micrometers wide and tens to hundreds of micrometers long. For a density difference $\mathrm{\Delta }\rho =100\hspace{0.17em}{\text{kg}\cdot \text{m}}^{-3}$, the settling speed reaches up to $100\hspace{0.17em}\mathrm{\mu }\text{m}\cdot {\text{s}}^{-1}$, and the Reynolds number is below 0.1.

For an ensemble of rods with random positions and orientations, the orientation-dependent settling velocity will induce relative motion between the rods, leading to encounters. We compute the corresponding geometric kernel ${\mathrm{\Gamma }}_{\text{rods}}$, neglecting hydrodynamic interactions. For monodisperse systems, the collision kernel $\mathrm{\Gamma }$ is defined as $\stackrel{.}{N}=\mathrm{\Gamma }{c}^2/2$, where $\stackrel{.}{N}$ is the collision rate per unit volume, $c$ is the particle concentration, and the factor of 2 corrects for double-counting pairs of identical particles (10). For a system with two types of particles of concentrations $c_1,c_2$, the kernel is defined as ${\stackrel{.}{N}}^{\prime }=\mathrm{\Gamma }\prime c_1{c}_2$ (4, 7). We first find the kernel ${\mathrm{\Gamma }}_{p_1{p}_2}$ between two subensembles of rods oriented parallel to two arbitrary directions $p_1$ and $p_2$. Averaging ${\mathrm{\Gamma }}_{p_1{p}_2}$ over $p_1$ and $p_2$ yields ${\mathrm{\Gamma }}_{\text{rods}}$.

To compute ${\mathrm{\Gamma }}_{p_1{p}_2}$, consider a subensemble of rods with random positions, all oriented parallel to $p_1$, and a single “target rod” oriented parallel to $p_2$. The rods from the subensemble and the target rod have relative velocity $\mathrm{\Delta }{u}_{12}$, which makes the collision possible. Moreover, since we neglect hydrodynamic interactions, all rods maintain their orientations as they settle. Eq. 1 implies that $\mathrm{\Delta }{u}_{12}$ is a linear combination of $p_1$ and $p_2$. Therefore, rods do not approach each other in a general position. Instead, from the ensemble of rods oriented parallel to $p_1$, only the rods that happen to move near the plane spanned by $p_1$ and $p_2$ and thus containing the target rod can collide with the target rod. As a result, the rod’s finite width must be taken into account when computing ${\mathrm{\Gamma }}_{p_1{p}_2}$.

For analytical tractability, we now treat rods as cylinders of length $l$ and aspect ratio $A$, rendering ${\mathrm{\Gamma }}_{p_1{p}_2}$ equal to, up to a factor of order $O\left(A^{-2}\right)$, twice the product of the rod width ($l/A$) and the sum of the rod lengths projected onto a plane perpendicular to $\mathrm{\Delta }{u}_{12}$ (Fig. 1A),

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_{p_1{p}_2}& =\frac{2l^2}{A}\left(|p_1\times \mathrm{\Delta }{u}_{12}|+|p_2\times \mathrm{\Delta }{u}_{12}|\right)\hfill \\ \hfill & =\frac{2l^2}{A}\frac{{\beta }_1}{8\pi \mu l}|p_1\times p_2|\left(|p_1\cdot f|+|p_2\cdot f|\right),\hfill \end{array}$$ [2]

where we used Eq. 1 to compute $\mathrm{\Delta }{u}_{12}$. Averaging over $p_1$ and $p_2$ yields the collision kernel (Materials and Methods)

$${\mathrm{\Gamma }}_{\text{rods}}=\frac{1}{{\left(4\pi \right)}^2}\iint d{p}_{1}d{p}_2{\mathrm{\Gamma }}_{p_1{p}_2}=l{\beta }_1\mathrm{\Delta }\rho V_{\text{rod}}g/\left(16A\mu \right).$$ [3]

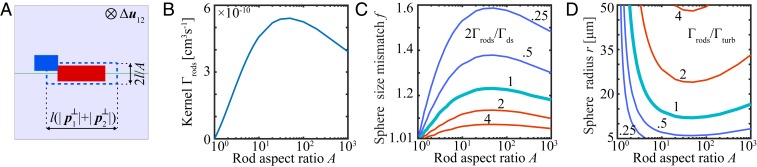
Numerical simulations agree with Eq. 3 to within less than 1%; if the cylinders are replaced with spheroids, the corresponding collision kernel ${\mathrm{\Gamma }}_{\text{rods}}^{\prime }$ can be bounded as $0.79{\mathrm{\Gamma }}_{\text{rods}}<{\mathrm{\Gamma }}_{\text{rods}}^{\prime }<{\mathrm{\Gamma }}_{\text{rods}}$ (Materials and Methods). For a fixed rod volume, the vanishing of ${\mathrm{\Gamma }}_{\text{rods}}$ as $A\to 1$ and as $A\to \infty$ represents, respectively, the lack of collisions between equal-size spheres (the bottleneck) and the fact that rods of fixed volume but increasingly larger aspect ratio cease to sink (Fig. 1B). Interestingly, Eq. 3 predicts that ${\mathrm{\Gamma }}_{\text{rods}}$ is maximal for $A\approx 50$ and that a broad range of aspect ratios are near this optimum. For example, for $A=5$, ${\mathrm{\Gamma }}_{\text{rods}}$ is only $36\%$ smaller than the optimum; such aspect ratios are typical among many elongated phytoplankton (8).

Fig. 1.

(A) The collision cross-section (blue broken line) between two rods is determined by their projections (blue and red rectangles) onto the plane perpendicular to their relative velocity $\mathrm{\Delta }{u}_{12}$. (B) The collision kernel ${\mathrm{\Gamma }}_{\text{rods}}$ for identical rods settling in a quiescent fluid (Eq. 3) as a function of the rod aspect ratio $A$ for a fixed rod volume (equivalent sphere radius $r=5\hspace{0.17em}\mathrm{\mu }\text{m}$) indicates an optimal aspect ratio of $A\approx 50$. (C and D) Comparison between ${\mathrm{\Gamma }}_{\text{rods}}$ and the collision kernels for (C) equal volume spheres colliding by differential settling due to size mismatch (Eq. 4) and (D) turbulence-induced encounters of identical spheres (Eq. 6). (C) The ratio of the encounter kernels $2{\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{ds}}$ (Eq. 5) as a function of $A$ and the sphere size mismatch factor $f$ (how much larger half of the spheres are compared to the other half). (D) The ratio ${\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{turb}}$ as a function of $A$ and the spherical particle radius $r$ (Eq. 7). Parameters are as follows: $ϵ=10^{-6}\hspace{0.17em}\text{W}\cdot {\text{kg}}^{-1}$, $\nu =10^{-6}\hspace{0.17em}{\text{m}}^2\cdot {\text{s}}^{-1}$, and $\mathrm{\Delta }\rho =100\hspace{0.17em}{\text{kg}\cdot \text{m}}^{-3}$.

Under favorable conditions, phytoplankton cells dwelling in the oceans can divide rapidly and reach concentrations of thousands of cells per milliliter, forming blooms that span kilometers and last for weeks. When blooms collapse, dead cells settle and aggregate into “marine snow” particles, which drive the biological pump, the climatically important vertical export of carbon from the ocean surface to its depth. To quantify the role of settling-induced encounters of rods in marine snow aggregation, we compare the collision kernel in Eq. 3 with the kernels for two main aggregation mechanisms for equal-size spheres (3): differential settling in a quiescent fluid due to a small size mismatch and turbulence-induced encounters of identical, neutrally buoyant spheres (Fig. 1).

For differential settling, we take half of the spheres to have radius $r$ and half to have radius $r\prime =fr$, where $f>1$ is the mismatch factor. Assuming spheres settle according to Stokes’ law, $u_{\text{sphere}}\left(r\right)=2\mathrm{\Delta }\rho g{r}^2/9\mu$, the corresponding kernel reads (2)

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_{\text{ds}}& =\pi {\left(r+fr\right)}^2|u_{\text{sphere}}\left(fr\right)-u_{\text{sphere}}\left(r\right)|\hfill \\ \hfill & =r{\left(1+f\right)}^2\left(f^2-1\right)\mathrm{\Delta }\rho V_{\text{sphere}}g/\left(6\mu \right).\hfill \end{array}$$ [4]

Taking the rods to be ellipsoids with volume equal to the volume of spheres with radius $r$, $V_{\text{rod}}=\pi l^3/6A^2=V_{\text{sphere}}$, yields the following relationship between the two kernels:

$${\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{ds}}=0.75{\beta }_1{A}^{-1/3}{\left(1+f\right)}^{-2}{\left(f^2-1\right)}^{-1}.$$ [5]

The ratio $2{\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{ds}}$ as a function of $A$ and $f$ shows that the kernels are of similar order over a broad range of aspect ratios (Fig. 1C). Unless the sphere radii differ by more than about $20\%$, we have $2{\mathrm{\Gamma }}_{\text{rods}}>{\mathrm{\Gamma }}_{\text{ds}}$, implying that orientation-dependent settling of rods causes more frequent collisions than differential settling of spheres; this holds for an even broader range of parameters if $V_{\text{rod}}$ is matched with the average $0.5\left(1+f^3\right)V_{\text{sphere}}$. The factor of 2 in the ratio arises due to the comparison between a monodisperse system of rods and the polydisperse system of two types of spheres. The collision rate in the first system is $\stackrel{.}{N}={\mathrm{\Gamma }}_{\text{rods}}{c}^2/2$ and, in the second, is $\stackrel{.}{N}\prime ={\mathrm{\Gamma }}_{\text{ds}}{c}_1{c}_2$, where $c_1=c_2=c/2$, which yields $\stackrel{.}{N}/{\stackrel{.}{N}}^{\prime }=2{\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{ds}}$.

In turbulent flow, the collision kernel for identical, neutrally buoyant spheres of radius $r$ is (7)

$${\mathrm{\Gamma }}_{\text{turb}}=1.3{\left(2r\right)}^3\sqrt{ϵ/\nu },$$ [6]

where $ϵ$ is the turbulence intensity and $\nu =\mu /{\rho }_{\text{fluid}}$ is the fluid’s kinematic viscosity. The value of $ϵ$ ranges from $10^{-10}\hspace{0.17em}\text{W}\cdot {\text{kg}}^{-1}$ in the deep ocean to $10^{-6}\hspace{0.17em}\text{W}\cdot {\text{kg}}^{-1}$ in the surface layer (11). For fixed $ϵ$, the ratio ${\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{turb}}$ reads ($V_{\text{rods}}=V_{\text{spheres}}$)

$${\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{turb}}\approx 0.05{\beta }_1{A}^{-1/3}r\mathrm{\Delta }\rho g/\left(\rho \sqrt{ϵ\nu }\right),$$ [7]

and is a function of the rod aspect ratio and the sphere radius (Fig. 1D). For a broad range of parameters, ${\mathrm{\Gamma }}_{\text{rods}}/{\mathrm{\Gamma }}_{\text{turb}}>1$, signifying that elongation can be more efficient than turbulence at forming marine snow. Clearly, the effect of shear (12) will be additional to that of settling, and turbulence will likely further increase the encounter rate between rods (13), although no general results seem to be available, to date, on turbulent encounters of rods in aquatic environments.

We have assumed isotropically distributed rods and have focused on the geometric part of the kernel, effectively setting the collision efficiency to unity (2). While Brownian effects should be negligible owing to the large typical rod length ($>100\hspace{0.17em}\mathrm{\mu }\text{m}$), rods may develop preferential orientation, and the collision efficiency will likely deviate from unity if other physical details are incorporated into the description of the collision process, most prominently, hydrodynamic effects. At nonzero Reynolds numbers, an isolated rod experiences a torque, which reorients it perpendicular to gravity (14). Furthermore, suspensions of settling rods undergo hydrodynamic instabilities (15), characterized by density fluctuations and preferential orientations, often in the direction of gravity (16, 17). For example, pairing during sexual reproduction in diatoms has been proposed to rely on such instabilities (18). When rods develop preferential orientation, an estimate of the encounter kernel may be obtained by replacing the average in Eq. 3 with a weighted average over the appropriate orientational distribution.

In summary, by finding a simple expression for the collision kernel of rods encountering one another in a quiescent fluid, we have added a fundamental case of wide applicability to the available repertoire of encounter rate kernels. We have rationalized the encounter process in terms of orientation-dependent settling velocity, which—unlike the case of spheres—leads to encounters also between identical rods. The encounter rate through this process is comparable with and often higher than the encounter rate between spheres that is induced by differential settling or turbulence. Since the latter two mechanisms are recognized as key coagulation mechanisms in marine snow formation (3), we conclude that orientation-dependent settling of elongated organisms or particles can be an important contributor to marine snow formation, and thus to the biological pump, even in the absence of turbulence.

Materials and Methods

Integrals.

To compute the average in Eq. 3, use Eq. 2 to obtain ${\mathrm{\Gamma }}_{\text{rods}}=l{\beta }_1/\left(32{\pi }^3\mu A\right)\int \int d{\mathit{p}}_{1}d{\mathit{p}}_2|{\mathit{p}}_1\times {\mathit{p}}_2\Vert {\mathit{p}}_2\cdot \mathit{f}|$, and note that $\int d{\mathit{p}}_1|{\mathit{p}}_1\times {\mathit{p}}_2|=2\pi {\int }_0^{\pi }d\theta {\sin }^2\theta ={\pi }^2$ and $\int d{\mathit{p}}_2|{\mathit{p}}_2\cdot \mathit{f}|\hspace{0.17em}=\hspace{0.17em}2\pi \mathrm{\Delta }\rho V_{\text{p}}g{\int }_0^{\pi }\hspace{0.17em}d\theta \sin \theta |\cos \theta |=2\pi \mathrm{\Delta }\rho V_{\text{p}}g$.

Numerical Tests.

We simulated $N_{\text{rods}}$ rods settling according to Eq. 1 in a cube (side $L$) with periodic boundary conditions over a time interval $T$. The kernel was estimated as ${\mathrm{\Gamma }}_{\text{sim}}=N_{\text{collisions}}{L}^3/\left(T{N}_{\text{pairs}}\right)$, where $N_{\text{pairs}}=N_{\text{rods}}\left(N_{\text{rods}}-1\right)/2$ and $N_{\text{collisions}}$ is the number of collisions. We used two protocols to sample initial conditions. In protocol A, rods were positioned randomly; the orientations were generated by $3\times 1$ vectors with normally distributed entries, normalized to unit length. In protocol B, rods were positioned on an equally spaced grid, and the orientations were generated from a spherical spiral (19). To detect collisions, we treated rods as cylinders with spherical caps: Collision occurred when the distance $d$ between the cylinder center lines satisfied $d<l/A$. Rods remained in the system after a collision.

For the two protocols, we obtained ${\mathrm{\Gamma }}_{\text{sim}}^{\text{A}}/{\mathrm{\Gamma }}_{\text{rods}}=1.0303$ and ${\mathrm{\Gamma }}_{\text{sim}}^{\text{B}}/{\mathrm{\Gamma }}_{\text{rods}}=1.0076$. Spherical caps in our collision detection scheme increased the collision cross-section by a factor of $1+\pi /2A\approx 1.016$. Correcting for this factor gave ${\mathrm{\Gamma }}_{\text{sim}}^{\text{A}}/\left(1.016{\mathrm{\Gamma }}_{\text{rods}}\right)=1.014$ and ${\mathrm{\Gamma }}_{\text{sim}}^{\text{B}}/\left(1.016{\mathrm{\Gamma }}_{\text{rods}}\right)=0.992$. Parameters were as follows: $N_{\text{rods}}=125$; $A=100$; $L=20l$; $T=8\times 10^3\tau$, where $\tau =8\pi \mu l^2/\left(\mathrm{\Delta }\rho V_{\text{rod}}g\right)$; and time step $\mathrm{\Delta }t=0.0005\tau$ (forward Euler scheme).

Cylinders vs Spheroids.

For spheroids, ellipses replace the rectangles in Fig. 1A, and the collision cross-section is an oval shape that appears to be analytically intractable. However, up to order $O\left(A^{-2}\right)$, its area is lower-bounded by the area of an ellipse with long and short axes given by $\left[l\left(\left|{\mathit{p}}_1^{\perp }\right|+\left|{\mathit{p}}_2^{\perp }\right|\right),2l/A\right]$ , which is a factor of $\pi /4\approx 0.79$ smaller than the rectangular cross-section. Thus, the collision kernel for spheroids ${\mathrm{\Gamma }}_{\text{rods}}^{\prime }$ satisfies $0.79{\mathrm{\Gamma }}_{\text{rods}}<{\mathrm{\Gamma }}_{\text{rods}}^{\prime }<{\mathrm{\Gamma }}_{\text{rods}}$.