Transcranial Focused Ultrasound Modulates Electrical Behavior of the Neurons: Design and Implementation of a Model

Abstract

Background:

Recently, ultrasonic neuromodulation research has been an important and interesting issue. Ultrasonic neuromodulation is possible by the use of low-intensity transcranial focused ultrasound (tFUS) to stimulate or inhibit the neural structures. The primary capability of this method is the improvement in the treatment progress of certain neurological and psychiatric disorders noninvasively. tFUS is able to modulate ionic currents and neural depolarization, causing the alteration in electrical properties of neurons

Objective:

The study aims to investigate the effect of tFUS waves on the electrical behavior of neurons using the simulation method

Material and Methods:

In the first part of this simulation study, the propagation of tFUS waves throughout the head was simulated to calculate the value of acoustic pressure at the cortex. In the second part, cortical neurons were simulated by a simple model of spiking neurons proposed by Izhikevich for three common dynamics. Then, the capacitance model was proposed to determine the alteration in the electrical behavior of the neurons during tFUS stimulation.

Results:

At the resting state, the electric potential of the neuron’s membrane through the tFUS stimulation has an amplitude of about 30 mv with the similar oscillatory behavior of the acoustic waveform; while,the ultimate electrical behavior of the neuron’s membrane indicates a decrease in the electric potential when the neurons fire

Conclusion:

The electrical behavior of the neuron and the range of its membrane voltage modulated during ultrasonic stimulation. The reduction in the amplitude of membrane potential was observed while neuron spikes

Introduction

In recent years, therapeutic focused ultrasound (FUS) has been an important issue not only for its noninvasive transmission through skull bone [ 1 - 3 ] but also for its ability to act upon biological tissues modulating cellular activity [ 4 ]. Apart from the use of ultrasound in diagnostic medical imaging, it can be used to interact with biological tissue as thermal or mechanical effects [ 5 , 6 ]. FUS at high intensities, known as a high-intensity focused ultrasound (HIFU), has been used for thermally ablated soft tissues with power over 1 kW/cm² [ 4 , 7 ]. On the other hand, it is shown that low-intensity focused ultrasound (LIFU) is able to modulate neural activity with no heating damage typically at the power less than 1 W/cm² [ 4 - 6 , 8 , 9 ]. Ultrasonic neuromodulation is the use of low-intensity transcranial focused ultrasound (tFUS) to stimulate or inhibit the neuronal activity without any concomitant brain damage.

Ultrasonic neuromodulation has superior advantages over conventional neuromodulation techniques such as deep brain stimulation (DBS), transcranial magnetic stimulation (TMS), and transcranial current stimulation (tCS). DBS technique, for example, requires a surgical procedure causing risk of infection and immune responses [ 10 ]. Furthermore, both TMS and tCS are limited by the fact that the stimulation fields cannot be highly controlled due to the lack of spatial specificity and penetrability required for targeting a deep-seated brain region [ 11 ]. However, repetitive TMS (rTMS) can treat certainly neurological and psychiatric disorders such as Parkinson’s disease, tinnitus, depression, stroke [ 12 - 14 ]. In efforts to overcome some of the limitations posed by these techniques, investigations into the use of ultrasound have begun to demonstrate new possibilities for interfacing with neurobiology using mechanical forces. Although the mechanism by which tFUS achieves neuromodulation is not known, it could be related to transient changes in cell membrane permeability [ 8 ]. With respect to the previous investigations at the microscopic level, high-intensity ultrasound can suppress neural activity due to widening synaptic clefts and decreasing the sizes of the presynaptic and postsynaptic densities [ 9 ]. Tyler et al. showed that low-intensity ultrasound (<300 mW/cm²) and low-frequency ultrasound (<0.65 MHz) are capable of stimulating action potentials and synaptic transmission [ 15 ].

Furthermore, considering the mechanosensitive properties of voltage-gated ion channels, acoustic radiation forces made by the interaction of ultrasound and lipid bilayers may lead to the opening of voltage-gated channels [ 16 , 17 ]. As a result, the hypothesis is that ultrasound may produce local membrane depolarization, and it is capable of modulating ion channel activity [ 18 ]. This study aims to provide a model to investigate the effect of transcranial focused ultrasound waves on the electrical behavior of neurons.

Material and Methods

Transcranial Focused Ultrasound Wave Simulation

In this simulation study, to gain the acoustic pressure of the transcranial focused ultrasound waves at the focal point, a simple numerical model was constructed using k-Wave MATLAB toolbox (http//k-wave.org) [ 19 ]. This model was designed for the time-domain simulation of propagating acoustic waves in 2D using a k-space pseudospectral method.

Geometry of simulation

The geometry of the simulation is a 2-dimensional medium shown in Figure 1. Since acoustical parameters of the cerebrospinal fluid and brain are close to each other, the simulated medium consists of the brain and skull with the following parameters given in Table 1. A bone layer was defined adjacent to the transducer, and both tissues were supposed as a homogenous tissue [ 20 - 22 ]. Calculations were performed in a computational grid with a 0.46 mm grid point size according to the Nyquist limit of two grid points per wavelength [ 23 ]. An absorption layer was defined around a computational grid with a thickness of 0.92 cm in order to absorb the acoustic waves when they reached the edges of the computational domain [ 24 ].

Figure1.

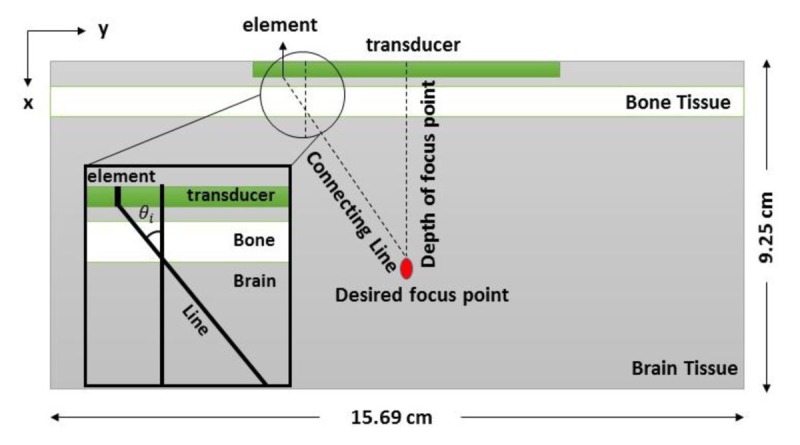
2-dimensional simulated medium and the linear phased array transducer.

Table1.

Acoustical properties of tissues in the simulated medium [22].

Tissue	Sound Speed (m/s)	Density (kg/m3 )	Acoustic Absorption Coefficient (dB/cm MHz)
Brain	1560	1040	0.58
Skull	3200	1990	3.5

tFUS waveform

According to the study carried out by the Hayner et al., the optimal gain between transcranial transmission and brain absorption for the acoustical neuromodulation is 0.4-0.7 MHz [ 25 ]. Moreover, there is a possibility of gaining appropriate power to stimulate the brain tissue at frequencies less than 0.5 MHz [ 26 ]. Hence, the frequency of 0.5 MHz was selected to be propagated in the medium with a linear Phased Array Transducers (PATr). The parameter of transcranial ultrasonic waveform was obtained from a study carried out by Mueller et al. To produce a stimulus duration of 0.5 s yielding a peak rare factional pressure of 0.80 MPa, the employed waveform for tFUS stimulation had parameters, including acoustic frequency(Af) = 0.50MHz, pulse duration (PD) = 360 µs, pulse repetition frequency (PRF) = 1.0 kHz and number of pulses (np) = 500 [ 27 ].

Neural Model Simulation

In order to simulate signals generated in the cerebral cortex, we used a simple model of spiking neurons proposed by Izhikevich [ 28 ]. According to the 20 neuro-computational features, Izhikevich model is not only biologically plausible as the Hodgkin–Huxley model but also computationally efficient as the integrate-and-fire model.

v'=0.04v²+5v+140-u+I

u'=a(bv-u)

With the auxiliary after-spike resetting


$\mathrm{if\; v\ge 30\; mV.\; then}\{\begin{array}{c}\mathrm{v\leftarrow c}\\ \mathrm{u\leftarrow u+d}\end{array}$

Four parameters of the model employ reproducing spiking and bursting behavior of common types of cortical neurons, including regular spiking (RS), intrinsically bursting (IB) and chattering (CH). The parameter α describes the time scale of the recovery variable u and its typical value is α=0.02. The parameter b describes the sensitivity of the recovery variable u to the subthreshold fluctuations of the membrane potential υ, and its typical value is b= 0.2. The values of c and d depend on the types of dynamics. For RS, IB and CH, the value of c is -65mV, -55mV and -50mV and the value of d is 8, 4 and 2, respectively

Mechanical-Electrical Model

To investigate the effect of tFUS on the electrical behavior of neurons, the capacitance model has been suggested. The main assumption of the model is that the acoustic pressure of tFUS modulates electrical properties of the neuron membrane during the stimulation. In this study, the membrane is considered as a capacitor. Therefore, the fact that how the cell membrane potential responses to the flow of ion channel currents is associated with both membrane capacitance and membrane resistance. The capacitance of a capacitor is altered since the mechanical force is applied to the membrane of a neuron. Capacitance changes because of decreasing the distance between the plates. The mass-spring model was employed to calculate the change in the membrane potential. In resting neurons, membrane potential was estimated based on time-variant acoustic pressure using the following equation

V (t) = (QA₁/kϵ₀KA) P (t)

Where Q is the electrical charge across the cell membrane of a neuron, and A₁ is the area of membrane affected by mechanical force; in addition, k, ϵ₀ and ϵare the spring constant, the permittivity of free space and the relative permittivity, respectively. Moreover, K, A, and d are the dielectric constant, the cell membrane surface and the distance between two phospholipid bilayer, respectively. Model parameters values are provided in Table 2. Besides, since the relative permittivity values depend on the frequency, Table 3 shows the value of gray matter relative permittivity in term of frequency [ 29 ].

Table2.

Parameters values for neuron

Q	A 1	k	ϵ0	K	A	ϵ
7 × 10-10 C	10 μm2	0.2 N/m	8.85 × 10-12 F/m	9	930 μm2	1181

Table3.

The value of gray matter relative permittivity in term of frequency [29].

f (KHz)	100	200	300	400	500	600	700	800	900	1000
ϵ × 10 3	3.222	1.961	1.55	1.324	1.181	1.08	1.005	0.946	0.899	0.86

In spiking neurons, the mechanical-electrical model was modified in respect of neural encoding hypothesis. Acoustic pressure and action potential considered as a stimulus and feature of the system, respectively; thus, neuron response could be predicted in reference to electric potential alteration.

Results

Simulated tFUS wave

According to the tFUS waveform parameters, US wave was simulated based on phased array transducer (PATr) propagating in the simulated geometry. In this method, the focal point is determined using the timing of the input electronic signals. Figure 2 reveals the distribution of the acoustic pressure waves surrounding the focal point throughout the whole time simulation. The amplitude of the transducer acoustic pressure is 0.8 MPa while the pressure obtained at the focal point is 0.6 MPa (Isppa = 58.85 w/cm²) indicating attenuation of propagating waves due to the presence of the bone layer.

Figure2.

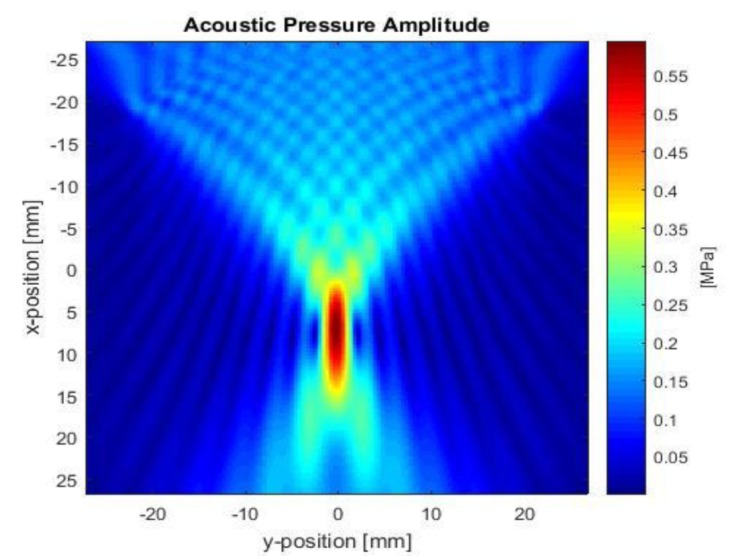
Ultrasound can be noninvasively focused through the human skull bone. The amplitude of acoustic pressure at the focal point is 0.6 MPa.

Neural modeling before and after tFUS stimulation

Electrical behavior of the cortical neurons was simulated based on different types of dynamics. Spiking and bursting behavior of RS, IB, and CH neurons are shown in Figure 3. Figure 4 displays a three-step approach to gain the ultimate time-variant electric potential of each neuron during the first 10 ms of tFUS stimulation. The first column is the action potential of a neuron depending on the spiking dynamic. The second column is the calculated electric potential resulting from the tFUS stimulation, and the third column is the final membrane potential of a neuron during tFUS stimulation. RS neurons fire as a spike frequency adaption which has a few spikes with short interspike period and then increases in the period. IB neurons fire a stereotypical burst of spikes followed by repetitive single spikes and CH neurons can fire stereotypical bursts of closely spaced spikes [ 28 ]. The electric potential resulting from the tFUS stimulation has a peak voltage of a 30 mV, which is the acceptable value according to the typical action potential value. When neuron spikes during the tFUS stimulation, the pattern and amplitude of action potential change. The modified action potential has a similar oscillatory behavior to the acoustic waveform, although its amplitude reduces from 30 mV to 1-4 mV.

Figure3.

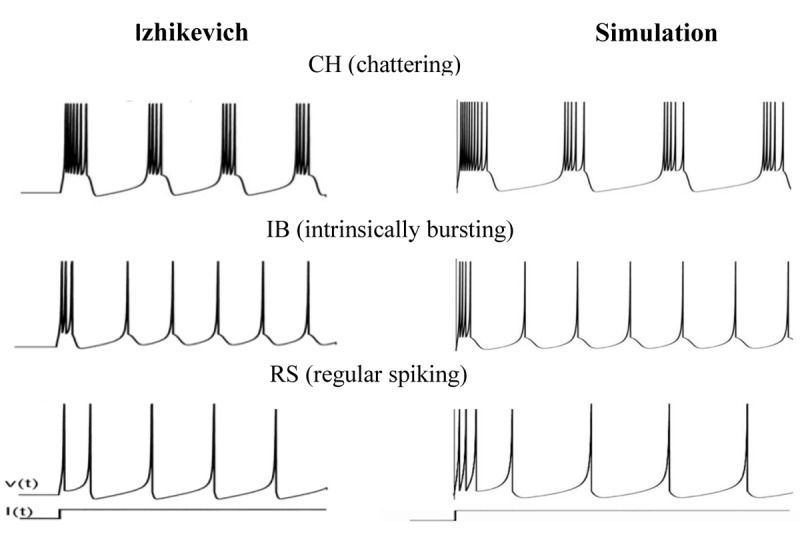
Firing patterns of cortical neurons in the Izhikevich model and simulated neural model [28].

Figure4.

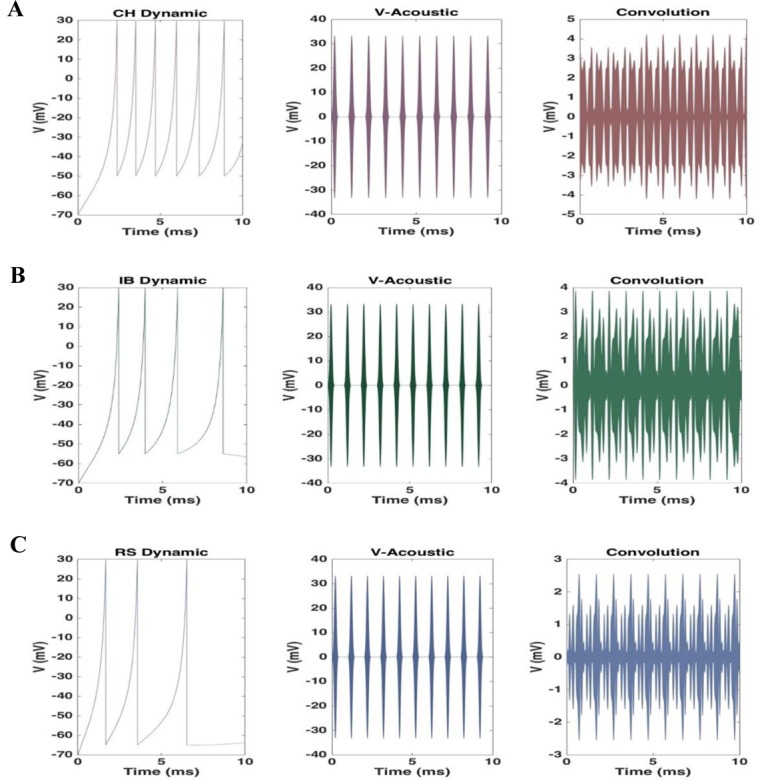
A three-step approach to gain the ultimate time-variant electric potential of each neuron during the first 10 ms of tFUS stimulation for A. CH dynamic, B. IB dynamic, and C. RS dynamic.

Discussion

Some years ago, significant advances were affirmed in the use of tFUS as a non-invasive tool for interacting with brain activity, not only for patients with neurological disorders or disabilities but also for the cognitive function. Ultrasonic Neuromodulation is possible through the use of tFUS to stimulate or inhibit the neural structures. In this study, a general model is proposed to simulate the effects of tFUS on the electrical behavior of neurons. First, the acoustic waves with effective neuromodulation parameters simulate through the head; then, the mechanical-electrical model shows how the acoustic pressure affects the neurons membrane potential. With respect to the proposed model as well as other experimental studies, tFUS may modulate the electrical behavior of neurons.

Acoustic wave

Ultrasound waves are able to destroy biological tissues; thus, it is crucial to exposure properties such as pressure amplitude, pulse duration, and frequency set properly. Significant thermal fluctuation and inertial cavitation can induce damage in soft tissues. In order to control thermal fluctuation, we used pulsed mode instead of continues mode in the tFUS transducer. Short stimulation time leads to generate low thermal in the tissue due to the absence of static waves, that is not sufficient for tissue damaging [ 30 ].

Furthermore, inertial cavitation rarely produces damage in soft tissues at pressures <40 MPa because there are no gas bodies in most soft tissues, including the brain [ 5 ]. Besides, ultrasound waves with peak rare-factional pressures<1 MPa have been effective for neuromodulation in the lack of cavitational damage [ 15 ]. As a result, 0.8 MPa, which is used in our study, is not only capable of modulating neuronal activity but also safe.

According to studies, the optimal gain between transcranial transmission and brain absorption for the acoustical neuromodulation is 0.4- 0.7 MHz [ 25 ]. If the frequency increases, the absorption in the tissue will also increase. Thus, there is a considerable possibility of tissue-damaging based on heat increment. On the other hand, the lower frequencies not only have no adequate absorbed energy for neuromodulation but also increase the chance of resonance in the skull [ 26 ]. Therefore, the aforementioned reasons led us to the fact that 0.5 MHz frequency is the best option for tFUS neuromodulation. In addition, the value of ISPPA in our study was calculated 58.85 w/cm² which is below the output limits established by the United States Food and Drug Administration for diagnostic imaging purposes = 190 w/cm²; and it is big enough for neuromodulation [ 15 ]. It is clear that if the acoustic pressure value is lower than the limit, the tissue will not have any damage during acoustic neuromodulation.

Microscopic level

The resting membrane potential of the neuron is about -70 mV. Besides, the ultimate value of the external voltage, which is applied to the membrane of a neuron in the presence of the ultrasonic stimulation, had a peak of about 30 mV. Therefore, the variation of the external electric potential is biologically meaningful, and neurons are able to conceive and response to these changes.

To better understand what happened to neurons and their membrane potential during ultrasound stimulation, we examined a dipole as a group of neurons instead of a single neuron. We know that the number of neurons in the cortex is about 24 billion, and the total area of the cortex is 2400 cm². Given that there is a dipole per square millimeter, the number of neurons in a dipolar is equal to 10⁵. The applied ultrasonic wave had a frequency and wavelength of 0.5 MHz and 3 mm, respectively, and also there is a dipole per mm square. Thus, each ultrasound pulse affected several neurons simultaneously (np = 500). Since some of these neurons are in the resting state, and some of them fire; the electrical behavior of all neurons may not be affected throughout one pulse duration. On the other hand, as previously mentioned in the method section, we used 1 KHz pulse train instead of a single pulse, which means that 500 pulses were applied to the neurons during tFUS stimulation. As a result, all the neurons were modulated by the ultrasound waves ultimately. Due to the constant exposure of tFUS, neurons modulated persistently. During one action potential, 10-15 ultrasound pulses applied to the neuron. Consequently, the electrical behavior of the neuron was expected to be entirely influenced by the acoustic pressure pulse. In the final convolution of an action potential and the external potential, the pattern of neuron’s dynamic would not be seen. Furthermore, the ultimate amplitude of electric potential of the neuron after stimulation indicates decrement into several mV in all dynamics in which the decrease in RS dynamic is more significant due to lack of bursting. These results are consistent with a study carried out by Juan et al. in 2014 that indicates the reduction of the action potential’s amplitude during ultrasound stimulation [ 31 ].

Hypothesis

The underlying mechanism of ultrasound neuromodulation has been still unclear. Tyler represented two approaches to investigate the possible mechanisms, including potential and continuum mechanism based on several studies [ 30 ]. Potential mechanism’s hypothesis which has the electrical activity of neural circuits, can be modulated using ultrasound. The mechanical change in membrane tension may alter ionic flux and local membrane depolarization activating voltage-gated Na+ channels and modulating K+ influx and efflux. [ 9 , 15 ]. These changes lead to the fact that ultrasound is able to induce action potentials and trigger synaptic transmission. In continuum mechanism, the effect of ultrasound on the dynamics of cerebrospinal fluid (CSF) in the extracellular space of the brain is discussed. The hypothesis reveals that the fluid-mechanical consequences such as acoustic streaming, acoustic radiation force, and stable cavitation occur due to the acoustic impedance mismatches between lipid bilayers and surrounding intracellular/extracellular fluids [ 32 , 33 ]. As a result, ultrasound can noninvasively modulate neuronal activity.

Conclusion

In this paper, we propose the mechanical-electrical model to investigate the effect of low-intensity tFUS on neuronal activity. With respect to the proposed model, the electrical behavior of the neurons and the range of theirmembrane voltage changed during ultrasonic stimulation. The reduction in the amplitude of membrane potential was observed while neuron spikes.