Lymphoidal chemokine CCL19 promoted the heterogeneity of the breast tumor cell motility within a 3D microenvironment revealed by a Lévy distribution analysis

Abstract

Tumor cell heterogeneity, either at the genotypic or the phenotypic level, is a hallmark of cancer. Tumor cells exhibit large variations, even among cells derived from the same origin, including cell morphology, speed and motility type. However, current work for quantifying tumor cell behavior is largely population based and does not address the question of cell heterogeneity. In this article, we utilize Lévy distribution analysis, a method known in both social and physical sciences for quantifying rare events, to characterize the heterogeneity of tumor cell motility. Specifically, we studied the breast tumor cell (MDA-MB-231 cell line) velocity statistics when the cells were subject to well-defined lymphoid chemokine (CCL19) gradients using a microfluidic platform. Experimental results showed that the tail end of the velocity distribution of breast tumor cell was well described by a Lévy function. The measured Lévy exponent revealed that cell motility was more heterogeneous when CCL19 concentration was near the dynamic kinetic binding constant to its corresponding receptor CCR7. This work highlighted the importance of tumor microenvironment in modulating tumor cell heterogeneity and invasion.

INSIGHT, INNOVATION AND INTEGRATION

Heterogeneity is a hallmark of cancer. However, quantitative understanding of tumor heterogeneity is lacking, in particular, in the context of tumor microenvironment. Using an integrated microfluidic and Lévy statistical analysis approach, we found that cytokines within the tumor microenvironment promoted the heterogeneity of the tumor cell motility. Our work provided a novel physical insight in which cytokines within tumor microenvironment modulated tumor invasion and metastasis.

INTRODUCTION

Mammalian cell motility plays critical roles in many homeostatic (e.g. immune response and tissue formation) and pathologic (e.g. tumor cell invasion and fibrosis) processes [1–4]. In all cases, cells migrate to perform their physiological function, e.g. immune cells move toward the site of infection to kill bacteria [3, 4]; tumor cells migrate to foreign organs to establish a new tumor [2, 5]. While it has been established that in these native states animal cells execute random walks within interstitial spaces [4, 6], it is only recently that single-cell migration statistics was examined carefully at a quantitative level [7–9]. These works reveal that results from population average are not sufficient to describe cell motility. Rather, rare cell events contribute significantly to the cell physiology and pathology, in particular in the case of tumor cell invasion.

Tumor cell heterogeneity is a hallmark of cancer [10, 11]. Although a majority of tumor invasion assays (e.g. Boyden chamber) only provide population-based information, recent development in microfluidic device and imaging technology has enabled the study of single-cell dynamics in both time and space [12, 13]. These studies revealed that mammalian cells did not execute random walks that followed the Gaussian distribution typically seen in the passive Brownian motion of micro- or nano-meter-sized particles in the equilibrium state established in a uniform environment [14]. Using an in vitro model, metastatic cancer cells migrating along linear micro-tracks were shown to follow Lévy like movement, in contrast to non-metastatic cells [9]. Tumor cells migrating within 3D collagen matrices demonstrated that the distribution of cell speed followed an exponential decay function [7]. Interestingly, immune cell migration within a mouse model showed that T-cell migration followed a generalized Lévy walk distribution [8]. Lévy walk has also been found recently in the motility of single swimming bacteria within a swarm where a group of bacteria move collectively [15]. Taken together, previous work revealed that rare cell statistics is a common feature of migrating cells, and we note that both Lévy statistics and exponential models feature a long tail favoring cell spreading in space or rare fast moving cell events. Lévy statistics has long been studied extensively in diverse fields, including the financial market, fluid mechanics and biological science, for the purpose of quantifying rare occurring events [16–18]. Indeed, rare tumor cell motility events such as the fast movers are important role players in cancer metastatic processes [19]. Here, we hypothesize that tumor cell migration follows a Lévy distribution, and its heterogeneity can be influenced by the cytokine concentration within the tumor microenvironment and quantified by the Lévy exponent.

Lymphoid chemokines are important components in the tumor microenvironment and have been implicated in breast cancer metastasis [20]. Lymph nodes are the first metastatic sites for many cancer types including breast and prostate cancers [21]. It has been estimated that ~80% of the solid tumors disseminate via lymphatic systems, in contrast to ~20% via blood vessels or direct seeding [22]. Traditionally, the lymphatic system is considered to play a passive role in tumor cell metastasis, and tumor cells landed in lymphatic system due to its high permeability and the absence of a basement membrane barrier. Recent work, however, suggests that the lymphoid system is an active player in mediating tumor cell invasion. Chemokine receptors were found to be highly expressed in malignant breast tumor cells [20], and the activation of the lymphatic system including lymphangiogenesis was associated with tumor progression and metastasis [23]. Muller et al. profiled all the chemokine receptors using 12 human breast tumor cell lines and found that the expression of CCR7 and CXCR4 peaked relative to other receptors [20]. CCR7 is a G protein-coupled receptor, known to regulate actin polymerization, pseudopodia formation, and consequently modulation of cell migration. CCR7 is also known as a lymphoid chemoreceptor, its binding ligands are CCL19 (soluble) and CCL21 (matrix binding). CCL21 is a potent chemokine in directing tumor cell migration and has been studied extensively [24, 25]. In contrast, the role of soluble ligand CCL19 in tumor cell migration is much less understood [2, 20, 21]. Here, we choose breast tumor cells (MDA-MB-231 cell line) embedded within a 3D collagen matrix as a model system to examine roles of the chemokine CCL19 in tumor cell invasion.

In this article, we explored breast tumor cell migration statistics under well controlled CCL19 gradients using a 3D microfluidic model. We focused on the quantitative evaluations of rare cell motility and its correlation with cytokine gradient within the tumor microenvironment.

RESULTS AND DISCUSSIONS

Microfluidic setup for creating cytokine gradients within a 3D extracellular matrix

Microfluidic model is an enabling technology for providing well-defined chemokine gradients for tumor cells. Its compatibility with optical imaging allows for probing single-cell dynamics in real time and space [12, 26]. Previously, we employed a microfluidic model for studying dendritic as well as tumor cells migrating within a 3D collagen matrix and in cytokine gradients [24, 25]. The 3D environment is important for cell migration studies as most mammalian cells require the architectural support within the 3D ECM to execute physiologically realistic motion. Indeed, results from studies of cell migration behavior on a 2D substrate are very different from those in 3D [27, 28]. Here, we used a microfluidic platform previously developed in our lab to study breast tumor cell (MDA-MB-231 cell line) dynamics in response to the gradients of lymphoid chemokine CCL19 [29]. As seen in Fig. 1a, three parallel microfluidic channels were patterned in a 1-mm-thick agarose gel membrane. CCL19 of various concentrations and buffer were introduced along the two side channels, respectively, and cell embedded collagen matrix was introduced into the center channel. A CCL19 gradient was established across the center channel via the molecular diffusion through the agarose gel walls [24, 25]. Four such devices were patterned on a single microfluidic chip for parallel experiments. Figure 1b is an image of the cells reconstructed from a z-stack image taken at a time t = 0 showing that cells were embedded in 3D. Due to the gel polymerization method we used (See Materials and Methods), most of the cells were located in the mid-z plane of the cell channel as seen in the x-z plane of the image. Using time series images such as the one shown in Fig. 1b, we evaluated cell migration speed, velocity and persistence length as illustrated in Fig. 1c.

Figure 1.

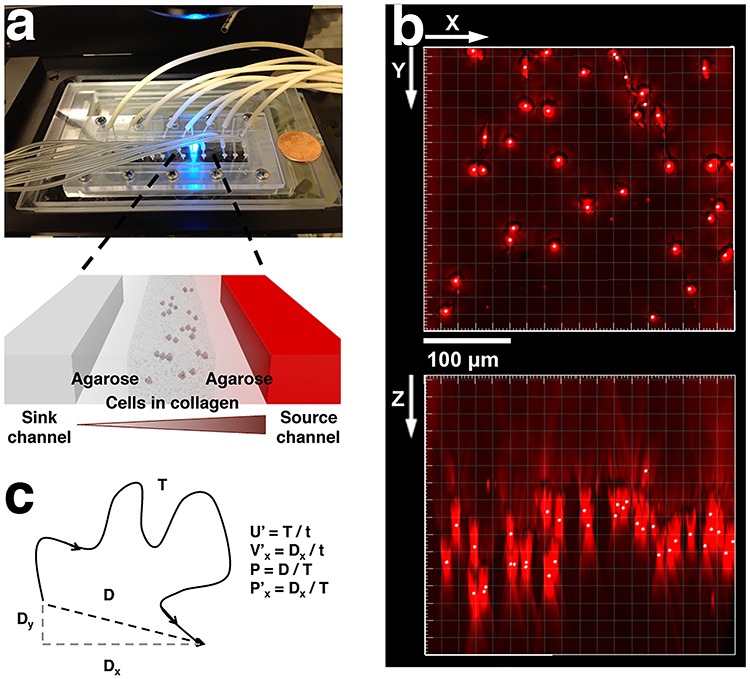
A microfluidic setup for 3D tumor cell migration in CCL19 gradients. (a) Top view shows a photo of the microfluidic chip on a microscope stage. Each chip contains four identical three-channel devices. Zoom in view shows that each device contains three parallel channels with a width of 400 μm and a depth of 250 μm. The gaps between the channels are 250-μm wide. Cell embedded collagen matrix is seeded in the center channel, cytokine/buffer flow through the two-side channels, respectively, and a concentration gradient of the cytokine is formed in the center channel via molecular diffusion. (b) 3D reconstruction of embedded cell images from a z-stack of images taken at time t = 0. Here, x-y represents the horizontal plane, and z the vertical direction. (c) Definition of migration parameters, speed, velocity, persistence length, and x-directional persistence length. Here, x-axis represents the direction of gradient.

Breast tumor cells displayed a distinct chemokinesis but a mild chemotactic tendency in CCL19 gradients

Individual cell tracks under various CCL19 gradients (Fig. 2a) were obtained using time series images. Tumor cell motility was clearly seen to increase with the increase of CCL19 chemokine gradients ranging from 0 to 111 nM/mm. This was also reflected in the percentage increase of migrating cells (Fig. 2b) and the average cell speed at five different CCL19 gradients (Fig. 2c). The cell speed peaked (or increased 34%) at CCL19 gradient of 111 nM/mm or average CCL19 concentration of ~ 50 nM. In contrast to the significant chemokinesis behavior (Fig. 2c), MDA-MB-231 cells showed mild chemotaxis behavior in CCL19 gradients (Fig. 2d). Here, the average velocity as well as the persistence length along the direction of CCL19 gradient (or + x direction) were positive in comparison to control but increased less than 5% of its control velocity (Fig. 2d and e).

Figure 2.

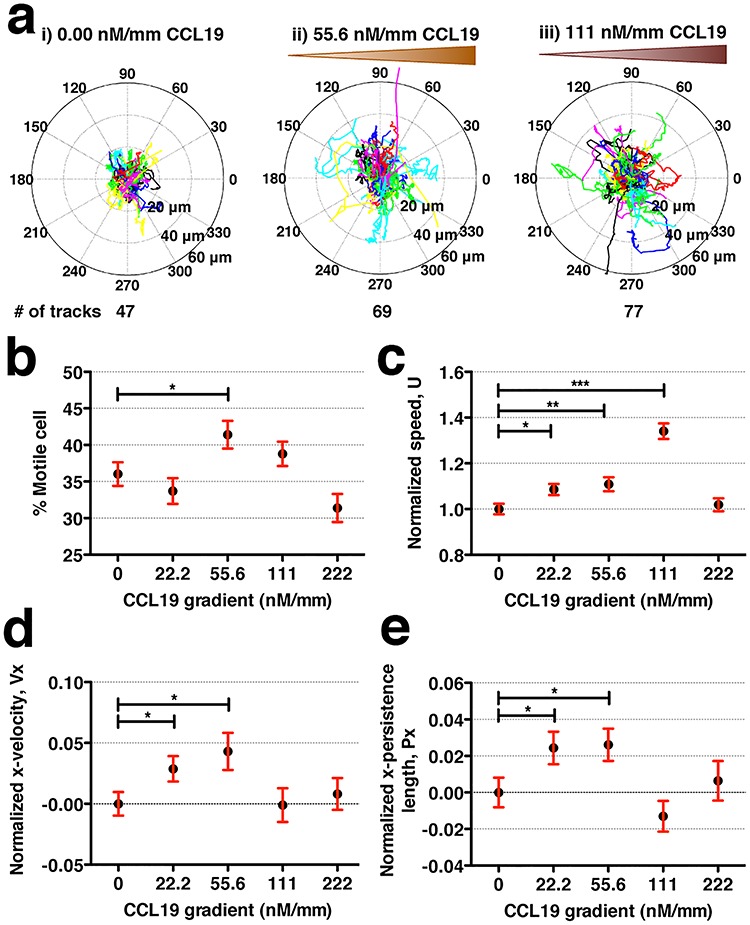
MDA-MB-231 cells show distinct chemokinesis and mild chemotaxis behavior in CCL19 gradients. (a) Polar plots of cell tracks, each 8-h long, under the CCL19 concentration gradient of (i) 0, (ii) 55.6 and (iii) 111 nM/mm CCL19. (b) Percent of migrating cells at various CCL19 concentration gradients. Here, the definition for migrating cells is that the standard deviation of cell displacement in x-direction is larger than 2 μm and y-direction is larger than 2.5 μm in 16 h. (c–e) Normalized cell speed (c), normalized cell velocity along gradients (d) and normalized persistence length along gradients (e) under various CCL19 concentration gradients. Student t-test is used for statistical analysis with ^* for 0.01 < P < 0.05, ^** for 0.001 < P < 0.01 and ^*** for P < 0.001.

Tumor cell speed responded to CCL19 gradients most sensitively at CCL19 gradients of 111 nM/mm or average concentration of 50 ± 25 nM (see Fig. 2c), which was close to the reported dynamic kinetic constant between CCL19 and CCR7 100 ± 40 nM [24, 25]. We previously obtained a dynamic kinetic binding constant of 100 ± 40 nM for CCL19 and CCR7 [25] using dendritic cell chemotaxis in CCL19 gradients, in which we demonstrated that the chemotactic sensitivity of dendritic cells to CCL19 gradients was proportional to the difference of the fractional ligand-receptor occupancy at the front and back of the cell [25]. Thus, the ultrasensitivity of G protein-coupled receptors to the external ligand close to the dynamic kinetic constant regime shown here was consistent with the ligand-receptor occupancy model proposed in [25]. We also note that this dynamic kinetic constant was close to the CCL19 concentration at which T-cell speed peaked in a separate study [30]. The kinetic binding constant from traditional biochemical assays using isolated CCR7 receptors along the CCL19-CCR7 axis was typically smaller and less accurately determined, reported to be 0.1–10 nM [31, 32].

The maximum cell speed increase of 34% due to CCL19 gradients is significant in comparison to the impact of other cytokines traditionally considered to be potent for promoting tumor cell invasion. Previously, we reported that the maximum speed increase of tumor cells (MDA-MB-231 cell line) was 12.5% in an epidermal growth factor (EGF) gradient and was 13.2% in an SDF-1α (ligand to chemokine CXCR4) gradient, two potent cytokines implicated in breast tumor metastasis [33]. There also existed distinct differences in the motility responses of tumor cells and murine dendritic cells (mDCs) to the presence of CCL19 gradients. A previous study in our labs using the same microfluidic setup showed that mDCs displayed mild chemokinesis but distinct chemotaxis in CCL19 gradients [25]. The highest speed percent change was 10% for mDCs, in contrast to 34% for tumor cells; the highest normalized x-velocity is 0.2 for mDCs in contrast to 0.05 for tumor cells when subjected to the same range of CCL19 gradients. These results indicate the intrinsic differences between immune and tumor cells; in that, immune cells utilized directed motion to reach their destination efficiently, while tumor cells may need to rely on enhancing its speed or heterogeneity when invading. We note that the steep response to the chemokine concentration gradients reflects the sensitive nature of G-protein-coupled receptor to the external ligands.

The heterogeneity of the tumor cell motility was modulated by CCL19 gradient

Tumor cells are known to display the high level of heterogeneity both in their genotypic and phenotypic behaviors. When taking a close look at the cell trajectories, we find various types of cell trajectories for breast tumor cells migrating within a 3D extracellular matrices. Figure 3a–c shows three sample trajectories typically seen in our experiments. Figure 3a is a breast tumor cell that stops and goes reminiscent of E. coli motion in which the cell runs or tumbles [34]. Note that the time between two consecutive dots in each trajectory is the same (8 min), and thus clustered dots indicate that the cell does not move. Figure 3c is a cell that moves smoothly. Figure 3b shows a track that a majority of cells follow, which is between a stop and go motion (Fig. 3a) and a smooth motion (Fig. 3c). To quantify cell motility heterogeneity, we first calculated the distribution of cell speed at various CCL19 gradients. In Fig. 3d, we see that the normalized speed distribution appears to become wider and shifts to the high speed end with the increase of CCL19 gradients. This means that there are more fast movers at high CCL19 concentration. At the single-cell level, the cell motility heterogeneity can be visualized by the scatter plots of persistence length versus cell speed as shown in Fig. 3e–h for various CCL19 gradients, where each dot represents one cell. Clearly, the rare events (represented by high speed and high persistence length) occur more often in Fig. 3h (111 nM/mm) than in Fig. 3e (no CCL19). Previously, we studied 3D breast tumor cell motility in the presence of EGF using a similar experimental setup. Performing a similar data analysis as in Fig. 3, we observed a similar trend for cells in the presence of EGF gradients (Supplementary Fig. S1). EGF is used here because it is a well-known growth factor that promotes tumor invasion and progression [33, 35].

Figure 3.

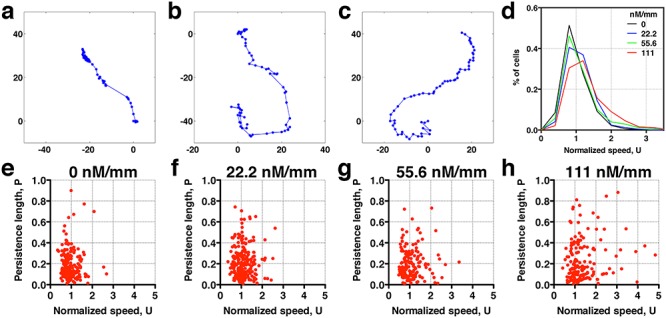
Rare cell motility events are modulated by cytokine (CCL19) availability. Sample single-cell trajectories: (a) stop and go; (b) in-between ‘stop and go’ and ‘smooth’ track motion; and (c) smooth motion. Here, each dotted line is a cell track of about 16-h long; the time between the two consecutive dots is 8 min. (d) Distribution of normalized cell speed under various CCL19 gradients. The occurrence of fast moving cells increases with CCL19 gradients, indicating thicker tail distribution. (e and f) Scatter plots of persistence length and normalized speed in various CCL19 gradient: 0.00 (e), 22.2 (f), 55.6 (g) and 111 (h) nM/mm. Each dot represents data taken from one cell track. The number of cells is 244 in each of the four concentration gradients.

MDA-MB-231 cell velocity followed a Lévy tail distribution

To establish that the tail end of the cell velocity distribution follows a Lévy function, we comparatively fitted the whole velocity distribution to a Gaussian versus a Crystal ball function (equations (1) and (2)), and also the tail end of the distribution to a Lévy versus an exponential function (equations (3) and (4)). Gaussian distribution is known to describe Brownian motion of small particles in fluids due to thermal fluctuation in an equilibrium system. Our choice of Gaussian function as a proposed model is based on the fact that cells are micrometer in length scale, and they execute random walks. Crystal ball function is composed of a Gaussian core in the low-velocity region and a Lévy function in the large-velocity region (equation (2)). It has been commonly used in high-energy physics to account for rare events. We used Crystal ball function here to account for the rare fast moving cells. Strictly speaking, it is the tail behavior of the Lévy stable distribution that converges to a power law; we thus used the tail end distribution to fit a Lévy function/power law. The exponential function was used here for comparison purpose due to a previous report where exponential function was used to describe tumor cell motility [7, 36].

The four functions we used are defined in the following:

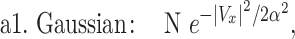(1)

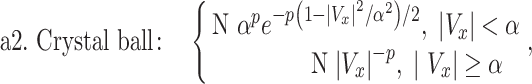(2)

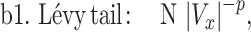(3)

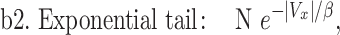(4)

where V_x is the normalized velocity along x-axis, N is the normalization factor for the distribution, α is the standard deviation in Gaussian distribution, p is Lévy exponent and β is an exponential decay factor. The crystal ball function is constructed such that the function and its derivative are continuous at the boundary between Gaussian core and power law at V_x = α. Equations (1) and (2) were used to fit the whole velocity distribution, while the tail end of the velocity distribution was used to fit equations (3) and (4).

We note that a modular scientific tool kit, root (an open source software, https://root.cern.ch), commonly used to perform statistical analysis in high-energy physics was used for all the fitting. Root is an easily adaptable and a highly versatile data analysis tool; it allowed us to fit various functions and to carry out statistical analysis in a straightforward way.

The fitted results in Fig. 4a showed that the distribution of V_x was best described by a Crystal ball function in contrast to a Gaussian distribution. To determine the goodness of a fit, we used the probability value (pv) evaluated from χ² and the number of degrees of freedom. In Fig. 4a, we obtained a probability value of 0.9996 from a fit to the Crystal Ball function, and 0.0003 to the Gaussian function. Note pv = 1 represents the best fit, and pv = 0 poor fit. We also used a second criterion, Akaike Information Criterion weight (wAIC), from AIC to determine which function is the best model. As seen in Fig. 4a, the results from Akaike weight calculation were consistent with the conclusion that crystal ball is a better model of the two.

Figure 4.

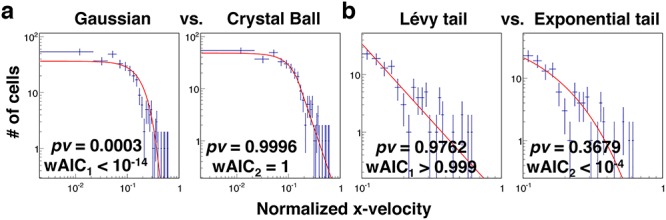
MDA-MB-231 cells follow Lévy but not Brownian statistics. The distribution of the normalized x-velocity is fitted to various statistical models. Dotted lines are from experiments with no CCL19 (control), and solid lines are fits to the models. (a) The fits to Gaussian versus Crystal ball function. (b) The fit to the tail end of the data to Lévy and exponential model. Here, pv is the probability value calculated using a chi-squared calculator, representing the goodness of fit. The best fit is represented by pv = 1. wAIC is the Akaike weight from Akaike Information Criterion, a second criterion used here to evaluate the goodness of fit.

The fitted results in Fig. 4b showed that the tail end of the distribution was better fitted to a Lévy function in contrast to an exponential function. The cutoff in V_x for tail end was determined by the α value obtained in the previous fitting (Fig. 4a, left panel). We obtained P-value (pv) of 0.9762 for Lévy function, 0.3679 for exponential tail function. This trend was reflected in the values of Akaike weight wAIC as well. To verify the robustness of the results, we repeated the above analysis using the data of MDA-MB-231 cells migrating in gradients of EGF obtained in a similar microfluidic platform [see Supplementary Fig. S2 and Kim et al. [33]]; the results also demonstrated that Lévy statistics was the best fit to the tail end of the velocity distribution.

Here, we showed that Lévy distribution was the best model to describe the tail end of the normalized velocity distribution. Our work is consistent with the previous report using migrating metastatic tumor cells along a contact line [9] and migrating T cells within a mouse model [8]. We note that the difference between Lévy and exponential function was subtle, not very pronounced. Previously, fibrosacoma HT 1080 cells migrating within collagen matrix were found to follow exponential function [7]. We conjecture that this difference may come from different cell types as well as cell culture condition. It is known that HT 1080 cells executed mostly mesenchymal motility in static culture which is an integrin-dependent motion; while MDA-MB-231 cells in microfluidic platform executed both mesenchymal and amoeboid (integrin independent motion) which may lead to a higher heterogeneity [33].

Chemokine CCL19 within tumor microenvironment promoted heterogeneity of MDA-MB-231 cell motility revealed by the Lévy exponent

To evaluate the level of heterogeneity of tumor cell motility to cytokine gradient, we fitted the tail end of the cell velocity distribution under various CCL19 concentration gradients to the Lévy distribution, 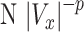. Here, a smaller exponent means a longer tail end, which leads to larger rare events or higher heterogeneity. Figure 5 showed that the Lévy exponent decreased with the increase of CCL19 gradients ranging from 2.68 to 1.95. Consistent results were obtained when the Crystal Ball function was used for the fitting (see Supplementary Fig. S3). These results indicated that the number of rare fast moving events increased significantly in the presence of the CCL19 gradients. Interestingly, we found that the Lévy exponent of the V_x distribution reached to a minimum value of 1.95 ± 0.14 and 2.04 ± 0.21 or the cell motility was most heterogenic when the average CCL19 concentration was between 50 and 100 nM, which was close to the measured dynamic kinetic constant between CCL19-CCR7, 100 ± 40 nM measured in our labs previously [25]. Similar results were obtained when we fitted data from EGF gradients to a power law (Supplementary Fig. S4) and a Crystal Ball function (Supplementary Fig. S5). An minimum exponent of 1.97 ± 0.31 was obtained at the average EGF concentration of 2.5 nM, close to the kinetic binding constant of EGFR and EGF, 2–5 nM [33].

Figure 5.

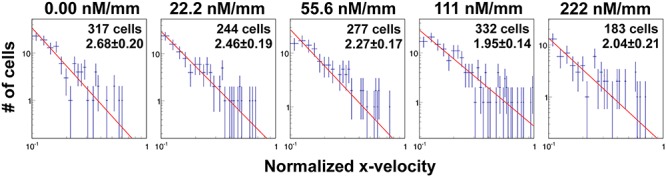
CCL19 gradients promoted the heterogeneity of tumor cell motility revealed by the Lévy exponent. Fit to a power law using the tail end of the x-velocity distribution. Dotted lines are experimental data taken at CCL19 gradients of (i) 0.00, (ii) 22.2, (iii) 55.6, (iv) 111 and (v) 222 nM/mm. The Lévy exponent decreases with the increase of CCL19 gradient and approaches to ~2.0 when the average CCL19 concentration is near ~111 nM.

Here, we found that the experimentally obtained Lévy exponent was close to 2.0 when the cytokine (either CCL19 or EGF) concentration was close to its dynamic kinetic constant. Early work [37] using flight length distribution of forager showed that an Lévy exponent of 2.0 represented an optimized search strategy for the foragers to find sparsely populated food. It is likely that tumor cells optimized its strategy to spread when the cells were most sensitive to their cytokines, that is when the cytokine concentration was close to its dynamic kinetic constant. Further work will be needed to verify this conjecture.

In summary, our data in Fig. 5 showed that tumor cell heterogeneity increased with the increase of CCL19 chemokine gradients. The measured Lévy exponent reached a minimum or a value of ~ 2.0 when CCL19 concentration was near its dynamic kinetic constant. This indicated that CCL19 promoted heterogeneity of the cell movement, highlighting the importance of cytokine gradients within the tumor microenvironment in tumor cell invasion.

CONCLUSION AND FUTURE PERSPECTIVES

Cellular heterogeneity is important in many physiological and pathologic processes including immune response and cancer progression. Here, we propose a new parameter, the Lévy exponent, for quantifying cellular heterogeneity. Using 3D breast tumor cell migration data, we showed that the migration velocity of breast tumor cells followed a Lévy distribution function. When challenged by chemokine CCL19 gradients within a microfluidic device, we found that the Lévy exponent reached to a minimum value of ~2.0 when average CCL19 concentration was ~50 nM, close to the currently reported dynamic ligand receptor (CCL19-CCR7) kinetic constant. We also showed that MDA-MB-231 cells displayed a mild chemotactic but distinct chemokinesis response in CCL19 gradients. A similar trend was also observed in the response of tumor cells to EGF gradients. Our work highlighted the importance of cytokines in modulating cellular heterogeneity, and its subsequent impact in tumor cell invasiveness. While our work is at single-cell level, the next level of inquiry will be to ask the question whether tumor cell motility follows Lévy walk when they are in aggregated form (tumor spheroids) for optimized invasion. We note that tools used here can be also used to explore the potential roles of genetic heterogeneity in tumor invasion and cancer metastasis.

MATERIALS AND METHODS

Device fabrication and assembly

A microfluidic platform previously developed in our lab was adopted for this project [25, 29]. Briefly, a silicon master with the pattern of four functional gradient generators was fabricated at the Cornell NanoScale Science and Technology Facility using a standard photolithography method. To make a device, we first placed a 1-mm-thick PDMS spacer on the silicon master surrounding the four functional units. A hot 3% agarose solution was then poured onto the silicon master inside of the spacer. A glass slide was immediately placed on the top of the spacer, and pressure was applied on the glass slide until the agarose gel was polymerized under room temperature. The agarose membrane, spacer, together with the glass slide were carefully peeled off from the silicon master. The agarose membrane typically was soaked in the media for 30 min before being assembled between a glass slide and a manifold. Lastly, the device was stored in an enclosure (upside down petri dish) to avoid evaporation before experiments.

3D cell culture

Cells

Human breast tumor cells (MDA-MB-231) were a generous gift from the Cornell University Center on the Microenvironment and Metastasis. The cells were maintained in DMEM (Invitrogen, Carlsbad, CA) with 10% FBS (Atlanta Biologicals, Lawrenceville, GA) and 1% Penicillin/Streptomycin (Invitrogen). When reaching 70–80% confluence, cells were detached with 2 mL of trypsin/EDTA and then re-suspended in fresh DMEM.

3D cell culture

The suspended cells in DMEM were first mixed with 0.5% type I collagen from rat tails (Pel-Freez, Rogers, AR) to reach a final concentrations of 1.5 mg/mL collagen and 10⁶ cells/mL. The cell-collagen mixture was then introduced into the cell channel of each of the four functional units. To prevent the cells from settling to the bottom of the channel due to gravity, we created the following procedures. The device was first incubated, in an upside-down position, at 37°C in a 5% CO₂ incubator for 7 min. The device was then turned upright way for an additional 13 min of incubation. Figure 1c showed that cells were distributed along z-direction, and most cells were in the mid-z plane, facilitating a 3D cell culture.

CCL19 gradient generation

CCL19 (R&D Systems, Minneapolis, MN) was reconstituted at 10 μg/mL insterile PBS (Invitrogen) containing 0.1% BSA (Sigma). At each experiment, three different concentrations of CCL19 solution were prepared by adding designated amount of growth medium to the reconstituted CCL19, while the control solution contained only growth medium. All mixture solutions were then transferred to the 3 mL syringes (BD, Franklin Lakes, NJ) whose tips were connected to a medical grade tubing (ID = 0.51 mm, PharMed BPT, Cole-Parmer, Vernon Hills, IL). The free ends of tubing were subsequently connected to the inlets of the source channels of the four functional units. The outlets of the flow channels were connected to a set of the tubing that was placed in a disposal container. For gradient generation, CCL19 solution and growth medium were pumped through the source and sink channels by a syringe pump (KD Scientific, Holliston, MA) at a rate of 1 μL/min. Since the chemokine can diffuse through the agarose barrier, a steady linear chemokine gradient was readily established across the center channel [24, 25]. For example, by flowing a 100 nM of CCL19 and buffer via source and sink channels, respectively, we create a CCL19 gradient of 100 nM/0.9 mm = 111 nM/mm gradient, with an average concentration of 50 nM. Note that the distance between the sink and the source channel is 0.9 mm.

Imaging

Images were taken in bright field using an inverted microscope (20× objective, Olympus IX81, Center Valley, PA) in the middle of the channel along the z-axis, at 8-min intervals for 16 h, and saved on hard drive for post-analyses. We used an image acquisition software, SlideBook (Intelligent Imaging Innovation, Inc., Denver, CO), a CCD camera (Orca-ER, Hamamatsu, Bridgewater, NJ), and a x-y controlled stage (OptiScan II, Prior Scientific, Inc., Rockland, MA). For each experiment, we imaged two locations in each of the four center channels at a given time point. Note, although cells were embedded within a 3D biomatrix, we image a single z-plane in the middle of the cell channel.

Data analysis

Time series images were used to obtain cell trajectories using Imaris (Bitplane, Zurich). An in-house MATLAB (The MathWorks, Inc., Natick, MA) script was used to compute migration parameters. To exclude non-motile cells from the analysis, we first calculated the standard deviations of the cell positions along the x-axis and y-axis (stdX and stdY) of each cell track (16-h duration). A cell was considered motile if its standard deviation stdX and stdY were greater than 2 and 2.5 μm, respectively. For each cell track, we first computed the total traveled distance T, the net displacement D, and the net displacement along the x-axis D_x as shown in Fig. 1c. From these, we computed speed, 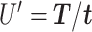, the x-directional velocity 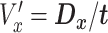, the persistence length 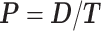, and the x-directional persistence length or chemotactic index 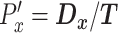. Here, t = 16 h, the duration of each track. The speed (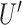) was normalized by the average control speed to minimize experiment-to-experiment variations. To normalize x-directional velocity, we subtract the average 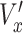of the control group from the 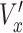of each cell, and the difference is subsequently divided by the average speed (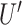) of the control population. The x-directional persistence length, 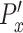is normalized by subtracting individual 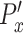with the average 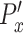of the control group such that the average of the normalized directional persistence length (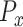) of the control group was set to zero. Student t-test was carried out in Prism (Graphpad, La Jolla, CA) for statistical analysis.

Statistical analysis

The goodness of fit was evaluated by two methods, probability value (pv) from Chi-Squared fitting and wAIC. The probability value calculates the probability that the assumed function simulates the real function using 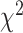criterion. Probability value (pv) = 1 represents the best fit indicating the assumed function is the real function. pv = 0 represents a poor fit indicating the assumed function is not suitable for the distribution. The probability value pv was obtained using the fitted chi-squared value and degree of freedom with an online Chi-Square calculator, https://www.mathsisfun.com/data/chi-square-calculator.html. Akaike Information Criterion weight is a measure that allows one to compare and rank multiple competing models and to estimate which of them best approximates the true process [16, 38]. AIC was computed using results from Chi-Square fit (details see https://en.wikipedia.org/wiki/Akaike_information_criterion). The relative likelihoods of candidate models were calculated using weights, with the weight (wAIC) of any particular model varying from 0 (no support) to 1 (complete support) relative to the entire model set. We used equation (8) in [38] for this calculation.

Author Contributions

B.J.K., A.R., M.A.S. and M.W. designed the project. B.J.K. and P.H. performed the experiments. B.J.K., P.H., A.R. and M.W. carried out data analysis. All authors participated in writing of the manuscript.

Competing interest statement

All authors have no competing interests.