A fully convolutional neural network for new T2-w lesion detection in multiple sclerosis

Highlights

• •A deep learning model for new T2-w lesions detection in multiple sclerosis is presented.
• •Combining a learning-based registration network with a segmentation one increases the performance.
• •The proposed model decreases false-positives while increasing true-positives.
• •Better performance compared to other supervised and unsupervised state-of-the-art approaches.

Graphical abstract

Abstract

Introduction: Longitudinal magnetic resonance imaging (MRI) has an important role in multiple sclerosis (MS) diagnosis and follow-up. Specifically, the presence of new T2-w lesions on brain MR scans is considered a predictive biomarker for the disease. In this study, we propose a fully convolutional neural network (FCNN) to detect new T2-w lesions in longitudinal brain MR images.

Methods: One year apart, multichannel brain MR scans (T1-w, T2-w, PD-w, and FLAIR) were obtained for 60 patients, 36 of them with new T2-w lesions. Modalities from both temporal points were preprocessed and linearly coregistered. Afterwards, an FCNN, whose inputs were from the baseline and follow-up images, was trained to detect new MS lesions. The first part of the network consisted of U-Net blocks that learned the deformation fields (DFs) and nonlinearly registered the baseline image to the follow-up image for each input modality. The learned DFs together with the baseline and follow-up images were then fed to the second part, another U-Net that performed the final detection and segmentation of new T2-w lesions. The model was trained end-to-end, simultaneously learning both the DFs and the new T2-w lesions, using a combined loss function. We evaluated the performance of the model following a leave-one-out cross-validation scheme.

Results: In terms of the detection of new lesions, we obtained a mean Dice similarity coefficient of 0.83 with a true positive rate of 83.09% and a false positive detection rate of 9.36%. In terms of segmentation, we obtained a mean Dice similarity coefficient of 0.55. The performance of our model was significantly better compared to the state-of-the-art methods (p < 0.05).

Conclusions: Our proposal shows the benefits of combining a learning-based registration network with a segmentation network. Compared to other methods, the proposed model decreases the number of false positives. During testing, the proposed model operates faster than the other two state-of-the-art methods based on the DF obtained by Demons.

1. Introduction

Multiple sclerosis (MS) is an inflammatory disease of the central nervous system, which is characterized by the presence of lesions in the brain and the spinal cord. Magnetic resonance imaging (MRI) has become a core paraclinical tool for diagnosing and predicting long-term disability and treatment response in MS patients. Follow-up brain MRI is required in patients who have not been diagnosed yet as MS patients but who show clinical and radiological findings suggestive of MS (Rovira et al., 2015). 3–6 months was suggested to be the optimal interval between the baseline and the follow-up scans. A third scan can be acquired 6–12 months later if no new lesions are seen in the first follow-up scan (Pestalozza, Pozzilli, Di Legge, Piattella, Pantano, Caramia, Pasqualetti, Lenzi, 2005, Rovira, Wattjes, Tintore, Tur, Yousry, Sormani, De Stefano, Filippi, Auger, Rocca, et al., 2015). Several criteria and strategies have been proposed for prompt identification of suboptimal responses in individual patients, based on a combination of clinical and MRI measures assessed during the first 6 to 12 months after initiating treatment (Freedman, Selchen, Arnold, Prat, Banwell, Yeung, Morgenthau, Lapierre, Group, et al., 2013, Prosperini, Mancinelli, de Giglio, de Angelis, Barletta, Pozzilli, 2014, Rio, Castillo, Rovira, Tintoré, Sastre-Garriga, Horga, Nos, Comabella, Aymerich, Montalbán, 2009, Sormani, Rio, Tintoré, Signori, Li, Cornelisse, Stubinski, Stromillo, Montalban, de Stefano, 2013, Sormani, de Stefano, 2013, Stangel, Penner, Kallmann, Lukas, Kieseier, 2015). These criteria are related to the detection of disease activity on follow-up brain MRI studies compared to baseline scans, defined as either gadolinium-enhancing lesions or new/enlarging T2-w lesions. However, the detection of active T2-w lesions in MS patients can be hindered by several factors, such as a high burden of inactive T2 lesions, the presence of small and confluent lesions, inadequate repositioning, and high interobserver variability (Altay et al., 2013). Automatic methods can overcome these issues and provide a robust estimation (Lladó et al., 2012).

Based on a review proposed by Lladó et al. (2012), methods can be classified into either lesion-detection approaches or change-detection approaches. In the lesion-detection approaches, both static and dynamic MS lesions on a single-time MR volume of a patient are detected. These segmentation-based methods, which can be supervised or unsupervised, rely on the intensity homogeneities of the tissues and typically apply data mining techniques (clustering or classification) to distinguish lesions from normal tissues. In longitudinal analysis, a lesion quantification approach is subsequently needed to compute the volumetric changes of each segmented lesion between two time points for the MS lesion evolution (Köhler et al., 2019). In change-detection approaches, the differences between successive MRI controls at both 2D and 3D image levels are analyzed instead of at a single time point. An MS lesion is generally seen as the combination of two different effects, tissue transformation and tissue deformation (Thirion and Calmon, 1999). Tissue transformation refers to the intensity change in the tissue of the lesion, while tissue deformation refers to the modification of its surrounding tissue, due to lesion expansion or contraction. These change-detection methods can be subclassified into either intensity-based approaches or deformation-based approaches.

In the intensity-based approaches, voxelwise comparisons are performed between successive scans to segment new lesions (Elliott, Arnold, Collins, Arbel, 2013, Ganiler, Oliver, Díez, Freixenet, Vilanova, Beltran, Ramió-Torrentà, Rovira, Lladó, 2014, Moraal, Meier, Poppe, Geurts, Vrenken, Jonker, Knol, van Schijndel, Pouwels, Pohl, et al., 2009, Moraal, Wattjes, Geurts, Knol, van Schijndel, Pouwels, Vrenken, Barkhof, 2010, Schmidt, Pongratz, Kster, Meier, Wuerfel, Lukas, Bellenberg, Zipp, Groppa, Smann, Weber, Gaser, Franke, Bussas, Kirschke, Zimmer, Hemmer, Mhlau, 2019, Sweeney, Shinohara, Shea, Reich, Crainiceanu, 2013). In the deformation-based approaches, the new T2-w lesion detection is performed by analyzing the deformation fields (DFs) obtained by nonrigid registration between successive scans (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Rey, Subsol, Delingette, Ayache, 2002, Thirion, Calmon, 1999). Nonrigid registration and the use of DFs between time points have been shown to improve the detection of new T2-w MS lesions in longitudinal studies (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018). These DFs can either be obtained using classic nonrigid registration approaches based on optimization or, recently, using learning-based approaches. In real cases, both tissue transformation (changes in intensity) and tissue deformation generally occur. Hence, the mass effect of the lesion should also be taken into account in order to define a precise lesion evolution. Deformation based approaches are sensitive to these changes in the brain. However, they do not provide information about stable lesions.

New lesion detection approaches have also been proposed, combining information from different sources. For instance, Fartaria et al. (2019) proposed a strategy for longitudinal analysis of MS lesions based on a combination of segmentation-based and intensity-based approaches to assess the performance of the partial-volume-aware lesion segmentation tool, and to propose a method for the generation of a lesion progression map between two time points. Moreover, several methods have been proposed as combinations of intensity-based and deformation-based approaches. Cabezas et al. (2016) improved the subtraction pipeline proposed by Ganiler et al. (2014) by combining subtraction and DF operators to decrease the number of false positive lesions detected by the subtraction pipeline. Salem et al. (2018) merged intensity- and deformation-based approaches in an automated multichannel supervised logistic regression classification. Their model used features taken not only from the baseline, follow-up, and subtraction images but also from the DF operators obtained from the non-rigid registration between time-points scans.

Classic registration approaches establish a dense nonlinear correspondence between a pair of 3D brain scans. For these approaches, registration is defined as an optimization problem that needs to be solved for each volume pair using a similarity metric while enforcing smoothness constraints on the mapping. Solving this optimization is computationally intensive and therefore, extremely slow in practice (Ashburner, 2007, Avants, Epstein, Grossman, Gee, 2008, Bajcsy, Kovai, 1989, Beg, Miller, Trouvé, Younes, 2005, Dalca, Bobu, Rost, Golland, 2016, Glocker, Komodakis, Tziritas, Navab, Paragios, 2008, Thirion, 1998). However, different graphics processing unit (GPU)-based accelerated approaches have been proposed to improve the efficiency and speed up the optimization (Han, Hibbard, Willcut, 2009, Punithakumar, Boulanger, Noga, 2017, Wu, Yang, Zhang, Chen, Mao, 2019).

Common learning-based approaches rely on classification algorithms to register the two scans. These algorithms involve a first stage in which a model is estimated on training data composed of a set of features and their corresponding ground truth (GT) and a second stage in which the model is tested on a new dataset to provide the desired results. Classic machine-learning methods require hand-crafting feature vectors to extract appearance information (Geremia et al., 2011). In contrast, convolutional neural networks (CNNs) can learn a set of features that are specifically optimized for the current task directly from the image data. Currently, CNNs have demonstrated superior performance in brain imaging specifically for segmenting tissues (Moeskops, Viergever, Mendrik, de Vries, Benders, Igum, 2016, Zhang, Li, Deng, Wang, Lin, Ji, Shen, 2015), brain tumors (Havaei, Davy, Warde-Farley, Biard, Courville, Bengio, Pal, Jodoin, Larochelle, 2017, Kamnitsas, Ledig, Newcombe, Simpson, Kane, Menon, Rueckert, Glocker, 2017, Pereira, Pinto, Alves, Silva, 2016) and white matter lesions (Brosch, Tang, Yoo, Li, Traboulsee, Tam, 2016, Valverde, Oliver, Roura, González-Villà, Pareto, Vilanova, Ramió-Torrentà, Rovira, Lladó, 2017). In the case of registration approaches, learning-based approaches learn a parametrized registration function from a collection of images during training. During testing, a registration field can be quickly computed by directly evaluating the function using the learned parameters. Some proposed methods (Sokooti, de Vos, Berendsen, Lelieveldt, Išgum, Staring, 2017, Yang, Kwitt, Styner, Niethammer, 2017) rely on a precomputed DF as the GT, and the others rely only on the images being registered or segmentation masks, without comparing the expected DF with a precomputed DF (Li, Fan, 2018, de Vos, Berendsen, Viergever, Staring, Išgum, 2017). Specifically, Balakrishnan et al. (2019) developed a new CNN approach that computes the deformation between two images by training the network using a similarity metric and a regularization term similar to classic registration methods, obtaining comparable results with current state-of-the-art approaches.

In this study, we propose a fully convolutional neural network (FCNN) approach to detect new T2-w lesions in longitudinal brain MR images. The proposed model combines intensity-based and deformation-based features within an end-to-end deep learning approach. To the best of our knowledge, this is the first longitudinal approach based on CNN that deals with lesion changes in brain MRI. Other longitudinal approaches based on CNNs have been presented before (Birenbaum and Greenspan, 2016), but those methods independently provide a cross-sectional segmentation of lesions at each time point using longitudinal information. Our proposed model is trained end-to-end. The DFs and the new T2-w lesions are learned simultaneously using a combined loss function. We evaluated the performance of the method using a leave-one-out cross-validation scheme on 36 patients with a clinically isolated syndrome (CIS) or early relapsing MS presenting new T2-w lesions on the follow-up scan and also on 24 patients with no new lesions.

2. Methods

2.1. Network architecture

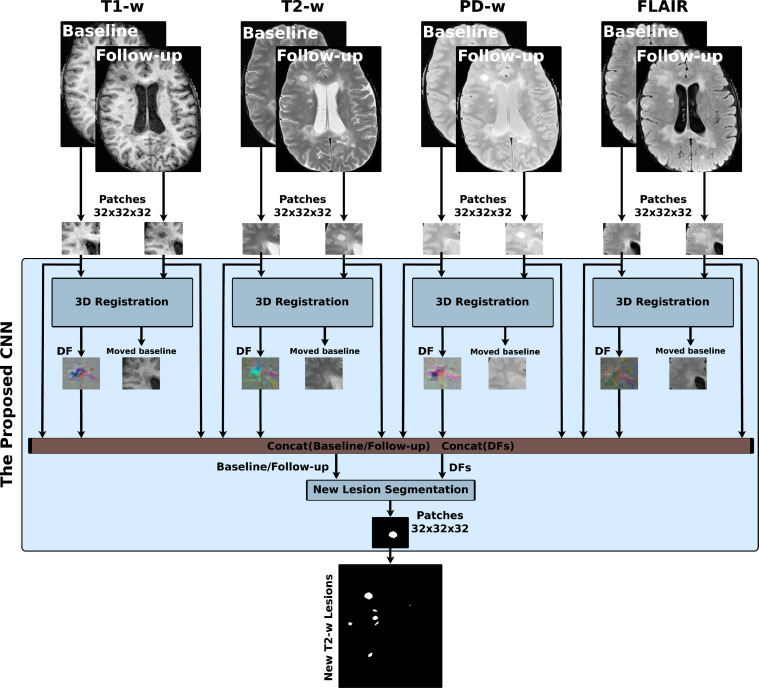
Fig. 1 shows the new T2-w MS lesion segmentation architecture. The proposed network is an FCNN that takes four image modalities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up as inputs and outputs the new T2-w lesion segmentation mask. The network consists of two parts. The first part is U-Net blocks that learn the DFs and nonlinearly register the baseline image to the follow-up image for each input modality. The learned DFs and the baseline and follow-up image modalities are then fed to the second part of the network, another U-Net that performs the final detection and segments the new T2-w lesions. The network is trained end-to-end with gradient descent and simultaneously learns both DF and new T2-w lesion segments.

Fig. 1.

Scheme of the new T2-w MS lesion segmentation network. The proposed network consists of four 3D registration blocks and one 3D segmentation block. The inputs are baseline/follow-up images of the T1-w, T2-w, PD-w, and FLAIR. For each input modality, there is a 3D registration block that learns the deformation field (DF) and nonlinearly registers the baseline image to the follow-up image. Afterwards, the learned DFs and the baseline and follow-up images are fed to the segmentation block, which performs the final detection and segmentation of the new T2-w lesions. The network is trained end-to-end using a combined loss function.

3D registration architecture: A 3D registration block is built for each input modality following the architecture shown in Fig. 2(a). This block is inspired by the work of Balakrishnan et al. (2019) (VoxelMorph), which is a learning framework for deformable medical image registration. The registration block learns the DF and nonlinearly registers the baseline image to the follow-up image. It is a fully convolutional network that follows a U-shaped architecture (Ronneberger et al., 2015). The U-Net architecture consists of four downsample (the contracting path) and upsample steps (the expansive path). The core element (CE) block is a two-3D convolution layer (kernel size = 3 and stride = 1) with K channels. Each convolution is followed by a LeakyReLU layer. The number of channels, K, of CE blocks are (64, 128, 256, and 512) and (512, 256, 128, and 64) for the contracting path and expansive path, respectively. The U-Net’s downsampling followed by the upsampling and skip connections allow the network to exploit information at large spatial scales while retaining useful local information. Moreover, as discussed in Drozdzal et al. (2016), skip connections facilitate gradient flow during training. The spatial transformation (Balakrishnan, Zhao, Sabuncu, Guttag, Dalca, 2019, Jaderberg, Simonyan, Zisserman, et al., 2015) warps the baseline image to the follow-up space using the learned DF and enabling end-to-end training. The LeakyReLU activations are used instead of ReLU so that the learned DFs can have both positive and negative values.

Fig. 2.

The 3D registration and segmentation architectures. Each input modality has its 3D registration block (a) that learns the deformation field (DF) and nonlinearly registers the baseline image to the follow-up image. The registration block is a U-Net architecture with four downsample and upsample steps. The spatial transform block is used to warp the baseline image to the follow-up space using the learned DF enabling end-to-end training. The four learned DFs and the baseline and follow-up images are then fed to the segmentation block (b), another U-Net that performs the final detection and segmentation of the new T2-w lesions.

3D segmentation architecture: A 3D segmentation block is used for segmenting the new T2-w lesions. It is a two-branch network where each branch is a U-Net following the architecture shown in Fig. 2(b). The U-Net architecture is exactly the same as the U-Net used in the registration block, but using a ReLU activation layer instead of the LeakyReLU layer. The inputs of the first branch are the four image modalities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up, while the second branch input is the four DFs learned from the first registration blocks. The outputs of the two branches are concatenated before the classification step. One UNetCore processes the DFs (deformation-based) and another UnetCore processes the baseline/follow-up modalities (intensity-based). Note that the model is merging the intensity with the DFs to segment the new lesions.

2.2. Loss functions

The loss function used in this work is the summation of two loss functions. One function is an unsupervised loss function that controls the registration part of the network (Balakrishnan et al., 2019). It consists of two components: A similarity part that penalizes differences in appearance between the moved baseline and follow-up images, and a regularization part that enforces a spatially smooth deformation and is often modeled as a linear operator on the spatial gradients of DF as stated in (Balakrishnan et al., 2019). Therefore, the registration block is trained in an unsupervised manner using the spatial transform block which is used to warp the baseline image to the follow-up space using the learned DF. The block learns the DF by minimizing the mean square error (MSE) between the warped baseline and the follow-up images during training. The other function is a supervised loss function L_CrossEntropy (Cross-Entropy) that controls the segmentation part of the network and penalizes differences between the segmentation and GT. The loss function L_Total is as follows:

$$L_{Total}=\underset{Segmentationlossfunction}{\underbrace{L_{CrossEntropy}(Seg,GT)}}+\underset{Registrationlossfunction}{\underbrace{{\sum }_{m\in Modalities}({\overbrace{\frac{1}{N}{\sum }_{i=1}^N{(F_{m_i}-B_m{\left(D{F}_m\right)}_i)}^2}}^{Similaritypart}+{\overbrace{\lambda {\sum }_{p\in DF}\parallel ▽D{F}_m\left(p\right){\parallel }^2}}^{Regularizationpart})}}$$ (1)

where F_m, B_m(DF_m), and DF_m are follow-up image, baseline image warped by DF (moved baseline), and DF for a modality m, respectively. Seg and GT are the automatic segmentation and the ground truth, respectively. N is the number of voxels in a patch and λ is a regularization parameter.

3. Experimental setup

3.1. Datasets

VH dataset: The database used in this paper consists of images from 60 different patients with a clinically isolated syndrome (CIS) or early relapsing MS who underwent brain MRI in the Vall d’Hebron Hospital’s center for monitoring disease evolution and treatment response. Each patient underwent brain MRI within the first 3 months after the onset of symptoms (baseline) and at 12 months’ follow-up after the onset. Thirty-six of the patients (13 women and 23 men; 35.4 ±  7.1 years of age) confirmed MS with new T2-w lesions, while 24 patients did not present new T2-w lesions. The baseline and follow-up scans for all patients were obtained in the same 3T magnet (Tim Trio; Siemens, Erlangen, Germany) with a 12-channel phased array head coil. The MRI protocol included the following sequences: 1) transverse proton density (PD)- and T2-weighted fast spin-echo (TR $=3080$ ms, TE $=21-91$ ms, voxel size $=0.78\times 0.78\times 3.0$ mm³), 2) transverse fast FLAIR (TR = 9000 ms, TE $=87$ ms, TI $=2500$ ms, flip angle $={120}^{\circ },$ voxel size $=0.49\times 0.49\times 3.0$ mm³), and 3) sagittal T1- weighted 3D magnetization-prepared rapid acquisition of gradient echo (TR $=2300$ ms, TE $=2.98$ ms, TI $=900$ ms, voxel size $=1.0\times 1.0\times 1.2$ mm³). The Vall d’Hebron Hospital’s ethics committee approved the study, and written informed consent was signed by the participating patients.

Only new T2-w lesions that were visually detected on the follow-up scan were annotated on the PD-w images and semiautomatically delineated using Jim 5.0 software.1 First, an expert neuroradiologist detected changes visually by using baseline and follow-up scans, and then a trained technician delineated them semiautomatically by using the subtraction image. The raters always annotated the complete new lesion or only the new part of the lesion in the case of large lesion growth. The dataset used in our study contained only two growing lesions, and the remainder were new lesions. Finally, the expert neuroradiologist confirmed the final segmentation. This analysis was used as the reference standard for comparison. The 36 patients with new T2-w lesions exhibited a total of 191 lesions. The lesions were distributed as 15.15% small (3–10 voxels), 53.53% medium (11–50 voxels), and 31.31% large (50+ voxels).

Preprocessing: For each patient, the same preprocessing steps were performed on both baseline and follow-up images. First, a brain mask was identified and delineated on the PD-w image using the ROBEX Tool2 (Iglesias et al., 2011). Second, the four images underwent a bias field correction step using the N4 algorithm from the ITK library3 with the standard parameters for a maximum of 400 iterations (Tustison et al., 2010). The T1-w and FLAIR images were linearly registered to the PD-w using Nifty Reg tools4 (Modat, Cash, Daga, Winston, Duncan, Ourselin, 2014, Modat, Ridgway, Taylor, Lehmann, Barnes, Hawkes, Fox, Ourselin, 2010). Finally, the baseline and the follow-up intensity values were normalized per modality and per patient (i.e., between the baseline and the follow-up scans, and not across the entire dataset) using a histogram matching approach based on Nyúl et al. (2000).5 To warp the baseline images to the follow-up space, the baseline PD-w image was linearly registered to the follow-up PD-w image using Nifty Reg tools. To avoid interpolation more than once, baseline T1-w and FLAIR images were warped using the combined affine transformation.

3.2. Training and implementation details

For training the network, 3D 32x32x32 patches with a step size of 16x16x16 were extracted from the baseline and follow-up images of the four input modalities. Zero padding was applied to all the input volumes. This configuration was chosen empirically to give the highest performance of the proposed model. Using smaller and larger patch sizes, did not significantly improve performance. Moreover, increasing the patch size was more computationally- and memory-expensive. Note also that we aimed to learn the registration part from all image locations and not only for those containing new lesions. Therefore, the whole model was trained end-to-end, including the registration and the segmentation part, using a uniform sampling of patches to cover all the image. The extracted patches were divided into training and validation sets (70% for training and 30% for validation). The training set was used to adjust the weights of the neural network, while the validation set was used to measure how well the trained model performed after each epoch. The model was trained using Adam (Kingma and Ba, 2014) with default parameters and regularization parameter $\lambda =0.01$ (Balakrishnan et al., 2019). The extracted patches were passed to the network for training in minibatches of size 4, and the network was set to train for 30 epochs. To prevent overfitting, the training process was automatically terminated when the validation accuracy did not increase after 5 epochs.

The proposed method was implemented in Python,6 using Keras7 with the TensorFlow8 backend (Abadi et al., 2015). All experiments were run on a GNU/Linux machine running Ubuntu 18.04 with 128 GB RAM. The training was carried out on a single TITAN-X GPU (NVIDIA Corp, United States) with 12 GB RAM memory. To promote the reproducibility and usability of our research, the proposed pipeline will be available for downloading at our research website.9

3.3. Evaluation

We evaluated the proposed framework in different scenarios. First, we analyzed the accuracy of the detection using a leave-one-out cross-validation strategy with the 36 patients with new MS lesions. We chose the leave-one-out cross-validation strategy to be able to perform a quantitative comparison with the results published in (Salem et al., 2018). In this evaluation strategy, the proposed network was trained using 35 patients and tested with the remaining patient. This process was repeated until all patient images were used as test images. Moreover, to demonstrate the contribution of simultaneously learning both the DF and the segmentation of new T2-w lesions, the following models were analyzed:

• •SimLearnedDFs: This is our main model in which the four registration blocks and the segmentation block were trained simultaneously end-to-end using the loss function explained in Section 2.2. The four image modalities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up combined with the learned DFs were fed to the segmentation block as first and second inputs, respectively.
• •SepLearnedDFs: In this model, the registration blocks and the segmentation blocks were trained separately. The four registration blocks were trained first to obtain the DFs. Then, the four image modalities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up combined with the learned DFs were fed to the segmentation block as first and second inputs, respectively. This model was used for comparison with the SimLearnedDFs model to highlight the impact of the end-to-end simultaneous training of the DFs and new T2-w lesions.
• •DemonsDFs (The proposed network using the DFs obtained from Demons (Thirion, 1998)): This model did not use the registration blocks of the proposed network shown in Fig. 1. It used only the segmentation block with four image modalities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up as the first input. The second input of the segmentation block was the DFs directly computed by the registering baseline image to the follow-up image for every input modality using a multiresolution Demons registration approach from ITK (Thirion, 1998). This model was used for comparison with the SimLearnedDFs model to highlight the impact of learned-based DFs with end-to-end training over the DFs from Demons.
• •NDFs (The proposed network without DFs): This model did not use the registration blocks of the proposed network shown in Fig. 1. It used only the segmentation block with only the four image modalities (T1-w, T2-w, PD-w, and FLAIR) in both the baseline and follow-up as input. This model was used for comparison with the other three models to highlight the impact of the addition of the DFs in increasing the detection of new T2-w lesions.

Second, we analyzed the specificity of the method with 24 patients with no new T2-w lesions. Testing the performance on these cases allowed us to further study how robust was the proposed method to avoid detecting false positives in patients with inactive disease. To do this, we performed a new training using all the 36 images with new MS lesions. In addition, we compared the obtained results with those of recent state-of-the-art approaches (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018, Schmidt, Pongratz, Kster, Meier, Wuerfel, Lukas, Bellenberg, Zipp, Groppa, Smann, Weber, Gaser, Franke, Bussas, Kirschke, Zimmer, Hemmer, Mhlau, 2019, Sweeney, Shinohara, Shea, Reich, Crainiceanu, 2013) applied to the same dataset used in this work. For the work of Schmidt et al. (2019), we used their implementation of the longitudinal pipeline available at https://www.statistical-modeling.de/lst.html. The lesion growth algorithm (Schmidt et al., 2012) was used to obtain the initial cross-sectional WM lesion segmentation per time point. The parameter κ was empirically optimized for the current dataset, selecting the value $\kappa =0.15$. Additionally, the Pearson correlation coefficient was used to analyze the linear relationship between manual annotations and the automatic detections obtained with the proposed model (SimLearnedDFs) in terms of number of new lesions and new lesion volume.

We also studied the performance of the proposed model (SimLearnedDFs), the three variants (SepLearnedDFs, DemonsDFs, NDFs), and the state-of-the-art approaches (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018, Schmidt, Pongratz, Kster, Meier, Wuerfel, Lukas, Bellenberg, Zipp, Groppa, Smann, Weber, Gaser, Franke, Bussas, Kirschke, Zimmer, Hemmer, Mhlau, 2019, Sweeney, Shinohara, Shea, Reich, Crainiceanu, 2013) on different brain regions. To the best of our knowledge, there is no current study that states that the location of the lesion is important for the longitudinal assessment of MS, although the lesion location (periventricular, juxtacortical, infratentorial, and deep white matter) is used to prove dissemination in space according to the McDonald criteria (McDonald et al., 2001). The motivation for performing this study was mainly to analyze the behavior performance of all the approaches on these specific regions. In particular, the analysis of the new MS lesion detection was divided into 4 types (periventricular, juxtacortical, infratentorial, and deep white matter) according to its location in the brain. An atlas with three segmented regions (cortex, ventricles, and (cerebellum and brainstem)) was resampled for each patient space after nonlinearly registering the atlas template to the T1-w image of each patient. After the registration, a new MS lesion was considered periventricular, juxtacortical, or infratentorial if it touched the cortex, ventricles, or (cerebellum and brainstem), respectively. Otherwise, it was considered a deep white matter lesion.

Standard measures such as the true positive fraction (TPF), the false positive fraction (FPF), and the Dice similarity coefficient (DSC), which was computed lesion-wise and voxel-wise, were used for the quantitative analysis and were computed as follows:

$$TPF=\frac{TP}{TP+FN}$$

$$FPF=\frac{FP}{FP+TP}$$

$$DSC=\frac{2\times TP}{2\times TP+FP+FN}$$

where TP, FN, and FP are the number of true positives, false negatives, and false positives, respectively. In terms of detection, a lesion was considered as a TP if there was at least one voxel overlapping (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Ganiler, Oliver, Díez, Freixenet, Vilanova, Beltran, Ramió-Torrentà, Rovira, Lladó, 2014, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018). In terms of segmentation, only the voxel-wise DSC was computed.

For all the evaluated pipelines, the automatic segmentation masks were obtained by thresholding the probability maps at 0.5 (using argmax). This thresholding value was not optimized. Since the outputs of the network were two probability maps (for the lesions and background), we used the argmax function which chooses the class with the highest probability. Since we are dealing with a binary problem, the highest probability is always 0.5 or greater. Therefore, using argmax is equivalent to using a threshold of 0.5. All automatic lesions with a size lower than three voxels were removed as done in previous works ((Battaglini, Rossi, Grove, Stromillo, Whitcher, Matthews, De Stefano, 2014, Roura, Oliver, Cabezas, Valverde, Pareto, Vilanova, Ramió-Torrentà, Rovira, Lladó, 2015, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018)). A paired t-test at the 5% level was used to evaluate the significance of the obtained results.

4. Results

Table 1 summarizes the new T2-w lesion detection and segmentation mean results for our proposed model (SimLearnedDFs) and the three variants (SepLearnedDFs, DemonsDFs, NDFs). We also included four state-of-the-art approaches for comparison (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018, Schmidt, Pongratz, Kster, Meier, Wuerfel, Lukas, Bellenberg, Zipp, Groppa, Smann, Weber, Gaser, Franke, Bussas, Kirschke, Zimmer, Hemmer, Mhlau, 2019, Sweeney, Shinohara, Shea, Reich, Crainiceanu, 2013) when analyzing the 36 MS patients. We note that our SimLearnedDFs model outperformed the three variants (SepLearnedDFs, DemonsDFs, NDFs) models and had the best values for all the evaluation measures. Additionally, it outperformed all the state-of-the-art approaches in terms of all evaluation measures. Regarding the mean runtime per patient, the SimLearnedDFs model could process a test case in less than 9 minutes while the other state-of-the-art methods (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018), that are based on DFs obtained using classic nonrigid registration approaches, took on average 18.36 and 18.55 minutes, respectively.

Table 1.

Lesion Detection Results: Comparison between the different models evaluated. The results represent the mean detection TPF, FPF, DSCd, mean segmentation DSCs, and the mean runtime in minutes when analyzing the 36 MS patients using a leave-one-out cross-validation scheme. The automatic segmentation masks were obtained by thresholding the probability maps at 0.5 (using argmax), and all automatic lesions with a size lower than three voxels were removed.

Method	TPF	FPF	DSCd	DSCs	Runtime (in minutes)
SimLearnedDFs	83.09  ±  21.06	9.36  ±  16.97	0.83  ±  0.16	0.55  ±  0.18	8.70  ±  0.09
SepLearnedDFs	57.77  ±  34.34	13.67  ±  21.99	0.60  ±  0.31	0.39  ±  0.22	9.08  ±  0.06
DemonsDFs	62.06  ±  32.74	11.98  ±  23.09	0.67  ±  0.29	0.42  ±  0.24	18.10  ±  0.05
NDFs	53.99  ±  38.01	17.20  ±  26.96	0.55  ±  0.35	0.37  ±  0.28	7.58  ±  0.09
Sweeney et al. (2013)	59.82  ±  37.59	33.59  ±  33.52	0.57  ±  0.33	0.44  ±  0.26	8.36  ±  0.01
Cabezas et al. (2016)	70.93  ±  34.48	17.80  ±  27.96	0.68  ±  0.33	0.52  ±  0.24	18.36  ±  0.02
Salem et al. (2018)	80.0  ±  27.77	21.87  ±  26.26	0.76  ±  0.25	0.55  ±  0.22	18.55  ±  0.02
Schmidt et al. (2019)	68.66  ±  35.26	31.89  ±  36.10	0.62  ±  0.34	0.40  ±  0.25	7.58  ±  0.03

Fig. 3 shows a visual example of the performance of our SimLearnedDFs model, where each column corresponds to the baseline T2-w image, follow-up T2-w image, GT annotated lesions, and the segmentation of SimLearnedDFs, NDFs, DemonsDFs, and SepLearnedDFs approaches. Fig. 4 shows the relationship between baseline, follow-up, the learned DF, GT, and the segmentation of the SimLearnedDFs model in the four input modalities.

Fig. 3.

Example of new MS lesion detection in a 12-month longitudinal analysis. (a) and (b) show one axial slice of the T2-w image at baseline and follow-up, respectively. (c) shows the new MS lesion annotations performed by an expert (GT). (d), (e), (f), and (g) show the segmentation of SimLearnedDFs, NDFs, DemonsDFs, and SepLearnedDFs approaches, respectively. The GT and the segmentations are overlaid in green and red, respectively, on the follow-up T2-w image. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 4.

Relationship between baseline, follow-up, the learned DFs, GT, and the segmentation of SimLearnedDFs in the four input modalities. All images are from the same patient and the same slice. The DFs are displayed in RGB (third column) and their magnitudes (fourth column) using a hot color map. The GT and the segmentation of SimLearnedDFs are overlaid in green and red, respectively, on the follow-up image. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Regarding false negatives, the SimLearnedDFs model missed about 17% of the total number of lesions being distributed as 48% small lesions, 38% medium lesions, and 14% large lesions. Fig. 5 shows two examples of false positive detections using the SimLearnedDFs model. Some of the false positives were due to inflammation areas that were not marked as new lesions by the experts and the remainder were mainly due to image artifacts.

Fig. 5.

False positive detection example. Some false positives (the first row) were due to inflammation areas that were not marked as new lesions by the experts and the others were mainly due to artifacts.

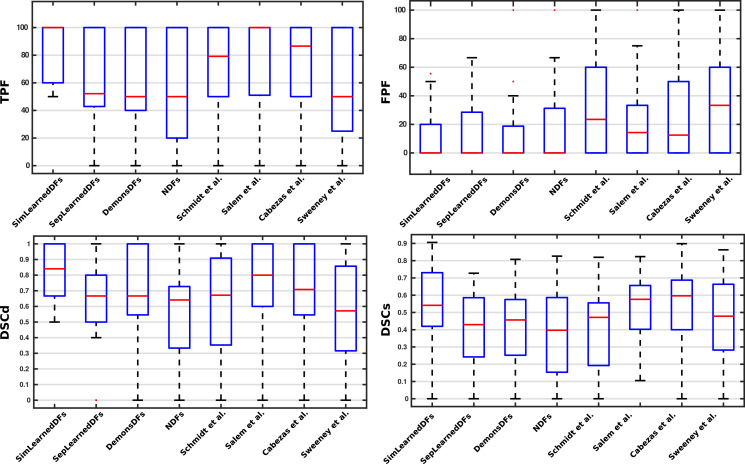
Analyzing the results per patient, Fig. 6 shows a box plot summarizing the performance of the SimLearnedDFs, the three variants (SepLearnedDFs, DemonsDFs, NDFs), and the state-of-the-art methods on the four metrics used in the evaluation. When this analysis was carried out on a per-patient basis, we observed that the proposed model (SimLearnedDFs) also provided better sensitivity for the cases that present few new lesions (i.e. 1, 2 or 3). For instance, for the 8 cases containing only one new lesion, our approach achieved a (TPF, FPF)=(100%, 0%), while the models used by Sweeney et al. (2013), Cabezas et al. (2016), Salem et al. (2018), and Schmidt et al. (2019) only achieved (71.43%, 25%), (85.71%, 0%), (85.71%,14.29%), and (71.43%, 38.33%), respectively.

Fig. 6.

Box plot summarizing the performance of the SimLearnedDFs, the three variants (SepLearnedDFs, DemonsDFs, NDFs), and the state-of-the-art methods on the four metrics used in the evaluation.

Fig. 7(a) shows the correlation between the number of new lesions manually annotated and those automatically detected (Pearson correlation coefficient: $R=0.97$; $p_{value}=2.7445e^{-21}$; confidence band = 95%). Fig. 7(b) shows the correlation between lesion volume in the GT and the automatically segmented (Pearson correlation coefficient: $R=0.98$; $p_{value}=5.0233e^{-24}$; confidence band = 95%). Regarding the number of the data points used, all the MS patients with lesion progression were used for this correlation (36 data points - 36 patients). However, several patients had the same number of GT and automatically-detected lesions and therefore some points are overlapping in the plot.

Fig. 7.

Correlation between (a) the number of GT lesions and the number of automatically detected ones using the proposed SimLearnedDFs model (Pearson correlation coefficient: $R=0.97;p_{value}=2.7445e^{-21}$) and (b) the volume (the number of voxels) of GT lesions and the volume of automatically detected ones using the proposed SimLearnedDFs model (Pearson correlation coefficient: $R=0.98;p_{value}=5.0233e^{-24}$). All the MS patients with lesion progression were used for this correlation (36 data points - 36 patients). Notice that different patients have the same combination of number of GT lesions and the SimLearnedDFs model detections. This means that several points are overlapping in the plot.

Fig. 8 shows the performance of the new T2-w lesion detection method when analyzed according to its location in the brain. Note that here the TPF and FPF were computed per-lesion type and not per-patient. The dataset had a total of 191 lesions (periventricular = 25, juxtacortical = 34, infratentorial = 12, and deep white matter = 120). In addition, we evaluated the behavior of the SimLearnedDFs model trained with all 36 patients when tested with the set of 24 patients with no new T2-w lesions. The results showed only 2 cases with one FP detection in each, and these results were better than those obtained with the other approaches.

Fig. 8.

Results of the new T2-w lesion detection for the 4 brain regions. The dataset had a total of 191 lesions (periventricular = 25, juxtacortical = 34, infratentorial = 12, and deep white matter = 120). TPF and FPF were computed per lesion type and not per patient.

To analyze the generalization and the performance of the proposed approach when tested on images from a different scanner and image-acquisition protocol, we performed a new experiment with data from another collaborating Hospital (Dr. Josep Trueta Hospital, so we refer to this dataset as the Trueta dataset). This dataset consisted of 17 MS patients, 9 of them with new T2-w lesions and 8 with no new T2-w lesions. The baseline and follow-up scans for all patients were obtained in a 1.5T magnet Philips scanner. The MRI protocol included the following sequences: 1) transverse proton density (PD)- and T2-weighted fast spin-echo (voxel size = 1.0 × 1.0 × 3.0 mm³), 2) transverse fast FLAIR (voxel size = 1.0 × 1.0 × 3.0 mm³), and 3) sagittal T1- weighted 3D magnetization-prepared rapid acquisition of gradient echo (voxel size = 1.0 × 1.0 × 1.0 mm³). The dataset was preprocessed in the same way as the VH dataset mentioned in Section 3.1. The experiment consisted in applying the SimLearnedDFs model and the approach of Salem et al. (2018) trained with the 36 cases from the VH dataset and then testing them on the unseen Trueta dataset. The results obtained for the 9 cases with new lesions showed that the SimLearnedDFs obtained a TPF of 72.1% and a FPF of 34.97%, while Salem et al. (2018) obtained a TPF of 54.81% and a FPF of 62.34%, respectively. Regarding the cases with no new lesions, the SimLearnedDFs model did not find any FP, while Salem et al. (2018) obtained at least 1 FP in each case of the 8 cases.

5. Discussion and future work

The proposed method is a fully convolutional neural network for detecting new T2-w lesions in longitudinal brain MR images. The model is trained end-to-end and simultaneously learns both the DFs and the new T2-w lesions. As the DFs are learned inside the network and not computed separately using classic nonrigid registration methods, the execution time of the network on a testing image is reduced compared to the time required by the state-of-the-art methods (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018). Moreover, the proposed model is fully automated, simple, and does not require hand-crafting feature vectors to extract appearance information similar to (Salem et al., 2018) because the convolutional neural networks (CNNs) learn a set of features that are specifically optimized for the task, directly from the image data. The inputs to our model are only the four image modalities (T1-w, T2-w, PD-w, and FLAIR) in both baseline and follow-up.

To analyze the effect of the end-to-end training, we trained the proposed model (SimLearnedDFs) and the other three variants (SepLearnedDFs, DemonsDFs, and NDFs). In terms of TPF, the SimLearnedDFs model was significantly better than all the other methods except Salem et al. (2018) method (p < 0.05). The TPF did improve by 3%. In terms of FPF, the SimLearnedDFs model was not significantly better than the SepLearnedDFs (4.31% improvement) and the DemonsDFs (2.62% improvement), but it was significantly better than the other methods (p < 0.05). Note that the model trained without any DFs (NDFs) detected new lesions with a TPF of 53.99% and an FPF of 17.20%. This result shows, as previously discussed in Cabezas et al. (2016); Salem et al. (2018), that the addition of DFs helps to increase the detection of new T2-w lesions while maintaining a low number of false positives. However, the results also show that training the model end-to-end, simultaneously learning both the DFs and the new T2-w lesions (SimLearnedDFs), performs better than either learning the DFs separately (SepLearnedDFs) or using DFs computed by classic deformable registration methods such as Demons (Thirion, 1998) (DemonsDFs). The increase in performance using simultaneous learning compared to the variants that compute the DF separately could be explained by the use of the combined loss function during the training process. The simultaneously learning model trained the two connected networks (registration and segmentation) end-to-end. That means, in each training epoch, the weights of the registration networks which compute the DFs were updated during the backpropagation to minimize the summation of the cross-entropy function (segmentation part) and the similarity function (registration part). These DFs (computed using the updated weights) were then used as inputs together with the intensity images to the segmentation network in the forward pass to compute the new lesion segmentation. Thus, the DFs were computed in a guided way that improved the new lesion segmentation. Note that the other variants did not include the connection between the registration and segmentation part, so DFs were computed blindly and independently from the segmentation. Moreover, our proposed model (SimLearnedDFs) improved the results over those of other unsupervised methods due to the use of a supervised classification model instead of an unsupervised rule-based approach (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Schmidt, Pongratz, Kster, Meier, Wuerfel, Lukas, Bellenberg, Zipp, Groppa, Smann, Weber, Gaser, Franke, Bussas, Kirschke, Zimmer, Hemmer, Mhlau, 2019). Compared with the state-of-the-art approaches, the proposed model (SimLearnedDFs) had better results than all the state-of-the-art approaches in terms of all the evaluation measures. It also operated orders of magnitude faster than (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018) during testing time due to the use of learning-based nonrigid registration. Regarding the analysis of the results when applied to the 24 patients with no new lesions, the proposed model (SimLearnedDFs) had high specificity, with no lesions found in 22 cases (only 2 patients had 1 FP).

Regarding the evaluation according to lesion location, the proposed model (SimLearnedDFs) appeared to learn well from most of the brain regions, and it had the highest sensitivity everywhere. When compared with the rest of the pipelines, there was a relevant increase in the performance in the juxtacortical lesions when both the deformation fields and brain lesions were learned jointly. The SimLearnedDFs model had a TPF of 91.18% (31 lesions out of 34) and FPF of 26.19% (11 FPs out of 42 candidates) with DCSd of 0.82 and DCSs of 0.65. The NDFs model also had a high TPF of 82.35% but with a high FPF of 51.02% (DSCd = 0.64 and DSCs = 0.57). In the periventricular region, the lesions were easily observed, which may be explained by the good contrast between ventricular and the new MS lesions. The difference in TPF of all CNN-based methods was not as high. The proposed method (SimLearnedDFs) showed the highest sensitivity while still maintaining some false positives (2 FPs out of 24 candidates, 8.33%) compared to the SepLearnedDFs and DemonsDFsmodels that had no FPs in the periventricular region. Regarding the deep white matter lesions, the SimLearnedDFs model detected the highest number of lesions (97 out of 120, 80.83%), which may be explained by the high number of lesions in this particular region (63% of the total number of lesions). The difference between the three variants in terms of FPs was very low. In contrast, the sensitivity of CNN methods was remarkably lower in the infratentorial region due to a lack of training data (infratentorial lesions were only 6% of the total number of lesions). Furthermore, this may also be one reason for the worse performances of both methods where DF were learned. In these methods, the learned DFs did not efficiently distinguish the complexity of the cerebellum, increasing the number of noninfratentorial lesion activations. The SimLearnedDFs model had only three FPs detected, and these FPs were only detected in one patient. All of the subtraction-based methods like (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Salem, Cabezas, Valverde, Pareto, Oliver, Salvi, Rovira, Lladó, 2018, Sweeney, Shinohara, Shea, Reich, Crainiceanu, 2013) had higher FP lesions in this region, which may be explained by the poor contrast between tissues in the infratentorial region and therefore, a noisy subtraction. We believe that more training data or the use of synthetic MS data as in (Salem et al., 2019) with more infratentorial lesions, may increase the sensitivity of all CNN-based methods while reducing FP lesions. The method of Schmidt et al. (2019) had high TPF in the periventricular, juxtacortical, and deep white matter regions but also a high FPF. It had (DSCd, DSCs) of (0.68, 0.49), (0.7, 0.51), and (0.54, 0.34) for the periventricular, juxtacortical, and deep white matter regions, respectively. We also observed that in the infratentorial region, it had better performance than the SepLearnedDFs and DemonsDFs models. However, these results should be further investigated using more cases containing periventricular and infratentorial lesions in order have a more robust analysis.

We also studied the use of conventional data augmentation methods like geometric transformations such as image translation, rotation, or flip. However, the performance did not increase. One reason might be due to the fact that the generated samples did not represent image appearances in real data, or that the generated samples were very similar to the existing images in the training dataset. Working on the development of a framework for generating new longitudinal synthetic MS lesions on patients or healthy MR images, could allow the creation of more data samples for particular lesion locations where few samples are available (i.e, the infratentorial region), helping to improve the trained models.

Regarding the experiment in which the proposed model (SimLearnedDFs) was applied to images from a different hospital, as expected, the TPF and FPF detection values were worse due to the change of domain (change in scanner and MRI protocol). Note however, that the SimLearnedDFs model provided a better generalization than the one not based on deep learning (Salem et al., 2018). Moreover, the obtained results with the SimLearnedDFs model in the Trueta dataset were also better than those of the unsupervised approaches (Cabezas, Corral, Oliver, Díez, Tintoré, Auger, Montalban, Lladó, Pareto, Rovira, 2016, Schmidt, Pongratz, Kster, Meier, Wuerfel, Lukas, Bellenberg, Zipp, Groppa, Smann, Weber, Gaser, Franke, Bussas, Kirschke, Zimmer, Hemmer, Mhlau, 2019), using the parameter configuration optimized for the VH Hospital. The performance without parameter tuning was actually poor, while the optimum configuration provided similar results to those shown on the VH dataset.

In conclusion, the obtained results indicate that the proposed end-to-end training model increases the accuracy of the new T2-w lesion detection. Given the sensitivity and limited number of false positives, we strongly believe that the proposed method may be used in clinical studies to monitor the progression of the disease.

CRediT authorship contribution statement

Mostafa Salem: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing - original draft, Visualization, Writing - review & editing. Sergi Valverde: Conceptualization, Validation, Writing - review & editing. Mariano Cabezas: Conceptualization, Validation, Writing - review & editing. Deborah Pareto: Resources, Validation. Arnau Oliver: Conceptualization, Writing - review & editing. Joaquim Salvi: Writing - review & editing, Funding acquisition. Àlex Rovira: Resources, Data curation, Writing - review & editing. Xavier Lladó: Conceptualization, Validation, Resources, Writing - review & editing, Supervision, Project administration, Funding acquisition.