Thermodynamic and thermoelastic data of georesources raw minerals: Zinc sulphide and apatite

Abstract

This article reports a dataset on the thermodynamic and elastic properties of two important raw minerals exploited in georesources and ore mining. The presented data refers to two zinc sulphide polymorphs, namely zinc-blende (low-pressure polymorph, space group $F\stackrel{-}{4}3m$) and rock-salt (high-pressure polymorph, space group $Fm\stackrel{-}{3}m$) [1], and of type-A carbonated apatite, [CAp, Ca₁₀(PO₄)₆CO₃, space group P1] [2]. The data here reported were calculated from ab initio quantum mechanical simulations at the DFT/B3LYP level, all-electron Gaussian-type orbitals basis sets and from the analysis of the phonon properties of the zinc sulphide polymorphs and of type-A CAp by means of the quasi-harmonic approximation. In addition, a correction to take into account the effects of dispersive forces was considered to obtain the dataset of type-A carbonated apatite. This dataset, which was validated against experimental thermodynamic data reported in literature, has been employed to construct the phase diagram between the two zinc sulphide polymorphs and discuss their stability over the temperature and pressure range 0–800 K and 0–25 GPa. The thermodynamic and thermoelastic data of CAp were obtained between 0 and 600 K and 0–3 GPa, below the temperature of thermal decomposition of the mineral. The reported data can be of use in several application fields, for instance fundamental georesource exploration and exploitation, and also in applied mineralogy, geology, material science, and as a reference to assess the quality of other theoretical approaches. Furthermore, the data of type-A carbonated apatite could be useful for designing and processing new biomaterials with tailored properties.

Specifications Table

Subject	Material Science
Specific subject area	Thermodynamics and thermoelastic of georesouces raw minerals
Type of data	Table Graph Figure
How data were acquired	Quantum mechanical simulations at the DFT/B3LYP level of theory, using the quasi-harmonic approximation (CRYSTAL17 code)
Data format	Raw Analyzed
Parameters for data collection	The temperature and pressure range used in the quasi-harmonic approximation for the calculation of the thermodynamic and thermoelastic data were 0–800 K (step of 1 K) and 0–25 GPa (step of 1 GPa) for zinc sulphides and were 0–600 K (step of 1 K) and 0–3 GPa (step of 1 GPa) for type-A carbonated apatite
Description of data collection	The data were obtained from quantum mechanical simulations conducted using Density Functional Theory, B3LYP functional and Gaussian-type orbitals basis sets. A correction for the dispersive forces based on the DFT-D2 method was also employed (B3LYP-D* scheme) for type-A carbonated apatite. The quasi-harmonic approximation, based on the volume dependence of mineral phonon properties at different temperatures and hydrostatic compression states, was employed to calculate the thermodynamic and thermoelastic dataset. Starting geometries used as input for the quantum mechanical simulations were taken from experimental structural results.
Data source location	The quantum mechanical simulations were conducted at the University of Bologna, Bologna, Italy.
Data accessibility	With the article
Related research articles	Ulian, G. & Valdrè, G. (2019) Thermomechanical, electronic and thermodynamic properties of ZnS cubic polymorphs: an ab initio investigation on the zinc-blende – rock-salt phase transition. Acta Crystallographica Section B, 75, 1042–1059, doi:https://doi.org/10.1107/S2052520619012630. Ulian, G., and Valdrè, G. (2019) First principle investigation of the thermomechanical properties of type A carbonated apatite. International Journal of Quantum Chemistry, 120, e26069, https://doi.org/10.1002/qua.26069.

Value of the Data •A detailed dataset on thermodynamic and thermoelastic properties of zinc sulphide polymorphs (zinc-blende and rock-salt ZnS) and of type-A carbonated apatite [Ca10(PO4)6CO3] represents a foundation for future fundamental and applied studies on these mineral phases. •Both theoretical and experimental researchers could employ this dataset as a valuable reference to compare the results of their studies. •This dataset provides also fundamental insights on the zinc-blende and rock-salt ZnS phases, which could be employed, for example, to devise pressure/temperature sensors. •In addition, being zinc sulphide an ore mineral, this dataset could be employed for development of ore mineral processing techniques. •Carbonated (hydroxyl)apatite is a key biomaterial for bone reconstruction and repair, and the provided data can drive future researches and developments in the biomaterial field.

1. Data description

1.1. Zinc sulphide polymorphs: zinc-blende and rock-salt ZnS

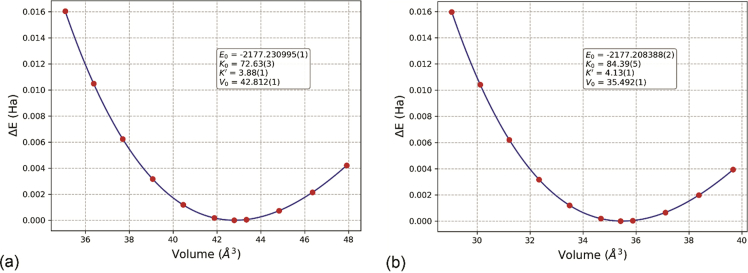
Zinc-blende (zb, also known as sphalerite from the mineralogical point of view) and rock-salt ZnS (rs) are two polymorphs of zinc sulphide, belonging to the space group $F\overline{4}3m$ and $Fm\overline{3}m$, respectively. zb-ZnS is stable at low pressure and temperatures, representing the main source of zinc from ore smelting, whereas rs-ZnS is found at high pressures. Sphalerite is found in several locations worldwide, such as Germany, Romania, Canada, USA and Mexico. To realize the present dataset, both polymorphs were optimized at equilibrium conditions and under the effect of hydrostatic expansion/compression at T = 0 K, starting from the experimental structures determined by Skinner [3]. The unit cell geometry optimization results for both zinc-blende and rock-salt polymorphs of zinc sulphide are reported in Table 1 [1], whereas Fig. 1 shows a graphical representation of the unit cell energy vs volume curves fitted by a volume-integrated 3rd-order Birch-Murnaghan equation of state.

Table 1.

Primitive unit cell volume (V_pc) and static energy (E_pc), Crystallographic unit cell volume (V_cc) and lattice parameter (a_pc) resulting from the geometry optimization results of zinc-blende and rock-salt ZnS polymorphs. Underlined values are related to the equilibrium geometry.

Zinc-blende ZnS					Rock-salt ZnS
P (Gpa)	Vpc(Å3)	Epc(Ha)	Vcc(Å3)	acc(Å)	P (Gpa)	Vpc(Å3)	Epc(Ha)	Vcc(Å3)	acc(Å)
21.30	35.080	−2.177214945324E+03	140.321	5.197	25.65	29.042	−2.177192422262E+03	116.170	4.879
16.23	36.377	−2.177220509835E+03	145.506	5.260	19.48	30.116	−2.177197962616E+03	120.462	4.939
11.81	37.704	−2.177224760714E+03	150.818	5.323	14.14	31.215	−2.177202180969E+03	124.860	4.998
7.95	39.064	−2.177227823064E+03	156.257	5.386	9.51	32.341	−2.177205213821E+03	129.362	5.058
4.59	40.456	−2.177229808849E+03	161.825	5.449	5.51	33.493	−2.177207182795E+03	133.972	5.117
1.67	41.881	−2.177230818510E+03	167.524	5.513	2.07	34.672	−2.177208195666E+03	138.691	5.176
0.05	42.781	−2.177230994348E+03	171.123	5.552	0.18	35.418	−2.177208385989E+03	141.670	5.213
−0.87	43.339	−2.177230942467E+03	173.355	5.576	−0.90	35.880	−2.177208348407E+03	143.518	5.236
−3.06	44.830	−2.177230262298E+03	179.320	5.639	−3.44	37.114	−2.177207726602E+03	148.457	5.295
−4.95	46.355	−2.177228851914E+03	185.421	5.702	−5.61	38.377	−2.177206406104E+03	153.507	5.354
−6.57	47.915	−2.177226778287E+03	191.658	5.766	−7.46	39.668	−2.177204454375E+03	158.671	5.414

Fig. 1.

Primitive unit-cell volume vs energy data (reported as ΔE = E – E_eq, with E_eq equal to the energy of the unit cell at equilibrium volume) of (a) zinc-blende and (b) rock-salt ZnS. The box reports the parameters obtained from fitting the data with a volume-integrated 3rd-order Birch-Murnaghan equation of state.

The thermodynamics and thermomechanics of both zb-ZnS and rs-ZnS were calculated from the phonon properties of the mineral phases between 0 and 800 K. The effect of pressure was evaluated from 0 GPa to 20 GPa for zinc-blende, whereas for the rock-salt polymorph, which presents phonon instability at low pressure [1], the properties were calculated in the pressure range 12–25 GPa. The results are reported in Tables S1–S22 in the Supplementary Material for both zb-ZnS (Tables S1–S11) and rs-ZnS (Tables S12–S22), subdivided as follows:

• •primitive unit cell volume (Tables S1 and S12);
• •isothermal bulk modulus, K_T (Tables S2 and S13);
• •adiabatic bulk modulus, K_S (Tables S3 and S14);
• •coefficient of thermal expansion (CTE), α_V (Tables S4 and S15);
• •isochoric heat capacity, C_V (Tables S5 and S16);
• •isobaric heat capacity, C_P (Tables S6 and S17);
• •entropy, S (Tables S7 and S18);
• •absolute enthalpy, H (Tables S8 and S19);
• •absolute Helmholtz free energy, F (Tables S9 and S20);
• •absolute Gibbs free energy, G (Tables S10 and S21);
• •absolute internal energy, U (Tables S11 and S22).

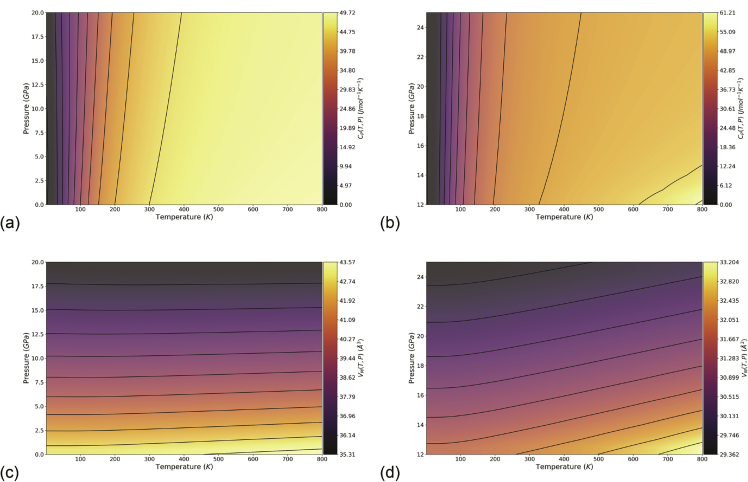
The obtained reported data can be employed, for instance, to create bidimensional plots of the desired thermodynamic and thermoelastic properties and to compare them to other theoretical or experimental results. Fig. 2 reports an example of this application.

Fig. 2.

Bidimensional contour plots of (a,b) isobaric heat capacity and (c,d) primitive cell volume as a function of temperature and pressure for (a,c) zb-ZnS and (b,d) rs-ZnS.

1.2. Type-A carbonated apatite

Type-A carbonated apatite [Ca₁₀(PO₄)₆CO₃, space group P1] belongs to the calcium apatite mineralogical family, which is used for several applications, such as production of fertilizers, gemstone cutting and as source of rare-Earth elements through ore smelting. Carbonated apatite is also an important mineral in the biomaterials field. Apatite minerals are commonly found in Canada, Brazil, USA and Mexico.

The thermodynamic and thermoelastic data here provided were calculated from the structural and vibrational properties of seven unit cell volumes in the temperature range 0–600 K (step of 1 K), below the temperature of thermal decomposition of the mineral phase [4], and between 0 GPa and 3 GPa (step of 0.5 GPa). The equilibrium geometry was theoretically determined in a previous work [5], where the experimental results of Fleet and Liu [6] were employed to model the type-A carbonated apatite. The results are reported in Tables S23–S33 in the Supplementary Material whose content is here summarized:

• •unit cell volume (Table S23);
• •isothermal bulk modulus, K^T (Table S24);
• •adiabatic bulk modulus, K^S (Table S25);
• •coefficient of thermal expansion (CTE), α^V (Table S26);
• •isochoric heat capacity, C^V (Table S27);
• •isobaric heat capacity, C^P (Table S28);
• •entropy, S (Table S29);
• •absolute enthalpy, H (Table S30);
• •absolute Helmholtz free energy, F (Table S31);
• •absolute Gibbs free energy, G (Table S32);
• •absolute internal energy, U (Table S33).

2. Experimental design, materials, and methods

The data here presented was obtained by first principle simulations on periodic systems, using the CRYSTAL17 code [7], which implements the Hartree–Fock and Kohn–Sham self-consistent field method.

Multielectron wave functions are constructed as an antisymmetrized product (Slater determinant) of monoelectronic crystalline orbitals (CO) that are linear combination of local functions (atomic orbitals, AO) centred on each atom in the system. In turn, atomic orbitals (basis set) are linear combinations of Gaussian-type functions (GTF). The all-electron basis sets employed for both Zn²⁺ and S²⁻ were described by the double-ζ basis set with polarization functions designed by Peintinger-Bredow-Oliveira (POB) [8]. For type-A CAp, it was the same basis sets adopted in previous works on OHAp and type A CAp [2,5]. Calcium has been described with a 86-511G(2d), with outer shell exponents α_sp = 0.453 bohr⁻², α_d1 = 3.1910 and 0.8683 bohr⁻² and α_d2 = 0.2891 bohr⁻². The phosphorus atom is described by the basis 85-21G(d), α_sp = 0.48105 bohr⁻² and α_d = 0.135 and 0.74583 bohr⁻², respectively. Oxygen was represented by a 6-31G* basis set with the outer shell exponents α_sp = 0.2742 and 0.190 bohr⁻² and α_d = 0.538 bohr⁻². The carbon atom is described by a 6-21G* basis set with α_sp = 0.26 bohr⁻² and α_d = 0.8 bohr⁻².

The hybrid B3LYP functional [9,10], which is well-known for its ability to produce high quality of crystal-chemical, vibrational/thermodynamic and elastic results [11,12], has been adopted for all calculations. Only in the case of type-A carbonated apatite, the DFT-D2 correction scheme was included in its recently adjusted form for B3LYP (B3LYP-D* approach) to take into account the effect of dispersive forces on both structural and thermodynamic properties [13]. The exchange–correlation contribution is performed over a grid of points and is the result of a numerical integration of the electron density and its gradient. The adopted pruned grid is given by 75 points and 974 angular points (XLGRID) and obtained from The Gauss–Legendre quadrature and Lebedev schemes. The tolerance thresholds that control accuracy of the Coulomb and exchange integrals were set to 10⁻⁷ and 10⁻¹⁶, respectively [7]. The Hamiltonian matrix has been diagonalized using a Monkhorst grid of k-points of size 8 × 8 × 8 for both zinc-blende and rock-salt polymorphs. The convergence on total energy was reached when the difference between the energy of two subsequent self-consistent field cycles was less than 10⁻⁸ Hartree during geometry optimization and less than 10⁻¹⁰ Hartree during phonon calculations.

The compressional behaviour of zinc sulphide and type-A carbonated apatite has been investigated carrying out a symmetry-preserving relaxation procedure by exploring ten volumes between 0.82×V_eq and 1.12×V_eq (step of 0.03×V_init) for both zinc-blende and rock-salt ZnS, whereas for type-A Cap seven unit cell volumes were considered between 0.92×V_eq and 1.08×V_eq, with a step of 0.04×V_eq under compression (two unit cell volumes) and 0.02 ×V_eq under expansion (four unit cell volumes). Here, V_init represents the volume of the unit cell of each mineral (zinc-blende, rock-salt ZnS, CAp) at equilibrium conditions. Each model was then geometrically optimized.

At each unit cell compressive state, the energy vs volume data, E(V) curve, was fitted with a volume-integrated 3rd-order Birch-Murnaghan equation of state (EoS) formulation [14]:

$$\begin{array}{c}E=E_0+\frac{9}{16}{K}_0{V}_0\left\{K^{\text{'}{\left({\eta }^2-1\right)}^3}+\left[{\left({\eta }^2-1\right)}^2\left(6-4{\eta }^2\right)\right]\right\}\end{array}$$ (1)

$$\begin{array}{c}\eta ={\left(\frac{V_0}{V}\right)}^{1/3}\end{array}$$ (2)

where V₀ is the unit cell volume at 0 GPa, E₀ its energy, K₀ the bulk modulus and K′ the pressure first derivative of the bulk modulus. The obtained parameters were employed in the well-known P–V formulation of the Birch-Murnaghan EoS to calculate the pressure state of the system:

$$\begin{array}{c}P=\frac{3}{2}{K}_0\left[{\eta }^{-7/3}-{\eta }^{-5/3}\right]\left\{1-\frac{3}{4}\left(4-K^{\text{'}}\right)\left({\eta }^{-2/3}-1\right)\right\}+P_0\end{array}$$ (3)

Thermodynamic and thermomechanics properties of each mineral phase were obtained from lattice dynamics results by means of the quasi-harmonic approximation (QHA) approach as described by Erba and co-workers [15]. Lattice dynamics was calculated on 4 × 4 × 4 supercells in the case of zinc sulphide polymorphs [1], whereas only Γ-point frequencies were considered for type-A carbonated apatite [2].

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: