Mechanism of μ-Opioid Receptor-Magnesium Interaction and Positive Allosteric Modulation

Abstract

In the era of opioid abuse epidemics, there is an increased demand for understanding how opioid receptors can be allosterically modulated to guide the development of more effective and safer opioid therapies. Among the modulators of the μ-opioid (MOP) receptor, which is the pharmacological target for the majority of clinically used opioid drugs, are monovalent and divalent cations. Specifically, the monovalent sodium cation (Na⁺) has been known for decades to affect MOP receptor signaling by reducing agonist binding, whereas the divalent magnesium cation (Mg²⁺) has been shown to have the opposite effect, notwithstanding the presence of sodium chloride. Although ultra-high-resolution opioid receptor crystal structures have revealed a specific Na⁺ binding site and molecular dynamics (MD) simulation studies have supported the idea that this monovalent ion reduces agonist binding by stabilizing the receptor inactive state, the putative binding site of Mg²⁺ on the MOP receptor, as well as the molecular determinants responsible for its positive allosteric modulation of the receptor, are unknown. In this work, we carried out tens of microseconds of all-atom MD simulations to investigate the simultaneous binding of Mg²⁺ and Na⁺ cations to inactive and active crystal structures of the MOP receptor embedded in an explicit lipid-water environment and confirmed adequate sampling of Mg²⁺ ion binding with a grand canonical Monte Carlo MD method. Analyses of these simulations shed light on 1) the preferred binding sites of Mg²⁺ on the MOP receptor, 2) details of the competition between Mg²⁺ and Na⁺ cations for specific sites, 3) estimates of binding affinities, and 4) testable hypotheses of the molecular mechanism underlying the positive allosteric modulation of the MOP receptor by the Mg²⁺ cation.

Significance

Overprescription of opioid drugs in the late 1990s, followed by abuse of both prescription and illicit opioid drugs, has led to what is nowadays called the “opioid overdose crisis” or “opioid epidemic,” with more than 130 Americans dying daily from opioid overdose at the time of writing. To reduce opioid doses, and thereby prevent or treat overdose and opioid use disorders, attention has recently shifted to the use of coanalgesics. Understanding how opioid receptor targets can be allosterically modulated by these elements, including cations, is key to the development of improved therapeutics. Here, we provide an atomic-level understanding of the mechanism by which magnesium binds to the μ-opioid receptor and enhances opioid drug efficacy by stabilizing the receptor activated state.

Introduction

Opioid analgesics such as morphine remain the “gold standard” for the treatment of acute (e.g., postoperative) or chronic (e.g., cancer) pain notwithstanding the multitude of side effects they cause, including respiratory depression, tolerance, addiction, dependence, constipation, nausea, vomiting, dizziness, fatigue, and itching (1). Among all side effects, respiratory depression is certainly the most feared by physicians given the almost 400,000 casualties from overdosing on prescription or illicit opioids during 1999–2017 in the United States alone (2).

Almost all clinically used opioid drugs act through the μ-opioid (MOP) receptor (3), a member of the G protein-coupled receptor (GPCR) superfamily. Like other GPCRs, this receptor exists as an ensemble of multiple inactive, active, and intermediate conformations, and this conformational plasticity forms the basis for the receptor signaling diversity achieved through receptor interaction with different intracellular proteins, such as G proteins (typically Gα_i/o subtypes) or arrestins (typically β-arrestin-2) (4). Depending on the MOP receptor conformation stabilized by the drug and the intracellular protein recruited by the receptor, biological functions that are either clinically desirable or detrimental can ensue. Indeed, although studies using MOP receptor knockout mice confirmed that the MOP receptor is responsible for the antinociceptive action of morphine (3), β-arrestin recruitment by the MOP receptor was shown to contribute to some of the side effects of this classical opioid drug (5, 6, 7), supporting the hypothesis that biasing the conformational equilibrium of MOP receptor toward the G protein pathway may lead the way to develop safer opioid therapies.

In principle, there are several ways one could possibly bias the conformational equilibrium of the MOP receptor toward a specific conformational state, whether using a small molecule, a peptide, a protein, or other allosteric modulators, including cations. Indeed, it has been known for more than 40 years that the MOP receptor can be differentially modulated by cations (8). Whereas the monovalent Na⁺ cation can decrease agonist affinity at the MOP receptor (8), most likely through stabilization of the inactive conformational state of the receptor (e.g., see (9,10)), the divalent Mg²⁺ cation has the opposite effect (e.g., see (11)), suggesting it stabilizes an active-like conformation of the receptor. Notably, similar conclusions were drawn for other GPCRs based on inferences from biochemical and pharmacological studies (12, 13, 14, 15, 16, 17, 18).

Although various high-resolution x-ray crystal structures of inactive forms of GPCRs have revealed the atomic details of Na⁺ binding (19, 20, 21, 22) and several molecular dynamics (MD) simulation studies have supported the stabilization of inactive conformations of the receptor by this monovalent cation (e.g., see (9,10,23,24)), limited information exists to date about the preferred binding site(s) of Mg²⁺ and the molecular mechanism underlying the positive allosteric effect of this divalent cation. A recent interdisciplinary study combining the results of ¹⁹F-NMR and MD simulations on another prototypic GPCR, the adenosine A_2A receptor (18), provided further support to the negative allosteric modulation of receptors by Na⁺ and their positive allosteric modulation by Ca²⁺ and Mg²⁺. Not only did this work allow quantification of the effects of these cations on the conformational ensemble of the adenosine A_2A receptor, but it also suggested important molecular determinants involved in the allosteric activation of this receptor in the presence of physiological cations. Notable results of these studies were the unexpected finding that Na⁺ also stabilized an intermediate state that had previously been associated with partial agonism, whereas Mg²⁺ cations drove G protein-binding cleft opening, and consequent receptor activation, upon bridging specific acidic residues on the extracellular region of transmembrane (TM) helices 5 and 6 (TM5 and TM6) of the receptor (18).

In our work, we studied the free binding of Mg²⁺ to the MOP receptor in the presence of physiological concentrations of Na⁺ by all-atom standard MD simulations of the receptor embedded in an explicit 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC)/cholesterol environment and supplemented them with a grand canonical Monte Carlo MD (GCMC-MD) method (25, 26, 27) to confirm thorough exploration of the Mg²⁺ bound states. The goal of this study was not only to predict energetically favorable binding sites of Mg²⁺ at the MOP receptor but also to provide atomic details of the molecular mechanism regulating the positive allosteric modulation of the receptor induced by this divalent cation. This information is important considering that magnesium is known to enhance opioid-induced analgesia in different types of surgical procedures without increasing opioid side effects at therapeutic doses, thus suggesting that its use in combination with opioid analgesics may be useful in clinical practice (28).

Methods

MD simulations and system setup

Three different simulation setups were built for the ligand-free murine MOP receptor (residues 65–347), using the CHARMM-GUI web server (29). Whereas one of them was based on the x-ray crystal structure of the inactive MOP receptor (Protein Data Bank (PDB): 4DKL (30)), the other two system setups used the crystal structure of the active MOP receptor (PDB: 5C1M (31)) and differed in the protonation state of the highly conserved D114^2.50 residue. The missing loop between TM5 and TM6 in 4DKL (residues M264–K269) was added using the Modeller software (32). Both ligand-free inactive and active MOP receptor models were embedded in a lipid bilayer with a POPC/cholesterol ≈ 9:1 ratio and an area of 7.5 × 7.5 nm². A POPC/10% cholesterol lipid bilayer is a typical membrane model used in MD simulations of GPCRs considering 1) the abundance of phosphatidylcholine lipids in cell membranes (33), 2) a 10% sterol/lipids ratio representing a mean value across membranes of different cell compartments, and 3) the suggested impact of cholesterol on the receptor conformational dynamics (34).

The membrane and protein were then solvated with explicit TIP3P water molecules and 0.15 M concentrations of both Na⁺ and Mg²⁺ cations and neutralized with Cl⁻ ions. All ions were placed randomly in the solvent volume, at least 10 Å away from the protein and membrane. Each full simulation system contained ∼70,000 atoms and had an initial volume of 7.5 × 7.5 × 11.9 nm³. The CHARMM36 force field (35) was used to model protein, lipids, and ions, and all-atom MD simulations were carried out using the GROMACS software package version 2018.1 (36). After a first energy minimization step, six short equilibrations runs with gradually decreasing harmonic constraints on lipid and protein heavy atoms were carried out, following the CHARMM-GUI membrane builder equilibration protocol. After these short equilibration runs, the three systems were further equilibrated for 100 ns in the NPT ensemble without constraints using the Nosé-Hoover thermostat (37) at 310 K (coupling constant ${\tau }_t=1.0$ ps) and the Berendsen barostat (38) at 1 atm (coupling constant ${\tau }_p=5.0$ ps). A final equilibration run of 20 ns was carried out under the production simulation conditions in which the Berendsen barostat was replaced by the Parrinello-Rahman barostat (39) (coupling constant of ${\tau }_p=5.0$ ps at 1 atm). Different production runs ranging between ∼0.7 and ∼2.4 μs, for a total simulation time of over 20 μs, followed, beginning from equidistant frames selected from the previous 20 ns equilibration (see Table S1 for details). Long-range electrostatic interactions (for interparticle distances beyond 1.2 nm) were taken into account using the particle mesh Ewald algorithm (40). The van der Waals interactions were switched off gradually between 1.0 and 1.2 nm. Periodic boundary conditions were applied to the simulation boxes, and an integration time step of 2 fs was used for all simulations.

GCMC-MD simulations

Despite extensive unbiased MD simulations, Mg²⁺ coordination complexes with direct interactions to acidic residues were not observed, possibly because of the large desolvation free energy for Mg²⁺ (41,42) and in agreement with the results of MD simulations carried out on another prototypic GPCR (18). To enable sampling of Mg²⁺ direct coordination complexes and check whether other important coordination sites had been missed by standard MD simulations, we applied a grand canonical Monte Carlo method combined with MD (GCMC-MD) (25, 26, 27) that successfully reproduced Mg²⁺coordination on RNA molecules (27). This method combines a Monte Carlo insertion/deletion protocol using an oscillating chemical potential with short MD trajectories to sample potential ion coordination complexes. Specifically, we utilized this method to insert and delete water molecules and Mg²⁺ ions into a defined GCMC region around the MOP receptor with a target concentration of water molecules and Mg²⁺ ions that matched their respective simulation concentrations. We used the previously described excess chemical potentials of −5.6 kcal/mol for water molecules and −437.38 kcal/mol for Mg²⁺ ions (25,43). This GCMC region was defined separately for different simulation systems as a cuboid with a volume of ∼52 × 52 × 94 Å³ centered on the geometrical center of each simulation box. We applied this protocol on representative conformations of the most populated Mg²⁺ macrosites extracted from our unbiased MD simulations (see below). For each protein conformation, we performed two initial iterations of GCMC to populate the GCMC simulation region with the target water molecules and Mg²⁺ ions. These were followed by 100 iterations of GCMC-MD sampling, each of which featured 200,000 steps of GCMC, a brief 5000-step steepest descent minimization, a 100 ps constant pressure equilibration, and finally a 1 ns constant volume run. The MD steps were performed with Gromacs version 2018.6. The MD trajectories of the GCMC-MD protocol were then analyzed to identify Mg²⁺ microsites and to calculate their bound population as described below.

Identification of cation binding sites

We used a two-step approach to identify the preferred binding sites for each cation on each of the simulated MOP receptor systems. First, so-called cation binding microsites were detected by the presence of either Na⁺ or Mg²⁺ cations within the closest minimum distance $\left(r_{\text{min}}\right)$ from heavy atoms of protein residues. The value of $r_{\text{min}}$ for the two cations was selected after inspection of the radial distribution functions of the Na⁺-protein and Mg²⁺-protein distances, respectively, calculated from combined MD and GCMC-MD trajectories of all simulated active and inactive MOP receptor systems. Based on the radial distribution functions shown in Fig. S1, values of $r_{\text{min}}=2.9$ Å or $r_{\text{min}}=2.5$ Å were chosen to indicate direct Na⁺ or Mg²⁺ coordination to protein residues, respectively. However, unlike Na⁺, the majority of Mg²⁺ coordination complexes were water mediated and we therefore chose to select a second closest minimum distance for Mg²⁺ cations ($r_{min}^{\left(2\right)}=4.5$ Å) to characterize microsites containing these coordination states. Given the large number of microsites obtained using the aforementioned criteria, for each simulated MOP receptor system, we aggregated microsites into macrosites of cation binding based on the location of coordinating residues within said microsites. For instance, microsites involving cation contacts with D147^3.32 were labeled as “orthosteric site,” whereas microsites involving coordination with D114^2.50 or N150^3.35 were labeled as “allosteric site.” Similarly, sites in the extracellular loop (ECL) region were labeled ECL1, ECL2, or ECL3 if containing G131–G136, A206–H223, or L305–T311 residues, respectively.

Calculation of cation binding affinity at macrosites

The cation binding affinity $K_d^i$ for the $i$th macrosite was estimated based on its marginal occupancy probability p_i, defined as the fraction of MD simulation frames in which the macrosite is occupied. This analysis was performed separately for frames sampled during the GCMC-MD protocol to assess the affinity of Mg²⁺ to equivalent macrosites identified during said protocol. Before running these calculations, we verified that the number of cation binding events at each macrosite, estimated in terms of the number of contacts formed by a cation at each macrosite across the multiple MD simulation trajectories, was sufficient to obtain reliable estimates of occupation probabilities from population counts. The results we obtained from analysis of the MD simulation runs, ranging from ∼40 to ∼1000 binding events for Mg²⁺ and 20 to ∼500 binding events for Na⁺ (see Table S2), confirmed that occupation probabilities could be calculated reliably. Assuming that binding to the protein does not change the ion concentration, the binding affinity $K_d$ can be estimated via the relation as follows:

$$K_d=C\frac{\left(1-p_i\right)}{p_i},$$

where C is the molar concentration of each cation species present in the simulation box.

Allosteric coupling between macrosites of cation binding

We assessed the effect of each cation species on the binding of the other by calculating cooperativity coefficients between pairs of binding macrosites derived from standard MD simulations. Specifically, we considered the joint probability distribution $p\left(o_i^x,o_j^y\right)$ of the cation species x occupying the macrosite i and the cation species y occupying the microsite j, marginalizing the occupancy of all the other macrosites on the receptor. Indicating with $K_i^x$ the affinity of the cation species x at macrosite i when macrosite j is not occupied, and correspondingly, with $K_j^y$ the affinity of the cation species y at macrosite j when macrosite i is not occupied, the presence of a cation at macrosite j changes the affinity of the cation species x at macrosite i to $K_i^x/{\alpha }_{ij}$, whereas the closure of the thermodynamic cycle ensures that when macrosite i is occupied, the cation binding affinity at macrosite j becomes $K_j^y/{\alpha }_{ij}$. We report these cation binding affinity changes as $\log {\alpha }_{ij}$, with negative values implying negative modulation (i.e., a reduction in the cation binding affinity at a given macrosite induced by the presence of another cation species). We estimate the values of ${\alpha }_{ij}$ from the ratios as follows:

$$\log {\alpha }_{ij}=\log \frac{p\left(o_i^x=1,o_j^y=1\right)}{p\left(o_i^x=1,o_j^y=0\right)}+\log \frac{p\left(o_i^x=0,o_j^y=0\right)}{p\left(o_i^x=0,o_j^y=1\right)}.$$

Quantification of cation effect on extracellular loop gating

To elucidate the effect of Mg²⁺ binding on the conformational plasticity of the extracellular loop 2 and 3 (ECL2/3) region of the receptor, which has often been linked to the allosteric modulation of ligand binding, we outlined a simple activation model of the MOP receptor and used our MD simulations to derive its thermodynamic properties. Frames sampled from GCMC-MD simulations were not included in this analysis because of a limited sampling of protein motions in this method. Specifically, our simple model only considers agonist binding and defines the active state of the receptor (with either neutral or charged D^2.50) as the ligand-bound state, whereas the inactive receptor conformation is classified as a ligand-unbound state. We consider two different states of the ECL2/3 region of the MOP receptor, which we labeled open (O) or closed (C), depending on whether the minimum distance $\left(d_{\text{Loop}}\right)$between the heavy atoms of residue pairs E310^ECL3−R211^ECL2 and Q212^ECL2−D216^ECL2 sampled during simulation was larger or smaller than 10 Å, respectively. Indicating with $K_O$ and $K_C$ the ligand binding affinity for the ECL2/3 region open and closed states, respectively, and with $H_B$ and $H_U$ the equilibrium constants for ECL2/3 region opening in the bound and unbound receptors, we have that $K_C/K_O=H_B/H_U$, and by applying the mass-action law, we can write the ligand-bound fraction of the receptor at ligand concentration $\left[L\right]$ as follows:

$$f_B=\frac{\left[L\right]}{\left[L\right]+\rho K_O}$$

where

$$\rho =\frac{1+H_U^{-1}}{1+H_B^{-1}}$$

is a coefficient that measures the allosteric coupling between ligand binding and loop dynamics.

If the dynamics of the ECL2/3 region do not depend on the presence of the ligand, then $H_U=H_B$ and $\rho =1$. In this case, the ligand binding thermodynamics are not affected by ECL2/3 region gating, and the ligand binding affinity is $L_{50}=K_O$, that is, the same as to the open receptor. If, however, the closed state of the ECL2/3 region is more stable in the ligand-bound complex, $H_U\ll H_B$ and $\rho \ll 1$. In this case, $L_{50}\ll K_O$ (i.e., the affinity of the ligand) and the stability of the active state are increased by ECL2/3 region closure. Accordingly, this model can capture the basic mechanism by which ECL2/3 region closure increases the binding affinity of a ligand.

To quantify the effect of Na⁺ and Mg²⁺ cations on ECL2/3 region gating, we assessed the coupling between the ECL2/3 loop region conformational dynamics and cation binding. For a given Mg²⁺ concentration [M], we characterized the dynamics between the Mg²⁺-bound state of the open ECL2/3 region $\left(O_M\right)$ and the Mg²⁺-free state of the open ECL2/3 region (O) as $O_M\left(i\right)=J_O\left(i\right)O\left(i\right)\left[M\right],$where $J_O\left(i\right)$ is the equilibrium constant reflecting the affinity of Mg²⁺ for the open state, and $i$ indicates the MOP receptor state (unbound/inactive, bound/active). Similarly, for the closed state of the ECL2/3 region, $C_M\left(i\right)=J_C\left(i\right)C\left(i\right)\left[M\right]$. Indicating with $H_0^{-1}\left(i\right)$ the equilibrium constant between the open and closed states of the ECL2/3 region in the absence of Mg²⁺, at magnesium concentration $\left[M\right]$, we have that the equilibrium between the ECL2/3 region open and closed states is as follows:

$$H_i^{-1}=H_0^{-1}\left(i\right)\frac{J_C\left(i\right)\left[M\right]+1}{J_O\left(i\right)\left[M\right]+1}.$$

Using this expression for $H_U^{-1}$ and $H_B^{-1}$, we obtain the dependence of the allosteric coefficient ρ on the Mg²⁺ concentration. Specifically, in the absence of magnesium, ${\rho }_0=\left(1+H_0^{-1}\left(U\right)\right)/\left(1+H_0^{-1}\left(B\right)\right)$, whereas for high-magnesium concentrations $\left[M\right]\gg J_s^{-1}\left(i\right)$, the allosteric coefficient is as follows:

$${\rho }_{\infty }\approx \frac{1+H_0^{-1}\left(U\right)J_C\left(U\right)/J_O\left(U\right)}{1+H_0^{-1}\left(B\right)J_C\left(B\right)/J_O\left(B\right)}.$$

The values of $J_C\left(U\right)$ and $J_O\left(U\right)$ (see Table S3) can be estimated from the occupancy of the extracellular binding sites in the closed and open states of the ECL2/3 region in the inactive MOP receptor trajectories, whereas the value of $H_0^{-1}\left(U\right)$ was obtained from the probability of the ECL2/3 region being in an open state in the same system. The values of $J_C\left(B\right)$, $J_O\left(B\right)$, and $H_0^{-1}\left(B\right)$ (see Table S3) were estimated from the corresponding fractions in the inactive and active MOP receptor trajectories. Values of ${\rho }_0$ and ${\rho }_{\infty }$are reported in Table S4.

Pocket surface area and mouth of the pocket area estimations

To quantify the accessibility of the orthosteric binding site through open or closed states of the ECL2/3 region in the three simulated MOP receptors, we calculated two commonly used geometrical descriptors of binding sites, specifically their pocket surface area and mouth of the pocket area, using the Computed Atlas of Surface Topography of proteins (CASTp) web server (44). The server uses the atomic van der Waals radii of the atoms provided in a molecular topology to detect concave surfaces in a structure, which are labeled as pockets. The mouth of each pocket is described as the constriction plane between the concave surface and the exterior convex surface of the molecule. The areas of both the mouth and concave pocket surface were calculated here using the α-shape method (45) and a probe radius of 2.0 Å. Table S5 lists these calculated quantities for representative protein conformations of the three most populated macrosites for each of the three simulated MOP receptors.

Calculation of coinformation

To elucidate the molecular determinants of the positive allosteric modulation of the MOP receptor induced by the Mg²⁺ cation binding, we calculated the coinformation between receptor residue pairs and Mg²⁺ occupancy of macrosites identified in MD simulations within the ECL2/3 region of the MOP receptor. Results of GCMC-MD runs were not included because of limited protein sampling in the protocol as implemented. Specifically, we describe residue dynamics using the Cartesian coordinates of the center of mass of the residue heavy atoms $R_i$, whereas Mg²⁺ binding was described using a binary variable representing the occupancy state of any of the Mg²⁺ macrosites in the ELC2/3 region, $o_{\text{ECL}}^{\text{Mg}}$. The mutual information $MI\left(R_i,R_j\right)$ is a common quantity used to describe the long-range allosteric coupling between the dynamics of different regions of the receptor. In this work, we assessed the modulatory effect of Mg²⁺ binding by calculating the so-called coinformation quantity:

$$CI\left(R_i,R_j,o_{ECL}^{Mg}\right)=MI\left(R_i,R_j\right)-MI\left(R_i,R_j|o_{ECL}^{Mg}\right),$$

where $MI\left(R_i,R_j\right)$ is the mutual information between the two residues, and $MI\left(R_i,R_j|o_{ECL}^{Mg}\right)$is the conditional mutual information between the residues, conditioned upon Mg²⁺ occupancy. This coinformation is the difference between the information shared by R_i and R_j for a given value of $o_{ECL}^{Mg}$ and the information shared by R_i and R_j irrespective of $o_{ECL}^{Mg}$ and thus measures the effect of $o_{ECL}^{Mg}$ on the amount of information shared between R_i and R_j. We note that negative values of the coinformation indicate that $o_{ECL}^{Mg}$ explains (some of) the observed correlation between R_i and R_j. Table S6 lists the normalized coinformation values derived from the following:

$$C{I}_{i,j}=\frac{CI\left(R_i,R_j,o_{ECL}^{Mg}\right)}{MI\left(R_i,R_j\right)}.$$

To reduce calculation time, trajectories were analyzed with a time step of 0.2 ns, and the mutual information and conditional mutual information values needed to calculate $C{I}_{i,j}$ were estimated using the MDEntropy python library (46) and the k-nearest neighbor algorithm with five bins per Cartesian dimension.

Results and Discussion

To elucidate the atomic details of the mechanism by which Mg²⁺ binds and allosterically modulates the MOP receptor in the presence of Na⁺ ions, we carried out MD simulations of experimentally determined inactive and active structures of the receptor embedded in a lipid-water environment and in the presence of both cations. Unlike the inactive MOP receptor state, in which the highly conserved D^2.50 residue is likely to be charged and bound to a Na⁺ cation, from previous simulation studies by us and others, we know that the D^2.50 does not bind Na⁺ in the receptor’s active state, and its protonation state depends on its proximity to cations (23,47). Thus, we carried out MD simulations of one ligand-free inactive MOP receptor crystal structure corresponding to PDB: 4DKL (30) and two forms of the ligand-free active MOP receptor crystal structure corresponding to PDB: 5C1M (31), differing only in the protonation state of the D^2.50 residue.

MD simulations were run at equal concentrations (0.15 M) of Na⁺ and Mg²⁺. Whereas the Na⁺ concentration is close to extracellular physiological conditions, the Mg²⁺ concentration is significantly higher than its normal value under the same conditions, but this choice was necessary to observe binding events of this divalent cation by standard MD simulations. Notably, the positive allosteric modulation of ligand-free receptors by Mg²⁺ cations can only be observed experimentally at high Mg²⁺ concentrations (0.1–0.5 M) as recently demonstrated for the adenosine A_2A receptor (18).

To assess whether the reported MD simulations had missed important bound states of Mg²⁺ ions because of their slow desolvation kinetics, we supplemented these simulations with a GCMC-MD procedure that overcomes desolvation barriers by sampling Mg²⁺ insertion around the protein. As reported below, the Mg²⁺ coordination complexes identified by GCMC-MD mostly matched those identified by MD and exhibited similar affinities (see Table 1), instilling confidence in the MD simulation results. A notable difference is the observed binding of Mg²⁺ to the allosteric and orthosteric binding sites of the inactive MOP receptor in the GCMC-MD simulations, but not in the MD simulations. Another difference concerns Mg²⁺ binding to the orthosteric binding site of the active MOP receptor with neutral D^2.50 in the GCMC-MD runs, an event that is also not seen in the MD simulations. A possible reason for this lack of agreement is the absence of Na⁺ ions in the GCMC-MD runs and their preferred occupancy of the orthosteric and allosteric sites in the MD simulations. However, one should not forget that interactions between metal ions and protein residues are notoriously hard to describe by MD simulations. Despite intense efforts (see (48) for a recent review), the reliability of these models is still under debate as evidence emerges that polarizable models or quantum calculations might be required to properly describe ion-binding events (49).

Table 1.

Magnesium Binding to the MOP Receptor

	Kd (MD)	Kd (GCMC)
Inactive MOP Receptor
E310ECL3/D216ECL2	0.73	0.37
D216ECL2/G1312.67	4.85	7.35
D216/C217ECL2	0.73	1.00
Allosteric site	–	0.10
Orthosteric site	–	1.35
Active MOP Receptor with Charged D2.50
E310ECL3/D216ECL2	0.64	1.99
D216ECL2/S214ECL2	0.85	0.21
Orthosteric site	0.56	0.39
Allosteric site	–	0.07
Active MOP Receptor with Neutral D2.50
E310ECL3/D216ECL2	4.85	1.35
D216ECL2/G1312.67	0.85	0.79
Q212ECL2/D216ECL2	0.92	1.21
Orthosteric site	–	0.22
Allosteric site	–	1.73

Estimates of Mg²⁺ binding affinity (in Molar units) to sites sampled by MD and GCMD-MD.

Mg²⁺ binds predominantly to the MOP receptor extracellular region and exhibits higher binding affinity for the active receptor conformation

To characterize likely binding sites of Mg²⁺ on the inactive or active MOP receptor (so-called macrosites) at physiological concentrations of Na⁺, we first identified microsites of single or multiple residues that were found to be forming direct interactions with Na⁺ and direct or water-mediated interactions with Mg²⁺ cations (see Methods for details). Given the large number of microsites obtained by this detailed classification, we grouped them into macrosites of cation binding at different regions of the receptor. The analysis of the occupancy probability of these macrosites (see Methods) revealed a small number of binding regions with significant marginal occupancy probability (>3%).

Figs. 1, 2, and 3 report the molecular and energetic details of all macrosites identified with cation binding affinity less than 5 M in MD simulations of ligand-free inactive MOP receptor, ligand-free active MOP receptor with charged D^2.50, and ligand-free active MOP receptor with neutral D^2.50, respectively. Values of the Na⁺ and Mg²⁺ binding affinities for these macrosites derived from occupancy probabilities in the MD or GCMC-MD simulation trajectories (see Methods for details) are listed in Tables 1 and 2 for Mg²⁺ and Na⁺ ions, respectively.

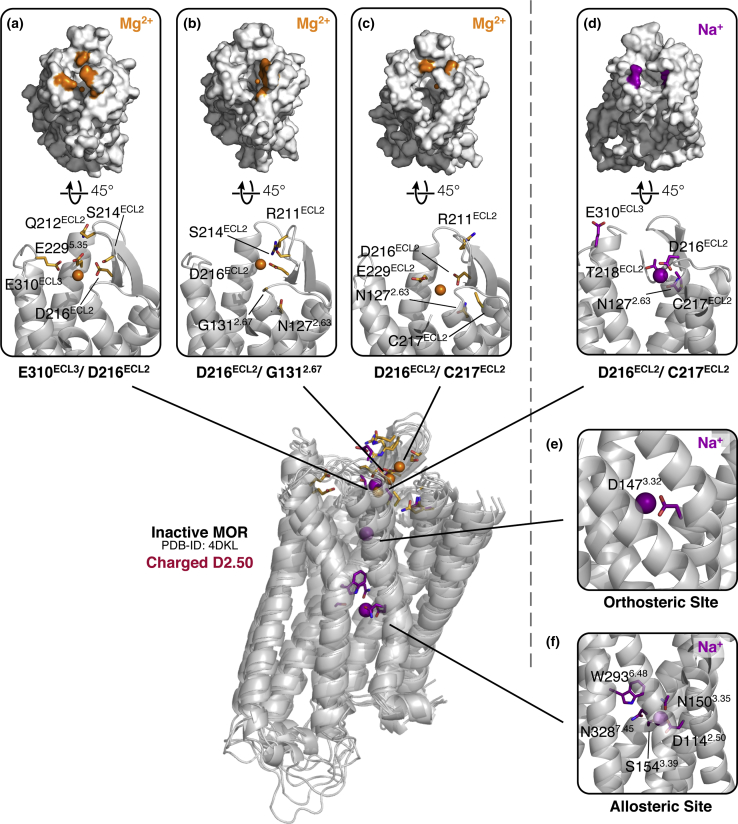
Figure 1.

Molecular and energetic details of all macrosites identified with cation binding affinity less than 8 M in simulations of ligand-free inactive MOP receptor. (a)–(c) and (d)–(f )show predicted binding sites for Mg²⁺ and Na⁺ ions, respectively. Representative residues of each cation binding macrosite (i.e., residues that are most frequently involved in Na⁺ and Mg²⁺ binding in microsites) are indicated in orange and purple colors, respectively, on the surface representations of the inactive MOP receptor. In the insets, the same residues are shown as sticks, whereas purple and orange spheres refer to Na⁺ and Mg²⁺ cations, respectively. Macrosites in the extracellular region of the MOP receptor are labeled by the residues that most frequently bind Na⁺ and Mg²⁺ cations in microsites. To see this figure in color, go online.

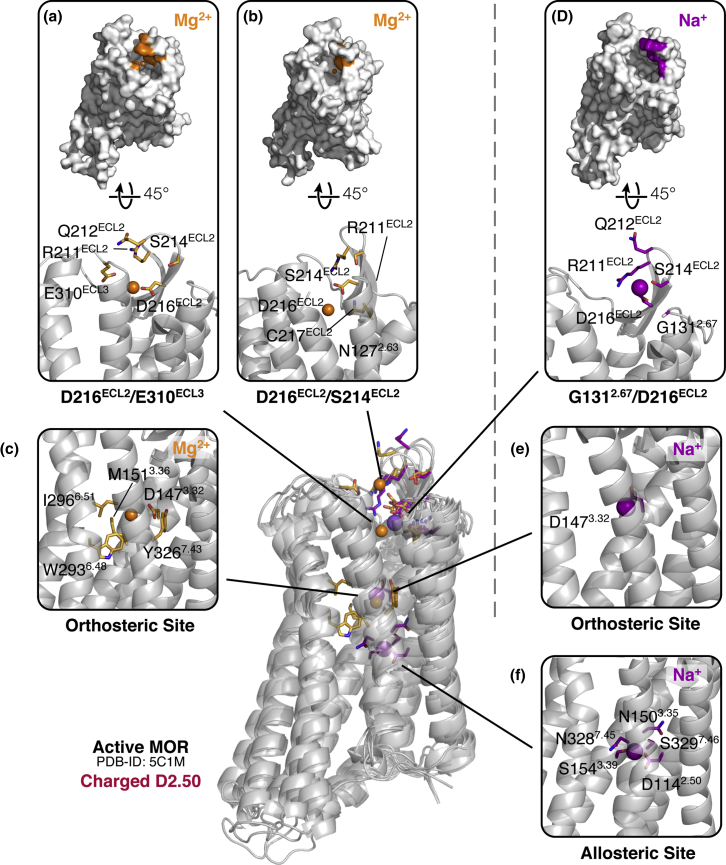
Figure 2.

Molecular and energetic details of all macrosites identified with cation binding affinity less than 8 M in simulations of the ligand-free active MOP receptor with a charged D^2.50 residue. (a)–(c) and (d)–(f )show predicted binding sites for Mg²⁺ and Na⁺ ions, respectively. See the caption of Fig. 1 for details. To see this figure in color, go online.

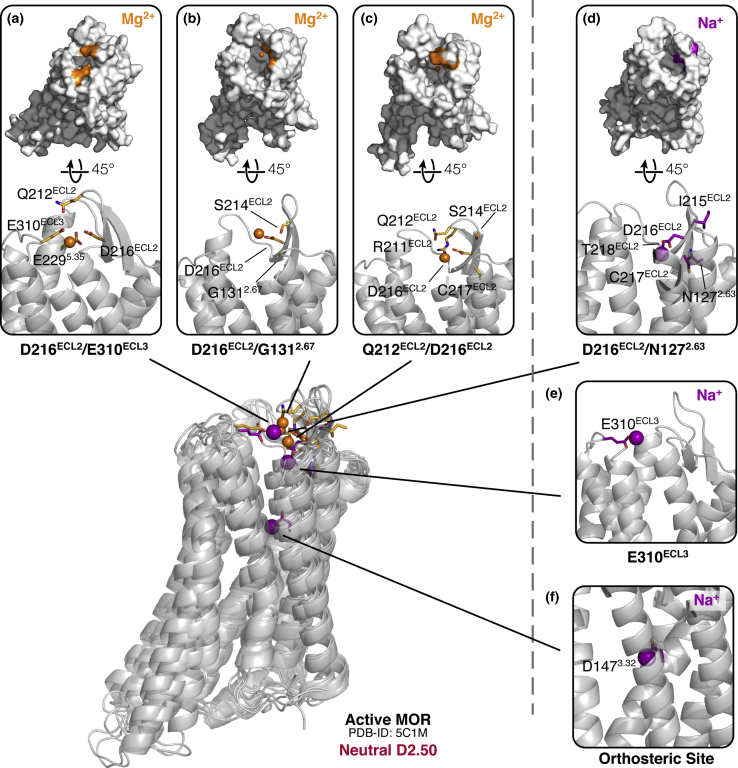
Figure 3.

Molecular and energetic details of all macrosites identified with cation binding affinity less than 8 M in simulations of the ligand-free active MOP receptor with a neutral D^2.50 residue. (a)–(c) and (d)–(f )show predicted binding sites for Mg²⁺ and Na⁺ ions, respectively. See the caption of Fig. 1 for details. To see this figure in color, go online.

Table 2.

Sodium Binding to the MOP Receptor

	Kd (MD)
Inactive
D216ECL2/C127ECL2	0.50
Orthosteric site	0.60
Allosteric site	0.01
Active Charged D2.50
G1312.67/D216ECL2	1.18
Orthosteric site	0.36
Allosteric site	1.29
Active Neutral D2.50
D216ECL2/N1272.63	0.62
E310ECL3	1.79
Orthosteric site	3.36

Estimates of Na⁺ binding affinities (in Molar units) to sites sampled by MD.

As expected, in the ligand-free inactive MOP receptor system (Fig. 1), the Na⁺ cation has the highest affinity for the allosteric binding site (in particular, residues D114^2.50, N150^3.35, S154^3.39, N328^7.45, and W293^6.48) revealed by high-resolution crystal structures of various GPCRs. We calculate K_d = 0.01 M for Na⁺ at this site (Fig. 1 f), which agrees with our previously published calculations from simulations of the MOP receptor in the presence of Na⁺ only and their experimental validation (9). In the absence of ligands, sodium ions can also bind to the orthosteric binding site, establishing direct interactions with the conserved D147^3.32 residue (Fig. 1 e). In addition to these binding sites within the transmembrane bundle, the Na⁺ cation was also found to bind at an extracellular site (specifically, residues N127^2.63, D216^ECL2, C217^ECL2, T218^ECL2, and E310^ECL3; see Fig. 1 d) in the inactive MOP receptor system, albeit with the significantly lower affinity of 0.5 M. Unlike Na⁺, Mg²⁺ ions bound primarily at three slightly different sites on the extracellular region of the inactive MOP receptor system, which all had the D216^ECL2 residue coordinating the cation (Fig. 1, a–c). The Mg²⁺ cation binding affinity for these sites was equally low, ranging from 0.7 to ∼5.0 M. As expected, in the presence of sodium ions, no binding of Mg²⁺ to the orthosteric and allosteric sites was observed. In GCMC simulations, which were carried out in the absence of Na⁺ ions, binding of Mg²⁺ was also observed to the orthosteric and allosteric binding sites of the inactive MOP receptor, where the ion established direct chelation with D147^3.32 or D114^2.50 residues. We note that in all GCMC-MD trajectories, Mg²⁺ never formed direct binding with residues in the extracellular region, except for a marginal fraction (<2% of frames) in the inactive MOP receptor, where direct contacts were established with E310^ECL2. Not shown in Fig. 1 is a Mg²⁺ binding site observed in the vicinity of helix 8, which is likely an artifact of having run MD simulations with a zwitterionic C-terminus.

Although Na⁺ had a much higher affinity than Mg²⁺ for the inactive MOP receptor, this difference was reduced in the simulations of the active MOP receptor systems (see Figs. 2 and 3). For instance, the affinity of Na⁺ for the crystallographic allosteric site decreased by two orders of magnitude from ∼0.01 to 1.3 M in the ligand-free active MOP receptor system with a charged D^2.50 (Fig. 2 f). This is consistent with the knowledge that this site is partially collapsed in active GPCR structures and not suitable to the same type of cation binding (19). Interestingly, the Na⁺ affinity for the extracellular region decreases, albeit less dramatically, from 0.5 to 1.2 M (Fig. 2 c). On the other hand, not only did the Mg²⁺ binding affinity for the extracellular loop regions slightly increase in the ligand-free active MOP receptor system with a charged D^2.50 compared to the simulated inactive receptor system (from 0.7–5.0 M to 0.6–0.8 M; compare Fig. 1, a–c with Fig. 2, a and c), but the Mg²⁺ cation was also found to bind at the orthosteric ligand binding site defined by residue D147^3.32 with a $K_d$ of 0.6 M, the highest affinity value for a macrosite for any ion in this system (see Fig. 2 c). Notably, although the orthosteric ligand binding site was equally accessible in the ligand-free inactive MOP receptor system (see Table S5), the Mg²⁺ cation did not bind at this site during MD simulation of the ligand-free inactive MOP receptor system. In contrast, GCMD-MD simulations carried out in the absence of Na⁺ did reveal binding of Mg²⁺ to both the orthosteric and the allosteric sites on the receptor. Notably, the Monte Carlo sampling revealed (data not shown) that the binding of Mg²⁺ to D147^3.32 at the orthosteric site is not via direct interaction, which was the case for the inactive receptor, but through water-mediated contacts, in agreement with the MD simulation results.

Not surprisingly, the change of the D^2.50 protonation state to neutral in the simulated active MOP receptor system had a significant impact on the binding affinity of both Na⁺ and Mg²⁺ cations for the ligand-free MOP receptor (Fig. 3) at macrosites within the TM bundle, therefore implying a relationship between cation binding and local electrostatics. In this system, both the Na⁺ affinity for the allosteric binding site defined by D^2.50 and the Mg²⁺ affinity for the orthosteric ligand binding site defined by D147^3.32 fell below the cutoff value of 5 M chosen for significance. GCMC-MD simulations of the active MOP receptor system with a neutral D^2.50 did not yield binding of Mg²⁺ to the allosteric site, and the Mg²⁺ binding to the orthosteric site was reduced with respect to that observed in the active receptor with charged D^2.50. Notably, the affinity values of Mg²⁺ for the extracellular loop region (ranging from 0.8 to 5.0 M; see Fig. 3, a–c) were closer to those recorded for the ligand-free inactive MOP receptor system than for the active receptor system with a charged D^2.50, whereas Na⁺ binding affinity for the extracellular region dropped to 1.8 M (Fig. 3, d and e).

Mg²⁺ binding to the extracellular region of the MOP receptor promotes occlusion of the ligand-binding pocket

A unique feature of Mg²⁺ binding to the MOP receptor extracellular region, particularly negatively charged residues D216^ECL2 and E310^ECL3, is that it can produce a transient closure of the orthosteric ligand-binding pocket by bringing ECL 2 and ECL 3 closer together. These two extracellular loops effectively act as a “gate,” and when closer together, they can hinder access of the ligand to the pocket as well as its departure from it. This phenomenon appears to be a unique feature of the divalent Mg²⁺ cation because it was not observed when the monovalent Na⁺ cation was bound at this site. The surface representations of the MOP receptor systems in Figs. 1, 2, and 3 and the mouth and pocket surface area quantifications reported in Table S5 clearly show the different degree of accessibility of the MOP receptor orthosteric ligand-binding pocket when Na⁺ or Mg²⁺ is bound at the extracellular region of the receptor. Notably, visual inspection of the trajectories, as well as smaller values of the equilibrium constant H_M (see Table S3), reveal that the Mg²⁺-induced ECL2/3 loop closure occurs with higher frequency in the simulated active MOP receptor conformations than in the inactive receptor system, suggesting a coupling between activation and ECL2/3 closure.

To quantify the effect of Mg²⁺-induced ECL2/3 closure on ligand binding and receptor activation, we calculated a coupling coefficient, as normally done to measure the allosteric modulation between different receptor degrees of freedom. Specifically, we considered a first approximation in which the agonist binding affinity is expressed as $L_{50}=\rho K_O$, where $K_O$is the agonist binding affinity to the receptor when the ECL2/3 gate is “open,” and $\rho$ is an “allosteric coefficient” that takes into account the Mg²⁺occupancy of the extracellular binding sites in the closed and open states of the ECL2/3 region, thus capturing the effect of cation binding on ECL2/3 closure. The same coefficient ρ was used to express the constitutive activity ratio between active and inactive MOP receptors as R/ρ, where R is the active/inactive receptor ratio in the absence of ECL2/3 gating. Values of the ρ coefficient calculated for different Mg²⁺ concentrations are shown in Table S4 (see Table S3 for values of its components and Methods for equations). In the absence of allosteric modulation by the cation, ρ is expected to be equal to 1. On the other hand, if ρ < 1, the agonist binding affinity is predicted to increase, as is the active fraction of the receptor. Comparison between the inactive MOP receptor system and the active MOP receptor with neutral D^2.50 yields $\rho \left(\text{high}{\text{Mg}}^{2+}\right)/\rho \left(\text{no}{\text{Mg}}^{2+}\right)\approx 0.25$, which suggests a 4-fold increase in agonist binding affinity in the presence of magnesium as well as a fourfold increase of the constitutively active fraction of the receptor (see Table S3). Similarly, comparing the inactive MOP receptor and the active MOP receptor with charged D^2.50 yields a value of $\rho \left(\text{high}{\text{Mg}}^{2+}\right)/\rho \left(\text{no}{\text{Mg}}^{2+}\right)\approx 0.20$, corresponding to a fivefold change (see Table S4).

Na⁺ and Mg²⁺ compete for binding at ECL2 sites

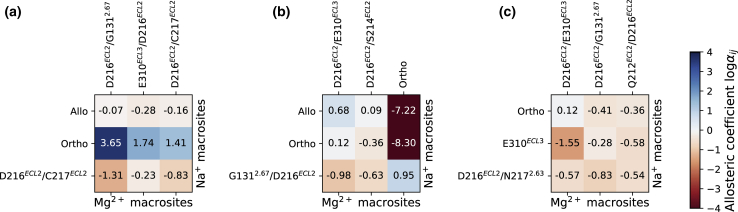
To address possible binding competition between Na⁺ and Mg²⁺ cations for specific sites on the MOP receptor, we calculated the allosteric modulation coefficient $\log \alpha \left(i_{Na},j_{Mg}\right)$ for the cation binding affinity for each of the three simulated MOP receptor systems. Negative values of this coefficient in the plots of Fig. 4 (red color) indicate a negative cooperativity, namely, that the binding of Na⁺ at site $i_{Na}$ decreases the affinity of Mg²⁺ at site $j_{Mg}$ (and vice versa), whereas positive values (Fig. 4, blue) would suggest that binding of one ion increases the affinity of the other. As expected, most of the coupling coefficients in the plots of Fig. 4 are negative, suggesting that there is active competition for the available binding sites in all simulated MOP receptor systems. Specifically, in the inactive MOP receptor system (Fig. 4 a), Mg²⁺ competes (negative values of $\log \alpha$) with Na⁺ for any of the extracellular binding sites. Notably, the coupling between the Na⁺ allosteric binding site and the Mg²⁺ E310^ELC3/D216^ECL2 site is also negative, albeit not very pronounced $\left(\log \alpha \approx -0.3\right)$, suggesting a reduction of the Na⁺ affinity for its allosteric binding site in the presence of Mg²⁺ at the E310^ELC3/D216^ECL2 site in the inactive MOP receptor. Conversely, this analysis reveals a strong positive cooperativity (up to $\log \alpha \approx 3$) between the presence of Na⁺ at the orthosteric site and magnesium binding in the loop region.

Figure 4.

Allosteric coefficients for cooperative binding at Na⁺ and Mg²⁺ binding sites in the simulated MOP receptor systems. (a)–(c) refer to inactive, active with charged D^2.50, and active with neutral D^2.50 MOP receptor, respectively. The coefficients are reported as $\log \alpha$, with negative values (in red) corresponding to negative cooperativity and positive values (blue) corresponding to positive cooperativity of the cation binding affinity. To see this figure in color, go online.

In the active MOP receptor (Fig. 4, b and c), a negative coupling is also observed between all pairs of binding sites in the extracellular region of the receptor. As expected from simple electrostatic considerations and from the proximity of the orthosteric and allosteric sites, we observe a strong negative modulation $\left(\log \alpha \approx -7.0\right)$ of the binding of Mg²⁺ to the orthosteric ligand-binding pocket induced by Na⁺ binding at the D^2.50 allosteric binding site in the active receptor with a charged D^2.50 (Fig. 4 b). This high negative cooperativity appears to be the reason for the lack of Mg²⁺ binding at the orthosteric ligand binding site when an Na⁺ cation is present at its allosteric binding site and vice versa.

Cation binding modulates the information flow across the receptor

To further elucidate the molecular mechanism underlying Mg²⁺ positive allosteric modulation of the MOP receptor, we analyzed the impact of Mg²⁺ binding on the information flow across the receptor. Reasoning that receptor allosteric modulation can be captured by the mutual information between residues, we characterized the residues mediating the modulatory effect of the cation by calculating the normalized coinformation between pairs of receptor residues (i, j) and Mg²⁺ occupancy of macrosites within the ECL2/3 region of the MOP receptor (see Methods).

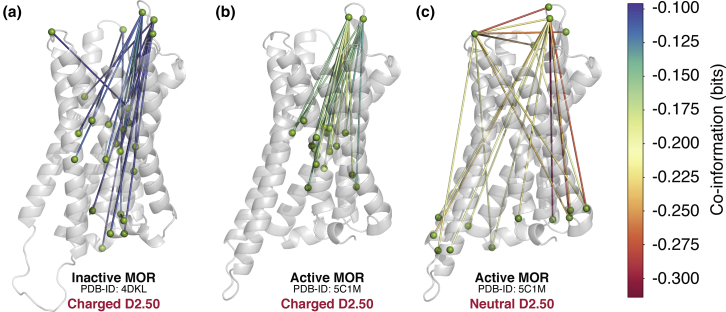
The receptor residue pairs whose correlation is maximally affected by Mg²⁺ binding (i.e., the top 20 pairs with the highest coinformation values) are listed in Table S6, and their location is shown in Fig. 5 for the three simulated MOP receptor systems. Accordingly, in the inactive MOP receptor system (Fig. 5 a), Mg²⁺ binding to the ECL2/3 region most dramatically affects the mutual information between specific residues in ECL2 (i.e., Y210, R211, I215, and S222), ECL3 (i.e., P309), TM2 (i.e., A102^2.38, N109^2.45, A113^2.49), TM3 (D147^3.32, Y149^3.34, N150^3.35, M151^3.36, and T153^3.38), intracellular loop (ICL) 2 (i.e., L176), TM5 (i.e., C235^5.41), TM6 (i.e., V288^6.43 and C292^6.47), the intracellular end of TM7, flanking the NPxxY motif (L324^7.41, C330^7.47, L331^7.48, L339^7.56), ICL4 (i.e., E341), and H8 (i.e., N342 and K344).

Figure 5.

Location of the MOP receptor residues pairs whose correlation is maximally affected by Mg²⁺ binding in the three simulated receptor systems. (a)–(c) refer to inactive, active with charged D^2.50, and active with neutral D^2.50 MOP receptor, respectively. Lines between residues are colored according to their coinformation value, with the most negative values shown in red. To see this figure in color, go online.

Notably, coinformation values are much more negative in the simulated active MOP receptor systems and especially in the system with a neutral D^2.50 (see Fig. 5 c; Table S6), reflecting a tighter coupling between magnesium occupancy of macrosites within the ECL2/3 loop region and the receptor dynamics in the active conformational state. In the active MOP receptor with a charged D^2.50 residue, the most affected regions of the receptor by Mg²⁺ binding share many similarities with those of the inactive MOP receptor (compare Fig. 5, a and b), involving specific residues within ECL2 (Y210^ECL2 and R211^ECL2), TM2 (N109^2.45), TM3 (N150^3.35, M151^3.36, and T153^3.38), TM6 (C292^6.47), and TM7 (L324^7.41 and L331^7.48). On the other hand, the coinformation observed in the active receptor with neutral D^2.50 is strikingly different from that of the MOP receptor with charged D^2.50 (compare Fig. 5, b and c). Notably, among the most affected receptor regions by cation binding in this system are ECL2/3 residue pairs, specifically P309^ECL3 with K209^ECL2, R211^ECL2, Q212^ECL2, or S222^ECL2 as well as the intra-ECL2 pair R211^ECL2-S222^ECL2. As expected by a positive allosteric modulator, magnesium binding also modulates the information transfer from ECL2/3 residues (i.e., R211^ECL2, S222^ECL2, and P309^ECL3) to the intracellular G protein-binding region of the MOP receptor, including the intracellular ends of TM1 (I93^1.57 and V94^1.58), TM3 (C170^3.55), TM4 (P181^4.39), TM5 (L257^5.63 and K260^5.66), and TM6 (D272^6.27 and R273^6.28) as well as ICL1 (M99), ICL2 (V173), and ICL4 (D340).

Taken together, these results support a mechanism by which Mg²⁺ binding to the MOP receptor active state with neutral D^2.50 (i.e., the expected most probable protonation state for an active receptor) has a direct effect on the dynamics of the ECL2/3 region, which in turn is strongly coupled with the dynamics of the intracellular region of the receptor, whereas this coupling is less effective in the inactive receptor. Notably, a similar mechanism was recently proposed for a different GPCR subtype (18), suggesting a possible molecular paradigm of GPCR allosteric modulation by cations.

Conclusions

Our simulations provide atomic details of the molecular mechanism by which magnesium cations preferentially bind to the extracellular region of the MOP receptor in the presence of sodium and allosterically modulate the G protein-binding region of the receptor. Specifically, the results reported here support a mechanism by which Mg²⁺ cations, unlike Na⁺ cations, promote states of the active MOP receptor with ECL2 and ECL3 folding back over the extracellular opening of the receptor TM bundle, thus impairing agonist unbinding and possibly enhancing agonist binding affinity. Mutations of residues involved in Mg²⁺ binding to the ECL2/3 region (e.g., the acidic residues E310^ELC3 and D216^ECL2) as well as mutations of residues identified as mediators of the cation allosteric effect (e.g., R211^ECL2, Q212^ECL2, and P309^ECL3) are predicted to affect its positive allosteric modulation of the MOP receptor.

Although Na⁺ and Mg²⁺ cations actively compete for binding to extracellular sites of the MOP receptor, a larger number of binding sites are available to Mg²⁺ in this region. Thus, despite the low (Molar) range of affinities for these sites, we would predict that Mg²⁺ cations bind to the extracellular region of the MOP receptor even at lower concentrations. Notably, in the presence of sodium, Mg²⁺ was never observed to bind to the Na⁺ allosteric site, most likely because of its double positive charge and an unfavorable balance between desolvation and binding. Mg²⁺ could, however, bind at the orthosteric ligand binding site with a significantly higher affinity than sodium. Furthermore, we observed a strong negative cooperativity between Mg²⁺ binding at the orthosteric site and Na⁺ binding at the allosteric site, suggesting that Mg²⁺ binding could reduce the fraction of bound Na⁺, thus reducing its inhibitory effect.

Author Contributions

X.H. and S.R. carried out the MD and GCMC-MD simulations, respectively. All authors analyzed the results and wrote the manuscript.

Editor: Vasanthi Jayaraman.