Abstract
Background:
There is consensus that early childhood lead exposure causes adverse cognitive and behavioral effects, even at blood lead levels (BLL) below 5 μg/dL. What has not been established is to what extent the effects of childhood lead exposure persist across grades.
Objective:
To measure the effects of early childhood lead exposure (BLL 1-10 μg/dL) on educational performance from grades 3-8; to determine if effects in lower grades persist as a child progresses through school; and if so, to characterize the pattern of persistence.
Methods:
We examine data from 560,624 children living in North Carolina between 2000-2012 with a BLL ≤ 10 μg/dL measured between age 0-5 years. Children are matched to their standardized math and reading scores for grades 3-8, creating an unbalanced panel of 2,344,358 student-year observations. We use socio-economic, demographic, and school information along with matching techniques to control for confounding effects.
Results:
We find that early childhood exposure to low lead levels caused persistent deficits in educational performance across grades. In each grade (3-8), children with higher blood lead levels had, on average, lower percentile scores in both math and reading than children with lower blood lead levels. In our primary model, we find that children with BLL = 5 μg/dL in early childhood ranked 0.90 – 1.20 (1.35 – 1.55) percentiles lower than children with BLL ≤ 1 μg/dL on math (reading) tests during grades 3-8. As children progressed through school, the average percentile deficit in their test scores remained stable.
Conclusions:
Our study shows that the adverse effects of early childhood exposure to low lead levels persist through early adolescence, and that the magnitude of the test-score percentile deficit remains steady between grades 3-8.
Keywords: Children, Education, Lead, Blood Lead Level, Cognitive Development
Introduction
Children are exposed to lead through a variety of sources, including lead paint, consumer products, and contaminated soil and water. While environmental policy has drastically reduced lead emissions from 1970 levels (U.S. EPA (2013)), many children in the United States continue to exhibit elevated blood lead levels (BLLs). The Flint, Michigan, drinking water crisis of 2014 was a stark reminder that lead exposure poses an ongoing threat.
There is consensus that childhood lead exposure leads to adverse health outcomes, including cognitive and behavioral deficits (Aizer et al. (2018); Bellinger et al. (1992); US EPA (2013); Evens et al. (2015); Lanphear et al. (2005); Magzamen et al. (2015); NTP (2012); Pocock et al. (1994); Reyes (2015a, 2015b)). What is less well understood is the persistence of the adverse effects, particularly at low BLLs, and whether the effects attenuate (or amplify) as children age. The first recorded case of lead poisoning in children was in 1892. The prevailing wisdom at that time was that if “the child recovered from the acute phase [of poisoning], no lasting effects would occur” (Needleman (1989)). In the 1940s, it was shown that children who survived acute lead poisoning continued to have significantly elevated lead levels and damage to their central nervous systems (Needleman (1989)).
Early studies on the effects of lead on children focused on IQ and the Bayley Mental Development Index for infants. These are small-sample studies of populations exposed to much higher mean or peak lead levels than are typically observed in today’s child population (BLL > 10 μg/dL). These studies uniformly found statistically significant, negative correlations between early childhood lead exposure and IQ (Pocock et al. (1994)). These studies did not address the issue of persistence in the effects of lead.
More recent literature has used individual-level blood lead surveillance data and public-school records to examine the relationship between BLL and achievement test scores. Achievement test scores reflect both intelligence and traits such as conscientiousness and neuroticism -- characteristics strongly associated with later-in-life outcomes (Borghans et al. (2016)). These studies found that higher BLLs led to significantly lower test scores in grades 3 or 4, but they did not examine the effects in later grades (Miranda et al. (2007, 2009); Magzamen et al. (2013, 2015), Evens et al. (2015); Aizer et al. (2018)). Zhang et al. (2013) and Elliott et al. (2015) found a positive relationship between less-than-proficient test scores and lead levels in grades 3, 5, and 8, but neither study examined the heterogeneity of lead’s effect by grade.
A few longitudinal studies have examined the effects of lead on longer-term outcomes using small cohorts. Studies examining IQ or education found negative correlations between early childhood lead levels and cognitive performance measured in later childhood or adulthood (Bellinger et al. 1992; Mazumdar et al. 2011, Needleman et al. 1990; Reuben et al. 2017). Studies examining other neurological or behavioral effects, including reduced brain volume and criminal arrests, also found long-term effects from early life lead exposure (Cecil et al. 2008; Brubaker et al 2009; Brubaker et al. 2010; Wright et al. 2008). While these studies showed that adverse effects of early childhood lead exposure persisted later in life, most did not quantitatively assess how the magnitude of those effects varied by age or grade. The exception is Reuben et al. (2017), who examined the change in IQ from childhood to adulthood among adults in New Zealand whose blood lead levels were measured as children. They observed that higher childhood BLL was associated with steeper declines in IQ from childhood to adulthood, but this analysis did not adjust for covariates.
In this study we estimate the effects of early childhood, low-level lead exposure on standardized test performance across grades in both math and reading. We study a cohort similar to that used by Miranda et al. (2007, 2009), but we follow those students every year from third through eighth grade, which allows us to estimate the change in trajectory of student performance across grades due to lead exposure. Our dependent variable is the student’s percentile score on their achievement test, which allows us to compare a student’s performance relative to their cohort. We focus our attention on two groups of children -- those with a maximum BLL ≤ 10 μg/dL and those with a maximum BLL ≤ 5 μg/dL. We use coarsened exact matching to construct “treatment” (children with BLL 2-5 μg/dL) and “control” (children with BLL ≤ 1 μg/dL) groups that have a better distributional balance across multiple covariates, improving our ability to identify the effect of BLL on test performance. Our research contributes to the literature in three ways: it adds to the understanding of how low-level BLL (≤ 5 μg/dL) affects a student’s performance relative to their cohort; it addresses how BLL affects the educational trajectory as children age; and it helps to inform the development of public policies to minimize the adverse effects of lead exposure.
Methods
Data and Summary Statistics
This research was conducted under an agreement with the Children’s Environmental Health Initiative (CEHI) at Rice University according to a research protocol approved by the University’s Institutional Review Board. CEHI provided BLL data from the North Carolina Childhood Lead Poisoning Prevention Program surveillance registry. As in most other states, BLL testing in North Carolina is not universal. North Carolina state guidelines require screening for all children participating in Medicaid and recommend screening for other “at-risk” children (Dickman & Safer Chemicals, Healthy Families, 2017). Approximately 20-30% of one- and two-year old children were screened in North Carolina in the 1990s and 2000s (North Carolina Childhood Lead Poisoning Prevention Program, 2004). We do not formally address selection bias in this study, but it is an important caveat when interpreting our results.
Our sample begins with all children who were born between 1990 and 2004 and were screened for lead in North Carolina at least once during age 0–5. The dataset includes information about the child’s birthdate, Medicaid enrollment status, BLL test date, blood sample method (capillary, venous), and the name of the laboratory responsible for the blood analysis. The majority of children in the registry were screened between the ages of 1-2 years using capillary (“finger prick”) blood samples analyzed by the North Carolina State Laboratory of Public Health. While capillary samples are easier to collect than venous samples, they are also more susceptible to contamination (Caldwell et al. 2017) and therefore may be a potential source of measurement error in statistical analysis. Approximately 95% of the observed blood lead measurements were from capillary blood samples, whereas the other 5% were from venous blood samples. Venous samples are typically used as follow-up tests to confirm an elevated BLL.1
While the majority of the children that we study had only a single blood lead test during childhood (61%), for children with multiple BLL tests, we take the geometric mean over all tests to create a single BLL measure. Aizer et al. (2018) found that using the child’s geometric mean BLL resulted in a larger estimated effect of BLL on test scores than a single random draw, suggesting that utilizing information from multiple tests can reduce attenuation bias coming from measurement error in a single BLL test result. North Carolina’s Department of Health and Human Services recognizes a level of detection for blood lead at 1 μg/dL, so children with a reported BLL below the level of detection were assigned a value of 1 μg/dL in the state database. Children with a BLL at or below the detectable level make up the counterfactual group in the empirical analysis. All other BLL values were rounded to the nearest integer by the North Carolina Childhood Lead Poisoning Prevention Program before being entered into the surveillance registry.
For our analysis, we study two overlapping groups of children. The first consists of children who had a maximum BLL ≤ 10 μg/dL between the ages of 0-5 (96% of the lead surveillance registry). This sample allows us to examine the effects of early childhood lead exposure by grade across a wide range of relevant exposure levels. We also consider a second, more restrictive sub-sample of children, who had a maximum BLL ≤ 5 μg/dL (74% of the surveillance registry). This smaller sample allows us to examine the effects of low-level BLL on a more representative sample of children, as it is estimated that less than 1% of the US population age 1 through 5 had a BLL exceeding 5 μg/dL as of 2013-2016.2
Our focus on these two groups helps isolate the impact of lead exposure from the potentially confounding effect of medical interventions that may be implemented for children with an elevated BLL. During our study period, North Carolina guidelines indicated that children who presented a BLL > 10 μg/dL must be re-tested.3 If their second test confirmed a BLL > 10 μg/dL then the child was eligible for a medical intervention. Finally, if the child also was determined to be living in housing with lead poisoning hazards, remediation would be required.4 During our sample period, children with a BLL ≥ 10 μg/dL were considered by the Centers for Disease Control and Prevention (CDC) as having a blood lead “level of concern.” For those children, the CDC recommended interventions such as conducting an environmental assessment and a detailed personal history to determine potential sources of lead exposure; providing nutritional counseling to increase calcium and iron intake to remove lead from the body; bowel decontamination if necessary; and oral chelation therapy in the case of dangerously high levels of lead. On the other hand, children having a BLL below the “level of concern,” were not eligible for any medical intervention.5 By examining samples of children with BLL values of 10 μg/dL and 5 μg/dL and below, we minimize this potentially confounding issue.
Every year, children living in North Carolina in grades 3 through 8 are administered end-of-grade standardized achievement tests in reading and mathematics. The North Carolina Education Research Data Center (NCERDC) maintains a database with records of those test scores. The NCERDC database also contains information on each student’s school, grade, gender, race, age, and enrollment status in a free/reduced-price school lunch. (Students enrolled in free/reduced-price lunch are hereafter referred to as “economically disadvantaged.”) We link students to their test results for each grade from 2000-2012, creating an unbalanced panel. We then merge the test-score panel data to the birth certificate records, provided by CEHI from the North Carolina Department of Health and Human Services, based on a common child identifier created by CEHI for matching purposes. The common child identifier used to link birth certificate records to student test records was created using combinations of first, middle, and last name, date of birth, and school district/county. Finally, we link the BLL data to the birth certificate records as well, which allows us to link the BLL data to our test-score panel data set. The birth certificate data includes the child’s birthdate and race, as well as the mother’s age, marital status, and mother’s self-reported smoking and alcohol use during pregnancy.6 Parental education level at child’s birth is also available from the birth certificate records.
Table 1 presents summary statistics for the different samples we study. The primary sample of children (BLL ≤ 10 μg/dL) consists of 560,624 students from 2000-2012, which represents 53% of the lead surveillance registry with BLL ≤ 10 μg/dL, and 2,344,358 student-year observations.7 The average BLL in the sample is 3.66 μg/dL. Based primarily on birth certificate information, students in this sample are 51% non-Hispanic White, 36% non-Hispanic Black, and 13% all other racial or ethnic groups. Consistent with the focus on screening at-risk children, 44% of the sample were enrolled in Medicaid at the time of the blood test, 59% were considered economically disadvantaged, and 43% were born to single mothers. 2,211 public schools are represented in the dataset. Our restricted sample of children with BLL ≤ 5 μg/dL includes 438,604 children with a mean BLL of 2.89 μg/dL.
Table 1.
Summary Statistics
| Full (≤ 10 μg/dL) | Full (≤ 5 μg/dL) | CEM (≤ 5 μg/dL) | ||||
|---|---|---|---|---|---|---|
| Variable | Mean | Std. Dev | Mean | Std. Dev | Mean | Std. Dev |
| BLLa (μg/dL) | 3.65851 | 1.904657 | 2.886765 | 1.182477 | 2.403745 | 1.237589 |
| Math Score | 45.59785 | 28.00918 | 47.36661 | 28.08836 | 59.46916 | 27.82358 |
| Reading Score | 45.61872 | 28.05972 | 47.43353 | 28.11505 | 59.06723 | 27.90667 |
| Male | 0.4968277 | 0.49999 | 0.4912944 | 0.4999243 | 0.4962058 | 0.4999862 |
| White | 0.5098598 | 0.4999029 | 0.5502916 | 0.4974645 | 0.8141953 | 0.3889495 |
| Black | 0.362643 | 0.4807631 | 0.3171912 | 0.4653827 | 0.1284981 | 0.334644 |
| Age in 3rd Grade | 8.423053 | 0.5674781 | 8.398993 | 0.5516493 | 8.338589 | 0.5044326 |
| EconDisadv | 0.5891152 | 0.4919945 | 0.5524484 | 0.4972417 | 0.2434874 | 0.4291873 |
| Medicaid | 0.4394414 | 0.4963192 | 0.425709 | 0.4944502 | 0.1828237 | 0.3865224 |
| Mother Not Married | 0.4325641 | 0.4954316 | 0.3985726 | 0.4896045 | 0.1566507 | 0.3634716 |
| Mother Used Alcohol | 0.0120613 | 0.1091596 | 0.0104295 | 0.1015909 | 0.0074116 | 0.0857709 |
| Mother Smoked | 0.1818511 | 0.3857218 | 0.1755077 | 0.3804009 | 0.104028 | 0.3052972 |
| Mother 21-29 years | 0.4991605 | 0.4999994 | 0.5032866 | 0.4999893 | 0.5210284 | 0.4995583 |
| Mother 30+ years | 0.2410306 | 0.4277089 | 0.2575049 | 0.4372599 | 0.393493 | 0.4885252 |
| Parents some high school | 0.1738625 | 0.3789913 | 0.1568569 | 0.3636659 | 0.0565226 | 0.2309284 |
| Parents graduated high school | 0.4003569 | 0.4899708 | 0.3866509 | 0.4869827 | 0.2220186 | 0.4156041 |
| Parents some college | 0.218569 | 0.4132755 | 0.2288427 | 0.4200879 | 0.2586863 | 0.4379135 |
| Parents graduated college | 0.1675384 | 0.373456 | 0.1895118 | 0.3919148 | 0.4446915 | 0.4969322 |
| No. of Observations | 2,344,358 | 1,789,255 | 387,794 | |||
| No. of Students | 560,624 | 438,604 | 136,910 | |||
| No. of Schools | 2,211 | 2,207 | 2,014 | |||
| No. of unique school-grade-year combinations | 70,548 | 69,870 | 39,562 | |||
Each child’s BLL is measured as the geometric mean of their BLL measurements taken during 0 – 5 years of age.
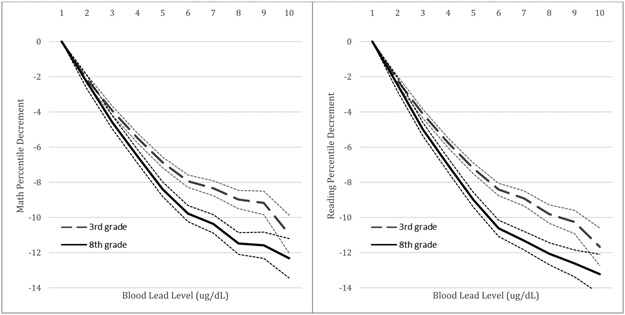
In Figure 1 we plot the average student performance deficit in math and reading in grade 3 and grade 8 by BLL for our main sample (BLL ≤ 10 μg/dL). For our measure of performance, we transform raw test scores into percentile ranks relative to the population of all students in the state of North Carolina who took the exam in a given grade and year. The “percentile deficit” is the average percentile difference between the various “treatment” groups (students with an early childhood BLL = 2, 3, 4, …, 10 μg/dL) and the “control” group (students with an early childhood BLL ≤ 1 μg/dL). First, we observe that on average, children with higher BLLs rank lower than children with lower BLLs. In addition, between third and eighth grade, children with higher BLLs do not improve their performance relative to their cohort. In math, a child with a BLL of 5 μg/dL has an average score that is 6.90 percentiles lower than a student with a BLL ≤ 1 μg/dL in third grade. By eighth grade, this differential worsens; a student with a BLL of 5 μg/dL is 8.40 percentiles below a student with a BLL ≤ 1 μg/dL. A similar pattern exists for reading test scores. The data suggest a strong pattern of persistence in the effects of lead exposure on school performance. These associations, however, are not adjusted for any student, mother, or school characteristics that may confound the relationship between BLL and achievement test scores.
Figure 1. Association between BLL and Math and Reading Test Score Percentiles at 3rd and 8th grade (without controlling for confounders).
Note: Dotted lines denote 95% confidence intervals. For 3rd and 8th graders in the main sample (BLL ≤ 10 μg/dL), the above plots display the average percentile decrement in math and reading test scores that is associated with each BLL.
Empirical Model
While Figure 1 suggests there may be a persistent pattern of educational deficit across grades associated with early childhood lead exposure, it does not provide evidence of a causal relationship or rule out the possibility that the observed pattern is due to spurious correlations. To better understand the effect of lead exposure on school performance across grades after controlling for other confounders, we start by estimating the following model:
| (1) |
where Percentile Scoreigst is the math or reading percentile score for student i, in grade g, at school s, in year t, normalized based on the population of all North Carolina students in grade g and year t. BLL enters as a vector of dummy variables denoting each BLL integer above 1 μg/dL, so the effect of BLL on percentile rank is allowed to vary non-linearly across BLLs. The omitted category in the vector BLL is students who had a BLL coded as 1 μg/dL in the data. This value reflects students whose early childhood lead exposure was at or below the detectable limit. This group serves as the counterfactual in our analysis.
Control variables include a vector of characteristics of both the student and the student’s parents (Xit). In particular, we account for the child’s sex, race/ethnicity, economically disadvantaged status, Medicaid enrollment, birth month, and age upon entry to grade 3. We also include the mother’s age, marital status, and self-reported alcohol and tobacco use and parents’ highest educational achievement at the time of the child’s birth. Mother’s age enters our model as a set of two binary variables to allow for a potential nonlinear relationship with school performance. For parental education, we include separate dummy variables indicating whether at least one parent had some high school, had graduated high school, had some college, or had graduated college at the time of the child’s birth, relative to the omitted category of having attended no more than middle school.
It would be ideal to include a vector of dummy variables representing the specific classroom each student was assigned to in a given year to control for teacher quality, peer effects, geographic effects, and other factors affecting educational quality which could affect a student’s test performance. Our dataset, however, lacks complete data on class or teacher assignments, so we instead include a vector of dummy variables (dgst) representing each unique school, grade, and year combination.8 The coefficient vector θ includes separate intercepts for each school-grade-year combination. The use of school-grade-year dummy variables allows us to estimate the effect of BLL on a student’s percentile rank relative to the average student in the same grade, same school, and during that same year, minimizing the effect of potential confounders.
To explore whether the educational trajectory of children across grades is affected differentially by early childhood lead exposure, we interact BLLi with the variable Gg, where Gg = 0 if the student is in third grade, 1 if the student is in fourth grade, through Gg = 5 if the student is in eighth grade.
The model we estimate is:
| (2) |
The parameter vector γ2 captures how educational outcomes change with grade at different levels of early childhood lead exposure. The interaction term Xit × Gg is included to allow the effects of other covariates to vary by grade, thus controlling for how educational outcomes evolve with other characteristics, irrespective of any lead exposure, as a student progresses through the grade levels.
Finally, to consider whether the effects of early childhood lead exposure across grades vary by race or socioeconomic characteristics, we add interaction terms between BLLi, Gg, and a subset of variables found in Xit, which we denote Zit:
| (3) |
β1 captures the effect of various child and mother characteristics on percentile rank, and γ3 allows the effect of BLL on percentile rank to differ across a subset of these characteristics. Of particular interest, estimates of γ4 shed light on whether the effects of early childhood lead exposure by grade are consistent across different racial and socioeconomic groups.
Coarsened Exact Matching
To interpret the coefficients on BLL as the causal effect on student test performance, the coefficient estimators must be unbiased. For this to be the case, there cannot be unobserved factors that directly affect percentile rank that are both correlated with early childhood BLL and are omitted from equations (1), (2), and (3). Such unobserved factors could include innate student ability, wellness, educational or medical interventions, and a supportive household.
We cannot completely eliminate the potential for bias due to such unobserved factors. However, we attempt to minimize any possible bias by pre-processing our data using a many-to-one coarsened exact matching (CEM) algorithm that is designed to better balance the distributions between the “treated” and “control” groups simultaneously for a set of observables that may affect percentile rank (Iacus, King & Porro, 2012). One motivation for this matching procedure is that if these two sub-samples are more balanced in terms of observed characteristics, then they may be more comparable in terms of unobserved characteristics as well. In addition, CEM provides a way to control non-parametrically for the observed characteristics.
CEM allows us to focus our analysis only on students who are similar in terms of key observed characteristics that may affect school outcomes (other than the variable of interest, BLL), thereby isolating the effect of BLL on percentile rank from that of other characteristics which may, themselves, be correlated with BLL. Balance is achieved by “pruning” observations in the control and treatment groups that cannot be matched and by using weights to balance the number of observations in each stratum across the groups. We define the “treated” group as students who had a geometric mean BLL > 1 μg/dL in early childhood. The “control” group again consists of children with a BLL ≤ 1 μg/dL. We use 1 μg/dL as our cutoff as this is the stated minimum level of detection by the State Laboratory (Miranda et al. 2007). Because the treatment variable is dichotomous, we focus on the ≤ 5 μg/dL sample for the CEM analysis. Children with higher BLLs become increasingly less comparable to the control group of children with BLL ≤ 1 μg/dL.9
The covariates we use for exact matching are race/ethnicity (non-Hispanic White, non-Hispanic Black, and all other categories); economically disadvantaged status; mother’s marital status at the time of birth (married or unmarried); enrollment in Medicaid at the time of the blood lead test; and school-grade-year indicators. We also match on mother’s age at the time of the child’s birth coarsened into three bins (less than 20 years, 20-29 years, and 30 years and above), and parent’s highest educational attainment at the time of the child’s birth coarsened into three bins (middle school or some high school; high school graduate; some college or college graduate). CEM allows us to compare, for example, the average percentile rank of Black eighth graders in 2012, attending a particular middle school, whose mothers were married, had at least one parent who attended college, did not receive Medicaid, were not economically disadvantaged, and had an early childhood mean BLL ≤ 1 μg/dL, against students with those exact same characteristics except that they had an early childhood mean BLL > 1 μg/dL. If the treatment and control groups are exactly balanced on the covariates and there are no additional confounders correlated with both lead levels and test scores, the effect can be estimated as the difference in the sample means across the two groups.
A measure of multidimensional imbalance, L1, is given by the rectilinear distance between the k-dimensional histogram, where k is determined by the number of covariates used in the matching algorithm (Iacus, King and Porro, 2012). The L1 parameter is bounded by 0 and 1 where an L1 value of 0 indicates perfect global balance, up to the level of “coarsening” or bin size, and an L1 value of 1 indicates complete separation. Prior to matching, we calculate the multidimensional imbalance measure on the sample of students with a BLL ≤ 5 μg/dL (1,789,255 student-year observations) as L1 = 0.30. After CEM, we retain 387,794 student-year observations and have an imbalance measure of L1 = 0.07. This is a reduction in the multidimensional imbalance of 77%. (The univariate imbalance parameters also show improved balance for each variable, except gender, where the imbalance measure increases slightly, from 0.020 to 0.025.)
The matching procedure shifts the distribution of BLL in the final matched sample such that a greater proportion of retained observations range from 1 to 3 μg/dL than in the unmatched sample. This results in a decline in mean BLL from 2.9 μg/dL in the full ≤ 5 μg/dL sample to 2.5 μg/dL in the matched ≤ 5 μg/dL sample. We also observe a reduction in both the fraction of non-Hispanic Black and economically disadvantaged children in the matched sample. This is not unexpected as children in these categories are more likely to exhibit higher BLL values.
Results
Our estimates for equation (1) are summarized in Table 2. The dependent variable for the first three models is the student’s percentile score in math. The dependent variable for the second three models is the percentile score in reading. We estimate cluster-robust standard errors for each model, where the cluster is at the student level to allow errors to be correlated across tests for a given student, but not between students.10 Models 1 and 4 in Table 2 are based on the full sample of students who had their BLL tested in early childhood and had a maximum BLL ≤ 10 μg/dL. In the subsequent models in Table 2, we examine the robustness of the results when focusing on students with a maximum BLL ≤ 5 μg/dL (models 2 and 5 in Table 2), a range that is more consistent with the current population of children. To further examine the robustness of our results, we use coarsened exact matching to obtain a more balanced sample across the control and treated groups within the BLL ≤ 5 μg/dL sample in terms of key covariates that may be correlated with both percentile rank and BLL (models 3 and 6 in Table 2).
Table 2.
Effects of BLL on Test Score Percentile: Base Regression Results
| Math Percentile | Reading Percentile | |||||
|---|---|---|---|---|---|---|
| Full BLL ≤ 10 (1) |
Full BLL ≤ 5 (2) |
CEM BLL ≤ 5 (3) |
Full BLL ≤ 10 (4) |
Full BLL ≤ 5 (5) |
CEM BLL ≤ 5 (6) |
|
| BLL 2 | −0.25* (0.11) | −0.22 (0.11) | −0.38 (0.19) | −0.32** (0.11) | −0.32** (0.11) | −0.55** (0.19) |
| BLL 3 | −0.44*** (0.11) | −0.36** (0.11) | −0.56** (0.20) | −0.69***(0.11) | −0.67*** (0.11) | −1.02*** (0.20) |
| BLL 4 | −0.69*** (0.12) | −0.68*** (0.12) | −0.96*** (0.23) | −1.03*** (0.12) | −1.06*** (0.12) | −1.31*** (0.23) |
| BLL 5 | −1.00*** (0.13) | −0.95*** (0.15) | −0.51 (0.30) | −1.42*** (0.13) | −1.41*** (0.15) | −0.97*** (0.30) |
| BLL 6 | −1.26*** (0.15) | −1.84*** (0.15) | ||||
| BLL 7 | −1.10*** (0.17) | −1.78*** (0.17) | ||||
| BLL 8 | −1.51*** (0.21) | −2.13*** (0.21) | ||||
| BLL 9 | −1.56*** (0.26) | −2.55*** (0.26) | ||||
| BLL 10 | −2.17*** (0.42) | −2.92*** (0.41) | ||||
| Male | 0.93*** (0.06) | 1.03*** (0.07) | 1.26*** (0.14) | −2.66*** (0.06) | −2.61*** (0.07) | −2.33*** (0.15) |
| White | 2.54*** (0.11) | 2.43*** (0.13) | 2.71*** (0.38) | 5.49*** (0.11) | 5.54*** (0.13) | 4.35*** (0.37) |
| Black | −10.52*** (0.11) | −10.72*** (0.13) | −11.48*** (0.43) | −7.50*** (0.11) | −7.51*** (0.13) | −9.94*** (0.42) |
| EconDisadv | −5.20*** (0.07) | −5.20*** (0.08) | −6.08*** (0.29) | −5.90*** (0.07) | −5.88*** (0.08) | −6.40*** (0.30) |
| Medicaid | −1.60*** (0.08) | −1.59*** (0.09) | −1.37*** (0.31) | −1.36*** (0.08) | −1.32*** (0.09) | −1.62*** (0.32) |
| Not Married | −1.05*** (0.08) | −1.13*** (0.09) | −1.12*** (0.33) | −0.40*** (0.08) | −0.42*** (0.09) | −0.65 (0.33) |
| Used Alcohol | 0.58* (0.27) | 0.32 (0.33) | 0.32 (0.83) | 0.80** (0.27) | 0.50 (0.34) | 1.23 (0.80) |
| Smoked | −2.05*** (0.08) | −2.11*** (0.10) | −3.03*** (0.24) | −1.32*** (0.08) | −1.30*** (0.10) | −2.22*** (0.25) |
| Age in 3rd Grade | −12.43*** (0.06) | −12.49*** (0.08) | −10.29*** (0.20) | −11.67*** (0.07) | −11.60*** (0.08) | −9.02*** (0.21) |
| Mother 21-29 years | −1.18*** (0.08) | −1.16*** (0.09) | −1.87*** (0.33) | −1.57*** (0.08) | −1.59*** (0.09) | −2.24*** (0.34) |
| Mother 30+ years | −0.02 (0.10) | 0.11 (0.12) | −0.16 (0.38) | 0.32** (0.10) | 0.38** (0.12) | −0.30 (0.38) |
| Parents some high school | −0.05 (0.16) | 0.00 (0.20) | 0.33 (0.55) | 1.72*** (0.16) | 1.89*** (0.19) | 2.30*** (0.54) |
| Parents high school grad | 2.77*** (0.16) | 2.94*** (0.19) | 3.46*** (0.56) | 5.00*** (0.16) | 5.36*** (0.19) | 6.37*** (0.56) |
| Parents some college | 7.40*** (0.17) | 7.52*** (0.20) | 8.54*** (0.61) | 9.85*** (0.17) | 10.10*** (0.20) | 11.57*** (0.60) |
| Parents college grad | 17.11*** (0.19) | 17.28*** (0.22) | 18.90*** (0.62) | 18.92*** (0.19) | 19.26*** (0.22) | 21.41*** (0.62) |
| Constant | 150.73*** (0.57) | 151.25*** (0.68) | 134.72*** (1.79) | 142.35*** (0.58) | 141.53*** (0.70) | 122.39*** (1.81) |
| N | 2,344,358 | 1,789,255 | 387,794 | 2,344,358 | 1,789,255 | 387,794 |
| R2 | 0.344 | 0.345 | 0.417 | 0.322 | 0.321 | 0.395 |
Note: The omitted categories for the categorical explanatory variables correspond to BLL = 1, female, all other races/ethnicities, not economically disadvantaged, not on Medicaid, mother married at the time of birth, mother did not use alcohol during pregnancy, mother did not smoke during pregnancy, mother less than 21 years old at the time of birth, and parents had no high school education as of the time of child’s birth. All estimates are from regression models that include school-grade-year dummy variables, and dummy variables denoting the month of birth. Robust standard errors clustered at the student level are presented in parentheses.
indicates the corresponding coefficient is significantly different from zero at the 0.1% level
indicates the corresponding coefficient is significantly different from zero at the 1% level
indicates the corresponding coefficient is significantly different from zero at the 5% level.
Blood Lead Level
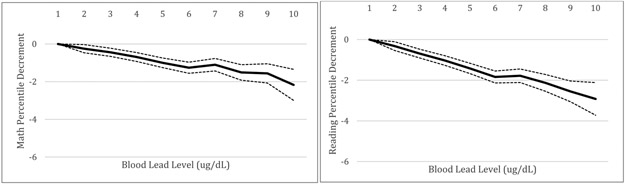
The coefficients corresponding to the BLL vector capture the effect of a student’s early childhood lead exposure on test performance.11 The estimates in models 1 and 4 in Table 2 are negative for both math and reading and are generally increasing in magnitude as BLL increases. Focusing on the effects of BLL on math percentile in model 1, we find that students with a BLL of 2 μg/dL rank 0.25 (p < 0.05) percentiles lower than students in the control group with BLL ≤ 1 μg/dL. This negative effect increases at higher lead levels, suggesting a 2.17 percentile decrement (p < 0.001) among students with an early childhood BLL of 10 μg/dL. These trends, also depicted in Figure 2, are similar when examining reading score percentiles. While these effects are statistically significant, they are substantially smaller in magnitude than the unadjusted associations between BLL and percentile rank shown in Figure 1, which confirms the importance of controlling for student and school characteristics in our regressions.
Figure 2. Effect of BLL on Math and Reading Test Score Percentiles (Average Across All Grades).
Note: Dotted lines denote 95% confidence interval. Left panel displays impact of BLL on end-of-grade math test score percentiles (from column 1 in Table 2). Right panel displays impact of BLL on end-of-grade reading test score percentiles (from column 4 in Table 2).
Focusing attention on the full and matched samples of children with BLL ≤ 5 μg/dL, we see that the results are extremely similar. This suggests that the estimates based on the full sample with BLL ≤ 10 μg/dL are not driven by unobserved heterogeneity across students with different BLLs, and lends greater support to a causal interpretation of the effects of early childhood lead exposure on later math and reading test performance.
Child and Mother Characteristics
Our models include control variables that are known to be important determinants of test scores and educational achievement (see for example, Jaffee et al. 2001; Sirin 2005). These variables describe the student at the time of birth or when in grade g, and the mother (or mother and father) at the time of the student’s birth. The corresponding coefficient estimates are shown in Table 2. In general, we find that percentile rankings in math are higher for males than for females, but the reverse is true for reading. Non-Hispanic Black students (Black) tend to score lower while non-Hispanic White students (White) tend to score higher relative to all other racial/ethnic groups. Students who are economically disadvantaged (EconDisadv) and enrolled in Medicaid also score lower than students who are economically better off. These findings are consistent with the education literature, which finds both the existence and persistence of an achievement gap for children who are minorities and are economically disadvantaged (Ladson-Billings, 2006). Children who are older in grade 3 (Age in 3rd Grade) also do less well, possibly reflecting selection bias driven by parent choice on when to enter a child into school.12
We find that children born to unmarried mothers and mothers who self-report smoking while pregnant have significantly lower percentile ranks on reading and math tests. The mother’s self-reported alcohol consumption during pregnancy (Alcohol Use) is positively associated with percentile rank, though this result is not statistically significant in all models. Parents’ highest level of education at the time of the child’s birth is also a strong predictor of a child’s test performance, with higher parental educational achievement associated with higher percentile scores. Mother’s age at the time of the child’s birth is a significant predictor of percentile rank, but in an unexpected way: children born to mothers age 21-29 perform less well than children with either younger or older mothers. This counter-intuitive result likely occurs because mother’s age at the time of the child’s birth is highly correlated with the parents’ highest level of educational achievement.
Putting our core results in context, we find that having a BLL of 5 μg/dL (relative to ≤ 1 μg/dL) leads to a similar percentile decline as that associated with having a mother who is unmarried at the time of the student’s birth (0.40 to 1.13 percentiles) or being enrolled in Medicaid (1.32 to 1.62 percentiles). On the other hand, this same elevated BLL has a less negative effect than that associated with being Black, being economically disadvantaged, or having parents with no high school education (relative to having at least one parent attend college), each of which are associated with losses of more than 5 percentiles.
Persistence of the Effects of Lead Across Grades
Equation (2) allows us to investigate whether the effects of early childhood lead exposure change as children progress through grade school and into adolescence. This is done by including interaction terms between BLL and the scalar variable, grade. All other control variables included in the model (except birth month) also are interacted with grade to allow the effects of the covariates on test score percentiles to vary. Table 3 presents the coefficients of primary interest, but the full set of coefficient estimates are available in the Supplemental Material, Table S4.
Table 3.
Changes in BLL Effects on Test Score Percentiles by Grade: Regression Results for Key Coefficients
| Math Percentile | Reading Percentile | |||||
|---|---|---|---|---|---|---|
| Full BLL ≤ 10 (1) |
Full BLL ≤ 5 (2) |
CEM BLL ≤ 5 (3) |
Full BLL ≤ 10 (4) |
Full BLL ≤ 5 (5) |
CEM BLL ≤ 5 (6) |
|
| BLL 2 | −0.22 (0.12) | −0.19 (0.12) | −0.50* (0.22) | −0.29* (0.12) | −0.30* (0.12) | −0.65** (0.23) |
| BLL 2 × grade | −0.03 (0.03) | −0.02 (0.04) | 0.05 (0.07) | −0.02 (0.04) | −0.02 (0.04) | 0.04 (0.07) |
| BLL 3 | −0.36** (0.12) | −0.28* (0.12) | −0.46 (0.24) | −0.61*** (0.12) | −0.59*** (0.12) | −0.85*** (0.24) |
| BLL 3 × grade | −0.05 (0.03) | −0.05 (0.03) | −0.05 (0.07) | −0.05 (0.03) | −0.05 (0.04) | −0.07 (0.07) |
| BLL 4 | −0.67*** (0.13) | −0.65*** (0.13) | −0.78** (0.29) | −1.03*** (0.13) | −1.06*** (0.13) | −1.12*** (0.29) |
| BLL 4 × grade | −0.03 (0.04) | −0.02 (0.04) | −0.07 (0.08) | −0.01 (0.04) | −0.01 (0.04) | −0.08 (0.08) |
| BLL 5 | −0.90*** (0.14) | −0.82*** (0.16) | −0.54 (0.40) | −1.35*** (0.14) | −1.31*** (0.16) | −1.11** (0.40) |
| BLL 5 × grade | −0.06 (0.04) | −0.06 (0.04) | 0.01 (0.11) | −0.04 (0.04) | −0.05 (0.04) | 0.05 (0.11) |
| BLL 6 | −1.11*** (0.16) | −1.67*** (0.16) | ||||
| BLL 6 × grade | −0.08 (0.04) | −0.08 (0.04) | ||||
| BLL 7 | −0.93*** (0.19) | −1.60*** (0.19) | ||||
| BLL 7 × grade | −0.08 (0.05) | −0.08 (0.05) | ||||
| BLL 8 | −1.22*** (0.23) | −2.11*** (0.24) | ||||
| BLL 8 × grade | −0.13* (0.06) | −0.01 (0.06) | ||||
| BLL 9 | −1.27*** (0.30) | −2.44*** (0.29) | ||||
| BLL 9 × grade | −0.13 (0.07) | −0.05 (0.07) | ||||
| BLL 10 | −2.23*** (0.48) | −3.02*** (0.47) | ||||
| BLL 10 × grade | 0.02 (0.10) | 0.04 (0.10) | ||||
| F-test of joint significance of grade x BLL variables (p-value) | 1.32 (p=0.22) | 0.83 (p=0.51) | 0.77 (p=0.55) | 0.97 (p=0.46) | 0.91 (p=0.46) | 0.97 (p=0.42) |
| N | 2,344,358 | 1,789,255 | 387,794 | 2,344,358 | 1,789,255 | 387,794 |
| R2 | 0.345 | 0.346 | 0.418 | 0.322 | 0.322 | 0.395 |
Note: The omitted categories for the categorical explanatory variables correspond to BLL = 1, female, all other races/ethnicities, not economically disadvantaged, not on Medicaid, mother married at the time of birth, mother did not use alcohol during pregnancy, mother did not smoke during pregnancy, mother less than 21 years old at the time of birth, and parents had no high school education as of the time of child’s birth. All estimates are from regression models that include school-grade-year dummy variables, dummy variables denoting the month of birth. All covariates listed in Table 2 are also included, both as a main effect and as an interaction term with grade. Only estimates corresponding to BLL are presented here, but for the full regression results see Table S4 in the Supplemental Material. Robust standard errors clustered at the student level are presented in parentheses.
indicates the corresponding coefficient is significantly different from zero at the 0.1% level
indicates the corresponding coefficient is significantly different from zero at the 1% level
indicates the corresponding coefficient is significantly different from zero at the 5% level.
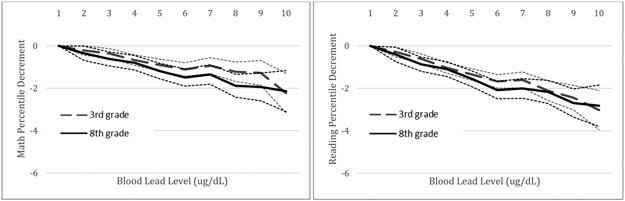
The series of coefficient estimates corresponding to BLL in Table 3 captures the average effect of early childhood BLL on third grade test score percentiles. The set of coefficients on the BLL×grade interaction terms capture the average incremental change in test score percentile for each successive grade in school from fourth through eighth grade at each BLL. For example, based on model 1 in Table 3, we find a 0.90 decrement (p < 0.001) in math percentile among students in third grade with a BLL of 5 μg/dL, relative to students with a BLL ≤ 1 μg/dL. The estimate corresponding to BLL 5 × grade, while negative, is small relative to the direct effect of BLL 5 and is not significantly different from zero. Summing the coefficient on BLL 5 with the coefficient on BLL 5 × grade multiplied by five gives the percentile deficit for eighth graders. We find a 1.2 decrement (p < 0.001) in math percentile for eighth graders with a BLL of 5 μg/dL, relative to students with a BLL ≤ 1 μg/dL. Effects on reading test scores are similar: model 4 in Table 3 shows a 1.35 decrement (p < 0.001) in percentile scores for third graders and a 1.55 decrement (p < 0.001) in percentile scores for eighth graders with a BLL of 5 μg/dL, relative to students with a BLL ≤ 1 μg/dL.
Our results indicate that the negative effect of early childhood lead exposure on test performance not only persists through subsequent grades, but it also does not attenuate as students reach higher grades. This suggests that children, on average, do not counteract the negative effects of low-level early childhood lead exposure on their educational performance. We find similar results at different BLL levels and across both math and reading test performance. This result is robust to models considering more homogenous samples (models 2, 3, 5, and 6 in Table 3), and as shown in Supplemental Material, Table S7, it is robust to using raw test scores or continuous z-scores in lieu of percentiles. Joint significance tests confirm the grade x BLL effects are not jointly significantly different from zero in all models (p = 0.22 - 0.55).
Figure 3 illustrates the results from models 1 and 4. The left panel shows the math percentile decrement with respect to BLL, and the right panel shows the same for reading. The dashed lines show this relationship among students in third grade and demonstrates the downward trend previously noted. Percentile ranks continue to decrease as BLL increases, reaching a decrement of approximately two to three percentiles among students with an early childhood exposure level of 10 μg/dL. The solid black line depicts the same relationship among eighth grade students. The two lines are quite close together, and the 95% confidence intervals overlap, suggesting that the negative effect of early childhood lead exposure on percentile rank persists as a child progresses through eighth grade.
Figure 3. Effect of BLL on Math and Reading Test Score Percentiles at 3rd and 8th grade.
Note: Dotted lines denote 95% confidence interval. Left panel displays impact of BLL on end-of-grade math test score percentiles (from column 1 in Table 3). Right panel displays impact of BLL on end-of-grade reading test score percentiles (from column 4 in Table 3).
Persistence of Lead Impacts Across Grades for Different Racial and Socioeconomic Groups
There is some question about whether the effects of lead on health and cognitive outcomes vary by race or socioeconomic status (Bellinger 2008; Hicken et al. 2013; Ferrie et al. 2015). The evidence on this issue is mixed for achievement test scores. For example, Magzamen et al. (2015) did not find statistically significant racial or socioeconomic heterogeneity in the effect of lead on test scores, but Evens et al. (2015) did find significant interactions, with a larger adverse effect of lead found in non-Hispanic White children than non-Hispanic Black or Hispanic children. In addition, Miranda et al. (2009) and Magzamen et al. (2015) found that BLL had different effects across the distribution of achievement test scores when using quantile regressions. We expand on this literature by examining whether there is heterogeneity in the impacts of early childhood lead exposure by grade across racial and socioeconomic groups.
We estimate equation (3), which includes interaction terms between the vector BLL with dummy variables identifying students who are Black (Black), economically disadvantaged (EconDisadv), and enrolled in Medicaid (Medicaid). The BLL and grade interaction terms are also interacted with these racial and socioeconomic group variables.
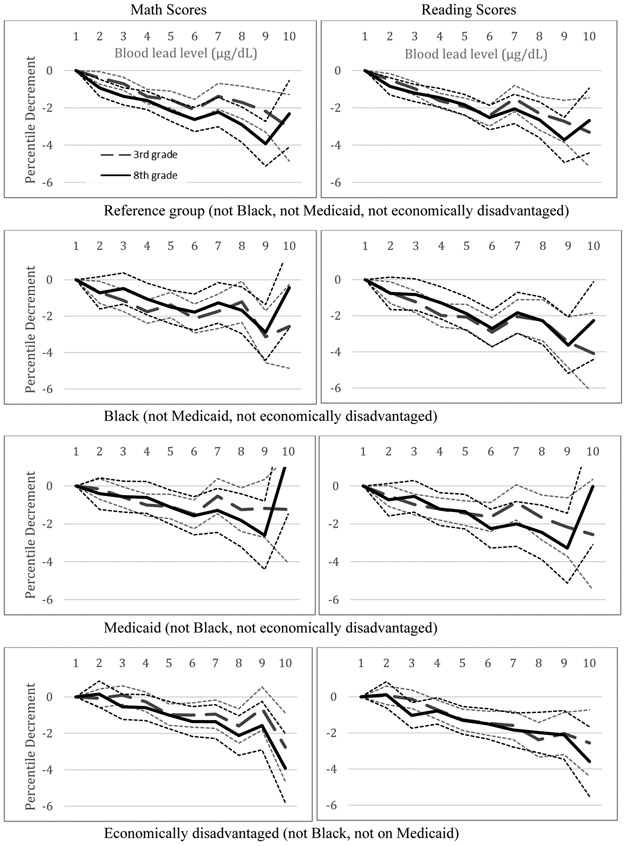
Figure 4 illustrates the results of interest, estimated using the full sample of students with BLL ≤ 10 μg/dL.13 The top panel in Figure 4 displays the test score percentile decrement with respect to BLL for math (left) and reading (right) for the reference group, which includes students identified as a race/ethnicity other than non-Hispanic Black, not listed as economically disadvantaged, and not enrolled in Medicaid. Lower panels display the results for each of the respective racial and socioeconomic groups. Compared to the previous model results, the confidence intervals are wider due to the additional parameter estimates through the added interaction terms, and there are some non-monotonicities introduced at higher BLLs. These results may occur due to the smaller number of observations in the higher BLL range when examining individual groups separately. Nonetheless, among all racial and socioeconomic groups, we see a similar downward trend showing that increases in BLL lead to a larger decrement in percentile rank. The one possible exception is among students enrolled in Medicaid. Here the trend is relatively flat, and not statistically different from zero at some BLL levels, though the confidence intervals are relatively wide among this group.
Figure 4. Effect of BLL on Math and Reading Test Score Percentiles at 3rd and 8th Grade across Race and Socioeconomic Groups.
Note: Dotted lines denote 95% confidence interval. Left panel displays impact of BLL on end-of-grade math test score percentiles (from column 1 in Table S5 in the appendix). Right panel displays impact of BLL on end-of-grade reading test score percentiles (from column 2 in Table S5 in the appendix).
Across all groups depicted in Figure 4, we see that the relationship between the test score percentile decrement and BLL is similar among third and eighth grade students. In other words, even when examining these racial and socio-economic groups separately, we still find a persistent negative effect of early childhood lead exposure on percentile rank as a student progresses into adolescence.
Discussion
While a substantial body of literature suggests that early childhood lead exposure has adverse effects on cognitive development, much of the evidence is based on tests taken by students in early grade school or is based on relatively high BLLs that are no longer representative of the population of children in the United States. To develop effective policies to protect the health and welfare of children, it is of fundamental importance to build knowledge on how low-level lead exposure affects a child’s long-term well-being.
This study is the first to examine how the effect of BLL on achievement test performance varies as a child progresses from early grade school into secondary school. We find strong evidence that even low-level lead exposure during early childhood has a negative effect on children’s school performance, and this effect is persistent from third through eighth grade. These findings are robust across different models and samples. Our findings are also consistent when restricting the BLL≤ 10 μg/dL and BLL≤ 5 μg/dL samples to a balanced panel that only includes students whose test scores are available for every year from third to eighth grade. In addition, our results are robust to alternative outcome variables, including a continuous variable measuring the raw test score, a continuous z-score, and a dichotomous variable representing whether the student’s score met the cutoff for “proficient” set by the North Carolina Department of Public Instruction, Division of Accountability.14
To better understand our results, it is useful to examine them in the context of other education effects. There are two bodies of literature that we consider. The first involves educational outcomes for children who belong to a minority group or who are economically disadvantaged. The disparities in standardized test scores between Black, Hispanic, and economically disadvantaged students vis-à-vis White students are well documented, and are persistent. (See Ladson-Billings (2006) for an overview of the “achievement gap” literature.) Our results are consistent with those findings. We see that students who are Black or in other non-White racial/ethnic groups, or are economically disadvantaged, have significantly lower test-scores than their White, not-economically disadvantaged counterparts, independent of blood lead level. Once we take into account these students’ early childhood BLLs, we find that academic performance is even further depressed, exacerbating the test-score gap. If children who belong to a minority group or who are economically disadvantaged are more likely to be exposed to lead in early childhood, they will be put at an even greater disadvantage.
The second body of literature that is of interest examines education effects of school improvement policies, such as reducing classroom size and improving teacher quality. In general, studies support the fact that students enjoy short-term benefits from placement in small classrooms (Kreuger (1999); Kreuger and Whitmore (2001); Schanzenbach (2006)) as well as classrooms with higher teacher quality (Chetty et al (2014)). 15 More specifically, Kreuger and Whitmore (2001) found that small classrooms increased averages test scores by 0.15 standard deviations. We find that for a child with an early childhood BLL of 5 μg/dL, their math and reading test scores are depressed by approximately 0.04 standard deviations. But unlike our findings, class-size studies uniformly show that the benefits from being in a small classroom decay rapidly once students are placed in regular-sized classrooms. Kreuger and Whitmore (2001) found that within the first year of moving to a regular-sized classroom, the percentile improvement in test scores declined by ½ to ¼ of its previous magnitude and continued to decline as the child progressed through at least grade 8. A similar pattern exists for teacher quality: while there are short term benefits for student test scores, studies have found that their effects on test scores rapidly “fade out” in subsequent grades (Chetty et al. (2014)).16 Our findings show that the effects of childhood exposure to lead do not dissipate – at best, they remain stable from grades 3-8. As Kreuger and Whitmore (2001) noted, even if the percentile gap over time is stable, the educational difference in higher grades may well be larger than in lower grades: so children exposed to lead are likely to be worse off as they progress through the school system.
Our study has some limitations. First, the sample of children screened for lead in North Carolina does not represent a random draw from the child population, which could lead to selection bias. Even though we have a large cohort of students in North Carolina, this cohort may not be representative of the general population of the state (or the United States). The children captured in the North Carolina Lead Prevention Surveillance Program are more likely to be economically disadvantaged or otherwise “at risk” for lead exposure. Although selection bias may affect inference to the broader population of children, it does not affect our within-sample estimates of how early childhood lead exposure impacts educational performance.
Second, most blood lead testing occurs when children are age 1 to 2 years, and there are very few observations in the lead surveillance data beyond five years. Although we examine the educational deficit from early childhood BLL, it is possible that continued low-level lead exposure into early adolescence partly explains our results. This is an important caveat to keep in mind when interpreting our findings. Given the paucity of data on BLL in older children and the positive association between past lead exposure and later BLL, disentangling the effects of early-childhood from later-childhood lead exposure is beyond the scope of our study, but this is an important area for future research.17
Third, we do not have reliable information on parent occupation or household income, which are known to be important determinants of a child’s school performance and may well be correlated with a child’s BLL. If so, this may introduce bias into our results, despite the inclusion of numerous observed covariates, including dummy variables denoting each grade at a particular school and in a specific year, and parents’ education level. The robustness of our results to exact covariate matching, where the control and treatment groups are balanced in terms of observed covariates (and presumably unobserved covariates as well) lends to the credibility of our findings.
Despite these limitations, our study advances the understanding of how low-level lead exposure in early childhood affects school performance across grades. First, by following the same children from third to eighth grade, we show that the negative effects of BLL on test performance in early grades persist in later grades. Second, by adopting a coarsened exact matching algorithm, we create balanced distributions between the “treated” (BLL > 1 μg/dL) and “control” (BLL ≤ 1 μg/dL) groups on a set of observables that may affect percentile rank non-parametrically, thereby reducing omitted variable bias and aiding our ability to interpret the results as a causal association. Due to the observational nature of our study, however, we cannot rule out the possibility that there are additional unobserved factors correlated with both lead levels and test scores that could bias our estimates. However, the robustness of our results across the matched sample and the full samples (BLL ≤ 10 μg/dL and ≤ 5 μg/dL) strengthens our argument that we have captured a causal relationship between early childhood lead exposure and educational deficits that persists across grades. Finally, by focusing on samples of children with low-level lead exposure (BLL ≤ 10 μg/dL and ≤ 5 μg/dL), our work provides information on some of the benefits of reducing early childhood lead exposure among the current population of children.
Conclusions
This is the first paper to examine how the effect of low-level early childhood lead exposure on educational performance varies as a child progresses from early grade school into secondary school. Our analysis demonstrates that even low BLLs have a measurable and persistent effect on a child’s educational performance in math and reading across grades. Furthermore, we find that the magnitude of the educational deficit is stable between grades 3-8. This indicates that physical maturation and additional schooling are not sufficient to offset the damage caused by early childhood exposure. Our results highlight the benefits to children’s educational performance from preventing early childhood exposure to lead.
Supplementary Material
Acknowledgements
Any opinions and conclusions expressed here are those of the authors and do not necessarily reflect those of the U.S. Environmental Protection Agency. In addition, although the research described in this paper may have been funded entirely or in part by the U.S. Environmental Protection Agency, it has not been subjected to the Agency’s required peer and policy review. No official Agency endorsement should be inferred. The authors declare they have no actual or potential competing financial interests. The authors thank the Children’s Environmental Health Initiative (CEHI) at Rice University, in particular, the CEHI Director, Marie Lynn Miranda, and Claire Osgood for their generosity in sharing their data and providing technical support, as well as Daniel Axelrad (EPA’s National Center for Environmental Economics), Juleen Lam (Cal State – East Bay), and three anonymous reviewers for their comments on previous drafts. The protocol for this study was approved by the Rice University Institutional Review Board. All results have been screened by the CEHI to ensure no confidential information, including any identifiable individual-level data, is disclosed.
Funding sources
None of the authors of this paper have received external funding to support this research.
Footnotes
Human subjects Institutional Review Board
The protocol for this study was approved by the Rice University Institutional Review Board.
Out of 1.6 million births from 1990-2004, the smoking variable is missing for 0.16% of the births, and the alcohol consumption variable is missing for 0.38% of the births. There is a high rate of overlap between missing observations.
Approximately 1,036,500 children born between 1990 and 2004 were screened for BLL by age 5. We were able to link 78% of these children (approximately 806,900) to the North Carolina birth certificate data. We then were able to link roughly 585,400 to the North Carolina education database. Approximately 17,000 students had missing test score data, so they had to be dropped from our sample. 24,100 students who we matched to the North Carolina education database had at least one BLL measurement > 10 μg/dL, so were also dropped from our sample. Finally, roughly 1,800 students were missing one or more of the following control variables: gender, economically disadvantaged status, mother’s marital status, smoking and/or drinking behavior during pregnancy. This led us to a final sample of 560,624 students (approximately 54% of the lead surveillance registry) and 2,344,358 student-year observations in North Carolina between 2000-2012.
For example, this vector includes a dummy variable set equal to one for all test scores from 3rd graders attending Charlotte Lab School in 2002 and set equal to zero for all other observations in the database. There are 70,548 unique school-grade-year combinations represented among the full sample of 2,344,358 student-year observations with BLL ≤ 10 μg/dL.
Our results remain consistent when we use CEM matching on the full sample but are not as precisely estimated due to pruning of observations at higher levels of BLL. Results are available in the Supplemental Material, Table S1.
We also estimated the models with cluster-robust standard errors clustered at the school level, which would allow errors to be correlated across all students within a given school. The results are similar with both clustering approaches.
While we use the geometric mean BLL in the models presented here, our results are robust to using either the maximum BLL or most recent BLL test result. Results are available in the Supplemental Material, Tables S2 and S3.
While not reported in Table 2, we find that students with late-fall birthdays—who tended to the be oldest students in their grade based on North Carolina school cutoff dates during our study period—outperformed relatively younger students, consistent with previous literature (e.g., Kinard and Reinherz 1986; Bell and Daniels 1990).
Results available in the Supplemental Material, Tables S6 through S8.
A notable exception to this literature is Hoxby (2000).
There have been other types of documented benefits to both types of school improvement policies, however, such as higher wages and greater numbers of students taking college entrance exams.
The half-life of lead in blood is roughly 30 days. Lead is also stored in bone, however, and can be released from bone to blood over much longer time spans (U.S. EPA 2013).
References
- Aizer A, Currie J, Simon P, & Vivier P (2018). “Do Low Levels of Blood Lead Reduce Children’s Future Test Scores?” American Economic Journal: Applied Economics 10(1), 307–341. doi: 10.1257/app.20160404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell J and Daniels S. 1990. Are Summer-born Children Disadvantaged? The Birthdate Effect in Education. Oxford Review of Education 16: 67–80. [Google Scholar]
- Bellinger DC (2008). “Lead Neurotoxicity and Socioeconomic Status: Conceptual and Analytical Issues.” Neurotoxicology 29(5), 828–832. doi: 10.1016/j.neuro.2008.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellinger DC, Stiles KM, & Needleman HL (1992). “Low-Level Lead Exposure, Intelligence and Academic Achievement: A Long-term Follow-up Study.” Pediatrics 90(6), 855–851. PMID: 1437425. [PubMed] [Google Scholar]
- Billings SB and Schnepel KT (2018). “Life after Lead: Effects of Early Interventions for Children Exposed to Lead.” American Economic Journal 10(3), 315–344. doi: 10.1257/app.20160056. [DOI] [Google Scholar]
- Borghans L, Golsteyn BH, Heckman JJ, & Humphries JE (2016). “What Grades and Achievement Tests Measure.” PNAS, 113(47), 13354–13359. doi/ 10.1073/pnas.1601135113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brubaker C, Schmithorst V, Haynes E, Dietrich K, Egelhoff J, Lindquist D, Lanphear B, and Cecil K. (2009). “Altered Myelination and Axonal Integrity in Adults with Childhood Lead Exposure: A Diffusion Tensor Imaging Study.” NeuroToxicology 30: 867–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brubaker C, Dietrich K, Lanphear B, and Cecil K. (2010). “The Influence of Age of Lead Exposure on Adult Gray Matter Volume.” NeuroToxicology 31: 259–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caldwell K, Cheng P-Y, Jarrett J, et al. (2017). “Measurement Challenges at Low Blood Lead Levels.” Pediatrics 140(2). doi: 10.1542/peds.2017-0272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cecil K, Brubaker C, Adler C, Dietrich K, Altaye M, Egelhoff J, Wessel S, Elangovan I, Hormung R, Jarvis K, and Lanphear B. (2008). “Decreased Brain Volume in Adults with Childhood Lead Exposure.” PLoS Medicine 5(5): 741–750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chetty R, Friedman J, & Rockoff J (2014). “Measuring the Impacts of Teachers II: Teacher Value-Added and Student Outcomes in Adulthood.” American Economic Review, 104(9); 2633–2679. 10.1257/aer.104.9.2633. [DOI] [Google Scholar]
- Dickman J & Safer Chemicals, Healthy Families. (2017) “Children at Risk: Gaps in State Lead Screening Policies.” https://saferchemicals.org/sc/wpcontent/uploads/2017/01/saferchemicals.org_children-at-risk-report.pdf [Google Scholar]
- Elliott MR, Zhang N, and Small D. (2015). “Application of Propensity Scores to a Continuous Exposure: Effect of Lead Exposure in Early Childhood on Reading and Mathematics Scores.” Observational Studies 1: 30–55. [Google Scholar]
- Evens A, Hryhorczuk D, Lanphear BP, Rankin RM, Lewis DA, Forst L, & Rosenberg D (2015). “The Impact of Low-Level Lead Toxicity on School Performance Among Children in the Chicago Public Schools: A Population Based Retrospective Cohort Study.” Environmental Health 14(21). 10.1186/s12940-015-0008-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrie JP, Rolf K, & Troesken W (2015). “Lead Exposure and the Perpetuation of Low Socioeconomic Status.” Working Paper. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.681.982&rep=rep1&type=pdf [Google Scholar]
- Hicken MT, Gee GC, Connell C, Snow RC, Morenoff J, & Hu H (2013) “Black-white blood pressure disparities: depressive symptoms and differential vulnerability to blood lead.” Environmental Health Perspectives. 2013 February;121(2):205–9. doi: 10.1289/ehp.1104517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacus SM, King G & Porro G, (2012). “Matching for Causal Inference Without Balance Checking: Coarsened Exact Matching.” Political Analysis 20(1), 1–24. doi: 10.1093/pan/mpr013. [DOI] [Google Scholar]
- Jaffee S, Caspi A, Moffitt T, Belsky J, & Silva P (2001). Why are children born to teen mothers at risk for adverse outcomes in young adulthood? Results from a 20-year longitudinal study. Development and Psychopathology, 13(2), 377–397. PMID: 11393652 [DOI] [PubMed] [Google Scholar]
- Kinard EM and Reinherz H. 1986. Birthdate Effects on School Performance and Adjustment: A Longitudinal Study. The Journal of Educational Research 79: 366–372. [Google Scholar]
- Lanphear BP, Hornung R, Khoury J, Yolton K, Baghurst P, Bellinger D, …, Roberts R (2005). “Low-Level Environmental Lead Exposure and Children’s Intellectual Function: An International Pooled Analysis.” Environmental Health Perspectives 113(7) 894–899. July. doi: 10.1289/ehp.7688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magzamen S, Imm P, Amato MS, Havlena JA, Anderson HA, Moore CF, & Kanarek MS (2013). “Moderate Lead Exposure and Elementary School End-of-Grade Examination Performance.” Annals of Epidemiology 23(11), 700–707. PMID 24095655. [DOI] [PubMed] [Google Scholar]
- Magzamen S, Amato MS, Imm P, Havlena JA, Coons MJ, Anderson HA, Kanarek MS, & Moore CF (2015). “Quantile Regression in Environmental Health: Early Life Lead Exposure and End-of-Grade Exams.” Environmental Research 137(108), 108–119. PMID: 25531815. [DOI] [PubMed] [Google Scholar]
- Mazumdar M, Bellinger D, Gregas M, Abinalla K, Bacic J, & Needleman H (2011). “Low-Level Environmental Lead Exposure in Childhood and Adult Intellectual Function: A Follow-Up Study.” Environmental Health 10:24 http://www.ehjournal.net/content/10/1/24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miranda ML, Kim D, Overstreet MA, Paul CJ, Hull AP, & Morgan SP (2007). “The Relationship between Early Childhood Blood Lead Levels and Performance on End-of-Grade Tests.” Environmental Health Perspectives 115(8), 1242–1247. doi: 10.1289/ehp.9994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miranda ML, Kim D, Reiter J, Overstreet MA, & Maxon P (2009). “Environmental Contributors to the Achievement Gap.” Neurotoxicology 30(6), 1019–1024. doi: 10.1016/j.neuro.2009.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Toxicology Program (2012), “NTP Monograph on Health Effects of Low Level Lead” U.S. Department of Health and Human Services; https://ntp.niehs.nih.gov/ntp/ohat/lead/final/monographhealtheffectslowlevellead_newissn_508.pdf. [PubMed] [Google Scholar]
- Needleman HL (1989). “Childhood Lead Poisoning: The Promise and Abandonment of Primary Prevention.” American Journal of Public Health, 88(12), 1871–1877. doi/ 10.2105/AJPH.88.12.1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Needleman HL, Schell A, Bellinger D, Leviton A, & Allred EN (1990). “The Long-Term Effects of Exposure to Low Doses of Lead in Childhood – An 11-Year Follow-up Report.” New England Journal of Medicine, 322(2), 83–88. doi: 10.1056/NEJM199001113220203. [DOI] [PubMed] [Google Scholar]
- North Carolina Childhood Lead Poisoning Prevention Program, (2004). North Carolina Childhood Lead Screening Data. Raleigh, NC: Children’s Environmental Health Branch, North Carolina Department of Environment and Natural Resources. [Google Scholar]
- Pocock SJ, Smith M, & Baghurst P (1994). “Environmental Lead and Children’s Intelligence: A Systematic Review of the Epidemiological Evidence.” British Medical Journal 309(6963), 1189–1195. doi: 10.1136/bmj.309.6963.1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuben A, Caspi A, Belsky DW, et al. (2017). “Association of Childhood Blood Lead Levels with Cognitive Function and Socioeconomic Status at Age 38 Years and With IQ Change and Socioeconomic Mobility between Childhood and Adulthood.” Journal of the American Medical Association 317(12):1244–1251. doi: 10.1001/jama.2017.1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes JW (2015a). “Lead Policy and Academic Performance: Insights from Massachusetts.” Harvard Educational Review. 85(1), 75–107. doi: 10.17763/haer.85.1.bj34u74714022730. [DOI] [Google Scholar]
- Reyes JW (2015b). “Lead Exposure and Behavior: Effects on Antisocial and Risky Behavior Among Children and Adolescents.” Economic Inquiry 53(3), 1580–1605. doi: 10.1111/ecin.12202. [DOI] [Google Scholar]
- Sirin SR (2005). Socioeconomic status and academic achievement: A meta-analytic review of research. Review of Educational Research, 75(3), 417–453. 10.3102/00346543075003417 [DOI] [Google Scholar]
- U.S. EPA. Integrated Science Assessment (ISA) for Lead (Final Report, July 2013). U.S. Environmental Protection Agency, Washington, DC, EPA/600/R-10/075F, 2013. [Google Scholar]
- Wright JP, Dietrich K, Ris MD, Hornung R, Wessel S, Lanphear B, Ho M, and Rae M. (2008). “Association of Prenatal and Childhood Blood Lead Concentrations with Criminal Arrests in Early Adulthood.” PLoS Medicine 5(5): 732–740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang N, Baker HW, Tufts M, Raymond RE, Salihu H, & Elliott MR (2013). “Early Childhood Lead Exposure and Academic Achievement: Evidence from Detroit Public Schools, 2008-2010.” American Journal of Public Health 103(3), e72–e77. doi/ 10.2105/AJPH.2012.301164. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.