Unbiased Estimation of Linkage Disequilibrium from Unphased Data

Abstract

Linkage disequilibrium (LD) is used to infer evolutionary history, to identify genomic regions under selection, and to dissect the relationship between genotype and phenotype. In each case, we require accurate estimates of LD statistics from sequencing data. Unphased data present a challenge because multilocus haplotypes cannot be inferred exactly. Widely used estimators for the common statistics r² and D² exhibit large and variable upward biases that complicate interpretation and comparison across cohorts. Here, we show how to find unbiased estimators for a wide range of two-locus statistics, including D², for both single and multiple randomly mating populations. These unbiased statistics are particularly well suited to estimate effective population sizes from unlinked loci in small populations. We develop a simple inference pipeline and use it to refine estimates of recent effective population sizes of the threatened Channel Island Fox populations.

Introduction

Linkage disequilibrium (LD), the statistical association of alleles between two loci, is informative about evolutionary and biological processes. Patterns of LD are used to infer past demographic events, identify regions under selection, estimate the landscape of recombination across the genome, and discover genes associated with biomedical and phenotypic traits. These analyses require accurate and efficient estimation of LD statistics from genome sequencing data.

LD is typically given as the covariance or correlation of alleles between pairs of loci. Estimating this covariance from data is simplest when we directly observe haplotypes (in haploid or phased diploid sequencing), in which case we know which alleles co-occur on the same haplotype. However, most whole-genome sequencing of diploids is unphased, leading to ambiguity about the co-segregation of alleles at each locus.

The statistical foundation for computing LD statistics from unphased data that was developed in the 1970s (Hill 1974; Cockerham and Weir 1977; Weir 1979) has led to widely used approaches for their estimation from modern sequencing data (Excoffier and Slatkin 1995; Rogers and Huff 2009). Although these methods provide accurate estimates for the covariance and correlation (D and r), they do not extend to other two-locus statistics, and they result in biased estimates of r² (Waples 2006). This bias confounds interpretation of r² decay curves.

Here, we extend an approach for estimating the covariance D introduced by Weir (1979) to find unbiased estimators for a large set of two-locus statistics including D² and ${\sigma }_D^2$. We show that these estimators are accurate for the low-order LD statistics used in demographic and evolutionary inferences. We provide an estimator for r² with improved qualitative and quantitative behavior over the widely used approach of Rogers and Huff (2009), although it remains a biased estimator. In general, for analyses sensitive to biases in the estimates of statistics, we recommend the use of D² or ${\sigma }_D^2$ over r².

As a concrete use case, we consider estimating recent effective population size (N_e) from observed LD between unlinked loci, a common analysis when population sizes are small, typical in conservation and domestication genomics studies. Waples (2006) suggested combining an empirical bias correction for estimates of r² with an approximate theoretical result from Weir and Hill (1980) to estimate N_e.

We propose an alternative approach to estimate N_e using our unbiased estimator for ${\sigma }_D^2$ that avoids many of the assumptions and biases associated with r² estimation. We first derive expectations for ${\sigma }_D^2$ and related statistics between unlinked loci and compare estimates of N_e based on ${\sigma }_D^2$ and r² using simulated data. As an application, we reanalyze sequencing data from Funk et al. (2016) to estimate recent N_e in the threatened Channel Island fox populations using ${\sigma }_D^2$. Our estimates are overall consistent with those reported in Funk et al. (2016) using the approach from Waples (2006), with the exception of the San Nicolas Island population where the ${\sigma }_D^2$-based estimate of 13.8 individuals is over 6 times larger than the r²-based estimate of 2.1 individuals. Our analysis further suggests population structure or recent gene flow into island fox populations.

Linkage Disequilibrium Statistics

Throughout, we assume that each locus carries two alleles: A/a at the left locus and B/b at the right locus. We think of A and B as the derived alleles, although the expectations of statistics that we consider here are unchanged if alleles are randomly labeled instead. Allele A has frequency p in the population (allele a has frequency $1-p$), and B has frequency q (b has frequency $1-q$). There are four possible two-locus haplotypes, AB, Ab, aB, and ab, whose frequencies sum to 1.

For two loci, LD is typically given by the covariance or correlation of alleles co-occurring on a haplotype (Lewontin and Kojima 1960; Hill and Robertson 1968). The covariance is denoted D:

$$\begin{array}{c}D=\text{Cov}(A,B)=f_{\mathit{AB}}-\mathit{pq}\\ =f_{\mathit{AB}}{f}_{\mathit{ab}}-f_{\mathit{Ab}}{f}_{\mathit{aB}},\end{array}$$

and the correlation is denoted r:

$$r=\frac{D}{\sqrt{p(1-p)q(1-q)}}.$$

Squared covariances (D²) and correlations (r²) see wide use in genome-wide association studies to thin data for reducing correlation between single nucleotide polymorphisms (SNPs) and to characterize local levels of LD (Speed et al. 2012). Although the average of D across sites is 0 under broad conditions, averages of D² and r² are nonzero and informative about demography: the magnitude and decay rate of r² between pairs of loci at varying distances reflect population sizes over a range of time periods (Tenesa et al. 2007; Hollenbeck et al. 2016), whereas recent admixture results in elevated long-range LD (Moorjani et al. 2011; Loh et al. 2013).

To measure the scale and decay rate of LD statistics, we compute averages over many pairs of loci across the genome. To build theoretical predictions for these observations, we take expectations over multiple realizations of the evolutionary process.

Sources of LD

When computing statistics from data, we typically work with a subset of samples from the full population. Our measurement of any two-locus statistic reflects both the underlying population-level quantity and details of the sampling process. Here, we assume that we randomly sample n diploid individuals from well-mixed, randomly mating population(s), so that contributions from the sampling process is entirely due to the given sample sizes.

To learn about the evolutionary and biological processes that shape LD, we are interested in population-level statistics. A major focus of this manuscript is to remove bias due to finite sample sizes when estimating LD. Below, we describe an approach to obtain unbiased estimators for any two-locus statistic that can be expressed as a polynomial in two-locus haplotype frequencies. However, r² is a ratio, complicating its estimation from data.

In addition, it is difficult to compute model predictions for population-level r² even in simple evolutionary scenarios. Here, we consider a related measure proposed by Ohta and Kimura (1969),

$${\sigma }_D^2=\frac{\mathbb{E}[D^2]}{\mathbb{E}[p(1-p)q(1-q)]}.$$

${\sigma }_D^2$ is not as commonly used or reported, although we can compute its expectation from models (Hill and Robertson 1968) and estimate it from data (as described in this study). Recent studies have demonstrated that ${\sigma }_D^2$ can be used to infer population size history (Rogers 2014) and, along with a set of related statistics, allows for powerful inference of multi-population demography and population structure (Ragsdale and Gravel 2019).

Finally, researchers typically exclude monomorphic sites when computing averages of r² or D² from data. This is in contrast to theoretical approximations for these quantities, which take expectations over all pairs of monomorphic and segregating loci (Hill and Robertson 1968; Ohta and Kimura 1969; Song and Song 2007), further complicating comparisons between observation and theoretical prediction. Using ${\sigma }_D^2$ instead of $\mathbb{E}[r^2]$ or $\mathbb{E}[D^2]$ avoids this issue, because including pairs where one or both loci are monomorphic does not change the expectation of ${\sigma }_D^2$.

Results

Estimating LD from Data

In the Materials and Methods section, we present an approach to compute unbiased estimators for a large family of two-locus statistics, using either phased or unphased data. This includes commonly used statistics, such as D and D², the additional statistics in the Hill–Robertson system ($D(1-2p)(1-2q)$ and $p(1-p)q(1-q)$, which we denote Dz and π₂, respectively), and, in general, any statistic that can be expressed as a polynomial in haplotype frequencies (f’s) or in terms of p, q, and D. We use this same approach to find unbiased estimators for cross-population LD statistics, which were recently used to infer multi-population demographic history (Ragsdale and Gravel 2019).

For a given pair of loci i and j, we use our estimators for D² and π₂ to propose an estimator for r² between loci i and j from unphased data, which we denote $r_{÷i,j}^2={\widehat{D^2}}_{i,j}/{\widehat{{\pi }_2}}_{i,j}$ (hereafter dropping the subscripts i, j). $r_{÷}^2$ is a biased estimator for r². However, it performs favorably in comparison with the common approach of first computing $\widehat{r}$ and simply squaring the result, as in Rogers and Huff (2009) (fig. 1).

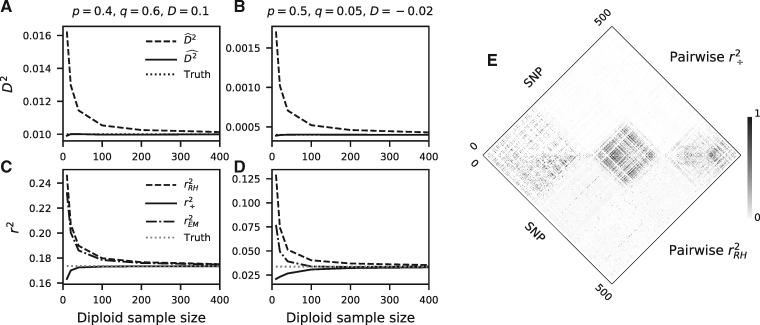
Fig. 1.

LD estimation. (A, B) Computing D² by taking the square of the covariance overestimates the true value, whereas our approach is unbiased for any sample size. (C, D) Similarly, computing r² by estimating r and squaring it (here, via the Rogers–Huff approach, $r_{\text{RH}}^2$, and the Excoffier–Slatkin EM approach, $r_{\text{EM}}^2$) overestimates the true value. Our approach, $r_{÷}^2$, does not overestimate the population-level r², although all estimators show variable biases depending on the underlying haplotype frequencies in the population. Comparisons with additional estimators and frequency configurations are in supplementary figure S1, Supplementary Material online. (E) Pairwise comparison of r² for 500 neighboring SNPs in chromosome 22 in CHB from 1000 Genomes Project Consortium et al. (2015). $r_{÷}^2$ (top) and $r_{\text{RH}}^2$ (bottom) are strongly correlated, although $r_{÷}^2$ displays less spurious background noise.

To explore the performance of this estimator, we first simulated varying diploid sample sizes with direct multinomial sampling from known haplotype frequencies (fig. 1A–D and supplementary fig. S1, Supplementary Material online). Estimates of D² were unbiased as expected, and $r_{÷}^2$ quickly converged to the true r² as sample size increases. Standard errors of our estimator were nearly indistinguishable from Rogers and Huff (2009) (supplementary fig. S2, Supplementary Material online), and the variances of estimators for statistics in the Hill–Robertson system decayed with sample size as $\sim \frac{1}{n^2}$ (supplementary fig. S3, Supplementary Material online).

Second, we simulated 1 Mb segments of chromosomes under steady-state demography (using msprime [Kelleher et al. 2016]) to estimate r² decay curves using both approaches. Our estimator was invariant to phasing and displayed the proper decay properties in the large recombination distance limit (fig. 2A). With increasing distance between SNPs, $r_{÷}^2$ approached zero as expected for population-level LD, whereas the Rogers–Huff r² estimates converged to positive values as expected in a finite sample (Waples 2006).

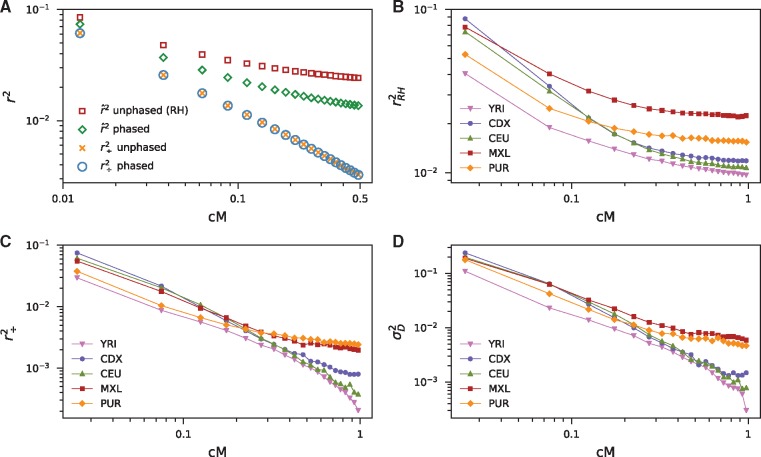
Fig. 2.

Decay of r² with distance. (A) Comparison between our estimator ($r_{÷}^2$) and Rogers and Huff (2009) (RH) under steady-state demography. The $r_{÷}^2$-curve displays the appropriate decay behavior and is invariant to phasing, whereas the RH estimator gives upward biased r², and this general approach is sensitive to phasing. Estimates were computed from 1,000 1 Mb replicate simulations with constant mutation and recombination rates (each $2\times {10}^{-8}$ per base per generation) for n = 50 sampled diploids using msprime (Kelleher et al. 2016). (B) $r_{\text{RH}}^2$ Decay for five populations in 1000 Genomes Project Consortium et al. (2015), including two putatively admixed American populations (MXL and PUR), computed from intergenic regions. (C) $r_{÷}^2$ Decay for the same populations. (D) Decay of ${\sigma }_D^2$ computed as $\sum \widehat{D^2}/\sum \widehat{{\pi }_2}$. The $r_{\text{RH}}^2$ decay curves show excess long-range LD in each population, whereas our estimator qualitatively differentiates between populations.

Finally, we computed the decay of r² across five population from the 1000 Genomes Project Consortium et al. (2015) (fig. 2B–D). $r_{÷}^2$ shows distinct qualitative behavior across populations, with recently admixed populations exhibiting long-range LD. However, r² as estimated using the Rogers–Huff approach displayed long-range LD in every population, confounding the signal of admixture in the shape of r² decay curves.

Estimating $N_e$ from LD between Unlinked Loci

Observed LD between unlinked markers is widely used to estimate the effective population size (N_e) in small populations (Hill 1981; Waples 1991, 2006; Waples and Do 2008; Do et al. 2014). This estimate of N_e reflects the effective number of breeding individuals over the last one to several generations, since LD between unlinked loci is expected to decay rapidly over just a handful of generations. Analytic solutions for $\mathbb{E}[r^2]$ are unavailable, although a classical result uses a ratio of expectations to approximate

$$\mathbb{E}[r^2]\approx \frac{c^2+{(1-c)}^2}{2N_{e}c(2-c)}$$ (1)

for a randomly mating population, where c is the per generation recombination probability between two loci (eq. 3 in Weir and Hill [1980] due to Avery [1978]). For unlinked loci (c = 1/2), equation (1) reduces to $\mathbb{E}[r^2]=1/3N_e$ (for a monogamous mating system, $\mathbb{E}[r^2]=2/3N_e$ [Weir and Hill 1980]). Rearranging this equation provides an estimate for N_e if we can estimate r² from data.

As pointed out by Waples (2006), failing to account for sample size bias when estimating r² from data leads to strong downward biases in ${\widehat{N}}_e$. Waples (2006) used Burrows’ estimator ${\widehat{r}}_{\Delta }^2$ (again following Weir and Hill [1980]) and used simulations to empirically estimate the bias in the estimate due to finite sample size (given by $\text{Var}({\widehat{r}}_{\Delta })$). Subtracting this estimated bias from ${\widehat{r}}_{\Delta }^2$ gives an empirically corrected estimate for r²,

$${\widehat{r}}_{\mathrm{W}}^2\approx {\widehat{r}}_{\Delta }^2-\text{Var}({\widehat{r}}_{\Delta }).$$ (2)

Waples showed that ${\widehat{r}}_{\mathrm{W}}^2$ removes much of the bias in N_e estimates (fig. 1C and D). Bulik-Sullivan et al. (2015) used a similar bias correction (via the δ-method) that appears to perform comparably with ${\widehat{r}}_{\mathrm{W}}^2$ (supplementary fig. S1, Supplementary Material online).

Predicting ${\sigma }_D^2$for Unlinked and Linked Loci

The Avery equation (1) was derived under the assumption that the expectation of ratios equals the ratio of expectation. By working directly with ${\sigma }_D^2$, we therefore save both a theoretical approximation and the need for empirical finite sample bias correction. In a random-mating diploid Wright–Fisher model with c = 1/2, we show in the Supplementary data that $\mathbb{E}[{\sigma }_D^2]=1/3N_e$, as suggested by the Avery equation, whereas monogamy leads to $\mathbb{E}[{\sigma }_D^2]=2/3N_e$. A similar approach allows us to show that $\mathbb{E}[D(1-2p)(1-2q)]$, another statistic from the Hill–Robertson system, is approximately zero for unlinked loci (its leading-order term is of order $1/N_e^2$).

In the opposite limit, for tightly linked loci ($c\ll 1$), Ohta and Kimura (1969) used a diffusion approach to approximate

$${\sigma }_D^2\approx \frac{1}{3+4N_{e}c-2/(2.5+N_{e}c)}.$$ (3)

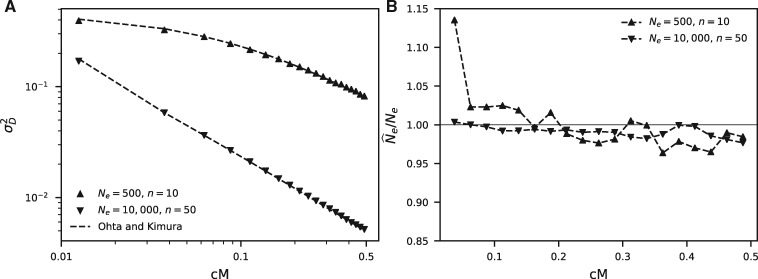
This approximation is accurate at demographic equilibrium for both large and small population sizes with low mutation rates and recombination distances (fig. 3A). Rearranging equation (3) then provides a direct estimate for N_e for any given recombination distance (fig. 3B), though the approximation is only valid for $c\ll 1$.

Fig. 3.

Using ${\mathit{\sigma }}_D^2$ to estimate ${\mathit{N}}_{\mathit{e}}$. (A) The approximation for ${\sigma }_D^2$ due to Ohta and Kimura (1969) is accurate for both large and small sample sizes. Here, we compare with the same simulations used in figure 2A for $N_e=$10,000 with sample size n = 50 and N_e = 500 with sample size n = 10. (B) Using ${\sigma }_D^2$ estimated from these same simulations and rearranging equation (3) provides an estimate for N_e for each recombination bin. The larger variance for N_e = 500 is due to the small sample size leading to noise in estimated ${\sigma }_D^2$.

Comparison of Methods for Estimating $N_e$Using Simulated Data

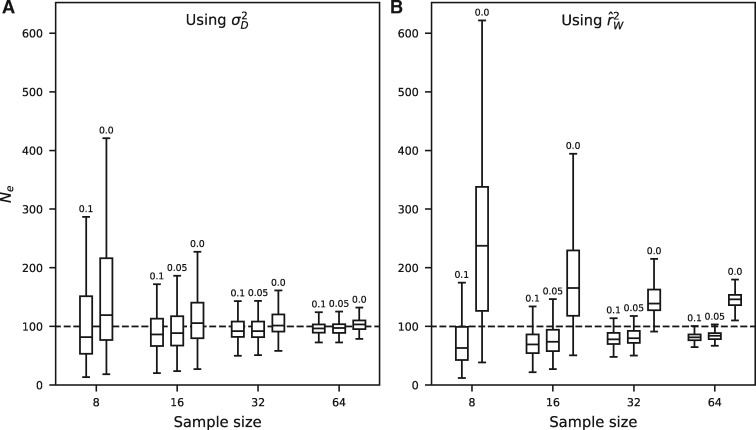
We simulated data with effective population sizes N_e = 100 and 400 using fwdpy11 (Thornton 2014) to compare the performance of inferring ${\widehat{N}}_e$ from NeEstimator version 2.1 (Do et al. 2014), which uses ${\widehat{r}}_{\mathrm{W}}^2$, and from ${\sigma }_D^2$ (see Materials and Methods for simulation details). Generally, using our estimators for ${\sigma }_D^2$ provided less biased estimates of N_e (fig. 4 and supplementary fig. S4, Supplementary Material online). This was the case even when data was filtered by minor allele frequency (MAF), a strategy recommended to reduce bias for NeEstimator but that is not required or desirable in the ${\sigma }_D^2$ approach. Estimates from ${\widehat{r}}_{\mathrm{W}}^2$ had smaller variance when filtering by MAF, but higher mean squared error (MSE) for larger sample sizes (supplementary table S1, Supplementary Material online). In practice, NeEstimator provides estimates with different cutoff choices and lets the user decide on the best cutoff choice.

Fig. 4.

Performance of ${\mathit{N}}_e$ estimation on simulated data. We used fwdpy11 (Thornton 2014) to simulate genotype data for the given sample sizes and N_e = 100 (see Materials and Methods section). Although estimates of N_e using (A) ${\sigma }_D^2$ had slightly larger variances than estimates using (B) equations (1) and (2) (computed using NeEstimator [Do et al. 2014]), estimates from ${\sigma }_D^2$ were unbiased when using all data and less biased when filtering by MAF, resulting in lower MSE (supplementary table S1, Supplementary Material online).

We also explored the effect of inbreeding on estimates of ${\sigma }_D^2$ and ${\sigma }_{\mathit{Dz}}=\mathbb{E}[\mathit{Dz}]/\mathbb{E}[{\pi }_2]$ using simulated data. Unsurprisingly, higher rates of inbreeding lead to higher values of ${\sigma }_D^2$ between unlinked loci, which results in deflated estimates of N_e (supplementary fig. S5A and B, Supplementary Material online). σ_Dz is robust to inbreeding, with expected value near zero even for large selfing rates (supplementary fig. S5C, Supplementary Material online). Although σ_Dz cannot be used to provide an estimate for N_e (as its expectation is zero), it could instead be used to distinguish between different violations of model assumptions: if we also measure σ_Dz to be significantly elevated above zero, it might suggest population structure or recent migration into the population (Ragsdale and Gravel 2019).

The Effective Population Sizes of Island Foxes

The island foxes (Urocyon littoralis) that inhabit the Channel Islands of California have recently experienced severe population declines due to predation and disease. For this reason they have been closely studied to inform protection and management decisions. More generally, they provide an exemplary system to study the genetic diversity and evolutionary history of endangered island populations (Wayne et al. 1991; Coonan et al. 2010; Funk et al. 2016; Robinson et al. 2016, 2018). A recent study aimed to disentangle the roles of demography (including sharp reductions in population size, resulting in strong genetic drift) and differential selection in shaping the genetics of island foxes across the six Channel Islands (Funk et al. 2016). In addition to genetic analyses based on single-site statistics, Funk et al. (2016) used NeEstimator (Do et al. 2014) to infer recent ${\widehat{N}}_e$ for each of the island fox populations (reproduced in table 1).

Table 1.

Inferred Island Fox Effective Population Sizes.

Population		${\widehat{N}}_e$ (95% CI) Reported in Funk et al. (2016)		${\widehat{N}}_e$ (95% CI) Using ${\sigma }_D^2$
San Miguel I.	13.7	$(13.2-14.1)$	15.3	$(14.5-16.1)$
Santa Rosa I.	13.6	$(13.5-13.7)$	13.3	$(13.0-13.6)$
Santa Cruz I.	25.1	$(24.6-25.5)$	22.8	$(22.4-23.3)$
Santa Catalina I.	47.0	$(46.7-47.4)$	40.9	$(40.4-41.6)$
San Clemente I.	89.7	$(77.1-107.0)$	59.1	$(53.0-66.7)$
San Nicolas I.	2.1	$(2.0-2.2)$	13.8	$(13.0-15.2)$

Note.—LD between unlinked loci provides an estimate for the effective number of (breeding) individuals in the previous several generations. Funk et al. (2016) used NeEstimator (Do et al. 2014) to estimate N_e for six island fox populations in the Channel Islands of California (left). We used this same data to compute N_e using our estimator for ${\sigma }_D^2$ instead (right), obtaining results largely consistent with Funk et al. (2016). Notably, Funk et al. inferred an extremely small size on San Nicolas Island (${\widehat{N}}_e\approx 2$), whereas our estimate is somewhat larger and on the same order of magnitude of ${\widehat{N}}_e$ from other islands with small effective population sizes. A 90% confidence intervals were computed via 200 resampled bootstrap replicates (see Materials and Methods).

Using the same 5,293 variable sites reported and analyzed in Funk et al. (2016), we computed ${\sigma }_D^2$ for each of the six island fox populations to estimate N_e. Results using ${\sigma }_D^2$ were generally consistent with those computed in Funk et al. (2016) using ${\widehat{r}}_{\mathrm{W}}^2$ (table 1 and supplementary table S2, Supplementary Material online). Perhaps most notably, the San Nicolas Island population, which was previously inferred to have the extremely small effective size of ${\widehat{N}}_e\approx 2$, was inferred to have ${\widehat{N}}_e\approx 14$. Although this size is still quite small in contrast to mainland populations, it is more encouraging from a conservation standpoint and similar to the effective sizes inferred in other island fox populations.

We also estimated σ_Dz for each population and found that it was significantly elevated above zero in each population (supplementary table S4, Supplementary Material online). This suggests that some model assumptions are not being met. From simulated data, neither inbreeding nor filtering by MAF should result in elevated observed σ_Dz (supplementary figs. S5 and S6, Supplementary Material online). The discrepancy could instead be caused by population substructure or recent migration between populations. It may also be driven by technical artifacts: we analyzed the data with the assumption that the separate RAD contigs were effectively unlinked (reads were not mapped to a reference genome). If some contigs were in fact closely physically linked on chromosomes, this could lead to larger LD statistics than expected for unlinked loci.

Discussion

We presented estimators for a range of summary statistics of LD, including Hill and Robertson’s D², Dz, and π₂, that account for both unphased data and finite sample sizes. Such estimators readily extend to two-locus statistics involving multiple populations, such as the covariance of D between two populations. This work naturally complements inference approaches that use LD, removing confounding from finite sample sizes and allowing for direct comparisons with expectations from evolutionary models (Loh et al. 2013; Rogers 2014; Ragsdale and Gravel 2019). As an illustration, here we demonstrated the use of our estimator for ${\sigma }_D^2$ to infer recent N_e from LD between unlinked loci (Waples 1991, 2006; Do et al. 2014).

Challenges of Estimating r²

We did not obtain an unbiased estimator for r². Computing estimates and expectations of ratios is challenging, and often intractable. One commonly used approach to estimate r² is to first compute $\widehat{r}$ via an EM algorithm (Excoffier and Slatkin 1995) or genotype correlations (Rogers and Huff 2009) and then square the result. Although we can compute unbiased estimators for r from either phased or unphased data, this approach gives inflated estimates of r² because it does not properly account for the variance in $\widehat{r}$. In general, the expectation of a function of a random variable is not equal to the function of its expectation:

$$r^2\cancel{\ne }\mathbb{E}\left[{\widehat{r}}^2\right].$$

For large enough sample sizes, this error will be practically negligible, but for small to moderate sample sizes, the estimates will be upwardly biased, sometimes drastically (figs. 1 and 2).

An alternative is to estimate D² and π₂ and compute their ratio for each pair of loci. Given unbiased estimates of the numerator $\widehat{D^2}$ and denominator $\widehat{{\pi }_2}$, the ratio $r_{÷}^2=\widehat{D^2}/\widehat{{\pi }_2}$ performs favorably to the Rogers–Huff approach (fig. 1C and D) and displays the appropriate decay behavior in the large recombination limit (fig. 2). It is still a biased estimator for r², however, since

$$r^2\cancel{\ne }\mathbb{E}\left[\frac{\widehat{D^2}}{\widehat{{\pi }_2}}\right].$$

Even if we were given an adequate estimator for r², obtaining theoretical predictions for its value is very challenging (McVean 2002; Song and Song 2007; Rogers 2014).

One approach to handle the finite sample bias for r² is to work directly with the finite-sample correlation, that is, the expected r² due to both population-level LD and LD induced by sampling with sample size n. This may be estimated by first solving for the expected two-locus sampling distribution for a given sample size (Hudson 2001; Kamm et al. 2016; Ragsdale and Gutenkunst 2017), and then using this distribution to compute $\mathbb{E}[r^2]$ for that sample size (as proposed by Spence and Song [2019]). This approach allows for a fair comparison between model expectations and r² as computed by the Rogers and Huff (2009) estimator. However, methods for computing the full two-locus sampling distribution are limited to a single population, preventing the exploration of models of admixture or migration between multiple populations. Furthermore, because finite-sample bias dominates signal for all but the shortest recombination distances, using biased statistics hinders comparisons across cohorts with differing sample sizes. Working directly with ${\sigma }_D^2$-type statistics, for which we presented unbiased estimators and can compute theoretical predictions for multiple populations under arbitrary demography (Ragsdale and Gravel 2019), avoids these complications.

Finally, Song and Song (2007) approximated $\mathbb{E}[r^2]$ using a series expansion of polynomials in p, q, and D. In theory, our approach can provide unbiased estimators for each term in that series, with accuracy determined by where we decide to truncate the series expansion. Although this may be an appealing strategy, it is likely to be quite computationally expensive as Song and Song (2007) suggest that many terms are needed for accurate estimation.

Tradeoffs and Limitations

Among caveats for the present approach, we find that the unbiased estimators are analytically cumbersome. For example, expanding $\mathbb{E}[D^2]$ as a monomial series in genotype frequencies results in nearly 100 terms. The algebra is straightforward, but writing the estimator down by hand is a tedious exercise, and we used symbolic computation to simplify terms and avoid algebraic mistakes. This might explain why such estimators were not proposed for higher orders than D in the foundational work of LD estimation in 1970s and 1980s.

Deriving and computing such estimators poses no problem for an efficiently written computer program that operates on observed genotype counts. The computational complexity of counting two-locus genotypes from unphased data and then computing $r_{÷}^2$ from genotype counts reasonably scales to sample sizes in the tens or hundreds of thousands, although our Python implementation remains slower than computing the Pearson product-moment correlation coefficients directly from the genotype matrix, as in the Rogers–Huff approach (supplementary fig. S7, Supplementary Material online). For very large sample sizes, the bias in the Rogers–Huff estimator for r² is negligible, and it may be preferable to use their more straightforward approach.

In computing sample variances from observations, there is a familiar tension between minimizing bias and minimizing the MSE of the estimate. For example, Bessel’s correction (the typical $n/n-1$ factor in the sample variance formula) provides an unbiased estimator of the sample variance, but often results in a larger MSE. The maximum likelihood estimator for r² or D² using the Excoffier and Slatkin (1995) approach reflects this tradeoff, providing a smaller MSE but a biased estimate of these quantities. In addition, it is worth noting that like many unbiased estimators, both $\widehat{D^2}$ and $r_{÷}^2$ can take values outside the expected range of the corresponding statistics: for a given pair of loci $r_{÷}^2$ may be slightly negative or greater than one.

Throughout, we assumed populations to be randomly mating. Under inbreeding, there are multiple interpretations of D depending on whether we consider the covariance between two randomly drawn haplotypes from the population or consider two haplotypes within the same diploid individual (Cockerham and Weir 1977). Given the existence of theoretical predictions for two-locus statistics in models with inbreeding, deriving unbiased statistics for this scenario appears a worthwhile goal for future work.

Materials and Methods

Notation

Variables without decoration represent quantities computed as though we know the true population haplotype frequencies. We use tildes to represent statistics estimated by taking maximum likelihood estimates for allele frequencies from a finite sample: for example, $\tilde{p}=n_A/n,\hspace{0.17em}{\tilde{f}}_{\mathit{AB}}=n_{\mathit{AB}}/n,\hspace{0.17em}\tilde{\pi }=2\tilde{p}(1-\tilde{p})$. Hats represent unbiased estimates of quantities: for example, $\widehat{\pi }=n/(n-1)\tilde{\pi }$. f’s denote haplotype frequencies in the population, whereas g’s denote genotype frequencies. Instead of writing $g_{\mathit{AABB}},g_{\mathit{AABb}},\dots ,g_{\mathit{aabb}}$, we use $g_1,\dots ,g_9$ as shorthand for genotype frequencies, and $n_1,\dots ,n_9$ as shorthand for the associated observed genotype counts (all nine genotypes are represented in table 2).

Table 2.

Expected Genotype Frequencies under Random Mating.

	BB	Bb	bb	Exp. Freq.
AA	g 1	g 2	g 3	p 2
Aa	g 4	g 5	g 6	$2p(1-p)$
aa	g 7	g 8	g 9	${(1-p)}^2$
Exp. freq.	q 2	$2q(1-q)$	${(1-q)}^2$	1

Note.—For a given pair or loci, the nine possible two-locus genotypes have frequencies which sum to 1. We assume random mating, so expected marginal genotype frequencies follow expected Hardy–Weinberg proportions. The g_i’s are shorthand for each of the possible observed two-locus genotypes. For example, a diploid sample where we observe the left locus heterozygous as Aa and the right locus homozygous bb contributes to frequency g₆.

Estimating Statistics from Phased Data

Suppose that we observe haplotype counts $(n_{\mathit{AB}},n_{\mathit{Ab}},n_{\mathit{aB}},n_{\mathit{ab}})$, with $\sum n_j=n$, for a given pair of loci. Estimating LD in this case is straightforward. An unbiased estimator for D is

$$\widehat{D}=\frac{n}{n-1}\left(\frac{n_{\mathit{AB}}}{n}\frac{n_{\mathit{ab}}}{n}-\frac{n_{\mathit{Ab}}}{n}\frac{n_{\mathit{aB}}}{n}\right).$$

We interpret $D=f_{\mathit{AB}}{f}_{\mathit{ab}}-f_{\mathit{Ab}}{f}_{\mathit{aB}}$ as the probability of drawing two chromosomes from the population and observing haplotype AB in the first sample and ab in the second, minus the probability of observing Ab followed by aB. This intuition leads us to the same estimator $\widehat{D}$:

$$\begin{array}{c}\widehat{D}=\frac{1}{2}\frac{\left(\begin{array}{c}{n}_{\mathit{AB}}\\ 1\end{array}\right)\left(\begin{array}{c}{n}_{\mathit{ab}}\\ 1\end{array}\right)}{\left(\begin{array}{c}n\\ 2\end{array}\right)}-\frac{1}{2}\frac{\left(\begin{array}{c}{n}_{\mathit{Ab}}\\ 1\end{array}\right)\left(\begin{array}{c}{n}_{\mathit{aB}}\\ 1\end{array}\right)}{\left(\begin{array}{c}n\\ 2\end{array}\right)}\\ =\frac{n_{\mathit{AB}}}{n}\frac{n_{\mathit{ab}}}{n-1}-\frac{n_{\mathit{Ab}}}{n}\frac{n_{\mathit{aB}}}{n-1}.\end{array}$$

In this same way we can find an unbiased estimator for any two-locus statistic that can be expressed as a polynomial in haplotype frequencies. For example, the variance of D is

$$\begin{array}{c}{D}^2={(f_{\mathit{AB}}{f}_{\mathit{ab}}-f_{\mathit{Ab}}{f}_{\mathit{aB}})}^2\\ =f_{\mathit{AB}}^2{f}_{\mathit{ab}}^2+f_{\mathit{Ab}}^2{f}_{\mathit{aB}}^2-2f_{\mathit{AB}}{f}_{\mathit{Ab}}{f}_{\mathit{aB}}{f}_{\mathit{ab}},\end{array}$$

with each term being interpreted as the probability of sampling the given ordered haplotype configuration in a sample of size four (Strobeck and Morgan 1978; Hudson 1985). An unbiased estimator for D² is then

$$\begin{array}{c}\widehat{D^2}=\frac{1}{\left(\begin{array}{c}4\\ 2,0,0,2\end{array}\right)}\frac{\left(\begin{array}{c}{n}_{\mathit{AB}}\\ 2\end{array}\right)\left(\begin{array}{c}{n}_{\mathit{ab}}\\ 2\end{array}\right)}{\left(\begin{array}{c}n\\ 4\end{array}\right)}\\ +\frac{1}{\left(\begin{array}{c}4\\ 0,2,2,0\end{array}\right)}\frac{\left(\begin{array}{c}{n}_{\mathit{Ab}}\\ 2\end{array}\right)\left(\begin{array}{c}{n}_{\mathit{aB}}\\ 2\end{array}\right)}{\left(\begin{array}{c}n\\ 4\end{array}\right)}\\ -\frac{2}{\left(\begin{array}{c}4\\ 1,1,1,1\end{array}\right)}\frac{\left(\begin{array}{c}{n}_{\mathit{AB}}\\ 1\end{array}\right)\left(\begin{array}{c}{n}_{\mathit{Ab}}\\ 1\end{array}\right)\left(\begin{array}{c}{n}_{\mathit{aB}}\\ 1\end{array}\right)\left(\begin{array}{c}{n}_{\mathit{ab}}\\ 1\end{array}\right)}{\left(\begin{array}{c}n\\ 4\end{array}\right)}.\end{array}$$

The multinomial factors in front of each term account for the number of distinct orderings of the sampled haplotypes. We similarly find unbiased estimators for the other terms in the Hill–Robertson system, $D(1-2p)(1-2q)$ and $p(1-p)q(1-q)$ (shown in the Supplementary data), or any other statistic that we compute from haplotype frequencies.

Estimating Statistics from Unphased Data

Estimating two-locus statistics from genotype data requires a bit more work because the underlying haplotypes are ambiguous in a double heterozygote, AaBb. Our first step is to derive expressions for D, p, and q in terms of the population genotype frequencies $(g_1,\dots ,g_9)$. We will then use these expressions to derive unbiased estimates in terms of the finite population sample genotype counts $(n_1,\dots ,n_9)$. Expressions for p and q in terms of genotype frequencies can be read directly from table 2: $p=(g_1+g_2+g_3)+1/2(g_4+g_5+g_6)$, and $q=(g_1+g_4+g_7)+1/2(g_2+g_5+g_8)$. To obtain an estimate for $D=f_{\mathit{AB}}{f}_{\mathit{ab}}-f_{\mathit{Ab}}{f}_{\mathit{aB}}$, we would like to have expressions for haplotype frequencies such as f_AB in terms of the g_i.

We can write a naive estimate for f_AB by reading from table 2 and simply assuming that the double heterozygote genotype $g_5=2f_{\mathit{AB}}{f}_{\mathit{ab}}+2f_{\mathit{Ab}}{f}_{\mathit{aB}}$ had equal probability of the two possible phasing configurations:

$$x_{\mathit{AB}}=g_1+\frac{g_2}{2}+\frac{g_4}{2}+\frac{g_5}{4}.$$

The correct expression for f_AB would replace $g_5/4$ by the probability of the correct haplotype configuration, $f_{\mathit{AB}}{f}_{\mathit{ab}}$. This probability can be expressed as $f_{\mathit{AB}}{f}_{\mathit{ab}}=g_5+2D/4$, so that

$$f_{\mathit{AB}}=g_1+\frac{g_2}{2}+\frac{g_4}{2}+\frac{g_5+2D}{4}=x_{\mathit{AB}}+\frac{D}{2}.$$

We can obtain similar expressions for all the $f_{··}$ and substitute in the expression for D to write

$$D=f_{\mathit{AB}}{f}_{\mathit{ab}}-f_{\mathit{Ab}}{f}_{\mathit{aB}}=x_{\mathit{AB}}{x}_{\mathit{ab}}-x_{\mathit{Ab}}{x}_{\mathit{aB}}+\frac{D}{2}.$$

Rearranging provides an estimate of D in terms of naive frequency estimates that depend only on genotypes:

$$D=2\left(x_{\mathit{AB}}{x}_{\mathit{ab}}-x_{\mathit{Ab}}{x}_{\mathit{aB}}\right).$$

This expression for D is equal to Burrows’ “composite” covariance measure of LD,

$$\Delta =\left(2g_1+g_2+g_4+\frac{1}{2}{g}_5\right)-2pq,$$ (4)

as given in Weir (1979) and Weir (1996), page 126.

Given this expression for D, as well as $p=x_{\mathit{AB}}+x_{\mathit{Ab}}$ and $q=x_{\mathit{AB}}+x_{\mathit{aB}}$, we can express higher-order moments as function of genotype frequencies. The Hill–Robertson statistics can be written as polynomials in the naive estimates

$$\begin{array}{c}{D}^2=4{(x_{\mathit{AB}}{x}_{\mathit{ab}}-x_{\mathit{Ab}}{x}_{\mathit{aB}})}^2,\\ D(1-2p)(1-2q)=2(x_{\mathit{AB}}{x}_{\mathit{ab}}-x_{\mathit{Ab}}{x}_{\mathit{aB}})\\ \times (x_{\mathit{aB}}+x_{\mathit{ab}}-x_{\mathit{AB}}-x_{\mathit{Ab}})\\ \times (x_{\mathit{Ab}}+x_{\mathit{ab}}-x_{\mathit{AB}}-x_{\mathit{aB}}),\end{array}$$

and

$$\begin{array}{c}p(1-p)q(1-q)=(x_{\mathit{AB}}+x_{\mathit{Ab}})(x_{\mathit{aB}}+x_{\mathit{ab}})\\ \times (x_{\mathit{AB}}+x_{\mathit{aB}})(x_{\mathit{Ab}}+x_{\mathit{ab}}).\end{array}$$

The next step is to obtain estimates from finite samples. Any statistic S written as a polynomial in $(x_{\mathit{AB}},x_{\mathit{Ab}},x_{\mathit{aB}},x_{\mathit{ab}})$ can be expanded as a monomial series in genotype frequencies g_j, $j=1,\dots ,9$:

$$S={\displaystyle \sum _i{a}_i}{\displaystyle \prod _{j=1}^9{g}_{j,i}^{k_{j,i}}}.$$

Each term of the form $a_i{\displaystyle \prod g_{j,i}^{k_{j,i}}}$ can be interpreted as the probability of drawing $k=\sum k_j$ diploid samples, and observing the ordered configuration of k₁ of type g₁, k₂ of type g₂, and so on. Then, from a diploid sample size of $n\ge k$, this term has the unbiased estimator

$$a_i\frac{1}{\left(\begin{array}{c}{k}_i\\ k_{1,i},\dots ,k_{9,i}\end{array}\right)}\frac{\left(\begin{array}{c}{n}_{1,i}\\ k_{1,i}\end{array}\right)\cdots \left(\begin{array}{c}{n}_{9,i}\\ k_{9,i}\end{array}\right)}{\left(\begin{array}{c}{n}_i\\ k_i\end{array}\right)}.$$

Summing over all terms gives us an unbiased estimator for S:

$$\widehat{S}=\sum _i{a}_i\frac{1}{\left(\begin{array}{c}{k}_i\\ k_{1,i},\dots ,k_{9,i}\end{array}\right)}\frac{\left(\begin{array}{c}{n}_{1,i}\\ k_{1,i}\end{array}\right)\cdots \left(\begin{array}{c}{n}_{9,i}\\ k_{9,i}\end{array}\right)}{\left(\begin{array}{c}{n}_i\\ k_i\end{array}\right)}.$$ (5)

We can use this approach to derive an unbiased estimator for D,

$$\begin{array}{c}\widehat{D}=\frac{1}{n(n-1)}\times \\ [\left(n_1+\frac{n_2}{2}+\frac{n_4}{2}+\frac{n_5}{4}\right)\left(\frac{n_5}{4}+\frac{n_6}{2}+\frac{n_8}{2}+n_9\right)\\ -\left(\frac{n_2}{2}+n_3+\frac{n_5}{4}+\frac{n_6}{2}\right)\left(\frac{n_4}{2}+\frac{n_5}{4}+n_7+\frac{n_8}{2}\right)],\end{array}$$

which simplifies to the known Burrows estimator (Weir, 1979),

$$\widehat{D}=\widehat{\Delta }\equiv \frac{n}{n-1}\tilde{\Delta }.$$

For statistics of higher order than D, such as those in the Hill–Robertson system, expanding these statistics often involves a large number of terms. In practice, we use symbolic computation software to compute our estimators. In some cases the estimators simplify into compact expressions, although in other cases they may remain expansive. However, even when there are many terms, the sums do not consist of large terms of alternating sign, and so computation is stable. Mathematica notebooks are provided as supplementary material, Supplementary Material online.

Simulations of Unlinked Loci

We used fwdpy11 (version 0.4.2) (Thornton 2014) to simulate data with multiple chromosomes and variable population sizes, sample sizes, selfing probabilities, and mutation and recombination rates. To simulate m chromosomes each of length L base pairs with recombination rate c per base pair, we defined m segments of total recombination rate Lc each separated by a binomial point probability of recombination of 0.5. The total mutation rate was then mLu, where u is the per-base mutation rate. fwdpy11 allows the user to define any selfing probability between 0 and 1.

For a given sample size of n diploids, we sampled from the N_e simulated individuals without replacement and assumed data from diploids was unphased. To compute ${\sigma }_D^2$ and σ_Dz, we constructed genotype arrays and used the Parsing features of moments.LD (Ragsdale and Gravel 2019), which makes use of scikit-allel (version 1.2.0) (Miles and Harding 2016), to compute statistics between each pair of chromosomes. We also output the same data in the genepop format, the required input format for NeEstimator (version 2.1) (Do et al. 2014), to compute ${\widehat{N}}_e$ using equations (1) and (2). For comparisons with Do et al. (2014), we considered MAF cutoffs of 0.1 and 0.05, as well as using all SNPs.

Island Fox Data and Analysis

Data

We reanalyzed data for six Channel Island fox populations studied by Funk et al. (2016) (with data deposited at https://datadryad.org/resource/doi:10.5061/dryad.2kn1v; last accessed November 19, 2019). In short, Funk et al. (2016) used Restriction-site Associated DNA sequencing to generate SNP data for between 18 and 46 individuals per population. No reference genome for the island foxes was available at the time, so they generated reference contigs from eight high coverage individuals to map reads from the remaining 192 sequenced individuals. They excluded loci that were called in fewer than half of all individuals and individuals with genotypes for less than half of all loci, and kept only SNPs with MAF greater than 0.1. They also reported only a single SNP per contig, keeping the first SNP for each contig if more than one SNP were observed.

Computing Statistics and N_e

The sequencing and filtering procedure from Funk et al. (2016) resulted in 5,293 SNPs, which were made available at the above URL. We converted the given genepop format to VCF, and used scikit-allel (Miles and Harding 2016) to parse the VCF and our software moments.LD to compute two-locus statistics using the approach described in this paper. We computed both ${\sigma }_D^2$ and σ_Dz for each of the six populations. Because contigs were not mapped to a reference genome, we did not know which chromosome each SNP was on. For this analysis, we assumed all SNPs were unlinked.

We computed ${\widehat{N}}_e=1/3{\sigma }_D^2$ for each population. To compute bootstrapped 95% confidence intervals, we randomly assigned the 5,293 SNPs to 20 groups and computed statistics between all $\left(\begin{array}{c}20\\ 2\end{array}\right)$ pairs of groups, and then sampled the same number of subset pairs with replacement to compute ${\sigma }_D^2$ and σ_Dz. We repeated this 200 times to estimate the sampling distributions and the $2.5-97.5\%$ confidence intervals for each.

Software

Code to compute two-locus statistics in the Hill–Robertson system is packaged with our software moments.LD, a python program that computes expected LD statistics with flexible evolutionary models and performs likelihood-based demographic inference (https://bitbucket.org/simongravel/moments). moments.LD also computes LD statistics from genotype data or VCF files using the approach described in this paper, for either phased or unphased data. Code used to compute and simplify unbiased estimators and python scripts to recreate analyses and figures in this manuscript can be found at https://bitbucket.org/aragsdale/estimateld.