A Traction Force Threshold Signifies Metastatic Phenotypic Change in Multicellular Epithelia

Abstract

Cancer metastasis has be en believed as a genetically programmed process that is commonly marked by biochemical signals. Here using extracellular matrix control of cellular mechanics, we establish that cellular force threshold can also mark in vitro metastatic phenotypic change and malignant transformation in HCT-8 cell colonies. We observed that for prolonged culture time the HCT-8 cell colonies disperse into individual malignant cells, and the metastatic-like dispersion depends on both cell-seeding gel stiffness and colony size. Cellular force microscopies show that gel stiffness and colony size are also two key parameters that modulate cellular forces, suggesting the correlations between the cellular forces and the metastatic phenotypic change. Using our recently developed biophysical model, we construct an extracellular traction phase diagram in the stiffness-size space, filled with experimental data on the colony behavior. From the phase diagram we identify a phase boundary as a traction force threshold above which the metastatic phenotypic transition occurs and below which the cell colonies remain cohesive. Our finding suggests that the traction threshold can be regarded as an effective mechano-marker for the onset of the metastatic-like dispersion and malignant transformation.

Introduction

Cancer metastasis is an enormously complicated process. Recent studies have accumulated evidence that tumors increase their metastatic potential through reciprocal interactions with their microenvironment that consists of various dynamically changing biochemical and biophysical factors¹. On the one hand, cancer progression and metastasis often results in changes in tumor microenvironment, spanning from increased stiffness of extracellular matrix (ECM)^{2, 3} to altered ECM composition⁴ and protein density⁵. On the other, tumor cells sense the bio-chemo-physical cues from their surroundings and respond by activating a cascade of biochemical and biophysical signals^6–8 that in turn regulate cancer progression. As metastasis is commonly believed as the primary reason of cancer mortality, identification and characterization of the markers that signify metastasis is critical to the prevention and treatment of cancer diseases. Indeed, tremendous efforts have been undertaken to identify possible biochemical markers for the onset of metastasis. In contrast, little is known about the role of cellular forces on the onset of metastasis, despite that it is now accepted from the study of mechanobiology that biochemical signaling pathway and cellular force transduction pathway coexist and interact in cancer progression.

Cell migration, particularly the onset of cancer metastasis, involves dynamic generation and transmission of intracellular, intercellular, and extracellular forces^9–14. For cells in isolation, actomyosin contraction is transmitted to integrin-mediated focal adhesions, generating extracellular traction on the ECM. The traction reacts back to the cell, generating cell body stress¹⁵. In multicellular microtissues, contractile forces are transmitted through both focal adhesions and cadherin-mediated adherens junctions, generating extracellular traction on the ECM on the one hand and long-range intercellular tension in the microtissues on the other^16–19. Though stress homeostasis has long been adequately described during cell morphogenesis, survival, and normal functions^20–22, how mechanical force evolves with malignant potential increase and cancer metastasis has remained elusive.

Here we report that cellular force evolution correlates with the metastatic-like dispersion and malignant progression in vitro. We first show that cohesive human colon carcinoma (HCT-8) cell colonies disperse into individual malignant cells upon prolonged culture on polyacrylamide (PAA) gels, and the dispersion is both gel stiffness and colony size dependent: dispersion occurs for cell colonies on stiff gels but not on soft ones; on stiff gels smaller colonies disperse statistically earlier than larger ones. Through advanced traction force microscopy (TFM)¹⁷ and monolayer stress microscopy (MSM)²³, we show that traction force and cell stress at the pre-dispersion stage are also gel stiffness and colony size dependent, manifesting their positive correlation with the dispersion behavior. Using a recently developed biophysical model we generate a traction force phase diagram in the parametric space of gel stiffness and colony size from which we identify a traction force threshold criterion that separates the cohesive and dispersive phenotypes observed in experiments. The combined experimental and modeling analyses reveal that the cellular force can serve as an effective mechano-marker for the onset of the metastatic-like dispersion and malignant progression in the multicellular epithelium.

Results

Dispersion of HCT-8 cell colonies is both gel stiffness and colony size dependent.

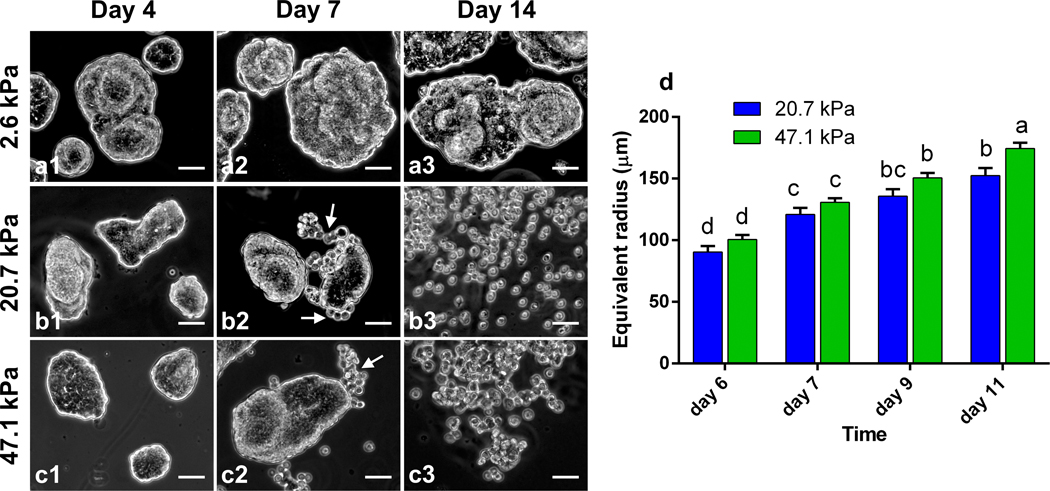
PAA gels of different stiffnesses were prepared (see Methods) and HCT-8 cells were cultured on the gels to examine the dispersion process. For all the PAA gels with Young’s modulus ranging from 1–50 kPa, the cells were able to attach to the substrates, spread and proliferate, and spontaneously adhere to each other to form cohesive colonies of different sizes (e.g., Figs. 1 a1 and b1) within 12 hours. Because of this spontaneity, the colony size spanned from very small (~30 μm in diameter) to fairly large (~300 μm), and the size distribution was dependent on the initial cell seeding density. On 20.7 kPa gels, the colonies continued to grow until day 3, after which the cell proliferation rate was rather low and the sizes of the colonies remained nearly unchanged; after ~6 days of culture, a number of round single cells began to disperse from the periphery of the colonies (Fig. 1b2, Fig. S1 a–c and Video S1). The entire colonies fully dispersed into scattered single cells in about two weeks (Fig. 1b3). Similar dispersion behavior was observed for cell colonies on 47.1 kPa gels (Fig. 1 c1–c3). On soft PAA gels (2.6 kPa), however, the cell colonies grew in a relatively slow rate and they remained cohesive without dispersion throughout the culturing time of 2 weeks (Fig. 1 a1–a3). Gels with stiffness higher than 50 kPa are physiologically irrelevant²⁴ for epithelial cells, and thus not considered here. These results suggest that colony dispersion is dependent on the hydrogel matrix stiffness. The colony dispersion was accompanied with malignant phenotypic change of the cells, marked by the abnormally shaped nuclei (Fig. S2), and more than 2-fold reduced E-cadherin expression level (Fig. S3) of the dispersed cells, all of which are hallmarks of the invasive phenotype of metastatic cancer cells^25–27. The phenotype change was also confirmed by evaluating gene and protein expression, in vitro invasiveness using cell invasion assay, and in vivo metastatic activity in nude mice using a splenic implantation model published elsewhere²⁷. In addition to the overexpression of metastasis-associated genes, dispersed cells display significantly enhanced basement membrane invasion in cell invasion assays and were able to generate significantly more metastasis sites in spleen, liver, and other tissues in the in vivo metastatic assays²⁷. Viability analysis showed that the dispersed cells remained alive (Fig. S4).

Fig. 1.

Substrate-stiffness and colony size dependent dispersion of HCT-8 cell colonies. (a1-a3) HCT-8 cell colonies on 2.6 kPa gels at day 4, day 7 and day 14 of culture. HCT-8 colonies remained cohesive without dispersion throughout the culture period of two weeks. (b1-b3) HCT-8 cell colonies on 20.7 kPa gels at day 4, day 7 and day 14 of culture. (b1) HCT-8 cells at day 4 of culture on the 20.7 kPa gel. HCT-8 cells formed isolated cell colonies of different sizes and morphologies. (b2) HCT-8 cells at day 7 of culture on the 20.7 kPa gel. Cells at the periphery of one of the cell colonies dispersed from their mother colony, as indicated by the arrows. (b3) HCT-8 cells at two weeks of culture on the 20.7 kPa gel. All the colonies dispersed into individual cells. (c1-c3) HCT-8 cell colonies on 47.1 kPa gels at day 4, day 7 and day 14 of culture. HCT-8 cells exhibited similar dispersion behavior as seen on 20.7 kPa gels. (d) Dispersion kinetics of HCT-8 colonies on the 20.7 and 47.1 kPa gels. Dispersion kinetics is colony size dependent as well as gel stiffness dependent. Scale bar: 50 μm. Two-way ANOVA (α=0.05) with Tukey’s post-hoc test was employed for analysis. Error bars denote standard error of the mean. Any two groups with a common letter are not significantly different, while any two groups without a common letter are significantly different.

While the stiffness dependent dispersion and phenotypic change have been previously observed²⁸, we also noted that the dispersion kinetics is colony-size dependent. As the cell colonies are irregularly shaped, the equivalent radius $R=\sqrt{A/\pi }$ is here used as a measure of the colony size, where $A$ is the area of the colony. We recorded the sizes of the cell colonies at the time when dispersion just started on the two relatively stiff gels, i.e., the onset time. In general, dispersion in smaller colonies occurred statistically earlier than in larger colonies (Fig. 1d). For examples, on 20.7 kPa gel, dispersion for a ∼90 μm colony is expected to occur at day 6, but at day 9 for a ∼130 μm colony (Fig. S1). The dispersion kinetics of the colonies on 47.1 kPa gels showed no statistical difference from that on 20.7 kPa gels. The co-dependence of the gel stiffness and colony size motivated our search of a single marker for the onset of the dispersion process.

Gel stiffness and colony size correlate to traction force and intercellular tension at the pre-dispersion stage.

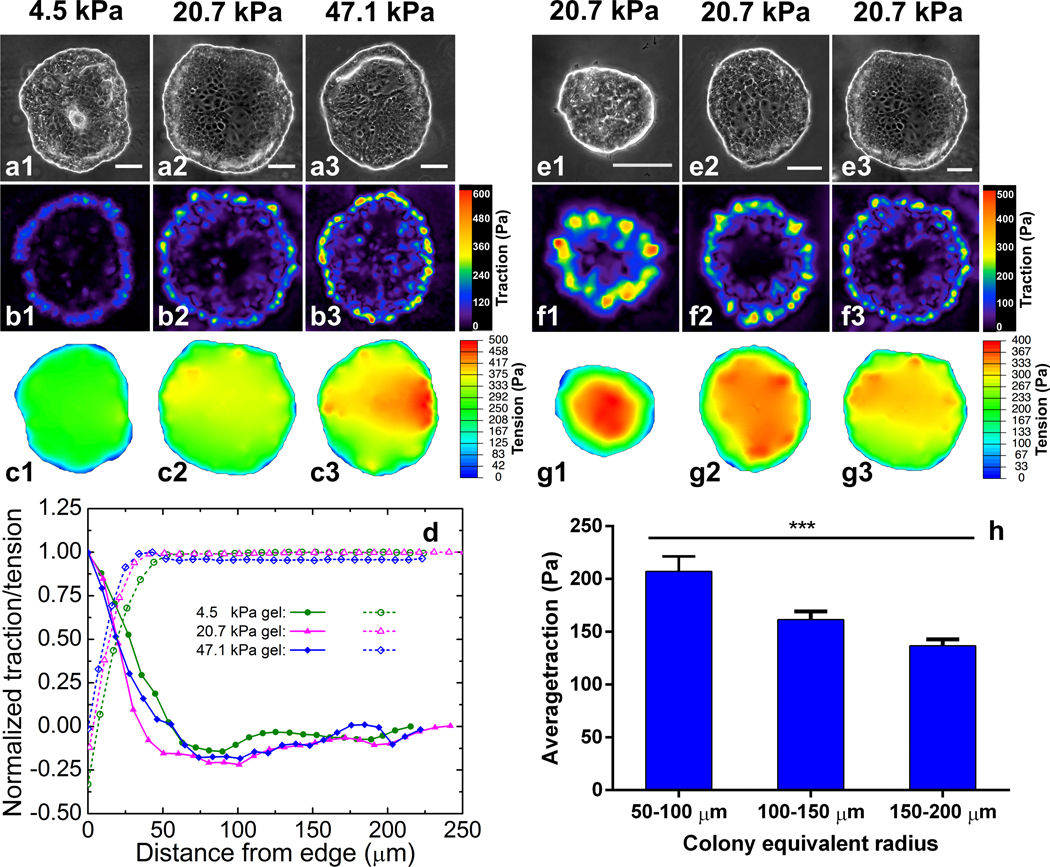
Since the tumor progression-associated dispersion process depends on both substrate stiffness and colony size, we then asked whether there is a unified biomechanical marker for the dispersion. As numerous studies have identified traction force as a dependent variable to substrate stiffness, traction force may be a target to explore. To correlate the traction force with substrate stiffness and colony size, we employed TFM²⁹ to measure the traction force 𝑇 (force per unit area, a 2D vector field) on the gels exerted by the cell colonies (SI text). The measurements revealed that at the pre-dispersion stage (day 2 of culture) traction force was localized at the boundary layers of the cell colonies and decayed rapidly from the periphery to the center, with a decay length scale of ∼50 μm. This characteristic is consistent with recent theoretical studies^{30, 31}. The characteristic decay length scale, i.e., the width of the boundary layer, is ~50 μm (about the width of 5 HCT-8 cells), independent of gel stiffness (Fig. 2 b1–b3 and d). Here the traction force is presented as the magnitude of the force vector. Consistent with the traction force distribution, the morphology of the cells at the boundary layer was noticeably different from that of the interior cells of the colonies. Cells at the interior of the colonies spread more than those at the boundary layers (Fig. S5). The interior region of the cell colonies was monolayer, while at the boundary layer of the cell colonies cells piled up into double layers. These morphological differences also indicate heterogeneous intercellular tension levels in the cell colonies. The maximum and the average traction forces are dependent on both gel stiffness (Fig. 2 b1–b3) and colony size (Fig. 2 f1–f3). Here for each colony the traction force is averaged over the 50 μm boundary layer, but not on the entire colony. The higher the gel stiffness, the higher the maximum and the average traction forces at the boundary layer of the cell colonies (Fig. 2, Left panel). The maximum traction force $T_{max}$ was 200.0±55.4 Pa on 4.5 kPa gel, 428.2±98.8 Pa on 20.7 kPa gel, and 571.6±132.5 Pa on 47.1 kPa gel, respectively. The average traction force within the boundary layer was 104.3±19.7 Pa on 4.5 kPa gel, 165.7±38.2 Pa on 20.7 kPa gel, 190.0±40.3 Pa on 47.1 kPa gel, respectively. For cell colonies with high circularity, we decompose the traction force into the radial ($T_r$) and tangential ($T_{\theta }$) components and notice that the tangent component is negligibly small compared to the radial component, i.e., $T_{\theta }\le T_r$, in the boundary layer (Fig. S6).

Fig. 2.

Dependence of traction force and intercellular tension at day 2 of culture on both gel stiffness and colony size. (a and e) Phase contrast images of cell colonies on different gel stiffness (a, with gel stiffness of 4.5 kPa, 20.7 kPa and 47.1 kPa, respectively) and with different sizes (e, on 20.7 kPa gels). Scale bar: 100 μm. (b and f) Traction force distributions of the cell colonies. For all the cases, the high traction forces are localized at the boundary layers of the cell colonies and coincide with the regions with high convex curvature. The stiffer the gels, the higher the average traction force (b); the small the cell colonies, the higher average traction force (f). (c and g) Intercellular tension (i.e., hydrostatic stress) distributions of the cell colonies. Intercellular tension ramps up from the boundary layer and reaches nearly uniform tension at the interior of the cell colonies. The uniform tension is proportional to the traction force at the boundary layer. (d) Spatial distribution of traction force (solid line) and intercellular tension (dash line), normalized by their maxima, respectively. (h) The average traction force at the boundary layer (the summation of traction force in the region within 50 μm from colony boundary divided by the area of the region). The average traction force is colony size dependent. ***p<0.001 (one-way ANOVA). Error bars denote standard error of the mean (n≥10).

The high traction forces were localized at regions of high convex curvature at the periphery of the cell colonies³², as consistently seen in all the colonies in Figs. 2 b1–b3 and f1–f3. In contrast, the traction force nearly vanished at the concave regions at the periphery of the cell colonies. The curvature-dependent traction localization suggests the role of line tension (regarding the cell colonies as 2D films) in the cellular force distribution, leading to the colony size dependence of the traction. The smaller the colony, the higher the average curvature at the periphery of the cell colonies, and hence the higher traction (Fig. 2 f1–f3). We have systematically measured the traction force of different sized colonies seeded on 20.7 kPa gels. For colonies of size ranging from 50–250 μm, the average traction force at the boundary layer monotonically decreases with colony size (Fig. 2h). Colonies with sizes less than 50 μm were rarely seen at the dispersion stage and thus their traction forces were not considered at the pre-dispersion stage. To summarize, the traction force at the pre-dispersion stage correlates to both the hydrogel stiffness and the colony size. Since the traction force unifies the effects of substrate stiffness and colony size, these results suggest that traction force may serve as the mechanical marker for the onset of the metastasis process.

The intracellular contraction generated by actomyosin motors is transmitted to both the focal adhesion points and cell-cell adherens junctions. The crosstalk between these two types of adhesion complexes dictates the distribution of the extracellular traction and intercellular tension^{18, 33}. We employed monolayer stress microscopy (MSM)^{14, 23} to quantify the stress in the cell colonies (SI text). We first digitalized the geometry of the cell colonies, which are simplified as an elastic, isotropic monolayer with homogeneous thickness (Fig. S7), and treat the measured traction force as a boundary condition. Solving the force balance equation in elasticity by the finite element method gives rise to the monolayer stress, which indicates both intercellular tension and cell colony stress. As shown in Figs. 2 c1–c3 and g1–g3, the calculated intercellular tension and colony stress ramps up from the boundary layer of the cell colonies and reaches a nearly uniform value at the interior of the cell colonies. Our microscopy analyses showed that the intercellular tension and colony stress at the interior is proportional to average traction force at the boundary layer, dictated by the force balance.

Spatiotemporal evolution of cellular forces correlates with colony dispersion.

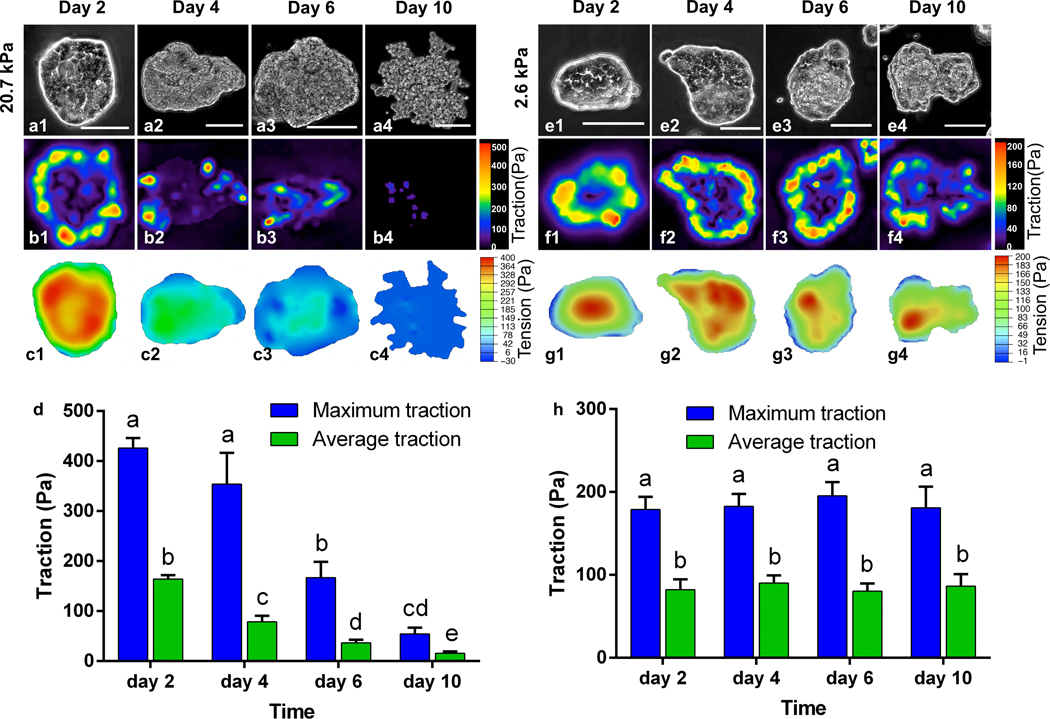
Cell scattering at the periphery disrupts the traction force and alters the intercellular tension of the colonies, which explains the sequential periphery-to-center dispersion. Figure 3 displays the spatiotemporal evolution of the extracellular traction and intercellular tension on 20.7 kPa (a-d) and 2.6 kPa gels (e-h), respectively. On 20.7 kPa gels, as the culture time went on, the traction force shifted from the periphery to the center; its magnitude (both the maximum and average) also decreased (Fig. 3 b1–b4 and d). Consequently, the area of uniform tension (red regions) reduced as dispersion progressed (Fig. 3 c1–c4). The magnitude of the intercellular tension also decreased (Fig. 3 c1–c4) as the boundary cells detached from the parent colony and relaxed their traction. The traction force completely vanished as the cell colonies were fully dispersed at day 10 of culture. In contrast, the periphery-to-center shift of the traction was absent for the cell colonies cultured on 2.6 kPa gels. Instead, both the extracellular traction (Fig. 3 f1–f4 and h) and intercellular tension (Fig. 3 g1–g4) maintained at nearly the same levels at the periphery and the interior of the colonies, respectively, throughout a culture time of 10 days. These results conclude that as cells disperse and migrate away from the colony, the cellular forces of the colony decrease, resulting in the correlation between the evolution of cellular forces and the colony dispersion process. Thus, the decreasing trend of the cellular forces may serve as a mechano-marker for the undergoing dispersion behavior.

Fig. 3.

Spatiotemporal evolution of traction and intercellular tension in cell colonies cultured on 20.7 kPa (Left panel, a-d) and 2.6 kPa gels (Right panel, e-h). (a and e) Phase contrast images; (b and f) traction force distributions; (c and g) intercellular tension distributions; (d and h) temporal evolution of traction force in HCT-8 colonies. On 20.7 kPa gels, the traction force shifts from the periphery to the center from day 1 to day 6, and completely vanishes on day 10, underlying the dispersion of cell colonies (b). Such periphery-to-center shift of the traction force is absent in the cell colonies cultured on 2.6 kPa gels (f). Correspondingly, the cell colonies cultured on 2.6 kPa gels maintains uniform tension inside the colonies (g), while those on 20.7 kPa gels lose the tension as the dispersion progresses (c). Scale bar: 100 μm. Two-way ANOVA (α=0.05) with Tukey’s post-hoc test was employed for analysis. Any two groups with a common letter are not significantly different, while any two groups without a common letter are significantly different.

Inhibiting cell contractility suppresses dispersion.

To further demonstrate the close correlation between cellular forces and the dispersion behavior, we next cultured the HCT-8 cells on stiff gels but with inhibited cell contractility using non-muscle myosin II inhibitor blebbistatin. Specifically, HCT-8 cells were seeded on 20.7 kPa gels and 12 hours later treated with 6 μM blebbistatin (Fig. 4a). Traction forces were measured at allotted times. Our measurements show that both maximum and average traction forces at the boundary layer measured at day 2 of culture time decreased by more than 3-fold due to the inhibition of cell contractility as compared to the untreated cell colonies on 20.7 kPa gels (Fig. 4 b1–b4). The level of the traction force was close to that of the cell colonies cultured on 4.5 kPa gels without blebbistatin treatment. The relatively low traction force is maintained without statistically significant differences during prolonged culture time of 10 days (see Fig. S8). Corresponding to the low traction force, the cell colonies remained cohesive over the entire culture time (Fig. 4 a1–a4), in contrast to the observed HCT-8 colony dispersion behavior on the same gel stiffness without the treatment. The blebbistatin treatment experiment confirms the strong correlation between the cellular forces at the early stage and the dispersion behavior of the HCT-8 cell colonies.

Fig. 4.

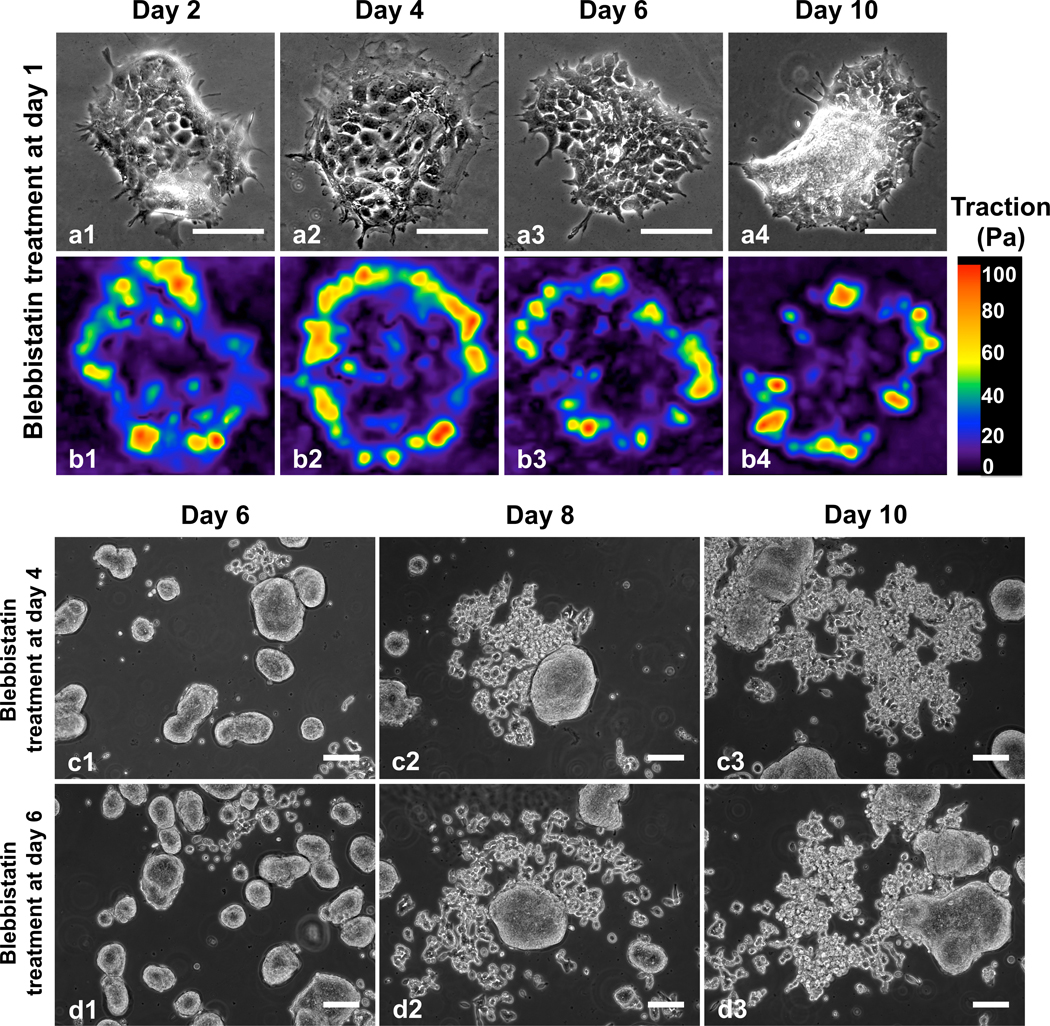
Dispersion behaviors of the HCT-8 colonies treated with 6 μM blebbistatin at different culture times on 20.7 kPa gels. (a) Cell colonies treated with blebbistatin at day 1. Colonies remained cohesive for a culture time of 10 days. (b) Corresponding traction forces of the colonies in (a). Relatively low traction force was maintained at the boundary layer of the cell colonies with blebbistatin treatment at day 1, showing the force-driving process. (c and d) Cell colonies treated with blebbistatin at day 4 (c) and day 6 (d). Dispersion occurred for cell colonies treated with blebbistatin at day 4 or day 6. Here the images show the representative colonies from parallel samples at different culture times, not the dynamics of one colony over time. Scale bar: 100 μm.

Interestingly, the dispersion behavior was dependent on the time at which the cell colonies were treated with myosin II inhibitor. While treating the colonies with 6 μM blebbistatin on day 1 of culture time inhibited the dispersion on 20.7 kPa gels (Fig. 4 a1–a4), treatment on day 4 (Fig. 4 c1–c3) or day 6 (Fig. 4 d1–d3) of culture time failed to inhibit the dispersion of HCT-8 colonies on 20.7 kPa gels. We recall that in the absence of the blebbistatin treatment the dispersion did not start for any of the colonies on the entire hydrogel (20.7 kPa) at day 4; at day 6, the dispersion occurred in only few small colonies but not in most of the colonies. This result agrees with our findings that while the cellular forces at the early pre-dispersion stage correlate with the dispersion behavior and thus can be regarded as a mechano-marker for the dispersion, cellular forces at later stage cannot, indicating that the decision of the metastasis phenotype change is made at the early stage correlating with cellular forces.

Cellular-force threshold exists at pre-dispersion stage for the dispersion behavior.

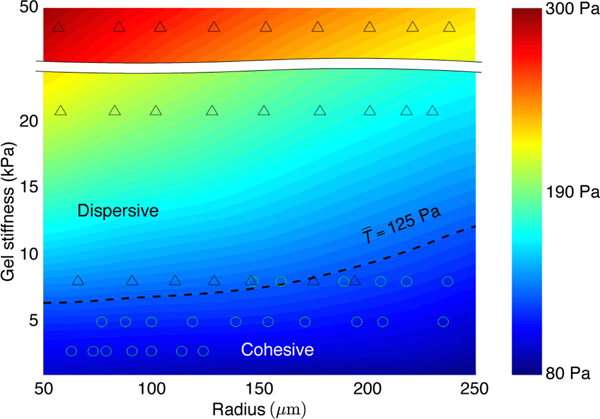
Finally, to elucidate whether there is a cellular force criterion that predicts the onset of the colony dispersion, we employ a recently established biophysical model to simulate the extracellular traction and intercellular tension with given hydrogel stiffness and the size of cell colonies³⁴. The biophysical model couples mechanical equilibrium conditions of the cell monolayer and the substrate through the traction force, which exerts on both the monolayer and the substrate. The distribution of focal adhesion points, which transmit the traction force, is in turn modulated by traction force, presenting a positive feedback. Since the biophysical model incorporates the molecular structures, it is molecularly based and simultaneously predicts the extracellular traction and monolayer stress³⁴. We here focus on the traction forces at the pre-dispersion stage during which morphologies of the cell colonies undergo little changes.

The biophysical model allows us to construct a phase diagram of average traction at the boundary layer ($\stackrel{-}{T}$) in the parametric space of gel stiffness (2 to 50 kPa) and colony size (50 to 250 μm radius), as shown in Fig. 5. Based on our experimental observations of a large number of colony samples, we mark down those dispersed cell colonies by “Δ” and those cohesive ones by “o” in the phase diagram. From the overlapping experimental data and modeling results, we identify a phase boundary that separates the cohesive and dispersive behaviors of the cell colonies, as marked by the dashed line, representing the force-threshold criterion, $\stackrel{-}{T}=T_c\approx 125$ Pa. This suggests a traction force-threshold criterion for the in vitro metastatic behavior: there exists a traction force threshold at the early stage of culture that signifies the onset of the metastatic-like dispersion and malignant progression of the HCT-8 cell colonies:

$$\stackrel{-}{T}\ge T_c.$$ (1)

Fig. 5.

Phase diagram of average traction at the boundary layer ($\stackrel{-}{T}$) in the stiffness-size plane computed by the biophysical model, overlapped with the dispersion behavior of a large number of cell colonies observed in the experiments. The dashed lines represent constant traction contours in the parametric space. A phase boundary of constant traction $T_c\cong 125$ Pa, separating the dispersive and cohesive cell colonies, is identified, representing a force-threshold criterion for the malignant phenotypic change.

Dispersion of the cell colonies initiates when the condition in Eq. (1) is met; the cell colonies otherwise remain cohesive. The phase diagram further suggests that at given gel stiffness, smaller colonies have a higher metastatic potential; while at a given colony radius, increasing the gel stiffness would drive the metastatic phenotypic change.

Discussions

Our in vitro experiments demonstrate that both the cellular forces (extracellular traction, intercellular tension, and intracellular contraction) and the tumor progression-associated colony dispersion depend on gel stiffness and colony size in a similar manner, and the dispersion behavior correlates with the cellular forces. However, it remains to identify the molecular mechanisms as to how cellular forces can foster the malignant phenotype change. As the tumor progression-associated dispersion behavior observed here correlates with sustained high cellular forces, this transition is unlikely a passive pulling-apart process, but rather an active process that involves mechanotransduction. It has been well established that mechanosensation of mechanical cues of the ECM through cell surface integrins activate the FAK/Rho/ROCK pathway, leading to increased actomyosin contractility³⁵. The increased intracellular contraction feeds back to the mechanotransduction pathway by promoting integrin clustering, focal adhesion assembly, and cytoskeletal remodeling, forming a positive feedback loop. The intracellular contraction transmits to the ECM, cell-cell adherens junctions, and cell body, generating counter-balancing extracellular traction, intercellular tension, and cell body stress. Since FAK as the early response in the mechanotransduction pathway activates and transduces the downstream intracellular signaling cascades, the activation level of FAK signifies the generated cellular forces. Indeed, immunofluorescence of FAK confirms the positive correlation between FAKpY397 expression and the cellular force distribution (see Fig. S9).

Our experimental studies and modeling analyses show that hydrogel stiffness and colony size are two key parameters that modulate cellular force landscapes, which signify the malignant phenotypic change and colony dispersion. This two-factor phenomenon suggests that the force-threshold marker holds irrespective of how the cellular forces are generated. That is, similar to the gel stiffness and colony size modulated cellular forces, other mechanical forces such as compression, tension, and flow shear applied to the cells may trigger the phenotypic change. In addition, since all cellular forces, namely intracellular contraction, intercellular tension, and extracellular traction, are correlated to each other, and thus they all correlate with gel stiffness and colony size. It is thus plausible to conclude that all cellular forces at pre-dispersion stage can be regarded as mechano-signals or mechano-markers for the onset of the metastatic-like dispersion in the multicellular epithelium.

It would be interesting to explore whether such a mechano-marker would exist for other cell lines. For non-cancerous cells, no experimental evidence has shown that substrate stiffness can trigger malignant transformation. However, a recent experiment has demonstrated that mechanically stretching a tissue can drive the non-cancerous cells within the tissue into a malignant phenotype, which supports the critical role of mechanical force in signifying and driving malignant transformation³⁶. For cancerous cell lines, we have observed that HeLa cells do not form cohesive colonies when culturing on the PAA hydrogels, suggesting that the mechano-marker is inapplicable to the HeLa cells³⁷. This is probably because the HeLa cells are already highly malignant. However, recent studies have demonstrated the same dispersion behavior in colon and prostate cancerous cell lines²⁷. It is possible that similar mechano-marker can be identified for these cell lines. Detailed experiments on these cell lines are needed to demonstrate the broader applicability of the mechano-marker.

Conclusions

In summary, we have demonstrated that the traction force threshold is an effective mechano-marker for the onset of the metastatic-like dispersion and malignant phenotype change in vitro in the HCT-8 multicellular epithelium. Different from the biochemical markers (e.g., over-expressed proteins) and elastic markers (reduced cell stiffness or stiffened tumor microenvironment) for cancer screening and detection^38–41, the mechanical criterion identified here present at an early stage of progression of malignancy, thereby opening up new insights in understanding force-regulated malignant activities and tumor progression.