Parallel Transmission for Ultrahigh Field MRI

Abstract

Magnetic resonance imaging (MRI) has been driven toward ultrahigh magnetic fields (UHF) in order to benefit from correspondingly higher signal-to-noise ratio and spectral resolution. Technological challenges associated with UHF, such as increased radiofrequency (RF) energy deposition and RF excitation inhomogeneity, limit realization of the full potential of these benefits. Parallel RF transmission (pTx) enables decreases in the inhomogeneity of RF excitations and in RF energy deposition by using multiple-transmit RF coils driven independently and operating simultaneously. pTx plays a fundamental role in UHF MRI by bringing the potential applications of UHF into reality. In this review article, we review the recent developments in pTx pulse design and RF safety in pTx. Simultaneous multislice imaging and inner volume imaging using pTx are reviewed with a focus on UHF applications. Emerging pTx design approaches using improved pTx design frameworks and calibrations are reviewed together with calibration-free approaches that remove the necessity of time-consuming calibrations necessary for successful pTx. Lastly, we focus on the safety of pTx that is improved by using intersubject variability analysis, proactively managing pTx and temperature-based pTx approaches.

The promise for higher signal-to-noise ratio (SNR), acquisition speed, and spatial resolution has been the driving force for ultrahigh field (UHF) MRI systems [B₀ ≥ 7 Tesla (T)].^1–3 UHF MRI is technically challenging due to inhomogeneities of the radiofrequency (RF) field and the increase in specific absorption rate (SAR) per unit flip angle.⁴ Inhomogeneity of the appropriately polarized transverse magnetic field B₁⁺ hampers clinical use of UHF MRI systems. This RF inhomogeneity is related to the reduction in RF wavelength at high field and causes inhomogeneities of the image contrast and SNR, which diminishes the quality and diagnostic value of MR images. In addition, the interaction of the electromagnetic (EM) field with dielectric tissues tend to exacerbate inhomogeneities in RF power deposition, which could potentially result in dangerous local hot-spots. These challenges have forced the MR community to go beyond traditional low-field approaches and to research new possibilities. Advances in RF array design have overcome some of the technical challenges to enable routine UHF imaging of brain and peripheral skeletal sites at 7T.^2,5 These developments resulted in a clinically approved 7T MR scanner for selected neurological and musculoskeletal applications in 2017.

During the last decade, parallel RF transmission (pTx) techniques^6,7 have been shown to offer promising solutions to the challenges of UHF by enabling decreases in B₁⁺ inhomogeneity and SAR. pTx is a developing technique and continued progress is required in order to fully explore the potential of UHF MRI in clinical applications. The fundamental concepts of pTx with the explanation of the technique and latest developments until 2015 were explained in detail in a review article by Padormo et al.⁸ We will give a brief overview of the general concepts and approaches for pTx and refer the reader to this article to review the basics of pTx and various pTx strategies developed before 2015 in detail. In this review article, we focus on the recent developments in pTx techniques that have been bringing us closer to the clinical use of UHF MRI. Relevant articles were identified through a PubMed search of articles published after 2015 using “parallel transmission” or “parallel transmit” as search terms. Recent research using pTx technique can be identified in overlapping 2 major categories: (1) pTx pulse design to mitigate B₁⁺ inhomogeneity and/or reduce SAR and (2) the safe use of pTx.

pTx PULSE DESIGN

In order to overcome patient-induced inhomogeneous RF excitation at UHF, several RF excitation methods have been proposed using multiple RF transmit coils. The first method was RF shimming,^4,9,10 in which multielement transmit coil arrays are driven with a single RF waveform by adjusting phase and amplitude in individual coils independently. This technique has been successful in improving the B₁⁺ homogeneity in excited volumes, especially in small local regions-of-interest (ROIs).¹¹ However, the efficiency of RF shimming diminishes as the ROI becomes larger. Thus, new approaches have been introduced to mitigate B₁⁺ inhomogeneities in large ROIs. For example, static RF shimming is improved by dynamically changing the RF shim weights,^12,13 which has been shown to reduce B₁⁺ inhomogeneity. Later, pTx techniques^6,7 combined and extended the benefits of these 2 approaches. pTx has been used to compensate for patient-induced RF inhomogeneities at UHF. In pTx, individual elements of multielement transmit coils are driven simultaneously with distinct tailored RF pulses sharing a common gradient waveform. The additional degrees of freedom available in pTx pulses can be used to shorten multidimensional pulses, improve spatial definition of the excitation pattern, and decrease RF power deposition.

Even though the pTx offers a means of overcoming technical problems associated with UHF, the technical development stage of parallel RF excitation has been slow compared with that experienced in the field of parallel MR reception.^14,15 The potential of pTx has not been fully explored in human studies due to the complexity and cost of additional equipment required, the computational complexity of designing RF pulses, especially for large-tip-angle (LTA) pulses, and importantly, the need for a real-time SAR/temperature assessment to ensure patient safety. The requirement of an additional RF pulse synthesizer and amplifier for each transmit channel increases the cost of parallel transmit equipment, as the number of transmit channels increases. The cost of parallel RF transmit systems is decreasing, as add-on prototype systems are replaced with fully integrated ones. Since the introduction of the first pTx pulse designs, various new approaches to the design of pTx pulses with reduced computational complexity have been proposed, first for small-tip-angle (STA)^16–19 and later for LTA.^20–22 Although the developments in pTx pulse design have been shown to mitigate B₁⁺ inhomogeneity effectively and enable application-specific tailored excitation profiles, the usage of pTx in a clinical setting is still limited to the lower field strengths (≤3T) due to concerns about SAR.

Simultaneous Multislice (SMS) pTx

In recent years, simultaneous multislice (SMS)²³ imaging has been extensively used in single RF excitation systems for scan time reductions in brain imaging, thanks to the advancements in high-field RF excitation and parallel imaging techniques.^24,25 SMS technique uses a multiband (MB) composite RF pulse with a slice-selective gradient to simultaneously excite multiple slice planes and parallel imaging techniques to distinguish the acquired aliased signal from multiple slice planes. Scan time reduction is especially critical in diffusion-weighted imaging and functional MRI improving the blood oxygenation level dependent contrast, SNR, and spatial resolution. Incorporating SMS techniques for achieving such benefits at UHF is limited by the inhomogeneous B₁⁺ field and high energy requirements of MB RF pulses leading to high SAR. Recent research has focused on solving these problems to bring the benefits of SMS techniques to UHF MRI.

pTx has been combined with SMS techniques in order to provide uniform excitations in multiple slices/slabs and to reduce the power demand/SAR of MB RF pulses. First, Wu et al²⁶ applied RF shimming to mitigate B₁⁺ inhomogeneity in multichannel MB excitation by finding a global RF magnitude and phase modulations for each channel that are applied to all the bands simultaneously. This type of RF shimming can be realized by using phase shifters and attenuators on a single-channel transmit system. In addition, the RF shimming approach was extended to calculate RF shim weights independently for each transmit channel and excited slice (lets abbreviate this by SMS-pTx). This extension necessitates the use of full pTx hardware. It was shown that the use of the more flexible RF shimming weight calculation approach using pTx system provides a more homogeneous flip angle patterns than global RF shimming alone. All MB RF pulses were designed using a single-spoke k-space traversal without using gradient encoding in the transverse plane. The power demand of the MB pulses was controlled by regularizing the average power of the total MB pulse. In another approach, Poser et al²⁷ used localized sensitivities of the transmit elements to reduce SAR while designing MB RF pulses for brain imaging. It was shown that the 8-channel pTx array with elements distributed in 2 rows in the slice direction can achieve the same mean flip angles with 30% reduction in RF power compared with conventional MB RF pulses. Recent research in SMS imaging using pTx at UHF focuses on improving the MB pulse design via incorporating multispokes, optimizing the spokes location,²⁸ moving toward LTA regimes,²⁹ and explicitly controlling SAR in addition to RF power.³⁰ Moreover, the feasibility of SMS imaging with pTx MB excitations has been demonstrated in the torso for cardiac MRI at 7T.³¹

Sharma et al²⁸ extended the design of MB RF pulses by optimizing the spokes’ k-space trajectory and the target in-plane phase patterns of each slice during calculation of the shim weights. They performed optimization using an interleaved greedy and local method by extending the STA spokes pulse design to the MB case. Moreover, the peak power of the pulses was controlled by solving a minmax problem after the MB RF pulse design incorporating Tikhonov-regularized average power. Jointly optimizing RF pulses, the target excitation patterns and the k-space trajectory resulted in improved flip angle homogeneity and controlled peak power for brain imaging at 7T.

In early applications of SMS-pTx, the peak and average power were reduced via Tikhonov regularization during RF pulse design. This achieves a control over power demands of MB RF pulses; however, it does not guarantee SAR reduction during design of SMS-pTx pulse. Unlike single-channel transmit systems, the control of RF power does not necessarily mean the control over SAR. To overcome this problem in previous SMS-pTx approaches, Guerin et al³⁰ proposed an MB RF pulse design method that explicitly controls the peak power, local SAR, and global SAR using simulated compressed SAR virtual observation points (VOPs). They have shown that the control of average power by Tikhonov regularization results in pulses that violate the hardware and SAR safety limits in many of the simulations performed at 7T head and 3T body. These findings for SMS-pTx approaches support the previous investigations that proposed to control the SAR explicitly during pTx RF pulse design.

All SMS-pTx pulse design approaches described above are based on STA approximation. Gras et al²⁹ proposed a method that covers the small and large flip angle regimes by replacing the numerical integration of Bloch equations with an analytical approximation derived from Average Hamiltonian Theory. This approximation provides a reduced computational burden and sufficient accuracy. Combination of joint optimization of spokes locations and RF pulses with explicit peak and average RF power, and the global and local SAR constraints are used to design SMS-pTx pulses for high-resolution T₂*-weighted 2D MRI protocol for a near whole-brain coverage. This implementation of LTA SMS-pTx approach is valuable for mitigating B₁⁺ inhomogeneities in SAR-demanding protocols.

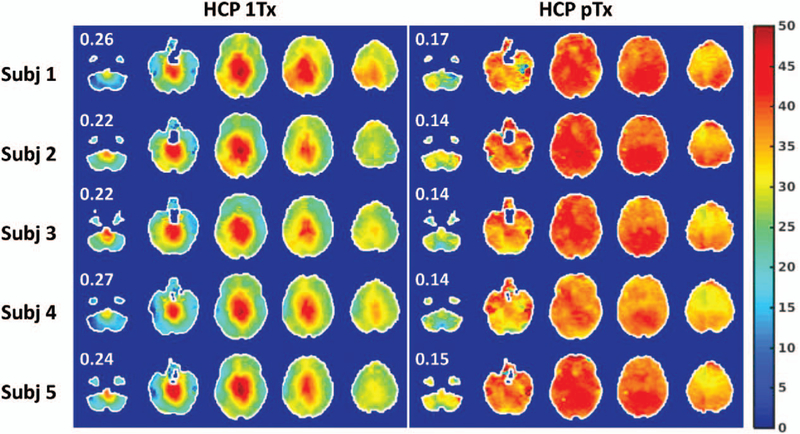
SMS-pTx pulse design was expanded to slab-wise framework from slice-specific pulse designs.²⁰ Time required for calibration scans, pulse calculation, and sequence preparation is drastically reduced with comparable RF performance for the head scans at 7T. This approach was recently used in whole-brain resting-state functional MRI acquisition³² at 7T and demonstrated the improvements on flip angle uniformity (Fig. 1), increased temporal SNR, enhancement in functional contrast-to-noise ratio, and more importantly lead to a better estimation of functional connectivity of brain. Moreover, the high-resolution whole-brain diffusion MRI at 7T was demonstrated with slab-wise framework with improved flip angle homogeneity and slice acceleration.³³

FIGURE 1.

Flip angle homogeneity comparison between single-channel excitation and 8-channel pTx for SMS brain imaging at 7T. Flip angle maps are shown in degrees using 5 gapped axial slices, with the number reported being the coefficient of variation (ie, std/mean) of the flip angles across the whole brain. pTx substantially improved flip angle homogeneities across the whole brain, with the coefficient of variation being reduced on average by 39%. Reprinted with permission from Neuroimage 2019; 184:396–408.

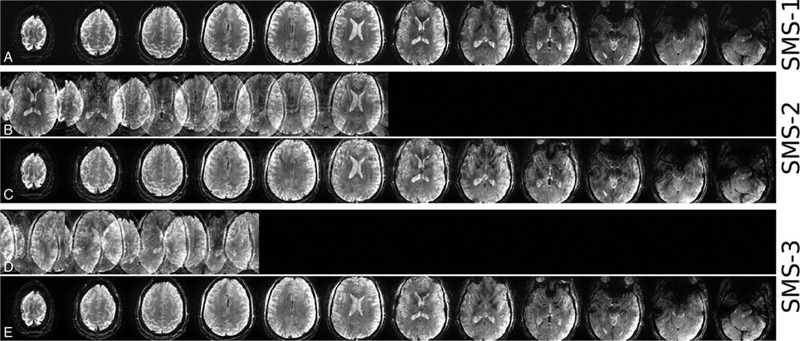
Recently, the use of the SMS-pTx approach has started to move beyond 7T brain imaging to higher field brain imaging and imaging of other organs. The inhomogeneity correction at 9.4T was successfully demonstrated for high-resolution (in-plane 0.28 × 0.28 mm²) in vivo brain imaging (Fig. 2).³⁴ The use of SMS-pTx also enabled shorter scans for near full brain coverage to a clinically acceptable time of under 7 minutes. SMS-pTx in dynamic cardiac MRI at 7Twas implemented to address the contrast heterogeneity for large slice coverage in cardiac MRI performed under breath-hold.³¹ Following the rapid extension of SMS techniques into clinical imaging,^24,25 we expect that the use of SMS-pTx approaches will continue to grow rapidly at UHF as well. In recent years, SMS-pTx has been shown to provide solutions to some of the technical problems associated with UHF-MRI. In a recent ISMRM challenge,³⁵ researchers competed to design the shortest SMS refocusing pulse achieving 5.1 times shorter pulse durations than conventional approaches, which highlights the importance of continued research progress on pTx pulse design methods.

FIGURE 2.

In vivo high-resolution SMS-GRE images acquired at 9.4 T using 16-channel dual row transmit and 31-channel receive array with 3-spoke (A) single-band, (B, C) SMS-2, and (D, E) SMS-3 excitations. Rows b and d show the SMS images before slice-GRAPPA reconstruction. Reprinted with permission from Magn Reson Med 2017; 78:1050–1058.

Inner Volume Imaging (IVI)

Apart from SAR and B₁⁺ homogeneity considerations, another emerging area of research in pTx involves the use of a transmit array for tailored regional excitations. For instance, by using accelerated multidimensional pTx, inner-volume excitations with high spatial selectivity have been experimentally realized³⁶ at UHF. Inner-volume excitation is expected to reduce total signal acquisition time or increase resolution for a constant acquisition time by reducing the extent of the volume that needs to be encoded to form an image. In addition, smaller inner-volume excitations tend to result in lower SAR for small acceleration factors,³⁷ which increases the importance of inner-volume excitations at UHF.

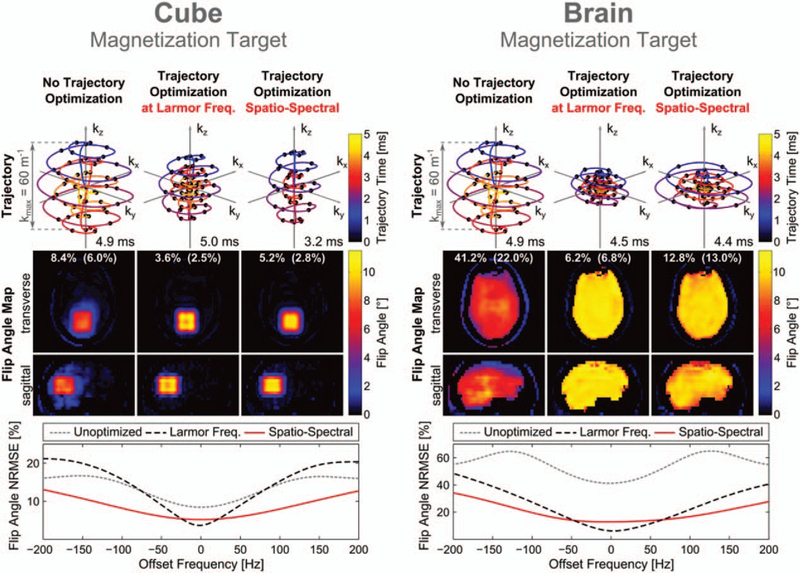
The use of pTx at UHF for excitations using 3D k-space trajectories was first realized to excite rat brain and kidneys on a 7Tanimal scanner where the powerful gradient systems enabled very short 3.2 ms pTx pulses.³⁶ Later, selective excitations for arbitrary 3D targets have been proposed for in vivo imaging at human scanners. One of the key aspects of inner volume imaging (IVI) is the design of excitation k-space trajectory. Several design methods have been proposed for optimizing the 3D excitation k-space trajectory to aim for shorter and more robust pTx pulse design. The parametrization of excitation k-space has been proposed using several control points and selecting the most contributed ones via greedy optimization in 2D³⁸ and its extension in 3D.³⁹ After selecting k-space points, the time optimal excitation trajectory design⁴⁰ obeying gradient amplitude and slew rate limits is followed by pTx pulse design. Recently, Davids et al⁴¹ extended the parametrization of the excitation k-space to a small number of shape parameters following the developments in k-space trajectory design in reception. Joint optimization of the STA pTx pulse and gradient waveforms using the shape parameters resulted in shorter pulses (<5 ms) and robust 3D excitations (Fig. 3). Experiments were performed using gradient echo sequence on a 7T scanner with an 8-channel pTx and clinical gradient system using a realistic head phantom. Moreover, it was found that the inclusion of B₀ robustness in the joint optimization pTx pulse problem significantly affected where the optimized excitation k-space trajectory traverses. The quality of inner-volume excitations is affected by the RF pulse length significantly. Joint optimization framework enabled shorter 3D pTx pulses than other approaches designed on clinical gradient system. However, the use of this method is currently limited to phantom studies due to long computation time (ranging from 0.8 to 7.7 hours based on the complexity of the optimization problem.)

FIGURE 3.

k-space trajectories and flip angle profiles obtained with the shells trajectory for excitation of the cube and brain-only target patterns (10°). For each target, 3 sets of results are shown corresponding to optimization of the RF waveform alone (left), joint optimization of the RF and gradient waveforms (center), and joint optimization with enforced off-resonance robustness (right). The 2 white numbers give the flip angle NRMSE in the entire field of excitation and outside of the cubic/brain-only target region (in parentheses). For each set of results, the off-resonance performance was evaluated in terms of the flip angle NRMSE as a function of the offset frequency (bottom). Reprinted with permission from Magn Reson Med 2016; 76:1170–1182.

In addition to GRE-based IVI approaches, spin echo-based sequences are used extensively for IVI. The translation of pTx hardware and design methods from UHF to 3T resulted in successful application of IVI using 2D selective excitations for turbo spin echo (TSE) sequences. IVI with 2D selective excitations has been applied to image prostate,^42–46 orbits,^47–49 kidneys,⁵⁰ and other organs.^51–53 Recently, Malik and Hajnal⁵⁴ proposed a 3D pTx pulse design method to improve background suppression for a TSE sequence with long echo trains and low refocusing angles. Proper background suppression is key for a successful IVI particularly for selecting small volumes for excitation. IVI with 3D pTx pulse of length 12.5 ms using a fixed 3D shells k-space trajectory was demonstrated for in vivo T2-weighted brain imaging at 3 T using 8-channel pTx system (Fig. 4). Their approach aimed at reducing the residual errors for background suppression by violating the CPMG condition. This approach achieved good image quality and sufficient background suppression. In another approach, Mooiweer et al⁵⁵ proposed to design a phased matched 2D pTx pulses for TSE imaging and combining IVI with parallel imaging. Phase matching with the nonselective refocusing pulses was demonstrated on 2-channel pTx system at 7T in vivo. The combination of IVI and parallel imaging has been used to provide higher acceleration factors in image reception and greater flexibility in excitation region definition and additional scan acceleration in IVI.⁵⁶ These approaches used pTx design approaches based on STA. Recently, 90° 2D spatially-selective pTx pulses were designed for in vivo brain stem imaging using the optimal control (OC)-based approach for 7T system with 8 transmit channels.⁵⁷ Spatially selective 2D pTx pulses have been also used to define shaped voxels for MR spectroscopy in human brain at 3T⁵⁸ and 7T.⁵⁹ Spectra using pTx showed a good agreement with the reference STEAM spectrum. Moreover, improved SAR management using pTx pulses could potentially improve the SNR of the spectra further.

FIGURE 4.

3D excitation results from an in vivo 3D-TSE scan compared with the standard nonselective excitation at 3T using 8-channel pTx body coil; columns represent sagittal, coronal, axial views. Top row: 3D-TSE with standard hard pulse excitation. Middle row: 3D-TSE with 3D-shells excitation pulse of length 12 ms. Top and middle row images were acquired at 1 mm isotropic resolution in 5 min. Bottom row: The small FOV 3D-TSE high-resolution image (0.8 mm isotropic) from the same subject shows no obvious artifacts. This image was acquired in 3 min 17 s. Reprinted with permission from Magn Reson Med 2016; 76:848–861.

Other pTx Pulse Design Approaches

Variants of RF shimming have been utilized for homogenizing the B₁⁺ field, improving transmit efficiency, reducing SAR, and facilitating adiabatic conditions. By using different shim settings during RF excitations played at different time points resulted in improved B₁⁺ homogeneity of the resulting MR image and reduced SAR. By using advanced/dynamic shim methods, researchers aimed to bridge the gap between pure RF shimming approaches via increasing the flexibility and full pTx RF pulse design solutions via reducing the system and design complexity. Recently, a direct signal control (DSC)¹² method has been proposed to control the uniformity of the excitation RF fields by changing the RF field pattern on a pulse-by-pulse basis. This approach requires an accurate signal model of the pulse sequence, which is provided by extending the spatially resolved extended phase graphs⁶⁰ to include steady-state response of the sequence. DSC method was first proposed at 3T for TSE brain imaging¹² and it has recently been extended to 7T for whole-brain 3D FLAIR imaging.⁶¹ In both field strengths, the signal homogeneity is substantially improved compared to static RF shimming. In another study, Beqiri et al⁶² extended the RF shimming approach to jointly optimize the sequence parameters such as TR. Minimizing TR in addition to B₁⁺ inhomogeneity is demonstrated on cardiac MRI using balanced SSFP sequence at 3T using an 8-channel pTx system.

In addition to the pTx pulse design methods aiming to reduce the inhomogeneity of the B₁⁺ field, B₁⁺ insensitive adiabatic pulses can benefit from pTx systems as well. RF shimming has been employed to improve the application of adiabatic pulses.^63–65 Recently, Jang et al⁶⁶ proposed a method to design 3D adiabatic pulses based on sub-pulse approach in pTx for inverting or refocusing spins. pTx was used to maintain the 3D selectivity while reducing the total pulse duration and/or eliminating the unwanted sidebands. Adiabatic pulses are generally power intensive that could impede the use at UHF due to safety concerns. Further studies are required to combine the adiabatic pulse design approach with explicit SAR constraints.

The OC approach has been used in RF pulse design since 1988.⁶⁷ In general, RF pulse design approaches focuses on solving the inverse problem using a linear approximation of the Bloch equation.^68,69 The OC approach removes the necessity of linear approximations by defining the RF pulse design problems using multiple controls based on Bloch equation. Several approaches for numerically solving the OC problem have been demonstrated for designing spatially selective RF pulses.⁷⁰ The OC approach has been successfully extended to pTx systems to design arbitrary flip angle pTx RF pulses.²² Recently, LTA pTx pulses using OC have been designed for 7T brain imaging satisfying strict regulatory local and global SAR limits and hardware peak power limits.⁷¹ The OC approach was combined with the kt-point method to design nonselective excitation, inversion, and refocusing pulses that are used in 3D T2-w brain imaging at 7T.⁷² In another approach, Sbrizzi et al⁷³ used OC techniques in extended phase graph formalism to design the tip angles and corresponding phases of the TSE train for 7T brain imaging. By providing the better control of Bloch equations and spin dynamics, it is expected that the OC methods will play an important role in pTx pulse design at UHF.

For formulating the pTx pulse design algorithm, Majewski and Ritter⁷⁴ used quaternion calculus for specifying first and second-order derivatives of the objective function efficiently. STA is defined as a first-order Taylor development from the exact first-order derivatives. The approach can be extended to arbitrary flip angle pTx design by defining the second-order derivative in addition to the first one. As opposed to previous design strategies, the z-axis rotation during the sample time interval is managed by additional sinc factors in these approximations and it resulted in shorter computation times. In a separate approach, Pendse et al⁷⁵ proposed an efficient pTx pulse calculation algorithm minimizing the cumulative SAR over a multi-slice scan while keeping the flip angle inhomogeneity under a predefined limit. In addition, this algorithm can handle large number of SAR matrices and slices without the need for additional SAR matrix compression based on VOP approach leading to a more efficient use of pTx system and on-scanner pulse design.

Joint-design pTx

PTx pulse design methods have focused on developing efficient design methods for improved B₁⁺ homogeneity and ensured subject safety. pTx employs gradients and RF pulses of multiple coils in order to tackle the problems associated with UHF. Initial experience on developing pTx pulse design methods using fixed excitation k-space trajectory is now enhanced by joint optimization methods that optimize both RF pulses and excitation k-space trajectory simultaneously.^76–78 Using an active set algorithm, Dupas et al⁷⁹ optimized the locations of 2-spoke trajectories during STA pTx pulse design with explicit SAR and power constraints. T2*-weighted images of the brain were acquired at 7T with good NRMSE. The SAR and power constraints have shown to impact the spoke replacement results, providing an evidence for the need for optimization facilitating those constraints. This concept was extended to LTA regime by jointly designing kt-points trajectory and pTx pulses.⁸⁰ In another study, Cao et al⁸¹ demonstrated improved spin echo BOLD fMRI at 7T using a LTA pTx pulse design approach by updating the gradient blip areas and RF pulses jointly.

Moving Toward Calibration-free pTx

pTx pulse design in general relies on calibration measurements performed before scanning subjects. B₁⁺ maps from each RF coil and B₀ offset distribution need to be acquired in order to calculate shim weights/RF pulses. To cover the whole region using multiple transmit elements increases the time required for a calibration before pulse design, as the calibration needs to be done for each slice/slab. In addition, the time to calculate RF pulses and their preparation on the scanner can become very time consuming, as the number of transmits channels and RF pulse duration increase. Calibration scans for ensuring patient safety also increase the time required for successfully applying pTx RF pulses before acquiring clinically relevant data. The time required for data calibration is usually on the order of 10 to 15 minutes that impedes the effective use of pTx approaches in routine clinical research. Researchers have focused on minimizing the time required for calibration measurements by developing fast B₁⁺ mapping, ΔB₀ mapping, and pTx RF pulse calculation techniques. Recently, the focus has shifted toward researching new ways to enable easy use of pTx systems by, for example, defining self-calibrating plug-and-play approaches, reducing the required number of RF transmit coils, and designing universal pulses.

Unlike other methods that try to improve the B₁⁺ inhomogeneity at UHF using measured field information, Cloos et al⁸² proposed a plug-and-play pTx method utilizing nonuniform RF fields with MR fingerprinting to achieve multiparametric MR imaging in heterogenous fields. Instead of trying to compensate B₁⁺ inhomogeneity at each location, the proposed method focused on incorporating complementary 2 or more distinct coil modes. These distinct coil modes are played in an interleaved fashion to mitigate B₁⁺ voids over the FOV. Plug-and-play pTx removes the necessity of time-intensive calibration steps. In addition, tailoring multiple coil modes to encode MR signal is beneficial for RF safety, as it avoids the constructive interference of electric fields using an interleaved RF excitation scheme. Simulations performed on the abdomen at 7T resulted in artefact-free multiparametric maps clearly overlaying the benefits of the proposed method at UHF.

Reducing the number of transmit coils via defining virtual coils has been proposed for pTx^83,84 and RF shimming.^85,86 In a recent work by Cao et al,⁸⁷ the array-compressed pTx pulse design method was proposed to jointly optimize the compression weights and RF pulses for the compressed array. Unlike previous approaches that defined a fixed coil combination before RF pulse design, this approach determines the coil combination weights, virtual coils, during RF pulse design. The array-compressed design framework achieved the lowest excitation error among other array compression techniques and recently experimentally realized on a hardware system.⁸⁸

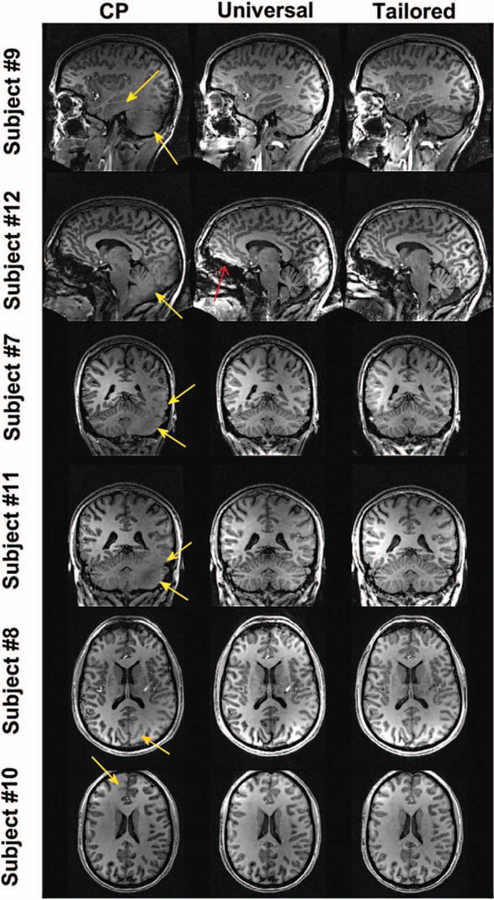
Gras et al⁸⁹ proposed to design a nonselective pTx pulse, called universal pulses, using a database of measured B₁⁺ and ΔB₀ maps from multiple subjects and use the designed pTx pulse on new subjects without the need for additional calibration scans. By reducing the variability of scans via carefully positioning of the subjects and building a database from a representative subject cohort, the authors demonstrated the benefit of using universal pulses with respect to CP and RF shim modes (NSMRS ~11% vs ~28% and ~20%). However, as expected, the excitation fidelity was worse when compared with subject-based optimized pulses (NRMSE ~7%) for brain imaging (Fig. 5). This study was performed using a home-made pTx array for 6 subjects who were scanned with pTx pulses generated by using a database from other 6 subjects. This approach later was extended to design 3D refocusing pulses using a commercial head arrays and a greater number of subjects.⁹⁰ In a separate study, the effect of the 7T system and pTx head array were analyzed using 2 different MR scanners and 2 different coil suppliers.⁹¹ The results suggested that the use of universal pulses lead to an improved flip angle homogeneity compared with CP mode. The application of similar calibration-free pTx pulse design approaches is expected to emerge for imaging other parts of the body. However, the greater variation of subject anatomy with respect to brain imaging could pose additional challenges.

FIGURE 5.

7T MPRAGE images acquired from multiple subjects using 8-channel pTx array. From left to right: CP-mode, universal and subject-based tailored pulses. The universal pulses are able to greatly mitigate the RF field inhomogeneity problem without B1 and ΔB₀ measurements (yellow arrows), while satisfying various hardware and safety constraints. The red arrow points to a small susceptibility artifact, which is better compensated by the subject-based tailored pulses. Some artifacts are also visible in the brainstem of subject #12 and are due to the nonlinearity of the used head gradient system (shoulder artifact). Reprinted with permission from Magn Reson Med 2017; 77:635–643.

Improved Calibrations

Hardware imperfections impede the successful use of designed pTx pulses resulting in decreased excitation fidelity and raise safety concerns. Using a field monitoring system, Çavuşoǧlu et al⁹² proposed to use the measured k-space trajectory during pTx RF pulse design for limiting the RF peak power via improved variable rate selective excitation (VERSE) method. They used the field monitoring system for simultaneously measuring gradient fields and RF pulses waveforms. This information later was incorporated into pTx pulse design for compensating timing imperfections, correcting gradient trajectory, and correcting RF waveform infidelities.⁹³ In another study to calibrate gradient delays for a spokes pTx pulses (a special case of k-space trajectory), Gras et al⁹⁴ proposed to use a simple method for measuring and correcting zero-order eddy currents and gradient delays. Similarly, the excitation errors were estimated and eliminated by using gradient delay corrections based on a navigator approach proposed by Tse et al.⁹⁵ In addition to corrections for system hardware imperfections, several methods have been proposed to improve the repeatability of pTx. Harada et al⁹⁶ proposed to use breath-holding during acquisition of B₁⁺ and B₀ maps in human brain. This improved the reproducibility of calibrations as well as GRE images. Kameda et al⁹⁷ used interleaved the acquisition of calibration scans to improve the pTx repeatability and image homogeneity. Schmitter et al⁹⁸ explored the effect of respiration on spokes pTx pulse design for cardiac imaging at 7T. By simultaneously using multiple B₁⁺ and ΔB₀ calibration scans from different phases of respiration cycle, they proposed a pTx formalism that allows pTx pulses to be robust against respiration. These developments underline the importance of calibration methods that reduce the mismatch between RF simulations and experiments and improve the repeatability of experiments.

SAFETY

The SAR behavior of pTx RF pulses has been studied extensively using a variety of excitation k-space trajectories,^99–101 coil designs,^84,102 acceleration factors,³⁷ and RF pulse design formalisms.^7,18,103 Evaluation and prediction of SAR consequences of designed pTx RF pulses have commonly relied upon EM simulations using virtual human body models¹⁰⁴ due to a lack of accurate means of measuring and predicting concomitant E fields inside the human body. Prescan-based individualized body models^105,106 have been used in the EM simulations in order to estimate SAR closely. Directly measuring the electrical properties of tissues has been proposed¹⁰⁷ to bring the accuracy of SAR estimations using EM field simulations close to reality. In another aspect of safety at UHF, pre-scan based SAR calibration methods have been proposed.^108–110 These methods enable accurate SAR predictions specific to coil-subject setup and do not require assumptions about the subject or the scanner setup. In addition to SAR prediction capability, an additional layer of system monitoring in the parallel RF excitation chain has been implemented to ensure subject safety, using either pick-up coils¹¹¹ or directional couplers.¹¹² These additional monitoring systems have been shown to detect system changes such as hardware failure, system instability, and patient position change, which were undetectable with previous RF monitoring systems. In recent years, the research on RF safety on pTx has more focused on improving the match between the EM field simulations and experiments to ensure patient safety while exploring the UHF without being limited by the safety concerns. For a more detailed review of SAR simulations and safety at UHF, we refer the readers to a review article by Fiedler et al.¹¹³ Here, we will review recent developments that could potentially help bringing the pTx into routine research and clinical use.

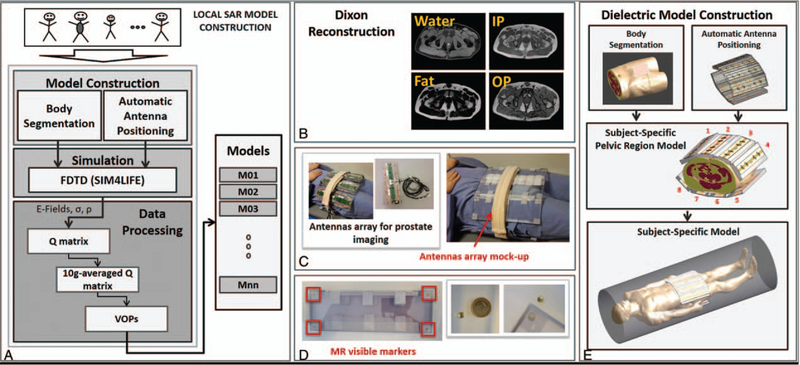
Researchers have focused on defining the intersubject variability of SAR for safe use of pTx systems at UHF. Le Garrec et al¹¹⁴ studied the variations of a head model on a 4-dimensional parameter space involving transformations to the head length, head breadth, and location shifts in 2 axes. On the basis of performing 33 EM simulations using different parameters from this space and testing on a large number of RF pulses, the authors found a safety margin of 1.5 that will keep the probability of exceeding a given peak 10 g SAR below 1% across the adult Caucasian population for the investigated parameters. In a separate study, Meliadò et al¹¹⁵ investigated the intersubject SAR variability by creating a database consisting of 23 virtual models for prostate imaging. Twenty-three subjects were scanned using a Dixon method 1.5Tand their images were segmented in 4 tissue types (muscle, fat, cortical bone, and skin) providing a sufficient SAR estimation accuracy (Fig. 6). Using the dielectric properties of these tissues at 7T, EM modeling was performed for an 8-channel pTx array for prostate imaging. The authors found that a safety factor from 1.8 to 2 needs to be taken into considerations to compensate for intersubject variability when a safety assessment of only 1 body model is performed. It seems that performing a range of EM field simulations for extensive SAR analyses in order to define safety margins will improve our understanding of the use and safety scenarios of pTx.

FIGURE 6.

A, Flowchart for an exemplary local SAR model construction using multiple subjects. B, Dixon reconstruction water/fat/in-phase (IP)/opposed-phase (OP) images were acquired to at lower field (1.5T) to differentiate different tissue types. C, For proper registration of the subject and array in EM field simulations, mockup array for prostate imaging were used with MR visible markers placed in the corners of each element (D). E, Subject-specific dielectric model was constructed, and EM simulations were performed. Reprinted with permission from Magn Reson Med 2019;81:2106–2119.

In addition to analyzing the intersubject SAR variability, researchers have worked on improving the patient safety via monitoring and proactively managing pTx. Following the early investigations on the pTx systems, UHF pTx systems now incorporate pTx safety infrastructure, which employs several calibration measurements that are used to start or terminate scans and track SAR from EM field simulations. Graesslin et al¹¹¹ implemented an RF safety concept for pTx at 3T using a database of EM field generated SAR matrices, an active decoupling among Tx coil elements, the predicted and actual SAR matching scheme using B₁⁺ measurements, and a scan termination. By using the in situ fast calibrations, Deniz et al⁸⁵ demonstrated a subject- and resource-specific RF power monitoring concept. Using a constrained optimization and pre-scan based multichannel calibration, pTx pulses were designed to obey the forward/reflected peak and average power limits of the RF power amplifiers and strict local SAR limits. In another study, Restivo et al¹¹⁶ improved the local SAR predictions by using in situ S-matrix measurements to match the simulated S-matrix to experimental condition using a cosimulation technique. While playing the pTx pulses during scan, deviations from the predicted pulse shape calculated using calibrations enable the safety system to stop the scan without causing safety issues. This could potentially result in scan interruptions on which the pTx pulse designer does not have a control. In an approach to overcome this challenge, Martin et al¹¹⁷ proposed a pTx pulse design approach with the knowledge of worst-case SAR estimation error calculated from potential RF deviations that are within the expected performance of the RF Tx chain (measured for spiral pulses 20% amplitude and 15° phase deviations). Combining mentioned calibration strategies with intersubject SAR variability analysis could potentially bring us close to the safe and efficient use of pTx.

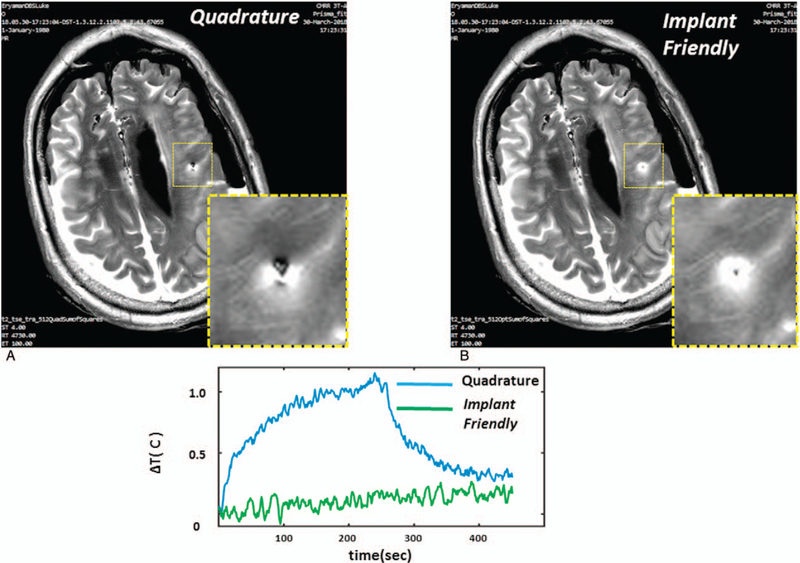
From the early days of invention, pTx has been proposed to reduce SAR via coordinating multiple transmitters. Eryaman et al¹¹⁸ used the flexibility of multiple transmitters to generate implant-friendly modes that are used to reduce SAR around deep brain stimulation (DBS) implants. During the MRI scan, RF-induced currents focus around DBS implant tips and this poses a safety risk affecting the patients. Due to the increased safety concerns, patients with DBS implants cannot benefit from full-fledged MR examinations effectively. The implant-friendly modes generated on a simulated head model at 3T resulted in lower controlled SAR while maintaining excitation homogeneity. Recently, this method was extended to a phantom and cadaver head studies using low power pre-scan calibrations and standard clinical protocols,¹¹⁹ and it demonstrated the feasibility of the approach to reduce the image artifacts and the temperature around the DBS implant tip (Fig. 7). Similarly, Etezadi-Amoli et al¹²⁰ used pTx to control RF-induced currents in elongated wires in general to decrease the heating risk. The experimental feasibility of the method is presented at 1.5 T using current sensor measurements on the wire and temperature measurements on a gel phantom.

FIGURE 7.

TSE images obtained around the lead using quadrature and implant-friendly (I F) patterns in the cadaver brain are shown. Quadrature pattern results in a signal loss mainly due to over-flipping of the spins at the vicinity of the lead. Axial image shows improved image quality as a result of using the I F pattern. In addition, I F pattern reduced the contact temperature significantly in comparison to quadrature excitation. Reprinted with permission from Magn Reson Med 2015; 73:1896–1903.

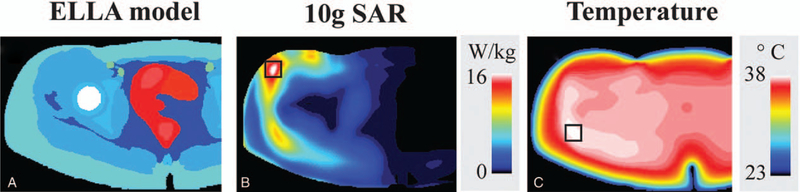
SAR and temperature limits during MRI scan are used to guarantee the subject safety during MRI examinations. SAR, either averaged over a 10 g tissue volume or over the exposed volume, is used to monitor safety and design pTx pulses obeying safety limits. Recently, replacing the use of SAR with the temperature during pTx pulse design has been proposed, as temperature has more direct relation to the tissue damage and it is also accepted as a safety metric internationally. Boulant et al¹²¹ proposed to calculate complex temperature matrices (similar to SAR matrices) for a 16-channel array using EM field simulations of head at 10.5T and Pennes Bioheat equation. Using these matrices, pTx pulses were designed under an explicit temperature rise constraints. It is found that the pTx pulse performance in some cases improved by a factor of 2 compared with pTx pulses designed with explicit SAR constraints. In another study, Deniz et al¹²² proposed to use local temperature correlation matrices to limit the maximum absolute temperature that is more relevant to subject safety than SAR and temperature rise limits. Performing experiments on regions with different perfusion characteristics (head and hip region) using a virtual model at 7T, better excitation fidelity was observed compared with designs with SAR constraints. Moreover, SAR and temperature hotspots were observed in different parts of the pelvis (Fig. 8). It was found that the benefit of using temperature correlation matrices diminish as the RF exposure duration increases, but the safe operation is always guaranteed by the pTx pulse design using strict maximum absolute temperature limits.

FIGURE 8.

Temperature and 10 g SAR resulting from RF pulses designed with temperature constraints in the hip region. Material distribution of the Ella virtual body model (A). Multiple intensity projections of 10 g SAR (B), and temperature (C), results from temperature constrained RF pulse designs. Maximum temperature and 10 g SAR are indicated by the black squares, which are located in different regions of the pelvis. The right-hand side of the simulations, which was not covered by the hip array, was cropped for visualization. Reprinted with permission from NMR Biomed 2017; 30:e3694.

The importance of coil-subject setup increases at UHF due to safety concerns. Deniz et al¹⁰³ analyzed the RF power requirements and SAR of pTx systems as a function of the distance between the transmit coil array and the subject in simulations. It was found that there are SAR benefits in moving transmit coils away from the subject. In another study, Erturk et al¹²³ proposed to use the combination of loop and dipole elements to improve SAR efficiencies of the pTx array. The importance of RF coil design enabling SAR reductions per unit angle for acquisition of MR images from different body organs is demonstrated through the pelvis and torso at 7T.

CONCLUSION

In the light of all these developments, parallel RF excitation, with appropriate SAR prediction and monitoring, is likely to continue to play an important role in the future of MRI by improving the diagnostic value of UHF-MRI.