Changes in genetic parameters for fitness and growth traits in pigs under genomic selection

Abstract

Genomic selection increases accuracy and decreases generation interval, speeding up genetic changes in the populations. However, intensive changes caused by selection can reduce the genetic variation and can strengthen undesirable genetic correlations. The purpose of this study was to investigate changes in genetic parameters for fitness traits related with prolificacy (FT1) and litter survival (FT2 and FT3), and for growth (GT1 and GT2) traits in pigs over time. The data set contained 21,269 (FT1), 23,246 (FT2), 23,246 (FT3), 150,492 (GT1), and 150,493 (GT2) phenotypic records obtained from 2009 to 2018. The pedigree file included 369,776 animals born between 2001 and 2018, of which 39,103 were genotyped. Genetic parameters were estimated with bivariate models (FT1-GT1, FT1-GT2, FT2-GT1, FT2-GT2, FT3-GT1, and FT3-GT2) using 3-yr sliding subsets. With a Bayesian implementation using the GIBBS3F90 program computations were performed as genomic analysis (GEN) or pedigree-based analysis (PED), that is, with or without genotypes, respectively. For GEN (PED), the changes in heritability from the first to the last year interval, that is, from 2009–2011 to 2015–2018 were 8.6 to 5.6 (7.9 to 8.8) for FT1, 7.8 to 7.2 (7.7 to 10.8) for FT2, 11.4 to 7.6 (10.1 to 7.5) for FT3, 35.1 to 16.5 (32.5 to 23.7) for GT1, and 35.9 to 16.5 (32.6 to 24.1) for GT2. Differences were also observed for genetic correlations as they changed from −0.31 to −0.58 (−0.28 to −0.73) for FT1-GT1, −0.32 to −0.50 (−0.29 to −0.74) for FT1-GT2, −0.27 to −0.45 (−0.30 to −0.65) for FT2-GT1, −0.28 to −0.45 (−0.32 to −0.66) for FT2-GT2, 0.14 to 0.17 (0.11 to 0.04) for FT3-GT1, and 0.14 to 0.18 (0.11 to 0.05) for FT3-GT2. Strong selection in pigs reduced heritabilities and emphasized the antagonistic genetic relationships between fitness and growth traits. With genotypes considered, heritability estimates were smaller and genetic correlations were greater than estimates with only pedigree and phenotypes. When selection is based on genomic information, genetic parameters estimated without this information can be biased because preselection is not accounted for by the model.

Introduction

The main purpose of genomic selection is to accelerate the genetic progress. This is accomplished by increasing the accuracy of selection and decreasing the generation interval. However, the breeder’s equation includes the genetic variance, and accuracies in multi-trait selection depend on genetic correlations (Walsh and Lynch, 2018). If genetic parameters change as a result of strong selection, the genetic gain as predicted using old parameters may not be realized.

In general, heritability and genetic correlations are expected to change under selection, with the amount of change dependent on the intensity of selection and initial genetic variance (Falconer and Mackay, 1996; Walsh and Lynch, 2018). Under directional selection, negative linkage disequilibrium (LD) is created introducing a negative correlation between pairs of loci, which decreases genetic variance, heritability, and selection response. Conversely, under disruptive selection, positive LD is generated introducing a positive correlation between pairs of loci (Bulmer, 1971; Walsh and Lynch, 2018). Two different genetic mechanisms contribute to genetic covariances, LD, and pleiotropy, and both can change over time. Selection creates LD, and alleles at different loci affecting single traits are co-inherited, creating a correlation between pairs of loci. With pleiotropy, 1 allele influences 2 or more traits.

The distribution of allelic effects is critical to predict medium- to long-term selection response in covariances. Changes in genetic covariances are likely to be more unpredictable than changes in genetic variances (Walsh and Lynch, 2018). Under directional selection, ignoring the reduction in genetic variance leads to an overestimation of the accuracy of selection (Bijma, 2012; Gorjanc et al., 2015). In the multi-trait selection, the genetic covariances also play an important role and appropriate estimates have to be used to calculate correct accuracies. Additionally, genetic covariances can evolve away from the direction favored by selection as a result of the introduced correlation between pairs of loci, making it harder to realize genetic changes in the desirable direction for each trait.

Estimation of genetic parameters over time is complex, especially under genomic selection. A general method would be to use a random regression model over time (Tsuruta et al., 2004). However, such a model is computationally expensive, especially with a large number of genotyped animals, and its ability to model complex changes is limited by the type and order of the regression functions. Another option is to use time intervals (i.e., slices) so that only a fraction of the data is utilized in each analysis. However, changes inside the intervals are averaged, and intervals need to be large enough to avoid biases due to earlier selection (Cesarani et al., 2019).

The objective of this study was to investigate changes in genetic parameters for fitness and growth traits in pigs under genomic selection using data in time intervals. We defined 3-yr intervals to have enough data and the subsequent intervals overlapped 2 yr, that is, the first interval included data from 2009 to 2011, the next included data from 2010 to 2012 and so on, and the last interval included 4 yr (2015 to 2018) because the last year contained few data points.

Materials and methods

Animal Care and Use Committee approval was not needed as data were obtained from preexisting databases.

Data

Data for fitness traits related to prolificacy (FT1) and litter survival (FT2 and FT3), and for classical growth traits (GT1 and GT2), recorded from 2009 to 2018, were provided by Smithfield Premium Genetics (Roanoke Rapids, North Carolina, USA). Initial pedigree consisted of 369,776 animals from one line born between 2001 and 2018, of which 39,103 were genotyped. The objective of the breeding program is to increase growth traits FT1 and FT2, and decrease FT3. Numbers of animals with genotypes, phenotypes, and in the pedigree per year and interval are shown in Table 1 and Table 2, respectively.

Table 1.

Number of animals with genotypes, phenotypes, and in the pedigree for fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2) per year

			Fitness traits			Growth traits
Year	Pedigree	Genotypes	FT1	FT2	FT3	GT1	GT2
2009	12,154	65	1,183	2,016	2,016	5,775	5,775
2010	16,474	923	2,182	2,237	2,237	7,858	7,858
2011	17,669	1,654	3,301	3,377	3,377	10,417	10,417
2012	26,177	1,455	2,506	2,579	2,579	14,656	14,656
2013	29,917	1,492	2,692	2,856	2,856	19,331	19,331
2014	27,947	1,957	3,438	3,620	3,620	18,391	18,392
2015	34,313	8,496	3,339	3,463	3,463	22,393	22,393
2016	39,536	10,881	2,018	2,203	2,203	24,783	24,783
2017	32,722	9,338	610	895	895	23,382	23,382
2018	13,309	2,842	—	—	—	3,506	3,506
Total	250,218	39,103	21,269	23,246	23,246	150,492	150,493

Table 2.

Number of animals with genotypes, phenotypes, and in the pedigree for fitness traits (FT1, FT2, and FT3) and growth traits (GT1 and GT2) per interval

			Fitness traits			Growth traits
Interval	Pedigree1	Genotypes	FT12	FT22	FT32	GT12	GT22
2009–2011	46,297 (24,479)	2,642	6,666 (2,151)	7,630 (2,195)	7,630 (2,195)	24,050 (2,582)	24,050 (2,582)
2010–2012	60,320 (35,131)	4,032	7,989 (3,334)	8,193 (3,400)	8,193 (3,400)	32,931 (3,971)	32,931 (3,971)
2011–2013	73,763 (47,075)	4,601	8,499 (3,821)	8,812 (3,915)	8,812 (3,915)	44,404 (4,597)	44,404 (4,597)
2012–2014	80,041 (56,168)	4,904	8,636 (3,943)	9,055 (4,055)	9,055 (4,055)	52,378 (4,894)	52,379 (4,894)
2013–2015	92,177 (65,098)	11,945	9,469 (4,238)	9,939 (4,351)	9,939 (4,351)	60,115 (10,851)	60,116 (10,851)
2014–2016	101,796 (72,249)	21,334	8,795 (4,087)	9,286 (4,177)	9,286 (4,177)	65,567 (4,177)	65,568 (4,177)
2015–2018	119,880 (84,171)	28,715	5,967 (3,112)	6,561 (3,358)	6,561 (3,358)	70,558 (25,892)	70,558 (25,892)

¹Total number of animals in the interval (number of animals used in the analyses after tracing back all animals with phenotypes or genotypes up to 3 generations of their ancestors).

²Number of animals with phenotypes (number of genotyped animals with phenotypes).

Analyses and computations

Variance components were estimated using a Bayesian approach via the Gibbs sampling algorithm as implemented in the GIBBS3F90 program (Misztal et al., 2014) with genomic analysis (GEN) or without genotypes pedigree-based analysis (PED). The analyses were separately performed in each interval. A single Gibbs chain of a total length of 100,000 rounds was initially generated. After discarding the initial 10,000 samples as burn-in, 1 in every 10 samples was stored to compute means and standard deviations of the posterior distributions. The means were used as estimates of the (co)variance components, and their posterior standard deviations were considered to be a measurement of their estimation errors.

The bivariate model could be expressed in matrix notation as:

$${\displaystyle \begin{array}{l}{\displaystyle \left[\begin{array}{l}{y}_f\\ y_g\end{array}\right]=\left[\begin{array}{cc}{X}_f& {\displaystyle 0}\\ 0& {\displaystyle X_g}\end{array}\right]\left[\begin{array}{l}{b}_f\\ b_g\end{array}\right]+\left[\begin{array}{cc}{Z}_f& {\displaystyle 0}\\ 0& {\displaystyle Z_g}\end{array}\right]\left[\begin{array}{l}{a}_f\\ a_g\end{array}\right]+\left[\begin{array}{cc}{W}_f& {\displaystyle 0}\\ 0& {\displaystyle 0}\end{array}\right]\left[\begin{array}{l}p{e}_f\\ 0\end{array}\right]+\left[\begin{array}{cc}0& {\displaystyle 0}\\ 0& {\displaystyle C_g}\end{array}\right]\left[\begin{array}{l}0\\ c{l}_g\end{array}\right]+\left[\begin{array}{l}{e}_f\\ e_g\end{array}\right]}\end{array}}$$

where f and g stand for fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2), respectively; y is the vector of observations; b is a vector of systematic effects (as stated below); a is the vector of direct additive genetic effects; pe is the vector of permanent environment effects; cl is the vector for common litter environment effects; e is the vector for random residual effects; X, Z, W, and C are incidence matrices relating the elements of y to elements of b, a, pe, and cl, respectively. The covariance matrix was assumed to be:

$${\displaystyle \begin{array}{l}{\displaystyle Var\left[\begin{array}{l}{a}_f\\ a_g\\ p{e}_f\\ c{l}_g\\ e_f\\ e_g\end{array}\right]=\left[\begin{array}{cccccc}\mathit{T}{\sigma }_{af}^{\mathbf{2}}& {\displaystyle \mathit{T}{\sigma }_{af,ag}}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}\\ \mathit{T}{\sigma }_{ag,af}& {\displaystyle \mathit{T}{\sigma }_{ag}^{\mathbf{2}}}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}\\ 0& {\displaystyle 0}& {\displaystyle \mathit{I}{\sigma }_{pef}^{\mathbf{2}}}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}\\ 0& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle \mathit{I}{\sigma }_{c{l}_g}^{\mathbf{2}}}& {\displaystyle 0}& {\displaystyle 0}\\ 0& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle \mathit{I}{\sigma }_{ef}^{\mathbf{2}}}& {\displaystyle 0}\\ 0& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle 0}& {\displaystyle \mathit{I}{\sigma }_{eg}^{\mathbf{2}}}\end{array}\right]}\end{array}}$$

where ${\sigma }_{af}^{\mathbf{2}}$, ${\sigma }_{ag}^{\mathbf{2}}$, and ${\sigma }_{af,ag}$ are variances for direct additive genetic effects for fitness traits, direct additive genetic effects for growth traits, and their covariances, respectively; ${\sigma }_{pef}^{\mathbf{2}}$ is the variance for permanent environment effects for fitness traits; ${\sigma }_{c{l}_g}^{\mathbf{2}}$ is the variance for common litter environment effects for growth traits; and ${\sigma }_{ef}^{\mathbf{2}}$ and ${\sigma }_{eg}^{\mathbf{2}}$ are variances of residual effects for fitness and growth traits, respectively; I is the identity matrix; T is equal to A when only pedigree information is used as the covariance structure for the direct additive genetic effects, or H when genomic and pedigree information are jointly used to compute relationships. According to Aguilar et al. (2010), the inverse of H is:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{H}}^{-1}={\mathbf{A}}^{-1}+\left[\begin{array}{cc}0& {\displaystyle 0}\\ 0& {\displaystyle {\mathbf{G}}^{-1}-{\mathbf{A}}_{22}^{-1}}\end{array}\right],}\end{array}}$$

where ${\mathbf{A}}^{-1}$ is the inverse of a pedigree-based relationship matrix for all animals included in the analysis, ${\mathbf{A}}_{22}^{-1}$ is the inverse of the pedigree-based relationship matrix for genotyped animals only, and ${\mathbf{G}}^{-1}$ is the inverse of a genomic relationship matrix. The systematic effects included in b were farm, year of farrowing, month of farrowing, age at measurement, and sex (included only for growth traits).

Results and discussion

Heritability

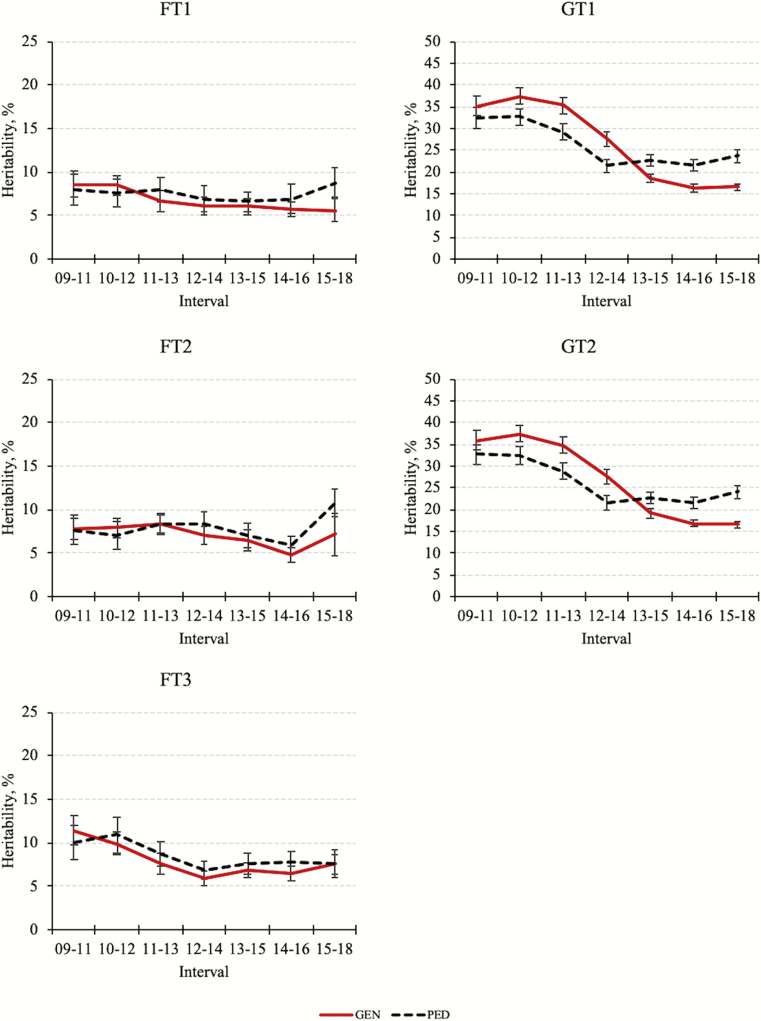
The changes in heritability estimated by GEN (PED) from the first to the last year interval, that is, from 2009–20011 to 2015–2018 were 8.6 to 5.6 (7.9 to 8.8) for FT1, 7.8 to 7.2 (7.7 to 10.8) for FT2, 11.4 to 7.6 (10.1 to 7.5) for FT3, 35.1 to 16.5 (32.5 to 23.7) for GT1, and 35.9 to 16.5 (32.6 to 24.1) for GT2. The posterior means and standard deviations for heritabilities estimated by GEN and PED are shown in Figure 1. The evolution of the heritabilities over time was similar with and without genomic information. Heritabilities for FT1 and FT2 were nearly stable, whereas heritabilities for FT3 and growth traits decreased over time. According to Walsh and Lynch (2018), the stronger the intensity of selection and the greater the heritability, the larger the LD and the stronger the reduction in the genetic variance.

Figure 1.

Posterior means and standard deviations for heritabilities of fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2) estimated with (GEN) or without (PED) genotypes. Heritabilities for FT1 and FT2 were nearly stable, while heritabilities for FT3 and growth traits decreased over time; estimates for FT2 increased in the last interval (2015–2018); and estimates for FT3 showed minor changes since 2012–2014.

In this population, the reduction in heritabilities was greater for growth traits, explained by their greater heritability and the stronger intensity of selection on these traits (evidenced by genetic trends; Figure 7). The reduction in the heritability for FT3 was observed in the first 3 intervals, accompanied by an undesirable slight increase in the genetic trend (Figure 7), suggesting that an unfavorable correlated response was the main cause.

Figure 7.

Genetic trends in standard deviation units of estimated breeding values (EBV) and genomic estimated breeding values (GEBV) for fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2). Genetic trends were similar for FT3. For FT1, FT2, and growth traits, the difference between genetic trends was nearly constant until 2015, but the 2 trends started to diverge in 2016.

Heritability for FT3 showed minor changes from 2012 to 2014, possibly as a result of weak selection (Figure 7). Another possible explanation is that this trait reached the equilibrium. Assuming an infinitesimal model and infinite population size with repeated cycles of selection, Bulmer (1971) showed that an equilibrium is eventually achieved in which the genetic variance lost by selection is regenerated by recombination. Villanueva and Kennedy (1990) studied the effect of selection in 2 traits. When selecting for 1 trait, variances of the directly and indirectly selected traits were reduced, and equilibrium values were reached in approximately 4 rounds of directional selection. Holm et al. (2004) reported constant heritability values for number born alive at first and second parities (0.10 ± 0.01) in a pig population under selection.

In a research related to survival in dairy cattle, van Pelt et al. (2016) found that the mean survival increased over time, whereas genetic and residual variances and heritability decreased. The heritability changed from 0.06 ± 0.07 (1989–1993) to 0.01 ± 0.06 (2009–2013). In a related study, the heritabilities for a productive life in dairy cattle (Tsuruta et al., 2004) were constant over time, most likely because of the lack of directional selection in this trait, which was evidenced by genetic trends. Haile-Mariam and Pryce (2015) reported a reduction in heritabilities for survival from 0.07 (1993–1994) to 0.03 (2007–2008) and for calving interval from 0.06 (1993–1994) to 0.03 (2007–2008). They stated that the observed decrease was related to a reduction in the genetic variance and an increase in the residual variance for calving interval.

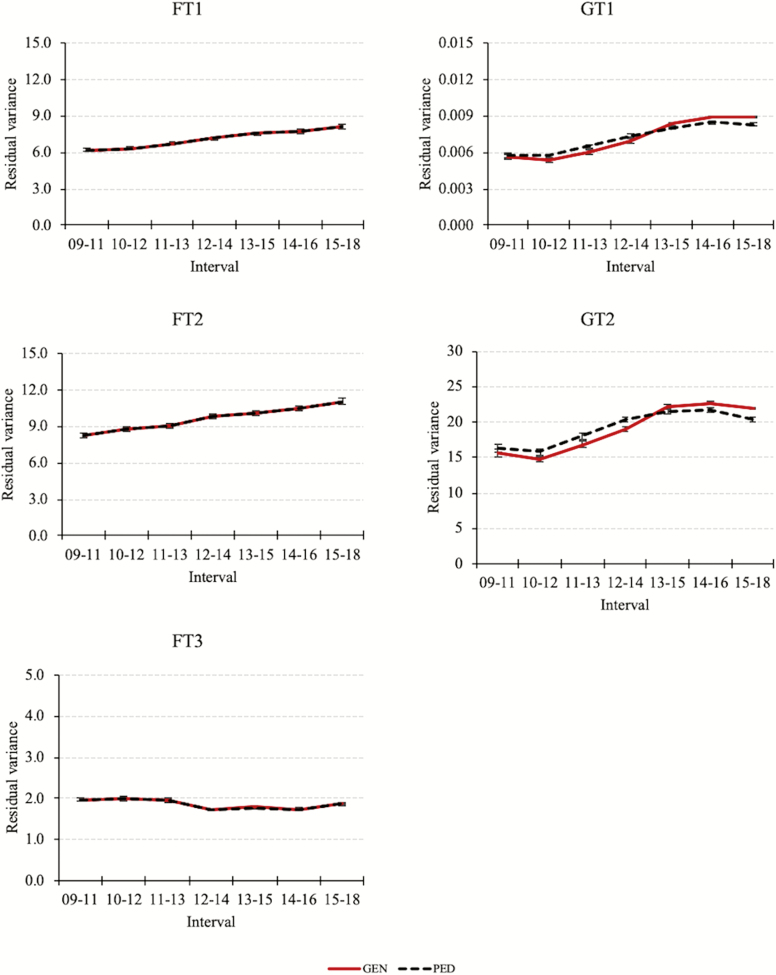
In this research, we found similar results, where the reduction in heritabilities was associated with a decrease in genetic variance and an increase in residual variance. Posterior means and standard deviations for additive genetic variance, environmental variance (permanent environment for fitness traits and common litter environment for growth traits), and residual variance are shown in Figure 2, Figure 3, and Figure 4, respectively. Genetic variance was nearly flat for FT1 and FT2, whereas for FT3 and growth traits it decreased. Environmental variance was stable for all the traits, except for FT3 where a reduction was observed. The residual variance increased over time for FT1, FT2, and growth traits, but was stable for FT3. The increase in the residual variance could be due to the scaling effect. As the means for FT1, FT2, and growth traits increased (improved), those residual variances increased, but mean for FT3 showed minor changes, tending to decrease (improve) as the residual variance for this trait.

Figure 2.

Posterior means and standard deviations for additive genetic variances of fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2) estimated with (GEN) or without (PED) genotypes. Genetic variance was nearly flat for FT1 and FT2, while for FT3 and growth traits it decreased.

Figure 3.

Posterior means and standard deviations for permanent environment (pe) variances of fitness traits (FT1, FT2, and FT3) and for common litter (cl) environment variances of growth traits (GT1 and GT2) estimated with (GEN) or without (PED) genotypes. Environmental variance was stable for all the traits, with exception for FT3 showing a reduction.

Figure 4.

Posterior means and standard deviations for residual variances of fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2) estimated with (GEN) or without (PED) genotypes. Residual variance increased over time for all the traits, with exception for FT3 showing a stable value.

In summary, the reduction in heritability for FT3 was associated with a reduction in the additive genetic variance, and the reduction in heritabilities of growth traits was due to the combination of a decrease in additive genetic variance and an increase in residual variance. However, it is important to highlight that the reduction in additive genetic variance played a key role in the observed changes, explaining an important part of it. Thus, breeding programs should take this into consideration.

Genetic correlations

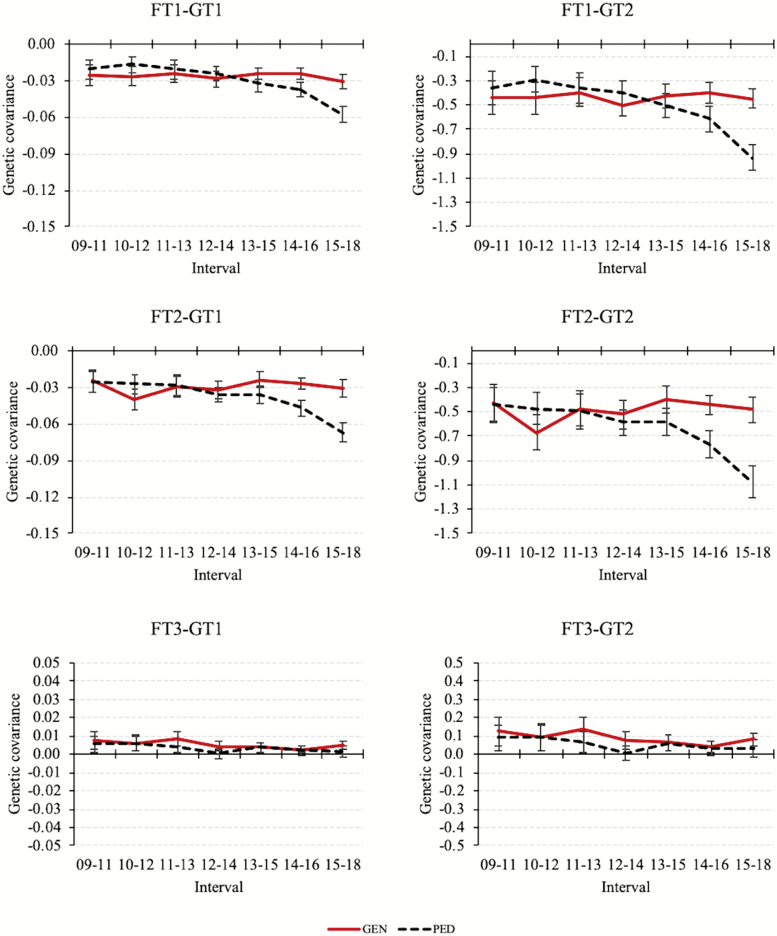
The changes in genetic correlations estimated by GEN (PED) from the first to the last year interval, that is, from 2009–2011 to 2015–2018 were −0.31 to −0.58 (−0.28 to −0.73) for FT1-GT1, −0.32 to −0.50 (−0.29 to −0.74) for FT1-GT2, −0.27 to −0.45 (−0.30 to −0.65) for FT2-GT1, −0.28 to −0.45 (−0.32 to −0.66) for FT2-GT2, 0.14 to 0.17 (0.11 to 0.04) for FT3-GT1, and 0.14 to 0.18 (0.11 to 0.05) for FT3-GT2. Posterior means and standard deviations for genetic correlations computed by GEN and PED are shown in Figure 5. The genetic correlations between FT3 and growth traits were roughly stable over time, whereas the genetic correlations of FT1 and FT2 with growth traits decreased. A possible explanation for the constant correlation between FT3 and growth traits is that the LD between these 2 traits has stabilized.

Figure 5.

Posterior means and standard deviations for genetic correlations among fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2) estimated with (GEN) or without (PED) genotypes. The genetic correlations between FT3 and growth traits were roughly stable over time, whereas the genetic correlations of FT1 and FT2 with growth traits decreased.

McMillan et al. (1995) studied the effects of simultaneous selection on the genetic correlation. They used selection index and concluded that positive and negative genetic correlations tended to decline. However, unequal heritabilities and unequal relative economic weights reduced the rate of change with the greatest imbalance tending to hold the genetic correlation constant or move it toward zero. In a study about selection in a single trait, Villanueva and Kennedy (1990) found that the genetic correlation between the trait under direct selection and the trait indirectly selected always decrease in absolute value, whereas genetic correlations between 2 traits indirectly selected can either decrease or increase in absolute value, depending not only on the signs but also on the magnitudes of the parameters involved.

Strandén et al. (1993) studied how the genetic correlation changes under selection on either single or both traits in a dairy breeding program using simulations. They simulated directional selection by truncation to increase 2 traits and reported that the absolute value of the genetic correlation usually decreased with single trait selection. However, when the initial genetic correlation was low and the residual correlation had the same sign and was high, the genetic correlation increased. With selection on both traits, the change in genetic correlation was always negative, that is, the traits became less positively correlated or more negatively correlated after selection, in agreement with the results found by McMillan et al. (1995).

Itoh (1991) theoretically demonstrated that multi-trait selection changes the genetic correlation always in an undesirable direction. These results agree with the ones found in the present study involving multi-trait selection. In fact, the genetic correlations of FT1 and FT2 with growth traits became more antagonistic and the remaining genetic variation upon which future selection must act for response will face a more undesirable genetic covariance. It is important to consider these changes in the breeding program, and genetic parameters need to be updated regularly. It is important to investigate the trends for the genetic variances and covariances and also for the mean breeding values to detect directional selection.

Holm et al. (2004) studied the effect of selection for production traits in pigs. They estimated genetic correlations for number born alive at first and second parities with adjusted age at 100 kg live weight (0.60 and 0.42), individual feed consumption from 25 to 100 kg (0.23 and 0.20), and percentage of lean meat content (−0.12 and −0.24). The authors concluded that directional selection for production traits resulted in more unfavorable genetic correlations in the second parity compared to the first parity.

In a study of dairy cattle, Haile-Mariam and Pryce (2015) reported that genetic correlations of survival with milk yield declined from 0.45 at the beginning of the study (1993–1994) to −0.15 at the end (2009–2010), whereas the genetic correlation between calving interval and milk yield became more unfavorable and increased from 0.31 to 0.50 over the same period. The genetic correlation between survival and calving interval also became more antagonistic, declining from −0.67 to −0.87. Similar results were found by Lawlor et al. (2002): the genetic correlation between milk yield and productive life decreased from 0.26 (1981) to −0.08 (1996). Another study reported changes in genetic correlations between somatic cell scores and milk yield from positive (0.25) to negative (−0.15) from first to later lactations (Banos and Shook, 1990). It is important to state that in dairy cattle, changes in genetic parameters could be affected by management practices.

According to McMillan et al. (1995), changes in the genetic parameters over time can affect selection decisions. The genetic covariance changes more rapidly than genetic variances. The use of initial genetic parameter estimates without considering the changes and unchanging selection weights for the traits in the selection index could have potentially negative effects on the overall genetic gain. In an example provided by Cheverud (1984), selection to increase 2 traits, with a genetic correlation of −0.80, was 5 times slower than if the genetic correlation was 0.0.

The posterior means and standard deviations estimated for additive genetic covariances are shown in Figure 6. The additive genetic covariances among FT3 and growth traits were stable. The additive genetic covariances of FT1 and FT2 with growth traits were stable with genomic information but decreased if only pedigree and phenotypes were used. The genetic correlations of FT1 and FT2 with growth traits decreased both with and without genomic information. Therefore, the changes observed in genetic correlations in our study are mainly due to the fluctuations in the additive genetic variances as they were stronger than in the genetic covariances.

Figure 6.

Posterior means and standard deviations for additive genetic covariances among fitness (FT1, FT2, and FT3) and growth traits (GT1 and GT2) estimated with (GEN) or without (PED) genotypes. The additive genetic covariances of FT1 and FT2 with growth traits were stable with GEN, whereas they decreased with PED.

Genomic vs. pedigree-based analyses

Heritability estimates were similar for fitness traits with GEN and PED, whereas for both growth traits, the heritabilities calculated with GEN were initially larger but declined faster (Figure 1). These greater initial heritabilities could be because genomic relationships in the limited interval were possibly more informative than the pedigree ones, and because the genomic selection effectively started around 2014, which was evidenced by genetic trends (Figure 7). The steeper decline past 2014 is likely because the analyses with the genomic information account for genomic preselection, which avoids estimation bias (Patry and Ducrocq, 2011b).

Using genomic data before the implementation of genomic selection, Forni et al. (2011) studying a pig population and Veerkamp et al. (2011) studying a dairy cattle population found similar genetic parameter estimates between genomic and pedigree-based analyses. These results are in agreement with our estimates of heritabilities for fitness traits.

Raidan et al. (2018) reported greater heritabilities in genomic analyses for adaptative and growth traits in beef cattle. Momen et al. (2017), in broiler chickens, found that heritabilities using genomic information were greater for body weight at 35 d of age and ultrasound area of breast meat. However, their results were mixed for hen-house egg production. In our study, the heritabilities for growth traits were larger at the beginning but lower at the end, suggesting that the use of time intervals is appropriate to study the changes in genetic parameters over time.

Genetic correlations with GEN, in general, were greater than the estimates with only pedigree and phenotypes (Figure 5). Momen et al. (2017) found similar results for genetic correlations in broiler chickens; genetic correlations between body weight at 35 d of age and hen-house egg production were −0.192 and −0.020 with pedigree-based and genomic analyses, respectively, and genetic correlations for ultrasound area of breast meat and hen-house egg production were −0.206 and −0.154 with pedigree-based and genomic analyses, respectively. The latter authors also reported that genetic correlations between body weight at 35 d of age and ultrasound area of breast meat were similar with pedigree-based (0.484) and with genomic analyses (0.497).

For populations undergone genomic selection, variance components or breeding values estimated using only pedigree and phenotypes are biased because an important piece upon selection is not used in the model. According to Patry and Ducrocq (2011a), this bias is due to preselection or because of the assumption that the mean of the mendelian sampling is 0. The preselection is clear when genetic trends under genomic and non-genomic (i.e., best linear unbiased prediction [BLUP]) analyses are compared. Masuda et al. (2018) showed that the trend for protein yield in U.S. Holsteins under BLUP leveled off, whereas the trend for single-step genomic best linear unbiased predictor (ssGBLUP) showed a greater genetic gain, which agreed with phenotypic trends. In our study, the bias was clear for the heritabilities estimated for growth traits.

Genetic trends estimated by GEN and PED are shown in Figure 7. When the goal of the breeding program is to increase the traits. According to Masuda et al. (2018), if there is a real downward bias using PED because an underestimation of breeding values, the trend by GEN should be greater than by PED for recent animals. Our results agree with this statement as genetic trends by GEN or genomic estimated breeding values (GEBV) were greater than those by PED or estimated breeding values (EBV) in the last 3 yr (2016–2018) for FT1, FT2, and growth traits. Over time, the genetic trends were similar for FT3, mainly due to the weak selection on this trait. However, for FT1, FT2, and growth traits, the difference between genetic trends by PED and GEN was nearly constant until 2015, but the 2 trends started to diverge in 2016.

In populations under selection with selective genotyping or when the genotyped population does not represent well the pedigree population (i.e., genotyped animals from only a few recent generations), a method that accounts for all available pedigree, genotypes, and phenotypes single-step genomic restricted maximum likelihood (ssGREML) produces the most accurate variance components compared with REML or genomic REML if only phenotypes of genotyped animals are considered (Cesarani et al., 2019).

The selection response is dictated by the breeder’s equation. With reduction of the genetic variance and assuming other parts of the breeder’s equation are constant (generation interval, intensity, and accuracy of selection), the selection response should be reduced. With increased accuracy due to the increasing number of genotyped animals (Table 1), again assuming other parts of the breeder’s equation constant, the selection response should accelerate. In our study, the selection response was not reduced (Figure 7), possibly because the reduction of the genetic variance was compensated by increased accuracy of selection.

Conclusions

Under genomic selection, the heritabilities of FT3 and growth traits decrease, and the negative genetic correlations become more negative. Subsequently, genetic gains may not be as high as computed using initial genetic parameters although they could keep constant if the accuracy of selection is increasing due to more genotyped animals. In populations undergone genomic selection, variance components estimated without genomic information are possibly biased. When the number of genotyped animals is large, variance components over time can be estimated using a model with time intervals.

Glossary

Abbreviations

BLUP

best linear unbiased prediction

FT

fitness trait

GEN

genomic analysis

GT

growth trait

LD

linkage disequilibrium

PED

pedigree-based analysis

Conflict of interest statement

The authors declare no real or perceived conflicts of interest.