Abstract
Although the spiral anatomy of the human cochlea seems evident, measuring the highly inter-variable true dimensions is still challenging. Today, only a few three-dimensional reconstruction models of the inner ear are available. Previously, spiral equations were applied to two-dimensional computed tomography (CT) images to predict the electrode insertion depth prior to cochlear implantation. The study aimed primarily to compare the clinical applicability of two analytical cochlear models using a recently introduced planning software to predict the insertion depth of the electrode array of 46 cochlear implant recipients. One was based upon the Escudé formula, which relies only on the basal turn diameter, and another based upon the Elliptic-Circular Approximation (ECA), using the diameter and width. Each case was measured twice by two ENT surgeons. Secondly, in order to measure the benefit of the new planning software over the use of the existing clinical routine method, the results were compared to the prediction based upon a two-dimensional CT image. The intra -and inter-observer agreement using the planning software was significantly better when the ECA was applied, compared to the Escudé formula (p < 0.01). As a reference, the predicted insertion depth was compared to the actual insertion depth measured on post-operative images. The mean absolute error was |2.36| (|1.11|) mm in case of the Escudé approach and |1.19| (|0.92|) mm in case of the ECA. The use of a new planning software that allows three-dimensional handling, integrating the diameter and width of the basal turn (ECA formula), resulted in the most accurate predictions of the electrode insertion depths.
Subject terms: Health care, Bone imaging, Tomography
Introduction
Cochlear implantation is the current standard for the treatment of severe-to-profound sensorineural hearing loss. Despite proliferation of cochlear implant (CI) technology, implantation remains a surgical procedure that requires specific preparation. In order to prepare the surgical procedure, a large number of surgeons create a mental map of the patient’s anatomy based upon interpreting two-dimensional computed tomography (CT) slices acquired preoperatively. The surgeon interprets the CT slices and tries to estimate the cochlear duct length (CDL), i.e. the length to accommodate the electrode array. This is not a trivial task, since the cochlea is highly variable in size1,2. It is hypothesized that preoperative estimation of the CDL can be used to provide surgeons with valuable information to assist with the selection of suitable electrode arrays. As we move towards atraumatic full electrode insertions in an attempt to preserve hearing and structures, the selection of the electrode array is crucial. By selecting an electrode array that optimally fits the cochlear anatomy of the patient, over-insertions can be avoided allowing preservation of cochlear structures3,4. Today, maximum structure preservation has become an important goal during cochlear implantation, since increasing research has proven that cochlear trauma limits the effectivity of electrical stimulation5,6. Avci et al. successfully provided a high-resolution visualization of the internal dimensions and the variability of different morphologies of the cochlea with a precision exceeding that of previous investigations. The described dimensions can be used to investigate the ideal location of the electrode array within the scala, with particular emphasis on the insertion depth of the implant7. Moreover, based upon previous literature, better speech understanding is expected in cases with deeper electrode insertions and should therefore be pursued8,9. The results of Buchman et al. suggest that deeper electrode insertions (and greater insertion angles) appear to offer better speech perception in the early post-activation period. They speculate that deeper electrode insertion angles produce greater degrees of cochlear coverage in the apical regions and therefore better tonotopic place representation for stimulation9.
As presented in the review of Koch et al., there have been a large number of studies introduced from 1884 to the present day that explicitly measured the CDL10. These methods have been measuring at both the bony lateral wall (LW) and at the level of the Organ of Corti (OC). The first method that was used to evaluate the CDL, was the direct method. This method measures the length from histologic sections by a micrometer under a microscope2,11. Later, consistent protocols were developed to graphically represent the CDL by using landmarks from histological sections or plastic casts12–14. However, this indirect method has some major drawbacks. An important drawback of using two-dimensional slices is the cutting angle effect. This effect is known as the effect of not choosing the correct plane for two-dimensional graphical reconstruction, which causes a false representation of the cochlear dimensions. Moreover, indirect measurements were found to underestimate the CDL, since they do not include the unique shape of the hook region15. Three-dimensional reconstructions on the other hand, consider the entire three-dimensional shape of the cochlea. Since they are not susceptible to the viewing angle effects, they are the most accurate models to measure the CDL10,16–18. Up until today, the reconstruction of such three-dimensional models has to be performed by trained experts and is too costly and complex to be integrated in clinical routine. The quality of the current cochlear clinical images is also not sufficient for a consistent three-dimensional reconstruction of the cochlea. To acquire better resolution, extra scanning or specific protocols are required19, which are not only time-consuming but also involve extra radiation exposure.
The basal turn of the cochlea is known as the most visible part on clinical CT images20. Therefore, spiral equations have been developed to rely on measurements of the basal turn parameters. Escudé et al. defined a logarithmic equation to determine the CDL at the level of the lateral wall at each cochlear angle θ using a single linear measurement of basal turn diameter A21. Alexiades then adopted the Escudé formula to estimate the CDL at the level of the electrode array (CDLi)22. Since the Escudé formula assumes a linear dependency of A and B, it does not account for the basal turn width B. However, a study of Meng et al. revealed that the ratio of A and B is not consistent but may vary substantially23. Therefore, Schurzig et al. introduced a new Elliptic-Circular Approximation, which uses both diameter A and width B of the cochlear basal turn20. Another key cochlear parameter that can affect the prediction outcomes is the height of the scala. However, due to the poor resolution of the clinical CT this measurement is not possible. To be able to investigate these analytical cochlear models, there is a need for a planning software that allows three-dimensional handling to provide a quick individualized oblique view of the cochlea based on clinically available CT images. Therefore, it should be easy to make decisions in advance and to plan the best possible outcome for each CI candidate. Recently, a new commercial otological planning software with special focus on cochlear implantation has been introduced24.
The primary aim of the retrospective single-centre study was to investigate the clinical applicability of two analytical cochlear models using a recently introduced planning software that allows three-dimensional handling to predict the electrode insertion depth prior to cochlear implantation. Secondly, the results were compared to the prediction using the traditional estimation based upon the A measurement on two-dimensional graphical CT reconstructions. Moreover, the predicted electrode insertion depths were validated by comparing them to the post-operative actual insertion depth.
Study Design
An experimental version of the planning software was used to analyse the existing pre- and postoperative CT images of 49 CI recipients of the Ear, Nose, and Throat (ENT) department of the Antwerp University Hospital, Belgium. The corresponding datasets were analysed by two experienced ENT surgeons, trained specifically in computer-assisted planning. The study was conducted in accordance with the recommendations of the ethics committee of the Antwerp University Hospital and the protocol was approved on September 9th 2017 (protocol number 17/35/395). The committee waived the need to obtain informed consents for this study.
Subjects
Subjects were selected if they were implanted with the FLEX28 electrode array (MED-EL, Innsbruck, Austria) and if there were pre- and postoperative CT images of their cochleae available. 49 consecutive CI candidates were screened for the study. After a preliminary screening of pre- and postoperative CT images, one otosclerosis case (Subj. 22) was excluded for further analysis because the location of the round window could not be optimally determined due to significant ossification. Subject 29 and subject 49 were also excluded for further analysis since, although complete insertion was predicted preoperatively, post-operative images exposed partial electrode insertion. Of the 46 remaining cases, 21 were male and 25 were female. The median age at the day of the preoperative CT scan was 56 years old ranging from 6 to 81 years. The entire overview of the included subjects (ear of implantation, gender and age at implantation) can be found as Supplementary Table A.
Statistical analysis
Using data from previous studies, the expected standard deviation of the measured linear insertion depth is ±1.5 mm10. Using a non-parametric (Wilcoxon) test, a sample of 42 cochleae would be needed to show that the mean determined by this study is inside this insertion depth range of the previous studies at a power of 90% (significance level of p = 0.05). To investigate the differences between the Escudé approach and ECA nonparametric Wilcoxon signed-rank tests were used. Degree of agreements between both observations (observation 1 and observation 2) and between both observers were analysed using intra-class correlation coefficients (ICC). IBM SPSS Statistics version 24 (IMB; Armonk, NY) was used for the statistical analyses.
Methods
Pre-operative intra and inter-observer agreement
The present study used the clinically available DICOM files (0.1875 * 0.1875 * 0.3 mm voxel), which are part of the clinical pre- and postoperative test protocol in CI. The intra- and inter-observer agreement analysis was performed on the pre-op measurements of the cochlear parameters and the electrode insertion depth predictions. The intra-observer agreement is defined as the repeatability or in ability of the same observer to come up with the same result on a second measurement performed on the same sample. Therefore, each observer measured the parameters two times, with at least an interval of one week between the two measurements. The inter-observer agreement on the other hand, is defined as the reproducibility of the measurements. To evaluate the extent of agreement, intraclass correlation coefficients (ICC) were calculated and Bland-Altman plots were created.
Equations used to predict electrode insertions depths
Typically, the insertion depth of the electrode refers to the covered angular (deg) and linear (mm) length of the cochlea at the electrode silicon tip. The electrode used in the study has a length of 28 mm from the silicon tip to the stopper (Fig. 1). Since this silicon tip is not visible in the post-op images, the validation of the electrode insertion depth prediction was performed on the 1st contact (C1), which is located 26.8 mm from the stopper (1.2 mm from the silicon tip). Therefore, the linear insertion depth of the electrode is taken as 26.8 mm for the flexible 28 mm lateral wall electrode array.
Figure 1.
Flexible 28 mm electrode array (MED-EL, Innsbruck, Austria). The presented electrode array has a length of 28 mm from the silicone tip to the stopper. The distance between the first contact (C1, left side) and the stopper (ride side) is 26.8 mm.
To predict the angular insertion depth of the electrode at C1 the adopted Escudé and ECA formulas were used. Both formulas project the full length of the electrode array (from stopper to the C1) to the estimated cochlear length and assume the electrode would follow a consistent path parallel to the level of the lateral wall, called CDLi.
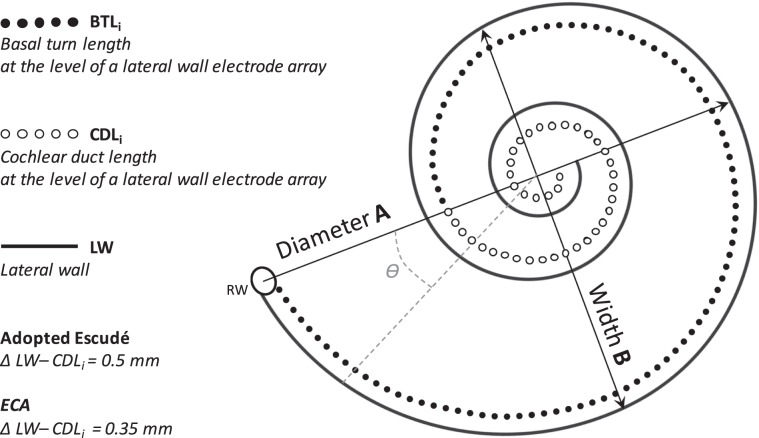
The first approach used an adopted version of the Escudé formula21. The original Escudé formula is based on the cochlear diameter (A) and estimates the length of the cochlear lateral wall at each specific angle (Ɵ). The adopted formula for electrode insertion length prediction implemented in the software assumes that the lateral wall electrode lies under the organ of Corti, 0.5 mm away from the lateral wall and therefore 1 mm is subtracted from the A value to accommodate for this distance (Eq. 1)22.
| 1 |
The second approach used the recently introduced Elliptic-Circular Approximation (ECA)20. In contrast to the Escudé formula, this estimation does not only rely on a single linear measurement of the basal turn diameter (A), but also includes the width of the basal turn (B). ECA assumes that the electrodes lie at a level of 0.35 mm from the lateral wall and therefore subtracts a 0.7 mm from the diameter and width (Fig. 2)22. In this formula, the basal turn length of the cochlea at the level of the electrode (BTLi) is estimated (Eq. 2), and then a percentage-based approximation is used to estimate the insertion depth of the electrode for each angle (Ɵ) (Eq. 3). Supplementary Table B presents for each insertion angle the corresponding basal turn length percentage (1–900 degrees in 1 degree steps). The derivation of the pBTL values is a result of a polynomial fit of the mean BTLLW and CDLLW values of 20 muCT datasets, which is described in detail in Schurzig et al. (Eq. 4)20.
| 2 |
| 3 |
| 4 |
Figure 2.
Schematic representation of the parameters of the cochlear duct. The lateral wall (LW), the Basal turn length (BTL) and the Cochlear duct length (CDL) at the level of a LW electrode array are shown. The arrows show the diameter (A) and the width (B) of the basal turn. The adopted Escudé approach uses 0.5 mm for the distance between the LW and the LW electrode array, while ECA uses 0.35 mm.
Measurement using planning software
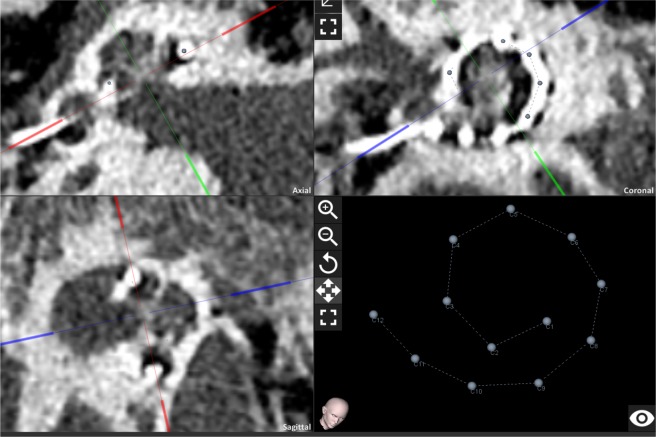
CTs were either imported automatically into the planning software through the PACS network of the hospital or imported from a memory stick. At first, the coronal oblique view, typically referred to as cochlear view, was created by three-dimensionally rotating against the body planes (axial, coronal, and sagittal). This three-dimensional handling is one of the main improvements of using the new planning software compared to the traditional estimations using 2D oblique views. Subsequently, the cochlear parameters of diameter (A) and width (B) were measured by two experienced ENT surgeons on the defined optimal cochlear view. The cochlear diameter (A) is defined as the linear measurement from the round window to the furthest point on the opposite wall of the cochlea, passing through the helicotrema. The cochlear width (B) is defined as the linear measurement perpendicular to the diameter passing through helicotrema connecting the two opposite lateral wall points (Fig. 3).
Figure 3.
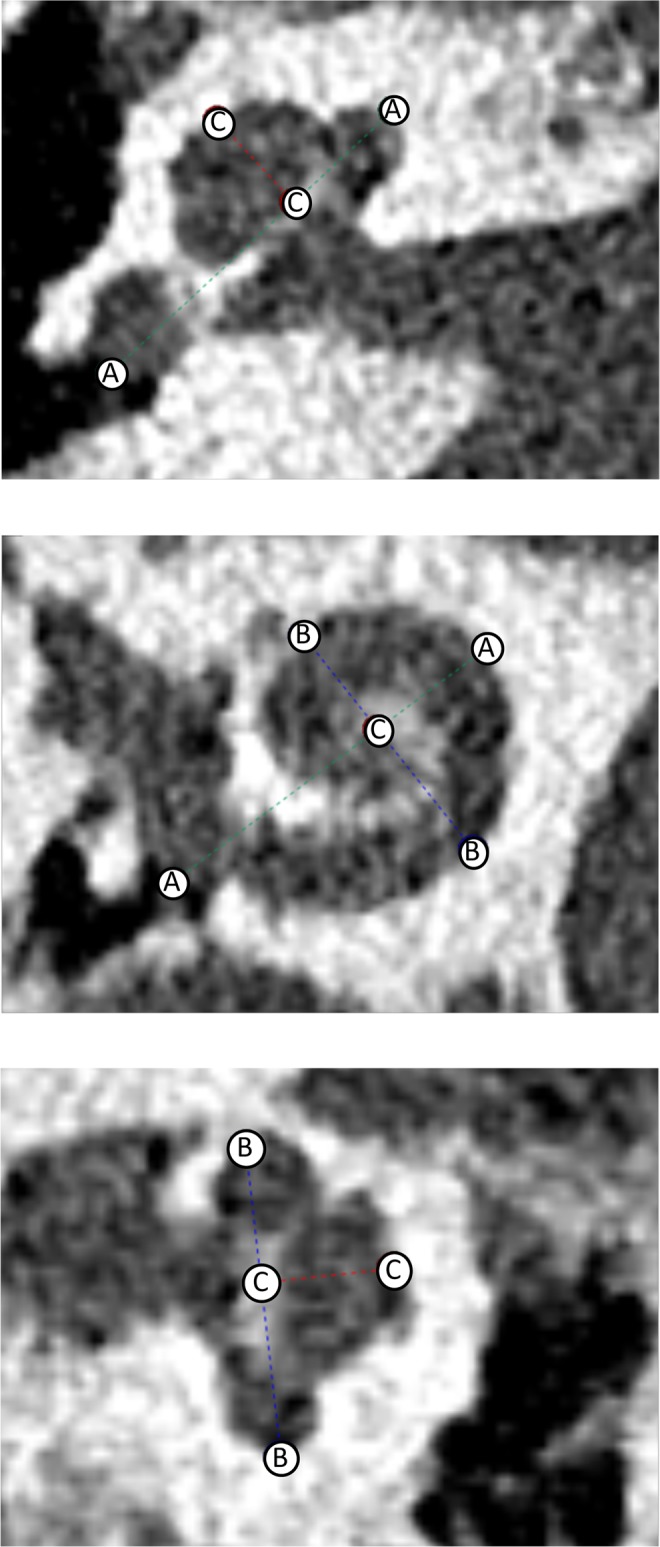
Measurement of the cochlear parameters on the defined optimal cochlear view using the new planning software. Cochlear diameter (A), width (B) and height (C) are shown.
Measurement using traditional 2D oblique view
To investigate the improvement of using the new planning software, the inter- and intra-observer agreement was compared to the agreement achieved with the previously used traditional A measurement, performed on the oblique slices in the Picture Archiving and Communicating System (PACS) viewer (Fig. 4).
Figure 4.
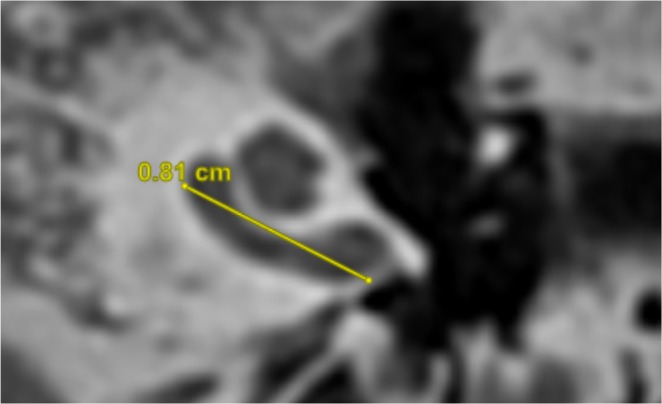
Example of a measurement of the A value on the traditional 2D oblique view in PACS viewer. Cochlear diameter, known as the A value is shown.
Postoperative validation of electrode insertion depth prediction
The postoperative CT images were used for the evaluation of the actual insertion status of the implanted electrode arrays inside the cochlea. In the first step, the cochlear view and coordinate system was set at the planning software using the cross-hairs and then both observers manually selected a point at the centre of each electrode contact (Fig. 5). The software then uses the user defined coordinate system to estimate the angular insertion depth of the selected centre of each electrode contact. In the next step the actual angular insertion angle of C1 is implemented in Eqs. 1–4 to calculate the actual linear insertion length of C1. To estimate the actual insertion depth of the electrode tip, 1.2 mm is added to the linear insertion depth of C1 (Eq. 5). For the subsequent conversion to the angular insertion depth at the tip, Eqs. 1–4 are used. To assess the accuracy of the predicated angular and linear insertion error the predicted values were subtracted from the actual insertion depth values (Eq. 6). The absolute values are used to assess the mean and standard deviation of the prediction errors for each formula.
| 5 |
| 6 |
Figure 5.
Postoperative tool of the planning software. User defined cochlear view and coordinate system by blue, green and red crosshairs and selected centre point of each electrode contact in the planning software.
Results
Intra and inter-observer agreement
Using planning software
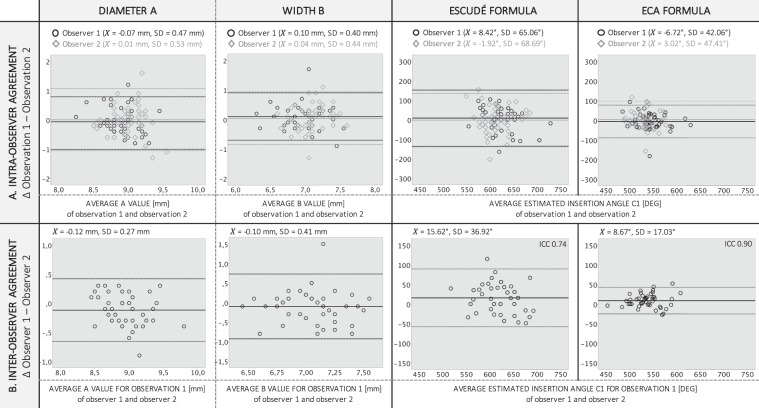
Intra-observer agreements of the preoperative predictions of A, B and the insertion depths of the electrode tip using the planning software are shown in the Bland-Altman in Fig. 6A for each observer. The mean difference of the A measurements at observation one and observation two was −0.07 (SD 0.47) mm for observer one and 0.01 (SD 0.53) mm for observer two. The mean difference of the B measurements at observation one and observation two was 0.10 (SD 0.40) mm for observer one and 0.04 (SD 0.44) mm for observer two. The standard deviation of the differences between the two observations reduced significantly (Wilcoxon Signed Rank test, p < 0.01) when ECA was used (SDOBSERVER_1 42.06°, SDOBSERVER_2 47.41°) for the prediction of the electrode insertion depth at C1 compared to the Escudé approach (SDOBSERVER_1 65.06°, SDOBSERVER_2 68.69°).
Figure 6.
Bland-Altman plots of the intra -and inter-observer agreements for the preoperative A and B measurements and the predictions of the electrode insertion angles, using the adopted Escudé approach and ECA. (A) INTRA-OBSERVER AGREEMENT. For each preoperative measurement the differences between observation 1 and observation 2 are shown against the respective averages of both observations. Data from observer 1 are displayed in black and from observer 2 in grey. The solid lines represent the mean differences between both observations. The top dotted lines show the upper 95% limit of agreement, and the bottom dotted lines show the lower 95% limit of agreement (2STDEV). (B) INTER-OBSERVER AGREEMENT. For each preoperative measurement the differences between observer 1 and observer 2 for their first observation are shown against the respective averages of both observers. The solid lines represent the mean differences between both observers. The top dotted lines show the upper 95% limit of agreement, and the bottom dotted lines show the lower 95% limit of agreement (2STDEV).
Inter-observer agreements of the preoperative predictions of A, B and the insertion depths of the electrode tip using the planning software are shown in the Bland-Altman in Fig. 6B. The mean difference between both observers was −0.12 (SD 0.27) mm for the A measurements and −0.10 (SD 0.41) mm for the B measurements. The standard deviation of the differences between the two observers reduced significantly (Wilcoxon Signed Rank test, p < 0.01) when ECA was used (SD 17.03°) for the prediction of the electrode insertion depth at C1 compared to the Escudé approach (SD 36.92°). The corresponding ICC for the Escudé approach was 0.74, indicating substantial agreement rate. The ICC for the ECA was 0.90, indicating an almost perfect agreement rate.
Using traditional 2D oblique view
The mean difference of the A measurements at observation one and observation two (intra-observer agreement) was 0.09 (SD 0.36) mm for observer one and −0.08 (SD 0.33) mm for observer two. The standard deviation of the prediction of the electrode insertion depth using the traditional 2D oblique view was significantly higher (SDOBSERVER1 = 83.97 and SDOBSERVER2 = 54.67) compared to the predictions with the planning software.
The mean difference between both observers (inter-observer agreement) was −0.65 (SD 0.48) mm for the A measurements. The standard deviation of the differences between the two observers was 97.32° for the prediction of the electrode insertion depth at C1, resulting in a corresponding ICC of 0.58, indicating moderate agreement.
Validation of electrode insertion depth prediction
The average of the actual angular insertion depth of the tip of the electrode using the planning software for both observers, was 562° (1.56 turns) and 572° (1.58 turns) using the ECA and the Escudé formula respectively. The pre-operative estimation of the angular insertion was the most accurate when the planning software used the ECA formula (573°), compared to the use of the Escudé formula in the software (668°) or the estimation based upon the 2D oblique view (795°). For all three estimation methods the preoperative measures overestimated the angular insertion depth.
In Table 1 the absolute angular and linear insertion depth prediction errors for both observers using the planning software (Escudé and ECA approaches) and the traditional estimation based upon a 2D oblique view are shown. It can be seen from the results that all measures overestimated the insertion depth of the electrode, although, when the B value was added (ECA) using the planning software, the overestimation of the predicted insertion angle reduced compared to the Escudé approach. For observer 1 the mean absolute angular and linear insertion error using the planning software was recorder as |98.99|° (SD |42.70|) and |2.50| mm (SD |1.06|) using the Escudé method and reduced significantly to |39.42|° (SD |30.49|) and |1.30| mm (SD |0.98|) using the ECA method. For observer 2 the absolute angular and linear insertion error using the planning software was recorder as |86.51|° (SD |44.52|) and |2.22| mm (SD |1.16|) using the Escudé method and reduced significantly to |32.55|° (SD |26.63|) and |1.10| mm (SD |0.87|) using the ECA method. Significant higher errors were found when the predictions were performed on 2D oblique views. The entire overview of the raw data of the predicted and the actual angular insertion depth of the electrode tip for observer 1 and 2 can be found as Supplementary Table A. For each observer the results are calculated for both observation 1 and observation 2 using both the adopted Escudé formula and using ECA.
Table 1.
Absolute angular and linear insertion depth prediction errors for the Escudé approach and ECA for both observers.
| Insertion prediction error at contact 1 | OBSERVER 1 | OBSERVER 2 | ||||
|---|---|---|---|---|---|---|
| Planning software | 2D oblique | Planning software | 2D oblique | |||
| Escudé | ECA | Escudé | Escudé | ECA | Escudé | |
| Angular [deg] | |98.99|SD |42.70| | |39.42|SD |30.49| | |275.26|SD 88.61 | |86.51|SD|44.52| | |32.55|SD |26.63| | |135.39|SD 63.86 |
| Linear (mm) | |2.50|SD |1.06| | |1.30|SD |0.98| | |5.46|SD 1.35 | |2.22|SD |1.16| | |1.10|SD |0.87| | |3.21|SD |1.34| |
Accuracy of the predicted angular (DEG) and linear (mm) insertion depth errors for both the planning software (using Escudé approach and ECA) and for the traditional estimation based upon a 2D oblique view. Preoperative predicted values were subtracted from the postoperative actual insertion depth values. Mean errors and their standard deviation (SD) of the absolute values are presented.
Discussion
The planning software used in the present study was found to be feasible to pursue optimal cochlear views on preoperative clinical CT images. The Elliptic-Circular approximation, which uses both diameter A and width B of the cochlear basal turn, resulted in more accurate predictions of the electrode insertion depth, compared to Escudé approach that relies on the single linear A measurement. This is in agreement with the findings of MENG et al. that confute the linear dependency of the cochlear basal turn diameter and width23. Moreover, the study of Pietsch et al. demonstrated that the geometry is not similar to a logarithmic spiral and that there are genuine inter-individual differences in cochlear geometry. They argue that logarithmic models are good enough to predict the metric length of the cochlear duct, but fail to predict the details of the spiral shape. Therefore, they developed a polynomial model that requires assessment of the basic individual parameters of cochlear base width, length and their intersection by the modiolus25.
Previous reconstruction models were too complex and therefore not suitable to complete within the available clinical timeframes. In 2017, van der Jagt et al. investigated in a large cohort an automatic tracing method based on voxel intensity to measure cochlear morphology in vivo up to and including the second turn of the cochlea. The possible benefit of the automatic method is the accuracy of the method and susceptibility for observer variability because of the use of 180 measurements per cochlear turn instead of four and because of its objectivity26. Such an automatic tracing method has a lot of potential in the near future to evaluate CI candidates preoperatively. Another methodology for measuring the cochlear duct length was introduced and evaluated by Würfel et al.27. This method uses clinically available high-resolution imaging modalities and relies on manually setting a three-dimensional spiral along the outer cochlear wall. However, up until today such methods are not clinical available yet. With the present planning software on the contrary, the preoperative planning takes on average five minutes and the postoperative analysis takes on average 15 minutes, as it takes longer to select all the electrode contacts on the image. So far, pre- and postoperative planning is only possible in normal anatomies. More research is needed to investigate the applicability and validity of the equations in malformed cochleas. The application may prove to be useful for electrode selection in dysplasia cases.
The intra-user variability largely depends on the image resolution. The consistency of the manual measurements performed in the study are expected to improve with increasing image resolution or when the planning software would be able to automatically provide the cochlear parameters. However, the identification of structures such as the round window membrane requires interpretations that can hardly be automated.
As shown in Table 1, all approaches resulted mainly in overestimations of the predicted insertion depths compared to the reference postoperative measurements, with only a small overestimation for the ECA method (OBSERVER1 = 39° and OBSERVER2 = 33°). A similar study performed by Rathgeb et al. used the adopted Escudé approach in the planning software. They reported a higher overestimation of 73 (96) degrees28. There are certain assumptions made during the pre-op electrode insertion depth prediction that can largely affect the prediction outcomes. Both formulas project the full length of the electrode over a consistent path along the lateral wall, 0.35 mm is case of ECA and 0.50 mm in case of Escudé. This presupposes that the application is for mid-range and lateral wall electrodes and not for modular hugging electrodes. One could argue that the higher overestimation rate found for the Escudé approach is due to the fact that (2*0.5) mm is subtracted from the A value22, whereas for ECA this was only (2*0.35) mm. However, only a small reduction of the overestimation was observed when using (2*0.35) instead of (2*0.5) in the Escudé approach as well. The angular insertion prediction error improved from 99.80° (SD 49.58) to 63.03° (SD 37.71) for observer one and from 84.19° (SD 47.86) to 55.13° (SD 34.39) for observer two. Both formulas also assume a full insertion of the electrode at which the stopper of the electrode array is exactly located at the level of the round window. They do not accommodate for the diameter of the scala, micro blockages inside the cochlea, surgeon’s preference or any other clinical reasons that would cause the electrode to bend. Another assumption made in the analytical cochlear models is the fixed position of the stopper at the level of the round window. However, the conical stopper is inserted up to the level of optimal ceiling. Since this is highly dependent of the anatomy of the round window niche, the distance between the stopper and the round window can cause a prediction error up to 1–2 mm. The ECA underestimates (one-tailed) the insertion depth of a lateral wall electrode on average with −0.58 mm. Taking into account that mean prediction error is about 1.19 mm, only 16% of the planned insertions will exceed the predicted insertion depth and only 2.5% will exceed it with more than 2.38 mm. Therefore, ECA offers a reasonable reliable tool to determine the electrode insertion depth, and it is up to the surgeon to decide on which limits are important i.e. whether not to pass a predefined depth, as is the case in residual hearing or to reach a least a certain insertion depth as in the case of severe hearing loss over all frequencies.
In addition to preoperative insertion predictions, the postoperative tool of the software allows the identification of the exact electrode location within the cochlea which would enable tonotopic stimulation15. This could optimize fitting strategies for CI patients and allow a preoperative or even pre-set fitting strategy based upon a postoperative CT scan to shorten the rehabilitation time with audiologists and speech therapists. Recent studies on CIs have suggested that speech perception is optimized when the frequency information is presented to the normal acoustic tonotopic cochlear location17,18,29,30. Frequency-place maps that are shifted or distorted relative to the normal tonotopic map may reduce speech recognition.
In conclusion, predictions of the electrode insertion depth were made using an experimental version of a new otological planning software, which allows guided three-dimensional handling. The ECA that is based upon two basal turn parameters (diameter and width) yielded more accurate predictions of the electrode insertion depth, compared to the adopted Escudé approach which is based upon a single diameter measurement.
Supplementary information
Acknowledgements
The Antwerp University Hospital is currently receiving a research grant from MED-EL (Innsbruck, Austria).
Author contributions
G.M., P.V., V.T. and V.V.R. conceived and designed the study. G.M. drafted the main manuscript text and undertook the analysis. V.V.R., P.V. and V.T. were involved with the pre –and postoperative measurements. E.G. contributed to the implementation of the planning software into the clinical practice. All authors critically reviewed and approved the final manuscript.
Data availability
The datasets generated in this study are available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
is available for this paper at 10.1038/s41598-020-58648-6.
References
- 1.Erixon E, Hogstorp H, Wadin K, Rask-Andersen H. Variational anatomy of the human cochlea: implications for cochlear implantation. Otol Neurotol. 2009;30:14–22. doi: 10.1097/MAO.0b013e31818a08e8. [DOI] [PubMed] [Google Scholar]
- 2.Hardy M. The length of the organ of Corti in man. Am J Anat. 1938;62:291–311. doi: 10.1002/aja.1000620204. [DOI] [Google Scholar]
- 3.Skinner MW, et al. In vivo estimates of the position of advanced bionics electrode arrays in the human cochlea. Ann Otol Rhinol Laryngol Suppl. 2007;197:2–24. doi: 10.1177/00034894071160S401. [DOI] [PubMed] [Google Scholar]
- 4.Aschendorff A, Kromeier J, Klenzner T, Laszig R. Quality control after insertion of the nucleus contour and contour advance electrode in adults. Ear Hear. 2007;28:75S–79S. doi: 10.1097/AUD.0b013e318031542e. [DOI] [PubMed] [Google Scholar]
- 5.Roland PS, Wright CG. Surgical aspects of cochlear implantation: mechanisms of insertional trauma. Adv Otorhinolaryngol. 2006;64:11–30. doi: 10.1159/000094642. [DOI] [PubMed] [Google Scholar]
- 6.Verberne J, Risi F, Campbell L, Chambers S, O’Leary S. The Effect of Scala Tympani Morphology on Basilar Membrane Contact With a Straight Electrode Array: A Human Temporal Bone Study. Otol Neurotol. 2017;38:47–53. doi: 10.1097/MAO.0000000000001259. [DOI] [PubMed] [Google Scholar]
- 7.Avci E, Nauwelaers T, Lenarz T, Hamacher V, Kral A. Variations in microanatomy of the human cochlea. J Comp Neurol. 2014;522:3245–3261. doi: 10.1002/cne.23594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yukawa K, et al. Effects of insertion depth of cochlear implant electrodes upon speech perception. Audiol Neurootol. 2004;9:163–172. doi: 10.1159/000077267. [DOI] [PubMed] [Google Scholar]
- 9.Buchman CA, et al. Influence of cochlear implant insertion depth on performance: a prospective randomized trial. Otol Neurotol. 2014;35:1773–1779. doi: 10.1097/MAO.0000000000000541. [DOI] [PubMed] [Google Scholar]
- 10.Koch RW, Elfarnawany M, Zhu N, Ladak HM, Agrawal SK. Evaluation of Cochlear Duct Length Computations Using Synchrotron Radiation Phase-Contrast Imaging. Otology & Neurotology. 2017;38:E92–E99. doi: 10.1097/Mao.0000000000001410. [DOI] [PubMed] [Google Scholar]
- 11.Ulehlova L, Voldrich L, Janisch R. Correlative study of sensory cell density and cochlear length in humans. Hear Res. 1987;28:149–151. doi: 10.1016/0378-5955(87)90045-1. [DOI] [PubMed] [Google Scholar]
- 12.Walby AP. Scala tympani measurement. Ann Otol Rhinol Laryngol. 1985;94:393–397. [PubMed] [Google Scholar]
- 13.Pollak A, Felix H, Schrott A. Methodological aspects of quantitative study of spiral ganglion cells. Acta Otolaryngol Suppl. 1987;436:37–42. doi: 10.3109/00016488709124974. [DOI] [PubMed] [Google Scholar]
- 14.Lee J, Nadol JB, Jr., Eddington DK. Depth of electrode insertion and postoperative performance in humans with cochlear implants: a histopathologic study. Audiol Neurootol. 2010;15:323–331. doi: 10.1159/000289571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Greenwood DD. A cochlear frequency-position function for several species–29 years later. J Acoust Soc Am. 1990;87:2592–2605. doi: 10.1121/1.399052. [DOI] [PubMed] [Google Scholar]
- 16.Green JD, Jr., Marion MS, Erickson BJ, Robb RA, Hinojosa R. Three-dimensional reconstruction of the temporal bone. Laryngoscope. 1990;100:1–4. doi: 10.1288/00005537-199001000-00001. [DOI] [PubMed] [Google Scholar]
- 17.Sridhar D, Stakhovskaya O, Leake PA. A frequency-position function for the human cochlear spiral ganglion. Audiol Neurootol. 2006;11(Suppl 1):16–20. doi: 10.1159/000095609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stakhovskaya O, Sridhar D, Bonham BH, Leake PA. Frequency map for the human cochlear spiral ganglion: implications for cochlear implants. J Assoc Res Otolaryngol. 2007;8:220–233. doi: 10.1007/s10162-007-0076-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Koch, R. W., Ladak, H. M., Elfarnawany, M. & Agrawal, S. K. Measuring Cochlear Duct Length - a historical analysis of methods and results. J Otolaryngol-Head N46, 10.1186/s40463-017-0194-2 (2017). [DOI] [PMC free article] [PubMed]
- 20.Schurzig D, et al. A Novel Method for Clinical Cochlear Duct Length Estimation toward Patient-Specific Cochlear Implant Selection. OTO Open. 2018;2:2473974X18800238. doi: 10.1177/2473974x18800238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Escude B, et al. The size of the cochlea and predictions of insertion depth angles for cochlear implant electrodes. Audiol Neurootol. 2006;11(Suppl 1):27–33. doi: 10.1159/000095611. [DOI] [PubMed] [Google Scholar]
- 22.Alexiades G, Dhanasingh A, Jolly C. Method to Estimate the Complete and Two-Turn Cochlear Duct Length. Otology & Neurotology. 2015;36:904–907. doi: 10.1097/MAO.0000000000000620. [DOI] [PubMed] [Google Scholar]
- 23.Meng J, Li S, Zhang F, Li Q, Qin Z. Cochlear Size and Shape Variability and Implications in Cochlear Implantation Surgery. Otol Neurotol. 2016;37:1307–1313. doi: 10.1097/MAO.0000000000001189. [DOI] [PubMed] [Google Scholar]
- 24.Gerber N, et al. Surgical planning tool for robotically assisted hearing aid implantation. Int J Comput Assist Radiol Surg. 2014;9:11–20. doi: 10.1007/s11548-013-0908-5. [DOI] [PubMed] [Google Scholar]
- 25.Pietsch M, et al. Spiral Form of the Human Cochlea Results from Spatial Constraints. Sci Rep. 2017;7:7500. doi: 10.1038/s41598-017-07795-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jagt A, Kalkman RK, Briaire JJ, Verbist BM, Frijns JHM. Variations in cochlear duct shape revealed on clinical CT images with an automatic tracing method. Sci Rep. 2017;7:17566. doi: 10.1038/s41598-017-16126-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wurfel W, Lanfermann H, Lenarz T, Majdani O. Cochlear length determination using Cone Beam Computed Tomography in a clinical setting. Hear Res. 2014;316:65–72. doi: 10.1016/j.heares.2014.07.013. [DOI] [PubMed] [Google Scholar]
- 28.Rathgeb Christoph, Demattè Marco, Yacoub Abraam, Anschuetz Lukas, Wagner Franca, Mantokoudis Georgios, Caversaccio Marco, Wimmer Wilhelm. Clinical Applicability of a Preoperative Angular Insertion Depth Prediction Method for Cochlear Implantation. Otology & Neurotology. 2019;40(8):1011–1017. doi: 10.1097/MAO.0000000000002304. [DOI] [PubMed] [Google Scholar]
- 29.Dorman MF, et al. An electric frequency-to-place map for a cochlear implant patient with hearing in the nonimplanted ear. J Assoc Res Otolaryngol. 2007;8:234–240. doi: 10.1007/s10162-007-0071-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Landsberger DM, Mertens G, Punte AK, Van De Heyning P. Perceptual changes in place of stimulation with long cochlear implant electrode arrays. J Acoust Soc Am. 2014;135:EL75–81. doi: 10.1121/1.4862875. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated in this study are available from the corresponding author on reasonable request.