Abstract.
Purpose: Bayesian theory provides a sound framework for ultralow-dose computed tomography (ULdCT) image reconstruction with two terms for modeling the data statistical property and incorporating a priori knowledge for the image that is to be reconstructed. We investigate the feasibility of using a machine learning (ML) strategy, particularly the convolutional neural network (CNN), to construct a tissue-specific texture prior from previous full-dose computed tomography.
Approach: Our study constructs four tissue-specific texture priors, corresponding with lung, bone, fat, and muscle, and integrates the prior with the prelog shift Poisson (SP) data property for Bayesian reconstruction of ULdCT images. The Bayesian reconstruction was implemented by an algorithm called SP-CNN-T and compared with our previous Markov random field (MRF)-based tissue-specific texture prior algorithm called SP-MRF-T.
Results: In addition to conventional quantitative measures, mean squared error and peak signal-to-noise ratio, structure similarity index, feature similarity, and texture Haralick features were used to measure the performance difference between SP-CNN-T and SP-MRF-T algorithms in terms of the structure and tissue texture preservation, demonstrating the feasibility and the potential of the investigated ML approach.
Conclusions: Both training performance and image reconstruction results showed the feasibility of constructing CNN texture prior model and the potential of improving the structure preservation of the nodule comparing to our previous regional tissue-specific MRF texture prior model.
Keywords: prelog shift Poisson model, convolutional neural network tissue-specific texture prior, machine learning
1. Introduction
Concerns about the radiation risk from the widely used computed tomography (CT) have motivated tremendous efforts toward producing clinically useful images at the lowest dose possible, i.e., ultralow-dose CT (ULdCT). However, the image quality will degrade seriously in the ULdCT case. To address ULdCT image reconstruction challenges, Bayesian theory establishes a sound framework with two terms for modeling the data statistics property (fidelity term) and incorporating a priori knowledge for the to-be-reconstructed image (prior term).1 This study aimed to investigate the feasibility of using a machine learning (ML) strategy, particularly a convolutional neural network (CNN), to construct a tissue-specific texture prior from previous full-dose CT (FdCT) and to integrate the prior with the prelog shift Poisson (SP) data property for Bayesian reconstruction of ULdCT images.
Tissue textures are recognized as useful biomarkers for clinical tasks and play an important role in computer-aided detection and diagnosis.2,3 Previously, we proposed a Markov random field (MRF)-based tissue-specific texture (MRF-T) prior4–6 to preserve the tissue textures in the ULdCT images, which demonstrated clinical benefit in the task-based evaluation.7,8 However, the MRF-T model assumed that the center pixel within the patch has a linear relationship with its neighbor pixels. Therefore, this study aims to investigate the feasibility of “learning” the relationship without any assumption (of linear, nonlinear, or other forms) to benefit from the development of ML, which has been successfully applied in various areas in medical imaging.9–15 Particularly, we propose to construct a CNN-based tissue-specific texture (CNN-T) prior taking advantage of its strength in pattern recognition, which may have the potential to preserve more detail, compared to our previous MRF-T model.
This study further integrates the proposed CNN-T model with the prelog SP data property for Bayesian reconstruction denoted as SP-MRF-T to address the low photon counts and high noise level in ULdCT. In a CT scanner, noise distribution is complicated by a cascade of random processes, such as photon generation, transmission, detection, electronic readout noise, and so on.16,17 The prelog model18–20 directly uses the transmission data from the detector, which can better utilize the statistical property of the x-ray quanta and the electronic background noise in its cost function. It also overcomes many difficulties associated with the log transformation of the postlog domain algorithm21–23 in the ultralow-dose situation, such as undefined negative values,24,25 weight estimation from the noisy data,23,26,27 and so on. Therefore, it has shown theoretical advantages in ULdCT image reconstruction. In the prelog domain algorithms, the SP model is a good approximation to describe the signal property20,28 and thus it is adapted for usage in this study.
In summary, the main contribution of this work is twofold. (1) We investigated the feasibility of constructing the CNN-T prior with no assumptions, comparing it to our previous MRF-T model. Compared to some existing CNN priors, which were proposed as a denoiser where the model parameters were trained with a pair of noise-free and noisy images,5 the presented CNN prior in this study not only denoises but also preserves tissue image textures by training the model parameters to learn the tissue textures, thereby improving the model’s clinical impact. (2) Comparing the presented SP-CNN-T method with our previous SP-MRF-T algorithm, we explored the potential benefit of CNN-T in texture preservation in ULdCT image reconstruction. Preliminary results were reported at the 15th international meeting on fully three-dimensional image reconstruction.29
The rest of this paper is organized as follows. Section 2 describes the proposed SP-CNN-T algorithm and the network design of the CNN priors. Section 3 describes the experiment design and presents the results. Section 4 describes discussion and conclusions.
2. Method
In this paper, we propose a machine-learning approach to construct a tissue-specific texture prior and integrate the prior with the prelog data statistical model under the Bayesian image reconstruction framework for the ULdCT imaging. This section first introduces the Bayesian image reconstruction framework. Then, we describe the “learnt” CNN-T prior within the Bayesian framework. The overall architecture of SP-CNN-T algorithm is presented in the following.
2.1. Bayesian Image Reconstruction Framework
Given a set of acquired transmission data, denoted by a vector , where is the number of data elements, we are interested in a solution, denoted by a vector with number of image voxels, which maximizes the posterior probability . By the Bayesian theorem, we have
| (1) |
where becomes a constant when maximizing the posterior probability; therefore, will be ignored.
For the acquired low-dose transmission data, following the description in the study of Xing et al.,28 we introduce an artificial quantity , which yields
| (2) |
where is the measured photon counts at the detector, and and are the mean and standard deviation of the electronic noise, respectively. Notation is the incident photon counts, and is the ’th line integral along the x-ray path. Let the log data likelihood or fidelity term be and the log prior term, , be described by an MRF model, then the solution for Eq. (1) can be obtained by minimizing the objective function , in which
| (3) |
where is the projection matrix and is the unknown prior, which will be learnt by CNN. Notation is the hyperparameter to balance the strength between the fidelity term and prior term. The introduced artificial quantity enables us to model the fidelity term with the SP distribution in the prelog domain for more accurate modeling. Here enables us to incorporate our prior knowledge as constraint to improve the image reconstruction performance, which could be any assumption, such as piecewise smooth and low-rank property. There are many types of prior or regularization with the purpose of image denoising, deblurring, edge preserving, piecewise smoothing, etc.30–32 In this study, we are more interested in the clinically important texture. In next section, we introduce how to construct the tissue-specific texture prior using the ML approach.
2.2. CNN-Based Texture Prior Learning
Tissue texture reflects the voxel gray-level distribution across the field of view or the contrast between one voxel and its neighboring voxels. Given a pixel and its surrounding neighbors, we define the tissue-specific texture prior to be the relationship between them, where the center pixel value could be inferred by its neighbors based on the pattern specified by its texture. Therefore, we proposed the tissue-specific texture prior in the following analytical form:4–6
| (4) |
where represents the texture prior weights of tissue , represents voxels index, denotes a small fixed neighborhood region of the voxel , and are voxels within . This tissue-specific texture prior has demonstrated certain advantages in clinical tasks.7,8 According to Eq. (4), the texture prior assumes that the center voxel has a linear dependence on its neighboring voxels. Therefore, we aim to construct such a prior without the linear assumption benefiting from the ML technology. We denote the trained CNN model as and the predication model can be expressed as
| (5) |
CNNs could learn a linear/nonlinear or other form model for the relationship between a pixel and its neighbors. Full-dose data were used to train this CNN network. After training, the CNN network can represent the relationship that all neighboring pixels follow.
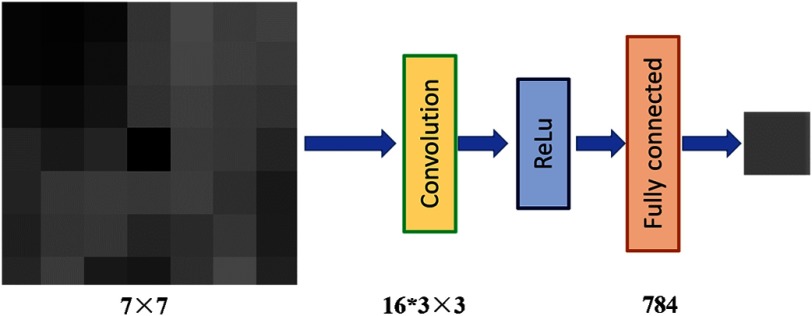
Following the idea of tissue texture, constructing the CNN texture prior is straightforward. We can input the neighboring voxel values to the machine model and ask the machine to predict the center voxel value. By training so, the machine can learn the relationship or the texture. The idea and network are shown in Fig. 1. We design a three-layer CNN model to learn such relationship from data. As our texture prior is tissue-specific, we build four CNN models for lung, bone, fat, and muscle, respectively. This model is trained offline to learn the texture-constrained predictions using the task of predicting a pixel value from its neighbors. Our CNN model has one convolution layer with 16 kernels of size . After the convolution, we use rectified linear unit as the activation function. In the last layer, we apply one fully connected layer with 784 and 1 neurons. The input of the model is a patch from with center pixel removed and to-be-estimated. The output is the estimated value of the center pixel. Mean square error (MSE) is used as training loss.
Fig. 1.
The network design of the proposed CNN model.
2.3. Proposed SP-CNN-T Algorithm
We construct one CNN texture prior, which is a built network saved in the computer. Now, we need to integrate this prior term with the Bayesian image reconstruction framework.
Let an auxiliary variable be , which satisfies . Equation (3) can be expressed as
| (6) |
By half–quadratic splitting method, we have
| (7) |
where the quadratic-type penalty was used. Here, is the penalty parameter, which varies in a nondescending order. Then, Eq. (7) can be solved by the following splitting iterative scheme:31
| (8) |
where indicates the iteration number. Using Eq. (8), the fidelity term and regularization term are decoupled. The fidelity term is associated with a quadratic regularized minimization problem, i.e., the first part of Eq. (8). Surrogate function strategy was used to detangle pixels in the first part of Eq. (8) as done in the study of Gao et al.33. Replacing the prior term of Eq. (4) from the study of Gao et al.,33 we obtained the updated formula for the first part of Eq. (8)
| (9) |
The regularization term is involved in the second part of Eq. (8) with two terms: constrains that the solution should not be too far away from updated by the fidelity. constrains that should satisfy some neighborhood relationship, which is produced by the CNN texture prior defined in Eq. (5), i.e., substituting with , we obtained
| (10) |
where the above equation builds the connection between the proposed CNN texture prior and the data fidelity constraint under Bayesian framework. Quadratic form penalty was used for both constraint and prior knowledge. As introduced above, the CNN texture prior was trained based on the FdCT. During the iteration, it takes the intermediate of low-dose CT (LdCT) and is used to predict the center pixel based on its neighboring pixels of LdCT. This is the key point of incorporating prior knowledge from FdCT into LdCT reconstruction. Unlike universal model for the whole image, such as Huber MRF weights, it considers the tissue types. In addition, this learning method makes the tissue-specific texture more image-adaptive, which means it can recognize more substructure. This is further discussed in Sec. 3.
Equation (10) could be simplified to Eq. (11) with representing the balance between fidelity and texture constraints
| (11) |
The solution of Eq. (11) is
| (12) |
Initially both and are set to zero. The attenuation map with zero initial was updated only by the fidelity term. After about 500 iterations, we start to increase the . Empirically, we varied in an exponentially increasing way, meaning changes slowly at the beginning, then much faster at later stages. We used , where is the iteration number since we start to change . The changed from around 1 to before the convergence criteria were met. The convergence criteria are MSE between and . As discussed above, represents the balance between fidelity and prior term. We choose , which gives us current reasonably good results.
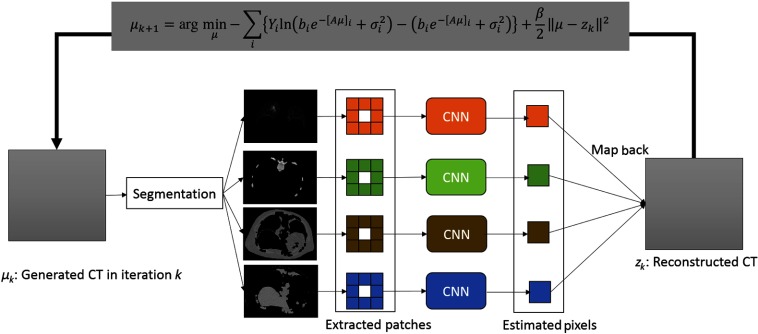
The flowchart of the proposed SP-CNN-T is shown in Fig. 2. The pseudocode of SP-CNN-T is summarized in Table 1.
Fig. 2.
Architecture of the proposed SP-CNN-T.
Table 1.
Pseudocode of the proposed SP-MRF-T algorithm.
| Algorithm: SP-CNN-T |
|---|
| Learn the tissue-specific MRF coefficients: |
| Segment the full-dose filtered back projection (FBP) reconstructed image into four tissue types. |
| Learn the MRF coefficients for each tissue type using the CNN model. |
| Prelog reconstruction for ULdCT: |
| Initialization by FBP. |
| Set parameters: and |
| While stop criterion is not met: |
| Update by Eq. (9). |
| Segment to lung, fat, muscle, and bone. |
| for pixel inside lung, fat, muscle, and bone: |
| determine tissue type for pixel ; |
| update by Eq. (12). |
| End |
| End until the stop criterion is satisfied. |
3. Experiments and Results
Two patients, who were scheduled for CT-guided lung nodule needle biopsy at Stony Brook University Hospital, were recruited for this study under informed consent after approval by the institutional review board. The patients were scanned with full-dose settings, the voltage at 120 kVp, and the tube current at 100 mAs. From here, we obtained the raw transmission data of two sets of FdCT for the following study.
Based on two patients’ scans, we first used one dataset to study the feasibility of constructing texture prior using the ML. Then, without changing any network design in the ML model and parameters in the image reconstruction, we performed the experiments on the other dataset. It not only validates the proposed method in a more diverse data but also helps us further understand whether the proposed CNN prior model is sensitive to the data variation or not. In addition, based on one patient’s scans, we first performed experiments using the learnt CNN prior and simulated ULdCT transmission data from the same FdCT slice, which means that the machine has “seen” the exact image during the training. Then, we performed the experiments using the CNN prior from the neighboring adjacent slices for the target slice reconstruction. Because this proposed tissue-specific CNN prior does not require strict registration between previous FdCT and current ULdCT scan, the second experiment can investigate the performance with the mismatch of slice location and the tissue regions.
3.1. CNN-Based Tissue-Specific Texture Prior
Following the instruction in Sec. 2, we first segmented the FdCT image into four tissue types. For each tissue type, patches with size were extracted and used as the training samples. For the experiment data, there are around 20,000 training samples for lung, fat, and muscles, and around 2500 training samples for bone region. To train CNN models, we select RMSprop optimizer,34 with learning rate set to . Early stop35 is adapted to prevent overfitting in training. We initialize the weights of convolution kernels with the method introduced in the study of He et al.36
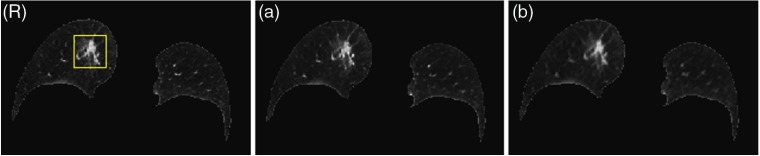
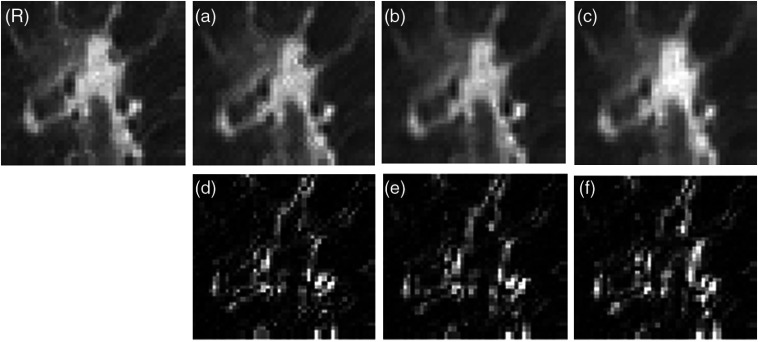
Figure 3 shows the training performance of the CNN model for lung region. Figure 3(R) refers to reference image, which is the ground truth. Figure 3(a) shows the CNN-predicted image by inputting patch of reference image and center pixels removed and Fig. 3(b) shows the linear MRF model-predicted image with the same input of CNN model. The structure predicted by CNN model keeps sharp at the edges and the blood vessels can also be seen clearly. There is a blurring in analytical MRF texture model, since we retreated the whole lung tissue as a region previously. Comparing the nodule region (yellow box in Fig. 3) of the two prediction models with ground truth, the CNN model can effectively learn the texture consistency constraint with better the local structures preserved.
Fig. 3.
The training performance of the CNN model for lung. (R) Reference image (ground truth). (a) Reference image predicted by CNN model. (b) Reference image by the linear analytical model. The display window is .
3.2. ULdCT Image Reconstruction
From the transmission data, we simulated the transmission data of the ULdCT level based on the physics mechanism of the CT signal generation. The signal is approximated as a combination of Poisson statistics and Gaussian statistics. The mean of the Poisson distribution for one certain mAs level can be obtained from the semiexperimental model in Refs. 27 and 37, where the photon count per ray is linearly dependent with the x-ray current settings at the fixed voltage setting. We then added Poisson noise to the x-ray quanta and combined it with the Gaussian-distributed electronic noise. In this study, the mean and standard deviation of the electronic noise are 10 and 25, respectively, similar to the setup in the study of Li et al.38
For comparison purpose, we implemented our previous proposed SP-MRF-T method, which use the SP model for the fidelity term and linear analytical MRF texture model for the prior term in the cost function. Moreover, SP-No Prior (with no prior applied) and SP-Huber-MRF (Huber MRF weights6) were also employed for comparison. The element of well-established Huber MRF weights is inversely proportional to the Euclidean distance between two voxels, which consider the piecewise smoothing spatially invariantly inside one region and preserve the edge sharpness of the region. For the analytical prior algorithms, all of them are MRF-type weights and with the same window size. They share the same optimized parameters. For example, the reconstruction stopped after 1500 iterations. The hyperparameter to tune the prior strength is set as 800. For CNN prior, the parameters have been discussed above.
The reconstruction results are compared in Fig. 4. First row shows the reference images. Second to fifth rows are the results of SP-No Prior, SP-Huber-MRF, SP-MRF-T, and SP-CNN-T, respectively. First and second columns are the reconstructed images and their zoomed-in images with display window . Third and fourth columns are difference images comparing to the reference images with display window . The nodule region, which is also our region of interest (ROI), is labeled in yellow box. In addition, one muscle region is also marked in a red circle for comparison. Without prior, high-level random noise is observed in images of SP-No Prior. It is clear that the prior can effectively suppress the noise. Comparing the ROI region, the SP-CNN-T outperforms other methods with least difference image.
Fig. 4.
Comparison of reconstructed images using different prior models. First row consists of reference images. Second to fifth rows contain results of SP-No Prior, SP-Huber-MRF, SP-MRF-T, and SP-CNN-T, respectively. First and second columns are reconstructed images and their zoomed-in images with display window . Third and fourth columns are difference images comparing to the reference images with display window .
Since the nodule is of the most clinical interest, we then focus our evaluation on the nodule. In this case, the nodule is glass-ground like, which is an important indicator for high chance to be cancer. We compared the nodules reconstructed by the aforementioned four methods. The comparison is presented in Fig. 5. According to Fig. 5(a), without any prior, the structure is buried in the noise. It is hard to identify the edges and blood vessels. The noise is suppressed significantly by applying Huber MRF prior in Fig. 5(b) and tissue-specific MRF prior in Fig. 5(c). However, the tiny structures were blurred to some extent. For example, the contrast of the “glass edge” of nodule (labeled by the yellow arrow in Fig. 5) is hard to identify. Our proposed CNN texture prior preserves the tiny structures well while suppressing the noise.
Fig. 5.
Comparison of ROI in reconstructed images using different prior models. (R) Full-dose image reconstructed by the FBP, which is treated as the golden standard reference. (a)–(d) The used priors are no prior, Huber MRF prior, tissue-specific MRF prior, and CNN prior, respectively. The display window is . (e)–(h) Difference between (a)–(d) and the reference (R).
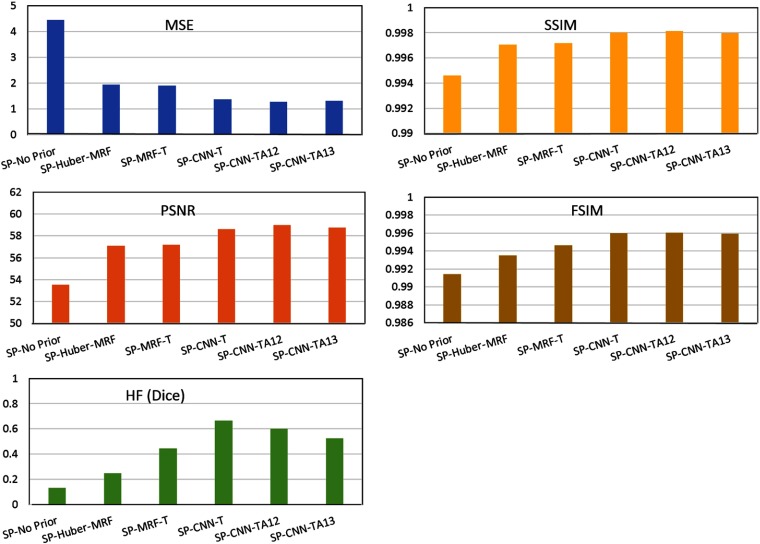
Quantified measures of the ROI are summarized in Table 2. We use the MSE, peak signal-to-noise ratio (PSNR), structure similarity (SSIM), feature similarity (FSIM),39 and Haralick feature (HF)40 metrics to quantify the image quality. MSE gives a quality score based on the pixel-based variation. PSNR evaluates the image quality in terms of noise suppression. SSIM evaluates the image similarity at the structure-based stage. FSIM mimics the human visual system to evaluate the image quality.39 HF gives the quality score from the task-based evaluation view, since HFs have been widely and successfully used in various clinical tasks.40,41 Since the HF is a set of quantities or in a vector form, we use the Dice coefficient to quantify the quality.42 For MSE, a smaller value means better image quality. For the other four metrics, higher values mean better image quality.
Table 2.
Quantified measures ROI in reconstructed images using different prior models.
| MSE | PSNR | SSIM | FSIM | HF | |
|---|---|---|---|---|---|
| SP-No Prior | 53.5226 | 0.9946 | 0.9914 | 0.1333 | |
| SP-Huber-MRF | 57.1175 | 0.9971 | 0.9935 | 0.2500 | |
| SP-MRF-T | 57.1902 | 0.9972 | 0.9946 | 0.4444 | |
| SP-CNN-T | 58.6137 | 0.9980 | 0.9960 | 0.6667 |
According to Table 2, quantified measures agree well with visual inspection. Without any prior, the image quality was worst for the five metrics. SP-Huber-MRF method improved the image quality. SP-MRF-T method achieved a further improvement over SP-Huber-MRF method, which agrees well with our previous study.4–6 The proposed SP-CNN-T outperforms the other models for all five metrics, which demonstrates the potential of ML to further improve the analytical model. There may be two main reasons for the gain of the CNN-T over MRF-T. One is the linear assumption as mentioned in Sec. 1. The ML model removes this assumption and could be any form inside its model, which may bring in the gain by higher order approximation. Another reason could be the power of ML model in texture pattern or substructure recognition. Therefore, the CNN-T can adapt the weights in the model according to the texture pattern described by the neighboring voxels. For example, there are some subsubstructures in the lung region, such as vessel, alveolus, etc. The CNN model can somehow recognize such substructures and adapt the corresponding weights to make the texture prior more accurate. Similar work was also explored in our previous analytical MRF texture model.4 In the initial work, we derived the texture MRF weights for each individual patch of the FdCT and then used the weights as prior for the corresponding patch in its LdCT image reconstruction.4 This patch-based MRF texture prior works perfectly, but it requires strict image registration between the FdCT and LdCT. Then, we developed the regional texture MRF model, which derives one set of MRF weights from the whole tissue and applies it into that tissue region, e.g., lung, bone, fat, and muscle.6 Despite the small variation within the same tissue region, the regional MRF texture prior model works well.7,8 Although the patched-based model works better than the regional model, the regional model makes it possible in practical use. Similarly, the ML model may have the ability to recognize substructures within the tissue region and thus works better than the analytical model, where one set weight is used for the whole tissue region.
3.3. Robustness Study
The proposed SP-CNN-T outperforms other comparison methods in one of our experimental dataset. Without changing any settings in the CNN training model and hyperparameter values in the image reconstruction, we evaluated this method on another dataset. Since experiments above have already shown the superiority of the texture prior, we now mainly compare the analytical texture prior model with the ML prior model.
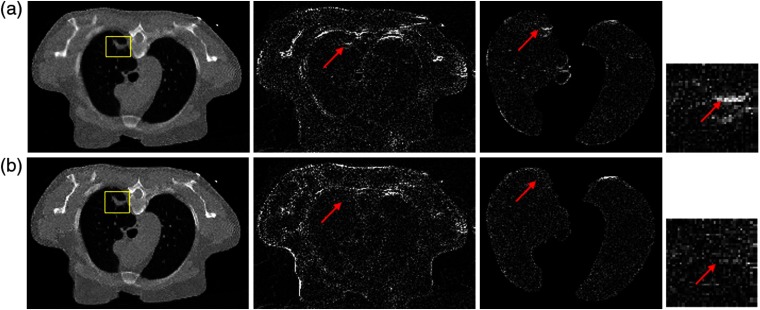
The reconstruction results of another dataset are shown in Fig. 6. The result on top is from SP-MRF-T method, and of the bottom from SP-CNN-T. For each row, from left to right, the picture is reconstructed image, the image difference from FdCT (reference), the image difference of lung from FdCT, and the image difference of nodule from FdCT, respectively. The nodule region is marked in yellow box. The difference image shows larger errors at lung nodule (labeled by the red arrows) in SP-MRF-T than SP-CNN-T but comparable error in the rest nodule region. This also indicated our analysis above. MRF-T and CNN-T perform similarly in most of tissue region, but differently at some substructure location. Quantified measures of the ROI are presented in Table 3. The metric values agree well with our visual judgment and also agree with our observation on the other dataset. Improved performance was observed in SP-CNN-T over SP-MRF-T through five quantified metrics in terms of noise suppression and texture preservation. Possible reasons for this gain have been discussed above in reference to the study by Zhang et al.4 because of their consideration of the neighboring information.
Fig. 6.
Comparison of reconstructed images by (a) SP-MRF-T and (b) SP-CNN-T. For each row, from left to right, the picture is the reconstructed image [the display window is ], the image difference from FdCT (reference), the image difference of lung from FdCT, and the image difference of nodule from FdCT. The nodule is labeled in yellow box.
Table 3.
Quantified measures ROI in reconstructed images using different prior models.
| Methods | MSE | PSNR | SSIM | FSIM | HF |
|---|---|---|---|---|---|
| SP-MRF-T | 55.3773 | 0.9941 | 0.9958 | 0.3529 | |
| SP-CNN-T | 57.8329 | 0.9977 | 0.9982 | 0.6000 |
Experimental results from both datasets agree well with each other. First, we demonstrate the superior performance of the proposed SP-CNN-T with different types of lung nodules. Second, the “learning” network designed based on the CNN is stable to the data variation. However, comparing both cases, we found that the training samples of each tissue type are comparable. For example, the lung region area of two patients is very similar. To further study the sensitivity of the network may require various data samples. For the hyperparameter, we chose it as 800 according to our previous experience. Usually, it will give us comparable and reasonable results when the parameter is within one range. There are also some studies43,44 to tune the hyperparameters using the ML method. This will be one of our future interests.
3.4. CNN-Based Tissue-Specific Texture Prior from Adjacent Slices
In our previous study,6 it is observed that the tissue textures from the nearest three neighboring slices are very similar to that of the target slice. This observation relieves the constraint of strict slice registration. Therefore, we further investigate the feasibility of extracting the CNN-T prior from the neighboring slices for the target slice. We first use the CNN prior, which was trained by adjacent slice (CNN-TA) around the target slice of the full-dose scan to predict the target slice of the FdCT. Then, we applied the CNN-TA prior to reconstruct the ULdCT images of the target slice.
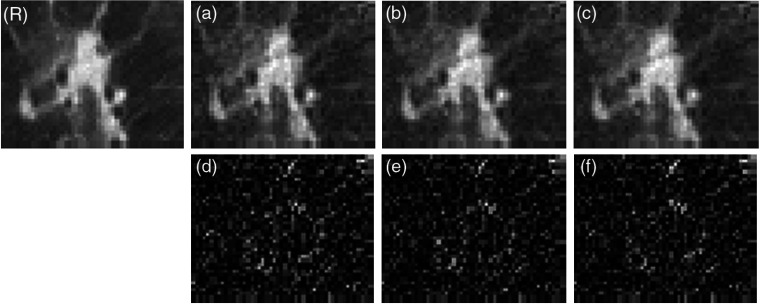
We denote the target as slice 11, of which two adjacent slices 12 and 13 are used to train the CNN model. Then, we use the trained CNN-TA to predict target slice directly by feeding in the patches of slice 11. Figure 7 shows the zoomed ROI of predicted target slice from CNN models trained by different slices as well as their difference to the reference. By visual assessment, the predicted images are very similar to each other, which agreed with our expectation that the adjacent two slices share the similar texture. From their difference, the farthest slice predicted images with relatively large difference comparing to the other two slices as expected.
Fig. 7.
Comparison of ROI in full-dose reconstructed images predicted by different CNN prior. (R) Full-dose image. (a)–(c) The used CNN priors are trained by slices 11 (target slice), 12 (adjacent slice), and 13 (adjacent slice) of the full-dose scans, respectively. The display window is . (d)–(f) The difference between (a)–(c) and the reference (R).
We use the CNN-TA as the prior in the SP-CNN-T algorithm to reconstruct the ULdCT scan of slice 11. The zoomed ROIs of reconstructed images are shown in Fig. 8. The CNN-TA has a similar performance with the CNN-T, where no obvious difference is shown among Figs. 8(a)–8(c). However, the difference images of Figs. 8(d)–8(f) show dissimilar pattern compared with Figs. 7(d)–7(f). In Fig. 7, the difference images have larger values around structure. The difference images of Fig. 5 seem following random distribution. This observation indicates the effect of different noise strength of the FdCT and ULdCT. In both FdCT and ULdCT cases, the CNN prior trained by adjacent slices can be used for the reconstruction of the target slice. In other words, no strict registration is required for the proposed CNN texture prior (Fig. 9).
Fig. 8.
Comparison of ROI in low-dose reconstructed images using different CNN prior. (R) Full-dose image reconstructed by the FBP, which is treated as the golden standard reference. (a)–(c) The used CNN priors are trained by slices 11 (target slice), 12 (adjacent slice), and 13 (adjacent slice) of the full-dose scans, respectively. The display window is . (d)–(f) The difference between (a)–(c) and the reference (R).
Fig. 9.
Performance comparison of different methods with MSE, PSNR, SSIM, and Haralick measures.
Quantitative measures on the results of different reconstruction methods mentioned above are summarized and shown in Fig. 7. The quantified measures agree well with our visual judgment. Overall, the proposed texture prior whether analytical or CNN type performs better than other comparison models in terms of noise suppression and texture preservation. The CNN texture prior performs better than the analytical texture model, which fits our expectation that the CNN prior removes the line assumption of the analytical prior, which may enable it a better approximation of texture pattern. Similar performance of CNN prior from adjacent slices is observed, which also makes the proposed CNN-T friendly and applicable in practice.
4. Conclusions and Discussion
In this paper, we proposed a way of constructing tissue-specific texture prior by ML from previous FdCT scan for current ULdCT image reconstruction. This work expanded our previously proposed analytically derived texture prior by removing the linear assumption of the previous model.6 We further integrated the machine-learnt texture, CNN-T, with the prelog SP model (SP-CNN-T) under the Bayesian law for ULdCT imaging reconstruction. The proposed SP-CNN-T method can adaptively extract the MRF textures because of its benefit from the power of CNN in pattern or substructure recognition. By applying this adaptive tissue texture prior, the nodule texture can be preserved significantly. The feasibility and potential of this investigated ML approach is evaluated by clinical patient datasets.
This paper utilized CNN to learn information from FdCT as a prior for ULdCT image reconstruction. This method can be adapted for applications with available previous FdCT, e.g., interval evaluation, image-guided interventions, dynamic studies, biopsy, etc. Even though promising results have been demonstrated, a task-based evaluation is needed by more clinical datasets for each specific clinical task. This is one of our future research tasks. Another remaining issue that shall be addressed is the availability of previous FdCT. Although the proposed CNN-T does not require strict registration between the FdCT and ULdCT, it still extracts information from its previous FdCT, which may not always be available in all clinical cases, such as lung screening. We have performed a pilot study of extracting texture information from previous FdCT database to remove this constraint based on the analytical MRF texture model,7 where encouraging results have been shown. In the future, we will also develop this CNN-T model to extract prior information from FdCT database and evaluate the developed model toward its application in clinical practice.
Acknowledgments
This work was partially supported by the Foundation for the National Institutes of Health (FNIH) (Grant No. CA206171).
Biographies
Yongfeng Gao received her PhD from the School of Physics at Peking University, Beijing, China, in 2018. She held a visiting scholar position in the Colliding and Accelerator Department, Brookhaven National Lab from January 2016 to October 2017. In 2017, she joined Stony Brook University as a specialist and now is a postdoctoral researcher in the Department of Radiology. Her research interests include low-dose CT reconstruction and machine learning (ML).
Jiaxing Tan received PhD in computer science from the City University of New York in 2019 with research area of computer vision and medical imaging. This work was done during his research internship at IRIS Lab, the Department of Radiology, State University of New York, Stony Brook, in 2018.
Yongyi Shi received his BSc and MSc degrees from Xi’an Jiaotong University, Xi’an, China, in 2014 and 2016, respectively. He is currently pursuing his PhD in the Institute of Image Processing and Pattern Recognition, Xi’an Jiaotong University. He was a visiting scholar in the Department of Radiology, Stony Brook University, New York, USA, in 2019. His research interests include CT reconstruction and ML.
Siming Lu received his MS degree in medical physics from Duke University in 2014, followed by two years of therapeutic medical physics residency training at Henry Ford Hospital. Then, in 2016, he became a therapeutic medical physicist at the Memorial Sloan Kettering Cancer Center. In 2019, he joined as a senior medical physicist in the Department of Radiation Oncology, Stony Brook University Hospital.
Amit Gupta completed medical school (2005) and a radiology residency (2009) in India. Then, he pursued four additional years of training at Cleveland Clinic, Cleveland, Ohio, USA, which included three clinical fellowships (one year each) in thoracic imaging, vascular and interventional radiology, and nuclear imaging and one year of clinical research fellowship in radiology. He is board certified by the American Board of Radiology and currently serving as an associate professor of clinical radiology at Stony Brook University Hospital, Stony Brook, New York, USA. The Society of Interventional Radiology has awarded him fellowship status. His research interests include postprocessing techniques to optimize quality of images obtained using low x-ray dose.
Haifang Li received his BS degree from the Department of Chemistry, University of Science and Technology, Heifei, China. He obtained his PhD in chemistry from the State University of New York, Stony Brook, USA. He is now a research faculty in the Department of Radiology, Stony Brook University.
Zhengrong Liang received his PhD in physics from the City University of New York in 1987, followed by a one-year research fellowship in nuclear medicine and radiation oncology at the Albert Einstein College of Medicine. He had been a research associate and then an assistant professor in radiology at Duke University Medical Center. He joined State University of New York, Stony Brook, in 1992 and currently holds a professorship in the Departments of Radiology and Biomedical Engineering.
Disclosures
The authors of this work declare no conflicts of interest.
Contributor Information
Yongfeng Gao, Email: Yongfeng. Gao@stonybrookmedicine.edu.
Jiaxing Tan, Email: jtan@gradcenter.cuny.edu.
Yongyi Shi, Email: yongyi.shi@stonybrookmedicine.edu.
Siming Lu, Email: siming.lu@stonybrookmedicine.edu.
Amit Gupta, Email: amit.gupta@stonybrookmedicine.edu.
Haifang Li, Email: haifang.li@stonybrookmedicine.edu.
Zhengrong Liang, Email: Jerome. Liang@stonybrookmedicine.edu.
References
- 1.Elbakri I., Fessler J., “Efficient and accurate likelihood for iterative image reconstruction in x-ray computed tomography,” Proc. SPIE 5032, 1839–1850 (2003). 10.1117/12.480302 [DOI] [Google Scholar]
- 2.Gatenby R., Grove O., Gillies R., “Quantitative imaging in cancer evolution and ecology,” Radiology 269(1), 8–15 (2013). 10.1148/radiol.13122697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ng F., et al. , “Assessment of primary colorectal cancer heterogeneity by using whole-tumor texture analysis,” Radiology 266(1), 177–184 (2013). 10.1148/radiol.12120254 [DOI] [PubMed] [Google Scholar]
- 4.Zhang H., et al. , “Deriving adaptive MRF coefficients from previous normal-dose CT scan for low-dose image reconstruction via penalized weighted least-squares minimization,” Med. Phys. 41(4), 041916 (2014). 10.1118/1.4869160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Han H., et al. , “Texture-preserved penalized weighted least-squares reconstruction of low-dose CT image via image segmentation and high-order MRF modeling,” Proc. SPIE 9783, 97834F (2016). 10.1117/12.2216428 [DOI] [Google Scholar]
- 6.Zhang H., et al. , “Extracting information from previous full-dose CT scan for knowledge-based Bayesian reconstruction of current low-dose CT images,” IEEE Trans. Med. Imaging 35(3), 860–870 (2016). 10.1109/TMI.2015.2498148 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liang Z., et al. , “Different lung nodule detection tasks at different dose levels by different computed tomography image reconstruction strategies,” in IEEE Nucl. Sci. Symp. and Med. Imaging Conf. (2018). 10.1109/NSSMIC.2018.8824410 [DOI] [Google Scholar]
- 8.Gao Y., et al. , “A feasibility study of extracting tissue textures from a previous full-dose CT database as prior knowledge for Bayesian reconstruction of current low-dose CT images,” IEEE Trans. Med. Imaging 38(8), 1981–1992 (2019). 10.1109/TMI.42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen H., et al. , “Low-dose CT with a residual encoder-decoder convolutional neural network,” IEEE Trans. Med. Imaging 36(12), 2524–2535 (2017). 10.1109/TMI.2017.2715284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jin K. H., et al. , “Deep convolutional neural network for inverse problems in imaging,” IEEE Trans. Image Process. 26(9), 4509–4522 (2017). 10.1109/TIP.2017.2713099 [DOI] [PubMed] [Google Scholar]
- 11.Kang E., Min J., Ye J. C., “A deep convolutional neural network using directional wavelets for low-dose x-ray CT reconstruction,” Med. Phys. 44(10), e360–e375 (2017). 10.1002/mp.2017.44.issue-10 [DOI] [PubMed] [Google Scholar]
- 12.Ledig C., et al. , “Photo-realistic single image super-resolution using a generative adversarial network,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 4681–4690 (2017). 10.1109/CVPR.2017.19 [DOI] [Google Scholar]
- 13.Wolterink J. M., et al. , “Generative adversarial networks for noise reduction in low-dose CT,” IEEE Trans. Med. Imaging 36(12), 2536–2545 (2017). 10.1109/TMI.2017.2708987 [DOI] [PubMed] [Google Scholar]
- 14.Chen H., et al. , “LEARN: learned experts’ assessment-based reconstruction network for sparse-data CT,” IEEE Trans. Med. Imaging 37(6), 1333–1347 (2018). 10.1109/TMI.2018.2805692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yang Q., et al. , “Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss,” IEEE Trans. Med. Imaging 37(6), 1348–1357 (2018). 10.1109/TMI.2018.2827462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fu L., et al. , “Comparison between pre-log and post-log statistical models in ultra-low-dose CT reconstruction,” IEEE Trans. Med. Imaging 36(3), 707–720 (2017). 10.1109/TMI.2016.2627004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang G., et al. , “Hybrid pre-log and post-log image reconstruction for computed tomography,” IEEE Trans. Med. Imaging 36(12), 2457–2465 (2017). 10.1109/TMI.2017.2751679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Erdogan H., Fessler J. A., “Monotonic algorithms for transmission tomography,” IEEE Trans. Med. Imaging 18(9), 801–814 (1999). 10.1109/42.802758 [DOI] [PubMed] [Google Scholar]
- 19.Man B. D., et al. , “An iterative maximum-likelihood polychromatic algorithm for CT,” IEEE Trans. Med. Imaging 20(10), 999–1008 (2001). 10.1109/42.959297 [DOI] [PubMed] [Google Scholar]
- 20.Elbakri I., Fessler J., “Statistical image reconstruction for polyenergetic x-ray computed tomography,” IEEE Trans. Med. Imaging 21(2), 89–99 (2002). 10.1109/42.993128 [DOI] [PubMed] [Google Scholar]
- 21.Fessler J. A., et al. , “Grouped coordinate ascent algorithms for penalized-likelihood transmission image reconstruction,” IEEE Trans. Med. Imaging 16(2), 166–175 (1997). 10.1109/42.563662 [DOI] [PubMed] [Google Scholar]
- 22.Li Q., Leahy R., “Statistical modeling and reconstruction of randoms precorrected PET data,” IEEE Trans. Med. Imaging 25(12), 1565–1572 (2006). 10.1109/TMI.2006.884193 [DOI] [PubMed] [Google Scholar]
- 23.Wang J., et al. , “Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose x-ray CT,” IEEE Trans. Med. Imaging 25(10), 1272–1283 (2006). 10.1109/TMI.2006.882141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kaufman L., “Maximum likelihood, least squares and penalized least square for PET,” IEEE Trans. Med. Imaging 12(2), 200–214 (1993). 10.1109/42.232249 [DOI] [PubMed] [Google Scholar]
- 25.Fessler J., “Penalized weighted least-squares image reconstruction for positron emission tomography,” IEEE Trans. Med. Imaging 13(2), 290–300 (1994). 10.1109/42.293921 [DOI] [PubMed] [Google Scholar]
- 26.De Man B., et al. , “Reduction of metal streak artifacts in x-ray computed tomography using a transmission maximum a posteriori algorithm,” IEEE Trans. Nucl. Sci. 47(3), 977–981 (2000). 10.1109/23.856534 [DOI] [Google Scholar]
- 27.Ma J., et al. , “Variance analysis of x-ray CT sinograms in the presence of electronic noise background,” Med. Phys. 39(7), 4051–4065 (2012). 10.1118/1.4722751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Xing Y., et al. , “Ultralow-dose CT image reconstruction with pre-log shifted-Poisson model and texture-based MRF prior,” in Int. Conf. Fully 3D Image Reconstr. Radiol. and Nucl. Med., pp. 254–258 (2017). [Google Scholar]
- 29.Gao Y., et al. , “A machine learning approach to construct a tissue-specific texture prior from previous full-dose CT for Bayesian reconstruction of current ultralow-dose CT images,” Proc. SPIE 11072, 1107204 (2019). 10.1117/12.2534441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Romano Y., Elad M., Milanfar P., “The little engine that could: regularization by denoising (RED),” SLAM J. Imaging Sci. 10(4), 1804–1844 (2017). 10.1137/16M1102884 [DOI] [Google Scholar]
- 31.Zhang K., et al. , “Learning deep CNN denoiser prior for image restoration,” in IEEE Conf. Comput. Vison and Patten Recognit., pp. 3929–3938 (2017). 10.1109/CVPR.2017.300 [DOI] [Google Scholar]
- 32.He J., et al. , “Optimizing a parameterized plug-and-play ADMM for iterative low-dose CT reconstruction,” IEEE Trans. Med. Imaging 38(2), 371–382 (2019). 10.1109/TMI.2018.2865202 [DOI] [PubMed] [Google Scholar]
- 33.Gao Y., et al. , “Characterizing CT reconstruction of pre-log transmission data toward ultra-low dose imaging by texture measures,” in IEEE Nucl. Sci. Symp. and Med. Imaging Conf., pp. 1–4 (2018). 10.1109/NSSMIC.2018.8824295 [DOI] [Google Scholar]
- 34.Hinton G., Srivastava N., Swersky K., “Neural networks for machine learning lecture, overview of mini-batch gradient descent,” Vol. 14, p. 8 (2012).
- 35.Girosi F., Jones M., Poggio T., “Regularization theory and neural networks architectures,” Neural Comput. 7(2), 219–269 (1995). 10.1162/neco.1995.7.2.219 [DOI] [Google Scholar]
- 36.He K., et al. , “Spatial pyramid pooling in deep convolutional networks for visual recognition,” IEEE Trans. Pattern Anal. Mach. Intell. 37(9), 1904–1916 (2015). 10.1109/TPAMI.2015.2389824 [DOI] [PubMed] [Google Scholar]
- 37.Zeng D., et al. , “A simple low-dose x-ray CT simulation from high-dose scan,” IEEE Trans. Nucl. Sci. 62(5), 2226–2233 (2015). 10.1109/TNS.2015.2467219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li Y., et al. , “Radiation dose reduction in CT myocardial perfusion imaging using SMART-RECON,” IEEE Trans. Med. Imaging 36(12), 2557–2568 (2017). 10.1109/TMI.2017.2747521 [DOI] [PubMed] [Google Scholar]
- 39.Lin Z., et al. , “FSIM: a feature similarity index for image quality assessment,” IEEE Trans. Image Process. 20(8), 2378–2386 (2011). 10.1109/TIP.2011.2109730 [DOI] [PubMed] [Google Scholar]
- 40.Haralick R., Shanmugam K., Dinstein I., “Textural features for image classification,” IEEE Trans. Syst. Man Cybern. SMC-3(6), 610–621 (1973). 10.1109/TSMC.1973.4309314 [DOI] [Google Scholar]
- 41.Hu Y., et al. , “Texture feature extraction and analysis for polyp differentiation via computed tomography colonography,” IEEE Trans. Med. Imaging 35(6), 1522–1531 (2016). 10.1109/TMI.2016.2518958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dice L., “Measures of the amount of ecologic association between species,” Ecology 26(3), 297–302 (1945). 10.2307/1932409 [DOI] [Google Scholar]
- 43.Bai T., et al. , “Z-index parameterization for volumetric CT image reconstruction via 3-D dictionary learning,” IEEE Trans. Med. Imaging 36(12), 2466–2478 (2017). 10.1109/TMI.2017.2759819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shen C., et al. , “Quality-guided deep reinforcement learning for parameter tuning in iterative CT reconstruction,” Proc. SPIE 11072, 1107203 (2019). 10.1117/12.2534948 [DOI] [Google Scholar]