Phenolic Hydrogen Transfer by Molecular Oxygen and Hydroperoxyl Radicals. Insights into the Mechanism of the Anthraquinone Process

Abstract

Hydrogen atom transfer (HAT) by ³O₂ and HO₂^• from arenols (ArOH), aryloxyls (ArO^•), their tautomers (ArH), and auxiliary compounds has been investigated by means of CBS-QB3 computations. With ³O₂, excellent linear correlations have been found between the activation enthalpy and the overall reaction enthalpy. Different pathways have been discerned for HATs involving OH or CH moieties. The results for ArOH + HO₂ → ArO^• + H₂O₂ neither afford a linear correlation nor agree with the experiment. The precise mechanism for the liquid-phase autoxidation of anthrahydroquinone (AnH₂Q) appears to be not fully understood. A kinetic analysis shows that the HAT by chain-carrying HO₂^• occurs with a high rate constant of ≥6 × 10⁸ M^–1 s^–1 (toluene). The second propagation step pertains to a diffusion-controlled HAT by ³O₂ from the 10-OH-9-anthroxyl radical. Oxanthrone (AnOH) is a more stable tautomer of AnH₂Q with a ratio of 13 (298 K) in non-hydrogen-bonding (HB) solvents, but the reactivity toward ³O₂/HO₂ is much lower. Combination of the computed free energies and Abrahams’ HB donating (α₂^H) and accepting (β₂) parameters has afforded an α₂^H(HO₂) of 0.86 and an α₂^H(H₂O₂) of 0.50.

1. Introduction

Autoxidation or combustion of organic matter (RH) with molecular (triplet state) oxygen is a complex (radical chain) process involving a plethora of individual reaction steps.¹⁻⁵ The hydrogen atom transfer (HAT) from RH toward molecular oxygen may be considered as the first radical-generating initiation reaction under (generally unrealistic) “clean” conditions.

1

Equation 1 constitutes a reverse radical disproportionation (RRD), whose enthalpy of activation is supposedly (almost) equal to the enthalpy of reaction, that is, ΔH^⧧(1) ≅ Δ_RH(1). In view of the high endothermicity for closed-shell species, this reaction may only be of some importance at elevated temperatures. Under low-temperature (autoxidation) conditions, an appropriate initiation process (e.g., homolysis of a thermally labile compound, photolytically initiated bond cleavage, radical generation by redox processes, and so forth.) is required for the formation of radical species. One of the exceptions seems to be the (aut)oxidation of anthrahydroquinone (9,10-anthracenediol, AnH₂Q), with molecular oxygen in the liquid phase at around 323 K, yielding hydrogen peroxide.⁶⁻⁸ This is the main industrial route (with 2-alkyl-AnH₂Q) to hydrogen peroxide, H₂O₂, an environmentally benign bleaching agent, with a worldwide manufacturing of more than 4 × 10⁶ tons/year.⁷ Following a vast body of studies dealing with autoxidation processes in chemistry and biology, the prevailing mechanism for the H₂O₂ synthesis can most reasonably be presented by a straightforward radical chain sequence (Scheme 1), involving initiation, propagation, and termination reactions.³⁻⁵ In the rate-determining propagation step (eq 2), the initially formed hydroperoxyl radical, HO₂^•, abstracts a hydrogen atom from AnH₂Q, leading to H₂O₂ and the anthraquinonyl (anthrasemiquinone) radical, AnHQ^•. Subsequently, the HAT from AnHQ^• to oxygen regenerates the radical chain carrier, HO₂, and yields anthraquinone, AnQ, as the second reaction product (eq 3).

Scheme 1. Anthraquinone Process for H₂O₂ Production.

In the next stage of the industrial process, AnQ is recycled back to AnH₂Q by means of catalytic hydrogenation. A frequently cited erroneous representation of this mechanism is displayed in the Appendix section.

This synthetic method has been developed around 70 years ago. However, in 2011, Yoshizawa et al. claimed that ... the reaction mechanism of the autoxidation process of AnH₂Q has remained unknown.⁹ or, in 2015, ... the reaction mechanism still remains a matter of debate.¹⁰ By means of a computational (density functional theory, DFT) investigation, the authors arrive at the conclusion that the rate-determining step consists of hydrogen atom abstraction by triplet oxygen from AnH₂Q (Scheme 2, eq 4a). This results in the formation of an intermolecular hydrogen-bonded complex, AnHQ^•–HO₂^•, with the hydroperoxyl radical acting as the hydrogen bond donor (HBD). Then, after intersystem crossing, the in-cage HAT (eq 4b) affords AnQ and hydrogen peroxide. Hence, AnH₂Q oxidation proceeds through a straightforward bimolecular reaction.

Scheme 2. Proposed One-Step Mechanism for AnH₂Q Oxidation.

However, it should be noted that hydrogen bonding (HB) is an equilibrium phenomenon and occurs at the nanosecond time scale. Under the liquid-phase conditions, the concentrations of other hydrogen bond acceptors (HBAs), such as AnH₂Q or AnQ, or even the solvent, are much higher than [AnHQ^•], which would greatly reduce the overall rate of eq 4. A ΔG^⧧(4a) of 12 kcal mol^–1 has been computed at the B3LYP/6-311G** level of theory, which leads to a rate constant of k(4a) = 1.4 × 10⁶ M^–1 s^–1 at 323 K.^8,9,11 This implies that under the conditions of constant oxygen concentration, the half-life of AnH₂Q would be around 50 ms. Such a fast reaction implies that the rate of dissolution of oxygen into the liquid becomes rate-limiting. This feature has not been reported in the literature; thus, it appears highly improbable that eq 4a can be considered as the rate-determining step.

The keto–enol tautomerization of arenols and methylacenes has been studied quite in detail by the experiment and theory.^12,13 In a CBS-QB3 computational study on the tautomerization of hydroxyarenes, we confirmed that the keto–enol ratio increases dramatically along the series phenol, 1-naphthol, and 9-anthrol.¹² For the latter, the keto form (anthrone) predominates in the gas phase at 298 K with a ratio of ≥10². These results are in satisfying agreement with the experimental observations concerning inert or poor HB solvents.¹² However, the anthrone/9-anthrol equilibrium ratio depends strongly on the applied solvent because of the formation of intermolecular hydrogen bonds with the tautomers. A preliminary calculation on the tautomerization of AnH₂Q shows that the keto form (oxanthrone, 10-OH-anthrone, AnOH) is present in about 10-fold excess in the gas phase at 298 K. In the liquid phase, the tautomeric ratio is expected to be determined as well by the HB and hydrogen-donating properties of the medium, as exemplified in Scheme 3 with S (e.g., toluene) as the HBA solvent.⁸ Interestingly, the role of AnOH in the H₂O₂ synthesis has not been documented before in a quantitative fashion.

Scheme 3. Intermolecular Hydrogen Bonding Determining the AnOH/AnH₂Q Ratio.

A literature survey shows that there are only a very few experimental studies dealing with the thermokinetics of the HAT between an O–H or a C–H bond to molecular oxygen from closed-shell molecules. The kinetic parameters of eq 1 may be determined by measuring the oxygen uptake at various temperatures, but the assignment of the experimental results to solely eq 1 would be questionable because of the unavoidable occurrence of various side reactions.

Remarkably, it appears that the thermokinetics for the individual steps in the conversion of AnH₂Q to AnQ and H₂O₂ has not been scrutinized in any thorough manner. Therefore, we embarked on a systematic study quantifying the thermodynamic parameters for the interaction of oxygen and hydroperoxyl with selected arenols, their tautomers, radicals derived therefrom, and auxiliary compounds employing the composite CBS-QB3 procedure. This computational method is known for its accuracy (1–2 kcal mol^–1 deviation from the experiment).¹⁴⁻¹⁷ Various families of compounds have been chosen in order to further increase the overall accuracy. The results are used to shed more light on the supposedly unknown mechanism for the oxidation of AnH₂Q. The solvent effect on the AnOH/AnH₂Q ratio has been investigated with the use of empirical solvent/solute parameters. Intermolecular HB between HO₂^• and H₂O₂ with various arenols and aryloxyls has been analyzed to quantify the HBD abilities of these species.

2. Computational Methods

Quantum-chemical computations on the CBS-QB3^18,19 level of theory were performed with the Gaussian 09 suite of programs.²⁰ All geometries were optimized to stationary points with keywords Opt = Tight and Grid = UltraFine. Transition states (TSs) (one imaginary frequency) were located employing the QST3 method. The vibrational displacement vectors related to the imaginary frequencies were examined in order to ensure the correct assignment of the TS. Zero-point vibrational energies were scaled by a factor of 0.99. Solvation was modeled by the solvation model based on density (SMD) continuum model.²¹

3. Results and Discussion

3.1. COH + ³O₂

The thermokinetic parameters for the HAT reaction with molecular oxygen for a series of arenols, aryloxyls, and auxiliary hydroxyl compounds (eqs 6a and 6b) have been computed by CBS-QB3. The auxiliary compounds have been (rather arbitrarily) selected in order to cover a wide range of reaction energies. The HAT process is formally a RRD reaction, but the TS for H-abstraction from closed-shell molecules is an electronic triplet state and not a singlet state as in RH + RH ⇌ R^• + RH₂^• because of the triplet ground-state configuration of ³O₂.¹³ For the radical species, the reaction with oxygen is computed to proceed on the doublet surface. Table 1 summarizes the results including the activation parameters [ΔG^⧧(6), ΔH^⧧(6), ΔS^⧧(6)], the overall reaction enthalpy, Δ_RH(6), the intermolecular hydrogen bond enthalpy, Δ_HBH(6), between the products (the lowest-enthalpy conformer, see 3.6), and the O–H bond dissociation enthalpy (BDE).¹¹ Pre-reaction triplet state hydrogen-bonded complexes of the nonradical educts with ³O₂ have been identified as well. Weak interactions (Δ_HBH = −0.67 ± 0.23 kcal mol^–1) for closed-shell compounds (ROH–³O₂) and quartet-state complexes of hydroxyl-substitued oxyl radicals (^•ROH–³O₂) are observed. Details are summarized in Table S1 of the Supporting Information. Further elaborations concerning these species are beyond the scope of this paper.

6a

6b

Table 1. CBS-QB3-Calculated RRD Activation Parameters for HAT Reactions from a Series of Arenols, Aryloxyls, and Auxiliary Hydroxyl Compounds by Molecular Oxygen (eqs 6a and 6b)^a.

compound	ΔG⧧(6)	ΔH⧧(6)	ΔS⧧(6)	ΔRH(6)b	–ΔHBH(6)c	BDEd
ethenol	39.4	30.0	31.5	35.6	9.0	84.8
2-OH-2-CN-ethenol	30.8	21.1	32.4	24.4	7.8	73.6
2-OH-2-CN-ethenoxyl	8.2	–3.0	37.7	0.8	5.6	50.1
dimethylhydroxylamine	26.5	17.6	30.1	24.7	10.1	73.9
phenol	39.1	30.3	29.4	37.8	10.5	87.1
4-OH-phenol	34.8	26.3	28.6	33.5	11.3	82.8
4-OH-phenoxyl	16.0	5.5	35.2	8.0	8.9	57.3
4-MeO-phenol	34.5	25.8	29.4	33.1	11.5	82.4
4-Cl-phenol	38.2	29.4	29.5	36.8	10.4	86.0
2,5-dimethyl-4-OH-phenol	32.2	22.1	33.9	31.4	11.9	80.6
2,5-dimethyl-4-OH-phenoxyl	14.0	3.0	37.0	6.1	9.5	55.4
TEMPOHe	22.1	12.3	32.8	20.8	12.5	70.1
1-naphthol	35.7	26.7	30.0	32.8	11.0	82.2
2-methyl-1-naphthol	32.2	23.0	31.0	30.6	9.9	79.9
4-OH-1-naphtholf	32.0	22.9	30.5	28.9	11.9	78.2
4-OH-1-naphthoxyl	9.4	–1.5	36.6	1.1	9.4	50.4
9-anthrol	28.9	18.3	35.6	23.3	10.2	72.6
10-OH-9-anthrol	23.8	14.8	30.1	20.1	10.6	69.4
10-OH-9-anthroxyl	3.1	–8.9	40.1	–6.4	9.1	42.9

^aIn (k)cal mol^–1 (K^–1) at T = 298 K. The CBS-QB3 computed Δ_fH⁰(³O₂) = −0.83 kcal mol^–1 and BDE(H–O₂^•) = 49.3 kcal mol^–1. The ΔG^⧧ and ΔS^⧧ data are corrected for the rotational symmetry numbers σ. All thermodynamic quantities refer to the standard state of 1 atm. To convert (for A + B → C, Δn = −1) to the standard state of 1 M at 298 K, ΔG_1M = ΔG_1atm – 1.89, ΔH_1M = ΔH_1atm – 0.59, ΔS_1M = ΔS_1atm – 8.34.

^bThe overall reaction enthalpy toward the non-hydrogen-bonded products.

^cThe intermolecular hydrogen bond enthalpy between the products; details are given in 3.6.

^dThe O–H BDE.

^e1-Hydroxy-2,2,6,6-tetramethyl-piperidine.

^fHydroxylic groups both in the away orientation.

An excellent linear [Bell–Evans–Polanyi (BEP)] correlation between ΔH^⧧(6) and Δ_RH(6) is observed for closed-shell molecules and radicals (eq 7, Figure S1a; n = 19, r² = 0.988).²² The range in Δ_RH(6) covers about 50 kcal mol^–123

7

Equation 7 pertains to the HAT between two oxygen centers. The enthalpy of activation, ΔH^⧧(6) is lower than Δ_RH(6), the reaction enthalpy for formation of the non-hydrogen-bonded products.²⁴ The variation in Δ_RH(6) is directly related to the O–H BDE(O–H), of the compounds under study (Table 1). The BDE(O–H)s for the arenols decrease when ortho and/or para hydrogens are replaced by electron-donating substituents (CH₃, OH) or by extending the aromatic system (phenol vs 9-anthrol).^12,25 It should be noted that eq 7 is only applicable when additional (neighboring) lone pair interactions in the TS can be ruled out.²⁶ The intermolecular hydrogen bond enthalpy, Δ_HBH(6), formed between the products shows only a minor fluctuation (see 3.6) and appears to be not correlated with Δ_RH(6). In Figures 1 and S2, the optimized TS structures for a family of compounds (arenols and derived aryloxyls) are displayed. The oxygen–hydrogen bond distances in the reactants are almost invariant with 0.9625 ± 0.0015 Å despite the fact that the BDE(O–H)s span a range of about 44 kcal mol^–1. In contrast, within the series (phenol to 10-OH-9-anthroxyl), the ArO–H bond length in the TS decreases from 1.3982 to 1.0992 Å with a concomitant increase of the H–O₂^• bond length from 1.0636 to 1.3410 Å, which is well consistent with the shift from a late to an early TS.

Figure 1.

B3LYP/CBSB7-optimized TS structures for the HAT from 9-anthrol, 10-OH-9-anthrol, and 10-OH-9-anthroxyl by ³O₂, showing bond distances (Å), bond angles, and the imaginary frequencies. r(OH)_ArOH denotes the O–H bond length in the parent ArOH reactant. Bond length in isolated HO₂^•, r(H–O₂) = 0.9754 Å.

The Arrhenius pre-exponential factor, A, using conventional TS theory, can be derived from the ΔS^⧧(6) data in Table 1.¹¹ For example, the gas phase A values at 298 K for phenol and 4-OH-phenoxyl are calculated as 4.2 × 10⁸ and 2.3 × 10⁷ M^–1 s^–1, respectively, suggesting a tight TS at least in the latter case. This may be associated with the formation of a hydrogen-bonded complex along the reaction coordinate. However, as has been concluded before, the computed entropies for complexes (such as a TS or an intermolecular hydrogen-bonded ensemble) are systemically underestimated, which is related to the erroneous handling of low-lying frequencies. Therefore, the use of ΔG^⧧(6) from Table 1 to predict absolute rate constants needs to be handled with some caution.

A typical enthalpy diagram for the HAT from an arenol (AnH₂Q) to molecular oxygen is displayed in Figure 2. The lowest-enthalpy pathway gives a hydrogen-bonded complex between the aryloxyl oxygen and the hydroperoxyl radical (ArO^•–HΟ₂^•). Hence, the overall reaction to the separate products involves a two-step mechanism: a HAT with simultaneous formation of an intermolecular hydrogen bond in the TS, followed by the dissociation of the hydrogen-bonded complex. This implies that based on the principle of microscopic reversibility, the disproportionation between an aryloxyl and a hydroperoxyl radical or the HAT with a quinone (the backward steps of eqs 6a and 6b) sets in with the formation of an intermolecular hydrogen-bonded complex. In the gas phase, such an encounter occurs without an enthalpic barrier, that is, ΔH^⧧(−6) ≅ 0 kcal mol^–1. Therefore, the overall activation enthalpy, ΔH^⧧(6), for the formation of the free species equals Δ_RH(6), that is, E_a(6) = Δ_RH(6) + 2RT.¹¹ In the liquid phase, a diffusional barrier of ΔH^⧧(−6) ≤ 2 kcal mol^–1 for organic solvents of low viscosity is expected.

Figure 2.

Enthalpy diagrams (kcal mol^–1) for the HAT by ³O₂ from anthrahydroquinone (AnH₂Q) and 10-OH-anthrone (AnOH).

A kinetic study in the liquid phase (benzene, ∼25 atm air) has afforded E_a(6a)s for phenol, 4-MeO-phenol, and 1-naphthol of 35, 27, and 25 kcal mol^–1 at 403 K, respectively, in poor agreement with the E_a(6a)s which can be derived from the data of Table 1.^27,28 The reported pre-exponential factor for phenol (A = 7.0 × 10¹² M^–1 s^–1) is unexpectedly about 10³ times higher than that for the other two arenols. To the best of our knowledge, experimental gas phase kinetic parameters for eq 6a dealing with phenol or any other compound listed in Table 1 are not available in the literature.

The HAT to oxygen with a series of aryloxyl radicals (4-OH-phenoxyl, 4-OH-1-naphthoxyl, and 10-OH-9-anthroxyl radicals) yields a closed-shell compound (a p-quinone) and HO₂^•. The thermodynamically favored product for the (formally) radical–radical disproportionation constitutes of an intermolecular hydrogen-bonded complex between the oxygen of the quinone and HO₂. The Δ_HBHs for the (C=O–HO₂^•) complexes, eq 6b, are quite comparable with those computed for HB in the (ArO^•–HO₂) ensembles, eq 6a (see 3.6).

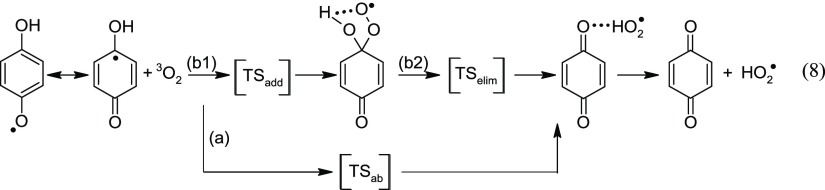
An alternative pathway can be pictured for the formation of p-quinones from the aforementioned aryloxyl radicals. As an example, the fate of the 4-OH-phenoxyl radical has been explored in more detail. The mechanism starting with the 1,4-semiquinone radical and oxygen leading to 1,4-benzoquinone and HO₂^• can be envisaged as an one- or a two-step process (Scheme 4): (a) by direct HAT (eq 8a) or (b) addition of oxygen to the ^•C₄OH moiety (eq 8b1), followed by an intramolecular elimination of HO₂ (eq 8b2). The two pathways have been confirmed by intrinsic reaction coordinate computations (see the Supporting Information, p S6). Unfortunately, a TS (TS_elim) for the intramolecular elimination of HO₂^• from the adduct (eq 8b2) could not be located. Numerous optimization attempts (by varying starting geometries and/or optimization conditions) always ended up with TSs reflecting conformational changes in the complexes with ³O₂ or HO₂ or the HO₂^• adduct, respectively.

Scheme 4. Two Distinct Pathways Leading to p-Benzoquinone.

The corresponding enthalpy diagram for eq 8 is shown in Figure 3. The computations reveal that the addition of oxygen to the ^•C₄OH moiety is, rather surprisingly, an activated process with ΔH^⧧(8b1) of 7.3 kcal mol^–1 [Δ_RH(8b1) = −0.1 kcal mol^–1]. For comparison, the para-addition of oxygen to the phenoxyl radical (^•C₄H moiety) requires an ΔH_add^⧧ of 7.8 kcal mol^–1 (Δ_RH_add = −1.8 kcal mol^–1).²⁹⁻³¹ In contrast, the experimentally determined rate constants for the addition of oxygen to (resonance stabilized) carbon-centered radicals in the gas phase are without an activation barrier, that is, ΔH_add ≅ 0 kcal mol^–1.³²

Figure 3.

Enthalpy diagrams (kcal mol^–1; see Table 1) for HAT from 4-OH-phenoxyl, 4-OH-1-naphthoxyl, and 10-OH-9-anthroxyl by ³O₂ yielding 1,4-benzoquinone, 1,4-naphthoquinone, and 9,10-anthraquinone, respectively; overall reaction enthalpies in italics. The Δ_addH^⧧ for 10-OH-9-anthroxyl is estimated (±1 kcal mol^–1), see text. The bond lengths (in Å) for the intra-HB in the three peroxyl radicals are as follows: r(C–OO): 1.6100, 1.6319, 1.6999; r(OO–HO): 1.8862, 1.8315, 1.6920; r(O–H): 0.9797, 0.9822, 0.9945; the dihedral angles (OOCOH) are 24.09, 20.25, 0.0°.

Stronger peroxyl bonds are formed with the cyclohexadienyl (para-addition) and allyl radicals, and lower activation enthalpies are predicted (ΔH_add^⧧ = 3.3 and 2.4, Δ_RH_add = −11.0³³ and −19.1³⁴ kcal mol^–1, respectively) (Scheme 5).

Scheme 5. Pathways (in kcal mol^–1) for Cyclohexadienyl and Allyl Radicals with ³O₂.

The TS for C–OO bond formation with a nonresonance stabilized radical, such as methyl, could not be located at this level of theory, meaning ΔH_add^⧧ ≈ 0 kcal mol^–1 (Δ_RH_add = −33.1 kcal mol^–135). These computational findings indicate, in a qualitative sense, a BEP-type relationship between ΔH_add and Δ_RH_add for the addition of oxygen to a carbon-centered radical. The Δ_RH_adds for the addition of oxygen to carbon-centered radicals by the theory and by the experiment are in good agreement, but that does not hold for the related activation enthalpies. More work is required to resolve this discrepancy.

The overall reaction enthalpy for eq 8 to the non-hydrogen bonded products amounts to 8.0 kcal mol^–1 (Table 1) which is in accordance with Δ_RH(8) = 9.2 ± 1.0 kcal mol^–1 derived from a compilation of experimental and computed thermodynamic data (see the Supporting Information, p. S7). The reverse reaction, 1,4-C₆H₄O₂ + HO₂^•, is without an enthalpic barrier, as outlined above. Therefore, irrespective of the mechanism, the overall E_a(8) obtained by theory measures in the gas phase 9.2 kcal mol^–1 (= Δ_RH(8) + 2RT) at 298 K. In the liquid phase, including a diffusional barrier, a E_a(8) ≅ 11 kcal mol^–1 is proposed. A rate constant, k(8), of ca. 43 M^–1 s^–1 is now calculated using an estimated pre-exponential factor of A(8) = 5 × 10⁹ M^–1 s^–1 for a bimolecular pathway. The inhibition by 1,4-hydroquinone (a natural occurring antioxidant) of styrene autoxidation has been studied, affording a k(8) = 2.7 × 10² M^–1 s^–1 for the 1,4-semiquinone radical (chlorobenzene, T = 323 K).³⁶ Extrapolation to 298 K gives a k(8) of ca. 80 M^–1 s^–1, in excellent agreement with the computational results. Such a low rate constant implies that eq 8 may only be of some importance at high oxygen concentrations. At low [O₂], the 4-OH-phenoxyl radicals will be involved in chain termination reactions (e.g., trapping peroxyl radicals). At high [³O₂], the generated hydroperoxyl radical by eq 8 starts to contribute to the chain propagation, making 1,4-hydroquinone a less effective chain-breaking antioxidant. A laser flash photolysis study on the HAT from the 2,5-di-tert-butyl-1,4-semiquinone radical to oxygen, eq 9, has yielded a k(9) of (1.3 ± 0.5) × 10⁶ M^–1 s^–1 (chlorobenzene, T = 298 K).³⁷ In the same work, a k(9) of (2.4 ± 0.4) × 10⁶ M^–1 s^–1 has been reported, based on the inhibition of styrene autoxidation by 2,5-di-tert-butyl-1,4-hydroquinone (chlorobenzene, T = 303 K).³⁷ Our CBS-QB3 computations (with the tert-butyl group modeled by methyl, which is assumed to have only a marginal effect on the reaction enthalpy) predicts a Δ_RH(9) of 6.1 kcal mol^–1 (≡Δ_RH(6b), see Table 1), 1.9 kcal mol^–1 lower than that for the 1,4-semiquinone radical. With E_a(9) ≅ 9 kcal mol^–1 (see above), a rate constant in solution of k(9) ≅ 1 × 10³ M^–1 s^–1 (298 K) is obtained, 10³ times lower than the experimental values.³⁷ Clearly, more experimental work needs to be done to clarify the disagreement.

9

The lowest enthalpy pathway for 4-OH-1-naphthoxyl reacting with oxygen involves the direct HAT mechanism. Figure 3 shows that the HAT process is associated with a small negative activation barrier (ΔH^⧧(6b) = −1.5 kcal mol^–1), while the barrier for addition amounts to 6.4 kcal mol^–1. According to the computations, Δ_RH(6b) = 1.1 kcal mol^–1, leading to E_a(6b) ≅ 4 kcal mol^–1 in solution with a concomitant overall rate constant, k(6b), of ca. 6 × 10⁶ M^–1 s^–1 at 298 K. An experimental k(6b) in a mixture of toluene and 10% (v/v) isopropanol has been reported as 6.2 × 10⁵ M^–1 s^–1 at 298 K. Hence, computations and experiment are in reasonable agreement.³⁸

The computed BDE(O–H) in 4-OH-1-naphthol (78.2 kcal mol^–1) is comparable with the BDE(O–H) of 77.1 kcal mol^–1 for the naturally occurring antioxidant α-tocopherol (vitamin E),¹ suggesting that 4-OH-1-naphthol may well be a robust radical chain-breaking compound. However, the facile generation of HO₂^• from the intermediate aroxyl radical greatly diminishes the inhibition properties.

In Figure 3, the enthalpy diagram is displayed for the various pathways concerning the 10-OH-9-anthroxyl radical + ³O₂ interaction. The TS_ab geometry for hydrogen abstraction (Figure 1, right) is similar to that for the almost thermoneutral reaction of 4-OH-1-naphthoxyl, but the barrier is significantly more negative [ΔH^⧧(6a) = −8.9 kcal mol^–1]. Thus, the direct H-transfer appears to be entropy-controlled [ΔG^⧧(6a) = 3.1 kcal mol^–1].³⁹ In this case, the TS for ³O₂ addition (TS_add) could not be located. A linear correlation predicts a ΔH_add^⧧ of around 5 ± 1 kcal mol^–1.⁴⁰ Therefore, the addition of oxygen is likely to be insignificant with regard to product formation. The direct HAT reaction is, in contrast to the other two aryloxyl radicals, exothermic by −6.4 kcal mol^–1 (see Figure 3). Accepting a linear BEP-type correlation for these reactions, the rate constant for the formation of anthraquinone from the 10-OH-9-anthroxyl radical in a non-HB solvent is clearly close to the diffusion-controlled limit, that is, k(6b) = k(3) ≥ 10⁹ M^–1 s^–1 at 298 K, in accordance with the experiment.³⁸

3.2. CH + ³O₂

The thermodynamic parameters for the HAT between C–H and oxygen, eqs 10a and 10b, involving closed-shell molecules (tautomers of arenols, methylaromatics, and their tautomers), derived radicals, and various auxiliary compounds/radicals have been computed by CBS-QB3. Table 2 summarizes the results, including the activation parameters, ΔG^⧧(10), ΔH^⧧(10), ΔS^⧧(10), the overall reaction enthalpy Δ_RH(10), the intermolecular hydrogen bond enthalpy Δ_HBH(10) between the product species, and the related C–H BDE.¹¹ Similar to what has been found for ^•R/ROH–³O₂ interactions (see 3.1), prereaction triplet state hydrogen-bonded complexes of the non-radical educts with ³O₂ (RCH–³O₂) are weak (Δ_HBH = −0.84 ± 0.60 kcal mol^–1) for closed-shell compounds. Details are presented in Table S3 of the Supporting Information. Further elaborations concerning these species are beyond the scope of this paper.

10a

10b

Table 2. CBS-QB3-Calculated RRD Activation Parameters for HAT Reactions (eqs 10a and 10b)^a.

compound	ΔG⧧(10)	ΔH⧧(10)	–ΔS⧧(10)	ΔRH(10)b	–ΔHBH(10)c	BDEd
ethyl	24.4	14.4	33.5	–13.9	3.7	35.4
1-hydroxy-ethyl, s-trans	21.0	11.8	30.7	–12.4	6.9	36.8
vinyl	23.6	14.1	31.9	–13.0	4.1	36.3
propene	47.2	39.9	24.7	37.9	3.4	87.2
allyl	31.6	21.1	35.0	8.2	3.5	57.5
formyl	9.1	–0.4	31.8	–33.8	2.6	15.6
iminyl	13.2	4.9	28.0	–31.1	6.2	18.2
methoxyl	16.1	5.9	34.2	–28.8	7.5	20.5
dimethylether	48.7	41.6	23.6	47.7	5.9	97.0
pentadienyl	36.5	26.3	34.2	16.0	4.0	65.3
cyclopentadiene	43.0	34.4	28.8	32.9	4.5	82.1
1,4-cyclohexadiene	35.5	27.9	25.6	25.0	5.5	74.4
cyclohexadienyl	14.0	3.8	34.1	–26.6	4.6	22.7
4-OH-cyclohexadienyl	12.9	1.3	38.9	–26.9	7.4	22.6
t-toluene	32.1	23.4	29.1	12.1	4.2	61.4
toluene	47.1	38.8	27.6	41.3	4.4	90.6
t-1-Me-naphthalene	35.5	26.0	31.8	18.4	4.7	67.7
1-Me-naphthalene	48.3	40.3	26.7	41.0	4.8	90.2
t-9-Me-anthracene	38.0	30.1	26.5	27.4	4.5	76.6
9-Me-anthracene	46.7	38.5	27.7	36.0	5.3	85.3
t-phenol	36.5	28.2	27.8	20.1	2.7	69.4
4-OH-t-phenol	33.9	24.1	32.6	10.8	6.3	60.0
2,5-di-Me-4-OH-t-phenol	32.8	23.0	32.7	11.3	6.3	60.6
t-1-naphthol	38.7	29.9	29.7	23.8	3.6	73.1
4-OH-t-1-naphthol	36.7	26.9	32.9	15.8	6.5	65.0
anthrone	39.9	31.3	28.6	27.1	4.3	76.4
10-OH-anthrone	37.4	27.5	33.0	21.5	7.1	70.7

^aSee also footnote a, Table 1. The compound prefix t denotes the para tautomeric form of the arenol or the methylaryl compounds.

^bThe overall reaction enthalpy toward the non-hydrogen-bonded products.

^cThe intermolecular hydrogen bond enthalpy between the products.

^dThe related C–H BDE.

In parallel with the O–H system discussed above, the plot of ΔH^⧧(10) versus Δ_RH(10) (Figure S4a) shows an excellent BEP correlation (n = 27, r² = 0.981) following eq 11(41)

11

This equation pertains to the HAT from carbon to oxygen, with a Δ_RH(10) range spanning more than 80 kcal mol^–1. A typical enthalpy diagram for the HAT from C–H (10-OH-anthrone) to oxygen is displayed in Figure 2. In contrast to the HAT from COH to oxygen, ΔH^⧧(10) > Δ_RH(10), with toluene as the only exception.

The intermolecular hydrogen bond enthalpies, Δ_HBH(10), between the products, that is, radical R^• or compound R_(−H2), and the hydroperoxyl radical, HO₂^•, are in the range of −3 to −7 kcal mol^–1. The formation of the HB product complex does not occur simultaneously with the transfer of a hydrogen atom in the TS as is the case with COH compounds (eq 6).

In Figures 4 and S5, the TS structures for selected compounds (such as the tautomers of arenols) are displayed. The elongation of the C–H bond in the TS for the formyl radical is only ca. 3% (an exothermic reaction) with Δ_RH(10b) (=–33.8 kcal mol^–1) while with oxanthrone (endothermic by 21.5 kcal mol^–1), the C–H bond length increases by ca. 25%.

Figure 4.

B3LYP/CBSB7-optimized TS structures for HAT from t-phenol, t-4-OH-phenol, and 10-OH-9-anthrone (AnOH) by ³O₂, showing bond distances (Å), bond angles, and the imaginary frequencies. r(CH)_tArOH denotes the C–H bond length in the parent tautomer. Bond length in isolated HΟ₂^•, r(H–O₂) = 0.9754 Å.

The number of kinetic studies dealing with the HAT from CH to oxygen from closed-shell molecules (all endothermic reactions) is rather limited. An experimental activation enthalpy, E_a,exp, of 39.0 ± 1.4 kcal mol^–1 for the propene + ³O₂ reaction in the gas phase (700–800 K) has been reported, which is in reasonable agreement with the computed E_a(10a) of 41.1 kcal mol^–1 (298 K, Table 2).⁴² However, an evaluation of all available gas-phase data has resulted in a preferred E_a,exp of 35.7 kcal mol^–1 (600–1500 K).⁴³ The agreement for toluene + ³O₂ is less satisfying, with a recommended gas phase E_a,exp of 44.9 kcal mol^–1 (500–2000 K)⁴³ (later remeasured as 46.0 kcal mol^–1),⁴⁴ while CBS-QB3 predicts E_a(10a) = 40.0 kcal mol^–1 (298 K). The E_a,exp of 32 kcal mol^–1 derived from liquid-phase experiments with toluene is incompatible with any data.²⁸ The E_a(10b) of 0.8 kcal mol^–1 (298 K) for the formyl radical (an exothermic reaction) is in line with the experiment.³²

The reactivity of carbon-centered radicals toward oxygen has been examined extensively in the gas³² and in the liquid phase.⁴ The addition of oxygen, leading to a peroxyl intermediate, is the predominant reaction channel. Studies dealing with C₆H₇^• + ³O₂ ⇌ products in solution have yielded k_exps of (1.2 ± 0.4) × 10⁹ M^–1 s^–1 (in cyclohexane⁴⁵) and 1.6 × 10⁹ M^–1 s^–1 (in benzene⁴⁶) at 298 K, hence, diffusion-controlled rate constants. They relate exclusively to the ortho and para addition route (see Scheme 5), yielding the corresponding C₆H₇OO^• radicals.^33,45,47 Conversely, a gas phase study has yielded a k_exp = 3.1 × 10⁷ M^–1 s^–1 at 298 K.⁴⁸ The apparent discrepancy between the liquid and gas phase k_exps is most likely due to a change in mechanism.⁴⁵ In the gas phase, the oxygen addition is (partially) reversible under the experimental conditions (e.g., at low oxygen concentration). This means that the HAT pathway toward benzene and HO₂ remains as the only exit channel.⁴⁵ The reversibility is associated with the weak incipient peroxyl bond in C₆H₇OO^•. The computed BDE(C–OO)s (at 1 M), 11.9 (ortho), and 10.8 (para) kcal mol^–1 in cyclohexane⁴⁹ are in good agreement with the experimental global value of 12 ± 1 kcal mol^–1 measured in isooctane.³³ According to the CBS-QB3 calculations in cyclohexane, the E_as for ortho and para addition amount to 4.6 and 3.4 kcal mol^–1, respectively, next to an E_a(10b) of 5.1 kcal mol^–1 for the HAT, suggesting a global rate constant to be much lower than the experimental ones in solution. With ΔG^⧧s for the three reaction channels, an addition/abstraction ratio in the gas phase of 10 is calculated, increasing to around 20 in cyclohexane. Thus, perhaps fortuitously, the selectivity (in solution) is in agreement with the experimental data.⁴⁹ As a consequence of the microscopic reversibility, the relationship between ΔH^⧧(−10) and Δ_RH(−10) [=−Δ_RH(10)] for disproportionation between two radical species (R^• + RH₂^• ⇌ RH + RH) can now be presented by eq 12

12

It is a general belief (dogma) that in the gas phase, the hydrogen atom shuttle is without an enthalpic barrier, whereas in solution, the rates are dictated by the temperature-dependent diffusion/viscosity. However, eq 12 evidently demonstrates that this is not the case. For the hypothetical thermoneutral radical disproportionation, an activation barrier as high as 18 kcal mol^–1 can be expected.¹³

The termination step in an autoxidation sequence involves radical–radical recombination and/or disproportionation reactions. With HO₂^• and ArO^• as the reactive species, the latter reaction may occur through formation of a hydrogen-bonded complex or by a direct HAT (Figure 2). The disproportionation of 10-OH-9-anthroxyl with HO₂ results in AnH₂Q and oxygen and is without an activation barrier (ΔH^⧧ ≅ 0, Δ_RH = −20.1 kcal mol^–1) (see Figure 2). In contrast, the HAT yielding AnOH is much slower with ΔH^⧧ = 6.0 and Δ_RH = −21.5 kcal mol^–1.

3.3. COH/CH + HO₂^•

The CBS-QB3-computed thermokinetic parameters for the O–H HAT by HO₂^• with series of arenols and aryloxyls radicals (eqs 13a and 13b) are compiled in Table 3.¹¹ The optimized TS structures are shown in Figures 5 and S6. The data refer to the lowest-energy species.

13a

13b

Table 3. CBS-QB3-Calculated Activation Parameters for the HAT Reaction (eqs 13a and 13b)^a.

compound	ΔG⧧(13)	ΔH⧧(13)	–ΔS⧧(13)	–ΔRH(13)b	–ΔHBHed(13)c	–ΔHBH(13)d
phenol	19.3	9.1	34.1	0.7	7.4	7.7
phenole	20.7	10.6	33.9	1.5	5.8	5.9
phenolf	22.8	12.8	33.6	2.4	4.3	3.9
phenolg	21.1	8.2	43.2	–2.3	5.6h	8.6
4-OH-phenol	16.3	6.5	32.9	5.0	7.3	8.2
4-OH-phenoxyl	17.0	5.1	40.1	30.5	6.3	8.2
4-MeO-phenol	16.2	6.1	33.8	5.3	7.6	8.3
4-Cl-phenol	19.0	8.9	33.9	1.7	7.1	7.1
1-naphthol	26.6	16.9	32.7	5.6	7.3	8.0
4-OH-1-naphtholi	20.5	10.6	33.2	9.5	7.6	8.6
4-OH-1-naphthoxyl	10.4	–1.8	40.8	37.3	6.5	7.0
9-anthrol	21.7	10.4	38.1	15.2	7.9	7.6
10-OH-9-anthrol	n.a.	n.a.	n.a.	18.4	8.1	7.2
10-OH-9-anthroxyl	n.a.	n.a.	n.a.	44.8	7.1	6.9

^aSee footnote a, Table 1; n.a.: no stable TS structure found. The computed Δ_fH⁰(HO₂^•) = 2.90, BDE(HO₂–H) = 87.7, and BDE((CH₃)₃COO–H) = 84.7 kcal mol^–1.

^bThe overall reaction enthalpy, Δ_RH, without HB in reactants or products.

^cΔ_HBH_ed, the intermolecular hydrogen bond enthalpy for the educt complex (ROH as the HBA), details are given in Table S7.1.

^dThe intermolecular hydrogen bond enthalpy for the product complex (RO^• as the HBA), details are given in Table S7.2.

^e(SMD)CBS-QB3: solvent cyclohexane.

^f(SMD)CBS-QB3: solvent water.

^gWith (CH₃)₃COO^• as the H atom abstracting peroxyl radical.

^hRefers to ROH as the HBD.

ⁱHydroxylic groups both in the away orientation.

Figure 5.

B3LYP/CBSB7-optimized TS structures for HAT from phenol, 4-OH-phenol, and 4-OH-phenoxyl by HO₂^•, showing bond distances (Å), bond angles, and the imaginary frequencies, d(HOOH) denotes the dihedral angle of the HOOH fragment. The r(O–H) bond lengths in the parent ArOHs are presented in Figure S2.

The Δ_RH(13) [=BDE(RO–H) – BDE(HOO–H)], without hydrogen-bonding in reactants or products, ranges from −0.65 (phenol) to −18.4 kcal mol^–1 (AnH₂Q). Table 3 shows that an (acceptable) BEP relationship between ΔH^⧧(13) and Δ_RH(13) is lacking. For example, the ΔH^⧧(13a)s for phenol and 9-anthrol are calculated as 9.1 and 10.4 kcal mol^–1, respectively, while the corresponding Δ_RH(13a)s toward the non-hydrogen-bonded products are −0.7 and −15.2 kcal mol^–1, respectively. However, the TS structures for the phenol/9-anthrol HAT differ clearly, in the O–H–OOH bond lengths (Figure S6). The r(O–H) decreases from 1.1539 to 1.0504 while the r(H–OOH) increases from 1.2193 and 1.4119 (in Å), in accordance with an earlier TS in the case of 9-anthrol. For the disproportionation reaction with the 4-OH-phenoxyl and 4-OH-naphthoxyl radicals, the large exothermicity suggest an early TS, but this is not reflected in the R(O–H) but rather in the dihedral angle of HOOH. There is an overwhelming amount of experimental kinetic information dealing with the HAT by peroxyl radicals from arenols (phenolic antioxidants). It is well established that the HAT rate with, for example, alkyl-peroxyls increases with a decreasing BDE(O–H).^3,4 The reason for this discrepancy between the theory and experiment is not entirely clear. It seems reasonable to attribute the larger scatter of the data, compared to the O₂ system, to the possibility to form additional HB (donor) interactions and/or adopting additional conformeric arrangements in the educt [ROH–HO₂^•] and in the product [RO^•–HO₂H] complexes, as well as in the TS. In fact, for most of the compounds in Table 3, more than one stable arrangement of the educt/product complex and/or the TS was found. Most likely, the HAT and the formation of the hydrogen bond occur concerted.

A literature survey learns that the computational outcome for the HAT by HO₂^• from phenol depends strongly on the applied level of theory (see Table S4). For this elementary reaction, the computed ΔH^⧧(13a) ranges from 1.5 to 13 kcal mol^–1. To the best of our knowledge, an experimental gas-phase study on this reaction has never been reported.

Additionally, we explored the thermodynamic parameters for the HAT (C–H) by HO₂^• with some prototype closed-shell compounds (eq 14).

14

The results, together with some data from the literature, are presented in Table S5. A reasonable BEP correlation (n = 12, r² = 0.957), eq 15, is found (see Figure S7).

15

However, the general outcome is inconclusive. For example, the calculated ΔH^⧧(14) of 5.4 kcal mol^–1 for RH = 1,4-cyclohexadiene suggests a much faster reaction compared to the experiment (see 3.5). Moreover, when an adjacent oxygen is present, that is, CH(OH), the linear correlation between ΔH^⧧(14) and Δ_RH(14) is not obeyed by all conformational arrangements of educts and TSs (compare 4-OH-t-phenol and 10-OH-anthrone, Figure S7). Also, the radical species (see Table S5) exhibit a stronger deviation from linearity. Clearly, more efforts are required to predict accurately by theory the ΔH^⧧s when dealing with HO₂^• as the hydrogen abstracting species.

3.4. Anthrahydroquinone Versus 10-OH-Anthrone: Solvent Effect

The anthraquinone process is carried out in the liquid phase (commonly referred to as the “working solution”) at around 323 K. The medium consists of, for example, a mixture of alkylaromatics and long-chain alcohols to accommodate the difference in solubility of the reactants and the products.⁸ The thermodynamic parameters for tautomerization (AnH₂Q ⇌ AnOH) are calculated as follows: Δ_tG = −1.52 kcal mol^–1, Δ_tH = −1.35 kcal mol^–1, and Δ_tS = 0.57 cal mol^–1 K^–1, with the OH in the s-trans orientation as the lowest-enthalpy keto conformer. This leads to an AnOH/AnH₂Q ratio (K_t) of 13.0 in the gas phase and inert solvents at 298 K (ca. 11 at 323 K). By ignoring the small difference in entropy between the two species, the keto–enol ratio for any arenol can be derived using Δ_tG ≅ Δ_tH = BDE(O–H)_enol – BDE(C–H)_keto (see Tables 1 and 2). The computations on a similar equilibrium, 9-anthrol ⇌ anthrone, have yielded a K_t of 95.6 (298 K), in satisfying agreement with the experiment.¹² The difference in the tautomeric ratios between AnH₂Q and 9-anthrol can be rationalized by considering the related BDE(O–H)s and BDE(C₁₀–H)s (see Tables 1 and 2). A more pronounced decrease in the BDE(C₁₀–H) in AnOH occurs because of the replacement of the C₁₀H moiety by the radical-stabilizing C₁₀OH.

Experimentally, it has been found that the anthrone/9-anthrol ratio in solution depends strongly on the applied solvent. For example, the ratio reduces from ca. 500 (isooctane)⁵⁰ to 6.6 (ethanol)⁵¹ to about 0.3 [dimethyl sulfoxide (DMSO)]⁵² at 298 K. The reason is not the change of the bulk solvent properties (i.e., the polarity) but rather the formation of 1:1 intermolecular hydrogen-bonded complexes between the tautomers (solutes) and the solvent.¹² The ratio is therefore determined by the hydrogen bond-accepting (HBA) and/or a hydrogen bond-donating (HBD) abilities of the species involved. The strong hydrogen bond between the S=O (DMSO) moiety (acceptor) and the arenolic OH (donor) ensures that 9-anthrol is present in excess in this solvent.

Quantitative data of the solvent effect on the AnOH/AnH₂Q ratio are scarce. In 1911, Meyer reported that AnOH did not tautomerize, even after prolonged heating in solvents such as CHCl₃, benzene, or ethanol. Starting with either AnOH or AnH₂Q, dissolved in ethanol and in the presence of a small amount of HCl, a K_t ≅ 0.03 at 298 K could be derived (after an equilibration time of two days).⁵³ Conversely, in 1969, Sterk measured a K_t of about 6 in neat 1-butanol at 313 K. The range in K_t (ca. 2 to 19) employing various solvents, such as CHCl₃, pyridine, and DMSO, is rather limited.⁵⁴ According to a study by Bredereck et al., K_t equals 0.13 (pH = 9.4, 298 K) in ethanol/water (50/50, v/v).⁵⁵ The noncatalyzed tautomerization is a slow process, and the presence of an acid or base is required to ensure a fully equilibrated mixture within the time frame of the experiment. For the noncatalyzed tautomerization of AnOH to AnH₂Q in ethanol (endothermic by only 1.4 kcal mol^–1), a rate constant of 3 × 10^–6 s^–1 has been reported, underscoring the sluggishness of the equilibration. The presence of 0.1 M HCl results in a hundred fold rate acceleration.⁵⁶

The HBD (acidity) and the HBA (basicity) abilities for an extensive range of compounds have been parametrized by the α₂^H and the β₂ descriptor, respectively, ranging from 0 to 1.^57,58 In most cases, these constants have been determined under dilute conditions and in inert solvents. The K_HB for the formation of a 1:1 intermolecular hydrogen bonded complex between a HBD and a HBA is given by eq 16

16

Numerous α₂^H and β₂ values are known from experimental studies, and eq 16 allows the calculation of K_HB for a large number of donor and acceptor combinations with remarkable precision. According to Scheme 3, the AnOH/AnH₂Q ratio in a neat HBA solvent, S, is given by eq 17

17

with K_HB1,1 and K_HB1,2 as the equilibrium constants for inter-HB formation with the two arenolic groups in AnH₂Q, and K_HB2 for the inter-HB formation with the OH in AnOH. Furthermore, [AnH₂Q]_s = [AnH₂Q] + [AnH₂Q(S)] + [AnH₂Q(S₂)] and [AnOH]_s = [AnOH] + [AnOH(S)]. In our study on the solvent effect on the 9-anthrol ⇌ anthrone equilibrium, it has been concluded that with ethanol (an HBA and an HBD) as a solvent, the HBD ability is greatly reduced. The hydroxylic hydrogens in neat ethanol are associated in cyclic oligomers and are not available for HB with the solute, that is, α₂^H ≅ 0.¹² For both arenolic hydroxyls in AnH₂Q, α₂ = 0.40 has been proposed.⁵⁹ Combined with α₂^H = 0.32⁵⁷ for the COH moiety in AnOH (as for a secondary alcohol) and the β₂s⁵⁸ for the S, eq 17 can be applied to predict the ratio in any HBA solvent. In neat methanol, eq 17 yields a [AnOH]_s/[AnH₂Q]_s ratio of 0.27, in reasonable agreement with the experimental observations. Hence, the percentage of anthracenyl moieties in solution increases from 7 (inert solvent) to 79%, but the total amount of non-HB hydroxyl groups in [AnH₂Q]_s decreases from 14 to 2.9%. In other HBA solvents, the ratios are calculated as 5.0 (toluene) and 0.02 (DMSO), all at 298 K. It should be noted that at high [AnH₂Q]⁸ and in a poor HB solvent, self-association may occur as well.

We have explored the effect of solvent on K_t on the (SMD)B3LYP/CBSB7 level of theory. In DMSO, K_t is predicted to increase (and not to decrease) from 13 to 77, while in water or ethanol, K_t drops to around 6 (see Table S6). The results reinforce that common continuum solvent models are not adequate for cases where intermolecular HB is determining the equilibrium ratio. Evidently, under the conditions (temperature, working solution) of the anthraquinone process, the AnOH tautomer is still present in excess.

3.5. Anthrahydroquinone Versus 10-OH-Anthrone: Kinetics

The Δ_RHs for the HAT by oxygen from AnH₂Q and AnOH, yielding the non-hydrogen-bonded products, are 20.1 (eq 6a) and 21.4 (eq 10a) kcal mol^–1, respectively. In contrast, the corresponding activation enthalpies are quite different with ΔH^⧧(6a) ≈ Δ_RH(6a) = 20.1 and ΔH^⧧(10a) = 27.5 kcal mol^–1 (see Tables 1 and 2 and Figure 2). Consequently, oxygen reacts about 10⁵ times faster with AnH₂Q than with AnOH in an inert solvent at 298 K. According to eqs 7 and 11, the intrinsic activation barrier for a hypothetical thermoneutral HAT from an OH moiety is substantially lower than that from a CH moiety. The magnitude of the TS barrier for RX–H–OO (X = O, C) can be associated with the stability of the RX–OO bond. A low BDE reduces the triplet repulsion (because of the three-electron ensemble) in the TS, and consequently, the ΔH^⧧ decreases.^2−5,60 Indeed, the RO–OO bond is much weaker than the RC–OO bond. Our CBS-QB3-computed activation free energy, ΔG^⧧(4a) [=ΔG^⧧(6a)], of 22.7 kcal mol^–1 for the formation of the hydrogen-bonded complex (10-OH-9-AnO^•–HO₂^•, see Scheme 2) is a far cry from the 12 kcal mol^–1 reported by Yoshizawa et al.^9,61 In any case, eq 4a is a rather slow reaction which may serve only as a radical initiating step and cannot be regarded as the rate-determining step in the oxidation of AnH₂Q.⁶²

At present, a reasonable estimate of the HAT rate constant by HO₂^• from AnH₂Q can only be obtained with the use of (experimental) thermokinetic data from the literature (see 3.3). Several studies in non- or poor HB solvents dealing with the H-transfer by an alkylperoxyl radical from phenol (an almost thermoneutral reaction)^63,64 have yielded an average rate constant of (2.6 ± 0.3) × 10³ M^–1 s^–1 at ca. 300 K (Table S4). For the HAT by HO₂ from the arenol 2,2,5,7,8-pentamethyl-6-chromanol (a model compound for α-tocopherol, vitamin E), a rate constant of 1.6 × 10⁷ M^–1 s^–1 (303 K) in CCl₄ (β₂^H ≅ 0) has been reported.⁶⁶ The corresponding Δ_RH has been estimated as −10.5 kcal mol^–1.¹ When postulating a BEP relationship for the HAT from the hydroxyl group of arenols by HO₂, the rate constant for the more exothermic H-transfer with AnH₂Q, eq 2, (Δ_RH = −18.4 kcal mol^–1, see Table 3) can be approximated as k(2) ≥ 10⁹ M^–1 s^–1 (per OH) in an inert solvent. Hence, eq 2 is an (almost) diffusion-controlled reaction, which may be the reason why CBS-QB3 calculations failed to locate the TS. Hydroxylic hydrogen involved in a linear intermolecular hydrogen bond is not available for HAT (the kinetic solvent effect).^67,68 With the use of eq 17, it is calculated that in toluene about 29% of the hydroxyls are non-hydrogen-bonded, leading to an apparent (experimental) rate constant of k(2) ≥ 6 × 10⁸ M^–1 s^–1 (per molecule).

The overall reaction enthalpy for the HAT by HO₂^• from the CH(OH) moiety in AnOH (Δ_RH = −17.0 kcal mol^–1) is 1.4 kcal mol^–1 less exothermic compared to the HAT from the OH group in AnH₂Q. However, the intrinsic activation barrier for AnOH is expected to be much higher, as outlined above for the HATs with oxygen.⁶⁹ Indeed, the HAT rate constant for 1,4-cyclohexadiene (1,4-CHD) has been reported as 2.3 × 10² M^–1 s^–1 (303 K, n-decane)⁷⁰ with a Δ_RH of −10.8 kcal mol^–1.⁷¹ The latter is almost equal to the Δ_RH for the HAT with 2,2,5,7,8-pentamethyl-6-chromanol, but the rate constants vary by a factor of 10⁵. While AnOH is present as the major tautomer, kinetic considerations learn that this compound is not directly involved in the H₂O₂ synthesis, despite claims to the contrary.⁷²

The AIBN-initiated autoxidation of 1,4-cyclohexadiene (1,4-CHD) affords exclusively benzene and hydroperoxide as the products (303 K, chlorobenzene). The reaction scheme is similar to that given by eqs 2 and 3, with HO₂^• as the chain-propagating radical. In the 1,4-CHD autoxidation, the only conceivable termination reaction pertains to the disproportionation between two hydroperoxyl radicals (eq 18), with 2k(18) = 1.34 × 10⁹ M^–1 s^–1 (303 K, n-decane).⁷⁰

18

Equation 18 is probably also the only relevant termination step in AnH₂Q autoxidation. In a radical chain process, the chain length is determined by the ratio between the propagation and termination rates [that is, k(2)/2k(18)^0.5].⁴ A large value of this ratio indicates that the oxidation products are (solely) determined by the two propagation reactions. The propagation rate constant (eq 2) is about 10⁶ times higher relative to the HAT from 1,4-CHD, thus underscoring that the AnH₂Q autoxidation is an extraordinary efficient long chain radical process.

3.6. Intermolecular HB

Tables 1 and 3 reveal that the hydroperoxyl radical (HO₂^•) and hydrogen peroxide (H₂O₂) form strong hydrogen bonds with acceptors such arenols and aryloxyl radicals. In Table S7.1, the thermodynamic parameters and the hydrogen bond distances are presented. For the interaction of HO₂ with phenol, three intermolecular hydrogen-bonded complexes (Ia, Ib, and Ic) could be identified (Scheme 6). In conformers Ia and Ib, the reactants are acting as amphoteric species, that is, as a HBD and a HBA. In complex Ic, HO₂^• behaves as a double HBA and phenol as a double HBD.

Scheme 6. Three Hydrogen-Bonded Complexes of HO₂^• with Phenol.

Hydrogen bond lengths (Å): (Ia) r₁(PhHO–HOO) = 1.8690, r₂(PhOH–OOH) = 2.0608; (Ib) r₁(PhHO–HOO) = 1.7893, r₂(PhH–OOH) = 2.4665; (Ic): r₁(PhOH–OOH) = 1.9858, r₂(PhH–OHO) = 2.6422. Thermodynamic data in (k)cal (K^–1) mol^–1 at 298 K and at 1 M standard state.

The lowest-enthalpy complex, Ia, consists of a planar five-membered ring with the phenolic OH group participating in two hydrogen bonds. From the HB bond distances, it can be concluded that the PhHO–HOO bond will be the strongest interaction. The Δ_HBHs for Ia and Ib are almost identical. Because of the free O–H vibration in Ib, the Δ_HBS is less negative, meaning that Ib is the lowest free energy conformer.

The effect of the solvent (cyclohexane, water) on the HB formation of HO₂^• with phenol has been explored with the SMD solvation model. The optimized geometries do not change significantly compared to those in the gas phase, and the Δ_HBSs remain almost constant (see Table S7.1). However, the Δ_HBH increases because of the partial loss of solvation enthalpy of the reactants, implying that the equilibrium constant in solution will be markedly different (lower) compared to the gas phase.

The HB-arrangement I, as depicted in Scheme 7, is the lowest enthalpy conformer for all arenols studied. The Δ_HBHs (−6.7 to −7.3 kcal mol^–1, see Table S7.1) demonstrate only a minor change when extending the aromatic system and/or replacing a para hydrogen by an OH group.⁷³ The ArHO–HOO bond distance shows no significant alteration, while the ArOH–OOH bonds with 9-anthrol or AnH₂Q are clearly elongated: 2.206 Å (AnH₂Q) versus 2.0608 Å (phenol). This is the consequence of a lower HBD ability for these compounds.⁵⁶ The foregoing results suggest that the Δ_HBH is largely determined by the acidity (α₂^H) of HO₂. Water and methanol are better HB acceptors compared to phenol with β₂^Hs of 0.38 and 0.41 versus 0.22, respectively.⁵⁸ The inter-HB complexes with HO₂ render shorter (O–HOO) bond lengths of 1.7661 Å (H₂O) and 1.7490 Å (CH₃OH) relative to phenol (1.8690 Å). Conversely, phenol is a stronger HBD,⁵⁷ which leads to an increase of the OH–OOH bond lengths, ranging from 2.0608 (phenol) to 2.2358 Å (CH₃OH).

Scheme 7. CBS-QB3-Calculated Lowest-Enthalpy Conformers of Hydrogen-Bonded HO₂^• Complexes with Arenols (I), Phenoxyl (II), and Naphthoxyl or Anthroxyl (III); Lowest-Enthalpy Conformers of H₂O₂ Hydrogen Bond Complexes with Phenoxyl (IV) and Naphthoxyl or Anthroxyl (V).

The lowest-enthalpy HB complexes for the interaction of HO₂^• with aryloxyl radicals are found to be a seven-membered (phenyl, II) or an eight-membered ring (naphthyl, anthracenyl, III) ensemble. Considering the hydrogen bond distances, the interaction of C–O^• with HO₂ (1.69 ± 0.01 Å) is much stronger than that for ArH and ^•OOH (ca. 2.20 Å). For the series investigated, the Δ_HBHs vary only slightly from −9.6 to −11.3 kcal mol^–1, and the HBs are 2–3 kcal mol^–1 stronger than with the corresponding arenols. It has been proposed that the aryloxyl radical can be regarded as a delocalized carbon-centered radical with the C–O^• moiety acting as a carbonyl group, which is a stronger HBA.⁶³ For comparison, the HB parameters have also been calculated for model compounds containing a C=O group (acetaldehyde, acetone, 1,4-benzoquinone, 1,4-naphthoquinone; see Table S7.1). The O–HOO bond lengths are somewhat longer than those in II, with a concomitant decrease in Δ_HBH. Hence, the HBA ability of aryloxyl radicals is estimated to be slightly higher than that of acetone, that is, β₂^H(ArO^•) = 0.52.

It is of interest to quantify the α₂^H for the hydroperoxyl radical using the computational data in order to predict the behavior in a HB environment (solution, troposphere⁷⁴). It is well known that the computed Δ_HBSs are underestimated values, leading to erroneous Δ_HBGs (and K_HBs). Therefore, eq 16 cannot be used in a straightforward way. An alternative approach is utilizing the difference in the computed Δ_HBGs (at 1 M, see Tables S7.1 and Scheme 6) for identical conformations (cancelation of errors) for the equilibria C₆H₅OH + HO₂ ⇌ Ib and C₆H₅O^• + HO₂^• ⇌ II. In this way, an α₂(HO₂^•) = 0.86 is derived using eq 15 combined with β₂(C₆H₅O^•) = 0.52 (see above) and β₂^H(C₆H₅OH) = 0.22.⁵⁷ The hydroperoxyl radical is a strong HBD, which is not unexpected in view of its low pK_a value (4.88).⁵⁹ Only one study has reported an estimated α₂(HO₂^•) of about 0.87, based on the analysis of the kinetic solvent effect on the HO₂ + HO₂^• self-reaction.⁷⁵

Finally, the HB of H₂O₂ (pK_a = 11.75) with aryloxyl radicals (Tables 3 and S7.2) consists of seven-membered (phenyl, IV) or eight-membered (naphthyl, anthracenyl, V) ring ensembles (Scheme 7). The solvent effect on the C₆H₅O^•–H₂O₂ HB complex is similar to that observed for the C₆H₅OH–HO₂^• ensemble. The Δ_HBHs are again almost invariant, ranging from −7.0 to −7.8 kcal mol^–1. With the computed Δ_HBGs (see above) for the equilibria C₆H₅O^• + HO₂ ⇌ II and C₆H₅O^• + HO₂H ⇌ IV, an α₂^H(HO₂H) = 0.51 is obtained, quite similar to the HBD ability of 2,2,2-trichloroethanol (pK_a = 12.02, α₂ = 0.50).⁵⁷

4. Conclusions

The kinetic parameters for the HAT by oxygen, ³O₂, from a broad range of arenols (ArOH) and aryloxyl (ArO^•) radicals has been quantified by means of CBS-QB3 calculations. The results show an excellent BEP correlation between the enthalpy of activation, ΔH^⧧ (TS: O–H–O) and the overall reaction enthalpy, Δ_RH. A similar excellent BEP relationship has been obtained for the HAT from the tautomeric forms of the arenols and auxiliary compounds (TS: C–H–O). However, the HATs from the OH and the CH moieties follow different pathways. The lowest-energy route for ArOH compounds (closed-shell species and radicals) involves a simultaneous transfer of the H atom and the formation of a strong intermolecular hydrogen bond (HB) between the product radicals ArO^• and HO₂^•, hence, ΔH^⧧ < Δ_RH. Conversely, ΔH^⧧ > Δ_RH holds for the HAT from CH, associated with a high intrinsic barrier. Because the number of experimental studies is quite limited, the computational findings may be of importance to predict the behavior of similar compounds under a variety of reaction conditions. With the hydroperoxyl radical, HO₂, as the HAT species, a reasonable BEP relationship could not be observed, while the predicted rate constants are quite at variance with the experiment. Equipped with the kinetic insights acquired from this study, the purportedly unknown mechanism for the (industrial) production of hydrogen peroxide (H₂O₂) from the autoxidation of anthrahydroquinone (AnH₂Q) has been debunked. The analysis shows that the two propagation steps in the radical chain sequence (eqs 2 and 3) are both at or near the diffusion-controlled limit. Oxanthrone (AnOH) is the thermodynamically more stable tautomer of AnH₂Q, and the ratio depends on the HB properties of the solvent. Furthermore, a HB donating ability, “the acidity”, for the hydroperoxyl radical of α₂^H(HO₂) = 0.86 has been derived from computational and empirical data.

Appendix

From a 2006 peer-reviewed paper entitled Hydrogen Peroxide Synthesis: An Outlook beyond the Anthraquinone Process, it can be learned that the oxidation of anthrahydroquinone (AnH₂Q) to H₂O₂ ... occurs by means of a well-documented free-radical chain mechanism.⁷⁶ Surprisingly, Scheme 3 presented in ref (76) does not refer to the autoxidation of AnH₂Q, as presented by eqs 2 and 3 but rather to that of 9,10-dihydroxy-9,10-dihydroanthracene (AnH₄Q).^77,78 Obviously unaware of the structural flaw, the authors (were forced to) proposed a more complex mechanism because an overall conversion of AnH₄Q to the final products anthraquinone (AnQ) and H₂O₂ would stoichiometrically require two molecules of ³O₂. The authors suggested a radical chain mechanism (see Scheme 8) that starts with a nonspecified initiation reaction whereby ketyl radical A is formed. The propagation involves the addition of oxygen to A (eq 19a) yielding a peroxyl radical B, followed by a HAT (eq 20) from AnH₄Q leading to an intermediate hydroperoxide (C), and regenerates A. The thermal decomposition of C affords oxanthrone, AnOH, and H₂O₂ (eq 21). Termination reactions have not been considered. The proposed mechanism is highly improbable. It is well known that ketyl radicals, for example, benzophenone ketyl, react with oxygen at the diffusion-controlled limit to yield ketone according to an addition/elimination mechanism (eqs 19a,b).³⁸ The proposed HAT by the peroxyl radical B (eq 20) will be a rather slow (CH to O) bimolecular reaction (this work). Consequently, the major pathway for ketyl A follows eqs 19a and 19b yielding 10-OH-anthrone (AnOH) and HO₂^•. Alternatively, a direct HAT by oxygen (eqs 22a and 22b) from A can be envisaged. In that case, the H-transfer from OH to ³O₂ (eq 22a) to give AnOH will be the preferred route (this work).

Scheme 8. Mechanism for the Anthraquinone H₂O₂ Process as Proposed in ref (76), with the CBS-QB3-Calculated Reaction Enthalpies in kcal mol^–1 (This Work).

The lowest-enthalpy conformer of AnH₄Q consists of the two hydroxyls in the s-trans orientation. BDE(C–H) in AnH₄Q is 77.8 kcal mol^–1. The bond lengths (in Å) for the intra-HB in B are as follows: r(C–OO): 1.6519; r(OO–HO), 1.7195; r(O–H): 0.9898; and the OOCOH dihedral angle is 0.0° (see also Figure 3).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.joc.9b03286.

• Two tables of CBS-QB3-computed thermochemical parameters of prereaction ³O₂ complexes; five figures pertaining to the BEP correlations for hydrogen atom abstraction by molecular oxygen and HO₂^•; assessment of the thermodynamics for the reaction of 4-OH-phenoxyl with oxygen; overview of the computed and experimental kinetic parameters for hydrogen abstraction from (4-OH/MeO−) phenol: CBS-QB3 computed thermokinetic parameters for the C–H hydrogen abstraction by HO₂ from various compounds; three figures showing selected computed transition structures for the foregoing hydrogen transfer reactions; effect of solvation on the AnH₂Q tautomeric equilibrium; thermodynamic parameters and bond distances for the intermolecular HB of HO₂^• and H₂O₂ with arenols and auxiliary species; and B3LYP/CBSB7- and CBS-QB3-computed energies and structure coordinates (PDF)

The authors declare no competing financial interest.

Dedication

This paper is dedicated to Keith U. Ingold on the occasion of his 90th birthday.