POST-TRAUMATIC CEREBRAL MICROHEMORRHAGES AND THEIR EFFECTS UPON WHITE MATTER CONNECTIVITY IN THE AGING HUMAN BRAIN

Abstract

Cerebral microbleeds (CMBs), a common manifestation of mild traumatic brain injury (mTBI), have been sporadically implicated in the neurocognitive deficits of mTBI victims but their clinical significance has not been established adequately. Here we investigate the longitudinal effects of post-mTBI CMBs upon the fractional anisotropy (FA) of white matter (WM) in 21 older mTBI patients across the first ~6 months post-injury. CMBs were segmented automatically from susceptibility-weighted imaging (SWI) by leveraging the intensity gradient properties of SWI to identify CMB-related hypointensities using gradient-based edge detection. A detailed diffusion magnetic resonance imaging (dMRI) atlas of WM was used to segment and cluster tractography streamlines whose prototypes were then identified. The correlation coefficient was calculated between (A) FA values at vertices along streamline prototypes and (B) topological (along-streamline) distances between these vertices and the nearest CMB. Across subjects, the CMB identification approach achieved a sensitivity of 97.1% ± 4.7% and a precision of 72.4% ± 11.0% across subjects. The correlation coefficient was found to be negative and, additionally, statistically significant for 12.3% ± 3.5% of WM clusters (p < 0.05, corrected), whose FA was found to decrease, on average, by 11.8% ± 5.3% across the first 6 months post-injury. These results suggest that CMBs can be associated with deleterious effects upon peri-lesional WM and highlight the vulnerability of older mTBI patients to neurovascular injury.

I. Introduction

Cerebral microbleeds (CMBs) are a consistent manifestation of traumatic brain injuries (TBIs) regardless of their severity. Although CMB impact upon clinical outcome is unclear, it has been proposed that TBI-related CMBs may result in widespread, long-term white matter (WM) alterations and in neurocognitive deficits [1]. Because CMBs are associated with neurotoxicity after the breakdown of the blood brain barrier (BBB), their sequelae may be more severe in geriatric TBI because the brains of older adults (A) exhibit greater BBB permeability and (B) have more deficient neuroinflammatory responses after TBI [1]. Given the uncertainty over the potential significance of TBI-related CMBs to clinical decision making, their identification from magnetic resonance imaging (MRI) and the assessment of their effects upon WM are worthwhile tasks. The detection of intra-parenchymal CMBs can be challenging because standard, anatomic, T₁- or T₂-weighted MRI does not obviate them clearly. In addition, MRI sequence parameters affect the ability to delineate CMBs, whereas magnetic susceptibility artefacts (e.g. flow voids in blood vessels, calcium deposits, deoxyhemoglobin in venules) can complicate their identification [2]. Recent studies utilize susceptibility weighted-imaging (SWI), which provides a higher contrast index for individual CMBs than conventional T₂-weighted MRI, and which has been shown to increase the sensitivity and reliability of CMB detection [3].

An important reason for which CMB effects upon WM have been difficult to study is the relative paucity of reliable techniques for the longitudinal comparison of WM connections via diffusion magnetic resonance imaging (dMRI). Tract-based spatial statistics (TBSS) is arguably the best-known such approach for both within- and between-subject comparison, and this method is available as part of the FMRIB Software Library (FSL) software library. Although adequate for voxel-wise analysis of WM fractional anisotropy (FA), TBSS is suboptimal for quantifying FA changes along specific WM bundles. By contrast, tract-based morphometry (TBM) uses a detailed dMRI WM atlas to facilitate the consistent and reliable identification of WM bundles across subjects, together with their grouping into WM streamline clusters [4]. When combined with streamline prototyping [5], this strategy allows one to identify WM connections confidently across subjects and to assess differences in FA across time.

The first aim of this study is to report on the efficacy of a gradient-based CMB identification algorithm which leverages gradient-based edge detection concepts to identify CMBs in mild TBI (mTBI) victims. The second aim is to utilize the said CMB segmentation algorithm in concert with automatic WM clustering to quantify longitudinal differences in WM FA in mTBI victims. The third aim is to report the statistical association between the presence of CMBs and the FA changes observed along WM streamlines which pass through their spatial neighborhoods (penumbras). The results of this study suggest that CMBs can be identified accurately using the proposed intensity gradient-based algorithm, and that cerebral microhemorrhages can be associated with statistically-significant and deleterious effects upon penumbral WM. These findings highlight the vulnerability of mTBI victims not only to neurovascular injury but also to changes in WM over the first 6–8 months post-injury.

II. Methods

A. Participants

The study was conducted with the approval of the Institutional Review Board at the University of Southern California and all participants provided written informed consent. Our cohort includes 21 individuals who suffered an mTBI about 51/2 months (mo) prior to SWI acquisition (μ = 5.6 mo, σ = 0.2 mo) and who had an acute Glasgow Coma Scale (GCS) score of at least 13 at the time of the initial medical assessment. Participants had to be adults over 21 years (y) of age with no clinical histories of neurological or psychiatric disease prior to their injuries. Volunteers consisted of adults over the age of 45 (N = 21; 8 females; age: μ = 66.2 y, σ = 7.8 y, range: 50–79 y).

B. Imaging

Imaging was performed at 3 T (Prisma MAGNETOM Trio TIM, Siemens Corp., Erlangen, Germany). T₁- and T₂-MRI, gradient recalled echo (GRE)/SWI and dMRI volumes were acquired. T₁-weighted images were acquired using a 3D magnetization-prepared rapid acquisition gradient echo (MP-RAGE) sequence [repetition time (T_R) = 1,950 ms; echo time (T_E) = 2.98 ms; inversion time (T_I) = 900 ms; voxel size = 1.0 × 1.0 × 1.0 mm]. T₂-weighted images were acquired using a 3D sequence (T_R = 2,500 ms; T_E = 360 ms; voxel size = 1.0 × 1.0 × 1.0 mm). Flow-compensated GRE/SWI volumes were acquired axially (T_R = 30 ms; T_E = 20 ms; voxel size = 1.33 × 1.33 × 1.6 mm). dMRI volumes were acquired axially in 64 gradient directions (T_R = 8,300 ms; T_E = 72 ms; voxel size = 2.7 × 2.7 × 2 mm). One volume with b = 0 s/mm² and another with b = 1,000 s/mm² were also acquired. All neuroimaging data were de-identified and de-linked after their acquisition.

C. Preprocessing

Volumes were corrected for motion and eddy current artefacts using the FSL image processing toolbox (https://fsl.fmrib.ox.ac.uk/fsl). The FSL brain extraction tool (BET) was used to exclude voxels outside the brain from analysis. Each subject’s SWI volume was skull-stripped and co-registered rigidly to her/his T₁ volume. Diffusion tensor estimation, dMRI streamline tractography and FA calculations were implemented using TrackVis (trackvis.org) software. WM streamlines whose lengths were smaller than 40 mm were discarded from the analysis.

D. CMB identification

First, the gradient of the image intensities I in the skull-stripped SWI volume was calculated at each brain voxel and the histogram of gradient magnitudes was computed over all brain voxels. The gradient magnitude volume was subjected to binary erosion using a morphological structuring element of spherical shape (11 mm radius). This allowed the exclusion of voxels on the outer edges of the brain volume. The resulting volume was thresholded to discard voxels whose gradient magnitudes belonged to the two tails of their distribution. All connected components consisting of contiguous non-zero voxels within this thresholded volume were identified and their volumes were computed. The components in question were found to be associated with groups of voxels straddling (A) boundaries between cerebrospinal fluid (CSF) and WM, (B) sulcal banks of the neocortex and boundaries between brain and blood vessels, and (C) boundaries between brain and CMBs. Voxels in components from group A could be set to zero by applying an island removal algorithm which targeted the connected component with the largest volume among all identified components. Components in group B could be distinguished from those in group C and isolated for removal by noting that GM and WM are isointense (within μ ± 2σ of the image intensity distribution) in SWI whereas the vasculature and CMBs are hypointense (I < μ – 2σ). After setting the voxels in group B to zero, the gradient magnitude map contained only connected components associated with CMBs (group C). The approach described above allowed connected components associated with CMBs to be identified with sensitivity and precision. Two raters trained in neuroimaging and blinded to the results of the automatic labeling process identified blood vessels and CMBs visually and independently from each other. All identified features of interest were either confirmed or infirmed by a third blinded rater. This allowed the sensitivity and precision of the classification algorithm to be calculated.

E. WM parcellation and prototyping

WM streamline parcellation was implemented using an anatomically-curated streamline clustering atlas described elsewhere [6]. Briefly, an annotation method was used to leverage expert neuroanatomical knowledge and population-based brain anatomical information and to then annotate and categorize streamline clusters. WM structures were annotated in an atlas containing deep WM bundles, including major long-range association and projection bundles, commissural bundles, bundles related to cerebellar connections and to the brainstem, as well as short and medium-range superficial bundle clusters organized into categories based on which brain lobes they connect. Potential false positive connections were annotated to facilitate their exclusion. The atlas allows whole-brain WM parcellation into 800 streamline clusters.

After parcellation, the most representative WM streamline in each cluster was identified using a streamline prototyping approach, as described elsewhere [4, 5, 7]. Briefly, this method can be applied to each WM cluster to facilitate the identification of a unique WM streamline whose trajectory and other properties are representative of the group of streamlines in the cluster. Streamline prototyping is necessary in a study like ours partly because dMRI tractography may generate spurious streamlines which are not associated with physical WM connections; the prototype of an entire cluster of streamlines is a more fiducial descriptor of the underlying WM architecture within the cluster and of its overall properties, including its trajectory.

F. Statistical analysis

The biological hypothesis of the WM analysis is that, within the first ~51/2 months after injury, a CMB leads to decreases in FA whose magnitudes are largest in the immediate spatial neighborhood (penumbra) of the CMB. In other words, the hypothesis is that TBI leads to substantial decreases in FA around the CMB, and that the magnitude of these decreases tapers off within the WM as a function of the distance to the nearest CMB. This hypothesis is inspired by the observation that CMBs are associated with breakdown of the BBB, with the release of neurotoxic compounds into the brain parenchyma and with the gradual infiltration of these compounds along WM tracts [1]. Formally, for each WM streamline prototype, the null hypothesis was formulated as the statement that there is no statistically significant correlation between (A) the longitudinal difference in FA measured at vertices along the prototype streamline and (B) the topological (along-tract) distance between the closest CMB and each vertex along the streamline prototype. The topological distance was selected over the Euclidean distance because the diffusion of neurotoxins away from the CMB site is thought to be constrained by WM axon trajectories [7]. This suggests that the topological (along-tract) distance is a measure which reflects the parameters of the biophysics problem more realistically. The statistical significance of the correlation coefficient between (A) longitudinal differences in FA at prototype streamline vertices and (B) topological vertex-to-CMB distances was evaluated using Student’s dependent t test for paired samples at a significance level a equal to 0.05, subject to the Benjamini-Hochberg correction for multiple comparisons.

III. Results

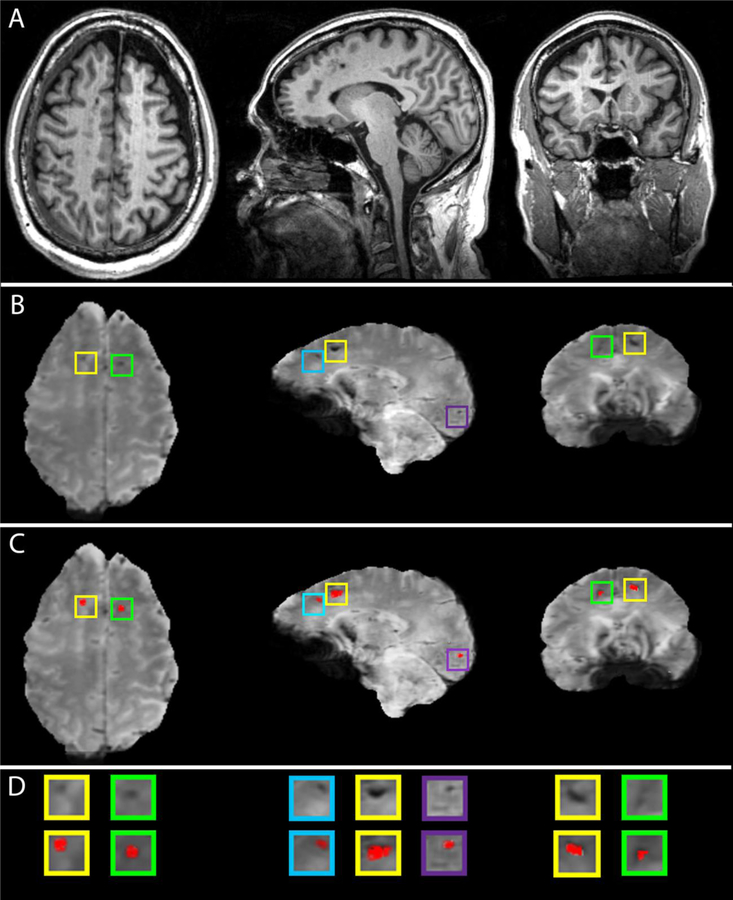
Examples of CMB segmentations are shown in Figure 1. Across all subjects, the average CMB count was 16.6 ± 11.5 (range: 5 to 44). Volunteers aged 65 or under had an average of 17.0 ± 11.8 CMBs (range: 5 to 38), whereas participants over 65 had 16.4 ± 11.8 CMBs (range: 5 to 44). No sex-related significant difference in CMB count was found: Welch’s t = 0.116, d.f. = 14.94, p > 0.909, 95% CI = (10.690, 11.921). The average sensitivity of the CMB classification was 97.1% ± 4.7% and its mean precision was 72.4% ± 11.0%.

Fig. 1.

Examples of automatic CMB segmentations in a geriatric mTBI patient. (A) T₁-weighted images. (B) SWI images with CMBs highlighted in color-coded boxes. (C) SWI images with superimposed CMB segmentations. (D) Enlarged views of CMBs in (B) and (C).

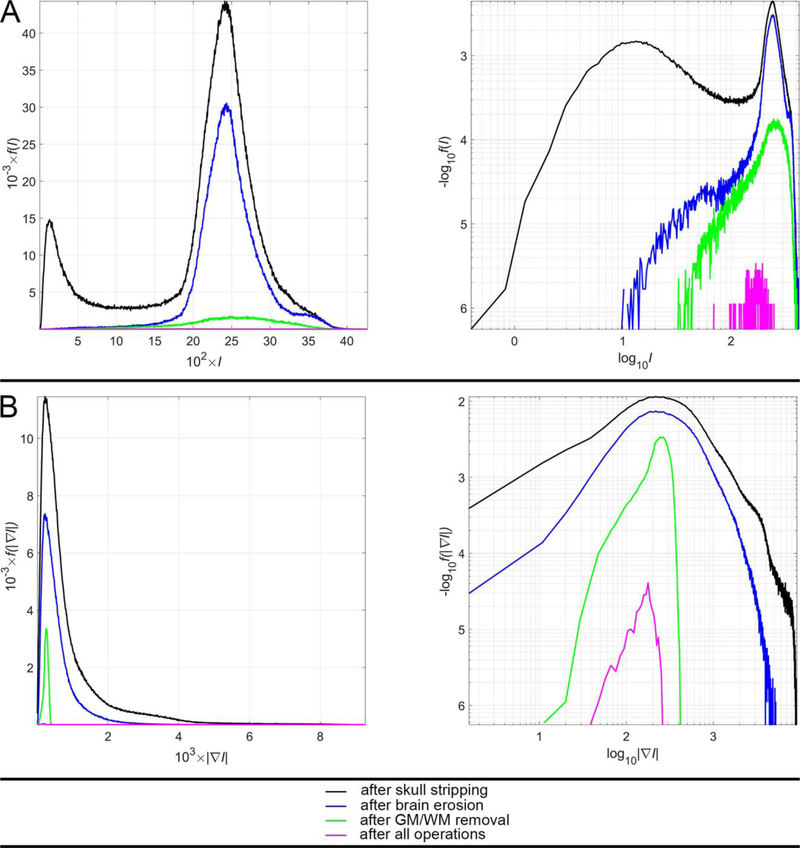
Figure 2 displays the probability density functions (PDFs) f of SWI intensities I (Figure 2A) and of SWI gradient magnitudes (Figure 2B) for voxels within the brain of a sample participant. In other words, Figure 2A depicts f (I) whereas Figure 2B depicts f (|∇I|) for voxels within the sample brain. In both A and B, the PDF computed over all voxels within the brain are plotted in black; that computed over voxels remaining after the brain erosion operation is drawn in blue; the PDF computed over remnant voxels after GM/WM removal is shown in green; the PDF associated with CMB voxels is plotted in magenta (see figure caption).

Fig. 2.

The PDFs f (⋅) for (A) SWI intensities I and (B) SWI intensity gradient magnitudes |∇I| in a sample participant. For convenience, plots are scaled either linearly (first column) or logarithmically (second column) along both axes. Traces depict the corresponding PDF computed over all brain voxels after skull stripping (black), over the subset of voxels remaining after brain erosion (blue), over voxels remnant after the subsequent removal of GM/WM (green) and over CMB voxels alone, after all operations (magenta). In the first column, for visual convenience, values are scaled linearly; for example, 10² × I is plotted on the abscissa in A (instead of I) and 10³ × |∇I| is plotted on the abscissa in B (rather than |∇I |). In the second column, the logarithm of the quantity being depicted is shown; thus, in A, the abscissa displays log₁₀ (I) rather than I; similarly, in B, the abscissa displays log₁₀ (|∇I |) rather than |∇I | itself. Thus, in each of A and B, the left and right columns display the same information, albeit using different scaling, i.e. linear scaling (first column) or logarithmic scaling (second column).

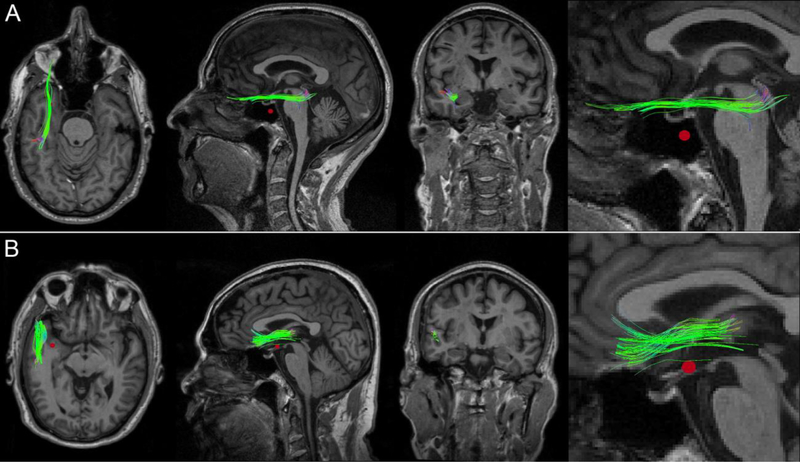
Figure 3 displays CMBs and dMRI-derived streamlines for a perilesional WM cluster in two representative mTBI victims. Across all participants, the null hypothesis was rejected (p < 0.05, corrected), on average, for 12.3 ± 3.5% of WM clusters (range: 6.34% to 17.43%). In other words, for 12.3 ± 3.5% of the WM clusters identified in the average participant, the magnitude of longitudinal FA changes observed along the streamline prototype of the cluster was negatively and significantly correlated with the distance to the closest CMB. Across subjects, the FA changes in question averaged 11.8% ± 5.3% of the FA measured at the first time point. No immediately obvious pattern in the spatial distribution of CMBs associated with significant WM FA changes was identified. WM structures whose FA decreases were found to be correlated significantly with the distance to the closest CMB included the inferior fronto-occipital, inferior longitudinal and superior longitudinal fasciculi.

Fig. 3.

WM streamline clusters in two mTBI victims who exhibit a CMB in the WM of the left anterior temporal lobe. In both (A) and (B), FA changes at vertices along the fasciculi were significantly correlated with the distances from these points to the nearest CMB (red). Whereas only some of the WM streamlines in each cluster pass through the CMB penumbra, the observed FA changes were found to extend beyond the immediate spatial neighborhood of the vascular lesion. From left to right: axial view, sagittal view, coronal view, and inset.

IV. Discussion

Figure 2 allows the reader to observe the effects of successive operations applied by the CMB identification algorithm to a sample sWI volume. The PDF of sWI intensities for voxels within the brain (black trace in the left plot of Figure 2A) reflects the presence of hypointense voxels around the brain (peak at I ≃ 200) in addition to that of isointense voxels associated with GM/WM (peak at I ≃ 2500). The former group of voxels is removed via 3D erosion, as reflected by the blue trace in the left plot of Figure 2A. The subsequent removal of GM/WM voxels, which account for most voxels in the brain, is reflected by the fact that the peak of the green trace in the left plot of Figure 2A is considerably smaller than that of the blue trace in the same plot. subsequent operations leading to the identification of the CMBs further reduce the number of voxels requiring labeling, such that only a logarithmic plot (right column of Figure 2A) allows one to inspect their distribution relative to other PDFs. The logarithmic plot in Figure 2A also allows one to take note of the fact that CMB-related voxels, although hypointense relative to GM/WM voxels, are nevertheless brighter than those which reside on—or close to—the outer edge of the brain. Finally, Figure 2B suggests that the magnitudes of the image intensity gradient at CMB voxel locations are similar to those at most other locations in the brain (right column of Figure 2B), despite the fact that CMB edges are hypointense relative to the GM/WM (right column of Figure 2B). This is consistent with the observation that the intensities of contiguous, CMB-related voxels are homogeneous relative to one another. Interestingly, however, the logarithmic plot in Figure 2B also suggests that CMB voxels have a much narrower SWI intensity range than other structures of similar SWI intensity in the brain. To segment CMBs, SVMs and similar methods entail the use of large training data sets as well as highly-precise feature scaling and class weighting. Semi-automatic methods using random forests have used hand-crafted features dependent on CMB shape and size, but this can lead to erroneous results because CMBs do not always have well-defined shapes [8]. Convolutional neural networks (CNNs) have required large training data sets and substantial processing times due the complex artificial neural layer architecture needed to solve this problem [9]. Because MRI scans are three-dimensional, conventional 2D CNNs are of limited applicability here, given that their kernels neglect information across slices whereas 3D CNNs are computationally intensive [9, 10].

Two prior ML studies report average sensitivities of 82% (SVM, [11]) and 93% (CnN, [9]) over multiple cross-fold validations. For the CNN method, the average precision of the classification was 44%. Whereas ML implementations are more computationally intensive and require cross-fold validations, our algorithm requires only one execution and achieves higher sensitivity and precision than the two ML approaches. Across subjects, our CMB identification method achieves an average sensitivity of 97.1 ± 4.7% and a mean precision of 72.4 ± 11.0%, which are higher than in the studies of ML applications to similar SWI data sets. These results suggest that concepts inspired by gradient-based edge detection methods can be applied to SWI data like ours to perform CMB identification with sensitivity and precision which are comparable to those of some ML methods. Nevertheless, our approach has several limitations. Firstly, we have not used either SVMs or CNNs to segment CMBs from our SWI data set. CMBs may have been more difficult to segment from SWI in previous studies due to reasons like image quality. Comparison of our method to SVMs, CNNs and to other ML approaches should therefore account for such factors unknown to us. Secondly, CMB presentation can vary substantially across mTBI cases; thus, it would be useful to validate the method proposed here in a larger sample. Thirdly, our method was tested on SWI volumes acquired using one set of acquisition parameters. Because the ability of SWI to identify CMBs is sensitive to these, the utility of our approach when applied to SWI volumes acquired with other acquisition parameters is unknown. Fourthly, methods like ours should be tested and validated on SWI volumes acquired not only from mTBI subjects, but also from individuals with other conditions involving CMBs, such as cerebral amyloid angiopathy and similar neurovasculopathies. Finally, sex and age may affect CMB presentation, and therefore confound the efficacy of our algorithm; future research should therefore investigate the effects of these biological variables upon the sensitivity and precision of methods like ours. Despite these limitations, this study illustrates how an interesting and clinically-relevant image analysis problem can be addressed efficiently and parsimoniously in cases like ours using concepts inspired from gradient-based edge detection, rather than more sophisticated methods like SVMs and CNNs.

The analysis of CMB effects upon WM suggests that, in middle-aged and geriatric mTBI participants, CMBs can have deleterious effects upon brain connectivity. The WM structures most frequently associated with such effects included the inferior fronto-occipital, inferior longitudinal and superior longitudinal fasciculi. These relatively long WM structures extend along the anteroposterior axis of the brain, and their association with CMB-related FA decreases may reflect the coup-contrecoup effects of fronto-occipital TBI, which is a very frequent mechanism of brain injury [1]. The statistical inferences made in this study appear to support the hypothesis that CMBs are associated with effects upon FA which are most deleterious in the CMB penumbra. Furthermore, the magnitude of these outcomes appears to decrease as the distance from the nearest CMB increases. This is consistent with the scenario where the occurrence of CMBs results in neurotoxic compounds being released into the brain parenchyma and in the gradual infiltration of such compounds into the WM, along the trajectories of WM tracts. One limitation of our analysis is that the statistical model involved only the distance to the nearest CMB, rather than distances to several CMBs. A corollary of this statement is that statistical interactions between distinct CMBs were not modelled and that their cumulative effects upon WM was not investigated. The effect of a CMB upon neighboring FA is likely much larger than the effects of more distant ones if CMBs are relatively far from one another. This assumption, however, may not hold if CMBs are close to each other, and future research should investigate this scenario.