Automatic recognition of breast invasive ductal carcinoma based on terahertz spectroscopy with wavelet packet transform and machine learning

Abstract

We demonstrate an automatic recognition strategy for terahertz (THz) pulsed signals of breast invasive ductal carcinoma (IDC) based on a wavelet entropy feature extraction and a machine learning classifier. The wavelet packet transform was implemented into the complexity analysis of the transmission THz signal from a breast tissue sample. A novel index of energy to Shannon entropy ratio (ESER) was proposed to distinguish different tissues. Furthermore, the principal component analysis (PCA) method and machine learning classifier were further adopted and optimized for automatic classification of the THz signal from breast IDC sample. The areas under the receiver operating characteristic curves are all larger than 0.89 for the three adopted classifiers. The best breast IDC recognition performance is with the precision, sensitivity and specificity of 92.85%, 89.66% and 96.67%, respectively. The results demonstrate the effectiveness of the ESER index together with the machine learning classifier for automatically identifying different breast tissues.

1. Introduction

Terahertz time-domain spectroscopy (THz-TDS) has emerged as a promising technique to characterize the properties of different biological tissues, because THz radiation is non-ionizing and highly sensitive to water and macromolecules [1,2]. Different types of tissues such as breast cancer, gastric tumor, brain glioma, and oral cancer have been detected using THz-TDS [3–6]. In particular, breast cancer is of high incidence and mortality among women. Furthermore, breast invasive ductal carcinoma (IDC) is the most common subtype among breast cancers [7]. The majority of the patients will conduct the lumpectomy to ensure that the cancer area together with a minimal margin of normal tissue are totally removed [8]. Various imaging techniques such as optical coherence tomography, Raman imaging and phase shifting interferometry have been adopted for breast cancer detection [9–11]. Particularly, THz-TDS has demonstrated great potential to differentiate the tumor region in breast tissue from the lumpectomy, which has attracted increasing interest recently [3,8,12–14].

Nonetheless, as there are generally no obvious absorbance peaks for the biological tissues in the THz frequency, effective spectroscopic feature extraction and classification methods are highly desired to distinguish the THz signals of different tissues [15]. To systematic and automatic recognition of different samples based on THz-TDS, many approaches have been proposed recently [16–22]. Cao et al. adopted a THz spectral unmixing strategy for recognizing the gastric cancer on the basis of frequency-domain absorption coefficient [16]. Park et al. proposed the spectroscopic integration method to increase the signal gap between melanoma and healthy tissues [17]. Zhang et al. introduced the composite multiscale entropy (CMSE) index to distinguish different tissues on account of the complexity analysis of THz signals [18]. Huang et al. used the maximal information coefficient method together with the Random Forests and AdaBoost algorithms to identify the mouse liver damage level [19]. Furthermore, different artificial intelligence analysis strategies, such as support vector machine (SVM), k-nearest neighbor (kNN), and decision tree (DT), were also applied to recognize the THz spectroscopic characteristics of various pathological samples [20–23]. Nevertheless, these studies generally adopted the THz time-domain and Fourier transformed frequency-domain indices.

As an alternative to Fourier transform, wavelet transform has also been widely applied to signal and image analysis due to the advantage of multi-scale resolution for non-stationary signal [24]. Moreover, it has also been adopted in the THz time-domain signal processing [25,26]. Many wavelet-based features such as energy, linear prediction cepstral coefficient and entropy have been proposed to characterize and distinguish different signals [27–29]. Particularly, wavelet entropy is sensitive to the signal singular point and can significantly decrease the data quantity [29]. The wavelet entropy feature has been successfully employed to characterize different physiological signals [30,31], which demonstrates a huge potential to provide a novel feature index for analysis of THz signals from various biological samples.

In this paper, we propose an automatic recognition strategy for transmission THz pulsed signal of breast IDC based on wavelet entropy feature extraction and machine learning classifier. To the best of our knowledge, we introduce the wavelet entropy approach into the complexity analysis of THz signal for the first time. A novel index of energy to Shannon entropy ratio (ESER) was proposed to distinguish different breast tissues. Moreover, the principal component analysis (PCA) method was employed to reduce the dimensionality of extracted feature. The performances of various machine learning classifiers were analyzed and compared for classification of the IDC and normal breast tissues. The results demonstrate the effectiveness of the ESER feature index together with the machine learning classifier for automatically identifying different breast tissues.

2. Materials and methods

2.1. Sample preparation and data acquisition

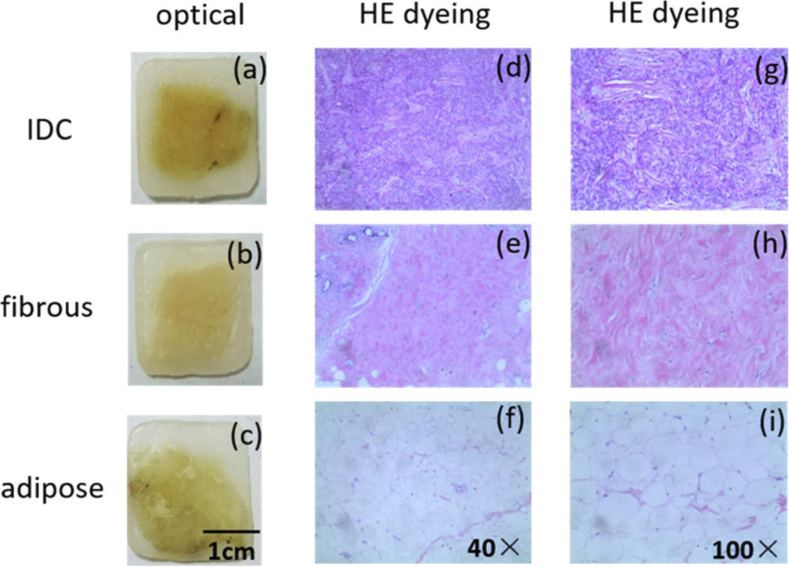
The tissue samples investigated in this study were obtained from the Shenzhen Maternity and Child Healthcare Hospital. These samples came from sixty-three patients (aged 32-65, mean age 46.54 ± 8.97) who were diagnosed with breast IDC and conducted the lumpectomy. The normal and cancerous breast tissues were retrieved from the surgically removed tissue samples and treated by the standard pathology procedure for histopathology examination. The group criteria for the IDC, normal fibrous and adipose tissue samples are as follows. First, the corresponding tissue components account for more than 90% region of the whole sample. Second, there is not any cancer tissue in the normal fibrous and adipose tissue samples. The obtained paraffin-embedded tissue samples were cut into slices by a cryotome, with an tissue area of about 10 mm × 10 mm and an average thickness of 1.996 ± 0.496 mm. To increase the sample quantity, two or three sliced paraffin-embedded tissue samples may come from one patient. The optical pictures of the three different paraffin-embedded samples and the corresponding HE (hematoxylin eosin) dyeing microscope images are demonstrated in Fig. 1. Finally, ninety-seven IDC samples, one hundred normal fibrous tissue samples and ninety-nine normal adipose tissue samples were obtained for the next step measurement and analysis.

Fig. 1.

Optical pictures of one paraffin-embedded IDC sample (a), one normal breast fibrous tissue sample (b) and one normal breast adipose tissue sample (c), HE dyeing microscope images (40×) of IDC (d), normal fibrous (e) and adipose (f) tissues, HE dyeing microscope image (100×) of IDC (g), normal fibrous (h) and adipose (i) tissues.

The THz time-domain signals were acquired using a self-built transmission THz-TDS system. The system mainly includes a femtosecond laser, a pair of photoconductive antennas as the THz pulse generator and detector. The detailed information of this system can be found in [32]. The tissue sample was placed at the focus point of the THz beam. The step scan was applied to measure the tissue region of each paraffin-embedded sample. During the measurement, the THz beam path was purged with dry nitrogen to decrease the absorption effect of water vapor (humidity: ∼5%, temperature: ∼22 ^oC).

2.2. Automatic recognition strategy

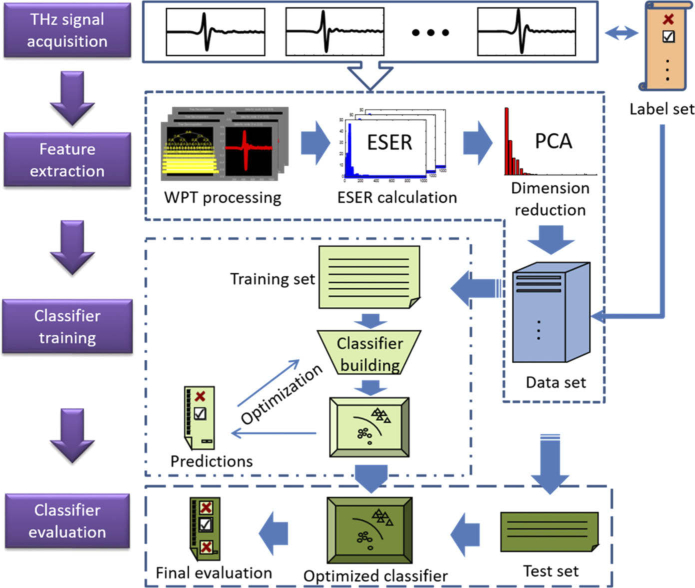
The flowchart of the proposed automatic recognition strategy for THz time-domain signals of breast cancer samples is shown in Fig. 2. The procedure contain the THz signal acquisition, wavelet packet transform (WPT) processing, WPT based ESER calculation, PCA dimension reduction, classifier building and optimization. Various machine learning classifiers were adopted to build the recognition system and train the feature database. The training set includes two hundred and seven samples (sixty-eight IDC, seventy normal fibrous tissue and sixty-nine normal adipose samples) and the test set contains eighty-nine samples (twenty-nine IDC, thirty normal fibrous tissue and thirty normal adipose samples). The corresponding classification results for the IDC and normal tissues were analyzed and compared.

Fig. 2.

Flowchart of the proposed automatic recognition strategy for THz time-domain signals of breast tissue samples.

2.2.1. WPT based ESER calculation

WPT is employed for wavelet entropy calculation in this study, which could provide sufficient analysis for both low and high frequency components of the signal. It has been widely applied in various areas such as speech analysis and image processing [28,30,33]. In general, WPT is performed by two recursive band-pass filtering processes, which are expressed as follows:

$$\{\begin{array}{l}{c}_{j+1}^{2n}(l)=\sum _{k}h(k-2l)c_j^n(k)\\ c_{j+1}^{2n+1}(l)=\sum _{k}g(k-2l)c_j^n(k)\\ c_0^0(l)=T(l)\end{array},n=0,1,2,\cdots 2^j,j=1,2,3,\cdots ,J$$ (1)

in which the original THz time-domain signal is denoted as $T(l)$ and the maximal WPT decomposition level is J. $h(\cdot )$ and $g(\cdot )$ are the low-pass filter and high-pass filter, respectively. The filters are formed by a mother wavelet and the relevant scale function. $c_j^n(\cdot )$ is the n_th sub signal at level j. $c_{j+1}^{2n}(\cdot )$ and $c_{j+1}^{2n+1}(\cdot )$ are the low-frequency and high-frequency parts of $c_j^n(\cdot )$.

For each sub signal, the WPT based Shannon entropy $H(c)$ is adopted in this study and calculated as follows based on normalized $p_i$ [30].

$$\begin{array}{l}H(c)=-\sum _{i=1}^I{|p_i|}^{2}log({|p_i|}^2),\\ p_i=\frac{{|c(i)|}^2}{\sum _{m=1}^I{|c(m)|}^2}\end{array}$$ (2)

where I is the length of the sub signal $c$. Moreover, the ESER is calculated and used as the feature index by considering not only the energy but also the complexity of the THz signal.

$$ESER(c)=\frac{E(c)}{H(c)}$$ (3)

in which $E(c)$ is the normalized energy of sub signal c with respect to that of the original THz time-domain signal and calculated as follows:

$$E(c)=\frac{\sum _{m=1}^I{c}^2(m)}{\sum _l{T}^2(l)}$$ (4)

About the mother wavelet choice, according to the Daubechies theory [34], the wavelets in Daubechies families are efficient as they have the minimal support set for specified number of vanish moments. In the present study, ten Daubechies wavelets (db 1∼10) were tested under different decomposition levels (3∼10) for the WPT analysis of the THz signal. The parameter of the summation of ESER ($S_{ESER}$) was adopted to evaluate the performance of different mother wavelets, and higher $S_{ESER}$ represents better performance of the mother wavelet [35]. The expression of $S_{ESER}$ is shown as follows:

$$S_{ESER}\text{ = }\sum _{n=1}^N\frac{E_n}{H_n}$$ (5)

in which $E_n$ is the energy of the n_th sub signal, $H_n$ is the Shannon entropy of the n_th sub signal, N is the total number of the sub signals. For the whole set of samples, we analyzed the $S_{ESER}$ results among different Daubechies wavelets (db 1∼10) and decomposition levels (3∼10). The db1 and decomposition level 10 acquired the highest mean $S_{ESER}$ among the whole set of samples. Thus, db1 and decomposition level 10 were employed in the next step WPT analysis for different breast tissue samples.

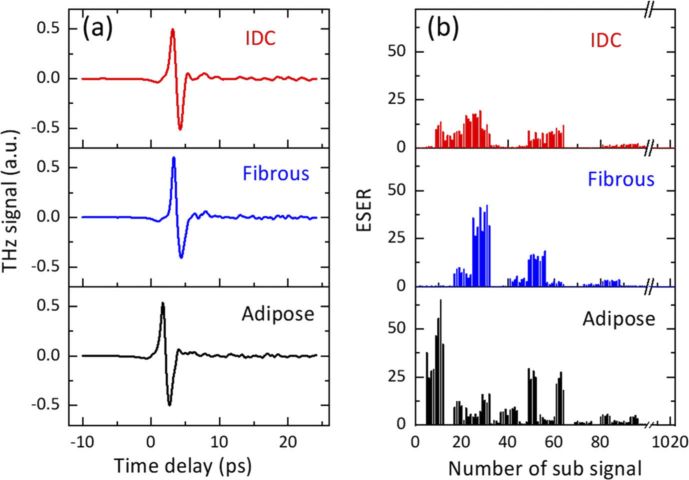
According to the above calculation, one THz time-domain signal can be transformed into an ESER feature vector $V_{ESER}=[ESE{R}_1,ESE{R}_2,\dots ,ESE{R}_N]$. The THz time-domain amplitudes and ESER analysis results for one IDC sample, one normal breast fibrous tissue sample and one normal breast adipose tissue sample are shown in Fig. 3. The differences in the profile and amplitude of the time-domain signals among the three tissues are small. However, a clear discrepancy of ESER exists among the three samples. Furthermore, to evaluate the discrepancies among the three tissue samples, we implemented one-way analysis of variance (ANOVA) for the THz time-domain signals and ESER features over the entire set of samples, respectively [36,37]. At the statistically significant difference level of p < 0.05, the ESER indices of three tissue sample are significantly different (p = 2.50×10⁻⁴) while there are no significant discrepancies in the time-domain amplitudes (p = 0.43). Moreover, the F value of ESER index (8.53) is much higher than that of time-domain amplitude (0.85), which means that the discrepancies of ESER indices between the three tissue samples are much larger than those of THz time-domain amplitudes. This demonstrates the feasibility of the ESER index for differentiating THz signals after interacting with different biological samples.

Fig. 3.

THz time-domain amplitudes (a), and ESER results (b) for one paraffin-embedded IDC sample, one normal breast fibrous tissue sample and one normal breast adipose tissue sample.

2.2.2. Machine learning classifier

To reduce the data dimensionality for classification, PCA is applied to the ESER database. PCA is an unsupervised feature extraction method, which contains an orthogonal transform of the data space to produce a series of uncorrelated principal components (PCs) [38]. Each consecutive PC has the largest variance possible under the orthogonal restraint. The combinations of PCs with increasing numbers were used and the corresponding classification performances were compared to determine the proper PC number.

Following the PCA feature extraction, the machine learning classifiers were constructed and trained to distinguish different breast tissue samples. To improve the classification performance, the included number of PCs and classifier parameters were optimized. In order to avoid overfitting of classifier parameters, we performed five-fold cross validation during the classifier building [39]. Three different classifiers including SVM, kNN and ensemble method were analyzed and compared in this study.

SVM utilizes an iteration approach to obtain the maximum boundary among different classes by using the minimal amount of support vectors [40]. The quadratic, cubic and Gaussian kernel functions in the SVM classifier were used in this study.

kNN is a supervised algorithm to determine which category the data should be classified by the vote of the nearest k points [41]. The cosine, cubic and Euclidean distance metrics in the kNN classifier were tested and k was set as ten for different distance metrics.

The Ensemble methods of bagged trees, subspace discriminant and subspace kNN were also compared to differentiate the three breast tissue samples [42].

The total accuracy was employed to determine the optimal combinations of PCs and classifier parameters. The receiver operating characteristic (ROC) curve and the area under the curve (AUC) were further adopted to assess the recognition performance for different breast tissue samples. The ROC curve represents how much true positive rate (TPR) is realized on condition of a prescribed false positive rate (FPR). The AUC score denotes the area under the ROC curve. Moreover, the criteria consisting of precision, sensitivity and specificity were further used to assess the breast IDC identification performance with different classifiers.

3. Results and discussion

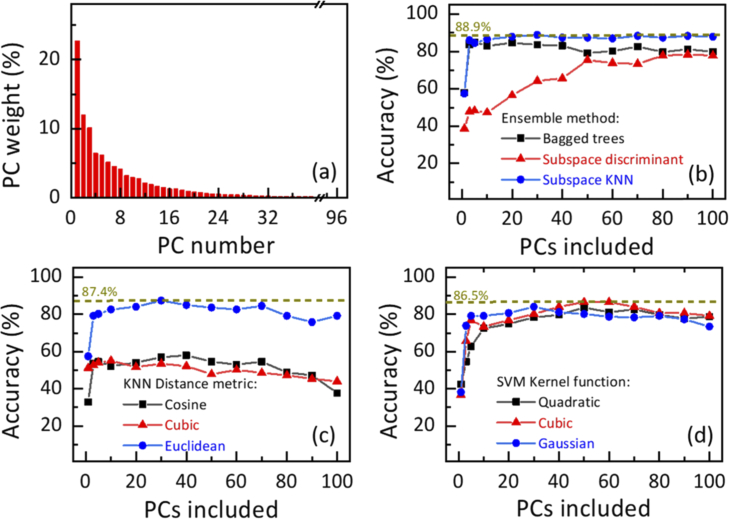
The data dimensionality reduction results for ESER database of the training set based on PCA is shown in Fig. 4(a). The corresponding total recognition accuracy results for Ensemble, kNN and SVM classifiers with different parameters based on increasing numbers of PCs are demonstrated in Fig. 4(b)–(d). The PC weight decreases significantly with the serial number of PC increases. Different amounts of PCs were applied to train the Ensemble, kNN and SVM classifiers. With more PCs included from 1 to 30, the total classification accuracy increases dramatically and reaches the highest value for the Ensemble classifier with subspace kNN strategy (88.9%) and the kNN classifier with Euclidean distance metric (87.4%). Then with the addition of the extra PCs, the total accuracy gradually drops for the kNN classifier, and it tends to saturation for the Ensemble classifier with subspace kNN strategy. For the SVM classifier with cubic kernel function, the total recognition accuracy increases significantly and reaches the maximal value of 86.5% with more PCs included from 1 to 50.

Fig. 4.

(a) Data dimensionality reduction results for ESER database based on PCA. Total recognition accuracy results for the Ensemble (b), kNN (c) and SVM (d) classifiers with different parameters based on increasing numbers of PCs.

The relation between the recognition accuracy and included number of PCs depends on the contribution to variance of different PCs, the architecture and parameter of the machine learning classifier. The present recognition results for different machine learning classifiers could be due to that the first fifty PCs, especially first thirty PCs, contribute most to the overall variance of the signal and the extra PCs may be related to the noise. The combination of the first thirty PCs was adopted for the Ensemble and kNN classifiers, while the first fifty PCs are used for the SVM classifier, in the next step recognition analysis of breast tissue samples. Moreover, the parameters in each classifier with better classification performance were also employed in the next step recognition analysis.

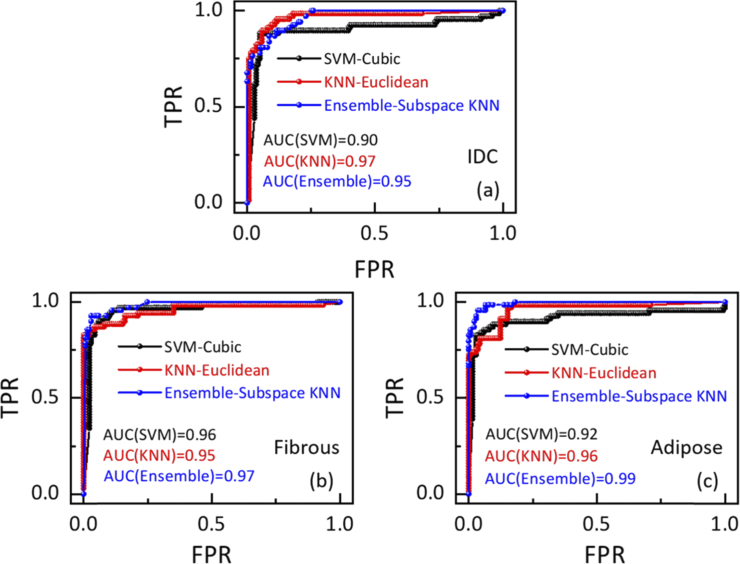
The ROC curves and AUC scores for breast IDC, normal fibrous and adipose tissue recognition in the training set are presented in Fig. 5 when Ensemble, kNN and SVM classifiers achieve the maximum accuracy. For the normal fibrous and adipose tissue samples, the AUC scores are all larger than 0.91 and the Ensemble classifier has the best performance. The AUC scores for IDC identification based on the Ensemble, kNN and SVM classifiers are 0.95, 0.97 and 0.90, which demonstrates the effectiveness of the ESER feature index together with machine learning classifier for identification of breast IDC. Moreover, the kNN and Ensemble classifiers have better performance than the SVM classifier for breast IDC recognition in the training set. For comparison, we also analyzed the recognition performance based on the original THz time-domain amplitude features in the same training set by using the same procedures. The corresponding AUC scores for breast IDC identification when Ensemble, kNN and SVM classifiers achieve the maximum accuracy are 0.85, 0.79 and 0.77, respectively. The ESER index has much better recognition performance for breast IDC than THz time-domain amplitude.

Fig. 5.

ROC curves and AUC scores for breast IDC (a), normal fibrous tissue (b) and normal adipose tissue (c) identification when Ensemble, kNN and SVM classifiers achieve the maximum accuracy.

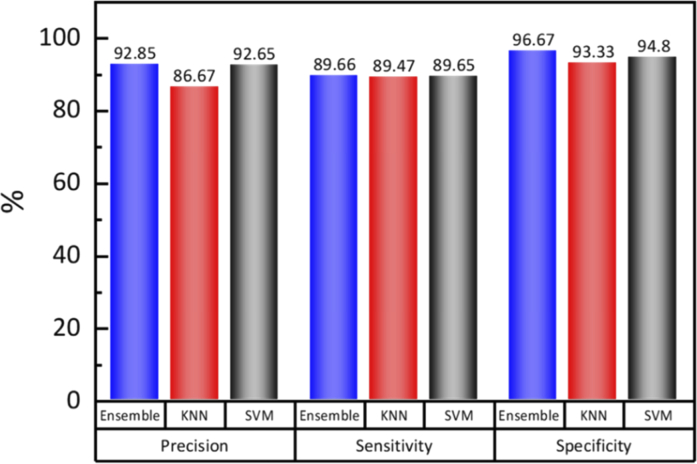
The precision, sensitivity and specificity results for breast IDC identification in the test set are shown in Fig. 6 when Ensemble, kNN and SVM classifiers achieve the maximum accuracy. In general, the increment of precision, sensitivity and specificity could realize higher diagnosis accuracy, lower misdiagnosis rate and smaller omission diagnostic rate, respectively. In particular, the Ensemble classifier has the highest precision and specificity among the three classifiers. Ensemble and SVM classifiers have a slightly higher sensitivity than the kNN method. In the present study, Ensemble classifier is most appropriate for automatic recognition of breast IDC based on THz spectroscopy with ESER feature index. These results indicate that the proposed strategy could be employed to largely decrease the misdiagnosis and omission diagnostic rates for paraffin-embedded breast IDC samples.

Fig. 6.

Precision, sensitivity and specificity for breast IDC identification when Ensemble, kNN and SVM classifiers achieve the maximum accuracy.

The wavelet-based ESER of THz signal could be adopted as a novel and complementary index for THz spectroscopic applications, which is suitable for discriminability of different tissues. It could further facilitate pathological tissue detection when combing with other THz indices. Moreover, by integrating ESER index with PCA and machine learning classifier, highly accurate and sensitive recognition of cancer tissue could be realized.

4. Conclusion

In conclusion, the feasibility and validity of an automatic recognition method for paraffin-embedded breast IDC samples based on transmission THz spectroscopy and machine learning classifier have been demonstrated. The WPT method was introduced to THz signal analysis and a novel index of ESER was proposed for distinguishing different tissues. Moreover, PCA and three different machine learning classifiers (Ensemble, kNN and SVM) were adopted and optimized for automatic identification of breast IDC. The Ensemble classifier with subspace kNN strategy and the kNN classifier with Euclidean distance metric achieve the highest recognition accuracy with thirty PCs included. For the SVM classifier, the cubic kernel function has the best classification performance with fifty PCs included. The results demonstrate that the AUC scores are larger than 0.89 for all the three classifiers and Ensemble classifier has the best identification performance of breast IDC with the precision of 92.85%. It provides an effective automatic recognition strategy for THz biomedical applications.

Ethical approval

This research was performed in view of the fundamental ethical principles stipulated in the Helsinki declaration and its later revisions. The tissue samples were acquired with the written approval from each patient undergoing the lumpectomy.

Funding

National Natural Science Foundation of China10.13039/501100001809 (61905271); Shenzhen Research Foundation (JCYJ20160608153308846, JCYJ20170413152328742); Youth Innovation Promotion Association of the Chinese Academy of Sciences10.13039/501100004739 (2016320); China Postdoctoral Science Foundation10.13039/501100002858 (2019M660217).

Disclosures

The authors declare that there are no conflicts of interest related to this article.