Qualitative and quantitative detection of liver injury with terahertz time-domain spectroscopy

Abstract

Terahertz technology has been widely used as a nondestructive and effective detection method. Herein, terahertz time-domain spectroscopy was used to detect drug-induced liver injury in mice. Firstly, the boxplots were used to detect abnormal data. Then the maximal information coefficient method was used to search for the features strongly correlated with the degree of injury. After that, the liver injury model was built using the random forests method in machine learning. The results show that this method can effectively identify the degree of liver injury and thus provide an auxiliary diagnostic method for detecting minor liver injury.

1. Introduction

Terahertz (THz) radiation consists of electromagnetic waves with a frequency in the range of 0.1-10 THz (1 THz = 10¹² Hz) and a wavelength in the range of approximately 0.03 mm to 3 mm [1]. THz waves have unique features such as transparency, low-energy, and fingerprinting. These waves provide an effective non-destructive method for the detection and analysis of biological macromolecules [2]. Moreover, the THz pulse has good time resolution, which permits the THz technology to be useful in fields such as defense and security [3,4], chemical and biological detections [5,6], and medical diagnosis [7–10].

Specifically, since the energy of THz photons is lower as compared to X-rays, the substances under detection are not damaged by photoionization. This has ushered in THz technology to become a critical detection method in medical diagnosis in the past decade [11–15]. For example, Mariia et al. did an investigation on water content in pork muscles by employing terahertz time-domain spectroscopy (THz-TDS). The quantitative calculation of the water concentration within the samples was conducted using the Landau-Looyenga-Lifshitz-based model [11]. Sim et al. [12] applied THz imaging for human oral cancerous tissue detection and obtained satisfactory results which covered features such as size, shape and internal position of the oral cancer. A single-channel THz endoscopic system was developed for fresh cancerous and normal colorectal tissue detection. They found that the level of contrast observed from the THz endoscopic system correlated well with the contrast levels observed in the free space ex vivo THz reflectance studies of human colonic tissue [14]. Normal and cirrhotic liver tissues were investigated by using terahertz reflection spectroscopy. The results showed that cirrhotic tissue had a higher absorption coefficient than the normal tissue because of higher water content [15].

Cancer is one of the most common cause of death in both economically developed countries and developing countries [16,17]. To date, the global morbidity and mortality of cancer is still rising [18,19]. There is no specific clinical manifestation in early stage of most cancers. Therefore, when the patients are diagnosed, they are mostly characterized as medium or high grades. Low grade cancers are often treated with surgery, while high grade cancers can only be treated with chemotherapy. Thus, chemotherapy has a crucial role in the treatment of high grade cancers [20]. However, with a better understanding of the effect of chemotherapy on cancers, the problem of liver injury associated with chemotherapy drugs has received increasing notice. This is because it may have adverse effects on treatment and prognosis.

Drug-induced liver injury (DILI) is a common clinical adverse drug side effect with a high incidence rate and exhibits different symptoms. In the United States, DILI is the leading cause of acute liver failure, which accounts for approximately 60% of all liver injury cases [21]. Chemotherapy drugs have a toxic effect on tumor cells. However, it can damage the normal cells of patients. This explains how chemotherapy drugs can cause many adverse effects. In fact, liver injury has always been one of the adverse effects of chemotherapy drugs. Some patients with severe liver injury may be at risk of getting life-threatening liver failure. It is involved in many complex biological processes such as bile secretion, detoxification, phagocytosis, metabolism, excretion, and immunity. Thus, DILI is a factor must be considered when it comes to chemotherapy.

At present, the main method for detecting DILI is a blood test. In addition, recently, many advanced diagnostic methods have been reported thanks to the advancement in medical technology. Anderson et al. [22] found that when the ratio of serum AST/ALT is progressively elevated to be greater than 1, the likelihood of developing cirrhosis is extremely high. Also, researchers have developed a metabolomic mass spectrometry-based approach for detecting drug-induced hepatotoxicity [23]. However, the specificity of blood test is not sufficiently high enough therefore making it difficult to detect low-level liver injury. Other methods are restricted by lack to provide mechanistic information or predictability. This also sets barriers in determining the surgical approach and predicting the likelihood of postoperative liver failure [24].

With this in mind, a method to detect the degree of liver injury in mice based on the THz-TDS was proposed. We applied the statistical method of boxplots for data cleaning since there were abnormal data existing in the process of data acquisition. Then, the maximum information coefficient method was used to find the top 20 features that were strongly correlated with the degree of liver injury. Finally, the random forests method was applied for building the detection model. In the results, the detection results of the two optical parameters were compared. It was found that the model built by the absorption coefficient can obtain a smaller root mean square error of prediction (RMSEP), and the model built by the refractive index can get a larger decision coefficient (R²).

2. Experiment

2.1. THz-TDS measurement

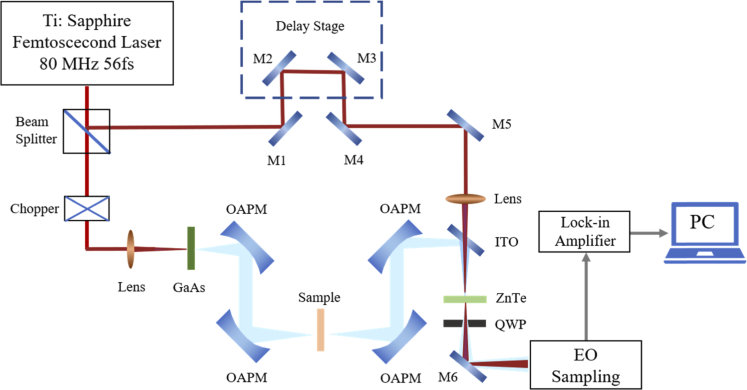
The Z3 THz-TDS system (Zomega Terahertz Corporation, USA) was used herein. Transmission mode was used to collect THz signal and its schematic diagram is shown in Fig. 1 . The THz excitation device adopts a commercial mode-locked Ti: sapphire laser (Coherent Company, USA). The pulse produced has a central wavelength of 800 nm, a repetition rate of about 80 MHz, and an average power of 960 mW. To reduce the error caused by THz absorption of water vapor, and to improve the signal-to-noise ratio, the air humidity was kept at about 1%, and the laboratory ambient temperature was maintained at 20°C. The radius of the THz beam is around 5 mm and the time for each measurement is 15 seconds. The effective detection range of the device is 0.2-2.0 THz, but because of the high water content in the biological samples, the actual available frequency band tended to be about 0.2-0.8 THz.

Fig. 1.

Schematic diagram of the terahertz transmission time-domain system.

2.2. Sample preparation

The chemotherapeutic drug 5-Fluorouracil (5-FU) has been widely used in the treatment of malignant tumors related to gastrointestinal tract, brain, breast, liver and pancreas [25]. 5-FU, whether applied solely or in combination with other drugs, is still the mostly used chemotherapy drug for gastrointestinal malignancies. Thus, in the experiments, we considered to inject different dose of 5-FU into mice to acquire five levels of liver injury. The 5-FU, a chemotherapeutic drug used in this experiment (Shanghai Xudong Haipu Pharmaceutical, China) and diluted in 0.9% normal saline. The drugs used in the experiments were prepared on the day of the experiment. The 30 Female BALB/C nude mice at a 5-week age weighted at 20 g on average were prepared for this experiment. The details of the mouse culture process are found elsewhere [26].

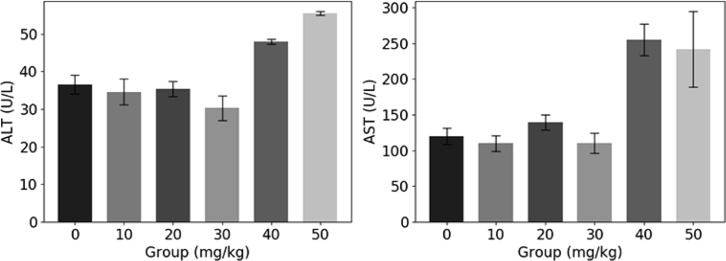
After one week of culture, the mice were randomly divided into six experimental groups, and 5-FU injections at concentrations of 0, 10, 20, 30, 40, 50 mg/kg were injected once daily, for five consecutive days, respectively. Only 26 mouse liver tissues were obtained, and four mice were excluded from other factors. The number of liver tissues in each group was 4-5. Figure 2 shows the serum ALT and AST values in six groups after three weeks of 5-FU injection. Since the 50 mg/kg injection dose was unacceptable to mice, the mice in this group were unable to survive for more than three weeks. Therefore, the biochemical indicators of the mice that died prior to three weeks were used as the test data before death. From the results of biochemical indicators, the liver tissue after injection of different concentrations of 5-FU was verified to be damaged to varying degrees.

Fig. 2.

Serum ALT and AST values of six groups after three weeks of 5-FU injection with associated error bars.

Furthermore, since each tissue had different size, the number of slices per tissue was 6-20 and the number of slices for each group were 62, 57, 63, 61, 60, and 54. The thickness of liver tissue sections of each mouse was controlled to be 350 µm. After that, the experiments were performed using the THz-TDS system. The THz experiments were carried out for two days, and the experimental steps and methods were consistent every day. According to the size of each slice, a total of 1-2 points were selected, and each test point was repeatedly tested twice to ensure the repeatability of the experiment. Finally, 85, 77, 76, 79, 78, and 69 time-domain spectra were obtained for the six groups, respectively, and 464 spectra in total.

2.3. Methodology

2.3.1. Liver injury recognition method

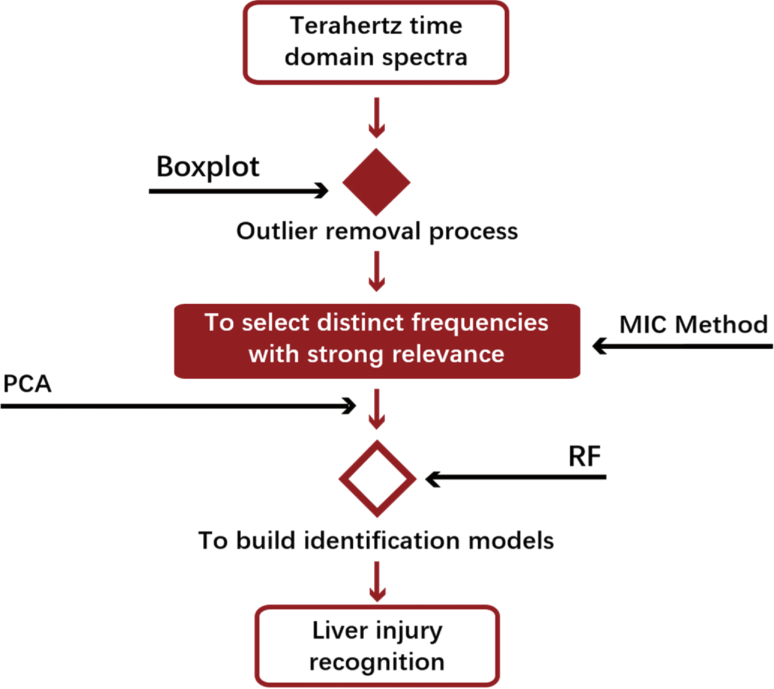
To detect the degree of liver injury in mice, we proposed an identification algorithm based on THz-TDS. The algorithm flow chart is shown in Fig. 3 . Due to inappropriate experimental operations and unstable factors in the system, some abnormal data existed in the process of detection. The data preprocessing was required in order to improve the recognition rate. We used the statistical method boxplot to remove the outliers with the parameter time-delay $\mathrm{\Delta }t$,

$$\mathrm{\Delta }t=t_{sam}-t_{ref}.$$ (1)

This parameter was selected because prior results showed good detection results could be obtained by using this parameter in the detection of biological samples [2]. Then, Fast Fourier Transform (FFT) was applied to transform the time-domain spectrum into frequency-domain spectrum. According to the optical parameter extraction model proposed by Dorney et al. [27], the equations of refractive index n(ω) and absorption coefficient α(ω) are as shown in Eqs. (2) and (3),

$$n(\omega )=\frac{\phi (\omega )c}{\omega d}+1,$$ (2)

$$\alpha (\omega )=\frac{2}{d}\ln \{\frac{4n(\omega )}{\rho (\omega ){[n(\omega )+1]}^2}\},$$ (3)

where d is the thickness of the sample slices, φ(ω) and ρ(ω) are the phase difference and the amplitude ratio between the sample signal and the reference signal.

Fig. 3.

Flow chart of liver injury discrimination algorithm based on terahertz spectra.

In the feature selection process, the distinct frequency points of the absorption coefficient and the refractive index were selected by the maximum information coefficient (MIC) method. The principal component analysis (PCA) method was used for feature dimension reduction, and the first five principal components were used as the input to the random forests (RF). In this study, we performed analysis of mouse liver injury based on two optical parameters absorption coefficients and refractive indices, respectively.

2.3.2. Distinct frequencies identification using MIC

The features with strong relevance with liver injury were found in the terahertz region. We considered the MIC technique because it can identify relationships between pairs of variables [28,29]. Specifically, MIC is able to provide a method to find big correlation between the distinct frequencies of absorption coefficient and refractive index spectra with injured liver tissues. The MIC is a correlation algorithm that evaluates the functional and statistical relationships between variables without making any assumptions about the data distribution. Using MIC permits an examination of a certain relationship between two variables, then a grid can be drawn on the scatterplot of the two variables that partitions the data to encapsulate that relationship.

The mutual information value of two variables can be calculated according to the marginal probability density function and the joint probability density function in the grid [30]. Given a finite ordered pair of dataset D, the x*y grid G is obtained only if the x-axes and y-axes are divided into x and y grids, respectively. The distribution of the values in x-y space locates in the cells of G is denoted as D|_G, where x and y are positive integers. If the number of mesh divisions is fixed, different mutual information values will be obtained by changing the mesh division position, and the maximum mutual information value of two variables is shown in Eq. (4).

$$I^{\ast }(D,x,y)=\text{max}I({D|}_G).$$ (4)

In order to facilitate comparison between different dimensions, the values are normalized by Eq. (5) to make values in the interval [0, 1]:

$$M{(D)}_{x,y}=\frac{I^{\ast }(D,x,y)}{{\log }_{\text{min}}\{x,y\}}.$$ (5)

$$MIC(D)=\underset{xy\le B(n)}{\text{max}}\{M{(D)}_{x,y}\}.$$ (6)

Knowing the ordered pair dataset D with a sample size of n, the MIC of the two variables X and Y in the dataset is shown as Eq. (6), where n is the number of samples, $B(n)=n^{\alpha }$ imposes an upper bounds on the sizes of G for searching the MIC value. $\alpha =0.7$ was used herein.

2.3.3. Identification by RF

Random forests (RF) are increasingly applied for classification and regression in recent years due to the high prediction rate and the ability to simulate complex interactions between large numbers of predictors [31,32]. It integrates decision trees and combines the idea of bagging integration and feature selection. RF method not only increases the diversity of individual decision trees, but also improves the generalization ability of the entire model. The measured mouse liver injury was used as the output variable of the model, and the parameters absorption coefficient and refractive index collected in the corresponding experiment were used as the input variables of the model. The output variables and input variables formed the training dataset D.

The bootstrap sampling technique was used to perform re-sampling of the training dataset, and n subsets D_n of the training datasets D and n regression trees T_n were randomly generated. Then, m features were randomly selected from M features to form a feature subspace for regression tree nodes to split. At each node of the regression tree, the optimal attribute was selected from the feature subspace according to the minimum principle of Gini impurity. The node was split using the optimal split attribute, and finally a regression tree was constructed. Each regression tree grew recursively from top to bottom. The regression tree stopped growing when the segmentation termination condition was attained. Finally, all the regression trees were combined to form a random forest. The predicted liver injury was estimated by averaging all the prediction results of each regression tree.

3. Results and discussion

3.1. Results for preliminary data processing

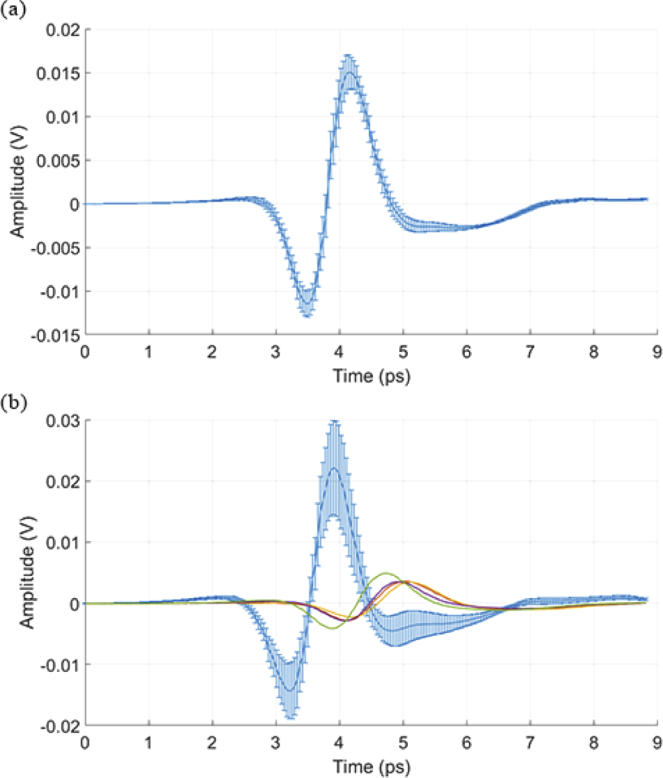
Figure 4 shows the average time domain spectra of two liver tissues injected with 0 and 50 mg/kg 5-FU with associated error bars, respectively. Standard deviations of time domain spectra were calculated and used as error bars. Since the volume of each liver tissue was slightly different, the number of slices of each tissue varied over a certain range. The average THz time domain spectra of the 1^st liver tissue in 0 mg/kg group (tissue 0-1) and the 2^nd liver tissue in the 50 mg/kg group (tissue 50-2) are shown in Figs. 4(a)–4(b), respectively. The result in Fig. 4(a) is clear while there are four abnormal spectra in Fig. 4(b). It can be seen from Fig. 4 that the overall trend of the time domain spectra of the same tissue is consistent, albeit there are obvious differences between the peak-peak values. As shown in Fig. 4(a), the tissue 0-1 exhibited universal results among multiple tests with relatively small standard deviation.

Fig. 4.

Average terahertz time domain spectra of two liver tissues. (a) Average terahertz time domain spectra of the 1^st liver tissue in 0 mg/kg group without clear abnormal data. (b) Average terahertz time domain spectra the 2^nd liver tissue in the 50 mg/kg group with clear abnormal data.

This indicates the external factors were well under control during the experiment. Conversely, data of the tissue 50-2 had substantially larger standard deviations compared to that of tissue 0-1. Although more tests were performed for tissue 50-2, the high standard deviation seems to indicate the presence of interference factors. In addition, there are four abnormal data points. These errors are introduced primarily due to the difference in THz target locations among different tissue samples. Despite a relatively higher homogeneity of the liver tissue in comparison to other tissues, compositional variations of the liver tissue can influence the analytical results. Secondly, invalid data may be generated as a result of sample misplacement. The results of these spectra were caused by the Tissue-Tek OCT compound which was used in the process of tissue sample acquisition. It was not removed completely.

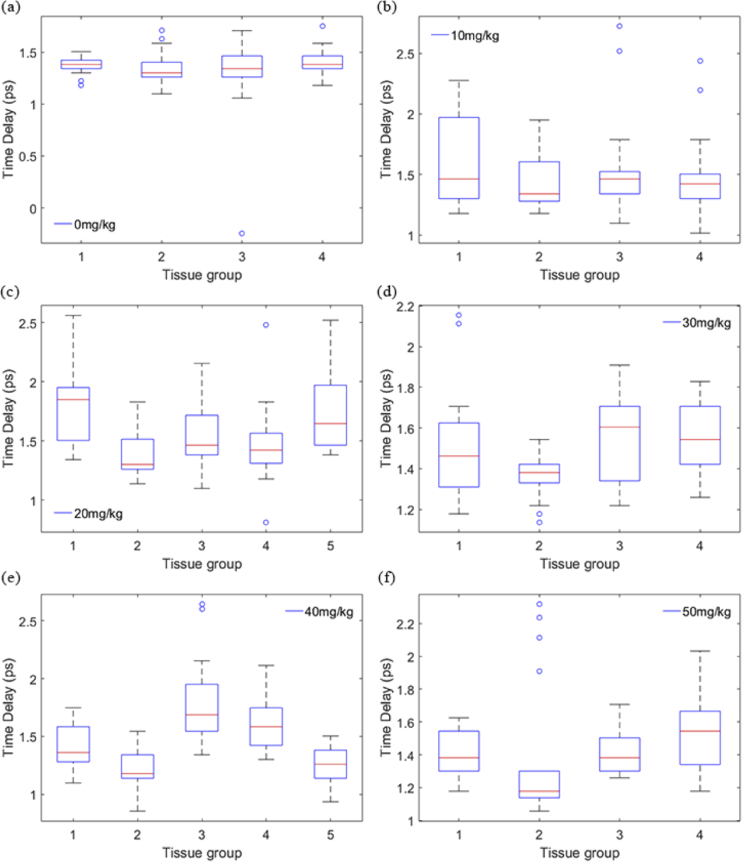
Hence, the statistical method boxplots were used for data cleaning. Figure 5 shows the abnormal spectra recognized by boxplots in all groups according to the parameters time-delay $\mathrm{\Delta }t$. The abscissa indicates the sample number of each group, of which only 5 mice were tested in the 20 and 40 mg/kg groups.

Fig. 5.

Boxplots showing the abnormal spectra in each tissue in one group with the parameter $\mathrm{\Delta }t$. (a) Boxplot result of 0 mg/kg group. (b) Boxplot result of 10 mg/kg group. (c) Boxplot result of 20 mg/kg group. (d) Boxplot result of 30 mg/kg group. (e) Boxplot result of 40 mg/kg group. (f) Boxplot result of 50 mg/kg group.

Boxplot is the most widely used exploratory data analysis tools in statistical practice that directly highlights outliers [33]. Hence, boxplot is used to assist visual identification of outliers. Figure 5 shows the boxplots of time-delay among different tissue groups, where outlier data points can be easily recognized. The x-axis represents the tissue number with drugs injected at different concentrations. In general, the time-delay of different tissues in the same group were relatively similar to one another. More specifically, with the exception of a seemingly invalid data point in the third tissue in the control group, the time delay of other samples varies within a small range. For the 10 mg/kg group, whereas the boxplot of the first tissue is wider vertically, the position and median of the other four boxplots are almost the same, indicating the experiment outcome of this group is relatively good. However, in the other four groups, the location of the boxplots displays different levels of fluctuations, indicating that there are differences in the level of tissue injury in each case.

This result correlates with AST and ALT values in the blood test to a certain extent. Due to large standard deviations of these two parameters in the blood test, the degree of liver injury to mice varies even though the same dose of drug was injected to the tissue at the same time. This is especially the case in the 20 and 30 mg/kg groups, where fluctuations are strong. This primarily can be attributed to the modulation of immune system in mice receiving non-lethal dose of drugs, which leads to the injury level fluctuated within a certain range. In addition, it can be seen from Fig. 6 that boxplot is useful in dealing with abnormal data points. A total of 22 abnormal data are removed.

Fig. 6.

Representative absorption coefficient and refractive index spectra of the 4^th tissue in 20 mg/kg group. (a) Absorption coefficient spectra of the 4th tissue in 20 mg/kg group. (b) Refractive index spectra of the 4^th tissue in 20 mg/kg group. The blue lines represent the original data and the red lines represent the data with boxplot process.

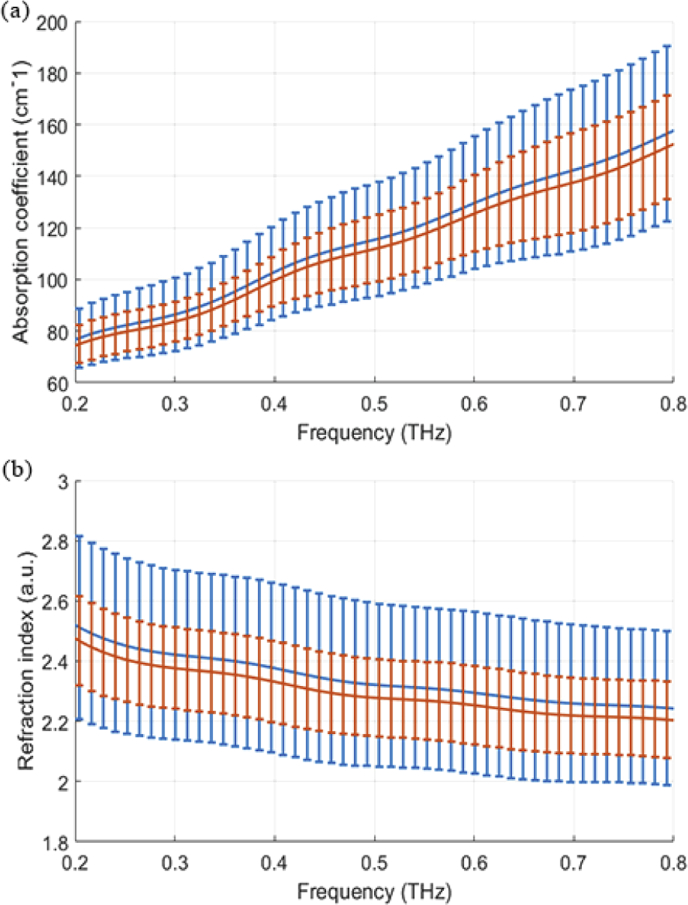
Figure 6 shows the average absorption coefficient and refractive index spectra with error bars of the 4^th tissue in the 20 mg/kg group (tissue 20-4) obtained after FFT process. The blue lines are the average absorption coefficients and refractive indices of original data, while the red lines represent the absorption coefficients and refractive indices with outliers removed. After removal of abnormal data points, standard deviations of all absorption coefficients and refractive indices of the same group are halved. Moreover, both the mean value of the absorption coefficient and the refractive index are reduced slightly. Regardless, the pattern and trend of the spectral lines between the treated and untreated data are almost identical.

3.2. Results for feature extraction

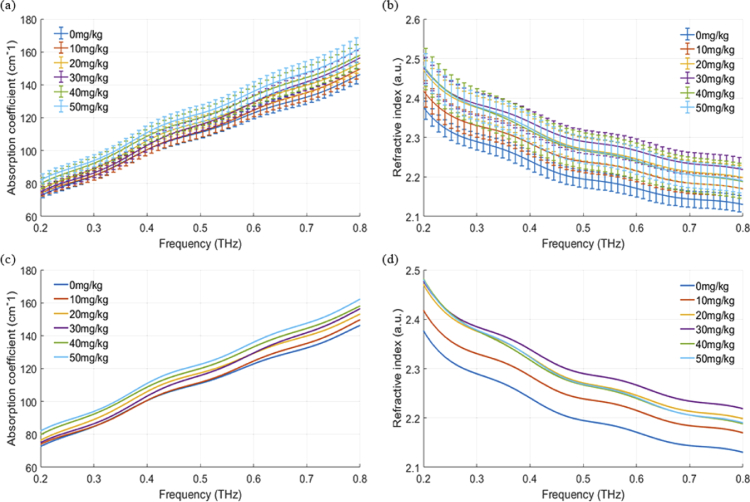
The absorption coefficient and refractive index of tissues with different degrees of liver injury are presented in Fig. 7 . As shown in Figs. 7(a)–7(b), the changes in the liver of the low degree of liver injury are relatively weak, and the actual degrees of liver injury in mice are also different to some extent with the injection of the same drug. This leads to the overlap of the mean values between one group and the adjacent groups. Figures 7(c)–7(d) show the mean values of each group. From the absorption coefficient spectra in Fig. 7(c), although the mean interval of each group is minimal, it can still be found that the absorption coefficient increases with the increase of the injection dose. In addition, it is found that the difference between the 0 and 10 mg/kg groups is small, and the mean values of the 20 and 30 mg/kg groups are crossed. This may be because the actual injury degree caused by the dose gradient of injection does not change significantly. However, as shown in the refractive index spectra in Fig. 7(d), the 30 mg/kg group is the largest in all of the six groups.

Fig. 7.

Average spectra of both absorption coefficient and refractive index of six groups. (a) Average absorption coefficient spectra of each group with error bars. (b) Average refractive index spectra of each group with error bars. (c) Average absorption coefficient spectra of each group. (d) Average refractive index spectra of each group.

From the blood test results, it can be seen that the biochemical indexes of the 30 mg/kg group are not very stable, showing the lowest results in both the ALT and AST indicators. This may be the reason for the fluctuations. In addition, the results of different groups overlap severely in the low-frequency band and have relatively visible differences in the high-frequency band. The results of the 40 and 50 mg/kg groups are almost the same, primarily because the injection doses of these two groups have exceeded the tolerance of mice, and the mice of the two groups hardly survived for three weeks during the culture process. The original 50 features of both the absorption coefficient and refractive index in the range of 0.2-0.8 THz are used for injury level recognition. All features are normalized before distinct feature selection and dimensional reduction. The 20 features with strong correlation are selected by the MIC method.

3.3. Results for liver injury identification

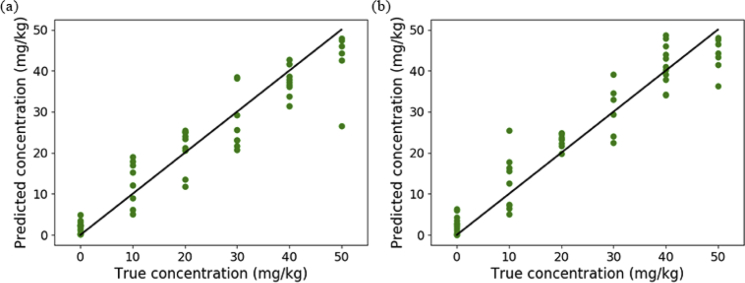
Figure 8 shows the results of the regression with the two parameter features of the absorption coefficient and the refractive index by RF after selecting the distinct frequencies using the MIC method. Figures 8(a)–8(b) represent the results of using the absorption coefficient and the refractive index as regression features, respectively. Through the two parameters, both the 0 and 50 mg/kg groups obtained relatively good predictive effects. For the 0 mg/kg group, the basic predicted injury concentration is kept below 5 mg/kg, while the results for the 50 mg/kg group are basically above 40. In fact, the injury intensities of these two groups are similar, because they both exceed the tolerance range of mice, so the biochemical indicators in blood tests are significantly increased, and the values are similar. As can be seen from Fig. 8(a), each group can be predicted substantially uniformly according to the feature of the absorption coefficient, except for several data. However, the refractive index in Fig. 8(b) is more sensitive to the 20 mg/kg group, and the recognition effect is better than the absorption coefficient. However, the detection results of the two parameters for the 10 mg/kg group are not satisfactory. This is primarily because there were individual differences among the experimental mice, some mice were more tolerant to 5-FU, while some mice were less tolerant. Thus, some highly tolerant mice were predicted with lower concentrations, and weakly tolerant mice were predicted with higher concentrations.

Fig. 8.

(a) Prediction plots with absorption coefficient. (b) Prediction plots with refractive index.

The reason for the instability of the 30 mg/kg group is that the dose may reach the tolerance limit of mice, thus causing a broad fluctuation range of the liver injury degree of mice. Table 1 shows the results of the R² and RMSEP of regression modeling of two parameter features through the RF method. In addition, the results of both features with PCA and MIC + PCA are compared. It is found that the MIC method can effectively select features with strong correlation and screen out some irrelevant features, which can effectively improve the performance of the model.

Table 1. Identification results of liver injury based on different features.

Features	Absorption coefficient		Refractive index
Methods	PCA	MIC + PCA	PCA	MIC + PCA
R2	0.830	0.914	0.824	0.930
RMSEP (mg/kg)	5.556	4.740	5.629	4.879

4. Conclusion

Herein, we proposed a method to detect the degree of liver injury in mice based on the terahertz time-domain spectroscopy. In this study, we used statistical methods and machine learning algorithms to conduct regression modeling analysis on different degrees of liver injury in mice. Firstly, there were factors that leaded to abnormal data in the process of data acquisition, so data preprocessing was required. We used the boxplots method for data cleaning. After that, the MIC method was used to find the top 20 features that were strongly correlated with the degree of liver injury, and then the dimension of the features was reduced by the PCA method. Finally, the RF method was used for analysis and detection. By comparing the detection results of the two parameters, it is found that the absorption coefficient can obtain a smaller RMSEP, and the refractive index can obtain a larger R². By comparing whether to introduce the MIC method for feature selection, it is found that the recognition results and the RMSEP of the model can be effectively improved after selecting the effective features. This method provides an auxiliary diagnostic method for detecting the low degree of liver injury and can detect the low degree of injuries within a certain range that cannot be detected by clinical blood tests. However, there is still a need for improving the intensive reading of the low concentration detection. More investigations are needed to improve the regression model.

Funding

National Natural Science Foundation of China10.13039/501100001809 (61473255, 61873234); Fundamental Research Funds for the Central Universities10.13039/501100012226 (2019FZA5007); National Human Genetic Resources Sharing Service Platform (2005DKA21300).

Disclosures

The authors declare that there are no conflicts of interest related to this article.