Abstract
An ultra-sensitive, wide-range force loading scheme is proposed for compression optical coherence elastography (OCE) that allows for the quantitative analysis of cervical tissue elasticity ex vivo. We designed a force loading apparatus featuring a water sink for minuscule incremental loading through a volume-controlled water droplet, from which the Young’s modulus can be calculated by fitting the stress-strain curve. We validated the performance of the proposed OCE system on homogenous agar phantoms, showing the Young’s modulus can be accurately estimated using this scheme. We then measured the Young’s modulus of rodent cervical tissues acquired at different gestational ages, showing that the cervical rigidity of rodents was significantly dropped when entering the third trimester of pregnancy.
1. Introduction
Every year, about one million children die worldwide due to preterm birth complications [1]. Preterm birth (PTB) is a complex problem for which some but not all causes are known. The cervix, located at the lowermost part of the uterus, is responsible for remaining closed until the fetus reaches full term. At the end of pregnancy, it loses rigidity and dilates to allow delivery. Cervical incompetence or insufficiency is one key risk factor that leads to preterm birth [1–3]. Quantitative analysis of cervical rigidity may allow us to identify abnormal or premature changes in cervical mechanical functions, and hence pave the way for developing biometrics for PTB prediction.
By now, a variety of technologies have been investigated for direct/indirect access of cervical biomechanical properties in ex vivo or in vivo settings, including mechanical testing [4,5], ultrasound elastography [6], electrical impedance spectroscopy [7,8], aspiration technique [9], two-photon microscopy [10,11], fluorescence imaging [12,13], and near infrared spectroscopy [14]. Mechanical testing, such as indention test, has been served as the golden standard for measuring the tissue biomechanics, but it was challenging to translate these methods to the in vivo settings. Optical techniques in general have the advantage of better resolution but they usually deliver the information that is remotely related to the tissue biomechanics. In contrast, ultrasound elastography techniques allow for quantitative analysis of tissue deformability in vivo, but with lower resolution. Contradictory results have been reported on cervical elasticity/deformability [15–19]. To reliably measure cervical mechanics, it is critical to develop an accurate elastography technique.
Optical coherence elastography (OCE) is an elastography technique based on optical coherence tomography (OCT), which is a non-contact, high-resolution, and three-dimensional imaging modality for biological tissues [20–22]. Compression OCE exhibits advantage in its higher spatial resolution, and higher sensitivity and contrast [23], which allows for detection of nanometer-scale deformation and delineation of tissue micro structures [24,25]. In comparison, dynamic OCE techniques often have a reduced lateral resolution, and thus are not as sensitive to tissue microstructures as compression OCE [26]. While elastograms mainly capture tissue deformation, the strain-stress relation or Young’s modulus is a direct measure of tissue elasticity and offers quantitative information about tissue biomechanics. To quantitatively analyze tissue elasticity via compression OCE, particularly for soft tissues such as brain, lung, and mucosa, it is important to only apply a minuscule stress, since soft tissues have low Young’s moduli and require very small force loading to induce nanometer-scale deformation. Conversely, for hard tissues, a relatively large force loading is needed to induce the deformation that is detectable. This represents one of the major challenges that compressive OCE faces: it lacks a force applicator with a high force sensitivity, a large dynamic range, and the capability of handling a large range of preload. It is also challenging to directly assess the stress that tissue experiences. Conventional piezoelectric stress sensors are not practical for static loading and do not meet all the aforementioned requirements. Recently, researchers introduced a self-referencing technique called optical palpation, where the stress applied to the tissue can be derived from the deformation of a optically clear, pre-characterized Ref. [27] sandwiched between the piezo actuator and the target tissue. However, introducing the reference material often complicates the study process: The reference needs to be fabricated and its stiffness to be calibrated beforehand; the material has to be chosen with respect to the targeted sample’s elasticity; and the accuracy of incremental stress measurement is dependent on the calibration accuracy of the reference material.
In this paper, we report an ultra-sensitive, wide-range force loading scheme that allows for quantitative analysis of tissue elasticity with a common-path high-resolution spectral-domain OCT system. We introduced a specially designed force loader composed of a water container for force loading and a glass window for imaging. The minuscule incremental stress was exerted to the tissue through a volume-controlled water droplet by a precision micropipette system. The strain of the tissue was estimated using the weighted least squares method, and the tissue’s Young’s modulus was calculated by fitting the measured stress-strain curve. We first tested the proposed approach on homogenous agar phantoms, showing that the Young’s modulus could be accurately estimated. We then measured the Young’s modulus in a well described mouse model of cervical remodeling using cervices at different gestational ages [28], demonstrating the potential ability of this loading scheme for accurately assessing cervical tissue biomechanics.
2. Methods
2.1. Phantom and mouse cervical tissue preparation
For demonstration of the Young’s modulus measurement using the proposed OCE system, we prepared multiple homogeneous one-layer agar phantoms with agar concentrations (w/w) of 0.5%, 1%, and 2%, respectively. To increase the scattering of the phantoms, we added 1% (v/v) Intralipid (from 20% Intraplid stock solution) to the agar solutions. The heated mixture was transferred into a vacuum chamber for 5 seconds to remove excessive air bubbles before the mixture was settled for curing. Each square-shaped phantom had a length/width varying between 10 mm and 15 mm, and a thickness of around 10 mm.
All animal studies were conducted in accordance with the standards of humane animal care as described in the NIH Guide for the Care and Use of Laboratory Animals. The research protocols were approved by the IACUC office at the University of Texas Southwestern Medical Center. Mice were housed under a 12 h-light/12 h-dark cycle at 22°C. Virgin C57B6/129sv two- to six-month-old female mice were caged with fertile males of the same strain for 6 hours. The presence of a vaginal plug at the end of 6 hours was considered as day 0 of pregnancy, with birth of the pups generally occurring in early morning of Day 19. Cervix and adjacent uterine tissue were isolated by dissection. Vaginal tissue was trimmed to expose the cervix. Tissue was pinned to wax, immersed in optimal cutting temperature embedding compound (Sakura Finetek USA, Torrence, CA), and frozen in liquid nitrogen. Samples were shipped frozen to Johns Hopkins University and stored frozen at -80°C until imaging performed. The frozen samples were imaged right after thawing under room temperature. The averaged thickness of the cervical tissues was 2.5 mm, with other details listed in Table 1 .
Table 1. Details of ex vivo rodent cervical tissue samples.
| Gestational Age | Non pregnant (NP) | 6 Days (6D) | 12 Days (12D) | 15 Days (15D) | 18 Days (18D) |
|---|---|---|---|---|---|
| Number of samples | 7 | 5 | 7 | 5 | 7 |
| Sample diameter (mm) | 3.1 ± 0.47 | 3.21 ± 0.97 | 2.82 ± 0.45 | 3.29 ± 0.07 | 4.39 ± 0.57 |
2.2. OCE system and imaging protocol
The simplified schematic of the sample holder of the compression OCE system with the ultra-sensitive force loading setup is shown in Fig. 1(a). The OCE system consisted of a home-built spectral-domain (SD) OCT system with a Ti:Sapphire laser as the light source (centered at ) and a customized linear-K spectrometer as the detector (not shown in Fig. 1) [29], and an ultra-sensitive water loading apparatus detailed in Fig. 1(b). The SD-OCT system had a measured axial resolution of 2.5 µm and a lateral resolution of 8.4 µm in air, with a shot-noise limited sensitivity of -106 dB at a sample arm power of 15 mW and an A-line rate of 70 kHz. Every OCT B-scan (cross-sectional image) comprised 1024 (axial) by 2000 (lateral) pixels, covering an area of 1.4 × 2.0 mm2 in air. The OCT system was equipped with a customized control/user interface (UI) software implemented in C++. The theoretical limit of the displacement measurement was estimated to be 0.15 nm by using [30]. The displacement noise floor was measured around 0.23 nm, close to the predicted value.
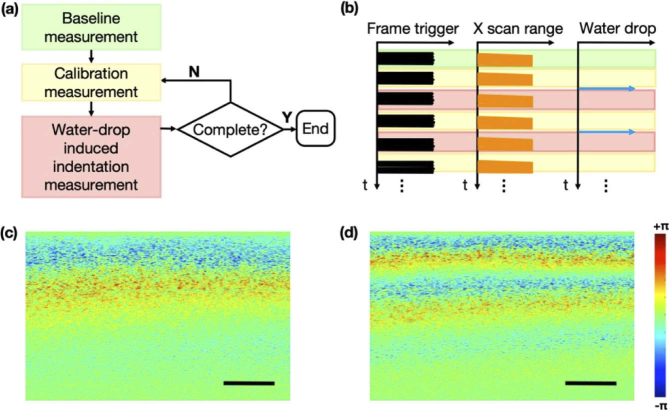
Fig. 1.
(a) A simplified schematic of the common-path compression OCE system with the ultra-sensitive force loading setup. (b) The detailed three-dimensional visualization of the water loading apparatus.
The force applicator (L 24 mm × W 24 mm × H 6 mm) was designed to have a light weight to allow for a wide range of controlled preload, as illustrated in Fig. 1(b). It should also be able to accommodate a wide range of incremental force. Therefore, its finalized design featured a platform that consisted of a water container (W 7 mm × D 6 mm) made of acrylic plastic, a transparent imaging window (Diameter 7 mm) with a No. 2 glass slide (2 cm by 2 cm) attached to the bottom (see Fig. 1(a)), and two near-zero-friction rails on a metal frame (height) allowing the platform to freely travel. The top surface of the glass slide was served as the reference for common-path OCT imaging, and the bottom surface was to bring in contact with tissue samples. The weight of the force applicator was merely 2.5 g, setting the lower limit of the preload (0.0245 N). The preload could be increased by adding weights to the water container. A syringe pump pushed water through a pipette tip to add droplets of a precisely controlled amount to the water container. The volume of the water drop determined the incremental force applied to the tissue. It could be set accurately via the pipette system, ranging from 10 µL to 200 µL. The time interval between water drops could be changed by varying the pumping speed. The droplet volume was uniform and varied with the pumping speed and surface tension of the solution in use. In this study, we used distilled water with the droplet volume set to 10 µL to 20 µL, which corresponded to a force range from 10−4 N to 2×10−4 N.
The imaging protocol is illustrated in Figs. 2(a)-(b). During the experiment, the loading apparatus was initially brought into contract with the sample (agar phantoms or mouse cervical tissues), and the preload was applied by the intrinsic weight of the loading apparatus. A baseline measurement was taken after the preload. It was a one-time measurement for every sample. Afterwards, two sets of measurement were made for every incremental stress applied by the micropipette system: (1) a calibration measurement was made before adding the water drop to measure the indentation of the sample due to the preload/previous loading; and another measurement made right after the incremental stress was applied (i.e., adding a water droplet to the water container). For every measurement, twenty frames at the same B-scan location were acquired. The time interval between any two consecutive measurements was approximately the same, about 2 seconds. Figure 2(c) shows the phase change exhibited in the sample during the time course between the baseline and calibration measurements. It is clear that the sample underwent minor deformation even without adding the incremental stress. This is most likely due to the compression after adding the preload. Figure 2(d) shows the phase change observed after adding the water drop, reflecting a sum of the deformation caused by both the incremental stress and the previous load. Therefore, it is crucial to include the calibration step in order to extract the true tissue deformation induced by water loading only. This is especially important for soft tissue samples which may take a longer time to stabilize in the loading system. It took no more than 5 minutes to complete the protocol for one sample, and there was no change in the tissue state during this short period.
Fig. 2.
(a) Flowchart for OCE imaging protocol and (b) illustration of synchronization and time sequences of OCE measurements. The time intervals are not necessarily drawn to scale. (c) Phase change exhibited between baseline measurement and the first calibration measurement. (d) Phase change measured after adding the incremental stress. All images presented were cropped, showing only the glass-tissue contact surface and the tissue underneath. Scale bars: 200µm.
2.3. Data processing
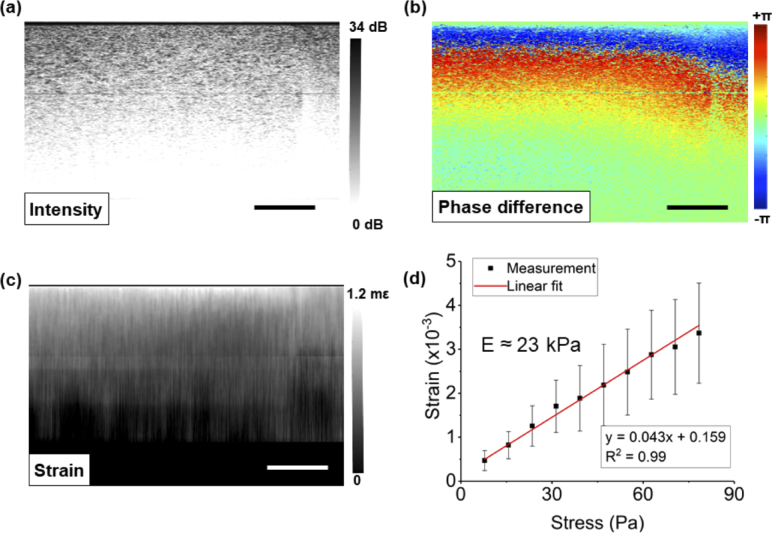
All images presented in this paper were cropped from the glass contact surface. In order to estimate the Young’s modulus of the sample, a strain-stress plot was created. The stress increment was estimated as , where is the water density, is the volume of water droplet, g is the gravitational acceleration constant, and A is the contact surface area at the interface between the tissue and the glass window before preload. For each agar phantom, the width and length of the square-shaped phantom was measured to estimate the contact surface area, while for the cervical tissues, the diameter of the sample was taken for the calculation. For each incremental stress , the phase difference between the complex B-scan signals and was extracted as . The complex B-scans were generated by inverse Fourier transform of the raw spectral data sampled by a linear-k spectrometer in the SD-OCT system. The mean phase change was obtained by averaging from 20 repeated measurements (Fig. 3(b)). It was then processed with a 2D phase unwrapping algorithm reported elsewhere [31], where ten (10) pixels along the axial direction and 20 pixels in the lateral direction were averaged to obtain the local phase. After the Nth incremental stress, the total stress was . The corresponding total phase change was calculated as , where is the unwrapped phase change caused by each incremental load. The total displacement can be written as with n as the tissue’s refractive index. The local strain built up in the tissue was then obtained by using the weighted least squares (WLS) method proposed by Kennedy B. et al [32], incorporating 100 pixels in the axial direction for calculation (equivalent to a strain resolution of 137 µm). A representative local strain image, obtained based on Figs. 3(a) and (b), is presented in Fig. 3(c). The actual strain of the sample was estimated by the averaged local strain values calculated from a region of interest (ROI). The ROI was selected with a size of 200 by 200 pixels over a 200 µm by 200 µm area in tissue (n = 1.4), right below the glass surface where the SNR is usually the highest. Finally, the Young’s modulus of the tissue was deduced from the fitting parameters of the linear part of the stress-strain curve. Specifically, in this study, the Young’s modulus was calculated as the inversed slope of the strain-stress curve, as shown in Fig. 3(d). Data points well above the noise floor were manually selected for the fitting process. The result was accepted if the R-squared value was above 0.9. All the OCT postprocessing and local strain calculation steps were implemented in MATLAB.
Fig. 3.
(a) OCT intensity B-scan for a 1% agar phantom. (b) The corresponding phase difference image and (c) local strain image after applying an incremental stress. (d) The stress-strain curve for Young’s modulus calculation. All images presented were cropped, showing only the glass-tissue contact surface and the tissue underneath. Scale bars: 200 µm.
2.4. Statistics
The one-way analysis of variance (ANOVA) test was applied for the resultant Young’s modulus of the mouse cervical tissues procured at different gestational ages. A p-value less than 0.01 was considered statistically significant. The statistical analysis was done in OriginPro (OriginLab, Northampton, Massachusetts, USA). All means in this paper are reported with the standard deviation (SD) unless otherwise noted.
3. Results
3.1. Phantom study
To assess the accuracy of the proposed sensitive OCE, we tested on the agar phantoms and compared the measured Young’s modulus using the methods described earlier with the reported values [33,34]. It is known that a higher agar concentration results in an increased sample hardness. A preload was first added by inducing approximately 10% strain in the phantom (thickness change = 10% of total thickness). The incremental volume of water drop was set to be 50 µL for 0.5% and 1% agar phantoms, and 100 µL for 2% agar phantoms. The measured Young’s modulus results were aggregated and listed in Table 2. In general, the measured Young’s moduli using the quantitative OCE system were in good accordance with previously reported values. Our results tended to be around the upper boundary. It is more likely caused by the overestimation in the stress calculation, since the contact area was measured before the incremental force application.
Table 2. Measured Young’s modulus of agar phantoms with different agar concentrations.
| Agar concentration | Number of samples | Measured Young’s modulus (kPa) | Previously reported Young’s modulus (kPa) |
|---|---|---|---|
| 0.5% | 10 | 10.4 ± 4.2 | 0.5 to 10 |
| 1% | 10 | 48.2 ± 12.0 | 30 to 50 |
| 2% | 4 | 107.0 ± 18.9 | 80 to 110 |
3.2. Ex vivo cervical tissue study
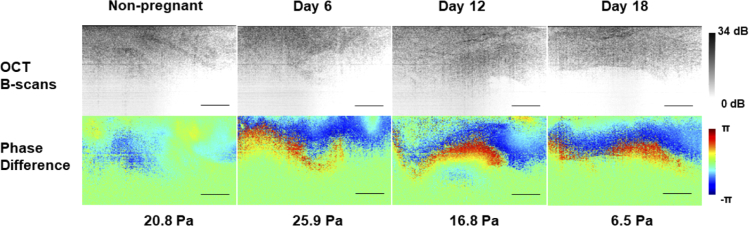
We then measured the Young’s modulus of ex vivo rodent cervical tissues harvested at different gestational ages. Figure 4 shows the representative quantitative phase difference images of the cervical tissues under different incremental stresses. The tissue sample acquired from a non-pregnant rodent underwent the smallest deformation despite a larger incremental stress, suggesting a higher Young’s modulus associated with it. Conversely, at the end of the gestational stage, the cervical tissue became so soft that even applying a small incremental stress resulted in a relatively large deformation. The trend from these images also indicates that the cervical tissue becomes less stiff across the gestational period.
Fig. 4.
Representative OCT intensity images and the corresponding phase difference images of cervical tissues acquired at different gestational ages. The incremental stress applied to induce indentation is provided in the bottom row. All images presented were cropped, showing only the glass-tissue contact surface and the tissue underneath. Scale bars: 200 µm.
In rodents, the aggregated Young’s modulus measurements are listed in Table 3, and illustrated in Fig. 5 with the mean and standard deviation (SD) marked out. It exhibits a power-law trend, which is also in accordance with the previously reported in vivo aspiration measurement of human cervix [6]. The averaged Young’s modulus measured for the non-pregnant rodent cervical samples is 260.13 kPa, significantly higher than the pregnant rodent cervices. It was very close to the previously reported cervical stiffness using a mechanical testing method [35]. For tissues acquired at gestational day 6, the averaged Young’s modulus is 61.98 kPa. It drops to 40.96 kPa for samples acquired at gestation day 12, and further reduces to 33.49 kPa for samples acquired at gestation day 15. Rodent cervical samples acquired at gestation day 18 has the lowest averaged Young’s modulus of 19.46 kPa. Nevertheless, the statistical result shows no significant differences among the pregnant rodent cervical sample groups in terms of Young’s modulus, except for the day 6 and day 18 groups. The gestational time points in the current study span early, mid and late pregnancy. The preliminary results in this study suggests that the cervical rigidity starts to show obvious change in the late pregnancy in mice.
Table 3. Measured Young’s modulus of cervical tissues harvested at different gestational ages.
| Gestational age | Measured Young’s modulus (kPa) | Averaged Young’s modulus (kPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| NP | 249.6 | 278.77 | 227.69 | 293.56 | 226.87 | 289.64 | 254.80 | 260.13 |
| 6D | 43.5 | 78.12 | 60.05 | 64.02 | 64.23 | 61.98 | ||
| 12D | 31.96 | 49.32 | 25.35 | 39.03 | 42.4 | 57.43 | 37.93 | 40.49 |
| 15D | 23.36 | 32.16 | 29.08 | 36.47 | 46.38 | 33.49 | ||
| 18D | 17.19 | 11.43 | 11.67 | 18.71 | 20.39 | 25.67 | 31.17 | 19.46 |
Fig. 5.
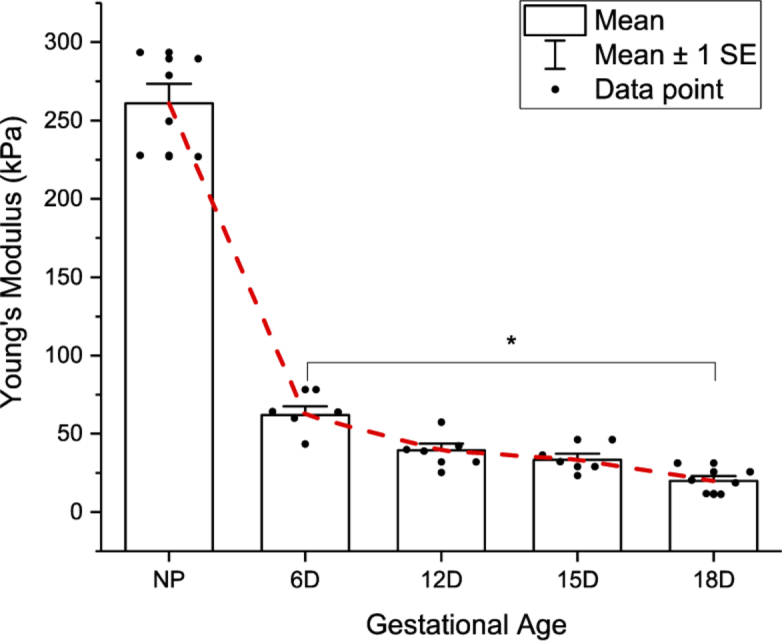
The measured Young’s modulus (detailed in Table 2) of cervical tissues at different gestational ages. Mean and standard deviation (SD) are computed and marked out. Among the pregnant sample groups, the measured Young’s modulus shows no significant differences, except for the day 6 and 18 groups (*: p < 0.01). The mean value of each group was connected by the red dotted line.
4. Discussion
We have shown the capability of the proposed sensitive OCE in terms of measuring Young’s modulus. Compared with conventional elastography techniques, OCE offers superior resolution, better suited for biopsy samples due to their size and small animal model tissues, and has the potential to be translated to in vivo imaging [36]. One advantage of this setup is that it offers direct access to the tissue’s elasticity/rigidity, which is one of the most important biomechanical properties and may be linked to complications in PTB [37,38]. It should be noted that the ultra-sensitive force loading apparatus allows for precise control of both the preload and the incremental stress. The minimal incremental stress induced by water droplets is only dependent on the resolution of the pipette, which can reach down to 0.1 µL. Therefore, its application can be extended to measure the rigidity of soft tissues with a very low Young’s modulus, such as brain, lung and mucosa. In the current study, we demonstrated the elasticity measurement based on repeated B-scans at one cross-sectional location. Three-dimensional (3D) elasticity map could also be possible if the pipette system is electronically synchronized with the OCT image acquisition channel. its use is far better suited for biopsy samples due to their size and small animal model tissues.
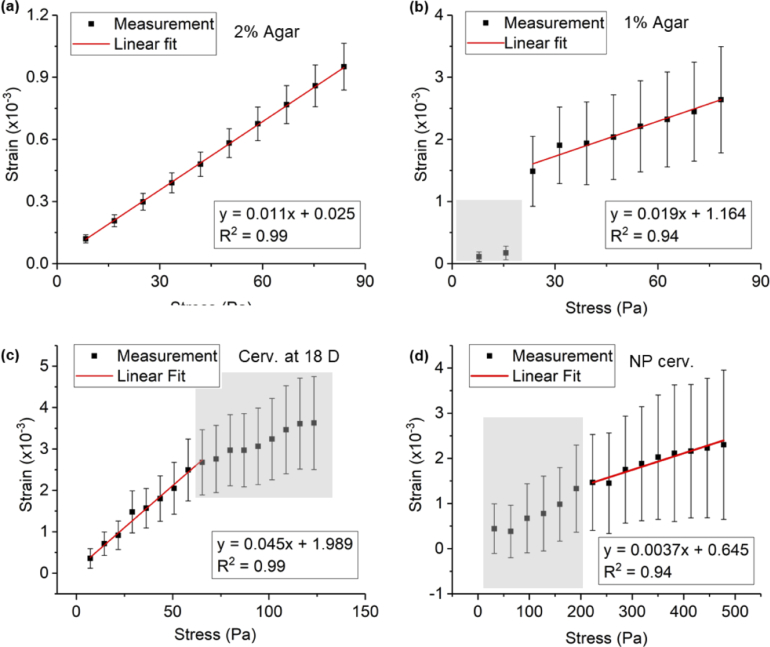
The performance of the proposed OCE system is nevertheless constrained by several factors. First, the force loader has no stabilization mechanism. Therefore, it may be subjected to disorientation when the samples are small in size, resulting in unreliable measurements. For cervical tissues, for example, the sample diameter was below 5 mm, which led to a relatively large variation in strain measurement compared to the phantom samples. The mechanical instability is more severe for larger incremental stress (i.e., large water drops). Second, the fitting process to obtain the Young’s modulus is monitored and adjusted semi-manually by examiners to ensure an R-squared value larger than 0.9. Hence, it is not fully objective. Figure 6 shows some examples for fitting region selection guidance. Figure 6(a) shows a perfect case where all measurements are well above the noise floor (at zero strain) and the errors are small. In this case, all the data points are included in the fitting process. This is usually the case where the tissue is hard and has a large surface area in contact with the imaging window. Figure 6(b) shows a case where the first two data points are excluded from the fitting to ensure an R-squared value larger than 0.9. For cervical tissue samples, the strain-stress curves are carefully examined to determine what to be included for the Young’s modulus calculation. In Fig. 6(c), for example, the strain measurement seems to reach saturation after 9 water drops, and therefore only the first 9 data points are incorporated for the fitting process. In fact, this happens frequently for soft tissues such as cervical tissues at gestation day 18, where the tissue deformation easily reaches saturation after incremental stress is applied for several times. We believe that observing this nonlinearity behavior can be associated to the preload, which might be already high for these very soft tissues. Figure 6(d) shows a case where the first few measurements are too noisy to be included into the fitting process. It happens for hard samples such as non-pregnant rodent cervical tissues, where large incremental stress may only result in minute deformation. Last but not the least, the strain estimation is always associated with the intrinsic SNR of the OCT signal. A higher SNR leads to a more accurate phase measurement. Therefore, the performance of the system may be affected for tissues showing a low SNR in OCT images.
Fig. 6.
Exemplary Young’s modulus measurements for (a) a 2% agar sample where the measurement was robust, (b) a 1% agar sample with first two data points (marked by gray area) excluded from fitting, (c) a rodent cervical tissue sample acquired at 18-day gestational age where the deformation reached saturation (marked by gray area), and (d) a non-pregnant rodent cervical tissue sample where the first batch of measurements (marked by gray area) were below the noise floor and were excluded from fitting. Error bars mark out ± 1 SD range.
It should also be noted that, while prior studies demonstrated a progressive decline in mechanical strength beginning in mid-pregnancy mouse cervix (from 12 days onwards) [35,39,40], our OCE study did not identify significant declines until Day 18 even though the trend for a decline from Day 12 was evident. This may be due to the relatively small sample sizes, which was a major limitation of this study. Another limitation of this study was that the Young’s modulus calculation was based on the local strain measurement within a selected ROI with highest SNR. Heterogeneity of the tissue’s elasticity was not covered in the current study and will be further studied in the future.
5. Conclusion
In this study, we reported an ultra-sensitive force loading scheme for accurate control of applied stress, enabling quantitative elasticity measurement via compression OCE. By using the apparatus, we were able to demonstrate accurate assessment of the agar phantoms’ Young’s modulus, and show distinctive biomechanical properties of the cervical tissues acquired from non-pregnant and pregnant rodents.
Acknowledgement
The authors would like to thank Ms Asha Varghese for preparing the rodent cervical samples, and Dr Wu Yuan, Mr. Ang Li, and Dr Wenxuan Liang for the enlightening discussion.
Funding
Hartwell Foundation10.13039/100006792; National Institutes of Health10.13039/100000002 (R01HL130804).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Goldenberg R. L., Culhane J. F., Iams J. D., Romero R., “Epidemiology and causes of preterm birth,” Lancet 371(9606), 75–84 (2008). 10.1016/S0140-6736(08)60074-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.House M., Socrate S., “The cervix as a biomechanical structure,” Ultrasound Obstet Gynecol 28(6), 745–749 (2006). 10.1002/uog.3850 [DOI] [PubMed] [Google Scholar]
- 3.Myers K. M., Paskaleva A. P., House M., Socrate S., “Mechanical and biochemical properties of human cervical tissue,” Acta Biomater. 4(1), 104–116 (2008). 10.1016/j.actbio.2007.04.009 [DOI] [PubMed] [Google Scholar]
- 4.Zhang M., Zheng Y. P., Mak A. F. T., “Estimating the effective Young’s modulus of soft tissues from indentation tests—nonlinear finite element analysis of effects of friction and large deformation,” Med. Eng. Phys. 19(6), 512–517 (1997). 10.1016/S1350-4533(97)00017-9 [DOI] [PubMed] [Google Scholar]
- 5.Akhtar R., Sherratt M. J., Cruickshank J. K., Derby B., “Characterizing the elastic properties of tissues,” Mater. Today 14(3), 96–105 (2011). 10.1016/S1369-7021(11)70059-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mazza E., Parra-Saavedra M., Bajka M., Gratacos E., Nicolaides K., Deprest J., “In vivo assessment of the biomechanical properties of the uterine cervix in pregnancy,” Prenatal Diagn. 34(1), 33–41 (2014). 10.1002/pd.4260 [DOI] [PubMed] [Google Scholar]
- 7.O’connell M., Avis N., Brown B., Killick S., Lindow S., “Electrical impedance measurements: an objective measure of prelabor cervical change,” J. Matern.-Fetal Neonatal Med. 14(6), 389–391 (2003). 10.1080/14767050412331312230 [DOI] [PubMed] [Google Scholar]
- 8.O’Connell M., Tidy J., Wisher S., Avis N., Brown B., Lindow S., “An in vivo comparative study of the pregnant and nonpregnant cervix using electrical impedance measurements,” BJOG 107(8), 1040–1041 (2000). 10.1111/j.1471-0528.2000.tb10410.x [DOI] [PubMed] [Google Scholar]
- 9.Badir S., Mazza E., Zimmermann R., Bajka M., “Cervical softening occurs early in pregnancy: characterization of cervical stiffness in 100 healthy women using the aspiration technique,” Prenatal Diagn. 33(8), 737–741 (2013). 10.1002/pd.4116 [DOI] [PubMed] [Google Scholar]
- 10.Zhang Y., Akins M. L., Murari K., Xi J., Li M.-J., Luby-Phelps K., Mahendroo M., Li X., “A compact fiber-optic SHG scanning endomicroscope and its application to visualize cervical remodeling during pregnancy,” Proc. Natl. Acad. Sci. 109(32), 12878–12883 (2012). 10.1073/pnas.1121495109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Akins M. L., Luby-Phelps K., Mahendroo M., “Second harmonic generation imaging as a potential tool for staging pregnancy and predicting preterm birth,” J. Biomed. Opt. 15(2), 026020 (2010). 10.1117/1.3381184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Maul H., Mackay L., Garfield R. E., “Cervical ripening: biochemical, molecular, and clinical considerations,” Clin. Obstet. Gynecol. 49(3), 551–563 (2006). 10.1097/00003081-200609000-00015 [DOI] [PubMed] [Google Scholar]
- 13.Schlembach D., MacKay L., Shi L., Maner W. L., Garfield R. E., Maul H., “Cervical ripening and insufficiency: from biochemical and molecular studies to in vivo clinical examination,” Eur. J. Obstet. Gynecol. Reprod. Biol. 144, S70–S76 (2009). 10.1016/j.ejogrb.2009.02.036 [DOI] [PubMed] [Google Scholar]
- 14.Hornung R., Spichtig S., Baños A., Stahel M., Zimmermann R., Wolf M., “Frequency-domain near-infrared spectroscopy of the uterine cervix during regular pregnancies,” Lasers Med. Sci. 26(2), 205–212 (2011). 10.1007/s10103-010-0832-7 [DOI] [PubMed] [Google Scholar]
- 15.Thomas A., “Imaging of the cervix using sonoelastography,” Ultrasound Obstet. Gynecol. 28(3), 356–357 (2006). 10.1002/uog.3813 [DOI] [PubMed] [Google Scholar]
- 16.Yamaguchi S., Kamei Y., Kozuma S., Taketani Y., “Tissue elastography imaging of the uterine cervix during pregnancy,” J. Med. Ultrasonics 34(4), 209–210 (2007). 10.1007/s10396-007-0150-2 [DOI] [PubMed] [Google Scholar]
- 17.Swiatkowska-Freund M., Preis K., “Elastography of the uterine cervix: implications for success of induction of labor,” Ultrasound Obstet. Gynecol. 38(1), 52–56 (2011). 10.1002/uog.9021 [DOI] [PubMed] [Google Scholar]
- 18.Molina F., Gomez L., Florido J., Padilla M., Nicolaides K., “Quantification of cervical elastography: a reproducibility study,” Ultrasound Obstet Gynecol 39(6), 685–689 (2012). 10.1002/uog.11067 [DOI] [PubMed] [Google Scholar]
- 19.Hernandez-Andrade E., Hassan S. S., Ahn H., Korzeniewski S. J., Yeo L., Chaiworapongsa T., Romero R., “Evaluation of cervical stiffness during pregnancy using semiquantitative ultrasound elastography,” Ultrasound Obstet. Gynecol. 41(2), 152–161 (2013). 10.1002/uog.12344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schmitt J. M., “OCT elastography: imaging microscopic deformation and strain of tissue,” Opt. Express 3(6), 199–211 (1998). 10.1364/OE.3.000199 [DOI] [PubMed] [Google Scholar]
- 21.Larin K. V., Sampson D. D., “Optical coherence elastography — OCT at work in tissue biomechanics [Invited],” Biomed. Opt. Express 8(2), 1172–1202 (2017). 10.1364/BOE.8.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kennedy B. F., Wijesinghe P., Sampson D. D., “The emergence of optical elastography in biomedicine,” Nat. Photonics 11(4), 215–221 (2017). 10.1038/nphoton.2017.6 [DOI] [Google Scholar]
- 23.Kennedy B. F., Kennedy K. M., Sampson D. D., “A Review of Optical Coherence Elastography: Fundamentals, Techniques and Prospects,” IEEE J. Sel. Top. Quantum Electron. 20(2), 272–288 (2014). 10.1109/JSTQE.2013.2291445 [DOI] [Google Scholar]
- 24.Shang W., Larin K. V., “Optical coherence elastography for tissue characterization: a review,” J. Biophotonics 8(4), 279–302 (2015). 10.1002/jbio.201400108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wang R. K., Kirkpatrick S., Hinds M., “Phase-sensitive optical coherence elastography for mapping tissue microstrains in real time,” Appl. Phys. Lett. 90(16), 164105 (2007). 10.1063/1.2724920 [DOI] [Google Scholar]
- 26.Hepburn M. S., Wijesinghe P., Chin L., Kennedy B. F., “Analysis of spatial resolution in phase-sensitive compression optical coherence elastography,” Biomed. Opt. Express 10(3), 1496–1513 (2019). 10.1364/BOE.10.001496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kennedy K. M., Es’haghian S., Chin L., McLaughlin R. A., Sampson D. D., Kennedy B. F., “Optical palpation: optical coherence tomography-based tactile imaging using a compliant sensor,” Opt. Lett. 39(10), 3014–3017 (2014). 10.1364/OL.39.003014 [DOI] [PubMed] [Google Scholar]
- 28.Mahendroo M., “Cervical remodeling in term and preterm birth: insights from an animal model,” Reproduction 143(4), 429–438 (2012). 10.1530/REP-11-0466 [DOI] [PubMed] [Google Scholar]
- 29.Xi J., Zhang A., Liu Z., Liang W., Lin L. Y., Yu S., Li X., “Diffractive catheter for ultrahigh-resolution spectral-domain volumetric OCT imaging,” Opt. Lett. 39(7), 2016–2019 (2014). 10.1364/OL.39.002016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hyle Park B., Pierce M. C., Cense B., Yun S.-H., Mujat M., Tearney G. J., Bouma B. E., Boer J. F. d., “Real-time fiber-based multi-functional spectral-domain optical coherence tomography at 1.3 µm,” Opt. Express 13(11), 3931–3944 (2005). 10.1364/OPEX.13.003931 [DOI] [PubMed] [Google Scholar]
- 31.Kennedy B. F., McLaughlin R. A., Kennedy K. M., Chin L., Curatolo A., Tien A., Latham B., Saunders C. M., Sampson D. D., “Optical coherence micro-elastography: mechanical-contrast imaging of tissue microstructure,” Biomed. Opt. Express 5(7), 2113–2124 (2014). 10.1364/BOE.5.002113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kennedy B. F., Koh S. H., McLaughlin R. A., Kennedy K. M., Munro P. R. T., Sampson D. D., “Strain estimation in phase-sensitive optical coherence elastography,” Biomed. Opt. Express 3(8), 1865–1879 (2012). 10.1364/BOE.3.001865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bin L., Ronghua Y., Peng Y., Awad M., Choti M., Taylor R., “Elasticity and Echogenicity Analysis of Agarose Phantoms Mimicking Liver Tumors,” in Proceedings of the IEEE 32nd Annual Northeast Bioengineering Conference(2006), pp. 81–82. [Google Scholar]
- 34.Li C., Huang Z., Wang R. K., “Elastic properties of soft tissue-mimicking phantoms assessed by combined use of laser ultrasonics and low coherence interferometry,” Opt. Express 19(11), 10153–10163 (2011). 10.1364/OE.19.010153 [DOI] [PubMed] [Google Scholar]
- 35.Yoshida K., Jiang H., Kim M., Vink J., Cremers S., Paik D., Wapner R., Mahendroo M., Myers K., “Quantitative Evaluation of Collagen Crosslinks and Corresponding Tensile Mechanical Properties in Mouse Cervical Tissue during Normal Pregnancy,” PLoS One 9(11), e112391 (2014). 10.1371/journal.pone.0112391 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu C.-H., Assassi S., Theodore S., Smith C., Schill A., Singh M., Aglyamov S., Mohan C., Larin K. V., “Translational optical coherence elastography for assessment of systemic sclerosis,” J. Biophotonics 12, e201900236 (2019). 10.1002/jbio.201900236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jayyosi C., Lee N., Willcockson A., Nallasamy S., Mahendroo M., Myers K., “The mechanical response of the mouse cervix to tensile cyclic loading in term and preterm pregnancy,” Acta Biomater. 78, 308–319 (2018). 10.1016/j.actbio.2018.07.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yoshida K., Jayyosi C., Lee N., Mahendroo M., Myers K. M., “Mechanics of cervical remodelling: insights from rodent models of pregnancy,” Interface Focus 9(5), 20190026 (2019). 10.1098/rsfs.2019.0026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Read C. P., Word R. A., Ruscheinsky M. A., Timmons B. C., Mahendroo M. S., “Cervical remodeling during pregnancy and parturition: molecular characterization of the softening phase in mice,” Reproduction 134(2), 327–340 (2007). 10.1530/REP-07-0032 [DOI] [PubMed] [Google Scholar]
- 40.Akins M. L., Luby-Phelps K., Bank R. A., Mahendroo M., “Cervical softening during pregnancy: regulated changes in collagen cross-linking and composition of matricellular proteins in the mouse,” Biol. Reprod. 84(5), 1053–1062 (2011). 10.1095/biolreprod.110.089599 [DOI] [PMC free article] [PubMed] [Google Scholar]