Abstract
Recent studies in mechanobiology have revealed the importance of cellular and extracellular mechanical properties in regulating cellular function in normal and disease states. Although it is established that cells should be investigated in a three-dimensional (3-D) environment, most techniques available to study mechanical properties on the microscopic scale are unable to do so. In this study, for the first time, we present volumetric images of cellular and extracellular elasticity in 3-D biomaterials using quantitative micro-elastography (QME). We achieve this by developing a novel strain estimation algorithm based on 3-D linear regression to improve QME system resolution. We show that QME can reveal elevated elasticity surrounding human adipose-derived stem cells (ASCs) embedded in soft hydrogels. We observe, for the first time in 3-D, further elevation of extracellular elasticity around ASCs with overexpressed TAZ; a mechanosensitive transcription factor which regulates cell volume. Our results demonstrate that QME has the potential to study the effects of extracellular mechanical properties on cellular functions in a 3-D micro-environment.
1. Introduction
The cell is subject to a range of physical forces that are intrinsically linked to the mechanical properties of both the cell and the extracellular matrix (ECM) [1]. Cells transform these physical forces into biochemical signals through mechanotransduction [2]. Forces and mechanical properties govern important cell functions including growth, movement, differentiation and apoptosis [3]. Furthermore, irregular ECM mechanical properties are implicated in many diseases including atherosclerosis, muscular dystrophy, and the onset and progression of cancer [4]. Taking a reductionist approach, early endeavors in mechanobiology studied cells cultured on two-dimensional (2-D) platforms such as glass coverslips and biomaterial surfaces. Measurement of forces and mechanical properties on 2-D substrates was brought to the forefront of mechanobiology with techniques such as traction force microscopy (TFM) and atomic force microscopy (AFM) [5,6]. However, 2-D cultures impose unnatural geometric constraints on cells, and cells respond differently to mechanical properties when cultured in 2-D compared to in three-dimensional (3-D) biomaterials [7,8]. In response, the majority of contemporary studies have shifted to a 3-D context, enabled by recent developments in biomaterial fabrication, which provide more physiologically-relevant 3-D environments in which to encapsulate cells [9, 10]. Consequently, techniques that measure forces directly, such as TFM, are now moving toward 3-D. For example, in TFM, cells are now typically cultured in 3-D biomaterials with known mechanical properties and biomaterial deformation is related to a force exerted by the cell [11]. Most commonly, confocal microscopy is used to measure deformation [12,13]. More recently, optical coherence tomography (OCT) has been proposed for use in TFM with a main advantage being that it has an increased penetration depth compared to confocal microscopy [14]. Techniques that deform a portion of a cell, such as AFM, have been used to measure cellular strain and elasticity with sub-nanometer spatial resolution [15]. Techniques that apply a mechanical loading over the entirety of the cell, such as optical trapping [16], and micropipette aspiration [17], have enabled the measurement of bulk cellular and sub-cellular mechanical properties. Shear-flow techniques, such as microfluidics, have been used to characterize the effect of shear stress on cell physiology with an advantage of increased throughput [18]. However, these techniques typically remain limited to surface measurements, or studying cells in isolation, making it challenging to study the influence of mechanical properties on cell physiology in 3-D biomaterials. Several techniques are emerging to address this problem including Brillouin microscopy [19] and optical coherence elastography (OCE) [20]. Brillouin microscopy measures longitudinal modulus throughout a sample volume and has a number of attractive features, including its high spatial resolution (0.5–5 µm) and that it does not require an external mechanical load [21]. However, the incompressibility and high water content of biomaterials introduce inaccuracies relating longitudinal modulus to a mechanical property more commonly used in mechanobiology, such as Young’s modulus [22]. Additionally, cell imaging with Brillouin microscopy in scattering materials has a limited penetration depth (0.1–0.2 mm) compared to low-coherence interferometry techniques such as OCE (0.5–1 mm) [23]. Initial efforts to apply OCE to the cellular scale focused on qualitative approaches that were unable to measure the elasticity of cells and their extracellular environment [24,25]. To address this, more recently, several studies have utilized quantitative micro-elastography (QME) to image tissue on the cellular scale. QME is a variant of compression OCE that maps tangent modulus (equivalent to Young’s modulus in a linear elastic material) throughout a sample volume [26]. QME is a non-invasive, label free technique that uses compressive loading of the entire sample to image over millimeter-scale fields of view. QME has been applied to breast tumor margin assessment [27] and an implementation based on an ultra-high resolution OCT system has been demonstrated on excised mouse aorta [28]. QME has also been incorporated in a rigid micro-endoscope to facilitate future in vivo cellular scale elasticity imaging [29]. However, using QME to image the elasticity of cells in 3-D biomaterials has yet to be demonstrated and, furthermore, the elasticity resolution of QME has been loosely defined, making its suitability for use in mechanobiology unclear.
In this study, for the first time, we explore the capability of QME to image cell and extracellular elasticity in 3-D biomaterials. Firstly, to establish the elasticity resolution of QME, we extend a framework for resolution that our group has previously developed in compression OCE [30] to QME for the first time. We demonstrate, on a phantom containing a cellular-scale inclusion, that we can achieve an elasticity resolution of 39 µm. This capability is enabled by a novel 3-D weighted least-squares (WLS) estimate of local axial strain, which improves the strain fitting range to 50 µm from the typical 100 µm used with this OCT system. We demonstrate QME on human adipose-derived stem cells (ASCs) encapsulated in 3-D methacrylated gelatin (GelMA) hydrogels over 3.8×3.8×0.45 mm (xyz) fields of view using a common-path OCT system with axial resolution of 4.8 µm and lateral resolution of 7.2 µm. Furthermore, we image ASCs with transcriptional co-activator with PDZ-binding motif (TAZ) activation. TAZ is a mechanosensitive co-transcription factor which regulates cell volume and has been shown to sustain the self-renewal and tumor-initiation capacities of mesenchymal stem cells when studied in 2-D substrates [31,32]. We show that TAZ activation further elevates cell and extracellular elasticity in 3-D. In addition, we increase the lateral resolution of the OCT system to 4.4 µm and utilize a dual-arm configuration to improve the visualization of cells in OCT images, enabling co-registration of local regions of elevated elasticity with individual cells identified in OCT images. Finally, we present 3-D visualizations of cell and extracellular elasticity to highlight the utility of the 3-D imaging provided by QME. This study suggests that QME may aid in understanding the influence of mechanical properties on cell function and disease mechanisms in 3-D biomaterials.
2. Methods
2.1. Encapsulating cells in hydrogels
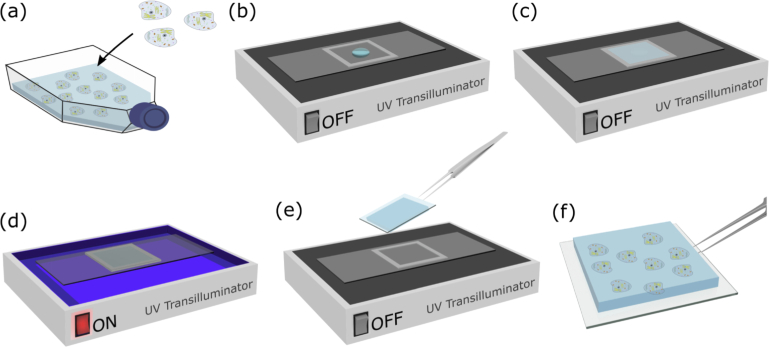
We analyzed the elasticity of 3-D GelMA hydrogels with encapsulated human ASCs. GelMA contains cell-attaching and matrix metalloproteinase responsive peptide motifs, which allow cells to proliferate and spread [33]. ASCs are commonly used to study mechanobiology due to their multi-linage differentiation capacity and unique immunobiological properties [34]. GelMA was synthesized by the methacrylation of gelatin, as described previously [35]. A 6.5% weight-to-volume GelMA solution was prepared 24 hours prior to use, by dissolving the GelMA monomer in phosphate-buffered saline at 37°C, and adding 0.1% weight-to-volume Irgacure-2959 (Sigma-Aldrich) dissolved in ethanol. The solution was kept at 4°C overnight, and reheated in a 37°C water bath for 1 hour before use. ASCs (ASC-F-SL, Zen Bio) were rapidly thawed and plated into a 37°C equilibrated T75 flask in standard media, containing Low Glucose Dulbecco’s Modified Eagle Medium (DMEM), 10% fetal bovine serum (FBS), and 1% antibiotic-antimycotic (AA), 24 hours before experiments. Prior to gel fabrication, 15 × 15 mm coverslips (Menzel-Gläser) were functionalized with (trimethoxysilyl)propyl methacrylate (Sigma-Aldrich), as described previously [36]. ASCs were trypsinized, collected in standard media, and centrifuged at 1,200 rpm for 5 minutes. The supernatant was discarded and 150 µL of GelMA per gel (a total of 750 µL) was added to the cell pellet (∼500,000 cells). 130 µL of cell-laden GelMA solution (Fig. 1(a)) was pipetted into a 13×13×0.5 mm (xyz) mold (Fig. 1(b)) comprised of a glass base with acrylic walls. A functionalized glass coverslip was placed on top, and the GelMA was polymerized using an ultraviolet (UV) transilluminator with center wavelength of 350 nm for 30 seconds (Figs. 1(c)–1(d)). Solidified hydrogels were ∼500 µm in height. These hydrogels, cast on glass coverslips, were removed from the molds (Figs. 1(e)–1(f)) and placed in standard media. Each hydrogel was incubated for fourteen days at 37°C and 5% CO2 to ensure cell growth and spread. ASCs and TAZ activated ASCs [37] were encapsulated in hydrogels under the same conditions.
Fig. 1.
Encapsulating cells in 3-D GelMA hydrogels. (a) Live cells are transferred into GelMA solution. (b) 130 µL of cell-laden GelMA solution is pipetted into a mold and (c) covered with a glass coverslip. (d) GelMA is polymerized into a solid hydrogel under UV exposure. The hydrogel, containing live cells, is then removed from the mold shown in (e) and (f).
2.2. Experimental setup
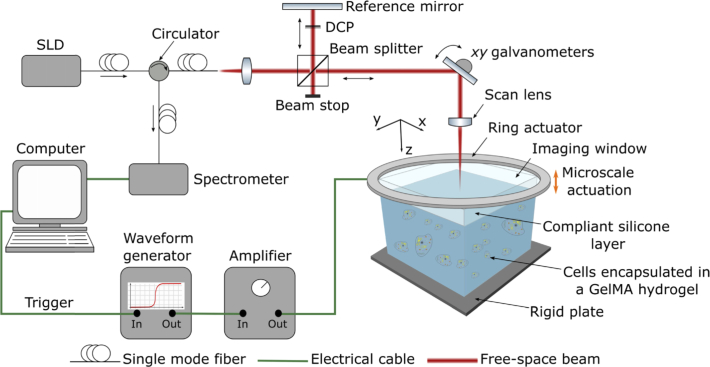
QME measurements were performed using a fiber-based spectral-domain OCT system (TEL320, Thorlabs Inc., USA). The schematic of the experimental setup is shown in Fig. 2. The light source is a superluminescent diode with a mean wavelength of 1300 nm and a spectral bandwidth of 170 nm. In this study, QME was performed using both common-path [38] and dual-arm configurations [39]. In both configurations, the measured OCT axial resolution in air is 4.8 µm (full-width at half maximum (FWHM) of irradiance). The scan lens (LSM03, Thorlabs) used in common-path has a numerical aperture (NA) of 0.063, a measured lateral resolution of 7.2 µm (FWHM) and a working distance of 25.1 mm. In common-path, the interface between the imaging window and a compliant silicone layer acts as the reference reflection. The compliant silicone layer is used to measure the stress applied at the sample surface and is described in the next paragraph. A concentration of 0.3% volume poly-methyl methacrylate (PMMA) beads (mean diameter = 1.3 µm) were added to the samples imaged in the common-path configuration to increase optical scattering and improve the OCT signal-to-noise ratio (SNR). Samples scanned using common-path were manually removed from the glass coverslips and placed on a non-reflective rigid metal plate to remove unwanted reflections. The scan lens (LSM02, Thorlabs) used in dual-arm has an NA of 0.11, a measured lateral resolution of 4.4 µm (FWHM) and a working distance of 7.5 mm. The samples analyzed in dual-arm were maintained on the glass coverslips and the scan lens was placed at a 4.5 degree angle from normal to the sample surface to remove unwanted reflections. The resulting tilt in QME and OCT images was corrected in post-processing. Operating QME in dual-arm enables the higher NA scan lens to be focused past the compliant silicone layer and into the sample. The higher NA scan lens focuses the equivalent optical power on a smaller region and collects a broader angle of back-scattered light, increasing the OCT signal and removing the need for PMMA to be added to the GelMA. Despite the reduced field of view, the improved lateral resolution and contrast of cells from surrounding GelMA enabled cells to be resolved and clearly distinguished from GelMA in OCT images, greatly facilitating the interpretation of corresponding QME images. Compression was applied to the samples using an annular piezoelectric actuator fixed to an imaging window through which the optical beam illuminates the sample. 10–15% bulk strain was applied to each sample to ensure uniform contact between the rigid plate, the sample, and the imaging window (Edmund Optics, USA). The ring actuator (Piezomechanik GmbH, Germany) has an aperture of 15 mm and a maximum stroke of 9.6 µm. A 20 mm diameter imaging window, fixed to the ring actuator, transfers the compressive load from the actuator to the sample. Scans taken in common-path comprised 2,000 A-scans per B-scan, and 4,000 B-scans per C-scan over a 4×4 mm (xy) lateral region, resulting in a lateral sampling density of 2 µm per voxel. Scans taken in dual-arm comprised 1,000 A-scans per B-scan, and 2,000 B-scans per C-scan over a 2×2 mm (xy) lateral region, also resulting in a lateral sampling density of 2 µm per voxel. Due to the reduced depth of field, and angle of the scan lens in dual-arm, there are regions with low OCT SNR on either side of the lateral field of view. As such, smaller, 1.25×1.25×0.28 mm (xyz) regions taken from the center of each scan are presented in Section 3.3. In all cases, the ring actuator was driven in a quasi-static regime by a 25 Hz square wave, collinearly with the imaging beam and synchronized with the acquisition of OCT B-scans. Similar GelMA hydrogels as those used in this study exhibit a linear stress-strain relationship and low viscoelasticity [40]. The 25 Hz actuation frequency was used to ensure we measured the instantaneous elastic strain in the sample. This was verified to be quasi-static as the difference in strain response to a lower 5 Hz actuation was within the strain sensitivity of the system. Two B-scans were acquired for each y-location such that alternate B-scans are acquired at different compression levels. Local axial displacement, uz, in the sample, is calculated from the phase difference between B-scans acquired at the same y-location [41]. Local axial strain, ɛ zz, is calculated as the gradient of axial displacement with depth using WLS linear regression over a 3-D fit length described in Section 2.3. To estimate the local stress at the sample surface, we utilize a 250 µm thick compliant silicone layer made from a soft silicone elastomer (P7676 1:1 crosslinker to catalyst ratio, Wacker) placed between the sample surface and imaging window [42]. Silicone oil is applied to lubricate the stress layer-imaging window interface. The thickness of the silicone layer is measured before and after the preload is applied to the sample to obtain an estimate of the bulk strain at each point on the sample’s surface. The local strain imparted to the layer by the ring actuator is used to calculate the local stress at the silicone layer-sample interface. The stress-strain relationship of the layer is characterized using a uniaxial compression testing apparatus as described previously [26,43]. Under the assumption that stress is uniform with depth, and by knowing the applied local stress and strain, the sample’s elasticity is calculated as a tangent modulus at the point of preload strain [26]. At low preload strains, tangent modulus is equivalent to Young’s modulus. QME images are presented in false color, overlaid on grayscale OCT images.
Fig. 2.
QME experimental setup using a phase-sensitive OCT system and compression loading applied from a ring actuator. SLD: superluminescent diode, DCP: dispersion compensation plate.
2.3. Signal processing
To improve the resolution of cellular-scale features in QME, we extend a framework developed by our group for analyzing spatial resolution in compression OCE [30]. In this framework, it is assumed that compression OCE resolution is determined by a convolution of mechanical deformation, OCT system resolution and strain fit length. Ultimately, mechanical deformation of the sample sets a limit to the achievable resolution. As such, the optimum scenario is that the system resolution, i.e., the OCT resolution convolved with the strain fit length, is below the deformation-limited case. In previous work, the system resolution was improved by using an ultra-high resolution OCT system with an axial and lateral resolution of 1.5 µm and 1.6 µm, respectively [28,29]. In this paper, we instead propose a novel approach for strain estimation to improve system resolution. Algorithms used to estimate strain in compression OCE typically use one-dimensional (1-D) WLS linear regression to calculate the gradient of axial displacement with depth over a sliding window of length, Δz [44]. For OCT systems with axial resolution comparable to our system, Δz is typically set to ∼100 µm [20,45]. The degradation to axial resolution from this fit length was shown to be approximately proportional to the fit length divided by [30]. Large fit lengths in z also lead to a mismatch between lateral and axial system resolution. In some applications, such a mismatch is acceptable, for example, in tumor margin assessment, images are typically presented in the (xy) lateral plane [27]. However, in this study, we are interested in the 3-D visualization of cell elasticity. To address this problem, we reduce the axial fit length, whilst maintaining sufficient sensitivity by implementing a 3-D WLS algorithm to estimate axial strain. This approach effectively obtains an improvement in axial resolution by trading off lateral resolution, such that the two are closely matched. In 3-D regression, the sample behavior in a local region is assumed to take the form:
| (1) |
where uzi is the axial displacement of the ith voxel, zi is its axial position, xi and yi are its lateral positions, and β1 is the local axial strain, ɛzz, that we are interested in estimating. β2 and β3 are the local gradients of axial displacement in x- and y-directions, respectively, β0 is an offset, and ei is the error term. We can then estimate uzi as:
| (2) |
The ordinary least-squares residuals are then:
| (3) |
The WLS model minimizes the weighted sum of squared residuals, RSS, for the parameter estimator β1:
| (4) |
where the weights, wi, are the OCT SNR at the ith voxel and N is the total number of voxels in the fit length. A detailed derivation of the algorithm is provided in Appendix 1. In this study, we reduce the axial fit length from 100 µm to 50 µm in z, and increase the lateral fit length to 50 µm in x and y. This fit length improves the axial system resolution from ∼72 µm to ∼35 µm and, while this degrades lateral system resolution by ∼35 µm, it uses two orders of magnitude more displacement data points, thus improving strain and elasticity sensitivity. We verified the improvement in strain and elasticity sensitivity by performing QME on a mechanically homogeneous phantom. The phantom was fabricated from Elastosil P7676 silicone (Wacker, Germany). The optical scattering properties of the phantom were controlled by adding titanium dioxide particles evenly mixed into the silicone at a concentration of 1 mg/ml [46]. QME was performed in common-path by acquiring 1,000 A-scans per B-scan, and 2000 B-scans per C-scan over a 2×2 mm lateral region with a lateral sampling density of 2 µm per voxel. The dataset was processed both with the conventional 1-D WLS algorithm using a 100 µm window length in z, and with the 3-D WLS algorithm using an isotropic 50 µm window length in x, y and z. Three 100×200 µm (zx) rectangular regions at different depths, and OCT SNR, were selected from the center B-scan and the mean strain and elasticity within this region was evaluated. Strain and elasticity sensitivity was evaluated as the standard deviation inside this rectangular region, as described previously [47]. The performance of the two algorithms is presented in Table 1. In each case, the 3-D WLS algorithm, with improved axial resolution, maintained higher strain and elasticity sensitivity compared to the 1-D WLS algorithm. The images presented in Section 3 are generated using an isotropic 50 µm window length which sets a system resolution of ∼35 µm in each dimension.
Table 1. Comparison of 1-D and 3-D WLS axial strain estimation techniques.
| Region | OCT SNR (dB) | Mean strain (mɛ) | Strain sensitivity (µɛ) | Mean elasticity (kPa) | Elasticity sensitivity (kPa) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1-D | 3-D | 1-D | 3-D | 1-D | 3-D | 1-D | 3-D | ||
| 1 | 21.2 | −0.6 | −0.6 | 59.4 | 48.1 | 10.5 | 10.5 | 1.1 | 0.9 |
| 2 | 12.8 | −0.6 | −0.6 | 83.9 | 46.8 | 9.8 | 9.8 | 1.4 | 0.7 |
| 3 | 4.4 | −0.7 | −0.7 | 169.1 | 125.1 | 9.8 | 9.8 | 3.2 | 1.8 |
3. Results
3.1. Common-path and dual-arm QME elasticity resolution
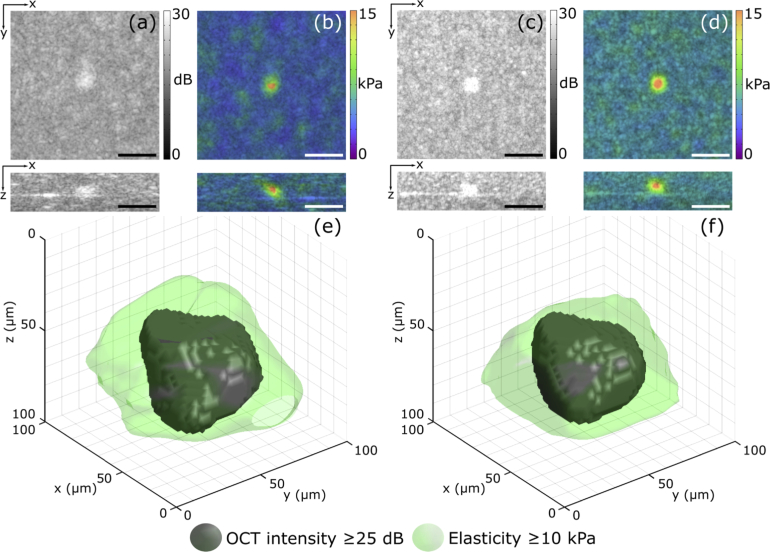
To verify the capacity of QME to resolve cellular-scale features, we use the approach developed previously by our group to measure strain resolution in compression OCE [30]. Extending this approach to QME, elasticity resolution is measured from the step response in elasticity across a stiff inclusion boundary in both x- and y-dimensions. A phantom was fabricated from Elastosil RT601, P7676, and AK50 Silicone oil (Wacker, Germany) that contained a stiff inclusion with dimensions of 50×45×44 µm (xyz), similar to a typical ASC analyzed in this study [48]. The optical scattering properties were controlled by adding titanium dioxide particles evenly mixed into the silicone in concentrations of 0.5 mg/ml in the bulk and 2.5 mg/ml in the inclusion [46]. Figures 3(a) and 3(b) are OCT images and OCT/QME overlays, respectively, of the phantom imaged using the common-path QME system. Both the axial and lateral elasticity resolution in Fig. 3(b) were 39 µm, respectively. Figures 3(c) and 3(d) are OCT images and OCT/QME overlays, respectively, of the phantom imaged using the dual-arm system. The higher lateral OCT resolution in Figs. 3(c) and 3(d) improves the visualization of the inclusion in the underlying OCT images. Both the axial and lateral resolution of elasticity in the dual-arm system, measured across the axial and lateral boundaries of the inclusion in Fig. 3(d), were 39 µm, respectively. This result is expected as, whilst the lateral OCT resolution of the dual-arm system (4.4 µm) is higher than the lateral OCT resolution of the common-path system (7.2 µm), the mechanical loading, and fit lengths of displacement used to estimate axial strain in both cases are equivalent and, as they are far larger than the OCT resolution, dominate the measured resolution.
Fig. 3.
OCT, QME and 3-D visualization of an inclusion phantom. (a) OCT and (b) OCT/QME overlay images of the inclusion imaged using common-path. (c) OCT and (d) OCT/QME overlay images of the same inclusion imaged using dual-arm. (e) and (f) are 3-D visualizations of the inclusion acquired using common-path, and dual-arm, respectively. In (e) and (f), the grey feature is the structure of the inclusion from the OCT intensity and the volume with elasticity above 10 kPa is overlaid in green. Scale bars represent 100 µm.
These results demonstrate that the elasticity resolution is similar in both the common-path and dual-arm configurations. Figures 3(e) and 3(f) are 3-D visualizations of the inclusion acquired using common-path and dual-arm, respectively, to highlight the 3-D imaging capability of QME. The solid grey feature in Figs. 3(e) and 3(f) is the structure of the inclusion extracted from the OCT volume using morphological filtering. The green region indicates the volume with elasticity above 10 kPa, and is overlaid on the inclusion structure. The threshold of 10 kPa was selected to separate the regions of high and low elasticity as it is in between the mean elasticity in the phantom bulk (∼5 kPa) and the mean elasticity inside the inclusion (∼15 kPa). Figures 3(e) and 3(f) help to highlight the impact of mechanical deformation and signal processing on elasticity resolution.
3.2. Imaging cells using common-path QME
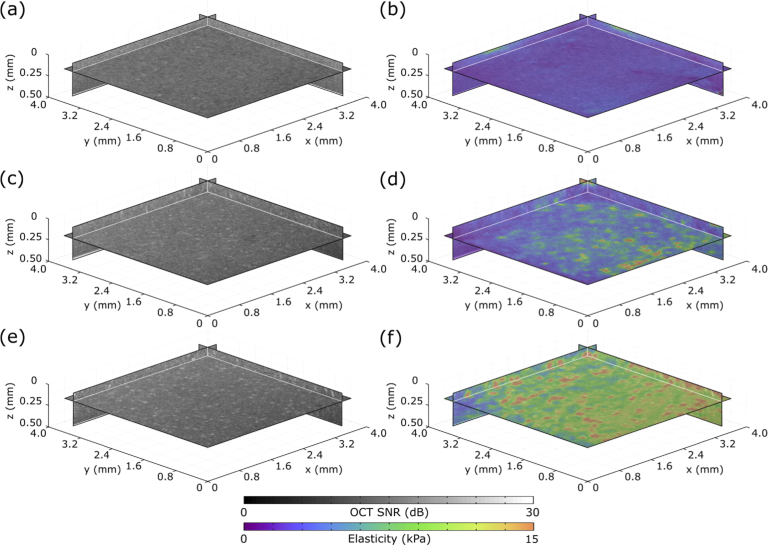
In Fig. 4, we demonstrate the capability of QME to distinguish between GelMA samples containing different cell types using a common-path configuration. We present one zx, zy and xy plane in each volume. Figure 4 shows OCT and OCT/QME overlays of GelMA, GelMA containing ASCs, and GelMA containing TAZ activated ASCs over 3.8×3.8×0.45 mm (xyz) fields of view, taken directly below the sample/stress layer interface. Figures 4(a) and 4(b) are OCT and OCT/QME overlays, respectively, of homogeneous GelMA without cells. The elasticity in Fig. 4(b) is relatively uniform, where the regions of non-uniformity may be due to slight differences in UV exposure in the curing process. Importantly, in Fig. 4(b) we observe no local regions of elevated elasticity. Figures 4(c) and 4(d) are OCT and OCT/QME overlays, respectively, of GelMA containing ASCs. In Fig. 4(d), we observe local regions of elevated elasticity, likely caused by cells. Cells interact with the extracellular environment via actin cytoskeletal filaments at the sites of cell adhesion. This enables cells to generate traction during migration and exert tension during matrix remodeling [49]. The increased elasticity is likely from cells exerting contractile forces and remodeling the ECM, which will be discussed further in Section 4. Whilst there are local regions of high OCT intensity in the OCT and OCT/QME overlays that likely correspond to cells, the low contrast between the cells and the surrounding GelMA, and the relatively low OCT lateral resolution, make it challenging to resolve individual cells in the OCT images. Figures 4(e) and 4(f) are OCT and OCT/QME overlays, respectively, of GelMA containing TAZ activated ASCs. In Fig. 4(f), we observe a greater number of local regions of elevated elasticity above 10 kPa when compared to GelMA containing ASCs. The local regions of elevated elasticity in Fig. 4(f) appear larger than in Fig. 4(d) and there is also an increase in GelMA elasticity over the field of view. The elevated elasticity with TAZ activation observed in Fig. 4 is consistent with results obtained on 2-D substrates [50]. TAZ activation in 2-D induces greater levels of actin production, which is likely to result in cells exerting greater traction force, and rates of ECM remodeling, further elevating the GelMA elasticity.
Fig. 4.
Volumetric images of the elasticity of GelMA, GelMA with ASCs, and GelMA with TAZ activated ASCs, acquired using common-path QME. (a) OCT and (b) OCT/QME overlay images of GelMA. (c) OCT and (d) OCT/QME overlay images of GelMA containing ASCs. (e) OCT and (f) OCT/QME overlay images of GelMA containing ASCs with TAZ activation.
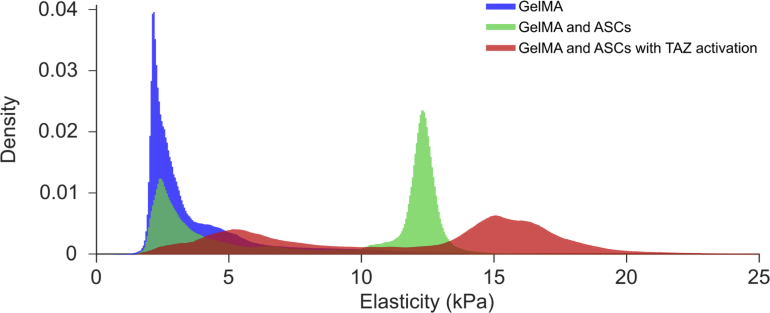
In Fig. 5, we present histograms corresponding to the elasticity of each volume in Fig. 4: GelMA (blue), GelMA containing ASCs (green), and GelMA containing ASCs with TAZ activation (red). The elasticity of homogeneous GelMA has a mean of 3.9 kPa and a positively skewed normal distribution. Both the measured elasticity from the GelMA containing ASCs and ASCs with TAZ activation exhibit bi-modal distributions. Throughout the sample volume, it is likely that the cells are elevating the elasticity of the GelMA in local regions. The first peak of these two elasticity distributions likely corresponds to the elasticity of the GelMA that is not affected by the cells and has a mean that matches closely with the peak observed in the homogeneous GelMA. The second peak likely represents the elasticity of local regions containing cells. In GelMA containing ASCs, this second peak occurs at ∼12 kPa. In GelMA containing ASCs with TAZ activation, this second peak occurs at ∼15 kPa, suggesting that the latter further elevates the cell and/or GelMA elasticity. Both the first and second peaks of the GelMA containing cells with TAZ activation are broadened relative to the respective peaks of the GelMA containing ASCs.
Fig. 5.
Histograms of the elasticity measured throughout the respective volumes presented in Fig. 4, GelMA (blue), GelMA containing ASCs (green), and GelMA containing ASCs with TAZ activation (red).
3.3. Imaging cells using dual-arm QME
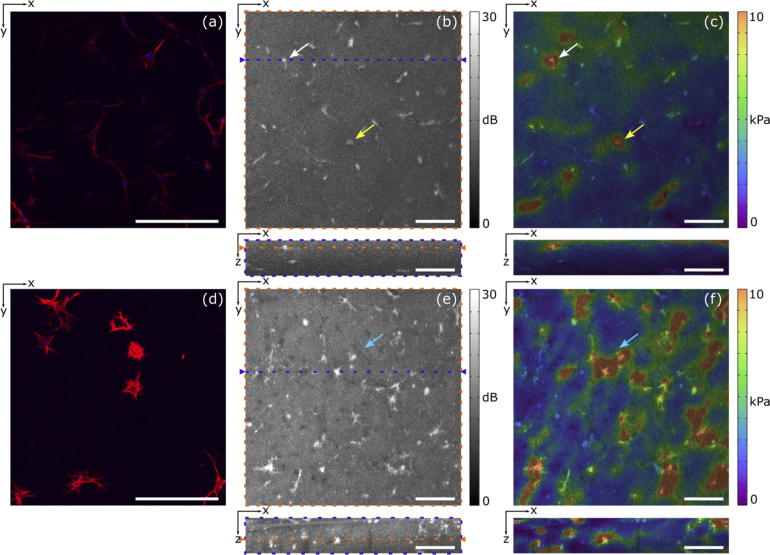
In Fig. 6 we utilize a dual-arm configuration with higher lateral OCT resolution to verify the capability of QME to resolve the elasticity of individual cells. We present OCT and OCT/QME overlay images of GelMA samples containing cells acquired over 1.25×1.25×0.28 mm (xyz) fields of view, acquired 50 µm below the sample surface. Despite the reduced field of view, the higher lateral resolution and increased contrast between cells and the GelMA in the OCT images helps to verify that local regions of elevated elasticity in the QME images correspond to individual cells. Figures 6(a) and 6(d) are representative confocal microscopy images of GelMA containing ASCs, and TAZ activated ASCs, respectively, acquired over a 0.65×0.65 mm (xy) field of view taken from samples prepared in the same batch as those scanned using QME. We present confocal microscopy alongside OCT and QME images to indicate differences in cell morphology between the two cell types. Confocal microscopy images were acquired using a Nikon C2+ confocal microscope running NiS Elements Advanced 4.0 (Nikon). 4’,6-diamidino-2-phenylindole (D9542, Sigma) staining was used to visualize cell nuclei, shown in blue, and Rhodamine Phalloidin (R415, Molecular Probes) staining was used to visualize actin filaments, shown in red. Descriptions of the straining procedures and confocal microscopy imaging parameters are provided in Appendix 2. We observe that TAZ activated ASCs (Fig. 6(d)) had more actin filaments, evident by brighter actin staining, compared to ASCs (Fig. 6(a)). As described in Section 3.2, contractile forces exerted by actin filaments in the cytoskeleton, and ECM remodeling, will likely elevate the elasticity in local regions around the cells. The respective cell morphologies of ASCs, and TAZ activated ASCs, observed in confocal microscopy can also be seen in the OCT images in Figs. 6(b) and 6(e), respectively. The OCT and OCT/QME overlays are presented as xy and zx cross-sections. In the OCT/QME overlays of ASCs, and TAZ activated ASCs, in Figs. 6(c) and 6(f), respectively, the arrows indicate example regions where individual cells have elevated elasticity. Similar to the results acquired in common-path, the local regions of elevated elasticity in Fig. 6(f) appear larger than in Fig. 6(c). In the region indicated by the blue arrow in Fig. 6(f) we observe three cells whose cell adhesions are extending toward each other. The boundaries of elevated elasticity in this region follow this cell group. Note that in Figs. 6(c) and 6(f) there are regions of elevated elasticity that are not co-registered with the presence of cells in the OCT image. As Figs. 6(c) and 6(f) present only one plane, these regions of elevated elasticity are likely due to cells either above outside of this plane. In addition, the planes in elasticity represents data from an axial and lateral range of 35 µm, whilst the OCT planes corresponds to an axial and lateral range of 4.4 µm.
Fig. 6.
Cells measured using confocal microscopy and dual-arm QME. Representative confocal microscopy of GelMA with (a) ASCs and (d) TAZ activated ASCs with cell nuclei shown in blue, and actin filaments in red. (b) OCT and (c) OCT/QME overlay images of ASCs. (e) OCT and (f) OCT/QME overlay images of ASCs with TAZ activation. Cross-sections in the OCT xy and zx planes are represented by orange and purple dashed rectangles, respectively. The arrows indicate example regions where individual cells have elevated elasticity. Scale bars represent 250 µm.
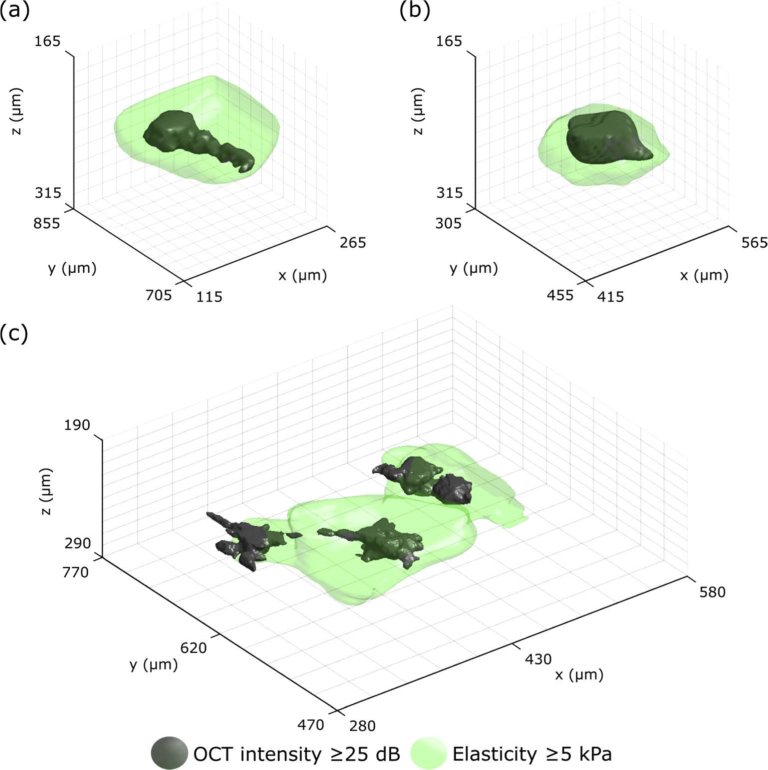
In Fig. 7, to provide a more complete representation, we present 3-D visualizations of cell and extracellular elasticity acquired from dual-arm QME. 3-D visualizations highlight the utility of the 3-D imaging of QME and overcome the issue of elevated elasticity potentially coming from cells above or below the xy plane presented. Figures 7(a) and 7(b) show 3-D visualizations of the ASCs indicated by the white and yellow arrows in Fig. 6 over 150×150×150 µm (xyz) fields of view. Figure 7(c) shows a 3-D visualization of three TAZ activated cells indicated by the blue arrow in Fig. 6(f), corresponding to a 300×300×100 µm (xyz) field of view. The cells (shown in grey) are extracted from the volumetric OCT image using morphological filtering. The green volume surrounding the cells denotes elasticity equal to, or higher than, 5 kPa. The threshold of 5 kPa was selected based on the histogram in Fig. 5 as it is in between the peaks corresponding to elasticity of the GelMA and local regions containing cells. The local volumes of high elasticity above this threshold are well correlated with the location of cells in the volumetric OCT images.
Fig. 7.
3-D visualization of cell and extracellular elasticity acquired from dual-arm QME. (a) and (b) are 3-D visualizations of the ASCs indicated by the white and yellow arrows in Fig. 6(c), respectively. (c) 3-D visualization of three TAZ activated ASCs from the region indicated by the blue arrow in Fig. 6(f). Cell structure is acquired from the OCT intensity (grey) and the volume with an elasticity above 5 kPa is overlaid in green.
4. Discussion
In this first study of QME in mechanobiology, we have demonstrated cell and extracellular matrix elasticity imaging in 3-D biomaterials. To more accurately compare differences in elasticity between cell types, we performed QME in common-path using a scan lens with an NA of 0.063 to increase the field of view and obtain a greater number of data points. This removed the need to place the sample at an angle from the scan lens, and enabled the imaging window, stress layer and sample to be in focus over a 3.8×3.8×0.45 mm (xyz) field of view. Although the resolution of elasticity is similar between both scan lenses used in this study, a scan lens with an NA of 0.11 improved the lateral resolution and contrast between the cells and GelMA in the underlying OCT images. However, the higher NA resulted in bright reflections at the imaging window, stress layer, and sample interfaces when configured in common-path and degraded image quality. To take advantage of the higher NA scan lens, we performed QME using a dual-arm configuration with the sample placed at an angle to the scan lens. Whilst this significantly reduced the field of view, making it less suitable to quantify the difference in elasticity between cell types, it provided the ability to co-register elevated regions of elasticity with the location of cells which greatly improved the interpretation of the QME images. Using both configurations, we have demonstrated the potential of QME to study changes in elasticity in response to upregulated mechanosensitive transcription factors over millimeter fields of view and the ability to resolve individual cells elevating the elasticity of GelMA in local regions. Such capacity can enable studies of cells in a variety of conditions including homogeneous and stiffness gradient 3-D biomaterials [36] that better replicate the conditions found in tissues and organs than conventional 2-D substrates.
The results presented in Section 3 suggest that TAZ activation in ASCs leads to an increase in cell and extracellular elasticity in 3-D substrates. Whilst this is a preliminary result, this is consistent with results obtained in 2-D substrates. In 2-D substrates, stiff extracellular environments induce the nuclear localization of TAZ, promoting the production of actin and inducing osteogenic differentiation, whereas soft environments inhibit the nuclear localization of TAZ and induce adipogenic differentiation [51]. Here, prior upregulation of TAZ is likely to induce ASCs to behave as they would on stiff substrates and stimulate actin production as indicated in the confocal microscopy images. Increased actin production represents indirect evidence that TAZ activation is contributing to greater contractile forces and elevated cell and extracellular elasticity. The increase in bulk elasticity near the bottom right side in the OCT/QME overlay in Fig. 4(e) is likely due to increases in local cell density and contractile forces as a result of TAZ activation. However, this is difficult to compare due to the lack of contrast in the common-path OCT images. It is possible that the increased elasticity is a result of a gradient in preload strain applied to the sample, however, we do not believe this is the case as each sample was loaded in identical conditions and we did not observe a similar increase in bulk elasticity in the corresponding bottom right regions in either Figs. 4(b) or 4(d). Additional explanations include increased rates of cell spread, proliferation and ECM remodeling. However, due to the lack of information on TAZ activation in 3-D, it still remains to be understood how the encapsulation process influences cell spread and proliferation in 3-D substrates. The focus of this study was to demonstrate the capability of QME to image cells in 3-D biomaterials and studying the impact of cell spread, proliferation and matrix remodeling on elasticity in 3-D represents a promising avenue for future research.
The results presented in Section 3 were acquired using a modified commercial OCT system, and our QME system resolution was sufficient to resolve the elasticity of cells to at least 39 µm. Whilst the ability to use commercial OCT systems is likely to improve the translation of QME to mechanobiology, the size of many cell types lies below this length scale. Importantly, the results in Section 3 show cells elevating elasticity in local regions, essentially acting as stiff inclusions. Previously, our group demonstrated that the degradation to resolution from mechanical deformation of stiff inclusions was approximately half the inclusion size [30]. Realizing the optimum, deformation-limited scenario will require a system that adequately samples this deformation. Typically, as is the case in this paper, the strain fit length is approximately an order of magnitude larger than the OCT resolution. QME based on ultra-high resolution [25,28,29], or visible light OCT [52], with axial and lateral resolutions of 1–1.5 µm, would likely result in system resolutions on the order of 10 µm. This suggests that QME could potentially resolve responses from cells as small as 20 µm. High resolution OCT systems are also likely to improve the resolution and contrast of cells in the underlying OCT images.
There are several techniques that could be combined with QME to provide new insight into mechanobiology. One such technique is TFM. For example, TFM typically contacts cells with a substrate with known mechanical properties and relates substrate deformation to a force exerted by the cell [11,12]. However, a challenge in relating deformation to a force is that it requires prior knowledge of both the mechanical properties of the cell and surrounding substrate, which are commonly either assumed or estimated from theoretical modeling [53]. TFM based on optical coherence microscopy (OCM), termed traction force optical coherence microscopy (TF-OCM) has recently been demonstrated on cells encapsulated in 3-D biomaterials [14]. As both QME and TF-OCM could be implemented using the same underlying OCM system, a multi-modal technique that employs QME to characterize local mechanical properties holds potential to improve the accuracy of the measured traction forces in TFM. Furthermore, florescence confocal microscopy could be combined with QME to verify the presence of proteins, such as TAZ, in cell nuclei to more accurately relate changes in mechanical properties to different cell types [7]. In addition, combining a molecular-specific method such as Raman spectroscopy [54] with QME could be used to co-register changes in mechanical properties with chemical composition.
Similar to conventional linear regression algorithms used to estimate axial strain in OCE, the 3-D WLS algorithm assumes displacement is linear over the fit length. However, in regions of mechanical heterogeneity, displacement is likely to be non-linear which will reduce strain accuracy. Ideally, the fit length would be as small as possible, however this limits strain sensitivity in the presence of noise [44]. Whilst increasing lateral fit lengths will likely reduce strain accuracy in x and y, reducing the axial fit length should increase strain accuracy in z and provide an isotropic system resolution. Importantly, for the typical cell size in this study, there is not an instantaneous response in elasticity, rather there exists a smooth gradient in elasticity which typically occurs over greater length scales than the fit length. For smaller cells, one approach to reduce the impact of non-linear displacement on strain accuracy is to improve displacement sensitivity and reduce the need for large fit lengths. This can likely be achieved by using specialized, high resolution OCT systems.
QME makes a number of assumptions that can, in some instances, limit the accuracy of the measurements. For example, in the current implementation of QME, stress determined at the sample surface is assumed to be uniaxial with depth. However, this assumption is routinely violated in mechanically heterogeneous samples. One approach to overcome the limitations in image quality imposed by these assumptions is to use computational solutions to the inverse elasticity problem [55,56]. Despite a significant increase in computational overhead, such approaches have the potential to remove the influence of mechanical heterogeneity and boundary conditions on QME accuracy and resolution. Computational solutions can also provide access to traction forces [57] which could potentially provide a rich insight into the influences of forces and mechanical properties on cell physiology in 3-D environments. Furthermore, consistent with the broader field of elastography, compression OCE techniques typically treat samples as linear elastic materials [20,45]. However, in general, many biomaterials and native ECMs exhibit regions of non-linear elastic behaviour [58]. In these cases, applying a preload strain will impart an offset along the non-linear stress-strain curve, which, at higher strains, will typically result in QME overestimating elasticity. In addition, more complex mechanical properties exist in many ECMs including time-dependent effects such as plasticity and viscoelasticity [3]. These time-dependent, non-linear mechanical characteristics are postulated to serve as important physical regulators in directing cell behaviour and ECM remodeling [10]. Non-linear OCE techniques have been demonstrated [59–61], and with further development toward applications in mechanobiology, could enable more accurate reconstructions of Young’s modulus and the opportunity to study time-dependent mechanical characteristics in 3-D biomaterials.
5. Conclusion
In conclusion, the visualization of cell and extracellular elasticity provided by QME represents a new technique to study the influence of mechanical properties on cell physiology in 3-D biomaterials. We have extended QME to volumetric imaging of cell and extracellular elasticity by developing the necessary sample preparation protocol, experimental setup and signal processing to resolve the elasticity of cells encapsulated in 3-D GelMA hydrogels. Our results demonstrate that QME can reveal elevated elasticity in local regions surrounding cells, and can distinguish between cell types when a mechanosensitive transcription factor is modified. This study also reveals the complementary nature of QME with structural images of cells in the underlying OCT images. QME shows promise for the characterization of cell mechanics with the potential to combine with multimodal imaging to study cell physiology and disease mechanisms in 3-D environments.
Appendix 1
The minimal residuals in Eq. (4) are found when the partial derivatives of RSS are 0. By applying the power rule and chain rule, we can calculate the partial derivatives as:
| (5) |
Solving for each parameter yields:
| (6) |
| (7) |
| (8) |
| (9) |
We can then rearrange these equations into WLS normal equations:
| (10) |
| (11) |
| (12) |
| (13) |
Equations (10)–(13) are solved simultaneously in matrix form using MATLAB to obtain an estimate of β1 as the gradient of axial displacement with depth (local axial strain) using a 3-D sliding window of length (Δx, Δy, Δz).
Appendix 2
Immunofluorescence was performed at two weeks to visualize cell morphological characteristics using a protocol developed previously [62]. Gels were removed from coverslips using a scalpel to increase the surface area through which immunostaining agents could access the gel. Samples were fixed in 4% paraformaldehyde (Santa Cruz) for 30 minutes, washed, then permeabilized in 1% Triton X-100 (Sigma-Aldrich) for 30 minutes and washed. Samples were stained for F-actin by incubation with Rhodamine Phalloidin (1:100, R415, Invitrogen) in 2% BSA at 37 °C for two hours, and washed. Samples were then incubated with DAPI (1:500, D9542, Sigma-Aldrich) in PBS for 20 minutes and washed. All washes were done three times in PBS. Samples were placed back on a coverslip and mounted with ProLong Diamond mountant (Invitrogen). Z-stack images (150 µm stack, 4 µm steps) were captured at 20 times magnification using a Nikon C2+ Confocal microscope (Nikon) and NIS-Elements BR 4.1 software.
Funding
Australian Research Council10.13039/501100000923; Cancer Council Western Australia10.13039/501100001170; Industrial Transformation Training Centre; The William and Marlene Schrader Trust of the University of Western Australia.
Disclosures
BFK: OncoRes Medical (F, I). The other authors declare that there are no conflicts of interest related to this article.
References
- 1.Ladoux B., Mège R. M., “Mechanobiology of collective cell behaviours,” Nat. Rev. Mol. Cell Biol. 18(12), 743–757 (2017). 10.1038/nrm.2017.98 [DOI] [PubMed] [Google Scholar]
- 2.Wang N., Tytell J. D., Ingber D. E., “Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus,” Nat. Rev. Mol. Cell Biol. 10(1), 75–82 (2009). 10.1038/nrm2594 [DOI] [PubMed] [Google Scholar]
- 3.Humphrey J. D., Dufresne E. R., Schwartz M. A., “Mechanotransduction and extracellular matrix homeostasis,” Nat. Rev. Mol. Cell Biol. 15(12), 802–812 (2014). 10.1038/nrm3896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jaalouk D. E., Lammerding J., “Mechanotransduction gone awry,” Nat. Rev. Mol. Cell Biol. 10(1), 63–73 (2009). 10.1038/nrm2597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lee G. Y. H., Lim C. T., “Biomechanics approaches to studying human diseases,” Trends Biotechnol. 25(3), 111–118 (2007). 10.1016/j.tibtech.2007.01.005 [DOI] [PubMed] [Google Scholar]
- 6.Moeendarbary E., Harris A. R., “Cell mechanics: principles, practices, and prospects,” Wiley Interdiscip. Rev.: Syst. Biol. Med. 6(5), 371–388 (2014). 10.1002/wsbm.1275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Caliari S. R., Vega S. L., Kwon M., Soulas E. M., Burdick J. A., “Dimensionality and spreading influence MSC YAP/TAZ signaling in hydrogel environments,” Biomaterials 103, 314–323 (2016). 10.1016/j.biomaterials.2016.06.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Engler A., Bacakova L., Newman C., Hategan A., Griffin M., Discher D., “Substrate Compliance versus Ligand Density in Cell on Gel Responses,” Biophys. J. 86(1), 617–628 (2004). 10.1016/S0006-3495(04)74140-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shao Y., Sang J., Fu J., “On human pluripotent stem cell control: The rise of 3D bioengineering and mechanobiology,” Biomaterials 52, 26–43 (2015). 10.1016/j.biomaterials.2015.01.078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li L., Eyckmans J., Chen C. S., “Designer biomaterials for mechanobiology,” Nat. Mater. 16(12), 1164–1168 (2017). 10.1038/nmat5049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tan J. L., Tien J., Pirone D. M., Gray D. S., Bhadriraju K., Chen C. S., “Cells Lying on a Bed of Microneedles: An Approach to Isolate Mechanical Force,” Proc. Natl. Acad. Sci. U. S. A. 100(4), 1484–1489 (2003). 10.1073/pnas.0235407100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Franck C., Maskarinec S. A., Tirrell D. A., Ravichandran G., “Three-Dimensional Traction Force Microscopy: A New Tool for Quantifying Cell-Matrix Interactions,” PLoS One 6(3), e17833 (2011). 10.1371/journal.pone.0017833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Legant W. R., Miller J. S., Blakely B. L., Cohen D. M., Genin G. M., Chen C. S., “Measurement of mechanical tractions exerted by cells in three-dimensional matrices,” Nat. Methods 7(12), 969–971 (2010). 10.1038/nmeth.1531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mulligan J. A., Feng X., Adie S. G., “Quantitative reconstruction of time-varying 3D cell forces with traction force optical coherence microscopy,” Sci. Rep. 9(1), 4086 (2019). 10.1038/s41598-019-40608-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mathur A. B., Collinsworth A. M., Reichert W. M., Kraus W. E., Truskey G. A., “Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy,” J. Biomech. 34(12), 1545–1553 (2001). 10.1016/S0021-9290(01)00149-X [DOI] [PubMed] [Google Scholar]
- 16.Fazal F. M., Block S. M., “Optical tweezers study life under tension,” Nat. Photonics 5(6), 318–321 (2011). 10.1038/nphoton.2011.100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hochmuth R. M., “Micropipette aspiration of living cells,” J. Biomech. 33(1), 15–22 (2000). 10.1016/S0021-9290(99)00175-X [DOI] [PubMed] [Google Scholar]
- 18.Vanapalli S. A., Duits M. H. G., Mugele F., “Microfluidics as a functional tool for cell mechanics,” Biomicrofluidics 3(1), 012006 (2009). 10.1063/1.3067820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Scarcelli G., Yun S. H., “Confocal Brillouin microscopy for three-dimensional mechanical imaging,” Nat. Photonics 2(1), 39–43 (2008). 10.1038/nphoton.2007.250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kennedy B. F., Wijesinghe P., Sampson D. D., “The emergence of optical elastography in biomedicine,” Nat. Photonics 11(4), 215–221 (2017). 10.1038/nphoton.2017.6 [DOI] [Google Scholar]
- 21.Scarcelli G., Polacheck W. J., Nia H. T., Patel K., Grodzinsky A. J., Kamm R. D., Yun S. H., “Noncontact three-dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy,” Nat. Methods 12(12), 1132–1134 (2015). 10.1038/nmeth.3616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wu P. J., Kabakova I. V., Ruberti J. W., Sherwood J. M., Dunlop I. E., Paterson C., Török P., Overby D. R., “Water content, not stiffness, dominates Brillouin spectroscopy measurements in hydrated materials,” Nat. Methods 15(8), 561–562 (2018). 10.1038/s41592-018-0076-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Izatt J. A., Hee M. R., Owen G. M., Swanson E. A., Fujimoto J. G., “Optical coherence microscopy in scattering media,” Opt. Lett. 19(8), 590–592 (1994). 10.1364/OL.19.000590 [DOI] [PubMed] [Google Scholar]
- 24.Leroux C. E., Palmier J., Boccara A. C., Cappello G., Monnier S., “Elastography of multicellular aggregates submitted to osmo-mechanical stress,” New J. Phys. 17(7), 073035 (2015). 10.1088/1367-2630/17/7/073035 [DOI] [Google Scholar]
- 25.Curatolo A., Villiger M., Lorenser D., Wijesinghe P., Fritz A., Kennedy B. F., Sampson D. D., “Ultrahigh-resolution optical coherence elastography,” Opt. Lett. 41(1), 21–24 (2016). 10.1364/OL.41.000021 [DOI] [PubMed] [Google Scholar]
- 26.Kennedy K. M., Chin L., McLaughlin R. A., Latham B., Saunders C. M., Sampson D. D., Kennedy B. F., “Quantitative micro-elastography: imaging of tissue elasticity using compression optical coherence elastography,” Sci. Rep. 5(1), 15538 (2015). 10.1038/srep15538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Allen W. M., Kennedy K. M., Fang Q., Chin L., Curatolo A., Watts L., Zilkens R., Chin L., Dessauvagie B. F., Latham B., Saunders C. M., Kennedy B. F., “Wide-field quantitative micro-elastography of human breast tissue,” Biomed. Opt. Express 9(3), 1082–1096 (2018). 10.1364/BOE.9.001082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wijesinghe P., Johansen N. J., Curatolo A., Sampson D. D., Ganss R., Kennedy B. F., “Ultrahigh-resolution optical coherence elastography images cellular-scale stiffness of mouse aorta,” Biophys. J. 113(11), 2540–2551 (2017). 10.1016/j.bpj.2017.09.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fang Q., Curatolo A., Wijesinghe P., Yeow Y. L., Hamzah J., Noble P. B., Karnowski K., Sampson D. D., Ganss R., Kim J. K., Lee W. M., Kennedy B. F., “Ultrahigh-resolution optical coherence elastography through a micro-endoscope: towards in vivo imaging of cellular-scale mechanics,” Biomed. Opt. Express 8(11), 5127–5138 (2017). 10.1364/BOE.8.005127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hepburn M. S., Wijesinghe P., Chin L., Kennedy B. F., “Analysis of spatial resolution in phase-sensitive compression optical coherence elastography,” Biomed. Opt. Express 10(3), 1496–1513 (2019). 10.1364/BOE.10.001496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Perez-Gonzalez N. A., Rochman N. D., Yao K., Tao J., Le M. T. T., Flanary S., Sablich L., Toler B., Crentsil E., Takaesu F., Lambrus B., Huang J., Fu V., Chengappa P., Jones T. M., Holland A. J., An S., Wirtz D., Petrie R. J., Guan K. L., Sun S. X., “YAP and TAZ regulate cell volume,” J. Cell Biol. 218(10), 3472–3488 (2019). 10.1083/jcb.201902067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Moroishi T., Hansen C. G., Guan K. L., “The emerging roles of YAP and TAZ in cancer,” Nat. Rev. Cancer 15(2), 73–79 (2015). 10.1038/nrc3876 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yue K., Trujillo-de Santiago G., Alvarez M. M., Tamayol A., Annabi N., Khademhosseini A., “Synthesis, properties, and biomedical applications of gelatin methacryloyl (GelMA) hydrogels,” Biomaterials 73, 254–271 (2015). 10.1016/j.biomaterials.2015.08.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Choi Y. S., Vincent L. G., Lee A. R., Dobke M. K., Engler A. J., “Mechanical derivation of functional myotubes from adipose-derived stem cells,” Biomaterials 33(8), 2482–2491 (2012). 10.1016/j.biomaterials.2011.12.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nichol J. W., Koshy S. T., Bae H., Hwang C. M., Yamanlar S., Khademhosseini A., “Cell-laden microengineered gelatin methacrylate hydrogels,” Biomaterials 31(21), 5536–5544 (2010). 10.1016/j.biomaterials.2010.03.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hadden W. J., Young J. L., Holle A. W., McFetridge M. L., Kim D. Y., Wijesinghe P., Taylor-Weiner H., Wen J. H., Lee A. R., Bieback K., Vo B. N., Sampson D. D., Kennedy B. F., Spatz J. P., Engler A. J., Choi Y. S., “Stem cell migration and mechanotransduction on linear stiffness gradient hydrogels,” Proc. Natl. Acad. Sci. 114(22), 5647–5652 (2017). 10.1073/pnas.1618239114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Park H. W., Kim Y. C., Yu B., Moroishi T., Mo J. S., Plouffe S. W., Meng Z., Lin K. C., Yu F. X., Alexander C. M., Wang C., Guan K. L., “Alternative Wnt Signaling Activates YAP/TAZ,” Cell 162(4), 780–794 (2015). 10.1016/j.cell.2015.07.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kennedy B. F., McLaughlin R. A., Kennedy K. M., Chin L., Curatolo A., Tien A., Latham B., Saunders C. M., Sampson D. D., “Optical coherence micro-elastography: mechanical-contrast imaging of tissue microstructure,” Biomed. Opt. Express 5(7), 2113–2124 (2014). 10.1364/BOE.5.002113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fang Q., Frewer L., Wijesinghe P., Allen W. M., Chin L., Hamzah J., Sampson D. D., Curatolo A., Kennedy B. F., “Depth-encoded optical coherence elastography for simultaneous volumetric imaging of two tissue faces,” Opt. Lett. 42(7), 1233–1236 (2017). 10.1364/OL.42.001233 [DOI] [PubMed] [Google Scholar]
- 40.Shin S., Park S., Park M., Jeong E., Na K., Youn H. J., Hyun J., “Cellulose Nanofibers for the Enhancement of Printability of Low Viscosity Gelatin Derivatives,” BioResources 12(2), 2941–2954 (2017). 10.15376/biores.12.2.2941-2954 [DOI] [Google Scholar]
- 41.Wang R. K., Ma Z., Kirkpatrick S. J., “Tissue Doppler optical coherence elastography for real time strain rate and strain mapping of soft tissue,” Appl. Phys. Lett. 89(14), 144103 (2006). 10.1063/1.2357854 [DOI] [Google Scholar]
- 42.Kennedy K. M., Es’haghian S., Chin L., McLaughlin R. A., Sampson D. D., Kennedy B. F., “Optical palpation: optical coherence tomography-based tactile imaging using a compliant sensor,” Opt. Lett. 39(10), 3014–3017 (2014). 10.1364/OL.39.003014 [DOI] [PubMed] [Google Scholar]
- 43.Sanderson R. W., Curatolo A., Wijesinghe P., Chin L., Kennedy B. F., “Finger-mounted quantitative micro-elastography,” Biomed. Opt. Express 10(4), 1760–1773 (2019). 10.1364/BOE.10.001760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kennedy B. F., Koh S. H., McLaughlin R. A., Kennedy K. M., Munro P. R. T., Sampson D. D., “Strain estimation in phase-sensitive optical coherence elastography,” Biomed. Opt. Express 3(8), 1865–1879 (2012). 10.1364/BOE.3.001865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Larin K. V., Sampson D. D., “Optical coherence elastography – OCT at work in tissue biomechanics [Invited],” Biomed. Opt. Express 8(2), 1172–1202 (2017). 10.1364/BOE.8.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lamouche G., Kennedy B. F., Kennedy K. M., Bisaillon C. E., Curatolo A., Campbell G., Pazos V., Sampson D. D., “Review of tissue simulating phantoms with controllable optical, mechanical and structural properties for use in optical coherence tomography,” Biomed. Opt. Express 3(6), 1381–1398 (2012). 10.1364/BOE.3.001381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chin L., Curatolo A., Kennedy B. F., Doyle B. J., Munro P. R. T., McLaughlin R. A., Sampson D. D., “Analysis of image formation in optical coherence elastography using a multiphysics approach,” Biomed. Opt. Express 5(9), 2913–2930 (2014). 10.1364/BOE.5.002913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ong W. K., Sugii S., “Adipose-derived stem cells: Fatty potentials for therapy,” Int. J. Biochem. Cell Biol. 45(6), 1083–1086 (2013). 10.1016/j.biocel.2013.02.013 [DOI] [PubMed] [Google Scholar]
- 49.Fletcher D. A., Mullins R. D., “Cell mechanics and the cytoskeleton,” Nature 463(7280), 485–492 (2010). 10.1038/nature08908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Nardone G., Oliver-De La Cruz J., Vrbsky J., Martini C., Pribyl J., Skládal P., Pešl M., Caluori G., Pagliari S., Martino F., Maceckova Z., Hajduch M., Sanz-Garcia A., Pugno N. M., Stokin G. B., Forte G., “YAP regulates cell mechanics by controlling focal adhesion assembly,” Nat. Commun. 8(1), 15321 (2017). 10.1038/ncomms15321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dupont S., Morsut L., Aragona M., Enzo E., Giulitti S., Cordenonsi M., Zanconato F., Digabel J. L., Forcato M., Bicciato S., Elvassore N., Piccolo S., “Role of YAP/TAZ in mechanotransduction,” Nature 474(7350), 179–183 (2011). 10.1038/nature10137 [DOI] [PubMed] [Google Scholar]
- 52.Shu X., Beckmann L. J., Zhang H. F., “Visible-light optical coherence tomography: a review,” J. Biomed. Opt. 22(12), 121707 (2017). 10.1117/1.JBO.22.12.121707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schwarz U. S., Soiné J. R. D., “Traction force microscopy on soft elastic substrates: A guide to recent computational advances,” Biochim. Biophys. Acta 1853(11), 3095–3104 (2015). 10.1016/j.bbamcr.2015.05.028 [DOI] [PubMed] [Google Scholar]
- 54.Kallepitis C., Bergholt M. S., Mazo M. M., Leonardo V., Skaalure S. C., Maynard S. A., Stevens M. M., “Quantitative volumetric Raman imaging of three dimensional cell cultures,” Nat. Commun. 8(1), 14843 (2017). 10.1038/ncomms14843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Dong L., Wijesinghe P., Dantuono J. T., Sampson D. D., Munro P. R. T., Kennedy B. F., Oberai A. A., “Quantitative compression optical coherence elastography as an inverse elasticity problem,” IEEE J. Sel. Top. Quantum Electron. 22(3), 277–287 (2016). 10.1109/JSTQE.2015.2512597 [DOI] [Google Scholar]
- 56.Dong L., Wijesinghe P., Sampson D. D., Kennedy B. F., Munro P. R. T., Oberai A. A., “Volumetric quantitative optical coherence elastography with an iterative inversion method,” Biomed. Opt. Express 10(2), 384–398 (2019). 10.1364/BOE.10.000384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Dong L., Oberai A. A., “Recovery of cellular traction in three-dimensional nonlinear hyperelastic matrices,” Comput. Methods Appl. Mech. Eng. 314, 296–313 (2017). 10.1016/j.cma.2016.05.020 [DOI] [Google Scholar]
- 58.Storm C., Pastore J. J., MacKintosh F. C., Lubensky T. C., Janmey P. A., “Nonlinear elasticity in biological gels,” Nature 435(7039), 191–194 (2005). 10.1038/nature03521 [DOI] [PubMed] [Google Scholar]
- 59.Sovetsky A. A., Matveyev A. L., Matveev L. A., Shabanov D. V., Zaitsev V. Y., “Manually-operated compressional optical coherence elastography with effective aperiodic averaging: demonstrations for corneal and cartilaginous tissues,” Laser Phys. Lett. 15(8), 085602 (2018). 10.1088/1612-202X/aac879 [DOI] [Google Scholar]
- 60.Qiu Y., Zaki F. R., Chandra N., Chester S. A., Liu X., “Nonlinear characterization of elasticity using quantitative optical coherence elastography,” Biomed. Opt. Express 7(11), 4702–4710 (2016). 10.1364/BOE.7.004702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wijesinghe P., McLaughlin R. A., Sampson D. D., Kennedy B. F., “Parametric imaging of viscoelasticity using optical coherence elastography,” Phys. Med. Biol. 60(6), 2293–2307 (2015). 10.1088/0031-9155/60/6/2293 [DOI] [PubMed] [Google Scholar]
- 62.Major L. G., Holle A. W., Young J. L., Hepburn M. S., Jeong K., Chin I. L., Sanderson R. W., Jeong J. H., Aman Z. M., Kennedy B. F., Hwang Y., Han D. W., Park H. W., Guan K. L., Spatz J. P., Choi Y. S., “Volume Adaptation Controls Stem Cell Mechanotransduction,” ACS Appl. Mater. Interfaces 11(49), 45520–45530 (2019). 10.1021/acsami.9b19770 [DOI] [PubMed] [Google Scholar]