A Robust Method Uncovers Significant Context-Specific Heritability in Diverse Complex Traits

Abstract

Gene-environment interactions (GxE) can be fundamental in applications ranging from functional genomics to precision medicine and is a conjectured source of substantial heritability. However, unbiased methods to profile GxE genome-wide are nascent and, as we show, cannot accommodate general environment variables, modest sample sizes, heterogeneous noise, and binary traits. To address this gap, we propose a simple, unifying mixed model for gene-environment interaction (GxEMM). In simulations and theory, we show that GxEMM can dramatically improve estimates and eliminate false positives when the assumptions of existing methods fail. We apply GxEMM to a range of human and model organism datasets and find broad evidence of context-specific genetic effects, including GxSex, GxAdversity, and GxDisease interactions across thousands of clinical and molecular phenotypes. Overall, GxEMM is broadly applicable for testing and quantifying polygenic interactions, which can be useful for explaining heritability and invaluable for determining biologically relevant environments.

Introduction

Many examples of gene-environment interaction (GxE) have been documented in humans at the level of individual genetic variants. In functional genomics, variants can have effects on expression that depend on external context,1, 2, 3, 4, 5 age,⁶ tissue,⁷ or cell type.^8,9 In complex traits, some genetic variants are known to interact with air pollution,¹⁰ microbe exposure,¹¹ or sex.12, 13, 14, 15 Variants can also interact with medical interventions and can render certain treatments ineffective.16, 17, 18

GxE tests can explain novel biology along two distinct, complementary axes. First, GxE can identify unappreciated genetic effects that elude linear models, which can increase genome-wide association study (GWAS) power and has recently received attention as a partial answer to the missing heritability question.19, 20, 21 Second, GxE tests can demonstrate that an environmental measurement is biologically trait relevant and quantify its impact, which can be important for public health and can illuminate intrinsic trait biology. More generally, genetic interaction tests can be used to assess the biological significance of any sample stratification, including (putative) phenotypic subtypes, quantitative covariates like age, or even other genetic variants.

However, investigation of GxE in nominally unrelated humans has been limited by the fact that individual variant effects are typically small. In the additive model context, genome-wide Genomic Restricted Maximum Likelihood (GREML) has been an invaluable complement to variant-based tests, powerfully characterizing aggregate polygenic effect sizes without attempting to resolve causal variants.²² Here, we propose an analogous mixed model for GxE, GxE Mixed Model (GxEMM), to characterize the aggregate polygenic contributions of GxE. Relative to single-variant GxE tests, GxEMM has higher power (for polygenic traits) but lower resolution, a tradeoff that makes it particularly useful for characterizing the biological relevance of environmental measures.

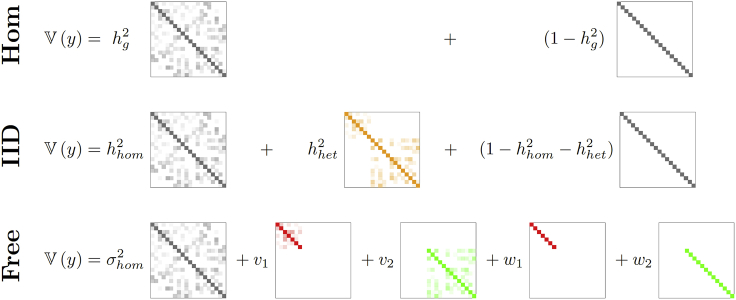
While complex in some settings, GxEMM is easily visualized for discrete environments (Figure 1). GxEMM incorporates three key, interpretable models. First, the Hom model is equivalent to standard GREML and models only the mean effects of the environment. We call the second model IID, as it allows environment-specific genetic variance and noise but assumes that these values are constant across every environment. We call the final model Free, because it allows the genetic and noise levels to freely vary between environments. We propose these three core models as a parsimonious, biologically informative representation of possible GxE models.

Figure 1.

The Three Key GxEMM Models in the Case of Two Discrete Environments

Entry shading indicates absolute value. Hom (top) fits homogeneous genetic ($h_g^2$) and noise (${\sigma }_e^2$) levels and is equivalent to GREML. IID (middle) adds a common effect for environment-specific heritability ($h_{het}^2$, orange), pictured as a block-diagonal matrix with each block corresponding to samples from one environment. Free (bottom) allows environment-specific genetic (v_k) and noise (w_k) levels.

Although GxEMM is simplest in the case of two discrete environments, GxEMM extends naturally to accommodate arbitrary environmental covariates. This is important because previous approaches require discrete environments (e.g., MV-GREML²⁰) or univariate environments (e.g., MRNM²³). A second significant component of GxEMM is the ability to model binary traits, like case/control disease studies. Third, GxEMM accommodates modest sample sizes, which can be important for applications like functional genomics. To obtain this flexibility, we implement three methods to estimate GxEMM parameters, each extending an existing approach to GREML: REML, for large sample sizes and continuous traits; phenotype-correlation-genotype-correlation (PCGC), for binary traits;^24,25 and Haseman-Elston regression (HE), for modest sample sizes, e.g., hundreds of samples.²⁶

We also make three important theoretical contributions. First, we demonstrate that noise heterogeneity must be modeled to avoid false positive GxE (Appendix A). Second, we provide a formally identified model description, which is essential for clear inference and future extensions (Appendix B). Third, we correct a misconception that G-E correlation generally causes GxE bias in the polygenic setting (Appendix C).

In this paper, we first provide a broad overview of GxEMM and the concept of polygenic interaction and then describe the details of the GxEMM method, our simulation study, and the three real datasets we analyze. Next, we perform a series of simulations and theoretical analyses that demonstrate that GxEMM is broadly reliable. We then apply GxEMM to study sex-specific heritability in 115 outbred rat traits and find strong, widespread signals of genetic and non-genetic heterogeneity, especially in bone and glucose-tolerance traits. Next, we find significant polygenic interactions with several stress indices and quantitative environments for major depression. Finally, we analyze RNA-seq data from postmortem brain and find strong evidence for bipolar- and schizophrenia-specific cis-heritability, both on average over the transcriptome and in nine known SCZ-associated genes. We conclude with a discussion on important caveats as well as future applications and extensions.

Material and Methods

Overview of GxEMM

GxEMM builds on GREML, an additive polygenic model that estimates heritability distributed across the genome. GxEMM additionally captures the GxE-based heritability due to polygenic gene-environment interactions. Assuming discrete environments, the model for phenotype y_i in environment k (i.e., $z_i=k$) is:

$$\begin{array}{ccccccccc}{y}_i|z_i=k& ~& \sum _q{X}_{iq}{\alpha }_q& +& {\sigma }_{hom}\sum _s{G}_{is}{\beta }_s& +& \sqrt{v_k}\sum _s{G}_{is}{\gamma }_{sk}& +& \sqrt{w_k+{\sigma }_{\mathrm{ϵ}}^2}{\mathrm{ϵ}}_i\\ & & \text{Covariate}& & \text{Hom G}& & \text{GxE}& & \text{Noise}\end{array}$$ (Equation 1)

In this model, X are covariates with fixed effects α, like age or genetic PCs. G is the genotype matrix, with additive effects β. As in GREML, we assume that β and the noise, ϵ, are i.i.d. standard normal, and the heritability is determined by the genetic and noise variances, ${\sigma }_{hom}^2$ and ${\sigma }_e^2$. GxEMM additionally captures SNP-environment interaction effects, γ, which are also assumed i.i.d. standard normal. Further, GxEMM allows environment-specific genetic (v_k) and noise (w_k) variances. Although we have assumed that z is discrete to simplify Equation 1 and Figure 1, GxEMM extends to general z, e.g., quantitative environments or proportional membership across discrete environments (see LMMs for Polygenic Interaction Effects (GxEMM)).

To unpack the model, imagine studying genetic effects on height across males and females. A SNP s that equally increases height in both sexes has a homogeneous effect $\left({\beta }_s>0\right)$ but has no sex-specific effects $\left({\gamma }_{sf}={\gamma }_{sm}=0\right)$, so s contributes to ${\sigma }_{hom}^2$ but not v_f or v_m. Conversely, a SNP $s^{\prime }$ that increases height only in females has ${\beta }_{s\text{'}}=0$ and ${\gamma }_{s^{\prime }f}>{\gamma }_{s^{\prime }m}=0$, so $s^{\prime }$ contributes to v_f but not ${\sigma }_{hom}^2$ or v_m. Finally, w_f > w_m means that females have higher non-genetic height variance.

We consider three distinct models for v: Hom, where all v_k = 0; IID, where $v_k=h_{het}^2$ for all k; and Free, where v is unconstrained. We use the same models for w, although the IID model is not identified in the case of discrete z. In the sex-height example, the IID model allows sex-specific genetic effects but assumes that, on balance, male- and female-specific sizes are identical; the Free model eliminates this assumption. In this paper, we assume that the genetic effects are exchangeable across environments, i.e., we assume that ${\gamma }_{sk}$ and ${\gamma }_{s{k}^{\prime }}$ are independent for $k\ne k^{\prime }$. We also theoretically describe a Full model allowing arbitrary correlations between environment-specific effects, which is richer but statistically and computationally challenging (see LMMs for Polygenic Interaction Effects (GxEMM)).

Of the many possible statistical tests available for GxEMM, we focus on a parsimonious set of biologically meaningful tests to characterize polygenic GxE:

• •Hom versus Null (i.e.: $h_g^2=0$?) tests whether there is any heritability.
• •IID versus Hom (i.e.: $h_{het}^2=0$?) tests polygenic GxE under homoscedasticity.
• •Free versus Hom (i.e.: $v_k=0$?) tests polygenic GxE allowing heteroscedasticity.

We implement both LR and Wald tests.

In the Free model with discrete z, each environment can have different levels of heritability and total variance. Assuming the kinship matrix is normalized, the heritability in environment k is:

$$h_k^2:=\frac{{\sigma }_{hom}^2+v_k}{{\sigma }_{hom}^2+v_k+w_k+{\sigma }_e^2}$$ (Equation 2)

Most previous approaches for polygenic GxE in unrelated samples assume discrete environments (Table 1). The GCTA GxE model fits an IID v.²⁷ The MV-GREML model fits Full v and Free w (and low-rank, polynomial sub-models, called RR-GREML).²⁰ iSet fits a similar model and can even fit Full w in the case that all samples are measured in all environments.²⁸ MetaSex fits the Hom model independently in each of two discrete environments, which implicitly resembles Free v and w.²⁹ Finally, StructLMM allows general (and potentially high-dimensional) environments, but only fits the IID model and a single SNP.²¹ Complementary to GxEMM, StructLMM powerfully identifies specific SNPs with environment-dependent effects but has low resolution to determine the biological significance of specific environments.

Table 1.

Recent LMMs for GxE Heritability

Publication	GxE	IxE	Binary y	Allowed Z	Notes
GCTA27	IID	unbiased	no	discrete	–
iSet28	full	unbiased	no	discrete	design-specific
MetaSex29.	free	unbiased	no	discrete	not MLE
MV-GREML20	full	unbiased	no	discrete	–
StructLMM21	IID	unbiased	no	general	$L=1$ SNP
RNM23	free	biased	no	bivariate	models G-E corr.
MRNM23	IID	unbiased	no	univariate	models G-E corr.
GxEMM (us)	free	unbiased	yes	general	–

GxE gives the richest fitted genetic heterogeneity model, and IxE indicates whether the method is biased under noise heterogeneity (Appendix A). Methods without specific notes are displayed with dash (–).

Most recently, Ni et al.²³ developed a Free model for v and w that allows gene-environment (G-E) correlation. In practice, Ni et al.²³ implement simpler submodels, and particularly focus on RNM and MRNM. RNM can fit up to two environments but ignores G-E correlation and noise heterogeneity (Appendix A). MRNM can fit only one environment, where the IID and Free models coincide. These constraints resolve computational and statistical limitations common to all GREML-based approaches, including GxEMM. The constraints also resolve non-identification issues specific to the model formulation in Ni et al.²³ By contrast, the formal model underlying GxEMM is well identified and naturally accommodates multivariate environments and genetic correlations between environments (Appendix B). For completeness, we extend the GxEMM model to accommodate G-E correlation in theory (see LMMs for Polygenic Interaction Effects (GxEMM)). Nonetheless, we theoretically demonstrate that this is unlikely to cause bias for GxEMM (Appendix C); moreover, no evidence to date has shown that polygenic G-E correlation causes GxE bias or test inflation in practice, in contrast to the single-variant case.³⁰

Overview of GxEMM with Binary Traits

Continuous trait models are inappropriate for binary traits like disease status. To address this, generalized linear models assume the binary trait is driven by an underlying quantitative liability. Binary trait heritability is then naturally defined as the heritability of this liability. To our knowledge, no other method has been developed to estimate polygenic GxE for binary traits.

One prominent approach to binary trait heritability estimation is to treat the 0/1 binary label as continuous in REML and then rescale post hoc. This transformation is exact without covariates³¹ and approximately extends to mild case ascertainment.^24,32,33 We attempt to extend this idea to GxE and evaluate the variance components both with and without rescaling (see GxEMM for Binary Traits).

Another method for binary trait GREML, phenotype-correlation-genotype-correlation (PCGC), uses moment-matching. When covariates are absent, PCGC amounts to comparing phenotypic and genotypic correlations, similar to HE regression for quantitative traits. PCGC extends this to incorporate covariates and preferential case ascertainment using an analytic approximation.^24,25 We can directly fit GxEMM with PCGC as it allows multiple relatedness matrices.

LMMs for Polygenic Effects (GREML)

The standard linear mixed model (LMM) for GREML assumes a quantitative trait measured on N samples, $y\in {\mathbb{R}}^N$. We allow Q background covariates in a matrix $X\in {\mathbb{R}}^{N\times Q}$ and L SNPs that we collect into the genotype matrix $G\in {\mathbb{R}}^{N\times L}$. The homogeneous LMM is:

$$y=X\alpha +G\beta +\mathrm{ϵ}$$ (Equation 3)

$${\beta }_j\stackrel{\text{iid}}{\sim }\mathcal{N}\left(0,{\sigma }_g^2/L\right);{\mathrm{ϵ}}_i\stackrel{\text{iid}}{\sim }\mathcal{N}\left(0,{\sigma }_e^2\right)$$ (Equation 4)

We assume $Q\ll N$ and estimate α as a fixed effect. In contrast, we allow $L\gg N$ and model β as a random effect. This can be motivated as a genuine prior that all SNPs have small, nonzero, i.i.d. effects, but GREML accurately estimates heritability under more realistic architectures.^34,35 Columns of G are demeaned and scaled based on some assumed relationship between MAF and effect size.^36,37

Marginalizing out β gives a simpler and equivalent (or almost equivalent, according to Steinsaltz et al.³⁸) formulation of GREML:

$$y\sim \mathcal{N}\left(X\alpha ,h_g^{2}K+\left(1-h_g^2\right)I_N\right)$$ (Equation 5)

defining I_N as the N-dimensional identity matrix and $K:=\frac{1}{L}G{G}^T$ as the $N\times N$ kinship matrix, a natural estimator of genetic similarity. Equation 5, and most expressions in this paper, assume the total phenotypic variance is 1, so that ${\sigma }_g^2=h_g^2$ and ${\sigma }_e^2=1-h_g^2$.

The GREML model in Equation 5 is commonly fit by restricted maximum likelihood (REML), which projects out X from K and y and then fits variance components by maximum likelihood. However, moment-matching methods are increasingly common, especially LD score regression³⁹ for very large N or meta-analyses—where implementing REML becomes challenging—or HE regression⁴⁰ for small N—where REML is biased³⁵ and computationally unstable.²⁶

LMMs for Polygenic Interaction Effects (GxEMM)

We now assume a matrix of P environmental variables, $Z\in {\mathbb{R}}^{N\times P}$. As for X, we allow arbitrary binary and/or continuous variables in Z and assume $P\ll N$. The GxE mixed model (GxEMM) adds environment main effects, polygenic interactions, and environment-specific noise to GREML:

$$y_i=\underset{\begin{array}{c}\text{Fixed}\\ \text{Effects}\end{array}}{\sum _q{X}_{iq}{\alpha }_q}+\underset{\begin{array}{c}\text{Hom}.\\ \text{Genetics}\end{array}}{\sum _s{G}_{is}{\beta }_s}+\underset{\begin{array}{c}\text{Gene}-\text{x}-\text{E}\\ \text{Interaction}\end{array}}{\sum _{s,p}{G}_{is}{Z}_{ip}{\gamma }_{sp}}+\underset{\begin{array}{c}\text{Noise}-\text{x}-\text{E}\\ \text{Interaction}\end{array}}{\sum _p{Z}_{ip}{\delta }_{ip}}+\underset{\begin{array}{c}\text{Hom}.\\ \text{Noise}\end{array}}{{\mathrm{ϵ}}_i}$$ (Equation 6)

X should include the main effect of Z. We define ${\gamma }_{sp}$ as the interaction effect of SNP s and environment p, and ${\delta }_{ip}$ is the noise contributed by environment p to person i.

We assume β and ϵ are random, as in Equation 4, and also model γ and δ as random effects:

$${\gamma }_{s,}\stackrel{\text{iid}}{\sim }\mathcal{N}\left(0,\frac{1}{L}V\right);{\delta }_{i,}\stackrel{\text{iid}}{\sim }\mathcal{N}\left(0,\frac{1}{N}W\right)$$ (Equation 7)

The interactions are independent between SNPs, as in β. For β, this means entries are independent, and for γ it means rows are independent. However, V allows the interaction effects to correlate across environments. Intuitively, ${\sigma }_{hom}^2$ captures the homogeneous effects (β) and V_pp captures the environment p-specific effects $\left({\gamma }_{,p}\right)$. Off-diagonal terms, $V_{p{p}^{\prime }}$, account for genetic effects shared between environments p and $p^{\prime }$ in excess of the homogeneous sharing across all environments, ${\sigma }_{hom}^2$.

W is interpreted analogously, where W_pp indicates environment p-specific noise and $W_{p{p}^{\prime }}$ indicates covariance between the noise contributed by environments p and $p^{\prime }$. In discrete environments, $W_{p{p}^{\prime }}$ is not identified and the W_pp can be assumed zero mean WLOG (Appendix B).

The model in Equation 6 can be simplified using ^∗, the column-wise Khatri-Rao product:

$$y=X\alpha +G\beta +\left(G\ast Z\right)\gamma +\left(I_N\ast Z\right)\delta +\mathrm{ϵ}$$ (Equation 8)

Just as the random β and ϵ can be marginalized for additive LMMs, giving Equation 5 from Equation 4, the random β, γ, δ, and ϵ in the GxEMM model in Equation 8 can be marginalized:

$$y\sim \mathcal{N}\left(X\alpha ,{\sigma }_{hom}^{2}K+\left(ZV{Z}^T\right)\circ K+\left(ZW{Z}^T\right)\circ I_N+{\sigma }_e^2{I}_N\right)$$ (Equation 9)

The GxE variance component nicely decomposes into the Hadamard product $\left(\circ \right)$ of environmental similarity (ZVZ^T) and genetic similarity (K).

Equation 9 defines a complex likelihood. But commuting the matrix multiplications in ZVZ^T and ZWZ^T through the (linear) Hadamard product simplifies the expression:

$$y\sim \mathcal{N}\left(X\alpha ,{\sigma }_{hom}^{2}K+\sum _{p,q}{V}_{pq}\left[\left(Z_{,p}{Z}_{,q}^T\right)\circ K\right]+\sum _{p,q}{W}_{pq}\left[\left(Z_{,p}{Z}_{,q}^T\right)\circ I_N\right]+{\sigma }_e^2{I}_N\right)$$ (Equation 10)

This phenotypic covariance matrix is easily visualized for discrete environments (Figure 1, with v_p = V_pp and w_p = W_pp). Since K and Z are known, Equation 10 is a standard variance component estimation problem. We typically fit the model with REML using LDAK.³⁷ For small sample sizes we also use HE regression, which is computationally stabler and unbiased.

Interestingly, this marginalization from Equations 8, 9, and 10 holds if and only if γ has the covariance in Equation 7 (under large N or random G, Appendix D). This matters because it links the simple visual intuition (Figure 1) underlying the variance component model in Equation 10 to the concrete linear model in Equation 8; prima facie, distinct linear models could give equivalent variance component models. This bridge also enables GxEMM to naturally generalize to arbitrary environments, as they are seamlessly accommodated by the linear regression model in Equation 3. Conversely, the pictorial representation in Figure 1 does not easily adapt to general environments, nor do models that directly start from variance components rather than the underlying linear model.

We use Wald and LR tests for GxEMM, with asymptotic standard errors derived from the information matrix and the delta method. We allow negative variance component estimates to reduce bias—which is important for aggregating estimates across traits³⁸—and because non-negative total heritability does not imply either that ${\sigma }_{hom}^2\ge 0$ or that V is positive definite. We test individual HE model fits using permutations. In psychENCODE, we permute within-disease to mitigate violations due to non-exchangeability across individuals by preserving any noise heterogeneity across the disease groups.^41,42

In this paper, we do not fit GxEMM with a general V or W (which we call the Full model) because it has $O\left(P^2\right)$ parameters, which is computationally and statistically difficult for the range of N where basic REML methods are computationally feasible. Instead, we consider several restricted models for V (and W): Hom, where V = 0; IID, where $V=h_{het}^2{I}_P$; and Free, where $V=\text{diag}\left(v_1,\dots ,v_P\right)$. Both IID and Free ignore correlation between genetic effects across environments (beyond the homogeneous sharing captured in ${\sigma }_{hom}^2$), which will perform well when environments are approximately exchangeable rather than structured, e.g., city or hospital indicators, but not discretized height. IID further assumes that genetics explain equal variance in each environment.

Ni et al.²³ develop two models similar to Free GxEMM, RNM and MRNM. For computational and statistical reasons, they are implemented only for special cases. RNM only fits bivariate environments and assumes Hom noise (which is unreliable, Appendix A). MRNM fits only univariate environments, where the Free and IID models coincide (Appendix B). A distinct strength of MRNM is modeling gene-environment correlation. In our model, this can be phrased as learning correlations between the genetic main and interaction effects (${\rho }_p:=\text{Cov}\left({\gamma }_{ps},{\beta }_s\right)$ for each SNP s). In the future, we will investigate G-E correlation with GxEMM by adding terms like ${\rho }_{p}K\circ \left(1_N{Z}_p^T\right)$ to our model in Equation 10.

Nonetheless, G-E correlation simulations in Ni et al.²³ suggest the bias is not likely to be severe in practice for GxEMM. Specifically, GxE estimates were unbiased in simulations so long as Z was adjusted as a fixed effect—which is well known, and GxEMM always includes Z as a fixed effect. Ni et al.²³ do observe that adjusting for Z changes the homogeneous variance components estimates, but this is entirely expected—cf. the distinction between “Marginal” and “Conditional” variances in Weissbrod et al.²⁵ Overall, generally fitting Full GxEMM with G-E correlation would be useful in large datasets, but this remains computationally and statistically unrealized in unrelated samples. Randomized methods may address this gap in the future.^43,44

GxEMM for Binary Traits

We extend two binary trait heritability estimation methods from the GREML context to GxEMM. The first uses REML and treats the 0/1 disease label as a quantititative trait, and then rescales the REML estimates post hoc:

$${\hat{h}}^2:=\frac{K^2{\left(1-K\right)}^2}{P\left(1-P\right){\left[\phi \left(\text{Φ}\left(1-K\right)\right)\right]}^2}{\tilde{h}}^2$$ (Equation 11)

where ${\tilde{h}}^2\in \left\{{\tilde{h}}_g^2,{\tilde{h}}_{hom}^2,{\tilde{h}}_{het}^2,{\tilde{h}}_k^2\right\}$ is any of the REML-based GxEMM heritability estimates; K is the disease prevalence in the population and P is the sample prevalence; and φ and $\text{Φ}$ are the standard Gaussian density and distribution functions. This scaling approach is well established for the Hom model³¹ and works well when covariates and ascertainment are modest,³² but otherwise can fail badly.²⁴

The second approach to fit GREML for binary traits, PCGC, directly models the binary nature of the trait and estimates parameters with the method of moments. PCGC incorporates covariates and ascertainment (approximately), making it far more robust than the REML rescaling approach for the Hom model.²⁴ We directly fit PCGC-based GxEMM using its LDAK implementation. We estimate standard errors using resampling²⁵ and the delta method.

The LDAK implementation discards on-diagonal entries in the variance component moment estimating equation. Although this is efficient for standard genetic similarity matrices, which have near-constant diagonals, this ignores important information for Free noise. A subtler and more significant problem, though, is that this off-diagonal approach treats the homogeneous noise variance component asymmetrically, as it captures both ${\sigma }_e^2$ and the residual moment estimating error. This caused estimates of w based on including K − 1 noise heterogeneity matrices to behave strangely, with the implicit component (the K-th, say) being upward biased relative to the other K − 1 as it combines both w_K and the overall PCGC approximation error. To mitigate this issue and enforce symmetry across environments, we use all K environmental noise similarity matrices in PCGC, which has a unique method-of-moments solution, enforces symmetry, and provides identified estimates of w_K by formally defining ${\sigma }_e^2=0$. We note this issue is relevant only for discrete environments (Appendix B).

Simulation Details

We tested GxEMM with simulations using real genotypes from CONVERGE (see CONVERGE Data). For each simulation, we randomly choose S = 1,000 SNPs to have both additive and interaction effects. Because causal SNPs are chosen uniformly at random, we use the standard GRM (the Gram matrix of G after column centering and scaling) inside GxEMM in these simulations. We do not use the causal relatedness matrix because it is unknown in practice. We independently draw 200 datasets per parameter set, except for the N = 1,000 simulations where we draw 500 datasets. We note that REML failed for a small number of simulations.

We define Z by assigning each sample to one of two discrete environments uniformly at random. We define X to include Z and the CONVERGE fixed effects (see CONVERGE Data) and draw ${\alpha }_q$ i.i.d. Gaussian with mean zero and variance such that X explains 10% of the variation in the raw phenotype (note, however, that α is irrelevant after residualizing in X in HE and REML). We scale columns of X and G to mean zero, variance one so that the effect sizes are easily interpretable.

We vary ${\sigma }_{hom}^2$, v, and w depending on the simulation setting, with different choices corresponding to either the Hom, IID, or Free GxEMM models. We always set the homogeneous noise level so that the phenotype has (residual) variance 1:

$${\sigma }_e^2:=\mathbb{V}\left(\mathrm{ϵ}\right)=1-{\sigma }_{hom}^2-\sum _k\left(\frac{v_k}{N}{\Vert Z_{,k}\Vert }^2\right)-\sum _k\left(\frac{w_k}{N}{\Vert Z_{,k}\Vert }^2\right)$$

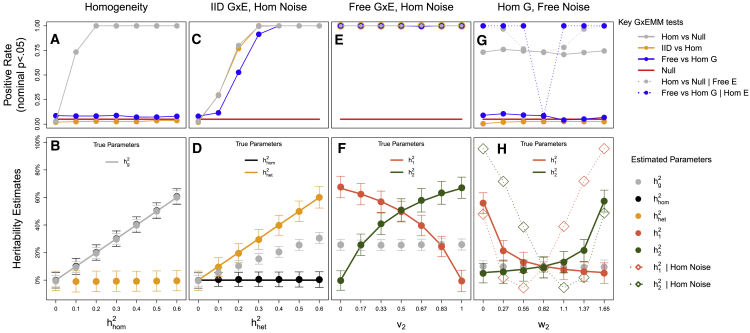
Given these parameter and data choices, we draw traits from the GxEMM model in Equation 6 (Figure 2).

Figure 2.

GxEMM Simulations

GxEMM simulations under (A and B) homogeneity, (C and D) IID heterogeneity, (E and F) Free genetic heterogeneity, or (G and H) Free noise heterogeneity. Results are shown for Hom, IID, and Free GxEMM and, in (G) and (H), the Free GxE model with Hom noise. In the top panels, the (true or false) positive rates are shown for Wald tests at nominal p < .05. In the bottom panels, mean GxEMM estimates are shown as points (±1 SD), with true generative parameters as background lines.

To simulate binary traits, we treat the generated quantitative trait, $y^{\left(0\right)}$, as a disease liability and then threshold to generate the disease label:

$$y_i=\{\begin{array}{ccc}1& \text{ if }& y^{\left(0\right)}\ge {\tau }_{80}\\ 0& \text{ if }& y^{\left(0\right)}<{\tau }_{80}\end{array}$$

where ${\tau }_{80}$ is the 80th percentile of $y^{\left(0\right)}$ so that y represents a disease with prevalence 20%.

We also perform a specific simulation study of large-effect covariates on binary traits (Figure 3, left). Rather than choose α randomly, we set all its entries to 0 except for the main effect of environment 1, i.e., the entry in α corresponding to $Z_{,1}$. This term, ${\mu }_1$, controls the relative prevalence of the binary trait between environments. We also assess a variant where the disease has low population prevalence but a 50/50 case/control cohort is ascertained by preferentially measuring diseased samples (Figure 3, right), setting ${\mu }_1=.4$. In these simulations, we simulate a population of size 500,000 and then ascertain 5,000 cases and controls; this strategy is computationally limited to modest population prevalences, e.g., $\approx 1\text{\%}$. We draw random SNPs i.i.d. with 50% frequency in these ascertainment simulations.

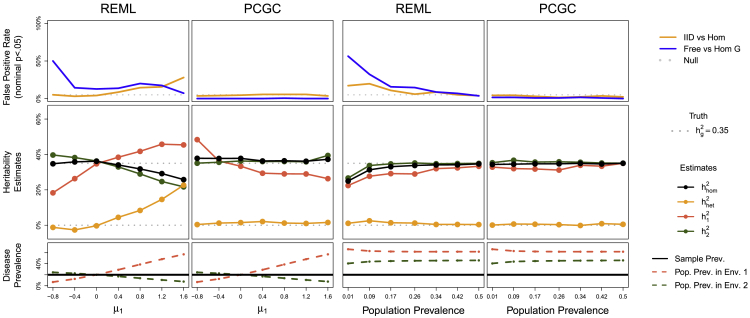
Figure 3.

REML and PCGC GxEMM in Binary Trait Simulations, with Liabilities Drawn from Hom GxEMM with $h_g^2=35\text{\%}$

Left plots vary the per-environment disease prevalences through the mean liability in environment 1, ${\mu }_1$, while fixing ${\mu }_2=0$. Right plots vary the population disease prevalence and then ascertain a 50/50 disease cohort. The top panels test for genetic heterogeneity between environments.

Finally, we performed simulations specifically designed to compare GxEMM to RNM (Figure S1). To mirror the simulations in Ni et al.,²³ we assume a continuous, centered, and scaled univariate environment and exclude other fixed effects. We then define the liability by drawing a 35% heritable trait with variance 1 and then adding the main environmental effect. We vary the main environment effect, ${\beta }_z$, to evaluate a range of realistic settings. We note that large environmental main effects are plausible in practice (e.g., Peterson et al.¹⁹), especially because candidate environments for GxE are generally proposed based on their direct trait relevance.

Rat Data

We studied 1,407 rats with genotype and partial phenotype information. We use the same 115 traits that we previously used,⁴⁵ which were deemed suitable for mixed model analysis in the original study.⁴⁶ We excluded one wound-healing trait where REML struggled to converge, and 24 traits with <1,000 observed samples.

The studied rats are an outbred mixture of eight inbred strains, a strategy designed to increase genetic association mapping power. The outbreeding strategy is not simple to describe, but it is designed to maintain the frequencies of the eight founder alleles at modest frequencies, avoid extreme inbreeding, and ensure mixing between founder strains.

We used the same kinship matrix, covariates, and trait transformations as in Baud et al.,⁴⁶ which we have summarized in Table S1. In particular, this involves adjusting for trait-relevant covariates—always including sex—and using trait-specific transformations.

To be conservative, we do not impute the phenotypes, though genetics-unaware imputation seems unlikely to substantially bias GxEMM.

CONVERGE Data

We studied 9,303 samples with genotype and covariate information and pairwise kinship <.05, following Peterson et al.¹⁹ We studied 14 binary stressors and 10 quantitative measurements as environmental covariates (Table S2). Two stress questionnaire items were very rare and excluded.

For each choice of environment variable (E), we used an intercept, age, ten genetic PCs (from an LDAK relatedness matrix³⁷), and E as fixed effects. We also always include the interactions between these terms and E, which can be important for reducing bias in GxE testing in large samples.⁴⁷

When fitting mixed models, we use the GCTA-based genetic relatedness matrix (GRM) in simulations and the LDAK-based GRM in real data. We previously found the difference between the LDAK and ordinary GRMs to be qualitatively minimal.¹⁹

To analyze a single quantitative covariate z, we linearly scaled it to have minimum 0 and maximum 1, and then defined $Z=\left(z|1-z\right)\in {\mathbb{R}}^{N\times 2}$. This is analogous to the discrete environment Z matrix: they exactly coincide when z covariate takes only two values, and in general z can be interpreted as proportional membership between two stylistic groups, the min and max values of z. In turn, v₁ (w₁) describes genetic (non-genetic) variance specific to low z, v₂ (w₂) describes the genetic (non-genetic) variance specific to high z, and ${\sigma }_{hom}^2$ describes heritability that is independent of z. This construction of z also allows naturally extending our definition of discrete environment-specific heritabilities (Equation 2) to quantitative environments: $h_1^2$ $\left(h_2^2\right)$ is the heritability for samples with the minimum (maximum) observed environmental value. We feel this coding of the environmental effect makes the interaction random effects more interpretable, but we emphasize that the simpler model which evaluates only z (instead of Z) is perfectly valid when its assumptions are met.

For higher-dimensional environments, the per-environment Z matrices could be concatenated by $Z=\left(z_1\left|1-z_1\right|\cdots \left|z_P\right|1-z_P\right)$. The environment-specific heritabilities from Equation 2 are not easily extensible to this setting, however.

psychENCODE Data

We analyzed the processed genotype and prefrontal cortex gene expression data from Gandal et al.⁴⁸ and Wang et al.⁴⁹ These data have already been adjusted for nonlinearity in raw expression measurements and large, non-genetic covariate effects, including biological factors like age, technical factors like RIN, and latent confounders as estimated by expression Surrogate Variables.⁵⁰ We restricted only to measurements from the pre-frontal cortex, as cerebullum and temporal cortex had much lower sample sizes.

We restricted only to autosomal SNPs and genes, and we only used SNPs with MAF > 5%, missingness < 10%, and Hardy-Weinberg p > .001. We then filtered our samples such that no pair had genome-wide relatedness above 0.05.²² After these filters, we obtained a sample size of N = 931 with both genotype and gene expression data.

For each autosomal gene, we extracted cis SNPs, which we define here as SNPs within 1 Mb of the gene transcription start or end site. This yielded 24,905 total genes. The median number of cis-SNPs per gene was 2,189. We then constructed cis kinship matrices for each gene by centering and scaling each SNP.

For each gene, we performed Hom, IID, and Free GxEMM with HE, due to the modest sample size. For comparison, we also fit two REML tools: REML-based GxEMM, and the Hom and IID models as implemented in GCTA.²⁷ As expected, GCTA and GxEMM with REML obtained essentially identical estimates for both Hom and IID (Figure S2). And, as expected, the HE estimates were also highly correlated $\left(\rho >.64\right)$ but noisier. We note that GCTA had substantially higher average $h_g^2$ than REML-based GxEMM (5.8% versus 4.2%), but this was driven almost entirely by GCTA’s lower rate of convergence: when restricting to genes where both methods converge, the methods gave similar results (5.8% versus 5.7%). This is redolent of the bias induced by restricting to genes with positive heritability estimates.³⁸

We assess significance in HE by using 10,000 permutations of samples within-disease class (Table S3). Even under noise heterogeneity, this approach is an exact permutation test when genetics are completely null because samples remain exchangeable within-disease class. More generally, our permutations are in line with approximate permutation tests used widely (e.g., for FEATHER⁴² or HE regression²⁶).

Results

Quantitative Trait Simulations

We simulate data from increasingly complex polygenic interaction models to assess GxEMM and to compare the Hom, IID, and Free models. We first simulate from the purely additive Hom model, equivalent to GREML, by varying $h_{hom}^2$ and fixing the heterogeneity terms to 0, i.e., v_k = w_k = 0. As expected, all GxEMM models performed well, as illustrated by the roughly unbiased Hom estimates of $h_g^2$ (Figures 2A and 2B, gray points). IID and Free also gave unbiased estimates for the total heritability, and their heterogeneity tests were appropriately null (Figure 2A, orange and blue lines).

Second, we draw from the IID model by varying the single heterogeneity parameter $h_{het}^2$ and fixing $h_{hom}^2=0$. As expected, fitting the IID model provides roughly unbiased estimates of both $h_{het}^2$ and $h_{hom}^2$ (Figures 2C and 2D), as does Free GxEMM. However, the Hom model underestimates total heritability (gray points, Figure 2D) and also gives the false impression that genetic factors are shared between environments.

Third, we simulate from the Free model by specifying different levels of genetic variance in each environment, varying $v_1\in \left[\mathrm{0,1}\right]$ and then setting v₂ = 1 − v₁; we keep ${\sigma }_{hom}^2$ = 0 and Hom noise $\left(w_1=w_2={\sigma }_e^2\right)$. For all v₁, Free GxEMM accurately estimates environment-specific heritabilities (dark orange and green lines in Figures 2E and 2F), but Hom GxEMM underestimates total heritability.

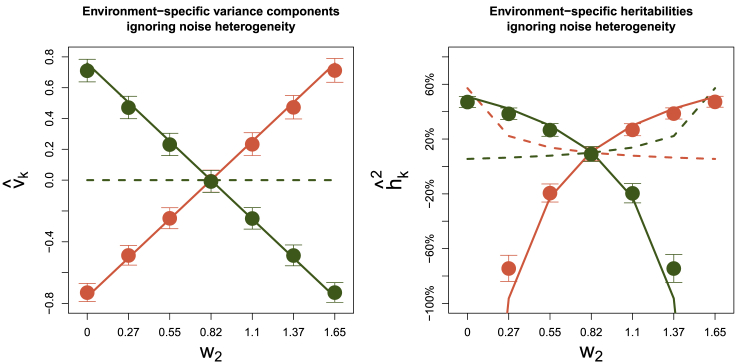
Our fourth setting again draws from the Free model, except now genetics are homogeneous(${\sigma }_{hom}^2=.1$, and v₁ = v₂ = 0) and we instead vary the distribution of noise per environment, taking $w_1\in \left[\mathrm{0,1.65}\right]$ and setting w₂ = 1.65 − w₁. Free GxEMM again performs well], correctly avoiding GxE false positives (Figure 2G, solid blue) and providing unbiased estimates (Figure 2H). Also, note that allowing Free noise increases Hom power (dotted gray, Figure 2G), showing that GxEMM can be useful even in the absence of GxE.

In this specific simulation, we also evaluate a variant of the Free model allowing Free GxE but assuming Hom noise. Related models have been used before.^23,51 However, this approach is susceptible to dramatic, replicating false positives under noise heterogeneity (Figure 2G, dotted blue lines) as well as severe bias: for example, consistently estimating a 10% heritable trait to have 100% heritability (dashed dark orange and green lines with diamonds, Figure 2H). We provide a theoretical characterization of this bias in Appendix A. Such GxE models that do not allow noise heterogeneity should almost never be used in practice.

We used Wald tests in these simulations, but results were similar when using LRT (Figure S3). Also, although we used two discrete environments here for simplicity, simulations with bivariate quantitative environments gave similar results (Figure S4). Finally, we also found that the GxEMM standard error estimates were accurate or slightly conservative (Figure S5).

We report the runtimes for the three GxEMM models on this simulated dataset, other simulated datasets, and the three real datasets in Table S4. Broadly, GxEMM runs in tens of minutes for thousands of samples, with higher costs for richer models and larger sample sizes.

Binary Trait Simulations

We next examine binary traits by simulating a 20% prevalence disease with $h_{hom}^2=.35\text{\%}$ and a discrete, binary environment with a 25%/75% split (Material and Methods), roughly based on the CONVERGE data (below). We focus on simulations from the Hom model to assess which approaches yield calibrated genetic heterogeneity tests. We compare fitting GxEMM either with REML, using the standard liability scale adjustment, or with PCGC, which directly models the binary nature of the trait.

We first assessed the impact of differential prevalence between environments by varying ${\mu }_1$, the mean liability in environment 1 (Figure 3, left). For ${\mu }_1\approx 0$, both estimators (PCGC and REML) and all GxEMM models (Hom, IID, and Free) perform well. PCGC continued to perform well for all tested ${\mu }_1$, giving calibrated heterogeneity tests and unbiased heritability estimates for the larger group, ${\hat{h}}_2^2$; however, the heritability in the smaller group, ${\hat{h}}_1^2$, was conservative (or very noisy at ${\mu }_1=-.8$, as basically no cases are observed in environment 1).

On the other hand, REML breaks down in several ways for $\left|{\mu }_1\right|>0$. First, the $h_g^2$ estimate is downward biased, as expected.²⁴ Second, $h_{het}^2$ becomes upward biased, and the IID heterogeneity test becomes inflated. Third, Free GxEMM gives severely biased environment-specific heritability estimates, and often badly inflated heterogeneity tests.

To assess power, we repeated these simulations under Free genetic heterogeneity and found that IID GxEMM had power to detect genetic heterogeneity for both REML and PCGC (Figure S6, left). However, Free GxEMM had low power, reflecting the loss of information from the liability thresholding process. Second, under Hom genetics and Free noise, PCGC was unbiased or slightly conservative while REML was again upwardly biased (Figure S6, right). Third, we performed binary trait simulations mirroring the quantitative trait simulations in LMMs for Polygenic Effects (GREML) to broadly test PCGC-based GxEMM (Figure S7). PCGC performed similar to REML for quantitative traits, except power is lower, as expected, and PCGC performed poorly under extreme variance heterogeneity, likely because the underlying first-order approximation breaks down in extreme settings.

Disease studies often preferentially ascertain disease cases to increase power. As ascertainment causes bias in GREML,²⁴ we assessed its impact on GxEMM through simulations. We fixed ${\mu }_1=.4$ (similar to CONVERGE) and ascertained 50/50 case/control cohorts (Material and Methods). Although GxEMM with REML breaks down under ascertainment—in particular, Free/IID GxEMM tests have roughly 50%/25% false positive rate for 1% prevalence—PCGC remains calibrated (Figure 3, right).

Finally, we evaluated the RNM model, a recent REML-based polygenic GxE model implemented in the MTG2 software package.⁵² To streamline comparison, we performed simplified versions of the above non-ascertained simulations with a continuous, univariate environment and no additional covariates. Consistent with our above results (Figure 3, left), we found that PCGC broadly performed well, as did REML-based GxEMM and RNM when the environment had no main effect (Figure S1). However, both RNM- and REML-based GxEMM become biased as the environment main effect grows. In particular, RNM obtains roughly 90% false positive rates when the environment explains roughly 50% of the liability-scale phenotypic variation.

In summary, repurposing standard tools for inferring polygenic GxE for quantitative traits is not viable. On the other hand, PCGC-based inference provides calibrated heterogeneity tests and approximately unbiased GxEMM parameter estimates. We caution, though, that PCGC estimator variances are large and, in particular, the Free model adds negligible value beyond the IID model for binary traits at these sample sizes.

Phenome-wide Sex-Specific Genetics in Outbred Rats

Our first application is to sex-specific genetic effects across 115 phenotypes in 1,407 outbred rats from the Rat Genome Sequencing and Mapping Consortium⁴⁶ (Material and Methods). These samples have high genetic relatedness, which aids mixed model power. Although many traits are known to be sexually dimorphic, it is not generally well known to what extent, and for which traits, sex differences are driven by autosomal genetic variation.

First, we fit Hom GxEMM and found 105/115 traits were heritable at p = .05/115, with average ${\hat{h}}_g^2=67.3\text{\%}$ (gray violin, Figure 4A). We next fit IID GxEMM, testing for GxSex interaction and found that the number of heritable traits increased to 112/115 (rust violin). The average IID heritability was 73.8%, which is 9.7% larger than the GREML heritability. The sex-specific component of the IID model explained 30.3% of trait variance on average and was Bonferroni significant for 12 traits (gold violin), including measurements of bone density, hemoglobin, platelets, serum composition, and glucose trial response (Figure S8, Table S1).

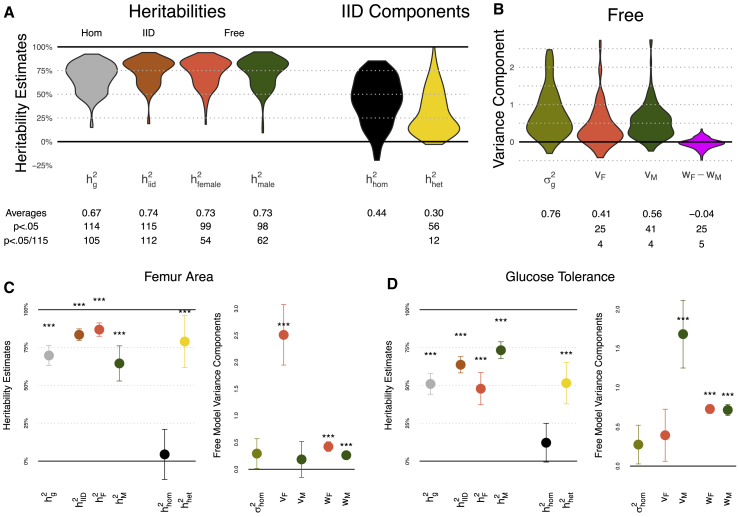
Figure 4.

GxEMM Estimates Aggregated across p = 115 Traits in Outbred Rats for the Hom, IID, and Free Models

p values marginally test whether variance components are 0.

(A, left) Heritability estimates from each model, with labels for which violins correspond to which GxEMM model.

(A, right) Homogeneous and heterogeneous heritability components in the IID model.

(B) Genetic variance component estimates for the Free model, as well as noise heterogeneity estimates ($w_F-w_M$). Middle table: for each component of the violin plots, we provide the average across traits as well as the number of traits where the component is significantly different from zero.

(C and D) Heritability and variance component estimates from GxEMM for two specific traits, bone density and glucose tolerance. Error bars represent 1 SE; *p < .05, **p < .01, and **p < .001.

On average across all traits, the Free heritability estimates were similar, for both sexes, to the IID model ($h_F^2$ orange violin and $h_M^2$ green violin, Figure 4A). Nonetheless, the Free model uncovered many traits with sex-specific genetic variance, including eight that were Bonferroni significant (orange v_F and green v_M violins, Figure 4B). All eight had significant $h_{het}^2$ in the IID analysis, but the Free analysis more precisely characterizes the genetic heterogeneity. For example, 3/8 of these traits have significantly different genetic effect sizes between sexes (Wald p < .05/115; 7/8 have p < .05): female-specific genetic effects drove two bone measurements, white blood cell count, and serum chloride; male-specific genetic effects drove two platelet traits, glucose response, and serum potassium (Figure S8). The Free model also found sex-specific noise levels for 5/115 traits (p < .05/115, pink violin), including three of the genetically heterogeneous traits and an additional bone density trait.

To further explore the data and illustrate the GxEMM model, we plot results for two of the traits with sex-specific heritability. The first is a femur size measurement (distal femur cortical area, Figure 4C). In Hom GxEMM, this trait has high heritability, roughly 75%. Nonetheless, heritability is increased to roughly 85% by the IID model and, moreover, the homogeneous component of IID GxEMM $\left(h_{hom}^2\right)$ is near zero. Finally, the Free model goes further by revealing that the sex-specific genetic effects are primarily active in females. This analysis shows that GxEMM can uncover dramatically non-additive genetic architecture even when ordinary GREML explains substantial heritability.

An approximate mirror image is obtained for a glucose tolerance trait (area under glycemia curve over baseline during intraperitoneal glucose tolerance test, Figure 4D): $h_g^2\approx 50\text{\%}$ is large, yet homogeneous heritability largely vanishes after accounting for sex-specific heritability in IID GxEMM, which is in turn revealed by the Full model to be driven largely by male-specific genetic effects. This result is consistent with a previously reported sex-APOE interaction effect for glucose.⁵³ This rich characterization of sex-specific architecture has clear implications for genetic association studies: power can be maximized by studying the sex with greater heritability, and associations can be interpreted in light of known average difference between sexes.

Polygenic Stress Interaction in Major Depression

We next apply GxEMM to major depression (MD), a moderately heritable disease that is likely genetically and environmentally heterogeneous.⁵⁴ We analyzed the CONVERGE cohort, which recruited about 10,000 Han Chinese women between 30 and 60 years old. Women were chosen because they have higher MD heritability than men (i.e., 42% versus 29%⁵⁵), and clinically ascertained MD-affected case subjects were selected for the same reason.⁵⁶ This strategy successfully led to replicated GWAS hits for MD⁵⁴ and later yielded three SNP effects specific to people without major lifetime stress.¹⁹ Here, we extend these SNP heterogeneity analyses to the polygenic level with GxEMM using our robust approach for binary traits based on PCGC.

We first fit Hom GxEMM with PCGC to MD and found ${\hat{h}}_g^2=38.5\text{\%}$ (SE 4.5%) assuming an 8.8% population prevalence (Figure 5).¹⁹ Importantly, we adjusted for interactions between genetic PCs and the environment, which can be essential for avoiding bias and false positives.⁴⁷

Figure 5.

GxEMM Stress-Specific Heritability Estimates for Major Depression

p values marginally test whether variance components are 0.

Estimates are shown aggregated over 14 different choices for the binary stress measurement that is used as the environment in GxEMM. All stress measures are correlated and have less than 50% prevalence in the dataset.

(A, left) Heritabilities from the Hom, IID, and Free models.

(A, right) IID heritability components.

(B) Free variance components.

We then fit 14 IID GxEMM models with each of 14 different binary stress measures (CONVERGE Data). IID modestly increased heritability on average (${\bar{h}}_{IID}^2=41.2\text{\%}$, Table S2), broadly supporting polygenic stress interactions. One stress measure (divorced/separated/widowed status) was Bonferroni significant (p = 0.0020 < .05/14). This measure had relatively high prevalence and MD effect severity, which both increase interaction test power; more severe measures (e.g., “Child Abuse”) were less frequent, and more frequent measures (e.g., “Natural Disaster”) were less severe. Altogether, the IID model supports polygenic stress interaction for MD, but large standard errors and high correlations between measures prevent conclusions about which specific major life stresses drive the interactions.

The Free model performed reasonably for the non-stress groups, finding slightly higher heritability relative to IID (41.2% versus 43.4%) but not finding any nonstress-specific genetic variance at Bonferroni significance. More importantly, however, the Free model performed badly in the smaller stress groups, consistent with simulations (Figure S6, left). Similarly, differential noise estimates had large standard errors and none were significantly different from 0.

Although we primarily focus on stress interactions due to prior knowledge that they are relevant to MD, we also investigated polygenic interaction across each of ten quantitative environmental measures (Material and Methods). IID results were qualitatively similar to the results from the binary stress measures, with average heritability increasing to ${\bar{h}}_{IID}^2=42.9\text{\%}$ (Figure S9) and one measure, “Cold Mother,” that was nearly Bonferroni significant for polygenic interaction (p = 0.0079 > .05/10; “Cold Father” point estimates were similar and had p = .0198). As for the binary stress measures, the Free model was not informative. Overall, IID GxEMM had power in this dataset and provided evidence for genetic heterogeneity, but larger sample sizes seem necessary for Free GxEMM to be useful.

Brain Expression Heterogeneity in Psychiatric Disease

Finally, we apply GxEMM to brain gene expression data from psychENCODE^48,49 to test for differential genetic and non-genetic factors governing transcriptional regulation in psychiatric disease relative to control subjects. In this analysis, disease state plays the role of the “environment” in GxEMM. After quality control (Material and Methods), the data include 931 samples, including 356 schizophrenia-affected case subjects (SCZ), 158 bipolar disorder (BPD)-affected case subjects, and 417 control subjects (CTRL), each measured on 24,905 genes. In this analysis, we focus on fitting GxEMM with HE regression because REML is computationally and statistically unstable at smaller sample sizes, especially for richer models.²⁶ (We note, though, that REML gave broadly consistent results when it converged [Figure S2].) For each gene, we estimate local cis-heritability by using relatedness matrices built specifically from SNPs within 1 Mb of the gene’s transcription start site.

We first fit Hom GxEMM and found $h_g^2=4.06\text{\%}$ (SE 0.07%) on average across the genome (Table 2). This is in line with previous transcriptome-wide heritability estimates from whole blood.^26,57 Here and below, we test transcriptome-wide averages with a Wald test, where standard errors are calculated assuming each gene is independent, which is an established approximation (e.g., Hernandez et al.²⁶).

Table 2.

Transcriptome-wide Average GxEMM Heritability Estimates under the Hom ($h_g^2$), IID ($h_{IID}^2$), and Free Models ($h_{BPD}^2$, $h_{SCZ}^2$, $h_{CTRL}^2$)

	$h_g^2$	$h_{IID}^2$	$h_{BPD}^2$	$h_{SCZ}^2$	$h_{CTRL}^2$
Mean (%)	4.06	4.12	4.32	4.34	3.82
SE (%)	0.07	0.07	0.08	0.08	0.07
Wald p for $h^2>0$	<2 × 10−16	<2 × 10−16	<2 × 10−16	<2 × 10−16	<2 × 10−16
Wald p for $h^2>h_g^2$	–	1.15 × 10−11	1.93 × 10−9	<2 × 10−16	1.00
Wald p for $h^2>h_{IID}^2$	–	–	3.83 × 10−6	<2 × 10−16	1.00

Because N is modest, we fit GxEMM with HE regression. We compare the models using Wald tests, estimating the standard errors of the transcriptome-wide averages assuming independence across genes. Dash (–) indicates that the comparison is not meaningful.

To investigate transcriptome-wide patterns of disease-dependent genetic architecture, we next fit the IID model. We estimated transcriptome-wide average heritability of $h_{IID}^2=4.12\text{\%}$, which slightly (1.5%) but statistically significantly (p < 2 × 10⁻¹⁶, paired t test) increased heritability over the homogeneous GREML model. We then fit the richer Free model, which estimated disease-specific heritabilities of 4.32% (SE 0.08%), 4.34% (SE 0.08%), and 3.82% (SE of 0.07%) for BPD, SCZ, and CTRL, respectively. For BPD and SCZ, the increase over $h_g^2$ is $\approx 7\text{\%}$ and significant (both p < 2 × 10⁻¹⁶); the increases over $h_{IID}^2$ are also statistically significant (p = 3.83 × 10⁻⁶ and p < 2 × 10⁻¹⁶). Conversely, $h_{CTRL}^2$ is lower than $h_g^2$, suggesting that GREML actually overestimates the heritability that is common across all disease states, consistent with simulations (Figures 2D and 2F). Overall, GxEMM shows statistically significant interaction between psychiatric disease state and genetic control of gene expression in the prefrontal cortex, and the Free model further suggests an increased role of genetics specifically active in the disease states.

To confirm that our results were not primarily driven by confounding from population structure, we performed the same analysis after restricting our dataset to samples from the “European” population, which was the most numerous population in our psychENCODE data (N = 872). We found that transcriptome-wide average estimates were essentially unchanged (Table S5).

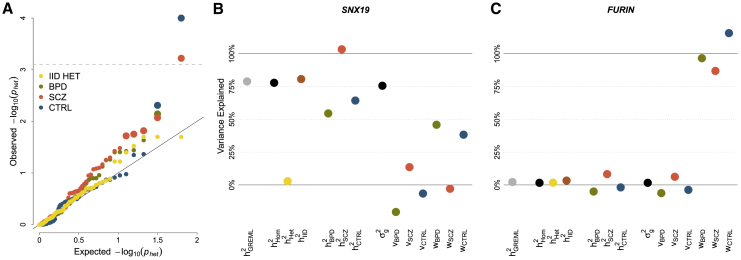
We next tested for genetic heterogeneity at individual genes, which is less powerful but more precise than transcriptome-wide average tests. Based on simulations, we have low power for genetic heterogeneity tests across all genes at this sample size (Figure S10). Instead, we test 63 genes with known significant gene-based genetic associations for SCZ.⁵⁸ We test for significance using within-disease group permutations (Material and Methods).

IID GxEMM does not find any gene with significant polygenic-disease interaction at 25% FDR (Benjamini-Hochberg, Figure 6A, Table S3). However, Free GxEMM detects 9 associations across the three subgroup-specific genetic variances (3 are Bonferroni significant). These results are consistent with our transcriptome-wide average tests, where we found that the Free model had considerably higher power than IID.

Figure 6.

Psychiatric Disease-Specific Heritability in Prefrontal Cortex Gene Expression

(A) IID and Free genetic heterogeneity tests based on permutations across 63 known SCZ-associated genes. Large points have FDR < 25%, and the horizontal line is Bonferroni-adjusted p < .05. The maximum BPD and CTRL points overlap at p = 1/(1+10,000), the minimum possible value after 10,000 permutations.

(B and C) GxEMM results for 2/9 candidate SCZ genes with significant genetic heterogeneity, SNX19 (B) and FURIN (C).

Figures 6B and 6C show the GxEMM estimates for two of these nine genes. First, SNX19 is an SCZ-associated protein coding gene that also has known experimentally validated functional eQTL that overlap SCZ risk loci.59, 60, 61, 62, 63 This gene has high cis-heritability in the Hom model (roughly 75%). Next, the well-established IID model fails to find even suggestive genetic heterogeneity. However, the rich Free model finds substantial heterogeneity that is largely driven by SCZ-specific genetics. This is consistent with simulation results showing low power for the IID GxE test when most of the specific heritability is concentrated in one group.

The second significant gene we illustrate, FURIN, is a protease that has been robustly associated with neurodevelopment in zebrafish and human neural progenitor cell development in vitro.⁶⁴ FURIN also has a strong cis-eQTL that colocalizes with GWAS-significant SCZ SNPs,⁶⁵ and this eQTL was experimentally shown to modify FURIN expression and, in turn, brain-derived neurotrophic factor.⁶⁶ In psychENCODE, we found that FURIN has essentially zero homogeneous or IID heritability, in contrast with SNX19. On the other hand, the Free model is able to reveal significant heritability specifically in SCZ. These stories both support the links between genotype, expression, and disease and demonstrate how GxEMM can be used to uncover genetic variants with disease-specific functional genomic effects. We also found Bonferroni-significant genetic heterogeneity for CHRNA2, a previously identified “high confidence” gene supported by association with SCZ and Hi-C interaction with nearby eQTL.⁴⁹

Finally, we tested for differential expression variance between disease groups transcriptome-wide. We find evidence for pervasive differences in expression variance across disease states: for example, 2,459 genes (roughly 10%) have Levene p < .001. This heterogeneity was driven primarily by higher expression variance in SCZ: of these 2,459 genes, 97.1% had higher variance in SCZ than CTRL. We also note that 92.2% of genes had higher variance in SCZ than BPD, but this is at least partially because SCZ has higher sample size (and thus power). Adding confidence in the Levene tests, we permuted disease labels and found no evidence of test inflation (e.g., 10% of genes have Levene p <.099 after permuting), suggesting disease state truly correlates with expression variance. Although this test does not establish genetic heterogeneity, it does show that Free GxEMM is likely more powerful than IID: in simulations, variance heterogeneity increased Free power over IID regardless whether it was genetic (Figure 2E) or non-genetic (Figure 2G).

Discussion

Gene-environment interactions (GxE) and polygenicity are separately well documented. We help bring these concepts together with a linear mixed model for polygenic GxE that we call GxEMM. GxEMM consists of three key models: Hom, IID, and Free. Each pairwise comparison adds biological interpretation: comparing Hom to IID can demonstrate the existence of GxE, and comparing IID to Free can demonstrate and appropriately adapt to heteroscedasticity across environments. Finally, comparing Hom and Free models can add power for detecting GxE over the IID model; for example, the Free model, but not the IID model, had power to show GxE for SNX19 and FURIN in psychENCODE. Generally, GxEMM can be used for any covariate putatively interacting with the genome, including genetic variants,⁶⁷ study indicators for meta-analysis^68,69 or genotype quality control,⁷⁰ or phenotypic subtypes.⁷¹

We have introduced several methods to fit GxEMM, based on REML, HE, and PCGC; all are implemented as an R wrapper of the LDAK software package. In practice, only one method is recommended for a given dataset: HE for small sample sizes, PCGC for binary traits, and REML for large sample sizes and continuous traits. These same concepts apply to standard homogeneous heritability estimates.

GxEMM unifies, formalizes, and solves several important biases in recent approaches to estimate GxE-based heritability. In particular, only GxEMM can accommodate general environments, noise heterogeneity, modest sample size, and binary traits, which we support with theory and simulation.

There are several methodological limitations to GxEMM. First, like most LMM methods, GxEMM is computationally intensive, as it fits several variance components to individual-level data. In special cases, the problem can be rewritten to roughly reduce the computational complexity from $O\left(N^3\right)$ to $O\left(N\right)$.^21,28 In the future, we will investigate larger sample sizes using randomized method of moments to fit GxEMM^43,44 (Material and Methods).

A second limitation is our assumption of Gaussian random effects—although the central limit theorem does support this for polygenic effects. But non-normality is not obviously more salient for GxEMM than for ordinary GREML, and we used quantile normalization in psychENCODE and trait-specific transformations for the rat traits to mitigate the impact of outliers.^26,42,72 We note that these normalizations, too, have downsides, and in particular reduce power for Levene tests for variance heterogeneity.

A third limitation to GxEMM is that we do not test or correct for gene-environment (G-E) correlation. This is a well-known source of bias in the fixed effect case.³⁰ Surprisingly, however, Ni et al.²³ did not observe inflation for polygenic interaction tests in simulations. In fact, we prove that this is due to a fundamental difference between the polygenic and single-SNP case (Proposition 3): absent systemic coordination between the main genetic effects on the environment and trait, the per-SNP biases average out over the genome. While such coordination would be intrinsically interesting, it has not been documented in real data and is not likely to be large in practice, and thus polygenic G-E is likely not to cause false positives for polygenic GxE tests. Nonetheless, we describe how to incorporate G-E interaction within the GxEMM model framework in the Material and Methods, for completeness.

Fourth, we did not fit Full GxEMM, which can learn structured genetic correlations across environments. Such models are flexible but complex, with many degrees of freedom and non-trivial identification concerns. However, at biobank-scale sample sizes, there will likely be sufficient power to fit the Full model.

A fifth limitation is that GxEMM does not currently allow random effects beyond the core Hom and GxE variance components. However, in the context of family studies (e.g., Diego et al.⁷³) or high-dimensional covariates (e.g., Moore et al.²¹), it can be valuable to model background confounding variables as random effects in GxE tests. In future work, GxEMM could in principle be easily extended to accommodate such additional variance components, e.g., Zaitlen et al.⁷⁴ jointly fit pedigree- and additive-relatedness matrices in the homogeneous setting. Nonetheless, in practice, we use and recommend standard filters on kinship and population structure corrections when analyzing natural populations, as is standard in GREML analyses.²² In the case of the rat experimental data, we did not perform these steps because confounding by cryptic relatedness is very unlikely;^45,46 however, additional random effects may still be helpful, e.g., for cage effects.

The results from our rat analysis shows widespread sex-specific heritability. The Free model, specifically, has strong statistical support for several traits even at stringent thresholds. This power derived from the high levels of genetic relatedness in these model organisms. Likewise, GxEMM will be powerful in other model organism and family studies, which can help build broad intuition about causal genetic architecture that can inform human disease studies. This is particularly true for autosome-sex interactions, which may be important for many complex human diseases.⁷⁵

There are several limitations to our analysis of the psychENCODE data. First, our LDAK-based REML approach often failed to converge, so we used HE regression, which is robust but less powerful than REML. Second, cell type proportions are known to vary between people and disease states, causing bulk differential expression across disease groups for any gene that is simply differentially expressed across cell types. In future work, we will extend GxEMM to partition expression heritability into cell type proportion effects and within-cell type effects.

GxEMM may also be useful for GWAS applications. An IID-based approach has been shown to improve power and calibration over the standard Hom model in some cases,⁴⁷ suggesting that Free GxEMM will likely yield further improvements when the IID assumption fails.

Declaration of Interests

The authors declare no competing interests.

Published: January 2, 2020

Appendix A: Unmodelled Heteroscedasticity Causes Bias in Polygenic Interaction Estimates

In this appendix we quantify the bias under the Free GxEMM model when environmental heterogeneity is ignored. We assume discrete environments and that the modeler fits the similarity matrices $\left\{K_k,I\right\}$, where K_k is the kinship matrix K with entries outside of environment k zeroed out. We assume that $\text{tr}\left(K_k\right)=n_k$ for all k. We also assume that the true variance of y is:

$$\mathbb{V}\left(y\right)=\sum _k{w}_k{E}_k+{\sigma }^{2}I$$ (Equation A1)

where E_k is the identity matrix with entries outside environment k zeroed out—i.e., we assume there is no genetic variance but that the noise variance may differ across environments when $w_k\ne w_j$ for some j and k. For simplicity, we also ignore the homogeneous genetic component and covariates. For identifiability, we assume $\sum _k{n}_k{w}_k=0$; under this constraint, ${\sigma }^2$ is the average phenotypic variance across all samples. Finally, we assume approximate independence between genetics and environment. It is worth noting how simple this model is—pure heteroscedastic noise.

We analytically study the behavior of the HE regression, which is more tractable than the MLE.

Proposition 1. Assume for all k that $n_k\approx n_0\gg 1$ and that $a\approx \mathbb{V}\left(diag\left(K_k\right)\right)$ and $b\approx \mathbb{V}\left(off-diag\left(K_k\right)\right)$ for all k. Under the pure heteroscedastic noise model (Equation A1), the bias in the Free genetic heterogeneity estimate with Hom noise is:

$$\mathbb{E}\left({\hat{v}}_k\right)\approx \frac{1}{1+a+n_{0}b}{w}_k$$ (Equation A2)

Proof. The moment estimating problem is:

$$\underset{v,{\sigma }^2}{\text{min}}{\Vert y{y}^T-\sum _k{v}_k{K}_k-{\sigma }^{2}I\Vert }_F$$

Note that modeling the diagonal terms, rather than regressing only on the strict lower triangular entries, is important when variance may be heterogeneous across samples.

The OLS solution for the parameters v and ${\sigma }^2$ is given by:

$$\left(\begin{array}{cc}{D}^{-1}& n\\ n^T& N\end{array}\right)\left(\begin{array}{c}\hat{v}\\ {\hat{\sigma }}^2\end{array}\right)=\left(\begin{array}{c}S\\ y^{T}y\end{array}\right)$$

where n is the vector of environment-specific sample sizes, $S_k:=y^T{K}_{k}y$, and D is diagonal (because $⟨K_k,K_j⟩=0$ for $k\ne j$) with $D_{kk}:=d_k:=\left(1/\text{tr}\left(K_k^2\right)\right)$. In expectation:

$$\mathbb{E}\left(y^{T}y\right)=\text{tr}\left(\mathbb{V}\left(y\right)\right)=\sum _k{n}_k{w}_k+{\sigma }^{2}N={\sigma }^{2}N$$

The last equality derives from our identification assumption on $\left(w,{\sigma }^2\right)$. Likewise, the expected values of the quadratic forms in S are:

$$\begin{array}{c}\mathbb{E}\left(S_k\right)=\text{tr}\left(K_k\mathbb{V}\left(y\right)\right)=\text{tr}\left(K_k\left(\sum _k{n}_k{w}_k{I}_k+{\sigma }^{2}I\right)\right)=\sum _j{w}_j\text{tr}\left(K_k{I}_j\right)+{\sigma }^2\text{tr}\left(K_k\right)\\ =w_k\text{tr}\left(K_k\right)+{\sigma }^2\text{tr}\left(K_k\right)=n_k\left(w_k+{\sigma }^2\right)\end{array}$$

Let $s:=\frac{1}{N-n^{T}Dn}=\frac{1}{N-{\sum }_j{n}_j^2{d}_j}$. The expected variance component estimates are (using block inversion in the second equality):

$$\begin{array}{c}\mathbb{E}\left(\left(\begin{array}{c}\hat{v}\\ {\hat{\sigma }}^2\end{array}\right)\right)={\left(\begin{array}{cc}{D}^{-1}& n\\ n^T& N\end{array}\right)}^{-1}\left(\begin{array}{c}n\circ \left(w+{\sigma }^2{1}_N\right)\\ {\sigma }^{2}N\end{array}\right)\\ =\left(\begin{array}{cc}D+sDn{n}^{T}D& -sDn\\ \cdot & s\end{array}\right)\left(\begin{array}{c}n\circ \left(w+{\sigma }^2{1}_N\right)\\ {\sigma }^{2}N\end{array}\right)\Rightarrow \\ \mathbb{E}\left({\hat{v}}_k\right)=d_k{n}_k\left(w_k+{\sigma }^2\right)+s{d}_k{n}_k\sum _j{n}_j^2\left(w_j+{\sigma }^2\right)d_j-s{d}_k{n}_k{\sigma }^{2}N\\ =d_k{n}_k\left[w_k-\frac{{\sum }_j{n}_j^2{d}_j{w}_j}{{\sum }_j{n}_j^2{d}_j-N}\right]\end{array}$$

The last line follows from some algebra and nicely emphasizes that the $\hat{v}$ are unbiased when w_k = 0 for all k, i.e., under noise variance homogeneity.

The d_k terms can be simplified assuming that the environments are independent of the genotypes and that each $n_k\gg 1$, so that:

$$\begin{array}{c}\text{tr}\left(K_k^2\right)=\sum _{i,j\in k}{K}_{ij}^2=\sum _{i\in k}{K}_{ij}^2+\sum _{i\ne j\in k}{K}_{ij}^2\\ =n_k+n_k\mathbb{V}\left(K_{ii\in k}\right)+n_k\left(n_k-1\right)\mathbb{V}\left(K_{i<j\in k}\right)\\ \approx n_k\left(1+a+n_{k}b\right)\end{array}$$

The approximation in the last line uses the assumption that the same a and b values can be used across k, which is implied by our assumed gene-environment independence and large n_k.

To approximate d_k, we assume that n_k = n₀ is constant across all groups, giving:

$$\begin{array}{c}\mathbb{E}\left({\hat{v}}_k\right)\approx \frac{1}{1+a+n_{0}b}\left[w_k-\frac{\frac{1}{1+a+n_{0}b}{\sum }_j{n}_j{w}_j}{\frac{1}{1+a+n_{0}b}{\sum }_j{n}_j-N}\right]\\ =\frac{1}{1+a+n_{0}b}{w}_k\end{array}$$

The last equality derives from our identification assumption on $\left(w,{\sigma }^2\right)$. This approximation could be expanded to capture modest variability across n_j by Taylor approximation around n₀.

□

In the case of noise homogeneity, w_k = 0 for all k, hence the HE estimate is unbiased, as is well known. The bias is also small in the case where the kinship matrix is very far from the identity (either because off-diagonals are large, increasing b, or because on-diagonals are highly variable, increasing a). However, in all other settings the expected estimate for environment-k-specific heritability v_k will be proportional to the true environment-k-specific noise (w_k), attenuated by a factor measuring the distance between K and I.

We show that this bias approximation can be accurate in practice by evaluating the HE regression model fits from the quantitative simulations performed in the main text. Specifically, we fit HE regression ignoring noise heterogeneity to the simulations with homogeneous genetics but heterogeneous noise (Figures 2G and 2H) and compare the estimated genetic heterogeneity with our bias approximation (Figure 7). We find that our bias approximation is accurate even though these simulations include nonzero heritability and fit a homogeneous genetic variance component, unlike our simplified theoretical analysis in this appendix—supporting the practical relevance of our bias approximation.

Figure 7.

Bias from HE Regression when Fitting Free GxEMM with Hom Noise

Estimates are based on the simulations used in Figures 2G and 2H, which assume Hom genetics and Free noise. Lines provide the bias approximation derived above. The true simulation model has v₁ = v₂ = 0; the true values are shown as dotted lines in the background.

Appendix B: Identification of V/W and Standardizing G/Z

Parameter Identification

The Free and IID assumptions resolve an identification problem that arises for the genetic variance parameters of the Full model, $\left({\sigma }_{hom}^2,V\right)$, when Z is discrete. Under the Full model, any constant λ can be passed between ${\sigma }_{hom}^2$ and V without changing the likelihood by $\left({\sigma }_g^2,V\right)\mapsto \left({\sigma }_g^2-\lambda ,V+\lambda 1_P{1}_P^T\right)$, with $1_P$ a vector of 1 s. Conceptually, this is equivalent to the fact that the population mean and the environmental main effects are not jointly identified in linear regression models with discrete environments.

Free and IID GxEMM break this symmetry because V_ij and $V_{ij}+\lambda$ cannot both be 0 for nonzero λ. Intuitively, the Free and IID models prioritize $\left(\beta ,\gamma \right)$ pairs where the mean effect across environments $\left({\bar{\gamma }}_s\right)$ is absorbed into ${\beta }_s$ (so ${\bar{\gamma }}_s=0$). We also note that some parameters in the model of Ni et al.²³ are not identified for this reason, and the problem grows as the number of environments increases.

W is also not fully identified for discrete Z. First, off-diagonal entries cannot be estimated, so the Full and Free models are identical. Second, $\left({\sigma }_e^2,W\right)\equiv \left({\sigma }_e^2+\lambda ,W-\lambda I\right)$, which eliminates a degree of freedom from the diagonal of W. In particular, the IID and Hom noise models coincide.

Covariate Scale Identification

Columns of G can be assumed mean zero WLOG because the restricted likelihood is invariant under the mapping $G\mapsto G+1_N{\mu }^T$ for all $\mu \in {\mathbb{R}}^L$:

$$\begin{array}{c}G\beta +\left(G\ast Z\right)\gamma \mapsto G\beta +\left(1_N{\mu }^T\right)\beta +\left(G\ast Z\right)\gamma +\left(\left[1_N{\mu }^T\right]\ast Z\right)\gamma \left(\text{linearity}\text{of}\text{Khatri}-\text{Rao}\right)\\ =G\beta +1_N\left({\mu }^T\beta \right)+\left(G\ast Z\right)\gamma +Z\left(\text{mat}\left(\gamma \right)\mu \right)\left(\text{direct}\text{computation}\right)\\ \equiv G\beta +\left(G\ast Z\right)\gamma \end{array}$$

where the equivalence is modulo the projection orthogonal to the fixed effects, which include 1_N and Z ($\text{mat}\left(\cdot \right)$ stacks γ into an K × L matrix column-wise).

Z, however, cannot be centered without changing the likelihood, because G is not projected out as a fixed effect. Mapping $Z\mapsto Z+1_N{\mu }^T$, now for $\mu \in {\mathbb{R}}^K$, the initial covariance parameters $\left(V,{\sigma }_z^2\right)$ are equivalent to the the new parameters $\left({\text{Σ}}_v,{\sigma }_v^2\right)$ iff

$$\begin{array}{c}{\sigma }_v^{2}K+K\circ \left(\left[Z+1_N{\mu }^T\right]{\text{Σ}}_v{\left[Z+1_N{\mu }^T\right]}^T\right)={\sigma }_g^{2}K+K\circ \left(ZV{Z}^T\right)\iff \\ K\circ \left(\left({\sigma }_v^2-{\sigma }_g^2\right)J_N+1_N{\mu }^T{\text{Σ}}_v{Z}^T+Z{\text{Σ}}_v\mu 1_N^T-Z\left(V-{\text{Σ}}_v\right)Z^T\right)=0\iff \\ \left({\sigma }_v^2+{\mu }^T{\text{Σ}}_v\mu -{\sigma }_g^2\right)1_N{1}_N^T+1_N{\mu }^T{\text{Σ}}_v{Z}^T+Z{\text{Σ}}_v\mu 1_N^T-Z\left(V-{\text{Σ}}_v\right)Z^T=0\iff \\ \left({\sigma }_v^2+{\mu }^T{\text{Σ}}_v\mu -{\sigma }_g^2\right)Z{1}_K{1}_K^T{Z}^T+Z{1}_K{\mu }^T{\text{Σ}}_v{Z}^T+Z{\text{Σ}}_v\mu 1_K^T{Z}^T-Z\left(V-{\text{Σ}}_v\right)Z^T=0\iff \\ Z\left(\left({\sigma }_v^2+{\mu }^T{\text{Σ}}_v\mu -{\sigma }_g^2\right)J_K-\left(V-{\text{Σ}}_v\right)+1_K{\mu }^T{\text{Σ}}_v+{\text{Σ}}_v\mu 1_K^T\right)Z^T=0\iff \\ \left({\sigma }_v^2+{\mu }^T{\text{Σ}}_v\mu -{\sigma }_g^2\right)J_K-\left(V-{\text{Σ}}_v\right)+1_K{\mu }^T{\text{Σ}}_v+{\text{Σ}}_v\mu 1_K^T=0\iff \\ {\text{Σ}}_v+\left({\sigma }_v^2+{\mu }^T{\text{Σ}}_v\mu -{\sigma }_g^2\right)J_K+1_K{\left({\text{Σ}}_v\mu \right)}^T+\left({\text{Σ}}_v\mu \right)1_K^T=V\end{array}$$

where J_K is a matrix of 1 s. So adding μ to the columns of Z comes WLOG if and only if there always exists a ${\sigma }_v^2$ such that the implied ${\text{Σ}}_v$ above remains in the set of allowed covariance matrices. In particular, demeaning the columns of Z comes WLOG only under the Full model, because the LHS in the final equation is non-diagonal for $\mu \ne 0$.

Fundamentally, this asymmetry between Z and G is because we treat the former’s main effect as fixed (α) and the latter’s as random (β).

The scale of columns of Z is irrelevant for Free GxEMM because the feasible set for V is closed under conjugation by diagonal matrices—multiplying $Z_{,k}$ by λ can be counterbalanced by multiplying row k and column k of V by ${\lambda }^{-1}$. However, the column scaling of Z can be very important for IID GxEMM. By default, we do not scale or center Z when it measures discrete environments in GxEMM. We do, nonetheless, require that ${\Vert Z\Vert }_F^2=N$, which comes without loss of generality and permits simpler formulas for heritability. We note that Moore et al.²¹ and common practice in many machine learning tasks centers and scales columns of Z; when environments are discrete, this corresponds to an assumption that rarer environments harbor larger specific genetic effects.

In the Full model, the columns of Z become identified only up to span$\left(Z\right)$. This has pros and cons: a benefit is invariance to linear transformations, but a con is that individual elements of V become meaningless. Conversely, individual elements of the diagonal V fit by Free GxEMM are meaningful, as the explicit assumption of diagonal V identifies a basis for span$\left(Z\right)$.

Appendix C: Gene-Environment Correlation and GxE Bias in Polygenic Setting

It is well known that gene-environment (G-E) correlation can cause bias in gene-environment interaction (GxE) tests if uncorrected. This is a general statistical issue in fixed effect regression, and main covariate effects should almost always be adjusted when testing interactions. This has been emphasized recently in the GxE literature for testing individual genetic variants; e.g., Dudbridge and Fletcher³⁰ provide a worked example analyzing the simplest case of a single causal genetic variant.

Ni et al.²³ recently introduced a polygenic GxE model that incorporates G-E. The motivation for modeling G-E was by analogy to the fixed effect setting, where the bias is not in dispute. However, Ni et al.²³ provide no reason this bias would persist in the polygenic setting, nor simulations where G-E causes false-positive GxE.

Here, we provide a theoretical analysis that answers these questions. It is possible for polygenic G-E to bias GxE, but only under a very specific condition that, to our knowledge, has never been evaluated in reality. In particular, we feel that G-E correlation is unlikely to be a significant source of false GxE in the polygenic setting.

Specifically, the condition for G-E correlation to bias GxE estimates is that the GxE effects for each SNP (γ) must correlate with the product of its direct effect on the phenotype (β) and its effect on the environment (α):

$$\eta :=\mathbb{E}\left(\alpha \beta \gamma \right)\ne 0$$

For example, in the case of GxSmoking for BMI, the fact that G-Smoking correlation exists $\left(\alpha \ne 0\right)$ is insufficient to cause bias. However, the polygenic GxSmoking estimates will be biased if the interaction of SNPs that both directly increase smoking likelihood $\left(\alpha >0\right)$ and BMI $\left(\beta >0\right)$ tend to have a positive interaction $\left(\gamma >0\right)$, indicating postive epistasis between main BMI effects and indirect effects mediated through smoking $\left(\eta >0\right)$. If, instead, we retain $\alpha ,\beta >0$ but assume $\gamma <0$, then these two pathways to BMI are instead negatively epistatic, meaning the total SNP effect is less than the sum of its direct and smoking-mediated effects.

Intuitively, the bias from G-E correlation on GxE per-SNP averages out to 0 across all SNPs. For a small number of causal SNPs, however, the contributions will not perfectly cancel. In the simplest, most studied case—a single causal SNP—the problem is at its most extreme.

Proposition 2. Assume the GxE model with G-E correlation²³ defined by:

$$y=\mu +Z\omega +G\beta +\left(G\ast Z\right)\gamma +ϵ$$

$$z=G\alpha +e$$

Assume also that both $\left(e_i,{\mathrm{ϵ}}_i\right)$ and $\left({\alpha }_l,{\beta }_l,{\gamma }_{\left(l\right)}\right)$ are i.i.d., and also independent of each other, where ${\gamma }_{\left(l\right)}\in {\mathbb{R}}^P$ are the GxE effects for SNP l. Then G-E correlation causes false positive inflation in the HE regression test for polygenic GxE if and only if:

$$\eta :=\sum _{p}Cov\left({\alpha }_{,p}\circ \beta ,{\gamma }_{\left(p\right)}\right)=\sum _{l,p}\mathbb{E}\left({\alpha }_{lp}{\beta }_l{\gamma }_{lp}\right)\ne 0$$

where ${\gamma }_{\left(p\right)}\in {\mathbb{R}}^L$ are the GxE interaction effects for environment p and ${\gamma }_{lp}$ is the SNP l-by-environment p interaction effect.

Proof. First, note that the fixed effects μ and ω are eliminated by residualizing covariates; we do not track the impact of this finite-sample projection going forward, however, which is not quite formal but is very standard. The model simplifies to:

$$\begin{array}{c}y=G\beta +\left(G\ast \left(G\alpha \right)\right)\gamma +\left(G\ast e\right)\gamma +\mathrm{ϵ}\\ =G\beta +\left(G\ast G\right)\left(\left[I_L\otimes \alpha \right]\gamma \right)+\left(G\ast e\right)\gamma +\mathrm{ϵ}\end{array}$$

In expectation—over the random variables e, ϵ, α, β, and γ—the quadratic form in y for $i\ne j$ is:

$$\begin{array}{c}\mathbb{E}\left(y_i{y}_j\right)=G_i\mathbb{E}\left(\beta {\beta }^T\right)G_j^T+\left(G_i\otimes G_i\right)\left(\mathbb{E}\left(\left[I_L\otimes \alpha \right]\mathbb{E}\left(\gamma {\gamma }^T|\alpha \right){\left[I_L\otimes \alpha \right]}^T\right)\right){\left(G_j\otimes G_j\right)}^T+\\ \mathbb{E}\left(\left(G_i\otimes e_i\right)\gamma {\gamma }^T{\left(G_j\otimes e_j\right)}^T\right)+G_i\mathbb{E}\left(\beta {\gamma }^T{\left[I_L\otimes \alpha \right]}^T\right){\left(G_j\otimes G_j\right)}^{T}2\\ ={\sigma }_{\beta }^2{G}_i{G}_j^T+\left(G_i\otimes G_i\right)\left(I_L\otimes \mathbb{E}\left(\alpha {\text{Σ}}_{\gamma |\alpha }{\alpha }^T\right)\right){\left(G_j\otimes G_j\right)}^T+\sum _{l_1,l_2,l_3,p}{G}_{i{l}_1}{G}_{j{l}_2}{G}_{j{l}_3}\mathbb{E}\left({\beta }_{l_1}{\alpha }_{l_{2}p}{\gamma }_{l_{3}p}\right)2\end{array}$$

defining ${\text{Σ}}_{\gamma |\alpha }:=\mathbb{E}\left({\gamma }_{\left(l\right)}{\gamma }_{\left(l\right)}^T|\alpha \right)$ and using the notation f(i,j)² = f(i,j) + f(j,i) for any two-argument term f.

The final term simplifies because the expectation is zero unless $l_1=l_2=l_3$, giving:

$$\begin{array}{c}\sum _{l_1,l_2,l_3,p}{G}_{i{l}_1}{G}_{j{l}_2}{G}_{j{l}_3}\mathbb{E}\left({\beta }_{l_1}{\alpha }_{l_{2}p}{\gamma }_{l_{3}p}\right)=\sum _{l,p}{G}_{il}{G}_{jl}^2\mathbb{E}\left({\beta }_l{\alpha }_{lp}{\gamma }_{lp}\right)\\ =\left(\sum _{l,p}{G}_{il}{G}_{jl}^2\right)\mathbb{E}\left({\beta }_{l^{\prime }}\sum _p\left[{\alpha }_{l^{\prime }p}{\gamma }_{l^{\prime }p}\right]\right)\Rightarrow \\ \sum _{l_1,l_2,l_3,p}{G}_{i{l}_1}{G}_{j{l}_2}{G}_{j{l}_3}\mathbb{E}\left({\beta }_{l_1}{\alpha }_{l_{2}p}{\gamma }_{l_{3}p}\right)\left[2\right]=\eta K_{ij}^{1.5}L\end{array}$$ (Equation A3)

where $l^{\prime }$ is an arbitrary dummy index (these terms are i.i.d. over $l^{\prime }$) and where we define $K_{ij}^{1.5}:=\frac{1}{L}\sum _l{G}_{il}{G}_{jl}^2+\frac{1}{L}\sum _l{G}_{il}^2{G}_{jl}$.

We allow the conditional variance ${\text{Σ}}_{\gamma |\alpha }$ to depend on α. But the GxE term $\mathbb{E}\left(\alpha {\text{Σ}}_{\gamma |\alpha }{\alpha }^T\right)$ is still proportional to $I_L$, because loci are assumed independent. Each diagonal entry is:

$$\mathbb{E}\left({\alpha }_{l,}{\text{Σ}}_{\gamma |\alpha }{\alpha }_{l,}^T\right)=:{\sigma }_{\gamma ,\alpha }^2$$

Together, these reductions give:

$$\begin{array}{c}\mathbb{E}\left(y_i{y}_j\right)={\sigma }_{\beta }^2{G}_i{G}_j^T+{\sigma }_{\gamma ,\alpha }^2{\left(G_i{G}_j^T\right)}^2+\eta \sum _l{G}_{il}{G}_{jl}^2\left[2\right]\\ =L{\sigma }_{\beta }^2{K}_{ij}+L{\sigma }_{\gamma ,\alpha }^2{K}_{ij}^2+L\eta K_{ij}^{1.5}\end{array}$$ (Equation A4)

This decomposes the expectation into the appropriate first two terms, for the homogeneous and GxE effects, and a third bias term. This bias is clearly zero when $\eta =0$. The second term, for GxE, also appropriately disappears under the GxE null—if γ is deterministically zero, then ${\text{Σ}}_{\gamma |\alpha }=0$.

□

A large-N argument could likely also be made that $K^{1.5}\to 0$ under certain genotype matrix structures.

η is closely related to the concept of coordinated interaction we are developing in related work. η conceptually measures the sum of coordinated interactions between the primary polygenic effect (β) and the indirect pathways through $Z_{,p}$ (${\alpha }_{,p}$).

Our proposition does not claim unbiasedness in general for the estimated GxE variance components, nor does it control any overdispersion of the estimated GxE parameter due to G-E correlation. Instead, we show that the GxE estimate is unbiased when $\eta =0$ under the null GxE hypothesis ($\gamma =0$). This is precisely the criterion used in Dudbridge and Fletcher³⁰ to argue that G-E correlation does cause bias for GxE. Our result differs substantially, however, because we model the full spectrum of polygenic SNP effects rather than individual SNPs.

This result also relates to calculations in Sulc et al.,⁷⁶ which focuses on a related problem where the “E” is unmeasured. However, they assume (1) $\alpha \propto \beta$ and (2) that $Z\in {\mathbb{R}}^N$ is univariate, which together make the math more straightforward⁷⁶ and also do not link their results to the equivalent assumptions on the SNP effect sizes, which is crucial for biological interpretation. In particular, it is not clear from their analysis that significant interaction results are obtained if and only if there is coordinated interaction via $\eta \ne 0$.

In summary, we provide a necessary and sufficient condition for G-E correlation to bias GxE interaction tests in the polygenic setting. This demonstrates that the bias is likely negligible in practice, as well as provides a proper theoretical characterization of the relationship between G-E and GxE bias under polygeneicity. This was previously unknown: for example, Ni et al.²³ did not demonstrate GxE bias in simulations with G-E correlation.

Appendix D: Marginalizing Random Interaction Coefficients

This section shows that the set of Gaussian GxE coefficients (γ) with covariance $D\otimes V$ (V for the environmental covariance, D for the SNPs covariance) describes essentially the same distributions as the set of linear mixed models with Hadamard kinship matrices $\left(GD{G}^T\right)\circ \left(ZV{Z}^T\right)$. The former are the natural model for polygenic GxE; the latter are intuitive (for discrete environments) estimates for environment-specific heritability and easily fit by REML. In practice, D is usually taken to be the identity matrix.

Proposition 3. Assume that $\gamma \sim \mathcal{N}\left(0,\text{Σ}\right)\in {\mathbb{R}}^{P\times L}$, that $G\in {\mathbb{R}}^{N\times L}$ has continuous, random entries, and that $Z\in {\mathbb{R}}^{N\times P}$ has rank P, with P < N. Write $K:=GD{G}^T$ for some fixed D. Then

$$\mathbb{V}\left(\left(G\ast Z\right)\gamma \right)=K\circ \text{Ω}\iff \left(\text{Σ},\text{Ω}\right)=\left(D\otimes W,ZW{Z}^T\right)forsome\text{W}$$

where ^∗ is the column-wise Khatri-Rao product; $\circ$ is Hadamard; and $\otimes$ is Kronecker.

Proof. First, note the identity:

$$\left(G_{i,}\otimes Z_{i,}\right)\left(D\otimes W\right){\left(G_{j,}\otimes Z_{j,}\right)}^T=\left(G_{i,}D{G}_{j,}^T\right)\left(Z_{i,}W{Z}_{j,}^T\right)=K_{ij}{\text{Ω}}_{ij}$$

Now, right to left is easy:

$$\mathbb{V}{\left(\left(G\ast Z\right)\gamma \right)}_{ij}=\left(G_{i,}\otimes Z_{i,}\right)\mathbb{V}\left(\gamma \right){\left(G_{j,}\otimes Z_{j,}\right)}^T=K_{ij}{\text{Ω}}_{ij}$$

The other direction assumes decomposition of the variance into Hadamard products holds, so

$$\left(G_{i,}\otimes Z_{i,}\right)\left(D\otimes W\right){\left(G_{j,}\otimes Z_{j,}\right)}^T=K_{ij}{\text{Ω}}_{ij}=\left(G_{i,}\otimes Z_{i,}\right)\sum {\left(G_{j,}\otimes Z_{j,}\right)}^T$$

Using the standard identity $\left(A\otimes B\right)\text{vec}\left(C\right)=\text{vec}\left(B^{T}CA\right)$, where $\text{vec}\left(\cdot \right)$ concatenates columns of a matrix, the above equality can be written as

$$\left(G_{j,}\otimes Z_{j,}\otimes G_{i,}\otimes Z_{i,}\right)\text{vec}\left(\text{Σ}-D\otimes W\right)=0$$

By assumption, this identity holds $\forall i,j$ and almost all genotypes $G_i,G_{j,}\in R^L$. The span of such pure four-way tensors is ${\mathbb{R}}^{L^2{P}^2}$, so its kernel has dimension zero and thus $\text{Σ}-D\otimes W=0$.

□

A similar result can be obtained if N grows large with fixed L.

We note that the easy direction appears implicitly in many human genetics papers (e.g., Robinson et al.,²⁰ Ni et al.,²³ Yang et al.²⁷). We do not know where to find a clear proof, however, and are unaware of any discussion of the other direction.

Web Resources

• GCTA, https://cnsgenomics.com/software/gcta

• GxEMM (free R implementation), https://github.com/andywdahl/gxemm

• GxEMM scripts to reproduce the simulations and rat analyses, https://github.com/andywdahl/gxemm-scripts

• GxEMM to reproduce the pyschENCODE analyses, https://github.com/nguyenkhiemv/GxEMM

• MTG2, https://sites.google.com/site/honglee0707/mtg2