Ambivert degree identifies crucial brain functional hubs and improves detection of Alzheimer’s Disease and Autism Spectrum Disorder

Highlights

• •A novel measure, ambivert degree, is proposed to detect hubs in the functional connectome.
• •Ambivert degree improves identification of crucial hubs compared to nodal degree and betweenness centrality.
• •Using ambivert degree as input features, deep neural networks detect AD and ASD from healthy controls.
• •The hubs detected in AD and ASD could be potential diagnostic biomarkers.

Abstract

Functional modules in the human brain support its drive for specialization whereas brain hubs act as focal points for information integration. Brain hubs are brain regions that have a large number of both within and between module connections. We argue that weak connections in brain functional networks lead to misclassification of brain regions as hubs. In order to resolve this, we propose a new measure called ambivert degree that considers the node’s degree as well as connection weights in order to identify nodes with both high degree and high connection weights as hubs. Using resting-state functional MRI scans from the Human Connectome Project, we show that ambivert degree identifies brain hubs that are not only crucial but also invariable across subjects. We hypothesize that nodal measures based on ambivert degree can be effectively used to classify patients from healthy controls for diseases that are known to have widespread hub disruption. Using patient data for Alzheimer’s Disease and Autism Spectrum Disorder, we show that the hubs in the patient and healthy groups are very different for both the diseases and deep feedforward neural networks trained on nodal hub features lead to a significantly higher classification accuracy with significantly fewer trainable weights compared to using functional connectivity features. Thus, the ambivert degree improves identification of crucial brain hubs in healthy subjects and can be used as a diagnostic feature to detect neurological diseases characterized by hub disruption.

1. Introduction

Evidence from several anatomical, physiological and neuroimaging studies have shown that the brain is composed of functionally diverse systems coordinating distinct inputs that result in cognition and behavior (Power and Petersen, 2013). While functional specialization is a key organization principle in the brain, there is increasing evidence of significant dynamic integration among functional regions in order to perform cognitive tasks as diverse as language perception (Friederici and Gierhan, 2013) and vision (Behrmann and Plaut, 2013). This integration or “coming together” of specialized brain regions depends on information flow between neurons in these regions, which is coordinated by a specific set of regions. These integrative or ‘hub’ regions together form a backbone for information transmission in the brain (Senden et al., 2018).

The functional brain organization is usually modeled using networks where brain regions consisting of a population of neurons are represented by nodes and the functional connections (as given by functional correlations) between brain regions are represented as edges with weights. Previous studies indicate that human brain connectome incorporates properties that promote functional specialization with a modular structure (for review refer to Sporns and Betzel, 2016) and efficient communication by virtue of network hubs (for review refer to van den Heuvel and Sporns, 2013). A recent study found that hubs are differentiated into three classes based on their connectivity to different functional modules (Gordon et al., 2018) and were shown to modulate different tasks. The central role of hubs in information processing makes their identification an important research problem.

Brain hubs were initially characterized by the nodes having large numbers of connections to other networks, that is, nodes having high nodal degrees (Buckner, Sepulcre, Talukdar, Krienen, Liu, Hedden, Andrews-Hanna, Sperling, Johnson, 2009, Cole, Pathak, Schneider, 2010, Tomasi, Volkow, 2011). However, later studies argued that since the brain modules had heterogeneous sizes and nodes had high within-module connections, simply taking the nodal degree would lead to giving undue weightage to nodes from large modules (usually the default mode network) (Power et al., 2013). Therefore, the nodes with high degree in comparison to the nodes in the same module (Power et al., 2013) were considered crucial for intra-modular communication and were termed as modular hubs. Conversely, the participation coefficient, a measure that quantifies the extent a node connects to other modules was proposed to detect heteromodal nodes facilitating inter-modular communication known as connector hubs (Gordon, Lynch, Gratton, Laumann, Gilmore, Greene, Ortega, Nguyen, Schlaggar, Petersen, et al., 2018, Nicolini, Bordier, Bifone, 2017, Power, Schlaggar, Lessov-Schlaggar, Petersen, 2013). The weighted average of scores derived from the two measures identified nodes with high intra-modular degree and heterogeneous connections often termed as network hubs.

Studies involving brain functional networks involve network sparsification steps that remove weak brain functional connections that are affected by experimental noise (van den Heuvel and Fornito, 2014). However, this affects not only the number of weak connections in the network but also the network’s underlying modular structure (Bordier et al., 2017). This can in turn affect the detection of network hubs because (i) disruption of brain modular structure leads to spurious detection of hubs; and (ii) a node may possess a very large number of weak connections and still be classified as a hub whereas a node with fewer but stronger connections may be ignored. In order to account for (i), we use the thresholding scheme proposed by Bordier et al. (2017), which preserves the network’s modular structure; and (ii), we propose a new measure called ambivert degree that considers both the nodal degree and the strength of connections. We also consider an extension of the participation coefficient, called gateway coefficient that considers information about the importance of a node’s neighbors in their module and the uniqueness of the node’s inter-modular connections (Vargas and Wahl, 2014). Considering both of these measures, we provide a new definition for brain functional hubs and study their importance in processing information in resting state brain functional networks of the 589 subjects from the HCP. By considering the effect of inducing artificial lesions in the brain functional networks, we found that the ambivert degree gives the most crucial modular hubs and instead of a node’s intra-modular degree (as previously thought), the ambivert degree combined with participation coefficient gives the most crucial network hubs.

Hubs are known to support brain information processing and alterations in the functional connectivity of hubs have global effect on brain network and function (Fornito, Zalesky, Breakspear, 2015, Gratton, Nomura, Pérez, D’Esposito, 2012). Previous research has shown that various neurological ailments such as Alzheimer’s disease (AD) (Guillon et al., 2017), Schizophrenia (Bordier, Nicolini, Forcellini, Bifone, 2018, Rubinov, et al., 2013), and Autism Spectrum Disorder (ASD) (Itahashi et al., 2014) affect brain functional hubs disproportionately and more than the other brain regions. These disruptions reflected in hub connectivity could be a result of the high information processing at the hub regions, causing high baseline activity and metabolic requirements of hub regions (Liang, Zou, He, Yang, 2013, Tomasi, Wang, Volkow, 2013) leaving the hub neurons vulnerable to metabolic stress or degeration due to high activity (Saxena and Caroni, 2011). In case of ASD, a developmental disorder characterized by a range of heterogeneous symptoms with varying degrees of severity, multiple resting state functional MRI (rs-fMRI) studies have found widespread impairment in intrinsic functional connectivity (for a review, see Hull et al., 2017), especially in the hubs (Itahashi et al., 2014). Similarly, research suggests that highly active heteromodal regions are preferentially affected in Alzheimer’s disease (AD). Buckner et al. (2009) used node degree centrality to define brain hubs and demonstrated that these hubs of healthy human brains overlap with regions showing higher Aβ deposition in patients with AD. de Haan et al. (2012) found that excessive neuronal activity that led to degeneration provides a possible explanation for hub vulnerability in AD. The Amyloid-β (Aβ) cascade hypothesis suggests that Aβ have a toxic effect on adjacent neurons and synapses, disrupting their normal functioning (Sheline and Raichle, 2013) in AD.

Based on prior studies, we hypothesized that nodal hub scores can be used to classify AD and ASD subjects from their respective healthy subject cohort. We apply our methods on rs-fMRI data for AD and ASD subjects to demonstrate how brain hubs can aid in diagnosis of brain diseases. We chose these AD and ASD for our analysis because of existing evidences of hub disruptions and availability of large sets of data for deep neural network modeling. We detected brain hubs from the functional scans and found that the brain hubs of AD and ASD patients were different from cognitively normal controls. Using both the nodal hub scores and functional connectivity as input features, we trained neural networks and SVM classifiers, and show that using hub scores gave a significantly higher classification accuracy with a much lower number of trainable weights.

2. Methods

Let $G=(\Omega ,W)$ denote the functional brain network (connectome) where Ω denotes the set of brain regions of interest (ROI) or nodes and $W=\left\{w_{ij}\right\}$ is the matrix of edge weights of the network with w_{i, j} denoting the weight between brain ROI i and j, and i, j ∈ Ω.

2.1. Detecting brain functional modules

While some previous studies detected brain modules and hubs by using subject averaged functional connectivity matrix (Bertolero, Yeo, D’esposito, 2017, Nicolini, Bordier, Bifone, 2017, Power, Schlaggar, Lessov-Schlaggar, Petersen, 2013), there are multiple studies pointing out varied individual differences in the functional connectome (Gordon et al., 2017). Therefore, inter-subject differences in functional architecture need to be considered while detecting functional modules (and subsequently network hubs) and combined group results from all the subjects need to be reported (Gordon et al., 2018). We, therefore, use the Iterative Consensus Spectral Clustering (ICSC) algorithm (Gupta and Rajapakse, 2019) that maximizes the similarity between group-level and subject-level modules, iterativly making them more similar.

The ICSC algorithm finds a modularization that groups of brain ROI into modules where connectivity among ROIs within modules are higher than connectivity with other ROIs. The ICSC minimizes the normalized-cut objective function to detect subject-level modularizations W^k of subject k. The group-level modularization $\mathcal{S}$ is obtained by performing consensus clustering on the subject-level modules (Lancichinetti and Fortunato, 2012). The ICSC algorithm then greedily refines the subject-level modularizations such that they are most similar to the group-level modularization by maximizing

$$S^k=\mathrm{sim}(S^k,S)$$ (1)

where the Adjusted Mutual Information is used to measure similarity between modularizations. The newly obtained subject-level modularizations are used to derive group-level modularizations using consensus clustering and so on, till there is no change in the similarity cost function given by (1).

Upon obtaining subject-level modularizations from ICSC, modular labels assigned to nodes for each subject were aligned with those at the group-level modularization. We align the subject-level modules, ${\mathcal{S}}^k,$ with the group-level modules $\mathcal{S}$ by using the Jaccard Index (JI) matching scheme (Lancichinetti and Fortunato, 2012). A module with index b in ${\mathcal{S}}^k$ is assigned to a group-level module label a if for both the group-level module a, $JI(a,b)>JI{(a,c)}_{c\in {\mathcal{S}}^k\setminus b}$ and subject-level module b, $JI(b,a)>JI{(b,c)}_{c\in \mathcal{S}\setminus b}$.

2.2. Thresholding connections

While our modularization method considers weighted unthresholded subject-level networks, weak connections that are most influenced by experimental noise (Birn, 2012, van den Heuvel, Fornito, 2014) need to be removed for further analysis. Researchers often select an a priori density for the network and compute a threshold that retains the target density of edges (Bertolero, Yeo, D’esposito, 2017, Gordon, Lynch, Gratton, Laumann, Gilmore, Greene, Ortega, Nguyen, Schlaggar, Petersen, et al., 2018, Power, Schlaggar, Lessov-Schlaggar, Petersen, 2013). Analyses over a range of densities have been performed to show the stability of derived topological features over a range of thresholds. However, weak correlations could still contain significant functional information, and therefore it is important to use methods that identify the optimal trade-off between the information gain by the removal of noisy edges and the loss due to removal of potentially useful weak edges. Bordier et al. (2017) used synthetic networks with known modular structure and noise similar to brain functional networks and showed that percolation analysis (Gallos et al., 2012), retains the minimum number of edges to keep the network connected while maximizing information on brain functional networks’ modular structure. Also, fixing the same edge density in brain functional networks of subject-groups may lead to inclusion of weak and spurious connections in a subject-group with disrupted functional connectivity and omission of strong connections in another subject-group. The latter becomes especially significant in our case since we perform analysis at the subject-level rather than at a group level. We perform percolation analysis on each subject’s functional network to determine the optimal threshold t for weights and assign zero weights for connections with weights less than t.

2.3. Modular hubs

The brain regions most critical for information processing within a brain module are known as modular hubs. While previous studies have assumed that modular hubs are defined by their intra-modular degree, we wanted to empirically find modular hubs.

2.3.1. Intra-modular degree

The nodal degree of a node i ∈ Ω in the functional connectome is defined as

$${\theta }_i=\sum _{j\in \Omega }{w}_{ij}$$ (2)

where functional connectivity matrix $W={\left\{w_{ij}\right\}}_{i,j\in \Omega }$. The number of connections is given by $n_i=\sum _{j\in \Omega }1(w_{ij}>0)$. The nodal degree θ_i and the number of connections n_i represent a node’s global network property.

With respect to a set of nodes in S, the degree θ_i,S for node i is given by:

$${\theta }_{i,S}=\sum _{j\in S}{w}_{ij}$$ (3)

and $n_{i,S}=\sum _{j\in S}1(w_{ij}>0),$ where 1( · ) is the indicator function. The nodes in the set S can represent a module from the network or all the nodes in the network. When $S=\Omega$. When the node i ∈ S, we refer to θ_i,S as the intra-modular degree. Similarly, the number of intra-modular connections to the node i ∈ S is given by $n_{i,S}=\sum _{j\in S}1(w_{ij}>0)$.

2.3.2. Ambivert degree

Nodes with high intra-modular degree are characterized by a large number of weak or strong intra-modular weights (determined by correlations of brain activations), or a combination of both. Although, nodes with a large number of weak correlations of brain activations do not convey meaningful information, under the existing techniques, these nodes are also classified as modular hubs. These nodes can be thought to be extroverts in social networks, i.e., nodes with a large number of weak ties to other nodes. We, on the other hand, are interested in ambiverts, i.e., nodes that not only connect with a sufficiently large number of nodes but also share meaningful relationships with them. For this purpose, we propose a measure called ambivert degree that identifies high intra-modular degree nodes that are synchronized with multiple nodes in the same module. The ambivert degree of node i ∈ S in module S is defined as

$${\alpha }_{i,S}={\theta }_{i,S}\left(\frac{{\theta }_{i,S}}{n_{i,S}}\right)$$ (4)

The ambivert degree is the intramodular degree weighted by average weight per connection.

2.3.3. Betweenness centrality

Besides the intra-modular degree, we also compute the intra-modular betweenness centrality β_i,S of a node i in module S to find nodes that lie on the shortest paths for information processing (Freeman, 1977):

$${\beta }_{i,S}=\sum _{i,j,k\in S}\frac{{\sigma }_{jk}\left(i\right)}{{\sigma }_{jk}}$$ (5)

where σ_jk measures the number of shortest paths between j and k and σ_jk(i) measures the number of shortest paths between j and k, which pass through node i.

2.3.4. Detection of modular hubs

Modular hubs are characterised by nodes having significantly high intra-modular connections and detected by using intra-modular degree, ambivert degree, or betweenness centrality. We compute the z-score ζ(m_i) by considering a univariate normal distribution of different modular hub measures m_i ∈ {θ_i,S, α_i,S, β_i,S} for a node i ∈ S over the module S. The modular hubs are characterized by the nodes that have significantly higher hub measures than the other nodes in the module.

2.4. Connector hubs

Modular hubs are central to the information processing within their respective modules. However, hubs not only play a role in intra-modular information processing but also act as bridges or connectors for inter-modular information transmission. The connector hubs refer to the nodes that represent heteromodal brain regions that participate in information processing between different functional modules. Traditionally, the participation coefficient has been used to measure the role of a node as a connector hub. Here we explore the participation coefficient as well as the gateway coefficient, a recent extension of the participation coefficient, to identify connector hubs.

2.4.1. Participation coefficient

Connector hubs are quantitatively identified using the participation coefficient p_i of the node i (Guimera and Amaral, 2005):

$$p_i=1-\sum _S{\left(\frac{{\theta }_{i,S}}{{\theta }_i}\right)}^2$$ (6)

2.4.2. Gateway coefficient

Although the participation coefficient has been widely used to characterize connector hubs, it discounts information about the importance of the neighbors of a node and the exclusivity of the node’s connections to other modules. For example, two nodes can have the same number of intra-modular connections and participation coefficient, but one of them may be more important since it may have the only connection between two modules, or its neighbors in a module could be more important in terms of degree or betweenness. This was rectified by the gateway coefficient (Vargas and Wahl, 2014) that renders an importance score to connections of a node to each module. The gateway coefficient of a node is given by:

$$q_i=1-\sum _S{\left(\frac{{\theta }_{i,S}}{{\theta }_i}\right)}^2{(1-{\gamma }_{i,S}{\gamma }_{i,S}^{intra})}^2$$ (7)

where γ_i,S measures the fraction of the edges of node i to the module S relative to other nodes in node i’s module; and ${\gamma }_{i,S}^{intra}$ measures the importance of nodes that are adjacent to node i. γ_i,S and ${\gamma }_{i,S}^{intra}$ are given by:

$${\gamma }_{i,S}=\frac{{\theta }_{i,S}}{\underset{S^{\prime }}{\max }\sum _{i,j\in S^{\prime }}{\theta }_{j,S}}$$ (8)

$${\gamma }_{i,S}^{intra}=\frac{\sum _{j\in S}1(w_{ij}>0){\beta }_{j,S}}{\underset{S^{\prime }}{\max }\sum _{k\in S^{\prime }}{\beta }_{k,S^{\prime }}}$$ (9)

2.5. Network hubs

The modular hubs represent brain regions that participate in intra-modular information processing while the connector hubs represent heteromodal regions that facilitate inter-modular information processing. Network hubs represent key brain regions that are crucial for information processing both inside and outside functional modules. In order to identify network hubs, we propose to combine modular and connector hub measures, giving equal weights to the node’s role in intra-modular and inter-modular information processing.

Given a node i, we define a network hub measure x_i to identify network hubs:

$$x_i=\zeta \left(m_i\right)+c_i$$ (10)

where modular hub measure m_i ∈ {θ_i,S, α_i,S, β_i,S} and connector hub measure c_i ∈ {p_i, q_i}. We explore different combinations of modular and connector hub measures to detect network hubs.

In order to find the network hubs in a subject, we compute x_i for each node and classify it as network hubs if x_i is in the top 2.5% to 20% percentile of nodes (Bertolero, Yeo, D’esposito, 2015, Gratton, Laumann, Gordon, Adeyemo, Petersen, 2016). We investigated the efficacy of this threshold in steps of 2.5%.

2.5.1. Inter-subject variability of hubs

The heterogeneously distributed inter-subject variability of brain functional architecture (Gupta, Rajapakse, 2019, Mueller, Wang, Fox, Yeo, Sepulcre, Sabuncu, Shafee, Lu, Liu, 2013) introduces variability to the hubs detected across subjects. Since we detect hubs for individual subjects and report group-level hubs, it becomes imperative to study the consistency with which a node is classified as a network hub over subjects. We define inter-subject variability λ_i of a hub node i as:

$${\lambda }_i=1-\frac{k_i}{K}$$ (11)

where k_i is the number of subjects where node i is classified as a hub and K is the total number of subjects in the dataset.

2.5.2. Artificial lesioning: efficacy of hubs

The hubs detected using different hub measures represent key brain regions with specific roles in brain information processing, and in order to understand their effects in detecting hubs at the modular and network levels, we simulated brain lesions by removal of different categories of hubs and examining the effects on the network path length. The path length of a network represents the efficiency of information transmission of the network where networks with long path length are inefficient in terms of information transmission. Given the shortest path length d_ij between nodes i and j, the path length l_S of a module S is given by:

$$l_S=\frac{1}{n(n-1)}\sum _{i,j\in S^{\prime },i\ne j}{d}_{ij}$$ (12)

If the module S is the brain network G, we refer to the path length as the global network path length and if the network is a brain module, we refer to the path length as modular path length.

We compute the change in path lengths after removal of hubs at both the network and modular level to understand the effect of removal of hubs on the network’s path length. For comparison between different hubs, we used Tukey’s paired t-test. Since there is no consensus on what percentage of nodes to denote as hubs, we repeat the hub removal for different percentages of nodes.

2.6. Detecting AD and ASD using ambivert degree and participation coefficient of nodes as features

Previous studies have shown evidence of hub disruption in several brain diseases including AD Guillon et al. (2017) and ASD Itahashi et al. (2014). We hypothesized that the large-scale disruption of hubs and alterations in hub measures in these diseases can render hub measures as effective biomarkers for these diseases. In order to investigate this, we obtained data of patients suffering from AD and ASD (along with their healthy age matched controls) and used deep neural networks (DNN) to classify patients and healthy subjects by using hub measures of functional nodes as input features. We compared classification performances achieved using nodal hub measures with those obtained using raw functional connectivity weights as features.

2.6.1. AD dataset

For AD, we used the ADNI dataset (URL: http://adni.loni.usc.edu/), which is the largest publicly available dataset for AD. Functional and structural MRI data were collected according to the ADNI acquisition protocol using a Philips 3 Tesla scanner. The rs-fMRI data for each subject consisted of 140 or 200 functional volumes, acquired with a repetition time (TR) = 3000 ms; echo time (TE) = 30 ms; flip angle = 80^∘; slice thickness = 3.313 mm; and 48 slices. Results included in this manuscript come from data pre-processed using fMRIPprep (Esteban et al., 2018) (details can be found in the appendix). We obtained 88 subjects of which 49 were cognitively normal (CN, age: 76.6  ±  5.5) and 29 subjects suffering from AD (age: 75.4  ±  8.2). Subjects classified as AD have Mini-Mental State Examination (MMSE) scores between 15.7 and 26.9, a Clinical Dementia Rating (CDR) between 0.5 and 3.0 and fulfilled the criteria for AD laid down by National Institute of Neurological and Communicative Disorders and Stroke and the Alzheimer’s Disease and Related Disorders Association (NINCDS/ADRDA). The CN subjects did not suffer from depression, cognitive impairment, or dementia, and had MMSE scores between 23.8 and 30.0 and a CDR of 0.0 and 1.0.

2.6.2. ASD dataset

For ASD, we used rs-fMRI data from the NYU Langone Medical Center available at Autism Brain Imaging Data Exchange (ABIDE, URL: http://fcon_1000.projects.nitrc.org/indi/abide/ (Di Martino et al., 2014), a consortium of brain imaging data for sharing within the scientific community. Specifically, rs-fMRI data of 73 ASD (age 13.9  ±  6.3) and 88 CN (age 15.8  ±  6.3) subjects were used, removing subjects with mean framewise displacement greater than 0.2mm. The data downloaded was preprocessed using the C-PAC pipeline from the Preprocessed Connectomes Project. The preprocessing of the fMRI data includes correction of slice timing, realignment of motion, voxel intensity normalization, nuisance signal removal and band-pass filtering.

2.6.3. Deep neural networks for disease classification

We compared classification performances with nodal hub measures and raw functional connectivity features. Considering a DNN with L layers, the output y_l of the hidden layer l ≠ L is given by:

$$y_l=f(V_l^T{y}_{l-1}+b_l)$$ (13)

where V_l and b_l denote the weights and biases of the layer l and f is the rectified linear unit (ReLU) activation function. For the input layer, $y_0=x_i$.

The output layer $l=L$ is a softmax layer and the output probabilities y of the input x belonging to patient and healthy classes is given by

$$y=\mathrm{softmax}(V_L^T{y}_{L-1}+b_L).$$ (14)

The class label is assigned to the class with the highest probability.

We used a two-class classifier for patients and healthy subjects. The weights and biases of the network are learnt using mini-batch stochastic gradient descent learning that minimises the cross-entropy cost. The networks were implemented in Python using the tensorflow library2.

3. Results

3.1. HCP dataset

The dataset included 589 healthy adults (males = 278, mean age = 28.33 years, range = 22 to 37 years) from the S900 release of the HCP (Van Essen et al., 2012) available at https://www.humanconnectome.org. All HCP rs-fMRI data were acquired on a Siemens Skyra 3T scanner at the Washington University. We used preprocessed data that had undergone image reconstruction with the R227 pipeline Glasser et al. (2013). In addition, 24 head motion parameters were regressed out of the time series. The functional connectivity of the brain was calculated as Pearson correlations of fMRI time-series on the 264 functionally diverse ROI identified in the Power atlas (Power et al., 2011).

3.2. Brain functional modules

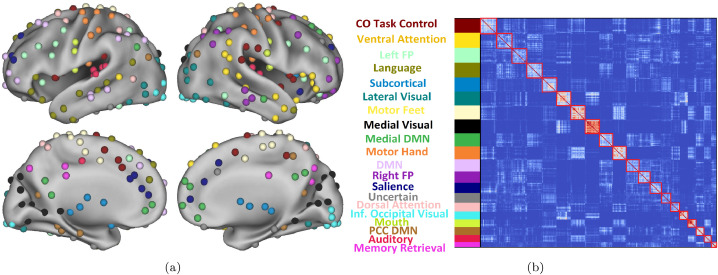
We ran 100 independent runs of the ICSC algorithm on unthresholded subject matrices until convergence and selected the run with the highest value for ICSC quality function. We used the subject-level and group-level modularizations for this run. The ICSC algorithm detected 19 group-level modules with the sizes of modules ranging from 6 to 18 (see Fig. 1), which correspond to previously defined functional networks of the human resting-state brain (Heine, Soddu, Gómez, Vanhaudenhuyse, Tshibanda, Thonnard, Charland-Verville, Kirsch, Laureys, Demertzi, 2012, Power, Cohen, Nelson, Wig, et al., 2011, Sun, Stepanovic, Andreano, Barrett, Touroutoglou, Dickerson, 2016, Yeo, Krienen, Sepulcre, Sabuncu, Lashkari, Hollinshead, Roffman, Smoller, Zöllei, Polimeni, et al., 2011). Using the Jaccard Index matching scheme, we assigned labels to subject-level modules and computed modular hub and network hub measures for network nodes.

Fig. 1.

The group-level modules detected by the ICSC algorithm on resting-state fMRI scans from the HCP dataset. 1(a) shows the functional ROI colored according to the modules they belong to. 1(b) the group consensus matrix with reordered node indices to bring nodes in the same module together. ROIs belonging to modules are ordered in the descending order of module size. The modules are given names based on functional networks identified by earlier studies or on the anatomical location of constituent regions.

3.3. Artificial lesioning to identify the most crucial modular and network hubs

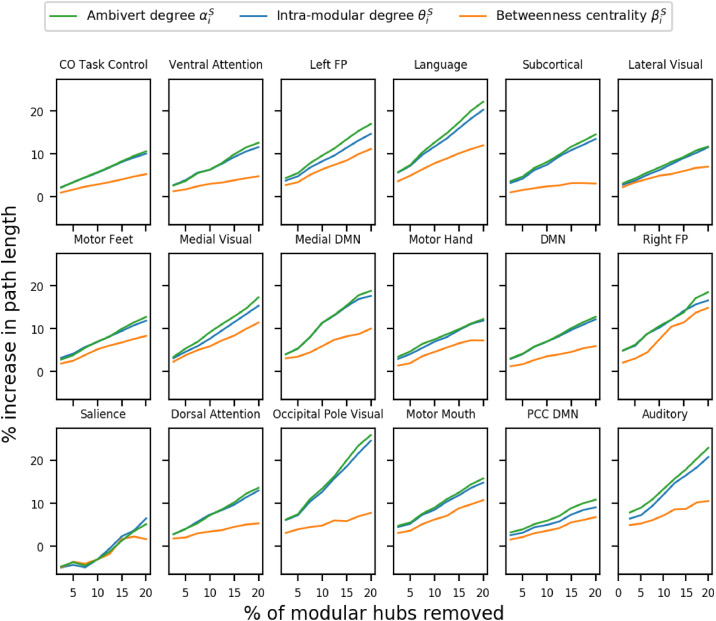
Previous studies assumed that the most crucial modular hubs are nodes with a high intra-modular degree (Nicolini, Bordier, Bifone, 2017, Power, Schlaggar, Lessov-Schlaggar, Petersen, 2013). We tested this assumption since finding nodes that were more crucial to inter-modular communication could also lead to detection of crucial nodes responsible for overall network communication. We computed the intra-modular degree θ_i,S, the ambivert degree α_i,S, and the betweenness centrality β_i,S for nodes in all subjects. Following the approach of (Bertolero, Yeo, D’esposito, 2015, Gratton, Laumann, Gordon, Adeyemo, Petersen, 2016) we classified different percentile of nodes as modular hubs, ranging from top 2.5% to 20% (in steps of 2.5%) and inspected the change in the modular path length l on their removal for a thorough analysis. In order to determine which hubs were the most crucial, we performed Tukey’s paired t-test on the path length of the network after removal of the hubs.

We performed the above set of experiments on all subjects after performing thresholding using percolation analysis. We found that for all the modules except the attention, motor, and salience modules, removal of nodes with a high ambivert degree led to a significantly higher increase in the modular path length (paired t-test p < 0.05) than removal of nodes with high intra-modular degree or betweenness centrality (refer Fig. 2). After the ambivert degree, the intra-modular degree gave the most crucial modular hubs.

Fig. 2.

The changes in path lengths of brain functional modules after artificial lesioning of modular hubs detected by different hub measures. Except the motor, attention and salience modules the removal of hubs detected by the ambivert degree led to significantly greater increase in path than the other modular hubs. The memory retrieval module was excluded from the analysis because it was found in fewer than 50 subjects.

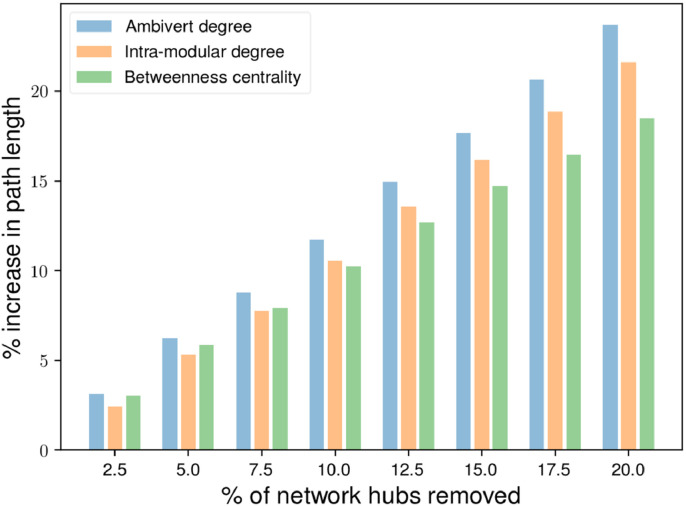
Since the ambivert degree gives more crucial modular hubs than those detected by intra-modular degree and betweenness centrality, we hypothesize that considering nodes with high ambivert degree, taking into weaker connections into considerations, as modular hub measure would yield more important overall brain network hubs. This hypothesis for each subject’s network tested by computing network hub measures and removed the nodes with top 20% scores (in steps of 2.5%) and inspected the change in the network path length l upon their removal.

To understand which hub measure gives the most crucial, we first compared the path length of different types of connector hubs with the same modular hubs. For modular hubs detected by different measures, we found that participation coefficient had a similar or larger impact on the path length than different gateway coefficient measures (Supplementary Fig. S1). We, therefore, compared the effect of removal of modular hubs only along with their participation coefficient on the network path length since these represented the most crucial network hubs detected using different modular hub measures (Fig. 3). We found that the removal of network hubs detected by ambivert degree led to a statistically significant higher increase in network path length than the removal of hubs detected by betweenness centrality (paired t-test p-value $<{10}^{-9}$), and intra-modular degree (paired t-test p-value $<{10}^{-45}$).

Fig. 3.

The increase in the path length after artificial lesioning of different percentiles of network hubs determined by different modular hub measures and their participation coefficient.

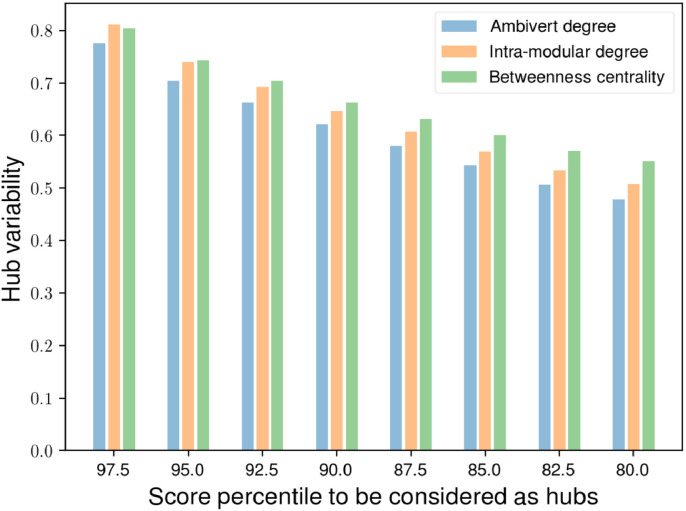
We also computed the inter-subject variability of network hubs across subjects, detected by different modular hub measures. For a complete analysis, we determined the hub variability across different percentiles ranging from 80 to 97.5 (with steps of 2.5). On comparison of variability of hubs detected by ambivert degree with betweenness centrality and intra-modular degree, we found that ambivert degree found the hubs that are most invariable across subjects. The difference in inter-subject variablity was statistically significant (p-value  < 0.05) for hubs detected by betweenness centrality but insignificant for those detected by intra-modular degree (refer Fig. 4).

Fig. 4.

The inter-subject variability of hubs detected by different hub measures and the participation coefficient at different percentiles.

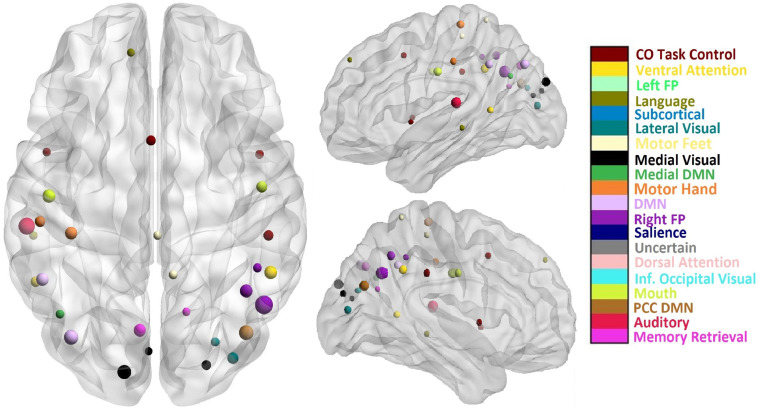
We computed the top 10% hubs given by ambivert degree and participation coefficient for each subject and determined a consensus over all the subjects. We found that the regions in the middle and superior temporal gyrus; the cuneus and precuneus; inferior parietal lobe; superior frontal gyrus, precentral and postcentral gyrus, and posterior cingulate were most frequently identified by ambivert degree combined with participation coefficient (Fig. 5).

Fig. 5.

The axial and sagittal views of the top 10% of the regions identified as network hubs by ambivert degree and participation coefficient. The size and color of the node correspond to its inter-subject variability and its functional module, respectively.

3.4. Disruption of network hubs in AD and ASD

We ran 100 independent runs of the ICSC algorithm on unthresholded subject matrices for the CN and diseased subjects from the ADNI and ABIDE datasets. We selected the run with the highest value for the ICSC quality function for both and used the subject-level and group-level modularizations from this run. We used the Jaccard Index matching scheme described before and assigned labels to each subject’s modules. We chose CN subjects taken from the respective datasets for comparison, because the subjects are age-matched (which removes the effect of age related changes), and the scans were collected on the same scanner. We observed that across thresholds hubs were disrupted in patients suffering from AD and ASD.

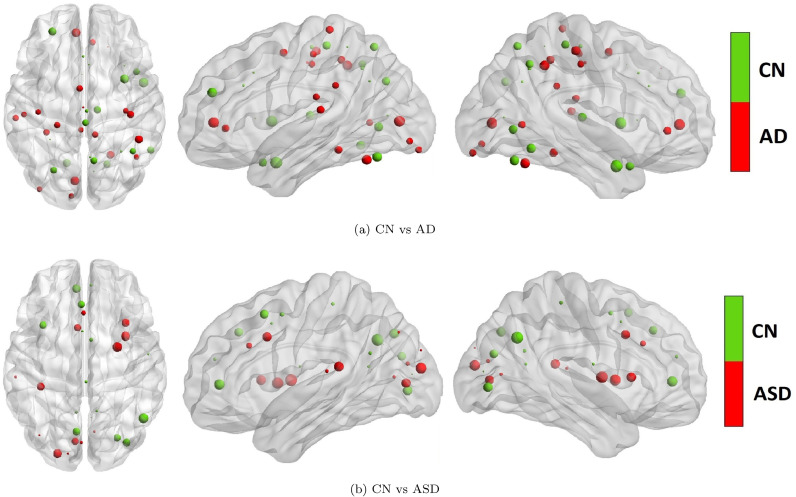
The top 10% ambivert participation coefficient hubs for the CN subjects were located in the cingulate gyrus, middle temporal pole (R: right), supplementary motor, precuneus, thalamus, calcarine (R), insula (R), superior medial frontal (L: left) and middle frontal (L) regions, whereas the hubs for the subjects suffering from AD were located in the middle cingulum, calcarine, anterior cingulate (L), inferior parietal, supplementary motor, precuneus, and fusiform gyrus. We observed that the CN hubs located in the middle temporal (R), insula (R), lingual (L), middle frontal (L), inferior temporal (R), thalamus (R), calcarine (R) and precuneus were disrupted in AD subjects (Fig. 6(a)).

Fig. 6.

The differences between brain regions that are identified as top 10% network hubs, using ambivert degree and participation coefficient in cognitively normal (CN) and diseased subjects. For Fig. 1(a) the subjects suffer from Alzheimer’s Disease (AD); and for Fig. 6(b) the subjects suffer from Autism Spectrum Disorder. The regions in red were identified as hubs in the diseased subjects but not in CN subjects whereas the regions in green were identified as hubs in CN subjects but not in the diseased subjects.

For the ASD subjects, the top 10% hubs detected by the ambivert degree were located in the supplementary motor area (L and R), anterior (L) and middle (R) cingulum, calcarine (L and R), angular gyrus (L), middle occipital (L and R) and insula (L and R); whereas the hubs for CN subjects were in supplementary motor area (L and R), frontal superior medial (L and R), anterior (R) and middle (L) cingulum, precuneus (L and R), middle occipital (R), and angular gyrus (L and R). We observed that the hubs located in the angular gyrus (R), anterior cingulum (L), precuneus (L), and medial superior frontal (L), and middle occipital (R) in normal subjects were disrupted in ASD subjects (Fig. 6). For other thresholds, please refer to Supplementary Fig. S3 (for AD) and S4 (for ASD).

We studied the regions with the highest disruption for both AD and ASD patients in comparison to their normal counterparts. For this, we computed the difference between the nodal hub measures (average ambivert degree and participation coefficient) for patients and cognitively normal subjects. For AD, we found that the network hubs were disrupted for regions in the middle and medial temporal gyrus, frontal orbital lobe, and occipital lobe (Table 1) whereas for ASD we found that regions in the thalamus, posterior cingulate cortex, and supplementary motor areas were most affected (Table 2).

Table 1.

Disrupted brain regions in AD. MNI coordinates of the most disrupted regions (R: Right, L: Left) detected by ambivert degree. Hub measures are given as the sum of ambivert degree and participation coefficient.

MNI			Hub measure
x	y	z	CN	AD	Anatomical Location
50	3	-24	1.39	0.67	Temporal Pole (R)
-20	36	-15	0.55	-0.06	Frontal Mid Orbital (L)
53	-48	12	0.80	0.27	Temporal Mid (R)
44	-48	-15	0.89	0.42	Fusiform (R)
8	42	-9	0.86	0.40	Rectus (R)
35	-81	0	1.07	0.65	Occipital Mid (R)
-44	27	-9	0.42	0.01	Frontal Inferior Orb (L)
23	-87	21	0.59	0.19	Occipital Superior (R)
-31	-78	-15	0.99	0.59	Occipital Inferior (L)
-50	0	-24	0.93	0.55	Temporal Mid (L)

Table 2.

Disrupted brain regions in ASD. MNI coordinates of the most disrupted regions (Right, L: Left) detected by ambivert degree. Hub measures are given as the sum of ambivert degree and participation coefficient.

MNI			Hub measure
x	y	z	CN	ASD	Anatomical Location
8	-7	8	0.76	0.43	Thalamus (R)
-2	-16	13	0.63	0.31	Thalamus (L)
51	-45	22	0.37	0.68	Temporal Superior (R)
9	17	30	0.54	0.85	Cingulum Anterior (R)
-7	-72	38	1.18	0.88	Precuneus (L)
-53	-15	-9	0.50	0.80	Temporal Mid (L)
-2	10	45	1.44	1.14	Suppl Motor (L)
-1	25	30	1.09	1.38	Cingulum Anterior (L)
5	3	51	1.46	1.16	Suppl Motor (R)

3.5. Classification of patients and healthy controls

We hypothesize that as there is widespread hub disruption in the patients suffering from AD and ASD, hub measures can be used as features to train deep neural networks to classify patients and healthy controls. We therefore used each node’s ambivert degree (z-score) and participation coefficient as features to perform classification with deep neural networks (DNN). The performance was also compared with a classifier trained on functional connectivity features from each subject’s unthresholded connectivity matrix W. Since W is symmetric, we formed a vector of its lower triangular elements, which results in a vector of 34, 716 functional connectivity features for each subject.

For DNN, we empirically set the number of hidden layers, number of neurons in each layer, batch size, and learning rate in the experiments. We added dropouts to the hidden layers and imposed early stopping criteria to prevent overfitting. For SVMs, we experimented with a range of parameters (C ∈ {0.001, 0.01, 0.1, 1, 10}, γ ∈ {0.001, 0.01, 0.1, 1}) and different kernels. The best hyperparameters were selected by performing a grid search on the average accuracy of different folds obtained from 5-fold cross validation.

The performance of the 5-layer DNN along with the best SVM model for different kernels are shown in Tables 3 and 4. All samples were included in the test set at least once and the experiment was repeated for 10 random seeds. We observed that the highest accuracy for both AD and ASD were obtained for a 3 hidden layer feedforward DNN using ambivert degree and participation coefficient as features. The SVM models gave a consistently poor classification accuracy. The improvement in classification accuracy by using hub score features in comparison to functional connectivity features was statistically significant for both AD (one tailed t-test, p-value $=0.0048$) and ASD (one tailed t-test, p-value $=0.045$). We also observed that usage of hub scores (that is, the sum of ambivert degree and participation coefficient) as features led to a significant increase in classification accuracy for ASD in comparison to their individual usage, which means that both measures carry crucial information.

Table 3.

Accuracies of classification of AD and NC using deep neural networks and nodal hub scores as features. * refers to a statistically significant result in comparison to all the others.

Model	Accuracy
Features: Ambivert degree + Part. coeff.
DNN (3 hidden layer of 50,32,10)	79.4%
SVM (Linear, C = 0.1)	66.5%
Features: (Ambivert degree, Part. coeff.)
DNN (3 hidden layers of 50,32,10)	81.2%*
SVM (Linear, C = 0.1)	64.5%
Features: Ambivert degree
DNN (3 hidden layers of 50, 20, 10)	77.5%
SVM (Linear, C = 0.1)	67.1%
Features: Part. coeff.
DNN (3 hidden layers of 40,20,10)	71.7%
SVM (Linear, C = 0.01)	62.8%
Features: Functional connectivity W
DNN (3 hidden layer sizes: 500, 50, 10)	76.7%

Table 4.

Classification of ASD and CN with deep neural networks with nodal hub measures and connectivity featues. * refers to a statistically significant result in comparison to all the others.

Model	Accuracy
Features: Ambivert degree + Part. coeff.
DNN (3 hidden layers of 40,20,10)	74.1%*
SVM (Poly, C = 0.01, $\gamma =0.1$)	59.1%
Features: (Ambivert degree, Part. coeff.)
DNN (3 hidden neurons layers of 50,32,10)	71.6%
SVM (Poly, C = 0.001, $\gamma =0.1$)	57.9%
Features: Ambivert degree
DNN (3 hidden neurons of 40,20,10)	71.3%
SVM (Poly, C = 0.01, $\gamma =0.1$)	59.2%
Features: Part. coeff.
DNN (3 hidden neurons layers of 40,20,10)	66.1%
SVM (Sigmoid, C = 1.0, $\gamma =0.01$)	53.7%
Features: Functional connectivity W
DNN (3 hidden layers of 1000,100,10)	72.1%

4. Discussion

4.1. Considering brain functional modules while detecting network hubs

Multiple studies have shown the modular nature of brain’s functional architecture with regions in the same modules having high synchronization with each other and thus high corresponding functional connectivity (Sporns and Betzel, 2016). It has also been shown that modules in brain functional networks have heterogeneous sizes (Gupta, Rajapakse, 2018, Nicolini, Bifone, 2016), leading to higher degree for nodes in a large module and vice versa (Power et al., 2013). Therefore, if only global degree of a node is considered to detect hubs, nodes in large modules would be invariably favored (Power et al., 2013), making it imperative to detect hubs at a modular level, considering the inherent brain functional modular structure.

A weak connection signifies weak correlation between neuronal activity of the brain regions involved, which in turn points to low probability of signaling and communication between neurons in the regions. However, several studies have pointed out the importance of considering weak functional correlations while analyzing brain functional networks (Bassett, Nelson, Mueller, Camchong, Lim, 2012, Cole, Yarkoni, Repovš, Anticevic, Braver, 2012, Santarnecchi, Galli, Polizzotto, Rossi, Rossi, 2014). Therefore, weak connections should be given due importance while computing brain functional network topology. In order to account for this, previous studies detecting modular hubs have thresholded the networks such that only a fraction of initial connections in the network are retained. However, thresholding strategies used in previous studies do not consider whether the underlying modular structure in functional networks is preserved. We took several measures to consider the modular architecture and considered the effect of weak connections on detection of hubs: (i) we used the ICSC algorithm which performs modularization on unthresholded networks; (ii) while computing network hub metrics, we used percolation analysis (Gallos et al., 2012) to find the threshold which preserves modular structure in brain functional networks (Bordier et al., 2017); and (iii) we proposed a new measure called the ambivert degree that incorporates the average weight per connection information to the node’s intra-modular degree.

Using the ICSC algorithm, we detected 19 group-level modules that corresponded to well-known functional systems. On performing percolation analysis, we found that even the functional networks derived from HCP subjects, which were in a narrow age range (mean 28.3  ±  3.7) and acquired on the same scanner with an average signal-to-noise ratio of 728, have a varied percentage threshold (mean 75.6  ±  10.3). Previous studies studying subject networks (Gordon et al., 2018) did not consider this, since they performed their analysis using the same percentage threshold for all subjects.

4.2. Using ambivert degree to detect modular and network hubs

We compare the detection of modular hubs for within module processing by using intra-modular degree, ambivert degree and betweenness centrality. We systematically analyzed the importance of nodes for intra-modular processing and global network processing by performing artificial lesioning where we remove a range of hubs and observe changes in the modular or network path length. We found that ambivert degree gives significantly more crucial modular hubs across different thresholds. At the global network level, we found that hubs detected by combining ambivert degree and participation coefficients are significantly more crucial than network hubs detected by intra-modular degree and betweeness centrality. It is to be noted that the gateway coefficient, an extension of the participation coefficient introduced to detect better connector hubs (Vargas and Wahl, 2014) did not have a significant impact on detecting crucial network hubs. This means that as long as the degree and weight per connection are being considered to derive network hubs, the participation coefficient is sufficient to detect network hubs.

The variability in hub locations is a by-product of widespread inter-subject variation prevalent in brain functional architecture. However, since we considered fMRI scans of healthy subjects in a narrow age range from the same scanner, the location of hubs should be relatively stable over subjects. On studying the variability of network hubs over multiple subjects, we found that while the hubs detected by ambivert degree hubs were more invariable than those detected by betweenness centrality significantly and intra-modular degree insignificantly.

Since many previous studies have reported nodes with high intra-modular degree and participation coefficient as functional brain hubs (Nicolini, Bordier, Bifone, 2017, Power, Schlaggar, Lessov-Schlaggar, Petersen, 2013), it is important to understand the differences in anatomical locations of these hubs and the network hubs characterized by ambivert degree and participation coefficients. We found that regions from the middle frontal gyrus (L) and superior temporal gyrus (R) which were classified as brain hubs using the old scheme are dropped, and instead regions from the cuneus (L), middle occipital gyrus (R) and inferior parietal lobe are added (Supplementary Fig. S2). While newly detected regions are known to be primarily involved in the dorsal and the ventral stream visual processing (Milner and Goodale, 2008), recent studies have also pointed to the role of the cuneus for internal directed attention activity in the brain during resting state (Benedek, Jauk, Beaty, Fink, Koschutnig, Neubauer, 2016, Benedek, Schües, Beaty, Jauk, Koschutnig, Fink, Neubauer, 2018).

4.3. Disruption of network hubs in AD and ASD

Numerous studies have investigated the changes in the brain functional and structural networks caused by AD and Mild Cognitive Impairment (Dai, Lin, Li, Wang, Yuan, Yu, He, Wang, 2019, Gupta, Chan, Rajapakse, Initiative, et al., 2019, Meszlényi, Buza, Vidnyánszky, 2017, Wang, Zuo, Dai, Xia, Zhao, Zhao, Jia, Han, He, 2013), specifically the disruption of brain hubs (Buckner, Sepulcre, Talukdar, Krienen, Liu, Hedden, Andrews-Hanna, Sperling, Johnson, 2009, Dai, Yan, Li, Wang, Wang, Cao, Lin, Shu, Xia, Bi, et al., 2014, Mutlu, Landeau, Gaubert, de La Sayette, Desgranges, Chételat, 2017). The changes in modular structure with cognitive decline and AD has been extensively studied with major alterations being reported in the default mode network, the salience network, and the fronto-parietal control network (Brier, Thomas, Snyder, Benzinger, Zhang, Raichle, Holtzman, Morris, Ances, 2012, Dickerson, Sperling, 2009, Weiler, Fukuda, HP Massabki, M Lopes, R Franco, P Damasceno, Cendes, LF Balthazar, 2014). Similarly, alterations in modular structure have been reported for ASD (Padmanabhan, Lynch, Schaer, Menon, 2017, Zielinski, Anderson, Froehlich, Prigge, Nielsen, Cooperrider, Cariello, Fletcher, Alexander, Lange, et al., 2012). Therefore, the modular structure of functional networks needs to be considered while detection of hubs, but previous studies investigating disruption of hubs in diseases either used traditional thresholding methods and did not consider preservation of network modular structure or used the global degree as a measure to find network hubs (Buckner, Sepulcre, Talukdar, Krienen, Liu, Hedden, Andrews-Hanna, Sperling, Johnson, 2009, Dai, Yan, Li, Wang, Wang, Cao, Lin, Shu, Xia, Bi, et al., 2014, Itahashi, Yamada, Watanabe, Nakamura, Jimbo, Shioda, Toriizuka, Kato, Hashimoto, 2014, Mutlu, Landeau, Gaubert, de La Sayette, Desgranges, Chételat, 2017), thus giving biased results. This warranted a fresh look at the disruption of hubs in the functional networks derived from AD and ASD subjects.

The hubs detected for the CN subjects from the disease datatsets are different from the healthy subject group from the HCP dataset. Besides factors like different scanner acquisition protocol, preprocessing, and gender ratio of participants the difference in network hubs between HCP subject cohort and CN subject cohorts (from the ADNI and ABIDE) can be primarily attributed to the difference in the age of the participants (Tomasi, Volkow, 2012, Yang, Tsai, Liu, Huang, Lin, 2016). The average ages for HCP, ADNI CN, and ABIDE CN participant cohorts are 28.3 years, 76.6 years, and 15.8 years, respectively. On computing hubs of subjects suffering from AD and ASD, we found that the network hubs for the patients were different from those for CN subject-group. Specifically, the hubs in the medial and inferior temporal lobe, precuneus, and posterior cingulate cortex in the CN subject group were found to be disrupted in the AD subject group. Atrophy in the medial temporal lobe has long been shown to be a biomarker for AD (Hu et al., 2019) whereas the functional connectivity of the precuneus with the default mode network and posterior cingulate cortex with the ventral attention network is known to be disrupted in AD patients (Klaassens, van Gerven, van der Grond, de Vos, Möller, Rombouts, 2017, Yamashita, Uehara, Prawiroharjo, Yamashita, Togao, Hiwatashi, Taniwaki, Utsunomiya, Matsushita, Yamasaki, et al., 2019) which validates our findings. Similarly, our results for hub disruptions in ASD subject group were corroborated by multiple previous studies, where disruption in connectivity of the angular gyrus (Kennedy, Courchesne, 2008, Padmanabhan, Lynch, Schaer, Menon, 2017, Zielinski, Anderson, Froehlich, Prigge, Nielsen, Cooperrider, Cariello, Fletcher, Alexander, Lange, et al., 2012) and precuneus (Itahashi, Yamada, Watanabe, Nakamura, Jimbo, Shioda, Toriizuka, Kato, Hashimoto, 2014, Padmanabhan, Lynch, Schaer, Menon, 2017, Zielinski, Anderson, Froehlich, Prigge, Nielsen, Cooperrider, Cariello, Fletcher, Alexander, Lange, et al., 2012) regions participating in the DMN have been studied and alterations of both functional and structural fibers in the anterior cingulum (Ikuta, Shafritz, Bregman, Peters, Gruner, Malhotra, Szeszko, 2014, Itahashi, Yamada, Watanabe, Nakamura, Jimbo, Shioda, Toriizuka, Kato, Hashimoto, 2014, Jou, Jackowski, Papademetris, Rajeevan, Staib, Volkmar, 2011, de Lacy, Doherty, King, Rachakonda, Calhoun, 2017, Thakkar, Polli, Joseph, Tuch, Hadjikhani, Barton, Manoach, 2008) have been reported.

4.4. Brain hubs as diagnostic features for AD and ASD

We hypothesized that the disruption of hubs in AD and ASD can be used as a potential diagnostic tool for detecting these diseases. Using multiple machine learning models, we found that a 3 hidden layer feedforward DNN using nodal hub measures as features were capable of detecting AD and ASD patients from CN subjects with an accuracy of 81% and 74%, respectively. We also found that combining both the inter-modular and intra-modular hub measures improves the classification accuracy.

Previous studies in the area have used functional connectivity measures (Iidaka, 2015, Ju, Hu, Zhou, Li, 2019, Wang, Chen, Fushing, 2012) or additional graph measures (Khazaee, Ebrahimzadeh, Babajani-Feremi, 2016, Li, Qin, Chen, Li, 2013) to perform classification of AD and ASD. The large number of training features not only causes overfitting of the models because of few available training samples but also uses high resources due to the large number of trainable weights (Gupta et al., 2019). In this study, we employed novel hub features including ambivert degree features for AD and ASD and demonstrated their use as diagnostic features for diseases. We observed that the hub disruption was more widespread in case of AD than ASD (refer Fig. 6), and correspondingly the difference in classification accuracy based on nodal hub measures and functional connectivity features was more for AD than ASD. While previous studies have used functional connectivity features for disease state classification, but For example: using just 0.09% (for AD) and 0.03% (for ASD) of the total number of trainable weights used in functional connectivity based models, we obtained a significantly higher classification accuracy. This work paves the way for using hub scores instead of functional connectivity as input features for diseases where hub disruption is a trademark.

5. Conclusion

Brain hubs are crucial for information processing and are often susceptible to neurological diseases. Previous studies did not consider the effect of weak connections and modular structure for detection of functional hubs. Using artificial lesioning, we showed that weak connections in the weighted brain functional networks can lead to the detection of sub-optimal hubs, and the newly proposed measure, ambivert degree, detect hubs that are more crucial for both intra-modular and whole network information processing. We use the ambivert degree to find widespread perturbation in the hubs in AD and ASD patients. We used this property to develop effective classifiers for these diseases and showed that these classifiers perform significantly better than functional connectivity based classifiers, with negligible number of trainable weights in comparison. The affected hubs detected by our methods could be used as biomarkers for neuropsychiatric and neurodegenerative diseases where hub disruption is a hallmark.

CRediT authorship contribution statement

Sukrit Gupta: Conceptualization, Methodology, Software, Writing - original draft, Writing - review & editing. Jagath C. Rajapakse: Conceptualization, Methodology, Writing - original draft, Writing - review & editing. Roy E. Welsch: Conceptualization, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no competing interests.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/