Predictive Accuracy of a Polygenic Risk Score–Enhanced Prediction Model vs a Clinical Risk Score for Coronary Artery Disease

Key Points

Question

Do polygenic risk scores have incremental value over and above prediction models that are currently used in clinical practice for cardiovascular risk stratification in general populations?

Findings

In this observational study of 352 660 individuals with no history of cardiovascular disease at baseline, the addition of a polygenic risk score to pooled cohort equations clinical risk score was associated with a modest but statistically significant improvement in discriminative accuracy for incident coronary artery disease (CAD) compared with pooled cohort equations alone (incremental C statistic, 0.02).

Meaning

The use of genetic information over the pooled cohort equations model warrants further investigation before clinical implementation.

Abstract

Importance

The incremental value of polygenic risk scores in addition to well-established risk prediction models for coronary artery disease (CAD) is uncertain.

Objective

To examine whether a polygenic risk score for CAD improves risk prediction beyond pooled cohort equations.

Design, Setting, and Participants

Observational study of UK Biobank participants enrolled from 2006 to 2010. A case-control sample of 15 947 prevalent CAD cases and equal number of age and sex frequency–matched controls was used to optimize the predictive performance of a polygenic risk score for CAD based on summary statistics from published genome-wide association studies. A separate cohort of 352 660 individuals (with follow-up to 2017) was used to evaluate the predictive accuracy of the polygenic risk score, pooled cohort equations, and both combined for incident CAD.

Exposures

Polygenic risk score for CAD, pooled cohort equations, and both combined.

Main Outcomes and Measures

CAD (myocardial infarction and its related sequelae). Discrimination, calibration, and reclassification using a risk threshold of 7.5% were assessed.

Results

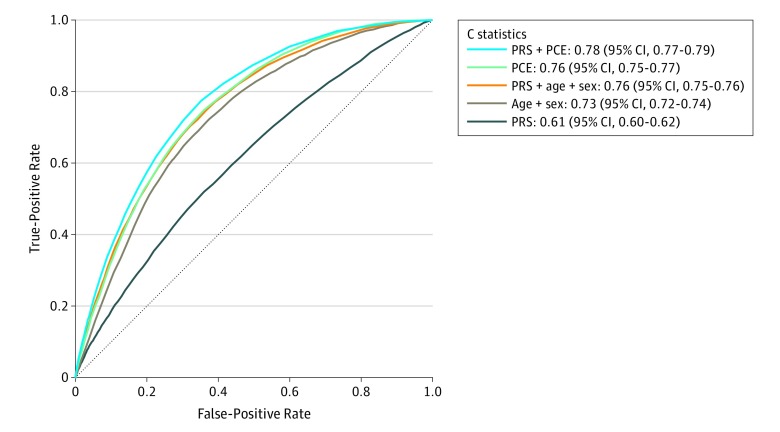
In the cohort of 352 660 participants (mean age, 55.9 years; 205 297 women [58.2%]) used to evaluate the predictive accuracy of the examined models, there were 6272 incident CAD events over a median of 8 years of follow-up. CAD discrimination for polygenic risk score, pooled cohort equations, and both combined resulted in C statistics of 0.61 (95% CI, 0.60 to 0.62), 0.76 (95% CI, 0.75 to 0.77), and 0.78 (95% CI, 0.77 to 0.79), respectively. The change in C statistic between the latter 2 models was 0.02 (95% CI, 0.01 to 0.03). Calibration of the models showed overestimation of risk by pooled cohort equations, which was corrected after recalibration. Using a risk threshold of 7.5%, addition of the polygenic risk score to pooled cohort equations resulted in a net reclassification improvement of 4.4% (95% CI, 3.5% to 5.3%) for cases and −0.4% (95% CI, −0.5% to −0.4%) for noncases (overall net reclassification improvement, 4.0% [95% CI, 3.1% to 4.9%]).

Conclusions and Relevance

The addition of a polygenic risk score for CAD to pooled cohort equations was associated with a statistically significant, yet modest, improvement in the predictive accuracy for incident CAD and improved risk stratification for only a small proportion of individuals. The use of genetic information over the pooled cohort equations model warrants further investigation before clinical implementation.

This study uses UK Biobank data to examine whether adding polygenic risk information to the pooled cohort equations improves the accuracy of risk prediction for coronary artery disease (CAD).

Introduction

Cardiovascular disease (CVD) is the leading cause of death worldwide.¹ Targeted CVD primary prevention strategies require timely identification of people at increased risk to focus effective lifestyle or pharmacological interventions. Risk prediction models have been developed to estimate the probability of developing cardiovascular outcomes in asymptomatic individuals.² Currently, risk assessment guidelines from the American College of Cardiology and American Heart Association recommend lipid-lowering treatment for individuals with 10-year absolute risk of atherosclerotic CVD greater than 7.5% based on pooled cohort equations.³

Over the past 10 years, considerable progress has been made in identifying genetic variants/single-nucleotide polymorphisms (SNPs) that are associated with coronary artery disease (CAD).⁴ Germline genetic variants are attractive biomarkers because they are stable throughout the lifetime and could potentially provide information about disease predisposition from an early age. While most common genetic variants individually make a small contribution to disease risk, taken together in the form of genetic or polygenic risk scores, they may enhance predictive ability for CAD and more efficiently stratify those at increased risk of future disease.⁵

Recently, studies^6,7 using (1) newly discovered genetic variants for CAD and (2) novel methods to generate polygenic risk scores that use genome-wide variation rather than only genome-wide significant variants showed improved performance of polygenic risk score for CAD prediction compared with earlier studies.^8,9,10,11,12 However, the added value of polygenic risk score on top of well-established and validated risk prediction models was not examined and, therefore, the clinical utility of polygenic risk score in risk prediction remains unclear. Here, using the UK Biobank cohort, the aim was to evaluate the potential of the polygenic risk score to improve risk prediction for CAD over and above pooled cohort equations and, in secondary analysis, QRISK3 models currently used for risk stratification in US and UK clinical practice, respectively.

Methods

Study Participants

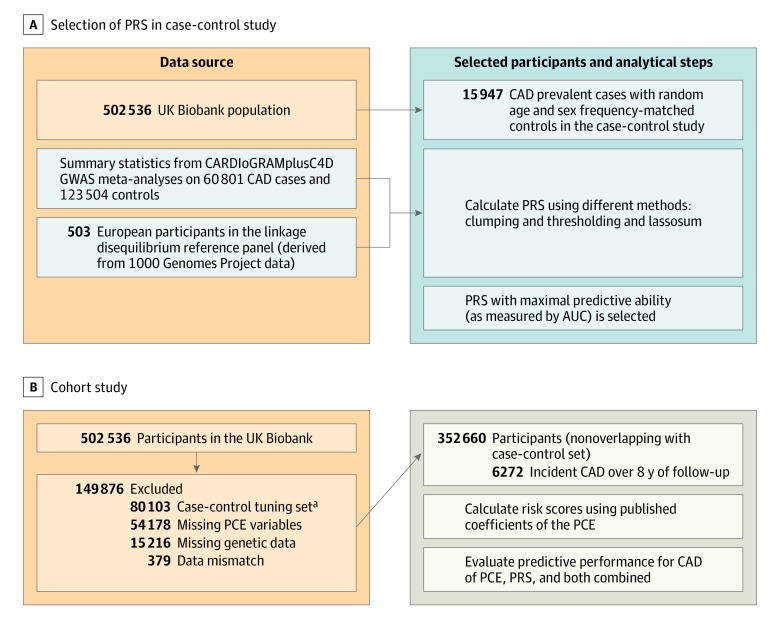
The UK Biobank includes 502 536 volunteers aged 40 to 69 years at baseline recruited through UK National Health Service registers. Participants attended 1 of 20 dedicated assessment centers nationally during 2006 to 2010.¹³ The study received ethical approval from the National Health Service’s National Research Ethics Service North West (11/NW/0382). All participants provided written informed consent for the study and completed a computer-based questionnaire on lifecourse exposures, medical history, and treatments and underwent a standardized portfolio of clinical measurements. Biomarkers were measured in stored serum and red blood cells as described in detail elsewhere.¹⁴ Our study design is shown in Figure 1.

Figure 1. Study Design and Flowchart for Coronary Artery Disease (CAD).

To select the method with the best discrimination based on area under the curve (AUC), clumping and thresholding and lassosum were used to calculate polygenetic risk scores (PRS) applied to a case-control set (prevalent cases). For this calculation, summary data from the largest genome-wide association study (GWAS) on CAD (CARDIoGRAMplusC4DREF¹⁵) that excludes UK Biobank and data on linkage disequilibrium were used. The resulting PRS was applied to a nonoverlapping set of participants from the UK Biobank with no preexisting cardiovascular disease, aged 40 to 69 years at baseline, and who were followed up for incident CAD events. In this population, the pooled cohort equations (PCE) model was calculated and different models (PRS, PCE, and PCE enhanced with PRS) were compared in terms of their predictive accuracy based on discrimination, calibration, and reclassification metrics.

^aCAD and cardiovascular disease tuning sets combined.

Our primary end point was CAD, taking advantage of large genome-wide association studies (GWAS) for CAD.¹⁵ In secondary analysis, CVD was examined (CAD as well as angina and stroke). The study population was divided into (1) a tuning set for the optimization of parameters of the polygenic risk score calculation (case-control study) comprising prevalent CAD cases (prevalent cases were defined by date of CAD event preceding the date of assessment or self-reported history of CAD at baseline) and randomly selected age and sex frequency–matched controls and (2) an independent cohort study (testing set) of participants with no history of CVD at baseline followed up for incident CAD events (Figure 1). The 2 data sets (tuning case-control and cohort testing set) had no overlapping participants. We aimed to maximize sample size for the incident analysis by using the prevalent cases of CAD for the polygenic risk score tuning. We were able to use prevalent cases along with matched controls for the polygenic risk score calculation as the genetic information is fixed at birth and therefore precedes these events. Study design for the CVD analysis is shown in eFigure 1 in the Supplement.

Definition of Variables for Risk Scores

The primary analysis was based on the pooled cohort equations model. Secondary analysis on the UK-recommended QRISK3 score is presented in the eMethods, eTables, and eFigures in the Supplement.¹⁶ We matched the predictors of the updated pooled cohort equations¹⁷ to the variables available in the cohort. The pooled cohort equation algorithm includes information on age, sex, race and ethnicity, smoking, total and high-density lipoprotein cholesterol, systolic blood pressure, and diabetes. Information on ethnicity was gathered via a self-reported questionnaire with a predefined list of categories. For the UK-based QRISK3 score in secondary analysis, the model uses a larger set of variables including body mass index, family history of heart disease, area deprivation score (Townsend), smoking intensity, and a number of prevalent conditions including chronic kidney disease stages 3 through 5, atrial fibrillation, migraine, rheumatoid arthritis, systemic lupus erythematosus, mental illness, erectile dysfunction, and antihypertensive medication use.¹⁸ Details on the definition of each variable are included in the eMethods in the Supplement.

Cardiovascular Outcomes

For all participants, retrospective and prospective linkage to electronic health data was available, including hospital episode statistics data on hospital admissions and Office for National Statistics cause of death data. Hospital episode statistics include coded data on diagnoses and operations. We defined CAD and CVD from hospital episode statistics and mortality data using the International Classification of Diseases and the Office of Population Censuses and Surveys’ Classification of Interventions and Procedures version 4 codes for CAD and CVD,^18,19 along with related codes for self-reported diagnoses and previous procedures (eTables 1 and 2 in the Supplement). This definition of CAD includes myocardial infarction and its related sequelae, whereas the CVD definition additionally includes angina, nonhemorrhagic stroke, and transient ischemic attack.

The recorded episode date, admission date, or operation date in hospital episode statistics was considered the date of the event. If none of these were available, one of elective date, episode end, or discharge date was used. For individuals with multiple CAD or CVD hospitalizations, the date of the earliest event was used as the date of event. Fatal CAD or CVD events from mortality data were included in the main outcomes. Prevalent disease at baseline was defined using self-reported and/or hospital episode statistics data with date of event preceding the date of attendance at study assessment center. Follow-up time for each participant was calculated as the number of days from assessment date until either event of interest, competing event (other cause of death), or censorship date according to origin of the hospital data (England: March 31, 2017; Scotland: October 30, 2016; Wales: May 30, 2016).

Polygenic Risk Score

Detailed information about genotyping and imputation in this study has been provided elsewhere.^20,21 Briefly, DNA samples of study participants were genotyped using initially custom Affymetrix arrays (49 950 participants) for the UK Biobank Lung Exome Variant Evaluation study and subsequently the UK Biobank Axiom array, designed to optimize imputation performance across the genome.^20,21 Genotype imputation was based on a merged sample of UK10K sequencing and 1000 Genomes Project imputation reference panels. Imputation was centrally carried out by the study using an algorithm implemented in the IMPUTE2 program.²² Genetic principal components to account for population stratification were centrally computed. We derived polygenic risk score for CAD as a weighted sum of risk alleles, using summary statistics from the largest GWAS on CAD that excluded participants from the present study (CARDIoGRAMplusC4D) (Figure 1).¹⁵

For the tuning (testing of different model parameters to optimize the model’s discrimination) of the polygenic risk score, we implemented 2 methods: (1) clumping and thresholding using PRSice-2 software (version 2.1.11) and (2) lassosum²³; detailed information on description and choice of polygenic risk score methods are described in the eMethods in the Supplement. Briefly, clumping and thresholding use several P value thresholds to maximize predictive ability of polygenic risk score. Lassosum implements a penalized regression model and accounts for linkage disequilibrium (LD) between SNPs using an external reference panel (eFigure 1 in the Supplement).²⁴ Lassosum is a recently proposed polygenic risk score method, which for CAD has been shown to perform as well as or better than the widely used LDpred method.^23,25 Lassosum has model parameters (s and lambda) that must be tuned, which we carried out in the case-control sample of prevalent CAD cases and sex and age frequency–matched controls, adjusting for genotype batch and first 10 genetic principal components. We ran lassosum (version 0.4.3) on 2 sets of SNPs with INFO score thresholds of 0.3 and 0.999, containing approximately 6.7 million and approximately 1 million SNPs, respectively. We then computed the area under the curve (AUC) of the receiver operating characteristic using logistic regression for prevalent CAD (and CVD in secondary analyses) and selected the polygenic risk score with the highest AUC for subsequent analyses. We calculated heritability estimates for genetic variants and CAD based on (1) LDHub to calculate the LD score regression (LDSR) (h²_LDSR = 0.0728, SE = 0.0054, using only HapMap 3 SNPs with 1000 genomes minor allele frequency >5%) and (2) the genomic-relatedness–based restricted maximum-likelihood (GREML) approach (h²_GREML = 0.22, SE = 0.03, using only SNPs with MAF >1%).²⁶

Statistical Analysis

We excluded participants with missing genetic data, mismatched data (eg, reported and genetic sex), or missing data on predictors, with the exception of imputation of missing smoking intensity data (light, moderate, heavy smoker) among current smokers for the QRISK3 model only (Figure 1 and the eMethods in the Supplement).

We calculated the updated pooled cohort equations score, and used the baseline hazard and weights for each constituent predictor variable, as previously published.¹⁷ We examined several models separately: (1) pooled cohort equations; (2) polygenic risk score for CAD; (3) age and sex; (4) age, sex, and polygenic risk score; and (5) pooled cohort equations and polygenic risk score. We used Cox proportional hazards regression with time of follow-up as the underlying time variable. The proportionality assumption was visually inspected using the scaled Schoenfeld residuals. We assessed the discrimination and calibration of models in the total cohort population, and separately in men and women and in those aged younger than 55 years old and those aged 55 years old and older. The discrimination of each model was assessed using Harrell’s C statistic and its 95% CI.^27,28,29 The C statistic is a rank-order statistic for predictions against true outcomes, with values ranging from 0.5 (no discrimination) to a theoretical maximum of 1.0. Calibration of the original models and their subsequent recalibration were graphically assessed by plotting the observed probability (Kaplan-Meier estimates) against the mean predicted probability within tenths of the predicted probabilities. For recalibration, we estimated the baseline survival function in the cohort (intercept) and combined this with the predicted hazard ratios from the published model to obtain recalibrated predicted probabilities. We calculated the calibration slope (b = 1 indicates perfect calibration) and the Greenwood-Nam-D’Agostino P value to quantitatively assess calibration of the models³⁰; this tests the null hypothesis that the observed and expected probabilities are identical in each group.

We calculated the net reclassification improvement (NRI) at the current recommended threshold for treatment in the United States (7.5%) and United Kingdom (10%), the associated integrated discrimination improvement (IDI), and the category-free NRI.³¹ A brief explanation of these metrics is included in eMethods in the Supplement.

In secondary analyses, we used CVD instead of CAD as the outcome of interest and QRISK3 instead of pooled cohort equations as the baseline model. Additionally, as a sensitivity analysis, we recalculated pooled cohort equations (and QRISK3) after excluding individuals taking lipid-lowering medications. Due to the potential for type I error caused by multiple comparisons, findings for secondary and sensitivity analyses should be interpreted as exploratory.

Statistical analyses were performed in R software, version 3.3 (R Project for Statistical Computing).³² We considered 2-sided P values less than .05 statistically significant.

Results

The case-control study comprised 15 947 participants with prevalent CAD and an equal number of controls for the tuning of the polygenic risk score (eTable 3A in the Supplement). The independent cohort study had 352 660 participants (mean age, 55.9 years), with a median follow-up of 8 years (interquartile range, 1.3) with 6272 incident CAD events. The median follow-up for CAD cases was 4.4 years (interquartile range, 5.4). Participants excluded due to missing covariates had similar baseline characteristics (demographic, lifestyle, and comorbidities) as those included in the cohort analysis (eTable 3B-eTable 3E in the Supplement).

In the case-control analysis (see eTable 3A in the Supplement for descriptive characteristics), among the approaches to obtain the polygenic risk score for CAD, the lassosum method applied to 1 037 385 SNPs using an INFO Score threshold greater than 0.999 showed the highest AUC of 0.63 (95% CI, 0.62-0.64) (eTable 4 in the Supplement).

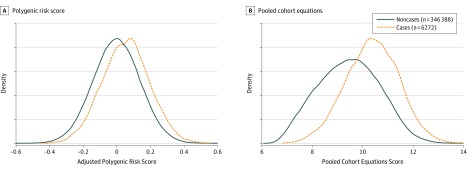
In cohort analysis, 54 178 individuals were excluded due to missing data on at least 1 covariate required for pooled cohort equation calculation. The discrimination of the polygenic risk score for CAD was lower than in the tuning case-control set (C statistic, 0.61 [95% CI, 0.60-0.62]) (Table) with associated overlapping distributions of polygenic risk score for CAD among incident CAD cases and noncases (Figure 2). The hazard ratio of polygenic risk score for CAD (per SD increase) for CAD was 1.32 (95% CI, 1.30-1.34; P = 2.3 × 10⁻²⁰⁹). Discrimination of the pooled cohort equations model measured by the C statistic was 0.76 (95% CI, 0.75-0.77) for CAD reflected by less overlapping distributions between incident cases and noncases compared with polygenic risk score (Table and Figure 2). Subgroup analysis by age group (younger or older than 55 years) and men and women separately showed overall higher discrimination in women than men and higher in younger age groups rather than older age groups (Table). The addition of polygenic risk score for CAD to the recalibrated pooled cohort equations model showed a statistically significant improvement in discrimination, with the C statistic increasing to 0.78 (95% CI, 0.77-0.79) and an associated change from pooled cohort equations alone of 0.02 (95% CI, 0.01-0.03) (Table and Figure 3). Results for individuals not receiving lipid-lowering medications at baseline (n = 306 421) showed similar discrimination performance (Table).

Table. C Statistics for Coronary Artery Disease in the Full Population and Stratified by Age Class (Older or Younger Than 55 Years of Age) and Sex^a.

	C Statistic (95% CI)
	All	Participants Aged <55 y	Participants Aged ≥ 55 y	Men	Women
All Participants	N = 352 660	n = 147 985	n = 204 675	n = 147 363	n = 205 297
Events, No.	6272	1350	4922	4493	1779
Polygenic risk score	0.61 (0.60-0.62)	0.64 (0.63-0.66)	0.60 (0.59-0.61)	0.61 (0.60-0.62)	0.61 (0.60-0.63)
Age and sex	0.73 (0.72-0.74)	0.73 (0.72-0.75)	0.68 (0.68-0.69)	0.64 (0.63-0.65)	0.68 (0.67-0.70)
Polygenic risk score + age and sex	0.76 (0.75-0.76)	0.76 (0.75-0.78)	0.71 (0.70-0.72)	0.68 (0.67-0.69)	0.71 (0.70-0.73)
Pooled cohort equations	0.76 (0.75-0.77)	0.78 (0.76-0.80)	0.71 (0.71-0.72)	0.68 (0.67-0.69)	0.74 (0.73-0.75)
Polygenic risk score + pooled cohort equations	0.78 (0.77-0.79)	0.80 (0.79-0.82)	0.74 (0.73-0.74)	0.71 (0.70-0.72)	0.76 (0.74-0.77)
Participants Not Receiving Lipid-Lowering Treatment at Baseline
	n = 306 421	n = 140 266	n = 166 155	n = 122 546	n = 183 875
Events, No.	4792	1149	3643	3381	1411
Polygenic risk score	0.61 (0.60-0.62)	0.65 (0.63-0.66)	0.61 (0.60-0.62)	0.62 (0.61-0.63)	0.61 (0.60-0.63)
Age and sex	0.74 (0.73-0.75)	0.74 (0.72-0.75)	0.69 (0.68-0.70)	0.65 (0.64-0.66)	0.69 (0.67-0.71)
Polygenic risk score + age and sex	0.76 (0.76-0.77)	0.77 (0.75-0.79)	0.72 (0.71-0.73)	0.70 (0.69-0.71)	0.72 (0.70-0.73)
Pooled cohort equations	0.77 (0.76-0.78)	0.78 (0.77-0.80)	0.72 (0.71-0.73)	0.69 (0.68-0.70)	0.75 (0.73-0.76)
Polygenic risk score + pooled cohort equations	0.79 (0.78-0.80)	0.80 (0.79-0.82)	0.74 (0.73-0.75)	0.72 (0.71-0.73)	0.76 (0.75-0.78)

^aCox proportional hazard models for coronary artery disease using recalibrated models for polygenic risk score, pooled cohort equations, and both combined.

Figure 2. Density Plots of the Adjusted Polygenic Risk Score and the Pooled Cohort Equations for Coronary Artery Disease Cases and Controls in Cohort Analysis.

After calculating the polygenic risk score on the selected single-nucleotide polymorphisms, residual values of the polygenic risk score are plotted from regression against sex, age, batch, and the first 10 principal components.

Figure 3. Receiver Operator Characteristic Curves and C Statistics for Different Models in Cohort Analyses of 352 660 Participants Aged 40 to 69 Years Old Over a Mean of 8 Years of Follow-up With 6272 Incident Coronary Artery Disease (CAD) Events.

See eTable 2 in the Supplement for the definition of CAD. PCE indicates pooled cohort equations; PRS, polygenic risk score.

When the observed and predicted cumulative incidences of CAD events were compared across each tenth of predicted risk, pooled cohort equations overestimated risk across the range of predicted probabilities (calibration graphs in eFigure 2 in the Supplement). On recalibration by fitting the predicted log–hazard ratios as covariates in the model, calibration was improved for pooled cohort equations and for pooled cohort equations plus polygenic risk score for CAD (eFigure 2 and eTable 5 in the Supplement).

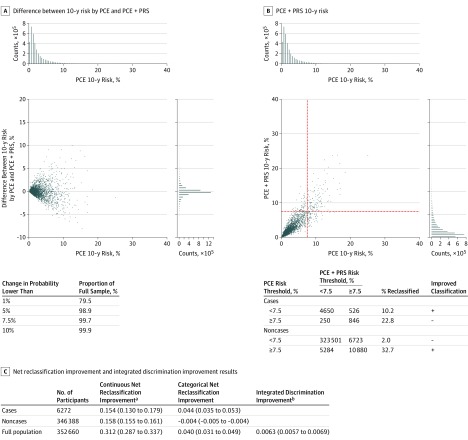
When polygenic risk score for CAD was added to the pooled cohort equations model, predicted risk changed by less than 1% for 79.5% of participants, and changed by 5% or more for 1.1% of participants (Figure 4A). At a risk threshold of 7.5%, 526 of 6272 cases (8.4%) were correctly reclassified to the higher-risk category and 250 of 6272 cases (4.0%) incorrectly moved to the lower-risk category. For the noncases, 5284 of 346 388 (1.5%) correctly moved down the 7.5% risk threshold, whereas 6723 of 346 388 (1.9%) incorrectly moved up (Figure 4B).

Figure 4. Change in Predicted Probabilities and Risk Reclassification.

A, Change in the predicted probabilities (expressed as a percentage) of the recalibrated model with pooled cohort equations (PCE) after the addition of the polygenic risk score (PRS) for coronary artery disease (CAD). The x-axis is the predicted probability from the original PCE model, and the y-axis is the difference in 10-year probabilities of an event between the PRS-augmented model and PCE. A random draw of 1% of the participants is represented on the scatter plot. Histograms along the x- and y-axes are based on all participants. The associated table shows the percentage of participants whose predicted probabilities changed by less than the given thresholds. B, Predicted probabilities by PCE and PCE plus PRS, with dotted lines showing the 7.5% threshold. The associated table shows the numbers reclassified according to a 7.5% risk threshold. Rows corresponding to an improved classification with the PCE + PRS model are denoted by a plus sign and a deterioration of the classification by a minus sign. C, Table of net reclassification improvement (NRI) and integrated discrimination improvement (IDI). The NRI is defined by (1) in the continuous case, the sum of proportions of cases and noncases with improved combined score (ie, higher combined score for cases denoted by P[up|case] {where P indicates probability} and lower for noncases denoted by P[down|noncase]) minus the sum of proportions with deteriorated combined score (ie, P[up|noncase]) and P[down|case]), and (2) in the categorical case, as changes in 7.5% predicted probability. A positive NRI indicates a better combined score overall. The IDI measures the increase in the difference of average probabilities of an event in cases (P_PCE+PRS[case] and P_PCE [case]) and noncases (P_PCE+PRS[noncase]) and P_PCE [noncase]). The higher the IDI, the more discriminant the combined score. In this case, the increase in risk difference between cases and noncases after addition of the PRS for CAD to PCE was only 0.6%, indicating a small difference.

^aNRI = P(up|case) − P(down|case) − P(up|noncase) + P(down|noncase).

^bIDI = P_pce+prs(case) − P_pce+prs(noncase) − P_pce(case) + P_pce(noncase).

Overall, the NRI was 4.4% (95% CI, 3.5% to 5.3%) for cases and −0.4% (95% CI, −0.5% to −0.4%) for noncases (Figure 4C). After addition of the polygenic risk score for CAD to pooled cohort equations according to the IDI metric, the increase in risk difference between cases and noncases was 0.006 (95% CI, 0.006 to 0.007) (Figure 4C).

Secondary Analyses

The median follow-up among CVD cases was 4.5 years (interquartile range, 4.0). When CVD was examined as the outcome of interest for pooled cohort equations (see eFigure 1 in the Supplement for study design), all prediction metrics (C statistic, NRI, and IDI) were smaller and the incremental value of polygenic risk score for CVD over and above pooled cohort equations was smaller (increase in C statistic, 0.007 [95% CI, 0.002-0.012]) than for CAD (eTables 5 and 6 and eFigures 3-6 in the Supplement).

The incremental value of polygenic risk score for CAD over and above QRISK3, which is the predictive model currently recommended in UK clinical practice, was also examined. For these analyses, 56 108 individuals with missing data for at least 1 QRISK3 covariate were excluded, and smoking intensity was imputed among current smokers for 7827 with missing intensity data (eMethods in the Supplement). Discrimination of QRISK3 and QRISK3 enhanced with polygenic risk score for CAD and reclassification analysis for a cutoff of 7.5% and 10%, respectively (as currently used in the United Kingdom), are presented in eTables 7-9 in the Supplement. QRISK3 performed slightly better than pooled cohort equations with regard to discriminative accuracy for incident CAD (C statistic, 0.79 [95% CI, 0.79-0.80]). The incremental value of polygenic risk score for CAD was smaller when added to QRISK3 compared with when added to pooled cohort equations (incremental C statistic, 0.015 [95% CI, 0.008-0.023]).

Discussion

In this analysis, adding genetic information to the pooled cohort equations clinical risk score was associated with only modest improvements in predictive accuracy for CAD and did not strongly influence the predicted probabilities for most participants.

Several other studies have investigated the potential for genetic variants to improve CAD risk prediction. They reported weak or no evidence for added value from risk scores based on GWAS significant variants^9,10,11,12 or LD-based approaches to select SNPs from GWAS findings.⁸ More recently, Khera et al⁷ and Inouye et al,⁶ using different methods to construct polygenic risk score with thousands or millions of genetic variants, supported a role for genetic information in risk assessment of CAD using UK Biobank data. However, both studies had limitations including the unavailability at that time of cholesterol measurements. Therefore, they did not assess the predictive accuracy of polygenic risk score over existing risk prediction models, such as pooled cohort equations or QRISK3, which are used in clinical practice, nor did they assess model calibration. In the present study, recalibrated pooled cohort equations plus polygenic risk score was used to assess and improve model calibration.

As previously shown, novel predictors, such as polygenic risk score, are more likely to show improved prediction over baseline models that are not well calibrated or not optimally defined.³³ Specifically, the incremental value of novel predictors depends on the discrimination potential of the baseline model. The same predictor may show greater discrimination when added to a poorly compared with a well-specified baseline model.³³ Inouye et al⁶ examined the incremental value of genetic information compared with a CVD risk factor model (though without cholesterol levels) with a C statistic of 0.67 whereas in the present study, pooled cohort equations had a C statistic of 0.76. This difference might explain some of the seemingly large improved risk prediction from addition of polygenic risk score in the study by Inouye et al⁶ compared with the present results. Similarly, the slightly greater improvement in discrimination here by addition of polygenic risk score to clinical models in men compared with women may reflect the poorer performance of these models in men, as previously reported.^19,34

Genotyping is already becoming a relatively inexpensive measure, requiring only a one-off assessment that can be obtained from birth. Germline genetic variants are therefore appealing as putative predictors of lifetime disease risk. However, the potential implementation of polygenic risk score in clinical practice needs careful evaluation. First, in this study, state-of-the-art polygenic risk score only modestly improved prediction. The number of people meaningfully changing risk category and, therefore, receiving different treatment strategies based on genetic information is relatively small, with improvements mainly seen among cases reclassified to higher risk by addition of polygenic risk score to pooled cohort equations whereas noncases had worse reclassifications (more noncases moved to the higher-risk category than were correctly reclassified to the lower-risk category). The relative benefit of those correct vs incorrect reclassifications in cases and noncases needs to take into account the risk-benefit profile of statins in a decision analysis and subsequent economic evaluation.³⁵ Still, the largest number of CAD and CVD events still occur among lower-risk categories (below treatment thresholds) arguing for continued population-based approaches to lower CVD risk such as programs to increase physical activity, improve nutrition, and prevent smoking.³⁶

Second, assuming polygenic risk score can predict lifetime risk early in life leading to earlier and more targeted prevention, the effect of obtaining genetic risk information at early ages is unknown. This is particularly important as the present results showed that a model with polygenic risk score and age and sex achieves similar discrimination as the pooled cohort equations model alone. Therefore, genetic information, which can be measured from birth, may have a role in risk prediction when clinical variables cannot be measured in middle age, eg, unavailability or low uptake of screening programs in certain populations. Nonetheless, current evidence shows that provision of genetic information to individuals does not motivate lifestyle modifications and therefore may have a limited role in risk communication strategies.³⁷ Furthermore, possible harms of providing genetic information (such as increased anxiety), especially at younger ages, need to be evaluated, eg, via randomized clinical trials.

This study has strengths. The presented analysis followed risk prediction reporting guidelines³⁸ to assess model discrimination and calibration and used previously validated models (pooled cohort equations and QRISK3) that are currently recommended in US and UK clinical guidance. The analysis benefited from the large sample size (including more than 6000 incident CAD events) and application of differing polygenic risk score methodologies to maximize predictive ability: clumping and thresholding and the lassosum method. The lassosum method uses penalized regression to calculate polygenic risk score while other recent studies⁷ have used an alternative method called LDpred, a Bayesian shrinkage approach; lassosum achieved slightly improved prediction of CAD over LDpred in the WTCCC data set.²³

Limitations

This study also has several limitations. First, this study was restricted to participants aged 40 to 69 years who were mostly of European ancestry and studies in people in other age groups and ancestries are needed. In addition, the value of continuous assessment of clinical risk factors over the lifetime has not been examined.

Second, this study evaluated CAD as the primary outcome whereas pooled cohort equations and QRISK3 were developed to predict CVD. Nevertheless, in the present study, pooled cohort equations and QRISK3 performed better for CAD than CVD, supporting their use for CAD as well as CVD prediction.

Third, pooled cohort equations and QRISK3 are designed to predict 10-year risk while median follow-up in this study was 8 years; this mismatch was, however, at least partially corrected by the recalibration process. While pooled cohort equations and QRISK3 overestimated risk in this study, this may be because the studied population includes a highly selected group of volunteers who are healthier than the general population¹³; again, this overestimation was corrected on recalibration. Conversely, before recalibration, polygenic risk score underestimated the risk in low-risk participants and overestimated the risk in high-risk participants. This may have been a result of the tuning process and was again remedied after recalibration. These findings underlie the importance of comprehensive assessment of calibration and careful recalibration of polygenic risk score models, a feature not commonly reported in polygenic risk score investigations. The high proportion of participants taking lipid-lowering treatment might also have driven the relatively low event rate in this population. Nevertheless, results were similar when analyses were restricted to individuals not taking lipid-lowering medications.

Fourth, the polygenic risk score in this study included low frequency and common variants (>0.5%)¹⁵ and did not examine the predictive value of rare genetic variants known to affect CAD risk such as familial hyperlipidemia.

Fifth, information on other potential important predictors, such as coronary artery calcium, was not available to examine the incremental value of genetic information over and above pooled cohort equations with these additional predictors.

Sixth, the adjudicated algorithm that incorporates self-report, death, and hospital inpatient data for the definition of incident CAD and CVD may have introduced some misclassification.

Seventh, the tuning of the PRS in the case-control analysis used prevalent CAD cases, which may have introduced survival bias. However, simulation studies have shown that potential survival bias has a limited effect on genetic effect estimates of subsequent event risk.³⁹ In addition, the case-control and cohort samples, although not overlapping, were derived from the same study, which may limit generalizability.

Eighth, participants with missing data in 1 or more predictors were excluded from the present analyses. However, individuals with missing data on covariates were not substantially different on demographic information and main characteristics compared with those included and therefore missing data are unlikely to have meaningfully affected the reported estimates.

Conclusions

The addition of a polygenic risk score for CAD to pooled cohort equations was associated with a statistically significant, yet modest, improvement in the predictive accuracy for incident CAD and improved risk stratification for only a small proportion of individuals. The use of genetic information over the pooled cohort equations model warrants further investigation before clinical implementation.

Supplement.

eMethods

eReferences

eTable 1. Definition of QRISK3 Variables in UK Biobank

eTable 2. Definition of Coronary Artery Disease (CAD) and Cardiovascular Disease (CVD)

eTable 3. Descriptive Characteristics

eTable 4. Association of Different Polygenic Risk Scores (PRS) With Coronary Artery Disease (CAD) and Cardiovascular Disease (CVD) in Tuning Case-Control Studies and in Prospective Cohort Study

eTable 5. Recalibration Coefficients for CAD and CVD Analyses From Cox Regression (PCE)

eTable 6. C Statistics (Derived From Cox Regression) for CVD Using Recalibrated Models in the PCE Prospective Cohort

eTable 7. Recalibration Coefficients for CAD and CVD Analysis From Cox Regression (QRISK3)

eTable 8. C Statistics (Derived From Cox Regression) for CAD and CVD Using Recalibrated Models in the QRISK3 Prospective Cohort

eTable 9. Risk Reclassification at 7.5% and 10% Thresholds for CAD and CVD Using Recalibrated Models: QRISK3 and QRISK3 Plus PRS

eFigure 1. Study Design and Flowchart for Cardiovascular Disease With PCE

eFigure 2. Calibration Plots for PCE, Polygenic Risk Score for Coronary Artery Disease (CAD) (PRS_CAD) and Both Combined, Using a UK Biobank Prospective Cohort Sample

eFigure 3. Distributions of PRS and PCE for CVD in the Prospective Cohort

eFigure 4. Calibration Plots for PCE, Polygenic Risk Score for CVD (PRS_CVD) and Both Combined, Using a UK Biobank Prospective Cohort Sample

eFigure 5. ROC Curves and C Statistics for Different Models in Prospective Cohort Analyses for CVD

eFigure 6. Change in the Predicted Probabilities (Expressed as a Percentage) of the Recalibrated PCE Model After the Addition of the Polygenic Risk Score for Cardiovascular Disease (CVD) (PRS_CvD)