Dynamic Multi-Atlas Selection Based Consensus Segmentation of Head and Neck Structures from CT Images

Abstract

Purpose:

Manual delineation of head and neck (H&N) organ-at-risk (OAR) structures for radiation therapy planning is time consuming and highly variable. Therefore, we developed a dynamic multi-atlas selection-based approach for fast and reproducible segmentation.

Methods:

Our approach dynamically selects and weights the appropriate number of atlases for weighted-label fusion and generates segmentations and consensus maps indicating voxel-wise agreement between different atlases. Atlases were selected for a target as those exceeding an alignment weight called dynamic atlas attention index. Alignment weights were computed at the image-level and called global weighted voting (GWV) or at the structure-level and called structure weighted voting (SWV) by using a normalized metric computed as the sum of squared distances of CT-radiodensity and Modality Independent Neighborhood Descriptors (extracting edge information). Performance comparisons were performed using 77 H&N CT images from an internal Memorial Sloan-Kettering Cancer Center dataset (N=45) and an external dataset (N=32) using Dice Similarity Coefficient (DSC), Hausdorff distance (HD), 95^th percentile of HD, Median of Maximum Surface Distance, and Volume Ratio Error against expert delineation. Pair-wise DSC accuracy comparisons of proposed (GWV, SWV) vs. single best atlas (BA) or majority voting (MV) methods were performed using Wilcoxon rank-sum tests.

Results:

Both SWV and GWV methods produced significantly better segmentation accuracy than BA (p < 0.001) and MV (p < 0.001) for all OARs within both datasets. SWV generated most accurate segmentations with DSC of: 0.88 for oral cavity, 0.85 for mandible, 0.84 for cord, 0.76 for brainstem and parotids, 0.71 for larynx, and 0.60 for submandibular glands. SWV’s accuracy exceeded GWV’s for submandibular glands (DSC=0.60 vs 0.52, p=0.019).

Conclusions:

The contributed SWV and GWV methods generated more accurate automated segmentations than the other two MABAS techniques. The consensus maps could be combined with segmentations to visualize voxel-wise consensus between atlases within OARs during manual review.

1. INTRODUCTION

Organ at risk (OAR) segmentation is a critical aspect of radiotherapy treatment planning. Clinically used manual delineations are time consuming to produce and are prone to high inter- and intra-observer variability.^1,2 Therefore, automating the segmentation of OARs particularly in sites involving large numbers of structures, such as the head and neck (H&N), is imperative to produce fast, reliable and consistent contours. Multi-atlas-based segmentation (MABAS)^3,4 or a combination of atlas and machine learning-based methods^5,6 have been used to generate OAR segmentations. Such methods seek to model anatomical variability within the medical images by leveraging population-based information computed directly through atlas label fusion, or through statistical modeling, respectively.

Multi-atlas based segmentation approaches consist of (a) registering a target image to a set of training images and their associated expert labels, called atlases, (b) propagating registered atlas labels onto the target image, and (c) selecting and fusing these labels in a meaningful way to estimate a new segmentation. These can be further refined using techniques such as active contours to generate smooth contour delineations⁴. Selection of the relevant set of atlases while reducing the influence of completely irrelevant atlases is important to achieve accurate MABAS segmentation. The selected set of relevant atlases for an incoming target scan may vary from a subset of the multi-atlas^7,8 to selection of all atlases in the multi-atlas^9,10. In addition to atlas selection, weighing the set of selected atlases is also important to reduce the effect of outlier propagated atlas labels and ensure good segmentation^11,12. This work addresses both issues for generating segmentations of OARs in the head and neck.

First, to reduce the adverse effect of combining segmentations from atlases that are outliers (those with large misalignment to target scan often arising due to highly different anatomy), we introduced a metric called dynamic atlas attention index (τ) that determines the appropriate number of atlases from the set of matching atlases for a given target scan. This selection is based on the relative weights assigned to the individual atlases with respect to all structures, in the case of global weighted voting, or with respect to a particular structure (in structured weighted voting) computed from a measure of target-to-atlas alignment and selecting only those with weights above this index. The target-to-atlas alignment is computed using the sum of squared distance metric of the CT density or an edge descriptor called the modality independent descriptor (MIND) that was previously developed for atlas registration. The τ parameter is determined as the minimum alignment required to maximize the segmentation accuracy for any given set of atlases in a multi-atlas set. This differs from prior approaches where the number of atlases to be used in weighted combination is pre-specified^9,13,14 and the label fusion involves computing the relative weights of those atlases.

Second, as opposed to prior MABAS methods that utilized voxel intensity, location, gradient and curvature texture features¹⁵, Dice Similarity Coefficient (DSC) score distribution¹⁶, or a constant value⁹ as weights for atlas fusion, our atlas weighting computation involves metrics (CT density or MIND) that are fast to compute. Sanroma et.al¹³ proposed using edge-based and Bayesian inference-based expected Dice similarity coefficient atlas weighting measures and exploited machine learning regression for expected segmentation performance during atlas weighting. We independently evaluated CT density and MIND descriptor-based image features to test whether image similarity-based metrics are indeed less optimal than other metrics. The presented multi-atlas label fusion generates a consensus segmentation together with a voxel-wise consensus probability map. Finally, we used the consensus map as a visual aid to determine the underlying variability within the produced probabilistic segmentations.

Our contributions are as follows: (a) an approach to automatically select and weight different atlases, either relative to the individual structures or for the entire image, to produce a multi-atlas consensus segmentation with voxel-wise consensus weights, (b) to compare two image features for evaluating atlas to target image similarity, and (c) visualization of segmentations using voxel-wise segmentation consensus maps.

2. MATERIALS AND METHODS

2.A. Overview

Figure 1 provides a schematic overview of our approach for generating multi-atlas segmentation and associated consensus maps for an unseen target scan. An incoming target scan was deformably registered to all atlases in the multi-atlas. Pairwise image similarity between the target scan and all atlases was computed. Then using the dynamic atlas attention index τ, our method selected the appropriate atlas set. The weights of the individual selected atlases were computed by normalizing and then exponentiating the atlas to target similarity. Voxel-wise weighted fusion of the atlas labels generated OAR consensus segmentation including voxel-wise consensus. Consensus is defined as the probability that a voxel is assigned a particular label based on the weighted frequency of that label being assigned by the individual atlases in the selected multi-atlas set. This voxel-wise consensus map was then used to visualize all voxels labeled by the different atlases for inclusion within the consensus segmentation. This color-coded map encapsulates the overall labeling variability within the segmentation, with voxels in red depicting higher consensus among the different atlases and blue voxels corresponding to lower consensus.

Figure 1:

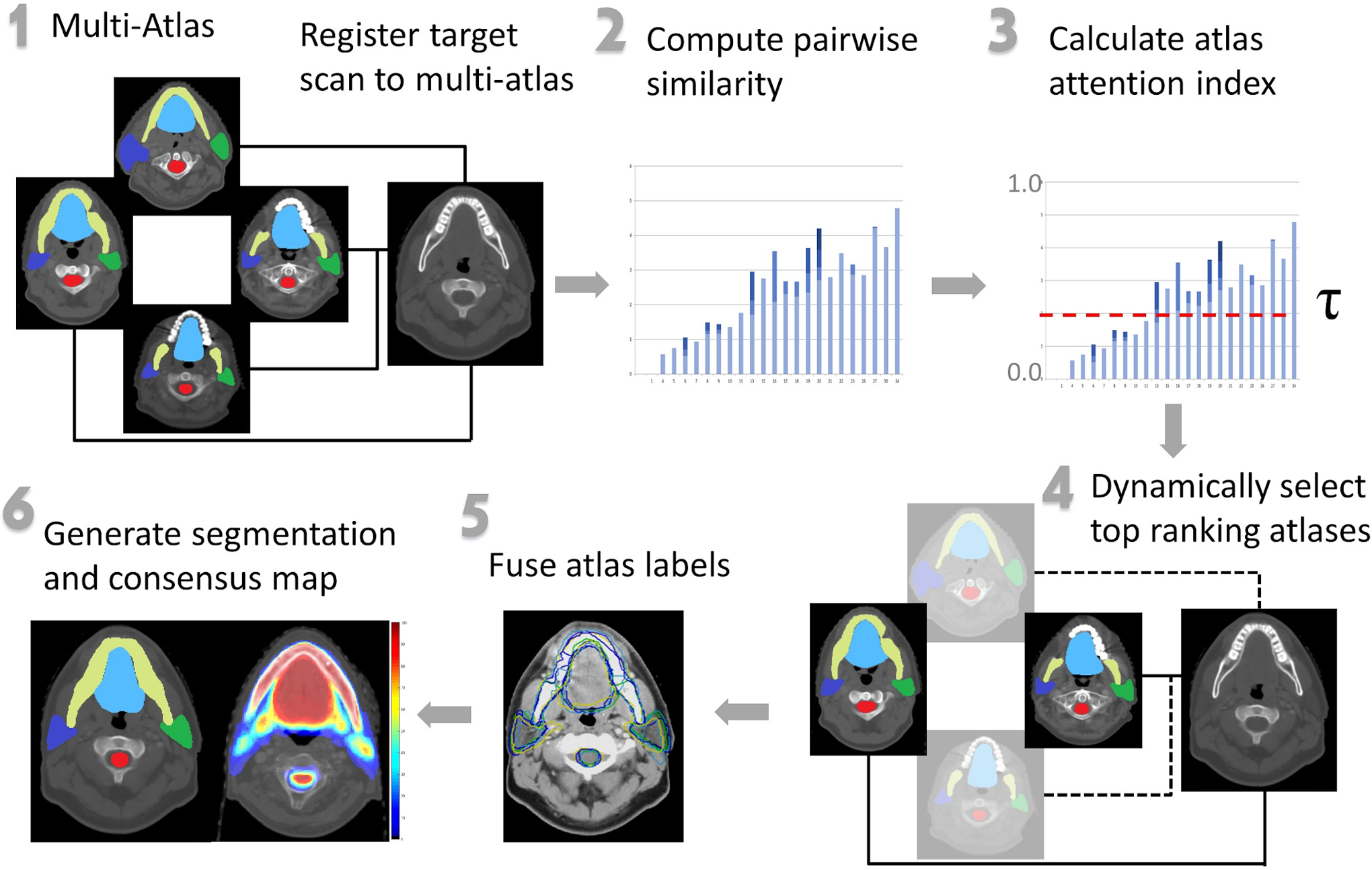
Schematic overview of our approach. A target scan was registered to all images and labels in the multi-atlas. Pairwise target to atlas similarities were computed. The atlas attention index was calculated. The set of atlases and their associated weights were dynamically selected. These selected labels were fused to produce segmentations and an associated consensus map that visualized underlying variability within generated OAR segmentations. Steps 2–6 represent modifications to the general MABAS scheme.

2.B. Analyzed datasets

We evaluated our approach using 77 H&N contrast-enhanced CT images, which included 45 clinical CT datasets of patients treated at our institution (INST). The average image resolution of this INST dataset was 1 × 1 × 2.5 mm³. The nine OAR manual delineations contained in the internal INST dataset were: larynx, bilateral parotids and submandibular glands, oral cavity, brainstem, mandible and spinal cord. Thirty-two CT scans from the publicly available, multi-institutional Public Domain Database for Computational Anatomy (PDDCA)¹⁷ curated from the Radiation Therapy Oncology Group (RTOG) 0522 study were used for external validation of our approach. The PDDCA dataset CT images had an average resolution of 1 × 1 × 3 mm³ and contained manual delineations of the following nine OARs: brainstem, chiasm, mandible, bilateral optic nerves, parotids and submandibular glands, as well as the presence of five bony landmarks. Clinically accepted delineations of nine OARs within each dataset that were performed by an expert radiation oncologist, physicist, or dosimetrist, depending on the organ, and were used for multi-atlas construction and considered the gold standard during segmentation validation. These expert delineations are referred to as atlases in this manuscript. The clinical datasets contained anatomical variability introduced by the underlying location of pathology as well as the existence of dental artifacts and bite blocks. The 3D images were cropped from above the eyes to the top of the sternum to reduce image size and thus registration computation time. Both the INST and PDDCA datasets include delineations of nine OARs with three non-overlapping structures. A table listing the above-mentioned structures contained within both datasets has been included in the supplementary Table 1.

Image Registration

The Plastimatch^16,17 algorithm was used to deformably register an incoming target image with all images in the multi-atlas. Registration between an atlas image and an incoming target scan required, on average, approximately three minutes of computation time, resulting in O(N × M) computation overhead for registering all N atlases to target. A mean squared error cost metric was used to minimize registration error. The target-atlas pair was registered in the following steps: (1) affine registration to centrally align and spatially resize the images (2) b-spline non-rigid registration in three stages. The image resolution, regularization parameter lambda, and maximum number of iterations were refined in three levels from (i) 4 × 4 × 2 mm³, 0.05, and 100 to (ii) 2 × 2 × 1 mm³, 0.005, and 50 and (iii) 1 × 1 × 1 mm³, 0.005, and 20. The regularization term lambda, as defined in the Plastimatch^18,19 method, is used to tradeoff the contribution between image intensity matching (for alignment) and deformable vector field smoothing (for smoothness of deformation of various structures in the image) during b-spline registration. As this term is relaxed during subsequent stages, the overall regularization of the control points is reduced to improve image matching and achieve better registration accuracy over the reduced grid space. Parameters used for performing registration are included in Supplementary Table 2.

2.C. Image features and atlas fusion strategies

We compared the performance of image similarity computed using CT radiodensity differences against the modality independent descriptor (MIND)²⁰ between the target and the registered atlas scans for assigning atlas weights during label fusion. The MIND feature computes local neighborhood descriptors that incorporate local image similarity including edges, the location and orientation of corner points, as well as image texture (i.e. the spatial arrangement of consistent intensity patterns in the image region) across the two CT images. The sum of squared difference (SSD) distance metric was used to quantify the differences between the registered atlas and the target image using either the CT-radiodensity or the MIND descriptors. The distances were converted to similarities as described in the subsequent Subsection 2.D. Normalized correlation coefficient, while being a more robust metric for calculating intensity differences between heterogeneous CT images, is computationally intensive and time-consuming. Therefore, SSD was used for calculating image similarity to reduce the overall computational burden during atlas selection.

Atlas-to-target similarities were computed using (i) the entire image (global weighted) similar to the global image-weighted voting (GWV)²¹, or (ii) a region-of-interest defined by each structure (structure weighted) and similar to the structure weighted voting (SWV).²² We compared the performance of GWV and SWV against single best atlas (BA) and majority voting (MV)²³ methods.

The multi-atlas segmentation $L_s^j$ for target scan I_S and structure label j using a multi-atlas set MA consisting of N atlases, MA = {A₁, A₂, …A_N}, where each atlas A_i is associated with an image I_i and label L_i, can be computed as the weighted sum of K (1 ≤ K ≤ N − 1) atlases in MA as

$$L_s^j\left(x\right)={\forall }_{j,}\sum _{i=1}^K{w}_i\left(x\right)\times s,\{\begin{array}{c}s=1\mathit{\text{\hspace{0.17em}if\hspace{0.17em}}}{L}_i\left(x\right)=j\\ s=0,\mathit{\text{otherwise}}\end{array}$$ (1)

where w_i is the weight associated with atlas A_i for a target scan I_S where s ≠ I, and $L_s^j\left(x\right)$. The weighted combination corresponds to the normalized consensus (0 to 1) among the different atlases of assigning a label j to each voxel x given that the individual atlas labels correspond to that label at the given location. In the case of overlapping labels, the voxel label with a higher consensus contributes towards the final segmentation.

The BA selection method selects the single best atlas that is the most similar to the target image such that K=1 and w=1. The MV atlas fusion approach combines the top K atlases with equal weights assigned (w/K) to each atlas. In contrast, our approach using GWV and SWV selects the appropriate number of atlases and assigns weights to the selected atlases corresponding to their similarity to the target image or structure, respectively.

2.D. Dynamic atlas attention index for selecting and weighting atlases for weighted fusion

Both BA and MV methods are known to produce less accurate segmentations. This is because similarity criteria based on CT-radiodensity, edge features, or metrics such as a histogram of oriented directions (HOG) assume that the compared images are highly similar, and the differences arise solely due to misalignment or anatomical differences. As a result, selecting the single best atlas or selecting all atlases with slightly different weights fails to produce a good segmentation. Therefore, we introduced a metric called the dynamic atlas attention index τ(0 to 1) that selects the number and set of atlases most suited for producing accurate segmentations of the individual OARs in each target scan. The metric τ is the lower limit on the similarity that must be achieved for an atlas to be considered suitable for label fusion. Higher values of τ reduce the number of selected atlases while lower values increase the number of atlases. In the extremes, τ = 1 corresponds to BA while τ= 0 corresponds to selecting all available atlases.

Our approach for atlas selection and fusion involves two steps, namely, selecting the appropriate number of atlases and then computing the weights for those selected atlases. The GWV weighting method differs from the SWV method in that the weights and the number of atlases for GWV are selected at the level of the image resulting in a single set of atlases and weights for all the structures. Whereas, in the SWV method, separate sets of atlas weights and associated atlases are selected per structure. Therefore, the overall technique for selecting and weighting atlases in the two methods is the same, with j = 1, corresponding to all structures taken as one unit for GWV atlas selection and weighting calculations, while j varies with each structure in SWV. To select the required number of atlases for the individual structure j, the atlas-to-target distance ${\phi }_S^j$ is computed for the target scan S, from the i atlases on a structure-by-structure basis ${\phi }_S^j=\left\{{\phi }_S^{1,j}\dots {\phi }_S^{i,j}\right\}$ where ∀i ∈ {1…N – 1, i ≠ S}. Normalized atlas similarity set ${\phi }_{\mathit{\text{SN}}}^j$ corresponds to the normalized similarities of the set of selected atlases for label fusion. It is calculated from the target-atlas similarity distances as:

$${\phi }_{\mathit{\text{SN}}}^j=1-\hspace{0.17em}\frac{{\phi }_S^{i,j}-\text{min}\left({\phi }_S^j\right)}{\text{max}\left({\phi }_S^j\right)-\text{min}\left({\phi }_S^j\right)}$$ (2)

where $\text{max}\left({\phi }_S^j\right)$ and $\text{min}\left({\phi }_S^j\right)$ are the maximum and minimum distances within the ${\phi }_S^j$ set for structure j. The normalized distance ${\phi }_S^j$ are subtracted by 1.0 to convert distance to similarity. Next, the appropriate number of atlases and the atlas set is extracted by selecting atlases that have a normalized similarity of at least τ. As a result of this step, at most K ordered atlases, where K≤N-1, that have atlas similarity greater than or equal to τ are selected.

As a second step, the weights w_i,j for the individual atlases i for each structure j in the selected atlas set are computed as:

$$w_{i,j}=\{\begin{array}{ll}{e}^{{\phi }_{\mathit{\text{SN}}}^{i,j}/{\sum }_{\text{i}=1}^{\text{K}}{\phi }_{\mathit{\text{SN}}}^{i,j}},\hfill & \mathit{\text{if\hspace{0.17em}}}{\phi }_{\mathit{\text{SN}}}^{i,j}\ge \tau \hfill \\ 0,\hfill & \mathit{\text{otherwise}}\hfill \end{array}$$ (3)

where 0 ≤ τ ≤ 1. If an atlas is a subset of K selected atlases that have similarity of at least τ, its associated label weight is calculated as the exponential of the probability of high atlas similarity value between structure j for atlas i and structure j for target scan S. This atlas weight assignment maximizes the likelihood of the propagation of relevant voxel-wise labels while reducing the effect of outlier labels. The calculated atlas weights are used to fuse the labels from the selected atlases using Equation (1) to produce the consensus map for each structure being segmented. The consensus map is converted into the range (0–100) through normalization and the consensus segmentation is computed through thresholding at a default value of 33. This normalization is done purely to have a sufficient range for visualization purposes.

The algorithm describing our approach to segment an incoming target CT scan using the multi-atlas leveraging dynamic atlas selection and weighting is included below (Table 1):

Table 1:

Step-by-step algorithm describing the procedure for segmenting OAR structures of the head and neck for an incoming target CT scan using the Structured Weighted Voting (SWV) and Global Weighted Voting (GWV) atlas fusion techniques using CT-radiodensity image similarity or MIND descriptor.

INPUT: Unseen target CT scan, Multi-atlas set with CT images and expert delineations of OARs

OUTPUT: Segmented CT scan with OAR segmentations and consensus map

Step 1: Deformably register all atlases to the target scan by using Plastimatch

Step 2: Propagate atlas labels to the target scan

Step 3: Calculate atlas similarity matrix using either CT-radiodensity or MIND descriptor image feature in Eq. 2

Step 4: Calculate weights and dynamically select top-ranked atlases using Eq. 3

IF fusion method == SWV THEN

Set τ = 0.5

ELSE IF fusion method == GWV THEN

Set τ = 0.8

Step 5: Fuse propagated atlas labels using Eq. 1 to produce the consensus map

Step 6: Extract segmentations using default consensus threshold = 33

2.E. Segmentation Evaluation

We employed leave-one-out validation using the internal and external datasets and subsequently compared the automated segmentations with the expert delineated structures, considered the gold standard, for each target scan using the Dice Similarity Coefficient (DSC), Hausdorff Distance (HD), 95^th percentile of HD (HD95), Median of Maximum Surface Distance (MMSD) and Volume Ratio Error calculated as (V_GS − V_AS)/V_GS, where V_GS is the gold standard segmentation. Statistical differences between segmentation performances were determined through the Wilcoxon rank-sum test performed on the DSC metric. A Bonferroni correction was applied to account for multiple comparisons and reduce the chances of obtaining false-positive results using the DSC metric.

3. RESULTS

3.A. Dynamic selection of atlases for label fusion leads to more accurate segmentation than selecting all atlases

Using sixteen randomly selected patients from the INST dataset as a calibration dataset, we tested whether varying the number of selected atlases through the τ parameter impacted segmentation accuracies. Leave-one-out validation was performed such that, for each patient, a maximum of fifteen atlases (τ=0) and a minimum of single best atlas (τ=1) could be selected for atlas fusion. The value of τ was varied from 0 to 1 with the increments of 0.1. Figure 2.(a) shows changes in the number of selected atlases for a randomly selected five out of sixteen patients with increasing values of τ using the GWV method. We chose GWV for showing the results to conserve space for plotting. Note that different numbers and different sets of atlases will be selected for SWV for each structure.

Figure 2:

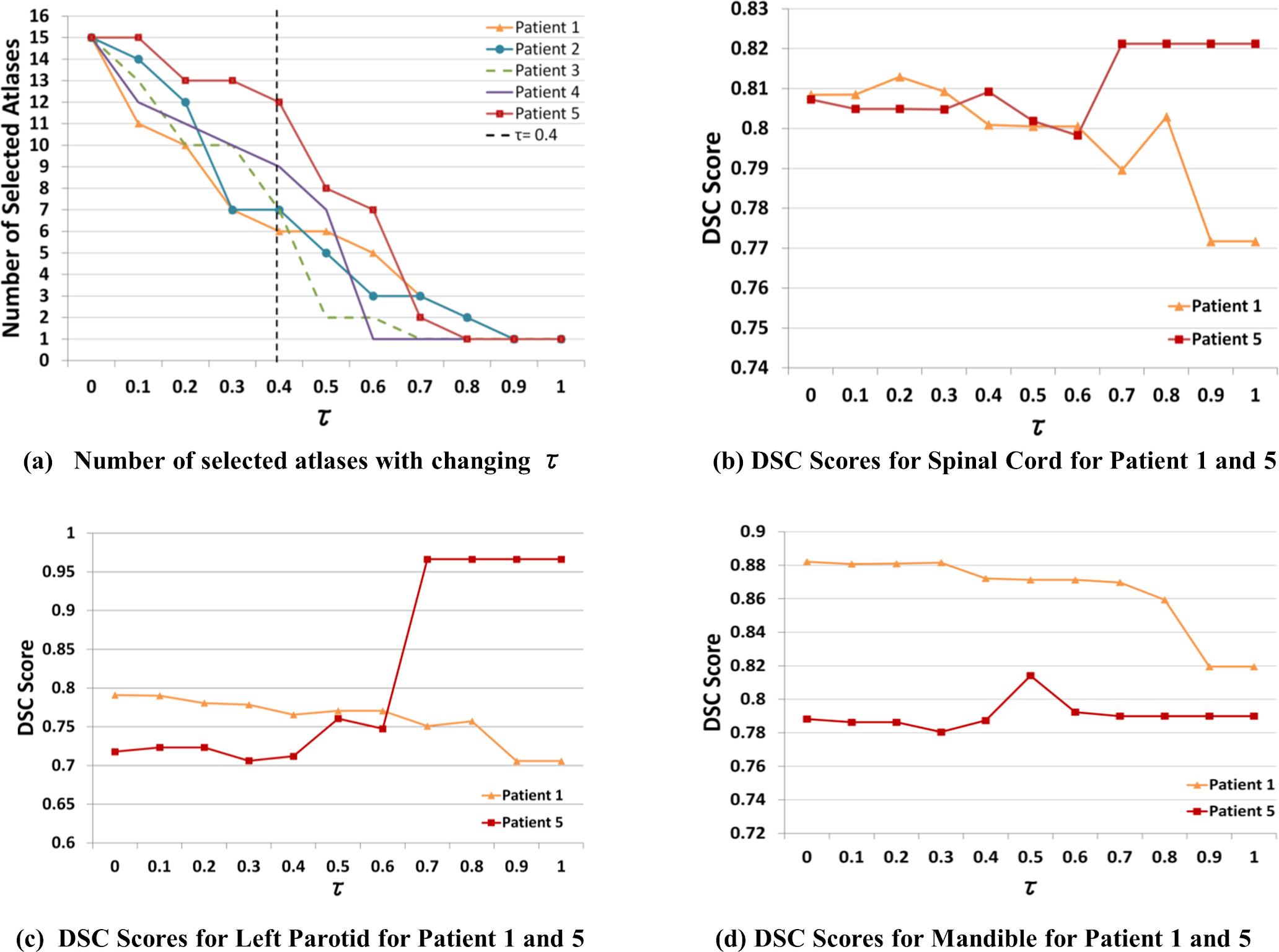
(a) Number of selected atlases with increasing τ (dynamic atlas attention index) using GWV and CT-radiodensity for five randomly selected patient scans, using fifteen atlases. Varying number of atlases are required for fusion to achieve a minimum similarity of τ=0.4. DSC comparison for Patients 1 and 5 for (b) spinal cord, (c) left parotid and (d) mandible with increasing τ demonstrate the difference in the number of atlases required for fusion to achieve high DSC accuracy.

As shown in Figure 2.(a), for a specific value of τ = 0.4, varying numbers of atlases were included for label fusion in all the patients. These differences are exemplified in the case of Patient 1 and Patient 5, where the former required 12 atlases while the latter required 6 atlases to reach the same value of τ= 0.4. We examined the effect of selecting different numbers of atlases on the segmentation performance for different normal structures including a long tubular structure, namely, the spinal cord (see Figure 2.(b)), a large soft tissue structure, the left parotid (see Figure 2.(c)), and a structure with high contrast, such as the mandible (see Figure 2.(d)). Figure 2.(b) illustrates that Patient 5 required fusion of two atlases (DSC = 0.82 with τ = 0.7) while Patient 1 required fusion of ten atlases (DSC = 0.81 with τ= 0.2) to the achieve highest possible segmentation accuracy for the spinal cord. This variability within the number of selected atlases was also observed for other patients across all OARs. As seen, arbitrarily selecting all (τ = 0.0) or the single best atlas (τ = 1.0) does not lead to the best performance for all three structures in both extreme cases Patients 1 and 5. On the other hand, segmentations with the highest DSC score were generated for both cases using an intermediate τ value. The SWV atlas fusion strategy uses the default threshold value of 33, which was empirically selected as the common threshold parameter for all structures by observing the preliminary segmentation results of these initial five test cases.

We optimized the segmentation accuracy across all structures for the appropriate τ value using all 45 patients in the INST dataset and found that a τ of 0.8 for GWV and 0.5 for SWV using CT-radiodensity image similarity, and a τ of 0.7 using MIND were appropriate for segmenting all structures (Figure 3(a–b)). The choice of τ has been fixed and used for segmentation of all OARs in the external PDDCA dataset.

Figure 3:

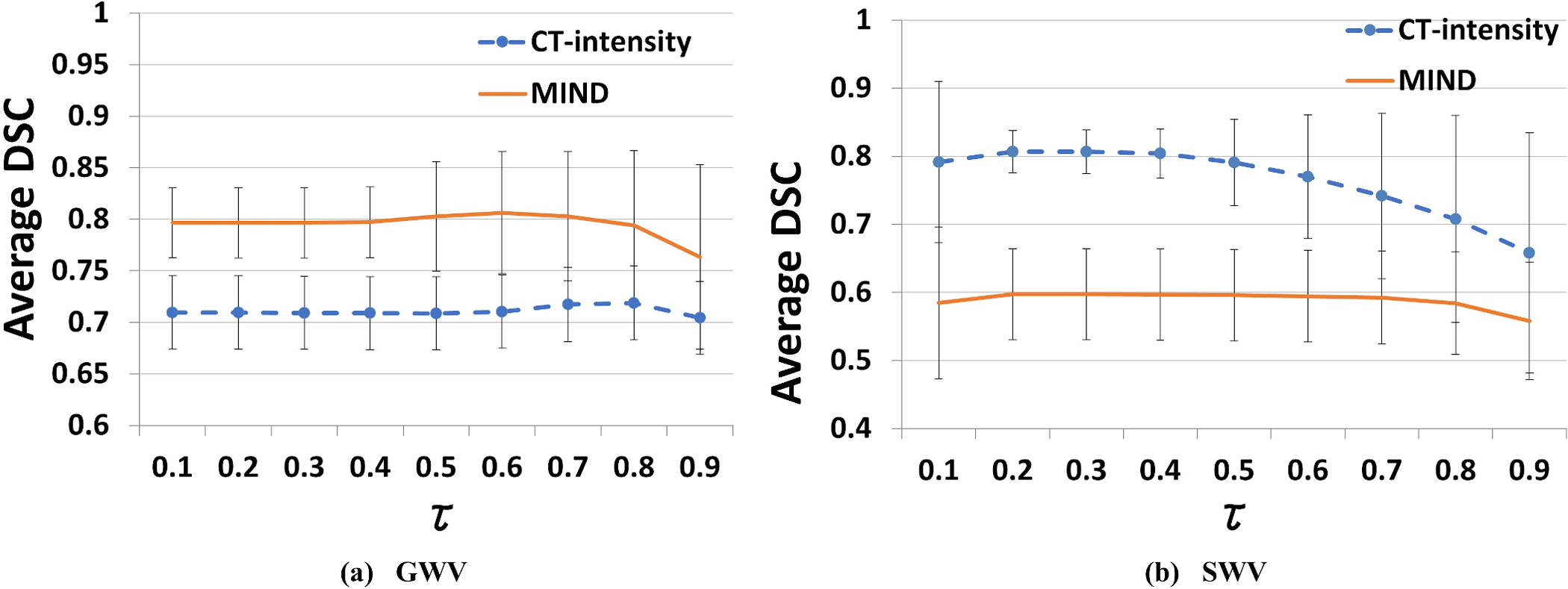
Average DSC segmentation accuracy, along with standard deviation, of 45 internal INST cases over all structures, generated using (a) Global Weighted Voting (GWV), and (b) Structured Weighted Voting (SWV) atlas fusion against expert delineation, using increasing values of τ. We investigate the effect of changing dynamic atlas attention index to segmentation accuracy for optimal τ parameter selection for CT-radiodensity and MIND image features.

3.B. Comparison of image similarity computed using CT-radiodensity with MIND for multi-atlas label fusion

Table 2 shows DSC accuracy computed for the 9 OARs when using CT-radiodensity and MIND for computing image similarity to assign atlas weights using the GWV and SWV methods. Accuracies were significantly different when using SWV between the two image similarity computations, but were highly similar for all other structures. This result suggests that the computationally simpler CT-radiodensity method is sufficient for computing similarity between target and atlas images. The combination of four atlas fusion and two image feature determination methods resulted in a total of eight approaches for generating automated segmentations for each evaluated target scan (Supplementary Figure 1).

Table 2:

Median Dice Similarity Coefficients of automated segmentations generated using different combinations of image similarity and atlas fusion methods against expert segmentation for all OARs of the internal INST dataset. DSC for the preferred combination, CT-radiodensity and SWV, are presented in bold. Values marked in ** and * were found to be statistically significant when compared against CT-radiodensity and SWV, with p-value < 0.001 and p-value < 0.05, respectively. SMG = Submandibular Gland.

OAR	CT-radiodensity DSC				MIND DSC
	BA	MV	GWV	SWV	BA	MV	GWV	SWV
Oral Cavity	0.77**	0.86*	0.86	0.88	0.7**	0.83**	0.81	0.84
Mandible	0.68**	0.82	0.84	0.85	0.65**	0.82**	0.80	0.84
Cord	0.76**	0.82	0.83	0.84	0.69	0.81	0.81	0.82
Brainstem	0.73	0.74	0.76	0.76	0.66**	0.74	0.74	0.75
Left Parotid	0.64**	0.73	0.75	0.76	0.58**	0.69**	0.71	0.72
Right Parotid	0.65**	0.71	0.73	0.74	0.48**	0.68	0.69	0.71
Larynx	0.50**	0.67	0.68	0.71	0.35**	0.63	0.67	0.63
Left SMG	0.47**	0.48**	0.52*	0.60	0.36**	0.38**	0.44	0.52
Right SMG	0.37**	0.44**	0.53*	0.59	0.24**	0.37**	0.43	0.48*

3.C. Comparison of MABAS segmentations produced using atlas fusion methods

Figure 4 displays two example patients with automated segmentations generated using the various methods overlaid with expert delineation using CT-radiodensity as a feature for computing image similarity. GWV and SWV generated consensus maps that were converted to segmentations using a pre-determined consensus threshold of 33. As seen, BA results in underestimation for all structures (shown in red) compared to manual delineation (shown in green). In contrast, MV, GWV and SWV methods produced segmentations much closer to the expert delineation for larger structures. All methods resulted in overestimation for the oral cavity and the spinal cord for the first example target scan, and overall slight underestimation for the second example target scan using the multi-atlas cohort.

Figure 4:

Example segmentations of two randomly selected target scans (in rows) from the INST dataset using (c) best atlas (BA), (d) majority voting, (e) global weighted voting, and (f) structure weighted voting atlas fusion methods and the CT-radiodensity image similarity feature. Figure shows expert delineated contours in (b) and in green in (c,d,e,f), and algorithm-generated segmentations in red (c, d,e,f).

Table 2 displays the segmentation accuracy comparison of the nine OARs using all image feature and atlas fusion combinations for the INST dataset. Statistical comparison was performed using the Wilcoxon-rank sum test to determine any statistically significant differences across all feature-method combinations. Bonferroni correction was applied to reduce the effect of false-positives on the DSC accuracies. As shown, both GWV and SWV atlas fusion methods outperformed the BA and MV methods. SWV method was similar to GWV in all but one structure. It significantly outperformed GWV for segmenting the submandibular glands, a structure with very poor soft-tissue contrast. Therefore, we chose SWV with the CT-radiodensity image feature as the preferred weighted atlas fusion scheme for external dataset validation.

3.D. SWV with CT-radiodensity as image feature produced similar segmentation accuracies for both internal and external datasets

DSC and HD95 segmentation accuracy results for each OAR using the CT-radiodensity image feature combined with SWV atlas fusion method are displayed in Figure 5. The smallest structures, such as the chiasm and the optic nerves, underperformed based on the DSC accuracy because this metric compares the volumetric ratios of the expert versus automatic segmentations and is thus biased against smaller structures. Volume Error, MMSD and HD results using SWV and CT-radiodensity are also presented in Figure 6 and Supplementary Figure 2, respectively. A negative volume error (Figure 6.(a)) depicts overestimation and a positive volume error refers to an underestimated MABAS result when compared against the gold standard. It can be observed that our algorithm slightly overestimated the volume for most structures in the internal dataset by less than 10%, except for the larynx and the submandibular glands. In contrast, larger structures in the external PDDCA dataset were slightly underestimated, with the worst median volume error observed for the mandible and the left parotid. This may be contributed to the anatomical variability within the atlases, as well as inherent registration errors propagated onto the target scan from the multi-atlas.

Figure 5:

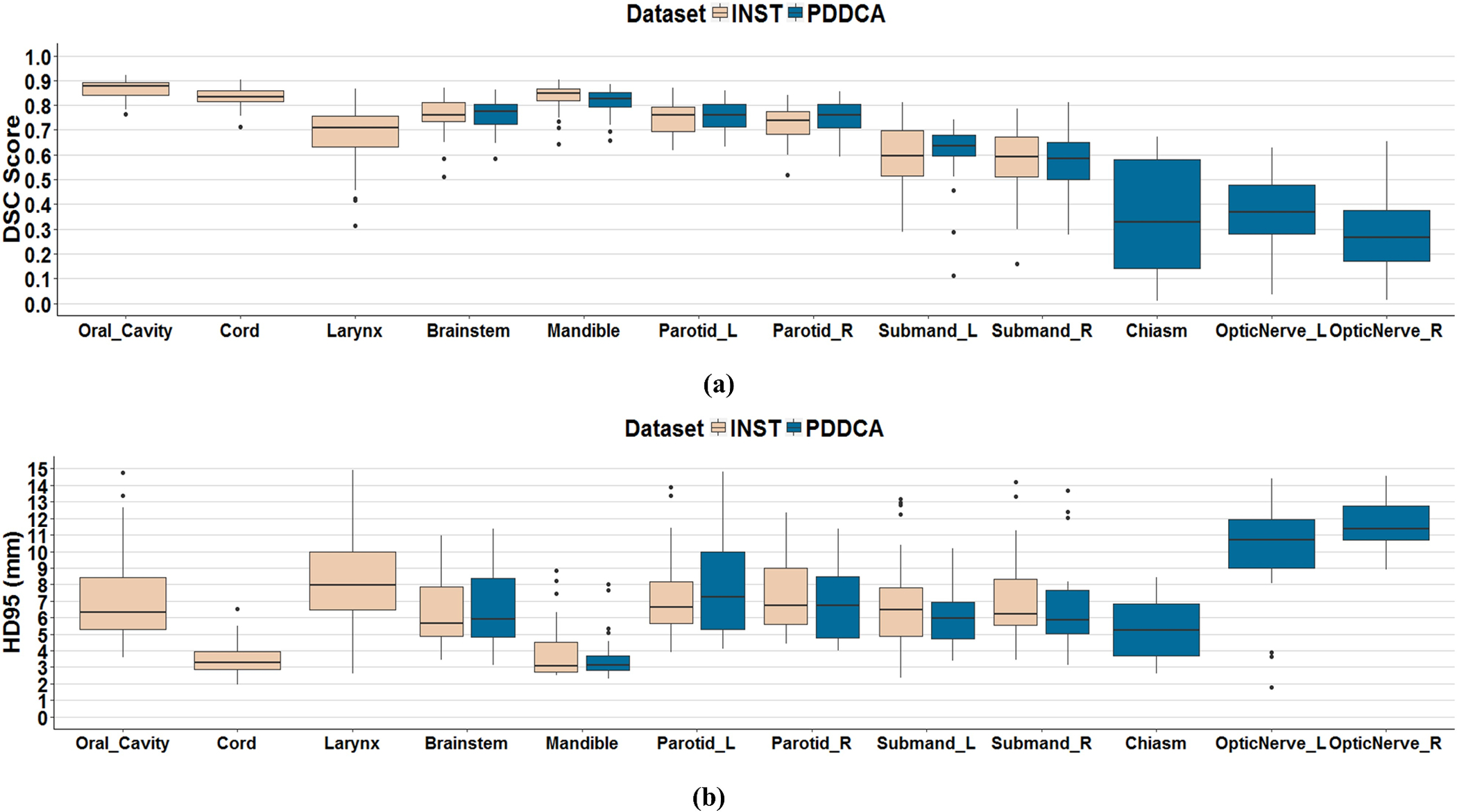
(a) Dice similarity coefficients (DSC) and (b) 95^th Percentile of Hausdorff Distance (HD95) (mm) using CT-radiodensity image similarity method and SWV atlas fusion against expert delineation for N=44 internal INST dataset (left) and N=32 external PDDCA (right) datasets.

Figure 6:

Median and interquartile range (IQR) of (a) Volume overlap Error and (b) Median of Maximum undirected Surface Distance (MMSD) (mm) comparing expert manual delineation to the CT-radiodensity image similarity and SWV atlas fusion method for INST (left) and external PDDCA (right) datasets.

Overall, the SWV atlas fusion and CT-radiodensity image feature method resulted in DSC accuracy greater than 0.75 for large structures, such as the cord, brainstem, mandible and oral cavity.

Results from the external validation dataset were consistent with our findings using the internal dataset. The highest DSC accuracy was achieved for the mandible. Large soft-tissue structures, such as brainstem and parotids achieved comparable median DSC accuracy of 0.83, 0.77 and 0.76 respectively. In contrast, small structures such as the chiasm and the optic nerves performed poorly due low soft-tissue contrast that the multi-atlas segmentation scheme was unable to capture.

Figure 7 presents example segmentation results of two typical dataset cases comparing expert clinical delineations against MABAS contours using CT-radiodensity image feature and SWV atlas fusion within the MABAS scheme. Maximum DSC accuracy for the patient shown in Figure b (a) was observed for the oral cavity OAR (0.88), and for the oral cavity and spinal cord (0.86) for patient shown in Figure 7(b). Overall, the MABAS-generated contours resulted in overestimation for the larynx, with DSC accuracy of 0.68 and 0.76 for patients shown in Figure 7(a) and Figure 7(b) respectively, and underestimated the superior-anterior portion of the parotids. This may be due to the lack of contrast close to the structure boundary, as well as the presence of dental artifacts at the anterior portion of the parotid close to the mandible. Segmentation consensus maps of two patients, along with their corresponding MABAS segmentations using SWV, are also displayed in Figure 7. Additional segmentation comparisons for two sample patients from the PDDCA dataset, depicting the best and worst submandibular gland, parotid and chiasm segmentations, are displayed in Supplementary Figure 3. The consensus maps highlight the highest label agreement and uncertainty within the atlases selected for weighted voting label fusion, corresponding to areas of red and blue, respectively.

Figure 7:

Comparison of MABAS segmentations using the CT-radiodensity image similarity and Structure Weighted Voting atlas fusion method (blue) against expert clinical delineations (green) for two patients (a-b). The segmentation consensus map for each patient is shown in the last column. A consensus value of 33% was used for the MABAS segmentations.

Table 3 displays comparison of achieved segmentation results against existing methods for segmentation of head and neck OARs. It should be noted that the external prior methods presented their results using different datasets, except for Ren et al.²⁴, who also utilized the external PDDCA dataset for validating their approach. Our method achieved results very similar to the deep learning method by Ibragimov et al.⁶ as well as the STEPS algorithm by Duc et al¹¹ and commercial MiM software as investigated by La Macchia et al.²⁵ However, our method was worse compared to the deep learning method by Ren et al.²⁴ for small structures including the submandibular glands and optic nerves.

Table 3:

DSC segmentation accuracies achieved using MABAS scheme versus various prior H&N segmentation methods in literature. Methods that report results using the publicly available PDDCA dataset are marked with an *.

Prior Methods	OAR	Dice Similarity Coefficient
		Prior Method	MABAS
Duc et al.11	Cord	0.76	0.84
	Parotids	0.65	0.77
	Brainstem	0.83	0.76
	OpticNerves	0.55	0.38
La Macchia et al.25 using MiM software	Cord	0.81	0.84
	Mandible	0.86	0.87
	Brainstem	0.81	0.76
	Parotids	0.79	0.77
Ibragimov et al.6	Parotids	0.77	0.77
	Cord	0.87	0.84
	Mandible	0.91	0.87
Ren et al.*24	Chiasm	0.58	0.33
	OpticNerves	0.71	0.38

4. DISCUSSION

We developed a novel approach to automatically select and weight the relevant number of atlases required to achieve high segmentation accuracy during MABAS atlas selection and fusion. Our results show that both dynamically weighted label fusion methods using entire-image based GWV and structure-based SWV significantly outperformed the MV (predefined K-atlas selection) and BA (single-atlas selection) based segmentation methods for all OARs. Our approach selects the best and appropriate number of atlases based on the image features that are required to achieve accurate segmentation while reducing the contribution of superfluous or insufficient outlier atlases during fusion. Segmentation results achieved for the PDDCA dataset indicate that the τ parameters, used for dynamic atlas selection during SWV and GWV, do not need to be optimized for an incoming H&N CT dataset, thereby mitigating any hyperparameter tuning computation overhead. We also evaluated the utility of the image similarity computed using MIND descriptors against the commonly used CT-radiodensity for computing atlas-to-target similarity and weights for multi-atlas label fusion. Our results show that both metrics and weighted-voting fusion techniques achieved similar performance except for the submandibular glands, where SWV combined with CT-radiodensity produced statistically significant results. This is because of the presence of low soft-tissue contrast in the region-of-interest that was better captured by fusing structure-specific relevant atlases to produce consensus segmentations.

Our results confirm the prior results including those by Aljabar et.al⁷ and Wolz et.al²³ which showed that selecting relevant sets of atlases for label propagation and fusion is imperative for achieving accurate segmentations. Unlike prior works that have typically fixed the number of atlases, we developed an approach to automatically identify the best number of atlases for each target. Sanroma et al.¹³ showed that varying the number of atlases in addition to atlas selection itself was required to achieve high segmentation accuracy.

Bayesian inference²¹ as well as machine learning regression for expected segmentation performance¹³ using edge-based features have been used to overcome the limitation of image similarities computed using image intensity including CT-radiodensity for assigning atlas weights. The limitation of intensity-based image similarities including local similarities²⁶ stems from the fact that these methods assume the differences in the atlas and target image are caused solely by mis-registration and not by any anatomic or intensity variations (due to artifacts) in the images. Therefore, we evaluated whether edge-based measures using MIND descriptors overcame such limitations. However, as shown in our results, both MIND and CT-radiodensity based measures were comparable in the achieved segmentation accuracies especially when using multi-atlas fusion methods.

Regardless of the method used for producing the OAR segmentations (manual or algorithm-based), all OAR segmentations should be subject to peer review^27–29 to ensure robust treatment plans. Therefore, we developed a visualization framework for viewing the consensus maps produced using the MABAS method and incorporated it within the Varian Eclipse system as a plug-in for clinical testing and internal validation. We used DSC and HD metrics for evaluating the accuracies to produce a more meaningful estimate as the DSC volumetric measure alone has been shown to be insufficient for evaluating clinical contour utility as demonstrated by Sharp at al.³⁰

As a limitation, we could not use the atlases computed from the internal dataset for segmentation with the external PDDCA dataset and vice versa because of difficulties in achieving registration without significant manual editing. Therefore, we only verified if the dynamic atlas-selection and weighted voting achieved similar performance in the two datasets. Atlas-to-target image registration is a crucial step for selecting relevant atlases. Any deformable image and label registration errors are inherently propagated onto image similarity calculations as well as atlas-label selections. Our presented atlas weighting scheme aims to mitigate these trickling errors by minimizing the effect of voxel-labels that may not highly correlate with overall atlas consensus during atlas label fusion. An alternate method may be to dynamically select the group of best performing atlases versus individual atlases for segmenting an incoming target scan, as demonstrated by Zaffiano et al.³¹

As a second limitation, we were not able to use multi-observer segmentations to test whether the segmentations produced using our method were within inter-observer variability. In addition, the default consensus threshold of 33 for producing SWV segmentations is not fine-tuned for all structure segmentations to mitigate the effect of hyperparameter tuning during multi-atlas segmentation. This threshold may vary depending on the anatomical and atlas variability within the individual structures being segmented. Similar to the work of Veeraraghavan et al.³², selection of an OAR-specific consensus threshold may improve structure segmentations. Finally, the gold standard clinical contours for the atlases were produced by different clinicians. Therefore, inter-observer segmentation variability is inherent in the atlases which likely led to lower than anticipated segmentation accuracies. In summary, we developed and implemented a framework for multi-atlas segmentation and visualization of OAR segmentations in head and neck CT images.

5. CONCLUSION

We developed a MABAS dynamic atlas selection and weighted approach for multiple normal organ at risk segmentation in head and neck CT images. We introduced a dynamic atlas attention index metric for selecting the number of atlases and weighting the atlases for label fusion using structure-wise voting and global image-wise voting techniques. Our approach produced more accurate segmentations than other MABAS techniques. This developed segmentation scheme has been incorporated as a plug-in within the Varian Eclipse clinical framework to provide users with tools to produce more consistent OAR contours along with their consensus maps for segmentation review. Also, consensus maps reflecting voxel-wise agreements between atlases produced using our method could be used together with segmentations for manual reviewing. Further studies could investigate the utility of combining these maps with segmentations for potential interactive editing applied to clinical treatment planning.

Supplementary Material

Supp FigS1

Supplementary Figure 1: Combination between image features and atlas fusion methods. Each combination of atlas fusion method and image feature generates an automated segmentation for a target scan, resulting in a total of eight automated segmentations.

Supp FigS2

Supplementary Figure 2: Median and interquartile range (IQR) of Hausdorff Distance (HD) (mm) comparing expert manual delineation to the MABAS CT-radiodensity image similarity and SWV atlas fusion results for INST (left) and external PDDCA (right) datasets.

Supp FigS3

Supplementary Figure 3: Automated segmentations (in red) compared against expert delineations (in green) for two sample patients selected from the external PDDCA dataset, which depict the best (top row) and the worst (bottom row) segmentation accuracies for the submandibular glands. Overestimation and underestimation of the OAR segmentations can be observed in (a) the submandibular glands, (b) the chiasm, and (c) the parotid glands. Associated consensus maps displaying the level of agreement with the underlying anatomy between the selected atlases for parotid segmentation are depicted in (d), with lowest agreement in blue, and highest regions of agreement displayed in red. Submand. = Submandibular glands.