Abstract
Purpose:
To evaluate fast-kV switching (FS) dual energy (DE) cone beam computed tomography (CBCT) using the on-board imager (OBI) of a commercial linear accelerator to produce virtual monoenergetic (VM) and relative electron density (RED) images.
Methods:
Using an polynomial attenuation mapping model, CBCT phantom projections obtained at 80 and 140 kVp with FS imaging, were decomposed into equivalent thicknesses of aluminum (Al) and polymethyl methacrylate (PMMA). All projections were obtained with the titanium foil and bowtie filter in place. Basis material projections were then recombined to create VM images by using the linear attenuation coefficients at the specified energy for each material. Similarly, RED images were produced by replacing the linear attenuation values of Al and PMMA by their respective relative electron density (RED) values in the projection space. VM and RED images were reconstructed using Feldkamp-Davis-Kress (FDK) and an iterative algorithm (iCBCT, Varian Medical Systems). Hounsfield units (HU), contrast-to-noise ratio (CNR) and RED values were compared against known values.
Results:
The results after VM-CBCT production showed good material decomposition and consistent HUVM values, with measured root mean square errors (RMSE) from theoretical values, after FDK reconstruction, of 20.5, 5.7, 12.8 and 21.7 HU for 50, 80, 100 and 150 keV, respectively. The largest CNR improvements, when compared to polychromatic images, were observed for the 50 keV VM images. Image noise was reduced up to 28% in the VM-CBCT images after iterative image reconstruction. Relative electron density values measured for our method resulted in a mean percentage error of 0.0 ± 1.8%.
Conclusions:
This study describes a method to generate VM-CBCT and RED images using FS-DE scans obtained using the OBI of a linac, including the effects of the bowtie filter. The creation of VM and RED images increases the dynamic range of CBCT images, and provides additional data that may be used for adaptive radiotherapy, and on table verification for radiotherapy treatments.
Keywords: dual energy imaging, cone beam computed tomography, relative electron density, fast-kV switching, image reconstruction
1. INTRODUCTION
Image-guided radiotherapy (IGRT) is used routinely during the course of treatment in order to improve its accuracy and precision. Cone-beam computed tomography (CBCT) is widely utilized for IGRT to aid in patient positioning and assessment of tumor response for possible adaptation (adaptive radiotherapy - ART) (Thörnqvist et al 2016, Lou et al 2013, Ghilezan et al 2013). However, CBCT presents some limitations including patient motion during image acquisition, photon scattering between the patient and detector, image noise and other artifacts (Landry and Hua 2018, Hansen et al 2018). These effects may result in inaccurate CT numbers and lower image quality than a diagnostic CT scanner (Peroni 2011). Moreover, the reduced contrast in CBCT can affect soft-tissue visibility, thereby limiting CBCT use for organ delineation and re-planning purposes (Lütgendorf-Caucig et al 2011, Lu et al 2011). However, since the on-board imager (OBI) used for CBCT acquisition is directly mounted to the linac gantry, it represents a convenient and efficient method for patient imaging in the treatment position. Thus, methods to improve CBCT image quality are desired.
In the diagnostic imaging community, there is increased interest in dual-energy (DE) CT imaging (Vaniqui et al 2017, Forghani et al 2017, Fredenberg 2018). DECT consists of imaging the patient with two different x-ray spectra to obtain more detailed information on the tissues within. There are multiple applications of DECT imaging that may benefit patients receiving radiotherapy. Among these applications is the generation of virtual monoenergetic (VM) CT scans (McCollough et al 2015). These image sets are produced from DE imaging data and the CT numbers represent the attenuation coefficients at an exact energy (Yu et al 2012). VM images offer the potential to reduce metal artifacts (Lewis et al 2013), increase soft tissue contrast (Noid et al 2018), and provide quantitative information on contrast agent concentration (Nasirudin et al 2015, Van Elmpt et al 2016, Larsson 2010). DECT can also provide additional information on material characterization (Lee et al 2016), including relative electron density (RED) and effective atomic number (Z) (Martz et al 2016). Such data has been shown to be valuable for treatment planning with low energy brachytherapy sources (Williamson et al 2006, Landry et al 2016). Recently, DECT has shown promising results for proton therapy, since relative stopping power (RSP) can also be derived from these images (Vilches-Freixas et al 2017, Zhang et al 2018b, 2018a, Landry and Hua 2018).
In this study, we examine the feasibility of fast-kV switching (FS) (Haytmyradov et al 2019) DE-CBCT on the OBI of a linac using material decomposition (Wong and Huang 1983). Based on this approach, the scatter-corrected projections are decomposed into images of effective basis material thicknesses on a pixel-by-pixel basis (Li et al 2012). The basis material projections are then recombined to create VM images by using the corresponding attenuation coefficients at the specified energy for each basis material. This technique may allow for the determination of the optimal energy for artifact reduction (Li et al 2012) and soft tissue contrast enhancement (Wu et al 2009). In addition, this approach is used to generate RED images that may be used for adaptive treatment planning (Vilches-Freixas et al 2017).
2. MATERIALS AND METHODS
DE imaging using material decomposition involves a number of steps. First, a mapping function must be created to relate high/low energy pixel values to equivalent thicknesses of basis materials. Next, following DE-CBCT image acquisition, scatter correction and image alignment between consecutive DE projections is performed followed by material decomposition. Lastly, selected VM or RED images are reconstructed using the basis material projections. Each of these steps will be described in the sections below.
2.1. Image Decomposition - Theory
The attenuation of an incident photon beam with intensity I0 can be expressed as a combination of photoelectric and Compton interactions along its path (Alvarez and Macovski 1976). In previous studies, this phenomenon was taken into account by approximating the attenuation as being due to two basis materials (Li et al 2013b, Wong and Huang 1983, Alvarez and Macovski 1976). One of the materials has a relatively high Z to represent the photoelectric effect while the other has a relatively lower Z to represent the Compton effect (Lehmann et al 1981). In practice, the basis materials that are used with this approach are often aluminum (Al) and polymethyl methacrylate (PMMA), representing high and low Z, respectively (Chuang and Huang 1988, Wong and Huang 1983). Therefore, using this approximation, the attenuation of a monoenergetic x-ray beam can be written as:
| (1) |
where I is the intensity of the exiting beam, t represents the thickness of each basis material (Al and PMMA) traversed by the incident beam and μ is the energy dependent linear attenuation coefficient for each material, respectively. For the case of monoenergetic x-ray beams irradiating at two different distinct energies (h and l), the transmitted intensities are described using the following equations:
| (2) |
| (3) |
The solution of these equations allows for the individual thicknesses of each basis material to be determined analytically (Chuang and Huang 1987).
Clinical x-ray beams, however, have a spectrum of energies. In this case, the high- and low- energy spectrum Sh (E) and Sl (E), result in transmitted intensities that can be represented as (Alvarez and Macovski 1976, Li et al 2012):
| (4) |
| (5) |
where S(E) implicitly includes the detector efficiency. Because detailed information on the x-ray spectra are required, it is difficult to analytically solve for the basis materials thicknesses in equations 4 and 5. Cardinal and Fenster (Cardinal and Fenster 1990, Li et al 2012) proposed a solution to this problem consisting of fitting a rational function to calibration data. In this study, a 3rd order polynomial was used to fit calibration data consisting of:
| (6) |
| (7) |
where H = −ln(Ih/I0) and L = −ln(Il/I0) are the scatter-corrected (or scatter-free if using simulated data) attenuations measured at both energies. That is, using data where the thicknesses of basis materials and scatter-corrected x-ray intensities are known, the parameters ai and bi (i=1–9) can be determined through a minimization process. By applying the calibration function to DE projection data, these images can be decomposed into equivalent thicknesses of the individual materials.
2.2. Calculation of Material Decomposition Parameters
In order to determine the material decomposition parameters of Eqs. (6) and (7), the scatter-free attenuations H and L, expected for a known thickness combination of tAl and tPMMA, were calculated using a virtual (calculational) phantom with thickness combinations ranging from 0 – 450 mm of PMMA (5 mm steps) and 0 – 24 mm Al (1 mm steps) with Eqs. (4) and (5). These calculations were performed by integrating the respective kV source spectra, for 80 and 140 kVp, with the detector efficiency and material attenuations for both thicknesses over all energies. The kV spectra used on these calculations were simulated previously, including the specific tube output window filtration and are used clinically for TrueBeam image reconstructions. The detector efficiency was also previously calculated by Monte Carlo simulations, taking into account the geometry (scintillator thickness and material) of the PaxScan 4030CB Flat Panel Detector (Varex Imaging, Salt Lake City, UT), calculated in 1 kV steps of the source spectra (Lehmann 2019). Following simulation, a least-square fit was performed to calculate the parameters a1 to a9 and b1 to b9.
2.3. DE-CBCT Image Acquisition
DE-CBCT scans were acquired of the Catphan 604 (The Phantom Laboratory Incorporated, Salem, NY, United States) using FS on a TrueBeam version 2.7MR3 (Varian Medical Systems, Palo Alto, CA) in Developer Mode. The FS software provides consecutive x-ray pulses that alternate between high and low energies using a programmed sequence. The image parameters used were 80 kVp (20 mA, 60 ms) and 140 kVp (20 mA, 10 ms). The relative exposures of low and high energies were chosen to generate similar pixel intensities as a precautionary measure, since possible lag effects were not quantified in this study. After a full rotation (360 degrees), the FS acquisition (11 frames/sec) generated 662 alternating projections (331 projections for each energy) with approximately 0.55 degree angular increment per energy, corresponding to total exposures of 400 and 66 mAs, respectively. The resultant DE frame rate is half of the programmed frame rate with each image pair resulting in one DE image. Projections were acquired using a frame grabber system (Matrox Imaging, Quebec, Canada) for off-line processing and encoded in 16-bit unsigned integers. Each projection consisted of 768 × 1024 pixels, acquired with dynamic gain mode and with both the titanium foil (0.89 mm) and bowtie filter, corresponding to the standard clinical CBCT protocols.
2.4. VM/RED Image Production
The method to create VM/RED images is outlined in Figure 1. Following FS-DE image acquisition, a scatter correction is first applied to the individual images using iTools Reconstruction (Varian). The scatter correction method is described by Sun et al. (Sun and Star-Lack 2010), and consists of a scatter kernel superposition (SKS) algorithm for deconvolving scatter from projection data. Following scatter correction, the images were normalized to the energy-specific air projections, thus treating the bowtie as part of the imaged object. To account for the angular separation between high- and low-energy projection pairs that is caused because of the rotational acquisition, a 2D image registration step was included in which projection pairs were rigidly registered by optimizing the mutual information (MI) metric (Wells et al 1996).
FIG.1.
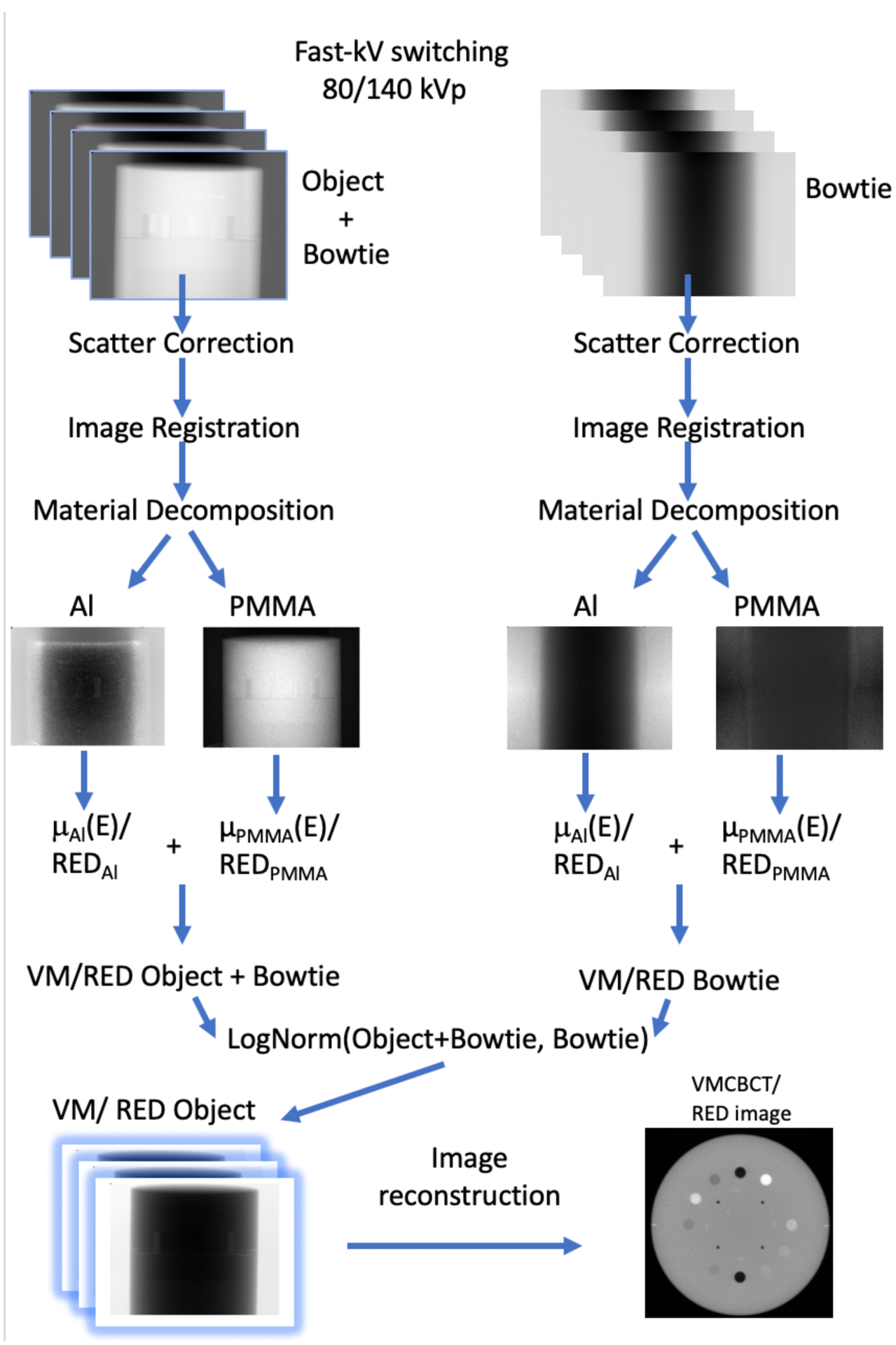
VMCBCT/RED image reconstruction steps. FS projections at low- and high-energies are acquired. Scatter correction is applied to the projections, rigid image registration is performed and the calibration functions are used to decompose the projections into thicknesses of Al and PMMA basis materials to be recombined. The VM/RED intensity images of the bowtie are used for log normalization before image reconstruction to remove the bowtie from the projections.
Based on the polynomial attenuation mapping (equations 6 and 7), the projections were then decomposed, using a custom MATLAB code, into equivalent thicknesses of PMMA and Al. New intensity projections for each VM were created by weighting the basis material projections by the material specific linear attenuation coefficients of the chosen energies (50, 80, 100 and 150 keV) and appropriate thickness values. These values were substituted into the following equation:
| (8) |
Additionally, RED images were produced by replacing the attenuation coefficient of Al and PMMA by their corresponding RED values in the decomposed projections (Men et al 2015).
The bowtie filter modifies the spectrum in a non-uniform way, therefore a positional-dependent approach needs to be performed. In order to compensate for the bowtie filter, rotational FS images were obtained with the bowtie in place. The wobbling effect from the bowtie (Zheng et al 2011) was taken into account by acquiring the scans in both the clockwise and counter-clockwise direction. As described previously, both scatter correction and image registration were performed prior to material decomposition of the bowtie images. VM/RED projections of the bowtie were created using the same approach described previously (Figure 1). Bowtie air normalization images were computed for 10 sectors, by averaging all air projections having the bowtie within a 36° sector. This was performed for both rotation directions. These VM bowtie images were placed in the respective air calibration folder within iTools. The program then normalized all projections with the bowtie air normalization image of the appropriate gantry sector. This normalization removed the bowtie from the VM/RED projections leaving only the object to be reconstructed. Conceptually, this is equivalent to subtracting the material thickness images of the bowtie-only measurements.
VM/RED projections were then loaded into iTools software for volumetric image reconstruction at the specified energies, using FDK (Feldkamp et al 1984) and iterative reconstruction with medium noise suppression with 0.5×0.5×2.0 mm3 voxels (detail of Varian’s iCBCT can be found in Laugeman et al 2019 and Mao et al 2019). Compared to the standard CBCT image reconstruction framework, the scatter correction and analytical spectrum correction (beam hardening correction) steps were removed. The former was removed because the scatter correction was already applied to the original projections and the latter was not used as the VM projections consisted of a single energy (not a spectrum). Moreover, the beam hardening correction was inherently taken into account during the decomposition process. As mentioned previously, iTools performs a normalization of the projections to the correspondent VM/RED bowtie image.
In order to assess the consistency of the Hounsfield Units (HU) values generated for VM-CBCT, a calibration was used to produce theoretical HU values according to the nominal linear attenuation coefficient values μVM of the Catphan 604 inserts provided by the vendor (The Phantom Laboratory Incorporated 2015). Theoretical HU values for each VM image (HUVM) were determined using the following equation:
| (9) |
where μVM and μWater are linear attenuation coefficients of the measured insert and water, respectively, at a particular VM value. The theoretical values extracted from equation 9 were used to determine the slope and intercept for our VM-CBCT HUVM calibration for each energy evaluated. Before reconstructing the VM-CBCT, the calibration curves for HUVM values were defined inside the reconstruction framework for each chosen energy. RED images were reconstructed using a similar approach.
2.5. Contrast-to-Noise Ratio
The VM images provide data at a particular energy value, and may provide improved soft tissue contrast (Noid et al 2018), particularly at low energies. However, the increased contrast often comes at the expense of increased image noise (Gondara 2016, Hatton et al 2009, Mentl et al 2017, Chen et al 2017). To evaluate this effect, the contrast-to-noise ratio (CNR) was assessed and defined as:
| (10) |
where Sins is the average CT number inside the insert with a circular region-of-interest (ROI - 242 pixels), Sbg is the average CT number for the background (region without inserts), and σmean is the mean standard deviation within the insert ROI. CNR values were calculated within the sensitometry slice of the Catphan 604 for the VM-CBCT images after FDK and iterative reconstruction. For comparison, these quantities were also calculated for the 80 and 140 kVp images reconstructed inside iTools, using standard FDK and iterative reconstructions with medium noise suppression.
3. RESULTS
3.1. Material Decomposition
The model for mapping the attenuations was evaluated and fit errors over all values used for the calibration are shown in figure 2. The error maps show the difference between the actual thicknesses used for the attenuation calculation and the polynomial fit, over a larger thickness range, expected to include most clinical situations. Within the fitting range (red rectangle), the residual errors are well below 1 mm for both materials. Outside the fitting range, even for large material thicknesses, such as 500 mm of PMMA and 30 mm of Al, the errors are within 2 mm. Of note, the errors of the two material thicknesses tend to be in opposite directions, thus reducing the total error when the materials are combined to create VM/RED projections. An example of the material decomposition for the Catphan 604 into equivalent thicknesses of Al and PMMA is shown in Figure 3.
FIG. 2.
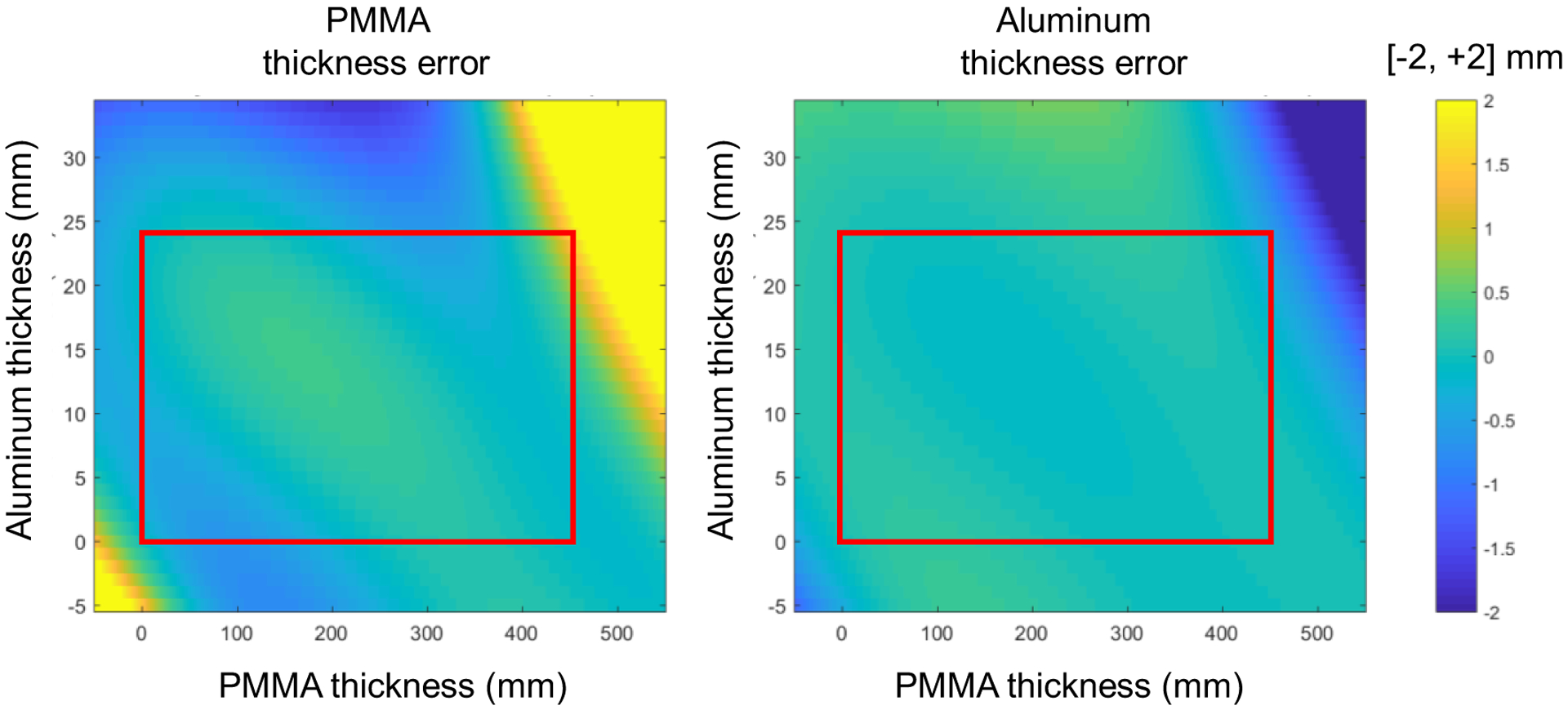
Representation of the 3rd order polynomial fit errors of PMMA thickness (left) and the Al thickness (right). The least square fit was based on material thickness pairs covering a range of 0 – 450 mm PMMA and 0 – 24 mm Al, as indicated by the red rectangle.
FIG. 3.

Projection images representing the thicknesses of Al (left) and PMMA (right) of the Catphan 604 following material decomposition. On the left, the bright part at the borders correspond the thickest part of the bowtie filter. The displayed Al thicknesses vary from 0 – 30 mm and PMMA thicknesses from 0 – 200 mm.
3.2. VM-CBCT
Figure 4 shows the reconstructed images of the Catphan 604 inserts for each selected VM. The theoretical and measured HUVM for each insert are summarized in Table 1. The inserts listed in the table begin with air, located at the 12 o’clock position on the figure, and proceed in a clockwise manner. Note that for the air inserts, the measured value of exactly −1000 HU is caused by the HU mapping implementation of the reconstruction, which clips values below −1000 HU. Following FDK image reconstruction, the HUVM resulted in RMSE of 20.5, 5.7, 12.8 and 21.7 HU for 50, 80, 100 and 150 keV respectively. After iterative image reconstruction, the HUVM resulted in RMSE of 21.1, 5.8, 11.3 and 20.5 HU for 50, 80, 100 and 150 keV respectively.
FIG. 4.

VM-CBCT images derived using our method. The FDK reconstructions are shown on the top row and iterative reconstruction on the bottom. Window/Level: [−1000/ 1251].
Table 1.
HU values comparison between theoretical and VM-CBCT for the energies of 50, 80, 100 and 150 keV.
| 50 keV | 80 keV | ||||||
|---|---|---|---|---|---|---|---|
| Theoretical | FDK | Iterative | Theoretical | FDK | Iterative | ||
| Air (Upper) | −1000 | −1000 | −1000 | −1000 | −1000 | −1000 | |
| Teflon | 1030 | 1061 | 1063 | 913 | 916 | 920 | |
| Delrin | 320 | 343 | 343 | 351 | 346 | 343 | |
| 20% Bone | 298 | 307 | 309 | 146 | 156 | 152 | |
| Acryllic | 79 | 79 | 78 | 122 | 109 | 110 | |
| Air (Lower) | −1000 | −1000 | −1000 | −1000 | −1000 | −1000 | |
| Polystyrene | −98 | −91 | −93 | −32 | −33 | −28 | |
| LDPE | −155 | −160 | −160 | −90 | −84 | −85 | |
| 50% Bone | 1092 | 1046 | 1043 | 545 | 544 | 540 | |
| PMP | −238 | −257 | −255 | −179 | −178 | −177 | |
| RMSE | 20.5 | 21.1 | 5.7 | 5.8 | |||
| 100 keV | 150 keV | ||||||
| Theoretical | FDK | Iterative | Theoretical | FDK | Iterative | ||
| Air (Upper) | −1000 | −1000 | −1000 | −1000 | −1000 | −1000 | |
| Teflon | 895 | 886 | 889 | 874 | 859 | 860 | |
| Delrin | 354 | 342 | 336 | 354 | 334 | 333 | |
| 20% Bone | 120 | 130 | 131 | 95 | 107 | 109 | |
| Acryllic | 132 | 108 | 116 | 141 | 109 | 113 | |
| Air (Lower) | −1000 | −1000 | −1000 | −1000 | −1000 | −1000 | |
| Polystyrene | −24 | −20 | −20 | −11 | −11 | −15 | |
| LDPE | −75 | −73 | −75 | −68 | −69 | −69 | |
| 50% Bone | 441 | 469 | 465 | 354 | 408 | 405 | |
| PMP | −165 | −166 | −166 | −159 | −158 | −157 | |
| RMSE | 12.8 | 11.3 | 21.7 | 20.5 | |||
The largest errors were observed for the high-density materials at lower energies (50% bone and Teflon). These errors were most likely due to uncertainties during the SKS scatter correction which is a water-based approach. Thus the scatter through high-density materials may not be modeled accurately (Maslowski et al 2018). Additionally, a polynomial fit is an approximation and these high density inserts may not be effectively modelled using the approach by Alvarez and Macovski (Alvarez and Macovski 1976). The materials with the smallest differences (excluding air inserts), across all energies, between theoretical and calculated values were the LDPE and polystyrene inserts. This effect may also be related to the HU calibration process, which tends to reduce errors for inserts in the mid HU range.
With respect to the individual VM images, the 50 keV image had the largest dynamic range in HUVM ranging from −1000 to +1063. This is expected as the photoelectric effect is dominant at low energies, resulting in attenuation coefficient related to Z3 of the materials. At 150 keV, the range in HUVM is −1000 to +860.
3.3. Contrast-to-Noise Ratio
The results for the CNR are presented for all energies in figure 5. The measurements were made for each insert, excluding air, Teflon and 50% Bone, since these are much higher contrast inserts and it was decided to focus on inserts with attenuation coefficients more similar to soft tissue. The background values were obtained from a circular region of the phantom without the inserts. For FDK reconstruction, the largest relative increase in CNR was from 6.2 (80 kVp) to 10.3 (50 keV) for the LDPE insert and the smallest relative increase in CNR was from 12.0 (80 kVp) to 15.2 (50 keV) for the Delrin insert. For the Acrylic (PMMA) insert, that mimics soft-tissue, the increase was from 2.8 (80 kVp) to 3.6 (50 keV). Overall, for the FDK reconstruction, the 50 keV image resulted in a mean improvement of 43% and 63% of the CNR compared to 80 kVp and 140 kVp respectively, for the materials shown.
FIG. 5.
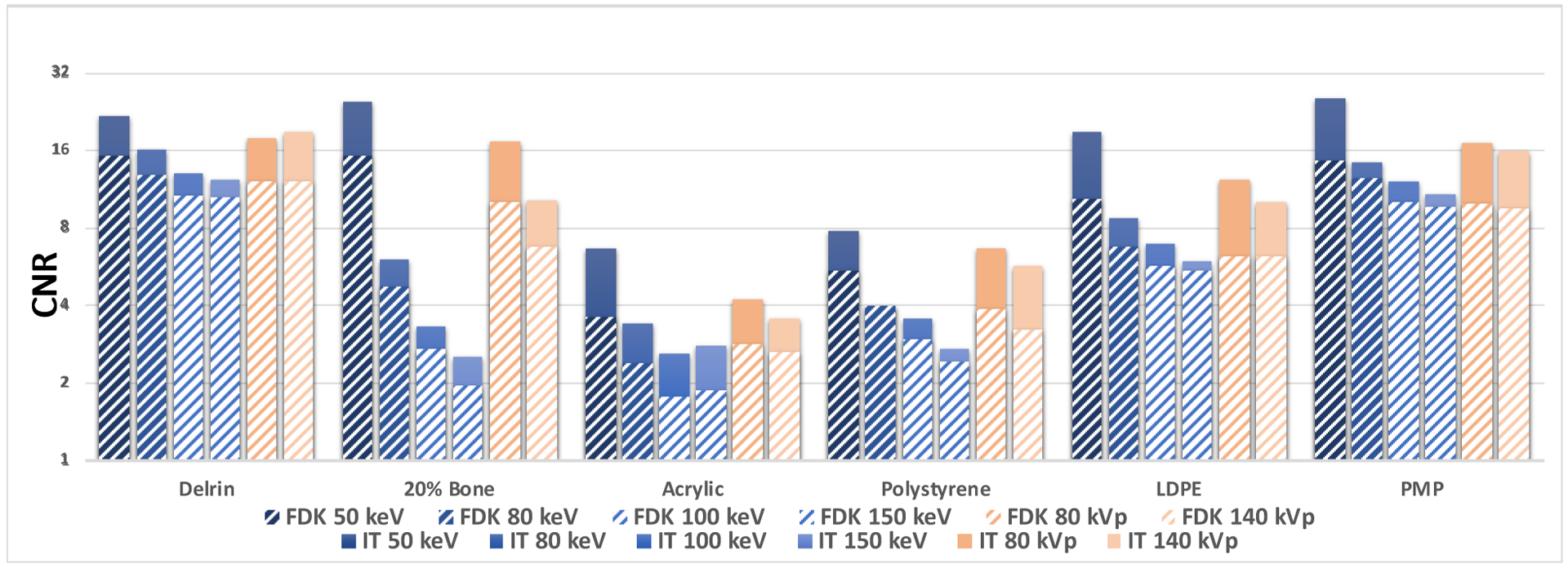
CNR measurements after FDK (stripes) and iterative reconstruction for 50, 80, 100 and 150 keV VM-CBCT and 80 and 140 kVp CBCT.
Following iterative reconstruction, the relative largest increase in CNR was from 10.2 (140 kVp) to 24.8 (50 keV) for the 20% Bone insert and the smallest relative increase in CNR was from 18.9 (140 kVp) to 21.8 (50 keV) for the Delrin insert. For acrylic, the improvement was from 3.6 (140 kVp) to 6.6 (50 keV). The 50 keV image resulted in a mean improvement of 41% and 71% of the CNR compared to 80 kVp and 140 kVp respectively, for the materials shown.
3.4. Relative Electron Density Images
By combining the equivalent thicknesses of Al and PMMA weighted by their respective relative electron density, RED images were created. This method reduces errors by avoiding the HU-RED conversion on single energy kVp images (Hatton et al 2009). For each insert, RED values were measured inside a circular ROI, as described previously. The measured RED values are presented and compared to reference values provided by the Catphan 604 vendor in Table 2. Overall, the average percentage difference between theoretical and measured values was 0.0 ± 1.8%. The measured median percent error was 0.2%. All values were obtained using FDK reconstruction. Iterative reconstruction did not result in any significant differences (data not shown).
Table 2.
Reference and measured RED values. The measurements were taken inside a circular ROI on a Catphan 604 reconstructed slice containing all inserts.
| Reference | FDK | Percent Difference | |
|---|---|---|---|
| Air (Upper) | 0.001 | 0.001 | 0.0% |
| Teflon | 1.868 | 1.856 | 0.7% |
| Delrin | 1.363 | 1.340 | 1.7% |
| 20% Bone | 1.084 | 1.101 | −1.6% |
| Acrylic | 1.147 | 1.120 | 2.3% |
| Air (Lower) | 0.001 | 0.001 | 0.0% |
| Polystyrene | 0.998 | 0.994 | 0.4% |
| LDPE | 0.945 | 0.942 | 0.3% |
| 50% Bone | 1.312 | 1.365 | −4.0% |
| PMP | 0.853 | 0.852 | 0.1% |
| Mean % difference | 0.0% | ||
| Standard deviation | 1.8% |
4. DISCUSSION
In this study, that is the first of its kind, we obtained FS DE-CBCT scans using the OBI of a commercial linear accelerator. The projections were subsequently processed off-line, using a material decomposition approach, allowing for the creation of VM and RED images. The HUVM and RED values from these images were compared with theoretical values, and showed good overall agreement. Previously, the evaluation of DE-CBCT has been studied mainly on bench-top systems (Li et al 2013a, Iramina et al 2018, Zbijewski et al 2014), and more recently on a Synergy linear accelerator (Elekta, Stockholm, Sweden)(Men et al 2017). Li et al.(Li et al 2013a, 2012). These approaches used a material decomposition approach based on attenuation measurements on scatter-corrected calibrations images of physical step wedges. Iramina et al.(Iramina et al 2018) used a filter-based DE separation technique on a bench-top micro-CBCT system. The authors evaluated a split-filter and alternate switching filters during image acquisition for spectral separation, and found the latter to be useful for metal artifact reduction. Zbijewski (Zbijewski et al 2014) et al. investigated the use of differential filtering and regularization for DE-CBCT material classification as a function of iodine concentration. This study was also performed on a bench-top system, and demonstrated a material classification accuracy over 90%. Kuo Men et al. (Men et al 2017) described a dual scan image acquisition, the creation of a look-up-table for basis material decomposition to produce RED images. However, none addressed the challenges of using DE-CBCT with the bowtie filter, which is highly desirable clinically (Mail et al 2009). Moreover, our studies were obtained using a FS acquisition on a linac, thus reducing the potential of motion artifacts when using a dual scan approach.
Compared to material decomposition calibration using a physical step wedge phantom, the virtual phantom allows for a much larger thickness range with user selected thickness increments. Moreover, this method avoids errors derived from imperfect scatter correction (Maslowski et al 2018), especially for thicker regions of a physical phantom. Within the fitting range, 0–24 mm for Al and 0–450 mm for PMMA, the residual errors were within 1 mm for both materials. The errors from the material mapping for the two materials tended to be in the opposite directions, which results in a total error reduction when the materials are combined in VM/RED projections. Therefore, our theoretical calibration is capable of providing material decomposition, being a fast and robust way to address this fundamental step for VM/RED image production. Finally, the theoretical approach allows for verification of the fit quality beyond the thickness range used for the least-square fit. However, such an approach requires detailed knowledge of x-ray spectra and detector response. An alternative approach to the presented calibration uses maximum likelihood basis-component decomposition (Schlomka et al 2008).
Overall, the HUVM values generated from our approach agree well with theoretical values. For the range 50–150 keV, the RMSE of 16.5 (FDK) and 16.0 (iterative) HU values are similar to those found in the literature. Zucca et al. (Zucca et al 2016) observed HUVM RMSE values of 26.8 HU and 13.4 HU, for GE and Siemens DE-CT scanners, respectively. In their study, VM images were created from 40–140 keV. The maximum RMSE values observed were 43.9 and 35.8 for the high Z material, for both scanners respectively. Sellerer et al. (Sellerer et al 2018) compared different DE-CT scanners using an abdominal phantom. The comparison was made between three types of DE-CT scanners: dual-layer CT (DLCT), rapid-kVp-switching CT (KVSCT) and dual-source CT (DSCT). Similar to our study, the authors concluded that the HU values agreed well with theoretical results.
VM-CT has been studied to define the optimal energy for tumor signal-to-noise (SNR), which would benefit clinical follow-up and improve contour delineation (Wichmann et al 2014, Albrecht et al 2015, Lam et al 2015). Further studies are required on VM-CBCT to determine the optimal energy for tumor and soft tissue contrast for each anatomical site. Wang et al. (Wang et al 2019) described a clinical protocol to determine the optimal VM in twin beam CT for organ segmentation of head-and-neck patients. In general, low energy VM images can provide enhanced image contrast, which in turn may result in improved organ segmentation (Lütgendorf-Caucig et al 2011, Lu et al 2011). Bazalova et al, demonstrated that DE imaging may also provide improved dose calculations compared to using single energy CT (Bazalova et al 2008); therefore the demonstrated accuracy in this study can potentially contribute to improved CBCT dose calculations.
In this study, RED images were created by replacing the μ values of the basis materials with the corresponding RED values when creating the projections. Following image reconstruction, RED values were measured within the inserts on the sensitometry slice of the Catphan 604 phantom. Compared to the reference values provided by the vendor, our method obtained a mean percent error of 0.0 ± 1.8%. The largest uncertainties were observed for the bone inserts, which are known to be a problematic region for correct RED and RSP measurement (Matsufuji et al 1998, Kanematsu et al 2012, Peng et al 2016). Nevertheless, the results for the other inserts compare well to the 2% maximum error observed in the Men et al. (Men et al 2015) study. The mean error measured for our RED estimation method was 0.00 ± 0.02 which compares well with Schyns et al. (Schyns et al 2017) who observed a mean error of 0.01 ± 0.03. In that study, they used 50 and 90 kVp with an integrated CBCT on a small animal irradiator that acquired the images consecutively. Our median error of 0.22% for RED compares favorably to the 1.4% found by Shen et al. (Shen et al 2018) which used 3 distinct energies.
The results of using the iterative CBCT reconstruction improved CNR by reducing image noise, consistent with the work published by Mao et al. (Mao et al 2019). The noise reduction improved the CNR values of the 50 keV images by approximately 71%, for the measured inserts, compared with the 140 kVp images. Note, however, that the exact amount of noise reduction related to the iterative reconstruction is somewhat arbitrary, since it depends on the selected noise suppression settings.
An important consideration of the proposed method is that the scatter correction performed on the projections uses a water-based approach. Therefore, a projection of the Catphan with high-density inserts would be interpreted and corrected as water slabs. This effect may explain the largest error found for HU values of high-density materials at lower energies, since we have a larger contribution of the Al base material when weighting the decomposed thicknesses into a VM projection. Future studies will involve the use of more sophisticated scatter correction algorithms, such as Acuros (Maslowski et al 2018, Wang et al 2018).
An advantage of our approach is that it uses the Varian image reconstruction algorithms, which are clinically available and computationally efficient. Therefore, this method allows one to decide the best energy for a desired task, and create a VM-CBCT in a timely manner for clinical applications such as image-guidance, treatment planning, dose recalculation for ART (Hudobivnik et al 2016, Zhu and Penfold 2016, Vilches-Freixas et al 2017, Men et al 2017, Peng et al 2016, Vaniqui et al 2017), among other applications discussed in the literature (Patino et al 2016, Fredenberg 2018, Forghani et al 2017, Van Elmpt et al 2016, Yu et al 2012). The iTools software allows for integration of a MATLAB script within its image reconstruction pipeline, which would completely automate our basis material decomposition and VM-CBCT production method.
There are a number of limitations with this study. First, the full scan takes approximately one minute. While this works well for phantoms, there can be a significant amount of organ or patient motion during the image acquisition. However, the implementation of FS DE-CBCT avoided the additional second scan used in a previous study (Men et al 2017). Additionally, the time can be further reduced by using half-arc scans or faster CBCT scan times (Mao et al 2019). Another limitation is that scans were obtained using a full-fan technique, resulting in a limited field of view (FOV). To facilitate the calibration, we assumed the beam spectra were spatially uniform, and the heel effect was not taken into account. To take into account a larger FOV, a half-fan scan, with the detector offset, would be required. In the latter case, the calibration process may exhibit a positional dependence that needs to be taken into account. Also, the high- and low-energy projections were acquired consecutively with a separation of approximately 0.55 degrees, resulting in the need to align the images prior to basis material decomposition. Thus, future studies are required to determine whether frame interpolation or an increased frame rate would present any improvement to current results. Future directions may also include determining the optimal kVp/mA settings for imaging with fast-kV switching.
5. CONCLUSION
We presented a method for obtaining FS DE-CBCT images using the OBI of a linear accelerator including the effects of the bowtie filter. The creation of VM and RED images increases the dynamic range of CBCT images, and provides additional data that may be used for adaptive radiotherapy, and on table verification for radiotherapy treatments.
6. ACKNOWLEDGMENTS
This work was funded by a research grant from Varian Medical System. Research reported in this publication was partially supported by the National Cancer Institute of the National Institutes of Health under Award Number R01CA207483. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Bibliography
- Albrecht MH, Scholtz JE, Kraft J, Bauer RW, Kaup M, Dewes P, Bucher AM, Burck I, Wagenblast J, Lehnert T, Kerl JM, Vogl TJ and Wichmann JL 2015. Assessment of an advanced monoenergetic reconstruction technique in dual-energy computed tomography of head and neck cancer Eur. Radiol 25 2493–501 Online: http://link.springer.com/10.1007/s00330-015-3627-1 [DOI] [PubMed] [Google Scholar]
- Alvarez RE and Macovski A 1976. Energy-selective reconstructions in X-ray computerized tomography. Phys. Med. Biol 21 733–44 Online: http://www.ncbi.nlm.nih.gov/pubmed/967922 [DOI] [PubMed] [Google Scholar]
- Bazalova M, Carrier JF, Beaulieu L and Verhaegen F 2008. Dual-energy CT-based material extraction for tissue segmentation in Monte Carlo dose calculations Phys. Med. Biol 53 2439–56 [DOI] [PubMed] [Google Scholar]
- Cardinal HN and Fenster A 1990. An accurate method for direct dual-energy calibration and decomposition Med. Phys 17 327–41 [DOI] [PubMed] [Google Scholar]
- Chen H, Zhang Y, Zhang W, Liao P, Li K, Zhou J and Wang G 2017. Low-dose CT via convolutional neural network Biomed. Opt. Express 8 679 Online: 10.1364/BOE.8.000679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chuang K-S and Huang HK 1988. Comparison of four dual energy image decomposition methods Phys. Med. Biol 33 455–66 [Google Scholar]
- Chuang KS and Huang HK 1987. A fast dual energy computational method using isotransmission lines and table lookup Med. Phys 14 186–92 [DOI] [PubMed] [Google Scholar]
- Van Elmpt W, Landry G, Das M and Verhaegen F 2016. Dual energy CT in radiotherapy: Current applications and future outlook Radiother. Oncol 119 137–44 Online: 10.1016/j.radonc.2016.02.026 [DOI] [PubMed] [Google Scholar]
- Feldkamp LA, Davis LC and Kress JW 1984. Practical cone-beam algorithm vol 1 [Google Scholar]
- Forghani R, De Man B and Gupta R 2017. Dual-energy computed tomography Neuroimaging Clin. N. Am 27 385–400 Online: http://linkinghub.elsevier.com/retrieve/pii/S1052514917300199 [DOI] [PubMed] [Google Scholar]
- Fredenberg E 2018. Spectral and dual-energy X-ray imaging for medical applications Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip 878 74–87 Online: 10.1016/j.nima.2017.07.044 [DOI] [Google Scholar]
- Ghilezan M, Yan D and Martinez A 2013. Adaptive Radiation Therapy for Prostate Cancer Semin Radiat Oncol 20 130–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gondara L 2016. Medical image denoising using convolutional denoising autoencoders 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW) (IEEE) pp 241–6 Online: http://ieeexplore.ieee.org/document/7836672/ [Google Scholar]
- Hansen DC, Landry G, Kamp F, Li M, Belka C, Parodi K and Kurz C 2018. ScatterNet: A convolutional neural network for cone-beam CT intensity correction Med. Phys 45 4916–26 Online: http://doi.wiley.com/10.1002/mp.13175 [DOI] [PubMed] [Google Scholar]
- Hatton J, McCurdy B and Greer PB 2009. Cone beam computerized tomography: The effect of calibration of the Hounsfield unit number to electron density on dose calculation accuracy for adaptive radiation therapy Phys. Med. Biol 54 N329–46 Online: http://stacks.iop.org/0031-9155/54/i=15/a=N01?key=crossref.9dd008871813121f70c0761d875c6426 [DOI] [PubMed] [Google Scholar]
- Haytmyradov M, Mostafavi H, Wang A, Zhu L, Surucu M, Patel R, Ganguly A, Richmond M, Cassetta R, Harkenrider MM and Roeske JC 2019. Markerless Tumor Tracking using Fast-kV Switching Dual Energy Fluoroscopy on a Benchtop System Med. Phys mp.13573 Online: http://www.ncbi.nlm.nih.gov/pubmed/31059124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudobivnik N, Schwarz F, Johnson T, Agolli L, Dedes G, Tessonnier T, Verhaegen F, Thieke C, Belka C, Sommer WH, Parodi K and Landry G 2016. Comparison of proton therapy treatment planning for head tumors with a pencil beam algorithm on dual and single energy CT images Med. Phys 43 495–504 [DOI] [PubMed] [Google Scholar]
- Iramina H, Hamaguchi T, Nakamura M, Mizowaki T and Kanno I 2018. Metal artifact reduction by filter-based dual-energy cone-beam computed tomography on a bench-top micro-CBCT system: Concept and demonstration J. Radiat. Res 59 511–20 Online: http://www.ncbi.nlm.nih.gov/pubmed/29718315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanematsu N, Inaniwa T and Koba Y 2012. Relationship between electron density and effective densities of body tissues for stopping, scattering, and nuclear interactions of proton and ion beams Med. Phys 39 1016–20 [DOI] [PubMed] [Google Scholar]
- Lam S, Gupta R, Levental M, Yu E, Curtin HD and Forghani R 2015. Optimal virtual monochromatic images for evaluation of normal tissues and head and neck cancer using dual-energy CT Am. J. Neuroradiol 36 1518–24 Online: http://www.ncbi.nlm.nih.gov/pubmed/26021623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landry G, Gaudreault M, van Elmpt W, Wildberger JE and Verhaegen F 2016. Improved dose calculation accuracy for low energy brachytherapy by optimizing dual energy CT imaging protocols for noise reduction using sinogram affirmed iterative reconstruction Z. Med. Phys 26 75–87 Online: https://www.sciencedirect.com/science/article/pii/S093938891500104X [DOI] [PubMed] [Google Scholar]
- Landry G and Hua C 2018. Current state and future applications of radiological image guidance for particle therapy Med. Phys 45 e1086–95 Online: http://doi.wiley.com/10.1002/mp.12744 [DOI] [PubMed] [Google Scholar]
- Larsson J 2010. The use of Dual-Energy in Computed Tomography (Sahlgrenska University Hospital; ) Online: https://radfys.gu.se/digitalAssets/1312/1312301_joel-larsson-thesis.pdf [Google Scholar]
- Laugeman E, Mazur TR, Mutic S, Park JC, Cai B, Kim H, Henke LE, Hugo GD and Li H 2019. Characterization of a Prototype Rapid Kilovoltage X-Ray Image Guidance System Designed for a Ring Shape Radiation Therapy Unit Med. Phys [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Kim YS, Choi S, Lee H, Choi S, Jo BD, Jeon PH, Kim H, Kim D, Kim H and Kim HJ 2016. Improvement of material decomposition and image quality in dual-energy radiography by reducing image noise J. Instrum 11 [Google Scholar]
- Lehmann LA, Alvarez RE, Macovski A, Brody WR, Pelc NJ, Riederer SJ and Hall AL 1981. Generalized image combinations in dual KVP digital radiography Med. Phys 8 659–67 Online: http://doi.wiley.com/10.1118/1.595025 [DOI] [PubMed] [Google Scholar]
- Lehmann M. Personal Communication - Varian Medical Systems. 2019.
- Lewis M, Reid K and Toms AP 2013. Reducing the effects of metal artefact using high keV monoenergetic reconstruction of dual energy CT (DECT) in hip replacements Skeletal Radiol. 42 275–82 Online: http://www.ncbi.nlm.nih.gov/pubmed/22684409 [DOI] [PubMed] [Google Scholar]
- Li H, Giles W, Bowsher J and Yin F-F 2013a. A dual cone-beam CT system for image guided radiotherapy: Initial performance characterization Med. Phys 40 021912 Online: http://doi.wiley.com/10.1118/1.4788654 [DOI] [PubMed] [Google Scholar]
- Li H, Giles W, Ren L, Bowsher J and Yin FF 2012. Implementation of dual-energy technique for virtual monochromatic and linearly mixed CBCTs Med. Phys 39 6056–64 [DOI] [PubMed] [Google Scholar]
- Li H, Yin F-F, Bowsher J, Colsher J, Dobbins JT, Qingrong I and Wu J 2013b. Investigation of Imaging Capabilities for Dual Cone-Beam Computed Tomography
- Lou Y, Niu T, Jia X, Vela P a, Zhu L and Tannenbaum AR 2013. Joint CT/CBCT deformable registration and CBCT enhancement for cancer radiotherapy Med. Image Anal. 17 387–400 Online: 10.1016/j.media.2013.01.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu C, Chelikani S, Papademetris X, Knisely JP, Milosevic MF, Chen Z, Jaffray D a., Staib LHand Duncan JS 2011. An integrated approach to segmentation and nonrigid registration for application in image-guided pelvic radiotherapy Med. Image Anal. 15 772–85 Online: 10.1016/j.media.2011.05.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lütgendorf-Caucig C, Fotina I, Stock M, Pötter R, Goldner G and Georg D 2011. Feasibility of CBCT-based target and normal structure delineation in prostate cancer radiotherapy: Multi-observer and image multi-modality study Radiother. Oncol 98 154–61 [DOI] [PubMed] [Google Scholar]
- Mail N, Moseley DJ, Siewerdsen JH and Jaffray D a 2009. The influence of bowtie filtration on cone-beam CT image quality. Med. Phys 36 22–32 [DOI] [PubMed] [Google Scholar]
- Mao W, Snyder KC, Kumarasiri A, Movsas B, Kim J, Wen NW, Chetty IJ, Gardner SJ, Siddiqui F, Zhao B and Liu C 2019. Evaluation and Clinical Application of a Commercially Available Iterative Reconstruction Algorithm for CBCT-Based IGRT Technol. Cancer Res. Treat 18 153303381882305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martz HE, Seetho IM, Champley KE, Smith JA and Azevedo SG 2016. CT dual-energy decomposition into x-ray signatures ρ e and Z e ed Ashok A, Neifeld MA and Gehm MEp 98470D Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.2228954 [Google Scholar]
- Maslowski A, Wang A, Sun M, Wareing T, Davis I and Star-Lack J 2018. Acuros CTS: A fast, linear Boltzmann transport equation solver for computed tomography scatter – Part I: Core algorithms and validation Med. Phys 45 1899–913 Online: http://doi.wiley.com/10.1002/mp.12850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsufuji N, Tomura H, Futami Y, Yamashita H, Higashi A, Minohara S, Endo M and Kanai T 1998. Relationship between CT number and electron density, scatter angle and nuclear reaction for hadron-therapy treatment planning Phys. Med. Biol 43 3261–75 Online: http://stacks.iop.org/0031-9155/43/i=11/a=007?key=crossref.1988133dae63d0c30f360ab8e8b9e47f [DOI] [PubMed] [Google Scholar]
- McCollough CH, Leng S, Yu L and Fletcher JG 2015. Dual- and Multi-Energy CT: Principles, Technical Approaches, and Clinical Applications Radiology 276 637–53 Online: http://pubs.rsna.org/doi/10.1148/radiol.2015142631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Men K, Dai J-R, Li M-H, Chen X-Y, Zhang K, Tian Y, Huang P and Xu Y-J 2015. A method to improve electron density measurement of cone-beam CT using dual energy technique Biomed Res. Int 2015 1–8 Online: http://www.hindawi.com/journals/bmri/2015/858907/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Men K, Dai J, Chen X, Li M, Zhang K and Huang P 2017. Dual-energy imaging method to improve the image quality and the accuracy of dose calculation for cone-beam computed tomography Phys. Medica 36 110–8 Online: 10.1016/j.ejmp.2017.03.023 [DOI] [PubMed] [Google Scholar]
- Mentl K, Mailhe B, Ghesu FC, Schebesch F, Haderlein T, Maier A and Nadar MS 2017. Noise reduction in low-dose CT using a 3D multiscale sparse denoising autoencoder 2017 IEEE 27th International Workshop on Machine Learning for Signal Processing (MLSP) vol 2017-Septe (IEEE) pp 1–6 Online: http://ieeexplore.ieee.org/document/8168176/ [Google Scholar]
- Nasirudin RA, Tachibana R, Näppi JJ, Mei K, Kopp FK, Rummeny EJ, Yoshida H and Noël PB 2015. A comparison of material decomposition techniques for dual-energy CT colonography Proceedings of SPIE--the International Society for Optical Engineering ed Hoeschen C, Kontos Dand Flohr TGp 94124F Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.2081982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noid G, Tai A, Schott D, Mistry N, Liu Y, Gilat-Schmidt T, Robbins JR and Li XA 2018. Technical Note: Enhancing soft tissue contrast and radiation-induced image changes with dual-energy CT for radiation therapy Med. Phys 45 4238–45 Online: http://doi.wiley.com/10.1002/mp.13083 [DOI] [PubMed] [Google Scholar]
- Patino M, Prochowski A, Agrawal MD, Simeone FJ, Gupta R, Hahn PF and Sahani DV. 2016. Material separation using dual-energy CT: current and emerging applications RadioGraphics 36 1087–105 Online: http://pubs.rsna.org/doi/10.1148/rg.2016150220 [DOI] [PubMed] [Google Scholar]
- Peng H, Kanehira T, Takao S, Matsuura T, Umegaki K, Shirato H and Xing L 2016. Feasibility Study of Using Dual-Energy Cone Beam Computed Tomography (DE-CBCT) in Proton Therapy Treatment Planning. Int. J. Radiat. Oncol. Biol. Phys 96 E697–E697 Online: https://linkinghub.elsevier.com/retrieve/pii/S0360301616327018 [Google Scholar]
- Peroni M 2011. Methods and algorithms for image guided adaptive radio- and hadron- therapy (Politecnico di Milano; ) Online: https://www.politesi.polimi.it/handle/10589/56740 [Google Scholar]
- Schlomka JP, Roessl E, Dorscheid R, Dill S, Martens G, Istel T, Bäumer C, Herrmann C, Steadman R, Zeitler G, Livne A and Proksa R 2008. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography Phys. Med. Biol 53 4031–47 [DOI] [PubMed] [Google Scholar]
- Schyns LEJR, Almeida IP, Van Hoof SJ, Descamps B, Vanhove C, Landry G, Granton PV and Verhaegen F 2017. Optimizing dual energy cone beam CT protocols for preclinical imaging and radiation research Br. J. Radiol 90 Online: 10.1259/bjr.20160480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sellerer T, Noël PB, Patino M, Parakh A, Ehn S, Zeiter S, Holz JA, Hammel J, Fingerle AA, Pfeiffer F, Maintz D, Rummeny EJ, Muenzel D and Sahani DV. 2018. Dual-energy CT: a phantom comparison of different platforms for abdominal imaging Eur. Radiol [DOI] [PubMed] [Google Scholar]
- Shen C, Li B, Lou Y and Jia X 2018. Element-resolved multi-energy cone beam CT realized on a conventional cone ceam CT platform. Int. J. Radiat. Oncol. Biol. Phys 99 S94–S94 Online: http://10.0.3.248/j.ijrobp.2017.06.227%0Ahttp://search.ebscohost.com/login.aspx?direct=true&db=aph&AN=124775670&site=ehost-live [Google Scholar]
- Sun M and Star-Lack JM 2010. Improved scatter correction using adaptive scatter kernel superposition Phys. Med. Biol 55 6695–720 [DOI] [PubMed] [Google Scholar]
- The Phantom Laboratory Incorporated. Catphan ® 604 Manual CTP604 34. 2015 Online: https://static1.squarespace.com/static/5367b059e4b05a1adcd295c2/t/56a78807c21b869ca68747b1/1453819924918/CTP604+Manual+9-15.pdf.
- Thörnqvist S, Hysing LB, Tuomikoski L, Vestergaard A, Tanderup K, Muren LP and Heijmen BJM 2016. Adaptive radiotherapy strategies for pelvic tumors - a systematic review of clinical implementations. Acta Oncol 1–16 Online: http://www.tandfonline.com/doi/full/10.3109/0284186X.2016.1156738 [DOI] [PubMed] [Google Scholar]
- Vaniqui A, Schyns LEJR, Almeida IP, van der Heyden B, van Hoof SJand Verhaegen F 2017. The impact of dual energy CT imaging on dose calculations for pre-clinical studies Radiat. Oncol 12 181 Online: http://www.ncbi.nlm.nih.gov/pubmed/29157265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilches-Freixas G, Taasti VT, Muren LP, Petersen JBB, Létang JM, Hansen DC and Rit S 2017. Comparison of projection- and image-based methods for proton stopping power estimation using dual energy CT Phys. Imaging Radiat. Oncol 3 28–36 Online: http://linkinghub.elsevier.com/retrieve/pii/S240563161730012X [Google Scholar]
- Wang A, Maslowski A, Messmer P, Lehmann M, Strzelecki A, Yu E, Paysan P, Brehm M, Munro P, Star-Lack J and Seghers D 2018. Acuros CTS: A fast, linear Boltzmann transport equation solver for computed tomography scatter – Part II: System modeling, scatter correction, and optimization Med. Phys 45 1914–25 Online: http://doi.wiley.com/10.1002/mp.12849 [DOI] [PubMed] [Google Scholar]
- Wang T, Ghavidel BB, Beitler JJ, Tang X, Lei Y, Curran WJ, Liu T and Yang X 2019. Optimal virtual monoenergetic image in “TwinBeam” dual-energy CT for organs-at-risk delineation based on contrast-noise-ratio in head-and-neck radiotherapy J. Appl. Clin. Med. Phys 20 121–8 Online: http://doi.wiley.com/10.1002/acm2.12539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells WM, Viola P, Atsumi H, Nakajima S and Kikinis R 1996. Multi-modal volume registration by maximization of mutual information. Med. Image Anal. 1 35–51 Online: http://www.ncbi.nlm.nih.gov/pubmed/9873920 [DOI] [PubMed] [Google Scholar]
- Wichmann JL, Nöske EM, Kraft J, Burck I, Wagenblast J, Eckardt A, Frellesen C, Kerl JM, Bauer RW, Bodelle B, Lehnert T, Vogl TJ and Schulz B 2014. Virtual monoenergetic dual-energy computed tomography: Optimization of kiloelectron volt settings in head and neck cancer Invest. Radiol 49 735–41 Online: http://content.wkhealth.com/linkback/openurl?sid=WKPTLP:landingpage&an=00004424-201411000-00006 [DOI] [PubMed] [Google Scholar]
- Williamson JF, Li S, Devic S, Whiting BR and Lerma FA 2006. On two-parameter models of photon cross sections: Application to dual-energy CT imaging Med. Phys 33 4115–29 Online: http://doi.wiley.com/10.1118/1.2349688 [DOI] [PubMed] [Google Scholar]
- Wong CK and Huang HK 1983. Calibration procedure in dual-energy scanning using the basis function technique. Med. Phys 10 628–35 [DOI] [PubMed] [Google Scholar]
- Wu X, Langan DA, Xu D, Benson TM, Pack JD, Schmitz AM, Tkaczyk EJ, Leverentz J and Licato P 2009. Monochromatic CT image representation via fast switching dual kVp SPIE Medical Imaging ed Samei Eand Hsieh Jp 725845 Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.811698 [Google Scholar]
- Yu L, Leng S and McCollough CH 2012. Dual-energy CT-based monochromatic imaging. AJR. Am. J. Roentgenol 199 9–15 [DOI] [PubMed] [Google Scholar]
- Zbijewski W, Gang GJ, Xu J, Wang AS, Stayman JW, Taguchi K, Carrino JA and Siewerdsen JH 2014. Dual-energy cone-beam CT with a flat-panel detector: Effect of reconstruction algorithm on material classification Med. Phys 41 021908 Online: http://www.ncbi.nlm.nih.gov/pubmed/24506629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Han D, Politte DG, Williamson JF and O’Sullivan JA 2018a. Impact of joint statistical dual-energy CT reconstruction of proton stopping power images: Comparison to image- and sinogram-domain material decomposition approaches Med. Phys 45 2129–42 Online: http://www.ncbi.nlm.nih.gov/pubmed/29570809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Han D, Williamson JF, Zhao T, Politte DG, Whiting BR and O’Sullivan JA 2018b. Experimental implementation of a joint statistical image reconstruction method for proton stopping power mapping from dual-energy CT data Med. Phys Online: http://www.ncbi.nlm.nih.gov/pubmed/30421790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng D, Ford JC, Lu J, Lazos D, Hugo GD, Pokhrel D, Zhang L and Williamson JF 2011. Bow-tie wobble artifact: effect of source assembly motion on cone-beam CT. Med. Phys 38 2508–14 Online: http://www.ncbi.nlm.nih.gov/pubmed/21776785 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J and Penfold SN 2016. Dosimetric comparison of stopping power calibration with dual-energy CT and single-energy CT in proton therapy treatment planning Med. Phys 43 2845–54 Online: http://doi.wiley.com/10.1118/1.4948683 [DOI] [PubMed] [Google Scholar]
- Zucca S, Loi S and Argiolas GM 2016. Virtual monoenergetic images on dual energy CT: An in phantom comparison of HU accuracy in two different scanners Phys. Medica 32 96 Online: https://linkinghub.elsevier.com/retrieve/pii/S1120179716003355 [Google Scholar]


