Accurate phase retrieval of complex 3D point spread functions with deep residual neural networks

Abstract

Phase retrieval, i.e., the reconstruction of phase information from intensity information, is a central problem in many optical systems. Imaging the emission from a point source such as a single molecule is one example. Here, we demonstrate that a deep residual neural net is able to quickly and accurately extract the hidden phase for general point spread functions (PSFs) formed by Zernike-type phase modulations. Five slices of the 3D PSF at different focal positions within a two micrometer range around the focus are sufficient to retrieve the first six orders of Zernike coefficients.

Wavefronts carry two fundamental types of information: (i) intensity information, i.e., photon flux, and (ii) optical phase information. Detectors typically used in optical measurements rely on the conversion of the incoming fields to electrons. Due to the physics of the detection process, without interferometry, only the intensity information of the incoming wavefront can be recorded, whereas the phase information is lost. However, it is possible to extract useful phase details to some extent from the recorded intensity information. This task has been coined the phase problem, an issue of fundamental importance not only in optical microscopy but also in many other areas of physics, e.g., x-ray crystallography, transmission electron microscopy, and astronomy.^1–3

The process of solving or approximating the phase problem is generally termed phase retrieval (PR), and numerous PR algorithms have been developed. Typically, they involve iterative optimization for the phase information under the constraints of the known source and target intensities as well as the propagating function.^4–9 For example, a set of images of a known point source at various axial positions has been used to estimate the pupil phase. A recent application of this approach has used PR for the design of tailored phase masks for 3D super-resolution imaging.¹⁰ While these approaches are useful, they are computationally demanding and, as a result, relatively slow. Moreover, they require oversampling of the feature space, i.e., a small increase in extracted phase information requires a large amount of additional intensity information.^11,12

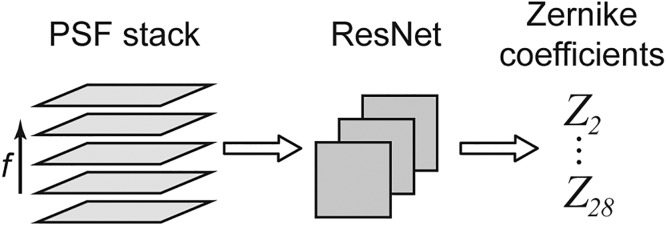
Deep neural nets (NNs) have recently been demonstrated to be useful tools in optics and specifically in single-molecule microscopy.^13,14 In these approaches, a learning process based on known image inputs trains the coefficients and weights of the NN, and the NN then processes unlearned images to extract position information or other variables. In general, aberrations can arise if the phase distortions from the microscope are not characterized. It has been shown that a residual neural net (ResNet)¹⁵ is capable of extracting wavefront distortions from biplane point spread functions (PSFs), which could be efficiently used to correct for aberrations with adaptive optics.^16,17 Also, deep learning can be used to recover images at low-light conditions¹⁸ and to accelerate wavefront sensing.^19–21 These findings led us to consider whether an approach based on a carefully chosen NN architecture might be able to tackle the fundamental and more general problem of PR of general PSFs, i.e., those generated from random superpositions of Zernike polynomials. In our design, after learning, the NN performs PR using a small set of measurements at a range of axial positions and directly returns the phase information as Zernike coefficients, as schematically depicted in Fig. 1.

FIG. 1.

Workflow. A stack with a few images of the PSF at different focal positions f is supplied to a deep residual neural net, which processes the images and directly returns the Zernike coefficients of order 1–6 (Noll indices 2–28) that correspond to the phase information encoded in the PSF images.

A cornerstone of any approach involving NNs is a sufficiently large dataset for training of the NN and an independent validation dataset to assess performance. To provide our NN with training and validation data, we turned to accurate PSF simulations. Images of a point emitter were simulated by means of vectorial diffraction theory^22,23 at focal positions of −1, −0.5, 0, 0.5, and 1 μm. The simulated emitter was positioned directly at a glass coverslip, as would be typical for a phase retrieval experiment. The emitter is placed in index-matched media in this study, but this choice is not fundamental, and index mismatch is straightforward to include in the PSF simulation if so desired.²⁴ Phase information was introduced by multiplying the Fourier plane fields from the point emitter by a Zernike phase factor with random Zernike coefficients of order 1–6 (Noll indices 2–28) with values between −λ and λ⁸—these coefficients define the shape of the final PSF. This choice of number of Zernike polynomials usually covers the dominant aberrations in an imaging system. Moreover, the higher-order Zernike coefficients tend toward zero in experimental settings, but as it was our goal to sample the parameter space equally, we did not impose any such limitation. The zero-order Zernike coefficient does not transport phase information, nor modify the detected image, and was hence not considered. Furthermore, we included camera properties typically encountered with electron multiplying charge-coupled device detectors (with the exception of excess noise, which arises from uncertainty in the gain resulting from the electron multiplication process), signal and background photons, and Poisson noise.²⁵ The relevant parameters are summarized in Table S1. Naturally, the chosen parameters are specific for a typical high NA experimental situation and can be changed according to the requirements of a specific problem.²⁶

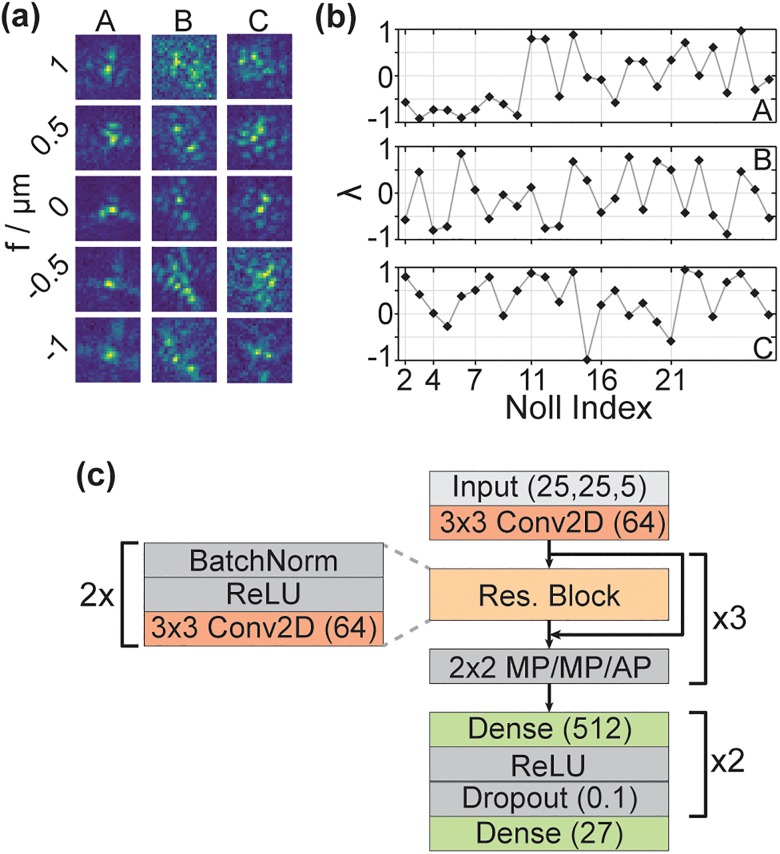
Figure 2(a) depicts three representative PSFs at the five simulated focal positions. The resulting PSFs display complex shapes and rapid changes in their appearance when the focal position is altered, an expected behavior given the variations as large as 2λ in the Zernike coefficients up to high-order as visible in Fig. 2(b).

FIG. 2.

(a) Three representative PSFs (A, B, and C) at focal positions from −1 to 1 μm. (b) Zernike coefficients for the three representative PSFs shown in (a). For clarity, only Noll indices that correspond to a change in the order of the Zernike coefficients are marked along the x-axis. (c) Schematic NN architecture. The PSF stack is supplied to the NN as a 25 × 25 pixel image with five channels, corresponding to the five focal positions. After 3 × 3 2D convolution with 64 filters, three residual blocks follow, each consisting of two stacks of batch normalizations, ReLU activation, and 3 × 3 2D convolution with 64 filters. After each residual block, the output of the residual block and its respective input are added. Then, 2 × 2 pooling is performed (MaxPooling, MP, after the first two residual blocks and average pooling, AP, after the third). Finally, two fully connected layers with 512 filters follow, each with ReLU activation and a dropout layer (dropout rate = 0.1). The last layer returns the predicted Zernike coefficients.

With realistic PSF simulations in hand, the challenge is to define the NN architecture and training. We focus on two key aspects identified during our optimizations: (i) training set size. The ability of the net to extract the Zernike coefficients sharply decreases when the training set is too small. For example, at a training set size of 200 000 PSFs, training was not successful. We used 2 000 000 training PSFs. (ii) Choice of architecture. Simple convolutional nets (ConvNets) were not able to return the Zernike coefficients. Presumably, a ConvNet with just few layers does not provide enough parameters to learn the complex phase information. However, a ConvNet deep enough to exhibit a sufficiently large parameter space likely suffers from the so-called degradation or vanishing gradient problem.¹⁵ In short, one might naively assume that for more complex problems, a deeper NN (i.e., a NN featuring more layers) offers the parameter space required. However, in praxis, one observes a saturation effect, that is, additional layers do not improve the performance. Frequently, deeper NNs even perform worse at some point. The reason lies in the backpropagation of the gradient from the later to earlier layers: during backpropagation, essentially many multiplications are performed. If the gradient is small at the beginning, repeated multiplications may yield an almost infinitely small result, which is not helpful in directing the net.

These issues are addressed by a simple ResNet architecture.¹⁵ The key features of ResNets are residual blocks that feature skip connections between earlier and deeper layers, allowing for residual mapping. The skipped connection provides a deeper layer with the output x of an earlier layer (i.e., an identity mapping of the earlier layer). The layers in between process the output, yielding F(x). These two outputs are added, giving the result H(x) = F(x) + x. If we consider a single residual block, then F(x) adjusts the input x during training to reduce the residual between prediction and ground truth. Importantly, if the NN already performs optimally, F(x) will go to 0, which is easy as the identity mapping of x to a later layer already provided the later layer with the output from the earlier layer. Without the skipped connection, i.e., in a normal ConvNet where each layer is only connected to the layer before, this task is much harder, which explains why ResNet architectures provide a solution to the vanishing gradient problem.

Our architecture is compact and, as a result, fast (analysis of the validation set with 100 000 PSFs took about eight minutes, i.e., about 5 ms per PSF, on a standard desktop PC, equipped with an i7–6700 processor and 16 GB RAM, not using a GPU). We note that with conventional PR algorithms, the analysis of 100 000 PSFs would take significantly longer. How long exactly depends on the chosen algorithm, the code implementation, stopping conditions, and so on, but even a very optimistic assumption of several seconds per PSF results in processing time of many days to weeks. Our approach is significantly faster, even if the initial NN training time of approximately 12 h is included in the calculation as a baseline. Moreover, starting conditions prominently contribute to the performance of conventional PR algorithms, and it was recently demonstrated that the convergence and speed of conventional PR algorithms benefit from NN-based parameter initialization.^20,27 Therefore, the rapid PR performed by the NN we developed could also be advantageous to initialize parameters if further optimization is desired. Finally, such fast analysis lends itself to difficult problems like calculation of phase aberrations varying throughout the field of view.^28,29

The network architecture is diagrammed in Fig. 2(c). The PSFs are supplied to the NN as five-channel images, corresponding to the five focal positions. After an initial 2D convolution, three residual blocks with batch normalization, ReLU activation, and 2D convolution follow with two maxpooling (MP) steps and one averagepooling step afterwards, respectively. As the term “residual” indicates, the output x of a layer n is stored before being passed on to the next layer. Later, the earlier output x is added to the output y of a deeper layer m. The joint outputs x + y are then passed as input to the next layer m + 1. Finally, two fully connected layers are implemented before the final output layer, which returns the 27 Zernike coefficients of order 1–6. After each of the two fully connected layers, dropout at a rate of 0.1 is implemented to avoid overfitting.³⁰ For a detailed description of the relevant concepts, see the supplementary material.

The NN was implemented in Keras with Tensorflow backend and trained on a standard desktop PC equipped with 64 GB RAM, an Intel Xeon E5–1650 processor, and an Nvidia GeForce GTX Titan GPU. The training parameters are summarized in Table S2. Convergence was reached after training for approximately 12 h and 77 epochs. This training time is reasonable for deep learning approaches¹⁶ and could be strongly reduced if a setup with tailored hardware is used. Furthermore, it should be noted that retraining is not necessary unless fundamental parameters of the experiment are changed, such as the numerical aperture, magnification, or a major realignment. As discussed above, the trained NN can perform hundreds of phase retrievals per second on a standard PC.

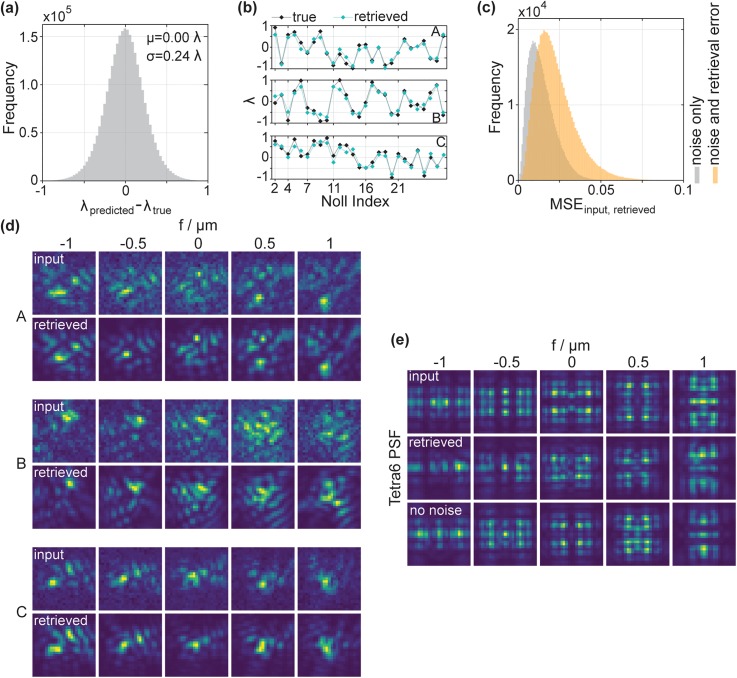
We now assess the performance of the NN on blind validation images not present in the training set, created as above with random Zernike coefficients. Figure 3(a) depicts the overall deviation in wavelength units between the predicted Zernike coefficients and their ground truth value for the validation dataset (all 27 values for the 100 000 PSFs are pooled). The deviations are symmetric and centered at zero, indicating that the NN does not exhibit a bias toward over- or underestimating. Also, the relatively small width of the histogram (standard deviation of approximately 0.24) indicates reasonably precise predictions.

FIG. 3.

(a) Histogram of the differences in wavelength units between the retrieved and the ground truth values for all Zernike coefficients in the validation dataset. (b) Representative examples for the agreement between retrieved and ground truth Zernike coefficients for three PSFs. Notably, the prediction is accurate over the whole range of Zernike coefficients, up to the highest order. (c) Histogram of mean squared errors between input and retrieved PSFs, calculated pixelwise for each PSF slice of the 100 000 validation PSFs (orange). Input and retrieved PSFs are normalized. The high agreement between the retrieved and true Zernike coefficients translates to low MSEs. A significant fraction of the error stems from Poisson noise in the input PSFs, evident from the MSE between input PSFs without noise and input PSFs that include noise (gray histogram—“noise only” refers to the influence of Poisson noise in the input PSFs). (d) Comparison between the input PSFs at the five simulated focal positions and the PSFs generated from the retrieved Zernike coefficients, corresponding to the data plotted in (b). The agreement is very good. Note that the retrieved PSFs do not include background or Poisson noise, whereas the input PSFs to be retrieved do. (e) PR of the Tetrapod PSF with the 6 μm range (Tetra6). Retrieval results from an additional NN are included, which was trained on PSFs not including noise (no noise). Note in this case, the input PSFs do not include noise as would typically be the case for a specific phase mask design. The retrieved PSF approaches the ground truth well. As expected, the NN that was trained on PSFs without noise performs slightly better.

In agreement with the overall small deviations between prediction and ground truth, the NN was able to predict the Zernike coefficients corresponding to single PSFs accurately. This is shown for three representative random phase cases in Fig. 3(b) (see Fig. S1 for more details).

The predicted Zernike coefficients are close to the ground truth values, but they are not perfect. Thus, we wanted to investigate if prediction and ground truth agree on the level of the PSFs as well. For this, we performed PR on PSFs using the NN and then calculated the shape of the PSFs with the predicted Zernike coefficients. The results are depicted in Figs. 3(c) and 3(d). Figure 3(c) shows the histogram of mean squared errors (MSEs) between input and retrieved PSFs, calculated pixelwise for each slice of all PSFs (orange). As is clearly visible, the MSE is low, indicating good agreement between input and retrieved PSFs at the level of the individual pixels. Notably, a significant part of the error is to be attributed to the Poisson noise in the input PSFs: we calculated the MSE between the input PSFs with Poisson noise and the same input PSFs, just without Poisson noise, which would obviously be the perfect result for phase retrieval. The MSE between these two sets of PSFs is depicted by the gray histogram, which shows large overlap with the orange histogram, i.e., with the MSE between retrieved and input PSFs. Figure 3(d) shows the retrieved PSFs corresponding to the plots in Fig. 3(b). Evidently, the retrieved PSFs agree very well with the input PSFs. As expected from the MSE analysis, there are minor differences, but not only the overall shape but also the intricate details of the complex PSFs are recovered at a high level of detail without the need to perform additional refinement using conventional PR algorithms.

To explore the utility of our PR approach, we asked whether the NN is able to perform PR on PSFs already used in praxis. One of the useful PSFs for extracting the 3D position is the Tetrapod PSF with the 6 μm range (Tetra6).^31,32 Here, we generated input PSFs under no-noise conditions to focus on the performance of the PR alone. The results are depicted in Fig. 3(e). Clearly, the Tetra6 PSF is well retrieved. In this context, it should be mentioned that some Zernike coefficients were accurately predicted to values well outside the training range of −λ to λ to retrieve the PSF, underscoring the robustness of the NN. Also, we note that including noise in training is not ideal when the NN is used for phase mask design given a desired PSF. In this case, it is more reasonable to train the NN in noise-free conditions to just concentrate the information on the effect of the phase mask: if a phase mask is to be designed, one provides the desired, ideal PSF without noise to our NN. Then, the calculation yields the Zernike coefficients that will return the desired PSF, which can subsequently be used for the phase mask. The validity of this approach was confirmed by retrieving the Tetra6 PSF with a NN that was trained on noise-free PSFs, which yielded an improved result [labeled “no noise” in Fig. 3(e)]. Nevertheless, as the figure shows, the NN that was trained on PSFs with noise still performs well for the Tetrapod. Thus, our approach also allows one to design a target PSF and then use the NN to develop a phase mask yielding this PSF, possibly in combination with other approaches for phase mask design developed recently.¹⁰ For a detailed analysis of different Zernike coefficient ranges, see Fig. S1.

In conclusion, we have developed a deep residual neural net that performs fast and accurate phase retrieval on complex PSFs from only five axial sample images of a point source. We investigated the net architecture and the training data parameters and verified the capability of our approach on realistic simulations of complex PSFs carrying Zernike-like phase information. We also demonstrated that the NN is able to perform accurate PR on the experimentally relevant Tetra6 PSF. From this, it will be straightforward to expand this approach to PR of non-Zernike-like phase information using different basis sets and to transfer the residual net concept to more applied tasks such as phase mask design. Fundamentally, we envision that this approach will be relevant not only for optics but also for any field where phase information needs to be extracted from intensity information.

See the supplementary material for PSF simulation and neural network training parameters, explanation of key concepts for neural network design, analysis of the neural network performance for varying Zernike coefficient ranges, and supplementary references.